A graph-embedded deep feedforward network for disease outcome classification and feature selection using gene expression data

Abstract

Motivation

Gene expression data represents a unique challenge in predictive model building, because of the small number of samples (n) compared with the huge amount of features (p). This ‘$n\ll p$’ property has hampered application of deep learning techniques for disease outcome classification. Sparse learning by incorporating external gene network information could be a potential solution to this issue. Still, the problem is very challenging because (i) there are tens of thousands of features and only hundreds of training samples, (ii) the scale-free structure of the gene network is unfriendly to the setup of convolutional neural networks.

Results

To address these issues and build a robust classification model, we propose the Graph-Embedded Deep Feedforward Networks (GEDFN), to integrate external relational information of features into the deep neural network architecture. The method is able to achieve sparse connection between network layers to prevent overfitting. To validate the method’s capability, we conducted both simulation experiments and real data analysis using a breast invasive carcinoma RNA-seq dataset and a kidney renal clear cell carcinoma RNA-seq dataset from The Cancer Genome Atlas. The resulting high classification accuracy and easily interpretable feature selection results suggest the method is a useful addition to the current graph-guided classification models and feature selection procedures.

Availability and implementation

The method is available at https://github.com/yunchuankong/GEDFN.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

In recent years, more and more studies attempt to link clinical outcomes, such as cancer and other diseases, with gene expression or other types of profiling data. It is of great interest to develop new computational methods to predict disease outcomes based on profiling datasets that contain tens of thousands of variables. The major challenges in these data lie in the heterogeneity of the samples, and the sample size being much smaller than the number of predictors (genes), i.e. the $n\ll p$ issue, as well as the complex correlation structure between the predictors. Thus the prediction task has been formulated as a classification problem combined with selection of predictors, solved by modern machine learning algorithms such as regression based methods (Algamal and Lee, 2015; Liang et al., 2013), support vector machines (Vanitha et al., 2015), random forests (Cai et al., 2015; Kursa, 2014) and neural networks (Chen et al., 2014). While these methods are aimed at achieving accurate classification performance, major efforts have also been put on selecting significant genes that effectively contribute to the prediction (Cai et al., 2015; Kursa, 2014). However, feature selection is based on fitted predictive models and is conducted after parameter estimation, which causes the selection to rely on the classification methods rather than the structure of the feature space itself. Beside building robust predictive models, the feature selection also serves another important purpose—the functionality of the selected features (genes) can help unravel the underlying biological mechanisms of the disease outcome.

Given the nature of the data, i.e. functionally associated genes tend to be statistically dependent and contribute to the biological outcome in a synergistic manner, a branch of gene expression classification research has been focused on integrating the relations between genes with classification methods, which helps in terms of both classification performance as well as learning the structure of feature space. A critical data source to achieve this goal has been gene networks. A gene network is a graph-structured dataset with genes as the graph vertices and their functional relations as graph edges. The functional relations are largely curated from existing biological knowledge (Chowdhury and Sarkar, 2015; Szklarczyk and Jensen, 2015). Each vertex in the network corresponds to a predictor in the classification model. Thus, it is expected that the gene network can provide useful information for a learning process where genes serve as predictors. Motivated by this fact, certain procedures have been developed where gene networks are employed to conduct feature selection prior to classification (Chuang et al., 2007; Li and Li, 2008; Wang et al., 2007; Wei and Pan, 2008). Moreover, methods that integrate gene network information directly into classifiers have also been developed. For example, Dutkowski and Ideker (2011) propose the random forest-based method, where the feature sub-sampling is guided by graph search on gene networks when constructing decision trees. Lavi et al. (2012) and Zhu et al. (2009) modify the objective function of the support vector machine with penalty terms defined according to pairwise distances between genes in the network. Similarly, Kim et al. (2013) develops logistic regression based classifier using regularization, where again a relational penalty term is introduced in the loss function. The authors of these methods have demonstrated that embedding expression data into gene network results in both better classification performance and more interpretable selected feature sets.

With the clear evidence that gene networks can lead to novel variants of traditional classifiers, we are motivated to incorporate gene networks with deep feedforward networks (DFN), which is closely related to the state-of-the-art technique deep learning (LeCun et al., 2015). Although nowadays deep learning has been constantly shown to be one of the most powerful tools in classification, its application in bioinformatics is limited (Min et al., 2017). This is due to many reasons including the $n\ll p$ issue, the large heterogeneity in cell populations and clinical subject populations, as well as inconsistent data characteristics across different laboratories, resulting in difficulties merging datasets. Consequently, the relatively small number of samples compared with the large number of features in a gene expression dataset obstructs the use of deep learning techniques, where the training process usually requires a large amount of samples such as in image classification (Russakovsky et al., 2015). Therefore, there is a need to modify deep learning models for disease outcome classification using gene expression data, which naturally leads us to the development a variant of deep learning models specifically fitting the practical situation with the help of gene networks.

Incorporating gene networks as relational information in the feature space into DFN classifiers is a natural option to achieve sparse learning with less parameters compared with the usual DFN. However, to the best of our knowledge, few existing work has been done on this track. Bruna et al. (2014) and Henaff et al. (2015) started the direction of sparse deep neural networks (DNNs) for graph-structured data. The authors developed hierarchical locally connected network architectures with newly defined convolution operations on graph-structured data. The methods have novel mathematical formulation; however, the applications are yet to be generalized. In both of the two papers, by using the two benchmark datasets MINST (LeCun et al., 1998) and ImageNet (Russakovsky et al., 2015), respectively, the authors have treated 2D grid images as a special form of graph-structured data in their experiments. This is based on the fact that an image can be regarded as a graph in which each pixel is a vertex connected with four neighbors in the four directions. However, graph-structured data can be much more complex in general, as the degree of each vertex can vary widely, and the edges do not have orientations as in image data. For a gene network, the degree of vertices is power-law distributed as the network is scale-free (Kolaczyk, 2009). In this case, convolution operations are not easy to define. In addition, with tens of thousands of vertices in the graph, applying multiple convolution operations results in huge number of parameters, which easily leads to over-fitting given the small number of training samples. By taking an alternative approach of modifying a usual DFN, our newly proposed graph-embedded DFN can serve as a convenient tool to fill the gap. It avoids over-fitting in the $n\ll p$ scenario, as well as achieves good feature selection results using the structure of the feature space.

The article is organized as follows: Section 2 reviews usual deep feedforward networks (DFNs) and illustrates our graph-embedded architecture. Section 3.1 compares the performance of our method with other approaches using synthetic datasets, followed by the real applications of two RNA-seq datasets in Section 3.2. Finally, conclusions are presented in Section 4.

2 Materials and methods

2.1 Deep feedforward networks

A DFN ( or DNN, multilayer perceptron) with l hidden layers has a standard architecture

$$\begin{array}{l}Pr\left(\mathbf{y}\right|\mathbf{X},\theta )=f({\mathbf{Z}}_{\text{out}}{\mathbf{W}}_{\text{out}}+{\mathbf{b}}_{\text{out}})\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathbf{Z}}_{\text{out}}=\sigma ({\mathbf{Z}}_l{\mathbf{W}}_l+{\mathbf{b}}_l)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\dots \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathbf{Z}}_{k+1}=\sigma ({\mathbf{Z}}_k{\mathbf{W}}_k+{\mathbf{b}}_k)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\dots \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathbf{Z}}_1=\sigma (\mathbf{X}{\mathbf{W}}_{\text{in}}+{\mathbf{b}}_{\text{in}}),\end{array}$$

where $\mathbf{X}\in {\mathcal{R}}^{n\times p}$ is the input data matrix with n samples and p features, $\mathbf{y}\in {\mathcal{R}}^n$ is the outcome vector containing classification labels, $\theta$ denotes all the parameters in the model, ${\mathbf{Z}}_{\text{out}}$ and ${\mathbf{Z}}_k,k=1,\dots ,l-1$ are hidden neurons with corresponding weight matrices ${\mathbf{W}}_{\text{out}},\hspace{0.17em}{\mathbf{W}}_k$ bias vectors ${\mathbf{b}}_{\text{out}},\hspace{0.17em}{\mathbf{b}}_k$. The dimensions of Z and W depend on the number of hidden neurons h_in and $h_k,k=1,\dots ,l$, as well as the input dimension p and the number of classes h_out for classification problems. In this paper, we mainly focus on binary classification problems hence the elements of y simply take binary values and $h_{\text{out}}\equiv 2$. $\sigma (·)$ is the activation function such as sigmoid, hyperbolic tangent (tanh) or rectifiers. $f(·)$ is the softmax function converting values of the output layer into probability prediction i.e.

$$p_i=f\left({\mu }_{i1}\right)=\frac{e^{{\mu }_{i1}}}{e^{{\mu }_{i0}}+e^{{\mu }_{i1}}}$$

where

$$\begin{array}{l}{p}_i:\hspace{0.17em}=Pr(y_i=1|{\mathbf{x}}_i)\\ {\mu }_{i0}:\hspace{0.17em}={\left[{\mathbf{z}}_i^{\left(\text{out}\right)}\right]}^T{\mathbf{w}}_0^{\left(\text{out}\right)}+b_0^{\left(\text{out}\right)}\\ {\mu }_{i1}:\hspace{0.17em}={\left[{\mathbf{z}}_i^{\left(\text{out}\right)}\right]}^T{\mathbf{w}}_1^{\left(\text{out}\right)}+b_1^{\left(\text{out}\right)},\end{array}$$

for binary classification where $i=1,\dots ,n$.

The parameters to be estimated in this model are all the weights and biases. For a training dataset given true labels, the model is trained using a stochastic gradient decent (SGD) based algorithm (Goodfellow et al., 2016) by minimizing the cross-entropy loss function

$$\mathcal{L}\left(\theta \right)=-\frac{1}{n}\sum _{i=1}^n\{y_i\hspace{0.17em}\text{log}({\widehat{p}}_i)+(1-y_i)\hspace{0.17em}\text{log}(1-{\widehat{p}}_i\left)\right\},$$

where again $\theta$ denotes all the model parameters, and ${\widehat{p}}_i$ is the fitted value of p_i. More details about DFN can be found in Goodfellow et al. (2016).

2.2 Graph-embedded DFNs

Our newly proposed DNN model is based on two main assumptions. The first assumption is that neighboring features on a known scale-free feature network or feature graph (Since in this paper we interchangeably discuss feature networks and neural networks, to avoid confusion, the equivalent term ‘graph’ is used to refer to the feature network from now on, while ‘networks’ naturally refer to neural networks.) tend to be statistically dependent. The second assumption is that only a small number of features are true predictors for the outcome, and the true predictors tend to form cliques in the feature graph. These assumptions have been commonly used and justified in previous works reviewed in Section 1.

To incorporate the known feature graph information to DNN, we propose the graph-embedded deep feedforward network (GEDFN) model. The key idea is that, instead of letting the input layer and the first hidden layers to be fully connected, we embed the feature graph in the first hidden layer so that a fixed informative sparse connection can be achieved.

Let $\mathbf{G}=(V,E)$ be a known graph of p features, with V the collection of p vertices and E the collection of all edges connecting vertices. A common representation of a graph is the corresponding adjacency matrix A. Given a graph G with p vertices, the adjacency A is a p × p matrix with

$$A_{ij}=\{\begin{array}{ll}1,\hfill & \hspace{0.17em}\text{if}\hspace{0.17em}\hspace{0.17em}{V}_i\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}{V}_j\hspace{0.17em}\hspace{0.17em}\text{are connected}\hspace{0.17em},\hspace{0.17em}\forall i,j=1,\dots ,p\hfill \\ 0,\hfill & \hspace{0.17em}\text{otherwise}.\hfill \end{array}$$

In our case A is symmetric since the graph is undirected. Also, we require A_ii = 1 meaning each vertex is regarded to connecting itself.

Now to mathematically formulate our idea, we construct the DNN such that the dimension of the first hidden layer (h_in) is the same as the original input i.e. $h_{\text{in}}=p$, hence ${\mathbf{W}}_{\text{in}}$ has a dimension of p × p. Between the input layer X and the first hidden layer ${\mathbf{Z}}_1$, instead of fully connecting the two layers with ${\mathbf{Z}}_1=\sigma (\mathbf{X}{\mathbf{W}}_{\text{in}}+{\mathbf{b}}_{\text{in}})$, we have

$${\mathbf{Z}}_1=\sigma \left(\mathbf{X}\right({\mathbf{W}}_{\text{in}}\odot A)+{\mathbf{b}}_{\text{in}})$$

where the operation $\odot$ is the Hadamard (element-wise) product. Thus, the connections between the first two layers of the feedforward network are ‘filtered’ by the feature graph adjacency matrix. Through the one-to-one $\mathcal{R}:p\to p$ transformation, all features have their corresponding hidden neurons in the first hidden layer. A feature can only feed information to hidden neurons that correspond to features connecting to it in the feature graph.

Specifically, let ${\mathbf{x}}_i={(x_{i1},\dots ,x_{ip})}^T,i=1,\dots ,n$ be any instance (one row) of the input matrix X, in the usual DFN, the first hidden layer of this instance is calculated as

$${\mathbf{z}}_i^{\left(1\right)}=\sigma \left({[\sum _{j=1}^p{x}_{ij}{w}_{1j}^{\left(\text{in}\right)}+b_1^{\left(\text{in}\right)},\dots ,\sum _{j=1}^p{x}_{ij}{w}_{h_{\text{in}}j}^{\left(\text{in}\right)}+b_{h_{i\mathrm{n}}}^{\left(\text{in}\right)}]}^{\stackrel{\hspace{0.5em}}{T}}\right),$$

where ${\mathbf{z}}_i^{\left(1\right)}$ is the i-th row of ${\mathbf{Z}}_1$, and $w_{kj}^{\left(\text{in}\right)},b_k^{\left(\text{in}\right)},k=1,\dots ,h_{\text{in}}$ are the weight and bias for this layer. Now in our model, $h_{\text{in}}=p$ and each $w_{kj}^{\left(\text{in}\right)}$ is multiplied by an indicator function i.e.

$${\mathbf{z}}_i^{(1)}=\sigma ({[\sum _{j=1}^p{x}_{ij}{w}_{1j}^{(\text{in})}\mathcal{I}(A_{1j}=1)+b_1^{(\text{in})},\dots ,\sum _{j=1}^p{x}_{ij}{w}_{pj}^{(\text{in})}\mathcal{I}(A_{pj}=1)+b_p^{(\text{in})}]}^T).$$

Therefore, the feature graph helps achieve sparsity for the connection between the input layer and the first hidden layer.

2.3 Evaluation of feature importance

Beside improving classification, it is also of great interest to find features that significantly contribute to the classification, as they can reveal the underlying biological mechanisms. Therefore, for GEDFN, we also develop a feature ranking method according to a relative importance score. The idea is analogous to the connection weights (CWs) method introduced by Olden and Jackson (2002). Extended from CW, we propose the graph connection weights (GCWs) method, which emphasizes the significance of the feature graph in our newly proposed neural network architecture.

The main idea of GCW is that, the contribution of a specific variable is directly reflected by the magnitude of all the weights that directly associated with the corresponding hidden neuron in the graph-embedded layer (the first hidden layer). Summing over the absolute values of the directly associated weights gives the relative importance of the specific feature, i.e.

$$s_j={\gamma }_j\sum _{k=1}^p\left|w_{kj}^{\left(\text{in}\right)}\mathcal{I}\right(A_{kj}=1\left)\right|+\sum _{m=1}^{h_1}\left|w_{jm}^{\left(1\right)}\right|,$$ (1)

$${\gamma }_j=\text{min}\left(c/\sum _{k=1}^p\mathcal{I}(A_{kj}=1),1\right),j=1,\dots ,p,$$ (2)

where s_j is the importance score for feature j, $w^{\left(\text{in}\right)}$ denotes weights between the input and first hidden layers, and $w^{\left(1\right)}$ denotes weights between the first hidden layer and the second hidden layer. A constant c is imposed to penalize feature vertices with too many connections, so that they will not be overly influential. In subsequent experiments, we take c = 50.

Note that the importance score consists of two parts according to Equation (1). The left term summarizes the importance of a feature according to the connection on the feature graph, coherent with the property of the graph-embedded layer. The right term then summarizes the contribution of the feature according to the connection to the hidden neurons in the next fully-connected layer. Input data are required to be Z-score transformed (the original value minus the mean across all samples and then divided by the standard deviation) before entered into the model, and this will guarantee all variables are of the same scale so that the magnitude of weights are comparable. After training GEDFN, the importance scores for all the variables can be calculated using trained weights, which leads to a ranked feature list.

2.4 Detailed model settings

For the choice of activation functions in GEDFN, the rectified linear unit (ReLU) (Nair and Hinton, 2010) with the form (in scalar case)

$${\sigma }_{\text{ReLU}}\left(x\right)=\text{max}(x,0)$$

is employed. This activation has an advantage over sigmoid and tanh as it can avoid the vanishing gradient problem (Hochreiter et al., 2001) during training using SGD. To train the model, we choose the Adam optimizer (Kingma and Ba, 2014), which is the most widely used variant of traditional gradient descent algorithms in deep learning. Also, we use the mini-batch training strategy by which the optimizer randomly trains a small proportion of the samples in each iteration. Details about the Adam optimizer and mini-batch training can be found in Goodfellow et al. (2016) and Kingma and Ba (2014).

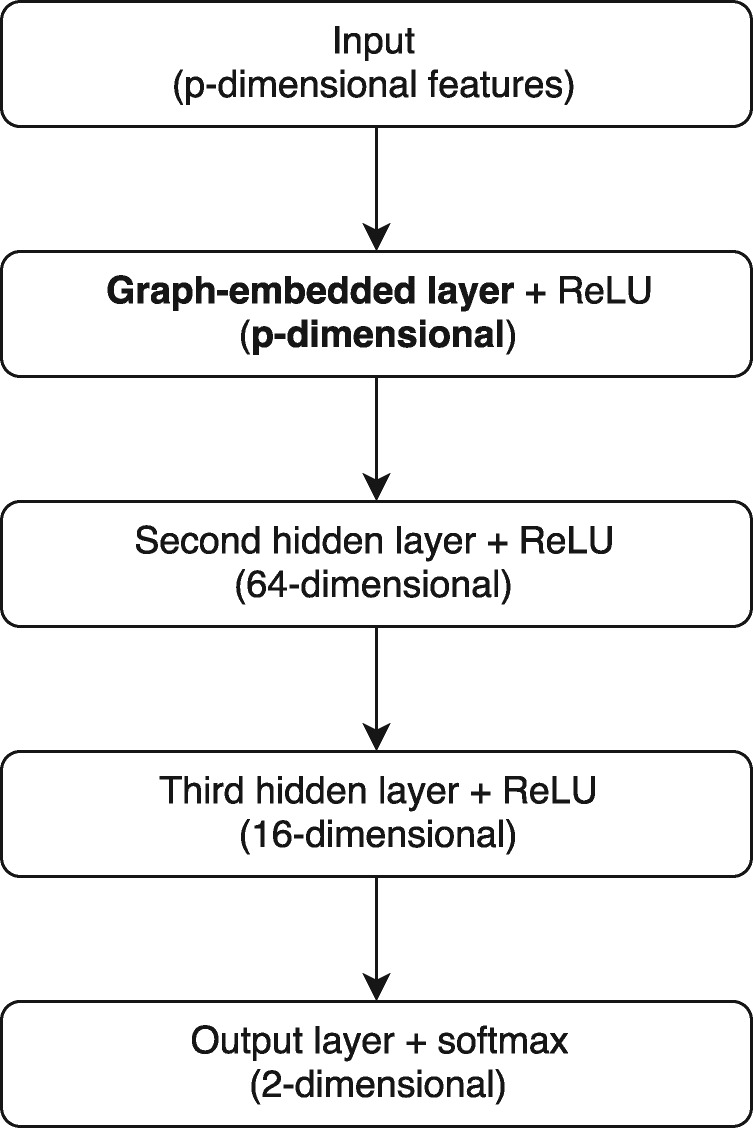
The classification performance of a DNN model is associated with many hyper-parameters, including architecture-related parameters such as the number of layers and the number of hidden neurons in each layer, regularization-related parameters such as the dropout proportion, and model training-related parameters such as the learning rate and the batch size. These hyper-parameters can be fine-tuned using advanced hyper-parameter training algorithm such as Bayesian Optimization (Mockus, 2012), however, as the hyper-parameters are not of primary interest in our work, in later sections, we simply tune them using grid search in a feasible hyper-parameter space. A visualization of our tuned GEDFN model for simulation and real data experiments is shown in Figure 1. More details of hyper-parameter tuning can be found in Supplementary Section S1.

Fig. 1.

Network architecture of the GEDFN model for experiments in Sections 3.1 and 3.2

3 Results and discussion

3.1 Simulation experiments

We conducted extensive simulation experiments to mimic disease outcome classification using gene expression and network data, and explored the performance of our new method in comparison with the usual DFN and other proven methods. Robustness was also tested by simulating datasets that did not fully satisfy the main assumptions. The method was applied to examine whether it could still achieve a reasonable performance.

3.1.1. Synthetic data generation

For a given number of features p, we employed the preferential attachment algorithm proposed by Barabási and Albert (1999) to generate a scale-free feature graph. The p × p distance matrix D recording pairwise distances among all vertices were then calculated. Next, we derived the covariance matrix by transforming the distances between verticies Σ by letting

$${\Sigma }_{ij}={0.7}^{D_{ij}},i,j=1,\dots ,p.$$

Here by convention the diagonal elements of D are all zeros meaning the distance between a vertex to itself is zero.

After simulating the feature graph and obtaining the covariance matrix of features, we generate n multivariate Gaussian samples as the input matrix $\mathbf{X}={({\mathbf{x}}_1,\dots ,{\mathbf{x}}_n)}^T$ i.e.

$${\mathbf{x}}_i\sim \mathcal{N}(0,\Sigma ),i=1,\dots \hspace{0.17em}n,$$

where $n\ll p$ for imitating gene expression data. Using this setup, vertices that are several steps away could naturally become negatively correlated when we sample the expression values from multivariate normal distribution using Σ as the variance–covariance matrix. Supplementary Figure S1 shows sample plots of the pairwise feature correlation distributions for the simulated data.

To generate outcome variables, we first select a subset of features to be the ‘true’ predictors. Following our assumptions mentioned in Section 2.2, we intend to select cliques in the feature graph. Among vertices with relatively high degrees, part of them is randomly selected as “cores”, and part of the neighboring vertices of cores are also selected. Denoting the number of true predictors as p₀, we sample a set of parameters $\beta ={({\beta }_1,\dots ,{\beta }_{p_0})}^T$ and an intercept β₀ within a certain range. In our experiments, we first uniformly sample β’s from (0.1, 0.2), and randomly turn some of the parameters into negative, so that we accommodate both positive and negative coefficients. Finally, the outcome variable y is generated through a generalized linear model framework

$$\begin{array}{l}Pr(y_i=1|{\mathbf{x}}_{\mathbf{i}})={\eta }^{-1}({{\mathbf{x}}_{\mathbf{i}}}^T\beta +{\beta }_0)\\ y_i=\mathcal{I}(Pr(y_i=1|{\mathbf{x}}_{\mathbf{i}})>t),i=1,\dots \hspace{0.17em}n,\end{array}$$

where t is a threshold and $\eta (·)$ is the link function. We consider two cases of ${\eta }^{-1}(·)$in our experiments, one is the sigmoid function, which is equivalent to the binary softmax and monotone

$${\eta }^{-1}\left(x\right)=\frac{1}{1+e^x}$$

and the other is a weighted tanh plus quadratic function, which is non-monotone

$${\eta }^{-1}\left(x\right)=0.7\varphi (\text{tan}\hspace{0.17em}h(x\left)\right)+0.3\varphi \left(x^2\right),$$

where $\varphi (·)$ is the min_max function scaling the input to [0, 1].

Following the above procedure, corresponding to the two cases of inverse link functions, we simulate two sets of synthetic datasets with 5000 features and 400 samples. We compare our method with the usual DFN, the feature graph-embedded classification method network-guided forest (NGF) (Dutkowski and Ideker, 2011) mentioned in Section 1, as well as the traditional logistic regression with lasso (LRL) (Tibshirani, 1996). In gene expression data, the number of true predictors account for only a small proportion of the features. Taking this aspect into consideration, we examine different numbers, i.e. 40, 80, 120, 160 and 200, of true predictors, corresponding to 2, 4, 6, 8 and 10 cores among all the high-degree vertices in the feature graph. However, in reality, the true predictors may not be perfectly distributed in the feature graph as cliques. Instead, some of the true predictors, which we call ‘singletons’, can be quite scattered. To create this possible circumstance, we simulate three series of datasets with singleton proportions 0, 50 and 100% among all the true predictors. Therefore, we investigate three situations where all true predictors are in cliques, half of the true predictors are singletons, and all of the true predictors are scattered in the graph, respectively.

3.1.2. Simulation results and discussion

In our simulation studies, as shown in Figure 1, the GEDFN had three hidden layers, where the first hidden layer was the graph adjacency embedded layer. Thus the dimension of its output is the same as the input, namely 5 000. The second and third hidden layers had 64 and 16 hidden neurons, respectively, which are the same for the usual DFN. The number of the first layer hidden neurons in the usual DFN, 1024 neurons, was selected using grid search.

For each of the data generation settings, ten independent datasets were generated, and the GEDFN, DFN, NGF and LRL methods were applied. For each simulated dataset, we randomly split the dataset into training and testing sets at a 4:1 ratio. The models were trained using the training dataset, and used to predict the class probabilities of the testing dataset. To evaluate the classification results, receiver operating characteristic (ROC) curve was generated using the predicted class probabilities and the true class membership of the testing dataset, and the area under the curve (AUC) was calculated. The final testing results were then averaged across the 10 datasets.

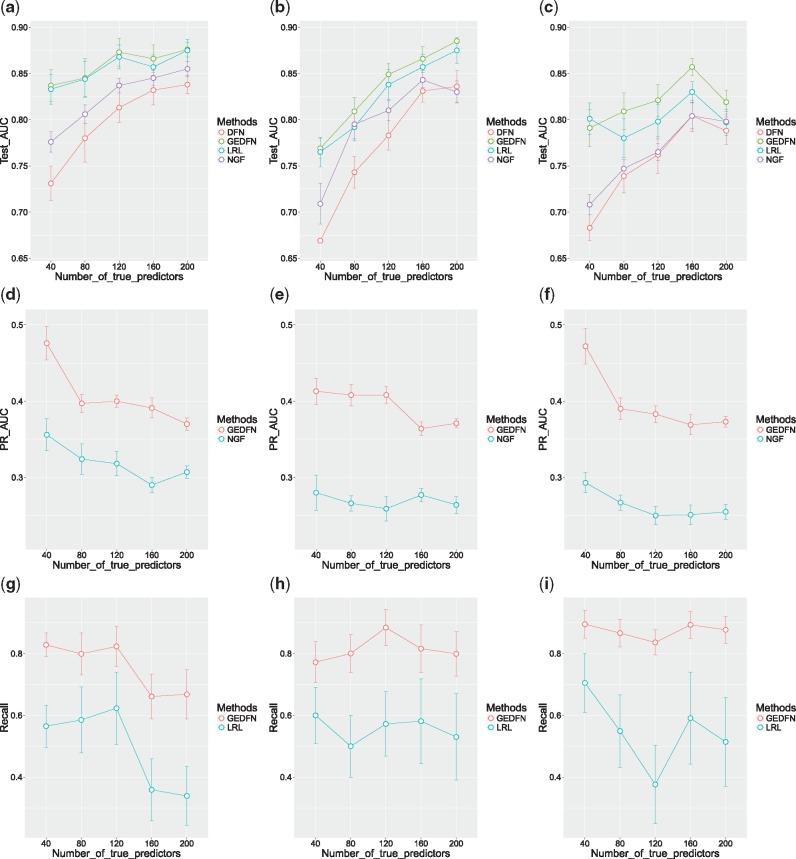
Figure 2 shows the results of the case with the sigmoid inverse link function. The error bars denote intervals of estimated mean AUC values plus/minus their standard errors. Corresponding to the case that singleton proportion is 0%, Figure 2a shows GEDFN and LRL outperformed the other two methods. As the number of true predictors increased, all of the methods performed better as there were more signals in the feature set. As the singleton proportion increased to 0.5 (Fig. 2b), GEDFN was the best among the four though the difference between GEDFN and LRL was not big. In Figure 2c, when the singleton proportion was increased to 1, all of the methods performed worse, but GEDFN performed better than the others overall. The close results of GEDFN and LRL were expected, as in the sigmoid case LRL was in fact the true model.

Fig. 2.

Plots of the classification and feature selection comparison for the case with the sigmoid inverse link function. Singleton proportions: left column 0%, middle column 50%, right column 100%. First row: AUC of ROC for classification; second row: AUC of precision-recall for feature selection; third row: recall plots given fixed precision from LRL. Error bars represent the estimated mean quantity plus/minus the standard error

As for feature selection, GEDFN uses Equation (1) to rank features. The feature ranking method for the usual DFN was similar to the one for GEDFN, except that for DFN each variable’s importance was given only by the second term in Equation (1) that was to consider only the weights connecting the input layer and the first hidden layer. For NGF, the variable importance calculation based on cumulative reduction of Gini impurity in random forests (Breiman, 2001) could be directly applied. Therefore, knowing the true predictors for simulated data, we were able to compare feature selection results for different methods by computing and comparing the AUC of the precision-recall curves, which were constructed using the feature ranking of the models and the 0/1 vector indicating the true predictor status of each feature. Figure 2d–f show the average precision-recall AUC (error bars: the intervals of mean AUC plus/minus one standard error) for each simulation setting of the sigmoid case. We found that DFN was not able to effectively rank features, resulting in precision-recall AUC <0.05 for all the datasets, and thus they were not included in the plots. From Figure 2d–f, one can conclude that GEDFN ranked features more effectively than NGF.

LRL did not rank features but directly gave the selected feature subset based on cross-validation. To compare feature selection between GEDFN and LRL, for each dataset, we fixed the precision of GEDFN to be the same as LRL, and then compared their recall values. The recall plots (error bars: the intervals of mean recall plus/minus one standard error) for different simulation settings are shown in Figure 2g–i. Again, it is evident that GEDFN achieved better feature selection results.

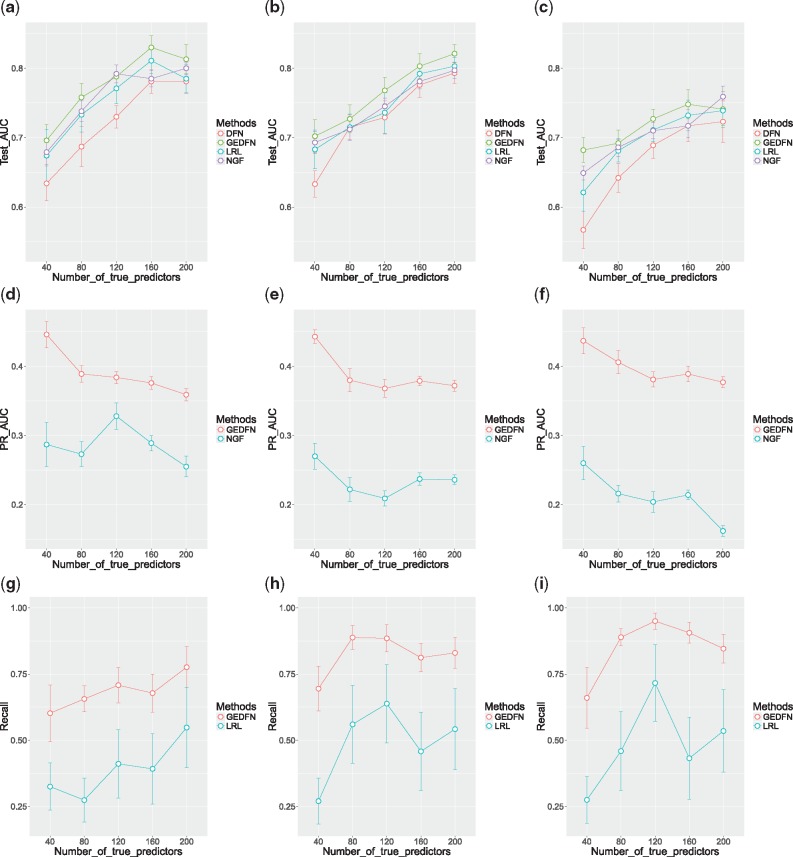
Simulation results for the case with the weighted tanh plus quadratic inverse link function are shown in Figure 3. From the first row of Figure 3, all the methods’ AUC decreased compared with their counterparts in the case of sigmoid inverse link, as the non-monotone function brought more difficulty to classification. However, GEDFN again outperformed the other methods in general, and the difference between GEDFN and LRL was enlarged compared with the sigmoid function case since the non-monotone inverse link was more challenging, and LRL was no longer the true model in this case. The second row and third row of Figure 3 indicate GEDFN’s better feature selection than NGF and LRL across all simulation settings in this case. DFN was again proved not to have good feature selection capability through the experiment, with precision-recall AUC no more than 0.04.

Fig. 3.

Plots of the classification and feature selection comparison for the case with the weighted tanh plus quadratic inverse link function. Singleton proportions: left column 0%, middle column 50%, right column 100%. First row: AUC of ROC for classification; second row: AUC of precision-recall for feature selection; third row: recall plots given fixed precision from LRL. Error bars represent the estimated mean quantity plus/minus the standard error

The above simulation experiment results showed nice performance of GEDFN in both classification accuracy and feature selection in both the sigmoid case and the tanh plus quadratic case. The method was robust across different number of true predictors and different proportions of singletons in feature graphs. To further test the robustness of GEDFN, we considered cases that the known feature graph was completely misspecified, i.e. the graph structure bears misleading information with regard to feature correlation and true predictor location. This extreme situation is unlikely in applications. We employed the synthetic datasets used above with singleton proportion 50%, destroyed the true feature graphs, and re-constructed random feature graphs using the preferential attachment algorithm. The comparison of classification and feature selection between the GEDFN with correct feature graph and the GEDFN with misspecified graphs is shown in Supplementary Figure S2. From the results, misspecified feature graphs negatively affected GEDFN regarding both classification and feature selection. For classification, GEDFN was robust enough to obtain acceptable accuracies. In contrast, feature selection was more influenced, which was expected as the feature ranking mechanism of GEDFN relied on the feature graph connections.

Another concern about the robustness of GEDFN is the reproducibility of feature selection. For a fixed dataset, we were interested in whether a relatively stable set of important features would be selected across different times of model fitting. To explore this, we randomly chose a synthetic dataset with 40 true predictors, 50% singleton and sigmoid inverse link, and experimented GEDFN feature selection repeatedly for 10 times. Ten ranked feature lists were obtained, and the top 40 ranked variables were selected for each experiment. Among the ten sets of 40 selected features, 19 features were repeatedly selected as top 40 over seven times, and they covered 40% of the 40 true predictors. Also, 70% of the union of the 10 sets of top 40 features turned out to be relevant for prediction. Here ‘relevant’ means a feature was either a true predictor, or a neighbor of a true predictor in the feature graph, since in our simulation settings, neighbors of true predictors can be useful in classification even if they were not chosen as true predictors themselves. This small specific experiment indicated the relative stable performance of GEDFN feature selection.

3.2 Real data applications

3.2.1. Breast invasive carcinoma data

We applied our GEDFN method to the Cancer Genome Atlas (TCGA) breast cancer (BRCA) RNA-seq dataset (Koboldt et al., 2012). The dataset consisted of a gene expression matrix with 20 532 genes of 707 cancer patients, as well as the clinical data containing various disease status measurements. The gene network came from the HINT database (Das and Yu, 2012). We were interested in the relation between gene expression and a molecular subtype of breast cancer—the tumor’s estrogen receptor (ER) status. ER is expressed in more than 2/3 of breast tumors, and plays a critical role in tumor growth (Sorlie et al., 2003). Elucidating the relation between gene expression pattern and ER status can shed light on the subtypes of breast cancer and their specific regulations. After screening genes that were not involved in the gene network, a total of 9 211 genes were used as the final feature set in our classification. For each gene, the expression value was Z-score transformed.

Using the HINT network architecture, we tested the four methods GEDFN, DFN, NGF and LRL on the BRCA data with 10 repeated experiments respectively. The computation time of GEDFN was around 3 min each time on a workstation with dual Xeon E5-2660 processors, 256 Gb RAM, and a single GTX Titan Xp GPU. The summary of test-set classification accuracies is seen in Table 1. From the classification results, all the methods achieved excellent AUC scores, and we concluded that the dataset contained strong signals for ER status. Thus, for this dataset, the improvement of incorporating feature graph regarding classification was limited, as traditional methods already pushed the performance to the upper bound.

Table 1.

Classification results for BRCA data

Methods	GEDFN	DFN	NGF	LRL
Mean AUC	0.945	0.938	0.922	0.940
SD	0.005	0.013	0.012	0.008

However, GEDFN exhibited advantages over other methods in terms of feature selection. To analyze the feature selection results for this dataset, we first averaged the importance scores across the ten repeated model trainings from GEDFN and NGF. DFN was proved not able to achieve good feature selection results in Section 3.1.2 and thus was excluded from this analysis. For LRL, the features selected over the ten times were quite stable with only one or two different variables, hence we took the union of the 10 selected feature sets as the feature selection result for LRL. In the end, selected features from LRL and the top 1% ranked features from GEDFN and NGF were compared. They contained 89, 92 and 92 features, respectively.

We invested the functional consistency of the selected features, as reflected by how close the selected features were in the original feature graph. On the feature graph, which was based on protein–protein interaction (Das and Yu, 2012), functionally related genes tend to be closer in distance. For each method, we extracted the sub-graph of the selected features from the entire feature graph, and examined the connection of the sub-graph. A better feature selection method was expected to choose features that fall into cliques of the overall graph, resulting in fewer connected components in the selected sub-graph. Table 2 shows the results of sub-graph analysis. The first row is the number of connected components for each sub-graph. The second row is the within-component average distances in the sub-graph. The third row is the average distances in the entire feature graph. From Table 2, one can see that features selected by GEDFN formed more closely connected sub-graphs (seen in Fig. 4), while NGF resulted in more scattered sub-graphs with 4 connected components. Features selected by LRL had no graph structure at all, with 89 features forming 80 connected components, meaning most of which were unconnected. The average distance in the entire feature graph for GEDFN was smaller than that for NGF, indicating the closer relationship among genes selected by GEDFN. Although the within-component average distance for LRL is the smallest, the large amount of connected components made this statistic meaningless for LRL.

Table 2.

Selected feature sub-graph analysis for BRCA data

Methods	GEDFN	NGF	LRL
No. of connected components	3	4	80
Within-component average distance	3.181	3.169	1.700
Average distance	2.263	2.393	3.822

Fig. 4.

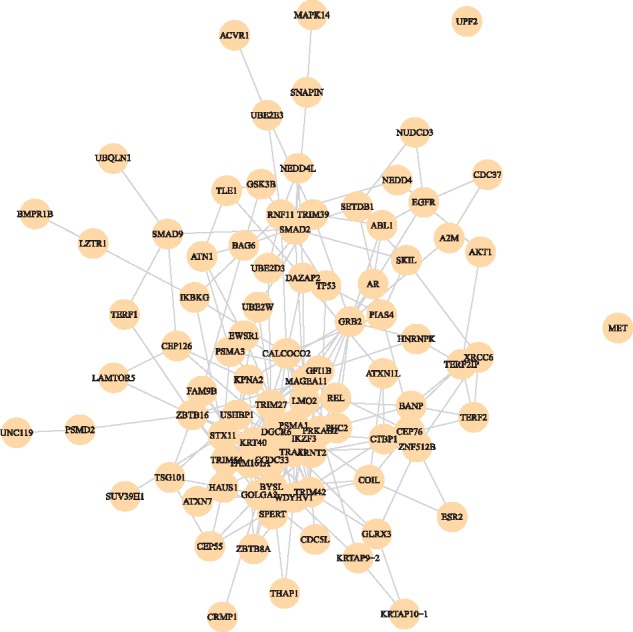
Feature sub-graph selected by GEDFN for BRCA data

Functional analysis of the genes selected by GEDFN was conducted by testing for enrichment of the gene ongoloty (GO) biological processes using GOstats (Falcon and Gentleman, 2007). The results can be found in Table 3. Fifteen of the 92 selected genes belong to the autophagy process, which was the most significant GO term. In addition, ‘regulation of apoptotic signaling pathway’ and ‘ubiquitin-dependent protein catabolic process’ were also among the top terms. Breast cancer cells that express ERα have a higher autophagic activity than cells that express ER-β and ER-cells (Felzen et al., 2015). It has been documented that the unfolded protein response and autophagy play a role in the development of anti-estrogen therapy resistance in ER+ breast cancer (Cook and Clarke, 2014).

Table 3.

Top GO biological processes for the sub-graph selected by GEDFN (BRCA data)

GOBPID	P-value	Term
GO: 0006914	5.02E-07	Autophagy
GO: 0045786	1.16E-05	Negative regulation of cell cycle
GO: 0030509	1.27E-05	BMP signaling pathway
GO: 2001233	1.74E-05	Regulation of apoptotic signaling pathway
GO: 0006511	1.78E-05	Ubiquitin-dependent protein catabolic process
GO: 0071363	3.01E-05	Cellular response to growth factor stimulus
GO: 0038061	5.56E-05	NIK/NF-kappaB signaling
GO: 0097576	5.97E-05	Vacuole fusion
GO: 0071456	6.68E-05	Cellular response to hypoxia
GO: 2001020	1.69E-04	Regulation of response to DNA damage stimulus

Note: Manual pruning of partially overlapping GO terms was conducted.

The second most significant term was ‘negative regulation of cell cycle’. ERα regulates the cell cycle by regulating the S and G2/M phases in a ligand-dependent fashion (JavanMoghadam et al., 2016). Several of the top terms were signal transduction process. It has been long established that there are cross-talks between BMP and estrogen signaling, as well as between growth factor receptor pathways and estrogen signaling (Osborne et al., 2005). BMPs are repressed by estrogen through ER signaling (Yamamoto et al., 2002). NF-κB is a crucial player in cancer initiation and progression. Direct binding to NF-κB is documented for p53 and ER (Hoesel and Schmid, 2013). It exhibits differential function in ER- and ER+ hormone-independent breast cancer cells (Gionet et al., 2009).

The remaining top GO terms were related to stress response. Breast cancer cells adapt to reduced oxygen concentrations by increasing levels of hypoxia-inducible factors. The increase of such factors causes higher risk of metastasis (Gilkes and Semenza, 2013). Hypoxia inducible factors can influence the expression of ER in breast cancer cells (Wolff et al., 2017). Estrogen changes the DNA damage response by regulating proteins including ATM, ATR, CHK1, BRCA1 and p53 (Caldon, 2014). Thus it is expected that DNA damage response is closely related to ER status. The full table containing all GO terms for the functional analysis can be found in Supplementary Table S1.

Finally, we analyzed the 69 genes that were only selected by GEDFN but not the other methods. The top five GO terms of this feature set are listed in Table 4. Clearly these functions agree very well with the biological processes based on all the selected genes listed in Table 3.

Table 4.

GO enrichment analysis for features selected by GEDFN only (BRCA data)

GOBPID	P-value	Term
GO: 2001233	4.81E-06	Regulation of apoptotic signaling pathway
GO: 0006511	1.12E-05	Ubiquitin-dependent protein catabolic process
GO: 0030509	2.39E-05	BMP signaling pathway
GO: 0071363	1.24E-04	Cellular response to growth factor stimulus
GO: 0045786	1.89E-04	Negative regulation of cell cycle

Note: Manual pruning of partially overlapping GO terms was conducted.

3.2.2. Kidney renal clear cell carcinoma data

We also tested GEDFN on the kidney renal clear cell carcinoma (KIRC) RNA-seq dataset from TCGA (Network et al., 2013). The dataset contained the gene expression matrix with 20 502 genes from 537 subjects, as well as the clinical data including survival information. The gene network again came from the HINT database. For KIRC, We tried to study the relation between gene expression and the five-year survival outcome, which was a much more difficult task compared with cancer subtypes. After screening genes that were not involved in the gene network, a total of 8630 genes were used as the final feature set in our classification. For each gene, the expression value was again Z-score transformed.

As in Section 3.2.1, we again tested the four methods GEDFN, DFN, NGF and LRL on the KIRC data with ten repeated experiments, respectively. The computation time of GEDFN was around 2.5min each time on the same workstation as for BRCA data. Classification results are summarized in Table 5. Given the 5-year survival outcome variable was much more challenging to predict, the AUC scores were much lower for all the methods. NGF was not able to classify instances at all with AUC of ROC near 0.5. At the same time, GEDFN performed substantially better than the other three methods. Therefore, the KIRC data demonstrate that incorporating feature graph would improve classification accuracy for DNN models.

Table 5.

Classification results for KIRC data

Methods	GEDFN	DFN	NGF	LRL
Mean AUC	0.743	0.643	0.521	0.698
SD	0.047	0.038	0.012	0.003

Due to the poor classification of NGF, it was unnecessary to examine its feature selection for KIRC. Similar to the BRCA results in Section 3.2.1, LRL selected scattered variables on the feature graph with few connections between them. For GEDFN, we obtained 86 top 1% important features that fall into 3 connected components, with an average within-component distance of 3.111, and an average distance in the entire feature graph of 2.257. In total 30 of the 86 genes overlap with the top genes in the breast cancer study, which was not a surprise given both datasets are based on tumor tissues.

The sub-graph of top 1% of genes selected by GEDFN is shown in Figure 5. GO enrichment analysis was conducted for the 86 genes, and the top 10 GO terms are shown in Table 6. The top GO terms were predominantly regulatory and signal transduction processes, several of which were well-known for their association with tumor development. However their role in survival was previously not clear. A key regulator in the oncogenesis of renal cell carcinoma inhibits apoptosis through apoptosis signaling pathway, which was the top GO term (Banumathy and Cairns, 2010). The second GO term, regulation of binding is a relatively broad term. The selected genes associated with this term fell mostly into protein and DNA binding processes. The 17 selected genes that were in this process include known oncogenes JUN (Jones et al., 2016) and TFIP11 (Tang et al., 2015), tumor suppressors CRMP1 (Cai et al., 2017) and LDOC1 (Ambrosio et al., 2017), target of tumorcide Manumycin-A PPP1CA (Carey et al., 2015), three SMAD family proteins SMAD2/SMAD3/SMAD4 that are involved in multiple cancers (Samanta and Datta, 2012), as well as several genes involved in various other cancers, e.g. PIN1 (Cheng et al., 2016), MDF1 (Li et al., 2017), AES (Sarma and Yaseen, 2011), MAPK8 (Recio-Boiles et al., 2016), CTNNB1 (Na et al., 2017), KDM1A (Ambrosio et al., 2017) and SUMO1 (Jin et al., 2017).

Fig. 5.

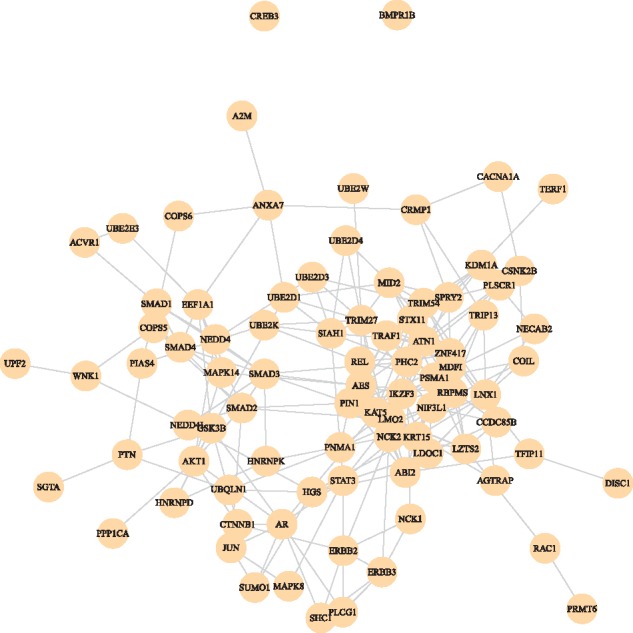
Feature sub-graph selected by GEDFN for KIRC data

Table 6.

Top GO biological processes for the sub-graph selected by GEDFN (KIRC data)

GOBPID	P-value	Term
GO: 2001233	7.10E-10	Regulation of apoptotic signaling pathway
GO: 0051098	1.14E-09	Regulation of binding
GO: 0071363	1.27E-09	Cellular response to growth factor stimulus
GO: 0007178	1.48E-07	Transmembrane receptor protein
		Serine/threonine kinase signaling pathway
GO: 1903827	2.27E-07	Regulation of cellular protein localization
GO: 0042176	5.72E-07	Regulation of protein catabolic process
GO: 0007507	1.66E-06	Heart development
GO: 0008285	1.72E-06	Negative regulation of cell proliferation
GO: 0048589	3.07E-06	Developmental growth
GO: 0007183	3.52E-06	SMAD protein complex assembly

Note: Manual pruning of partially overlapping GO terms was conducted.

The term ‘cellular response to growth factor stimulus’ includes the epidermal growth factor receptor (EGFR) pathway, and BMP signaling pathway. Both are related to the development of renal cell cancer (Edeline et al., 2010; Zhang et al., 2016). Increased EGFR expression occurs in some renal cell carcinoma patients with an unfavorable histologic phenotype (Minner et al., 2012). Many genes in the ‘heart development’ and ‘developmental growth’ processes are also part of the response to growth factor stimulus, causing those terms to be significant.

The serine/threonine kinase signaling pathway includes SMAD and mTOR signal transduction, both of which are involved in renal cell cancer development (Edeline et al., 2010). Both cell proliferation regulation and ubiquitin-dependent protein catabolism are commonly affected pathways in multiple cancers. Specifically, the ubiquitin-dependent protein catabolic process is impacted by a key genetic defect of clear cell kidney cancer in the VHL tumor suppressor gene, which is part of a multiprotein E3 ubiquitin ligase (Corn, 2007). The full table containing all GO terms for the functional analysis can be found in Supplementary Table S2.

Overall, with the KIRC data, GEDFN was able to achieve better prediction, and select genes that were easily interpretable. The results pointed to several important pathways, the behavior of which may predispose patients to certain survival outcomes.

4 Conclusion

We presented a new DFN classifier embedding feature graph information. It achieves sparse connected neural networks by constraining connections between the input layer and the first hidden layer according to the feature graph. Simulation experiments have shown its relatively higher classification accuracy and better feature selection ability compared with existing methods, and the real data applications demonstrated the utility of the new model in both classification and the selection of biologically relevant features.