Self-consistency test reveals systematic bias in programs for prediction change of stability upon mutation

Abstract

Motivation

Computational prediction of the effect of mutations on protein stability is used by researchers in many fields. The utility of the prediction methods is affected by their accuracy and bias. Bias, a systematic shift of the predicted change of stability, has been noted as an issue for several methods, but has not been investigated systematically. Presence of the bias may lead to misleading results especially when exploring the effects of combination of different mutations.

Results

Here we use a protocol to measure the bias as a function of the number of introduced mutations. It is based on a self-consistency test of the reciprocity the effect of a mutation. An advantage of the used approach is that it relies solely on crystal structures without experimentally measured stability values. We applied the protocol to four popular algorithms predicting change of protein stability upon mutation, FoldX, Eris, Rosetta and I-Mutant, and found an inherent bias. For one program, FoldX, we manage to substantially reduce the bias using additional relaxation by Modeller. Authors using algorithms for predicting effects of mutations should be aware of the bias described here.

Availability and implementation

All calculations were implemented by in-house PERL scripts.

Supplementary information

Supplementary data are available at Bioinformatics online.

Note

The article 10.1093/bioinformatics/bty348, published alongside this paper, also addresses the problem of biases in protein stability change predictions.

1 Introduction

Protein stability, a feature largely defined by protein sequence (Anfinsen et al., 1961; Tanford, 1968), is one of the most important factors that defines the function of globular proteins (Tanford, 1968). Experimental measurements of change of protein stability caused by mutations are laborious and feasible only for proteins that can be purified (Stevens, 2000). Therefore, the computational prediction of the effect of amino acid changes on protein structure and stability has become vital to many fields, including medical applications (Kiel and Serrano, 2014), protein design (Goldenzweig et al., 2016) and evolutionary biology (Shah et al., 2015; Tokuriki et al., 2007) to name a few key fields.

Several computational methods for prediction of the effect of amino acid changes on protein stability are available, which differ in processing time and accuracy (Benedix et al., 2009; Capriotti et al., 2005b; Gilis and Rooman, 2000; Guerois et al., 2002; Rohl et al., 2004; Seeliger and de Groot, 2010; Yin et al., 2007). The molecular dynamics protocol that uses alchemical free energy simulations is the most time-consuming method that shows the highest correlation with experimental data, up to r = 0.86 (Seeliger and de Groot, 2010). Programs such as FoldX (Guerois et al., 2002; Schymkowitz et al., 2005), Eris (Yin et al., 2007) and Rosetta (Rohl et al., 2004) manipulate structures more quickly, resulting in correlations with experimental change in free energy in independent tests of r = 0.50 for FoldX and r = 0.26 for Rosetta (Eris was not assessed) (Potapov et al., 2009). Machine-learning methods such as I-Mutant (Capriotti et al., 2005a,b) work even faster; I-Mutant achieves correlation of r = 0.54 (Potapov et al., 2009) based solely on the original protein structure or sequence, without requiring construction of the mutant protein structure.

Accuracy is usually used as the main and only descriptor of a method’s utility. Developers and testers of the programs for prediction of the change in protein stability attempt to maximize and quantify accuracy (Potapov et al., 2009). Although it has been reported that some methods are biased, the datasets used to detect the bias were small (Capriotti et al., 2008; Christensen and Kepp, 2012; Frappier et al., 2015; Thiltgen and Goldstein, 2012), and it has not been systematically investigated.

A straightforward approach to detect the bias in the measurements of protein stability is to rely on the principle of symmetry, a common feature in several areas of physics. Specifically, for a state function the values of the function for forward and reverse changes sum up to zero. This idea was used by several authors to detect the bias in different programs predicting the effect of protein substitutions. First, Capriotti et al. (2008) noticed that the methods could suffer from the bias without quantifying the effect. Frappier et al. (2015) found the bias after application of the prediction methods to a dataset containing 303 stabilizing and destabilizing mutations. To estimate the bias quantitatively, Christensen and Kepp (Christensen and Kepp, 2012) measured the deviation of the reverse change of stability from that expected from the forward ones, where both wild-type and mutant structures were produced by homology modeling. Next, Thiltgen and Goldstein measured the bias on the small dataset of 65 pairs (Thiltgen and Goldstein, 2012). Finally, Fariselli et al. when developing the INPS method (Fariselli et al., 2015), avoided the bias by adding symmetrical mutations to the training dataset to make it ideally balanced.

Here we measure systematically and accurately the bias inherent to methods predicting change of protein stability as a function of the number of introduced mutations. Compared to previous realizations, our approach has one or more of the following advantages. First, it does not use any experimental data on protein stabilities or change of protein stability. Second, it uses protein crystal structures and the computational method without requiring additional structure predictions or manipulations. Our dataset contains thousands of protein structure pairs. Finally, it is independent of protein structures being wild-type because processing forward and reverse substitutions are identical in terms of computational procedures. We explored the presence of the bias for four of the most popular prediction algorithms, FoldX (Guerois et al., 2002; Schymkowitz et al., 2005), Eris (Yin et al., 2007), Rosetta (Rohl et al., 2004) and I-Mutant (Capriotti et al., 2005a,b). We found that all four algorithms have an inherent bias, whereby for many instances the effect of the forward and the reverse substitution was predicted to be substantially different in magnitude. The value of the bias increases with the number of introduced amino acid substitutions.

2 Materials and methods

2.1 Dataset

We created a high-quality dataset of the protein structures differing by few amino acid residues (from one to ten). For that, we retained from protein data bank (PDB, www.rcsb.org) (Berman et al., 2000):

1. X-ray determined structures with resolution lower than 2.5 Å;

2. monomeric structures (according to the REMARK 350 of PDB header). If several chains were presented in the PDB file, we selected the first one;

3. PDB structures without unresolved backbone atoms coordinates;

4. PDB structures without non-standard residues.

In the dataset built from the sequences of the selected PDB files we found pairs of structures differing by one to ten amino acids (the number of found pairs is given in the Supplementary Table S1) using stand-alone version of BLAST (Altschul, 1997). From every set of pairs differing by a given number of mutations, we selected all pairs if their number was lower than 1000; otherwise, we chose 1000 pairs at random to minimize the computation time, the list is given in the Supplementary Table S2.

2.2 FoldX

We used FoldX (Guerois et al., 2002; Schymkowitz et al., 2005) 4.0 version (http://foldxsuite.crg.eu/products), predictions are given in Supplementary Table S2. At the moment, FoldX does not have a web-server version.

During a single run of ‘BuildModel’ procedure, FoldX samples different rotamers of the new amino acid residue from the rotamer library to achieve a lower free energy. The recommendation is to make one run; to check the convergence, multiple runs can be done (FoldX manual, http://foldxsuite.crg.eu/command/BuildModel). We found that the bias itself is not changed (both for the default protocol and for the modified one, see Section 3.4), while the standard deviation of the bias decreases with the number of models. So, to increase the reliability of the presented results we used ten-run modeling.

2.3 Eris

We used the stand-alone version v1.0 of Eris (Yin et al., 2007) with default parameters. We renumbered amino acid residues in PDB files starting with 1 and retaining only the first protein chain with small molecules belonging to that chain. The web-version can be found at http://redshift.med.unc.edu/eris/login.php.

2.4 Rosetta

We used Rosetta (Rohl et al., 2004) version 32.58837. We renumbered amino acid residues in PDB files starting with 1 and retaining only the first protein chain with small molecules belonging to that chain. Then we made five relaxed structures by ‘relax’ procedure of Rosetta package with parameters ‘-relax: dualspace true; -ex1; -ex2; -use_input_sc; -flip_HNQ; -no_optH false; -relax: min_type lbfgs_armijo_nonmonotone; -ignore_unrecognized_res; -database $ROSETTA/main/database; -nstruct 5; -nonideal’. Then we chose the structure with the lowest free energy. In that structure we calculated change of stability using the ‘ddg_monomer’ procedure of Rosetta package with parameters ‘-ddg::iterations 3; -ddg::dump_pdbs false; -ignore_unrecognized_res; -ddg::local_opt_only false; -ddg::suppress_checkpointing true; -in::file::fullatom; -ddg: min_cst true; -ddg: mean false; -ddg: min true; -ddg: sc_min_only false; -ddg: ramp_repulsive true; -ddg: opt_radius 12.0; -score: fa_max_dis 9.0; -ddg::output_silent true’.

2.5 I-Mutant

I-Mutant (Capriotti et al., 2005a,b) is a machine-learning method trained to estimate free energy change of single mutations in two modes: based on protein structure or protein sequence alone. The algorithm was trained to rely on the character of the mutation and the environment of the mutated position. For structural prediction the neighboring residues in physical space are used (or their absence in case of solvent-accessible position), and for sequence-based prediction a sequence window of ±9 residues is used (Capriotti et al., 2005a,b). The web-version can be found at http://folding.biofold.org/cgi-bin/i-mutant2.0.cgi. We used stand-alone version of I-Mutant 3.0 in PDB mode (i.e. predicting change of stability using the protein crystal structure) with default options.

2.6 Relaxation of structure by Modeller

We used Modeller (Webb and Sali, 2014) version 9v4 following the basic procedure for modelling a sequence with high identity to template. For each protein structure in question we generated with Modeller ten models of wild-type sequence and ten models of mutant sequence. Then for each Modeller model we ran ten rounds of FoldX RepairPDB and took final stability. Finally, we calculated the difference between average stability of ten mutant models and ten wild type models.

3 Results

3.1 Measurement of the bias

Using pairs of homologous proteins with known structure, we used the following protocol for accurate measurement of the bias in prediction of protein change of stability after mutation, which can be described as follows [see also (Christensen and Kepp, 2012; Frappier et al., 2015; Thiltgen and Goldstein, 2012)].

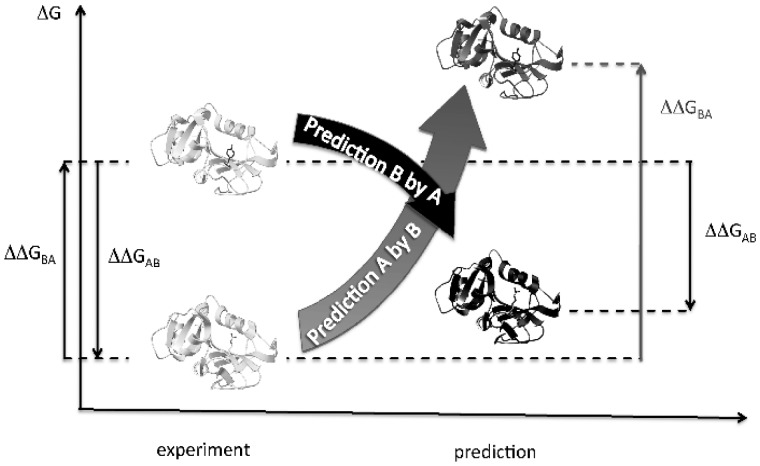
Suppose, we have protein structures A and B having free energy change of folding ΔG_A and ΔG_B differing by one amino acid in the position X: structure A has residue X_A, while structure B has residue X_B (Fig. 1). Let ΔΔG_AB = ΔG_B – ΔG_A be the free energy change of structure A due to mutation X_A -> X_B, where ΔG_A and ΔG_B are folding free energies of the structures A and B, respectively. Similarly, ΔΔG_BA = ΔG_A – ΔG_B is the free energy change of structure B due to mutation X_B -> X_A. From the definition of ΔΔG_AB and ΔΔG_BA:

$${\Delta \Delta \mathrm{G}}_{\text{AB}}{=–\Delta \Delta \mathrm{G}}_{\text{BA}}, \text{or}$$

$${\Delta \Delta \mathrm{G}}_{\text{AB}}{+\Delta \Delta \mathrm{G}}_{\text{BA}}=0.$$

However, calculations are not ideal: to obey this equation, programs should generate the lowest energy structure B from the structure A and vice versa, which may be hard, considering internal specific features of the programs. FoldX, for instance, does not move backbone chain upon mutation; it also does not move sidechains of all residues but neighbors. As a result, we expect the modeled structure B to be less stable than the crystal structure B by some value δ_AB. Similarly, modeled structure A is expected to be less stable than the crystal structure A by some value δ_BA:

$${\Delta \Delta \mathrm{G}}_{\text{AB}}{+\Delta \Delta \mathrm{G}}_{\text{BA}}{=\delta }_{\text{AB}}{+\delta }_{\text{BA}}, \text{or}$$

$${\Delta \Delta \mathrm{G}}_{\text{AB}}{=– \Delta \Delta \mathrm{G}}_{\text{BA}}{+(\delta }_{\text{AB}}{+\delta }_{\text{BA}}).$$

In this way, we can measure sum of the two delta values (δ_AB + δ_BA) and calculate the average bias per mutation as  <(δ_AB + δ_BA)/2> = <(ΔΔG_AB + ΔΔG_BA)/2>  considering all available protein pairs A and B.

Fig. 1.

Design of the protocol. Two example protein structures, A and B, differing by one amino acid residue are shown on the left. If we measure free energy change for the forward and reverse mutations, their sum must be zero: ΔΔG_AB+ΔΔG_BA=0 (arrows on the left). For predicted destabilizations (shown on the right), their sum may not be zero due to errors. Here, the case is given, when ΔΔG_AB+ΔΔG_BA>0

The used approach can be extended to pairs of structures that differ by more than one amino acid substitution. The advantage of the approach is that it does not depend in any way on the experimental determination of the free energy of the protein structure. Furthermore, it does not depend on the knowledge of which of the two sequences, if any, is the wild type variant.

3.2 The bias for single and multiple substitutions

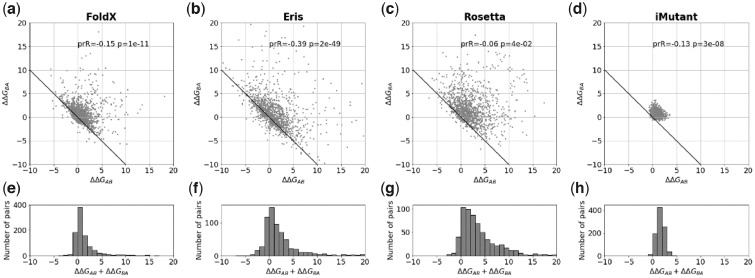
For single substitutions the average bias (ΔΔG_BA + ΔΔG_AB)/2 significantly deviates from zero (Table 1 and Fig. 2), ranging from 0.74 ± 0.05 kcal/mol for FoldX to 2.08 ± 0.12 kcal/mol for Rosetta. The clouds in Figure 2a–d consist of pairs near the non-biased line ΔΔG_BA = –ΔΔG_AB that do not contribute to the bias and a dispersed group of points that comprises the bias. We investigated influence of different factors for one of the program, FoldX. We found that mutations in more buried positions and mutations with more dramatic change in the amino acid size tend to give larger bias (Supplementary Fig. S3). The change in hydrophobicity, change in charge of the mutated residues, and other factors have little or no influence on the bias (Supplementary Fig. S3).

Table 1.

Bias for single substitutions

Program	Bias, kcal/mol	r (P-value)	Binary fraction of errors
FoldX	0.74 ± 0.05	−0.15 (10−11)	0.35
Eris	1.25 ± 0.11	−0.39 (2 × 10−49)	0.27
Rosetta	2.08 ± 0.12	−0.06 (0.04)	0.51
I-Mutant	0.80 ± 0.01	−0.13 (3 × 10−8)	0.74

Note: Bias is given for an individual substitution, i.e. bias = (ΔΔG_AB + ΔΔG_BA)/2, with the standard error of mean. r, Pearson correlation coefficient with the associated P-value. Binary fraction of errors is the fraction of errors in binary classification. A pair was considered as correctly classified if the signs of forward and reverse change of stability were opposite.

Fig. 2.

The bias for single substitutions for FoldX, Eris, Rosetta and I-Mutant. (a–d) The relationship between predicted changes of stability ΔΔG_AB and ΔΔG_BA for the forward and reverse mutations, where the structures A and B differ by a single substitution. The ‘ideal’ relationship ΔΔG_AB+ΔΔG_BA=0 is shown as a solid line. Because of symmetry of the protocol, every pair of structures A and B is plotted as (A; B) and (B; A), so the plot is symmetric relative to the y=x line. ‘prR’ and ‘p’ are the Pearson correlation coefficient and the associated P-value. (e–h) The histograms of the sum of two changes of stability ΔΔG_AB+ΔΔG_BA for the forward and reverse mutations for FoldX, Eris, Rosetta and I-Mutant, respectively

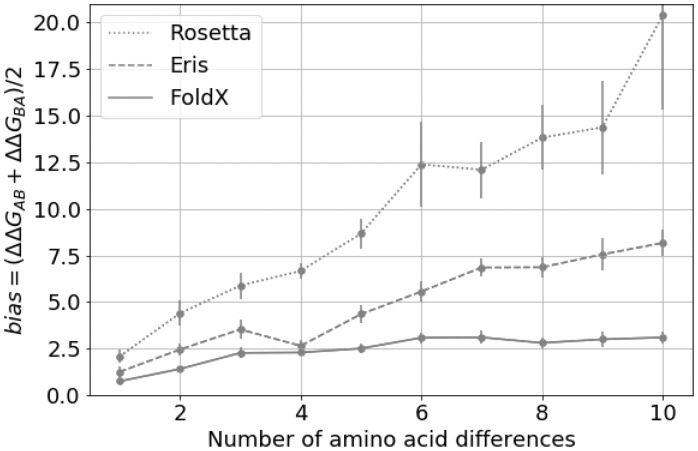
We also investigated the bias for multiple mutants (Fig. 3) for FoldX, Eris and Rosetta (I-Mutant was not studied because it does not allow input of multiple mutations). The bias increases with the number of introduced mutations (from two to ten); however, the increment becomes less pronounced with additional mutations.

Fig. 3.

The bias for multiple mutations for FoldX, Eris and Rosetta. The individual value of the bias depending on the number of amino acid substitutions separating protein variants A and B in pair of structures. The error bars represent 3 standard errors of mean

3.3 Influence of additional parameters on the bias for FoldX

We took one program, FoldX, as an example, and introduced some modifications in its default protocol to reduce or eliminate the bias. To reduce the running time of the modeling, we sampled 100 random pairs from the original pool of pairs differing by the one to ten substitutions. For reference, the bias for the default protocol of FoldX for 100-pairs subsample for single substitution was 0.80 ± 0.16 kcal/mol.

3.3.1 Initial relaxation of protein structure

Most programs manipulating protein structures as the first step of the algorithm prepare the protein structure to avoid artifacts coupled with the initial unrelaxed structure. In FoldX this procedure is called ‘RepairPDB’. First, it recovers all absent atoms and residues in the protein, then flips Asp, Gln and His side chains to avoid incorrect 180-degree rotation. Then, for amino acid residues with high free energy it tests different rotamers from the rotamer library to obtain a better free energy estimation. The recommendation of the FoldX manual is to use RepairPDB once (http://foldxsuite.crg.eu/command/RepairPDB), as we have done to obtain the data shown in the previous section.

In a computational experiment, one may want to consider changes of free energy of completely different proteins in one pool. To avoid possible artifacts coupled with unequal relaxation of different proteins, one may require the full relaxation of protein structures, i.e. the free energy after the relaxation should reach a plateau (within a reasonable threshold, we chose here 0.1 kcal/mol). We found that FoldX reaches a plateau only after 7–10 rounds of RepairPDB (Supplementary Fig. S4).

Thus, a possible concern for the default FoldX procedure is that an incomplete initial relaxation influences the predicted values of stability change and the bias. To test this possibility, we made ten rounds of RepairPDB instead of the default single round. We found that, on average, change of stability (r = 0.99, slope = 1.01 when intercept fixed at zero) and the bias (r = 0.99, slope = 0.97 when intercept fixed at zero) were the same (Supplementary Fig. S5). So, full initial relaxation of the structures, although being physically reasonable, does not reduce the bias.

3.3.2 Additional relaxation after introducing mutations

The residues are mutated in FoldX by the procedure called ‘BuildModel’. In the mutated position, BuildModel removes the original residue and assigns different rotamers for the new residue from the rotamer library. Simultaneously, BuildModel reconsiders the side-chain of the residues neighboring the mutated residue in physical space since the new amino acid residue may bump into its neighbors. The final prediction of the free energy change is calculated as the difference in free energy between the mutant structure and the reference wild-type structure. For better prediction, BuildModel moves ‘the same neighbours in the WT and in the mutant producing for each mutant PDB a corresponding PDB for its WT’ (FoldX manual, http://foldxsuite.crg.eu/command/BuildModel).

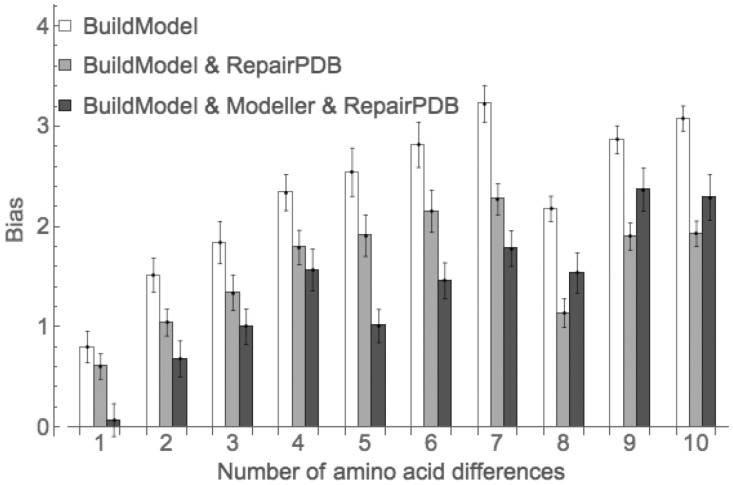
FoldX changes only the mutated position and several neighbors keeping the rest of the protein structure the same, which may seem like a biologically unrealistic requirement. We checked if the independent relaxation of the rest of the structure of mutant and the corresponding wild-type protein can decrease the bias. The additional relaxation indeed helps, and ten rounds are needed again to achieve full relaxation (Supplementary Fig. S6) decreasing the bias to 0.61 ± 0.13 kcal/mol for single mutations (Fig. 4, gray bars), or ∼25% lower than before. For multiple mutants, the reduction was even more significant (Fig. 4, white and gray bars).

Fig. 4.

The bias for different modifications of the default protocol of FoldX. The error bars represent standard error of mean

3.4 Using Modeller to decrease the bias of FoldX

FoldX does not move the backbone upon mutation, which may be the reason for the bias found here. To test this hypothesis, after mutation we used Modeller (Webb and Sali, 2014) to relax the structure including the backbone. After that, we applied ten-fold relaxation by FoldX, because the Modeller force-field could not be optimal for FoldX force-field.

We found that using Modeller for single mutants of FoldX removes the bias (Fig. 4, black bars) but at a cost of increasing the noise of the predictions (Supplementary Fig. S7). For multiple mutants using Modeller did not eliminate the bias; nevertheless, it was reduced significantly for structures differing by as many as eight substitutions. For sequences with eight to ten mutations Modeller did not reduce the observed bias (Fig. 4).

All physically reasonable modifications to the default protocol suggested here require additional computations; however, for more careful analysis one might prefer a more accurate but slower protocol, with the necessary computations, which can be performed in a feasible timeframe on a computational cluster.

4 Discussion

We accurately and systematically measured the bias for programs predicting the effect of substitutions on protein stability, for one to ten substitutions. The design of the protocol allows its application without knowing any experimental data on protein free energy change (Christensen and Kepp, 2012; Frappier et al., 2015; Thiltgen and Goldstein, 2012). The protocol uses two protein structures differing by one or several mutations. A program predicts protein free energy change upon mutations in the forward and reverse directions, and the bias is detected if the sum of free energy changes deviates, on average, from zero. We used the protocol on four representative programs, FoldX (Guerois et al., 2002; Schymkowitz et al., 2005), Eris (Yin et al., 2007), Rosetta (Rohl et al., 2004) and I-Mutant (Capriotti et al., 2005a,b), and showed that they have an inherent bias in the prediction of the mutation effect. For single mutants, the bias was 0.74 ± 0.05 kcal/mol for FoldX, 1.25 ± 0.11 kcal/mol for Eris, 2.08 ± 0.12 kcal/mol for Rosetta and 0.80 ± 0.01 kcal/mol for I-Mutant (Table 1).

The bias was noticed before. For example, Christensen and Kepp (2012) in their investigation of beta-lactamase mutants estimated the bias for FoldX equal to ∼0.5 kcal/mol. It is close to our results for single mutants; however, their estimate characterizes both single and multiple mutants together, making it impossible to differentiate between the influence of single mutations and their interactions. Moreover, to estimate the bias they used protein models obtained by homology modeling. These manipulations lead to additional uncertainty about the nature of the observed bias. In the work (Thiltgen and Goldstein, 2012) the authors found the values for the bias, which agrees to our results, but only for single mutations and using only 65 protein pairs.

The exact reasons for the observed bias and reduced accuracy on a balanced dataset remain largely obscure. One of the reasons, general to all the programs, could be that programs are trained on experimental datasets which have much more destabilizing mutations than stabilizing ones, as discussed in (Capriotti et al., 2008). Therefore, if such programs are given a balanced dataset (as we use here), then the algorithm will predict more destabilizing mutations, reflecting the tendencies of the training dataset.

The reason specific to FoldX could be that FoldX fixes the backbone when making the mutant structure. Obviously, the fixed backbone is optimal for the starting structure, not the mutated one, which is expected to estimate the prediction to be more destabilizing. When applying FoldX to a balanced dataset of 84 mutations (42 forward and 42 reverse) in the original paper (Guerois et al., 2002) the authors used additional relaxation by WHATIF program (Vriend, 1990) for the mutation increasing the sidechain. In that way, they were able to obtain unbiased results [see Fig. 3 in Guerois et al. (2002)]. Using WHATIF program was similar to our usage of Modeller in the present work.

For I-Mutant, the specific factor could be that it considers the sequence/structure context of the mutated position. The context contribution is the same both for forward and reverse mutations. Being trained on a dataset containing more destabilizing mutations it may erroneously predict that some context on average creates more destabilized predictions.

The identification of the bias does not immediately lead to a better prediction of experimental mutation effects because it is not clear if the bias results from misestimating the impact of the forward or the reverse mutation. For example, in independent tests I-Mutant showed the strongest correlation between experimental and predicted effects of mutations (Potapov et al., 2009); however, I-Mutant was also the noisiest method in our test (Fig. 2d). This suggests, that in our work we tested for different parameters of quality of prediction programs than are explored by test for agreement with experimental data. Hopefully, the bias explored here may be addressed in the course of development of new approaches [as in INPS (Fariselli et al., 2015)], or modification of the existing methods for prediction of free energy change (Christensen and Kepp, 2013, 2012). For example, the protocol used here can be utilized as an independent training part of new programs, when a program requires the forward and reverse mutations to have opposite effects.

There are situations when the bias does not influence the interpretation of the results. One of them is when we compare protein variants that have the same number of mutations and are generated from the same template structure. In this case the bias is, on average, the same for all mutants (Sarkisyan et al., 2016; Tokuriki et al., 2007). Otherwise, mutant structures obtained from the same reference structure but with different number of substitutions will have different bias, which will make them hard to compare.

To summarize, we measured accurately and systematically the bias in prediction of change in protein structure stability, both for single and multiple substitutions, utilizing the protocol based on self-consistency. The users might evaluate if the bias can influence the interpretation of their results. The developers could reduce or remove the bias from the predictions by using artificially completed balanced datasets or by requiring the method to predict the same but opposite in sign effects for forward and reverse mutations. Our findings have important applications in the studies involving the protein structure destabilization predictions.