MODE-TASK: large-scale protein motion tools

Abstract

Summary

MODE-TASK, a novel and versatile software suite, comprises Principal Component Analysis, Multidimensional Scaling, and t-Distributed Stochastic Neighbor Embedding techniques using Molecular Dynamics trajectories. MODE-TASK also includes a Normal Mode Analysis tool based on Anisotropic Network Model so as to provide a variety of ways to analyse and compare large-scale motions of protein complexes for which long MD simulations are prohibitive. Beside the command line function, a GUI has been developed as a PyMOL plugin.

Availability and implementation

MODE-TASK is open source, and available for download from https://github.com/RUBi-ZA/MODE-TASK. It is implemented in Python and C++. It is compatible with Python 2.x and Python 3.x and can be installed by Conda.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Conventional analysis of Molecular Dynamics (MD) trajectories may not identify global motions of macromolecules. Normal Mode Analysis (NMA) and Principal Component Analysis (PCA) are two popular methods to quantify large-scale motions, and find the ‘essential motions’; and have been applied to problems such as drug resistant mutations (Nizami et al., 2016) and viral capsid expansion (Hsieh et al., 2016).

MODE-TASK is an array of tools to analyse and compare protein dynamics obtained from MD simulations and/or coarse grained Elastic Network Models (ENMs). Users can perform standard PCA, kernel and incremental PCA (IPCA). Data reduction techniques [Multidimensional Scaling (MDS) and t-Distributed Stochastics Neighbor Embedding (t-SNE)] are implemented. This is the first set of tools with various extensions of PCA and other dimensionality reduction techniques for protein MD simulations. Users can also analyse normal modes by constructing ENMs of a protein complex. This tool forms the first complete set of scripts that have been developed specifically for NMA of biological assemblies. A novel coarse graining technique has been incorporated that allows the user to analyse the normal modes of a biological assembly without the use of high performance computers. The MODE-TASK coarse graining algorithm offers an alternative approach to the rotation-translation of blocks (RTB) method (Durand et al., 1994; Tama et al., 2000). The algorithm was recently validated in a virus study (Ross et al., 2018).

Beside the command line MODE-TASK, a GUI has been developed as a PyMOL plugin for easy access to all the rich and diverse functionality of MODE-TASK tools. This makes MODE-TASK and its associated pyMODE-TASK GUI a complete, unique and diverse package for analysing the large-scale motion of proteins and protein complexes.

2 Materials and Methods

2.1 Implementation

MODE-TASK was developed using C++ and Python programming languages on Linux/Unix-based systems. The C++ scripts were wrapped and are accessible from Python, and all scripts are compatible with Python 2 and 3. Python libraries, including NumPy, SciPy, Matplotlib (Hunter, 2007), MDTraj (McGibbon et al., 2015) and Scikit-learn (Pedregosa et al., 2011), were used. The C++ ALGLIB (www.alglib.net) was also utilized. MODE-TASK supports a wide variety of MD trajectory and topology formats including binpos (AMBER), LH5 (MSMBuilder2), PDB, XML (OpenMM, HOOMD-Blue), .arc (TINKER), .dcd (NAMD), .dtr (DESMOND), hdf5, NetCDF (AMBER), .trr (Gromacs), .xtc (Gromacs), .xyz (VMD), .mdcrd (AMBER) and LAMMPS. PyMODE-TASK – a PyMOL plugin was developed using Python, Tkinter and Pmw1.3 (Python megawidgets). Tkinter is a standard Python interface to Tk GUI toolkit. Tk is a cross platform, free and an open source library for creating a graphical user interface.

2.2 Model analysis by elastic network models

2.2.1 Mode calculation

MODE-TASK employs the Anisotropic Network Model (ANM) (Atilgan et al., 2001) to construct an ENM of the protein where all pairs of nodes separated by a defined cutoff are connected. For a given PDB file, the algorithm builds the Hessian matrix on the atomic co-ordinates of the C_α or C_β atoms of each residue in the complex. It incorporates the ALGLIB library to calculate the pseudoinverse of the Hessian by singular value decomposition. This process leads to the eigenvalues and eigenvectors associated with the normal modes.

2.2.2 Coarse graining

An elastic network of a macromolecular system gives rise to a Hessian matrix with dimensions that are too large for time-feasible decomposition. MODE-TASK implements a novel coarse graining algorithm that selects a sub-set of the carbon atoms that are evenly spaced across the structure of biological assemblies of macromolecules. The algorithm exploits the symmetry of the assembly by first identifying a sub-set of atoms from selected residues in an individual asymmetric unit, and then selecting the corresponding atoms from the identical residues in all other asymmetric units of the complex. In comparison to the RTB approach, the primary difference is that in MODE-TASK the criterion for selection is derived from the distance between the atoms in the structure; therefore, the coarse-grained model reflects the number of contacts between individual atoms, supporting the analysis of more localized motions. In the standard RTB approach the network is defined by a set of rigid blocks, where each block is based on the centre of mass of a single protein in the complex (Durand et al., 1994; Tama et al., 2000). This network only accounts for the connections between the proteins in the complex; while the higher level of intraprotein connectivity is lost. In contrast, the MODE-TASK network incorporates the interconnection of nodes within the individual proteins as well as across the protein-protein interfaces. This reduces the rigidity of the relative motions of the proteins that is enforced by the RTB method and may capture local motions within the proteins of the complex. The difference between the two networks has been depicted in Supplementary Figure S1.

The MODE-TASK algorithm was validated in a previous study of the Enterovirus 71 (EV71) capsid (Ross et al., 2018). The EV71 capsid is icosahedral with T = 3 symmetry. NMA of symmetrical structures yield degenerate and non-degenerate modes. Degenerate modes present with identical eigenvalues and correspond to modes for which any spatial rotation will result in a valid representation of the mode with identical frequency (Yang et al., 2009). As degenerate modes arise from symmetry, for any given structure there is a precise set of allowed degeneracies. The MODE-TASK algorithm was applied to the full EV71 capsid and to an individual pentamer of the capsid. The modes calculated for the coarse-grained capsid and pentamer presented with the allowed degeneracies defined for an icosahedron and pentagon, respectively. Moreover, such results were observed regardless of an increase in the level of coarse-graining. The NMA of the EV71 capsid, coarse grained at different levels, captured three modes that contributed to capsid expansion. Of these three modes, radial expansion of the capsid was reported. In a previous study, the RTB approach was used to investigate the normal modes of virus capsids comprising different quasi-equivalent symmetries (Tama and Brooks, 2005). Included in the study was the T = 3 Cowpea Chlorotic Mottle Virus (CCMV). The RTB approach only captured a single dominant mode (radial expansion) for the CCMV capsid. It was suggested that the two additional modes captured by the MODE-TASK algorithm represent the local motions within a pentameric unit (Ross et al., 2018).

Pseudocode, describing the MODE-TASK algorithm has been included in Supplementary Appendix A1. The script, specifically developed for the analysis of proteins only, can accept a standard PDB file or a biological assembly of a protein complex (.pdb1). In the initial step, the algorithm selects the C_α/C_β atom from a starting residue defined by the user. The algorithm then determines the distance between this atom and every other C_α/C_β in a single asymmetric unit of the assembly. For a specified level of coarse graining, the algorithm selects the nth closest C_α/C_β to the starting point and defines a minimum distance as the distance between the initial and the selected nth closest atom. The algorithm then expands outwards and iteratively steps through the (n + 1)^th closest atom. The atom is selected only if the distance between all atoms that have already been selected is greater than the defined minimum distance, thus avoiding the selection of clustered atoms. If the atom is not selected it will be marked and excluded from possible selection in subsequent iterations. The algorithm stops when all atoms in a single asymmetric unit have been scanned for possible selection. For an assembly of multiple asymmetric units, the algorithm extends to select the C_α/C_β of residues in each unit that correspond to the selected atoms. As such, the symmetry of the assembly is retained and selected atoms are evenly distributed across the molecule.

2.2.3 Analysis and visualisation

MODE-TASK has an array of tools to extract and visualise individual modes. In comparison to other tools developed for NMA of proteins such as ProDy (Bakan et al., 2011), MODE-TASK includes specialized algorithms for the extensive analysis of biological assemblies. MODE-TASK contains a tool to identify modes that act in the direction of a known conformational change between two crystal structures. The tool calculates the overlap and Pearson coefficient between a predicted displacement and an experimental conformational change. The calculation can be performed across the entire biological assembly, or the user can calculate the overlap/correlation per each asymmetric unit and each individual chain in the complex. This allows the user to determine which region of the complex contributes the most towards the conformational change for a given mode. MODE-TASK also contains a tool to plot covariance matrices for a given set of modes. The user may produce a plot that represents the complete assembly, or construct the covariance plots between a set of specified asymmetric units across the complex. For example, in the analysis of a virus capsid the user may analyse the covariance between protomers within a single pentamer, in comparison to protomers across the pentamer-pentamer interface. Basic tools to calculate the mean square fluctuations for each atom in the system for a given set of modes are also included. In addition, the user can compare fluctuations between two alternative models. This allows the user to compare two different protein structures or two models of the same complex that have been coarse grained to a different level.

2.3 Modal analysis by PCA

2.3.1 Standard PCA

MODE-TASK takes the MD trajectory and topology file as input and extracts the atomic coordinates of a set of atoms of the user’s choice. Before applying the PCA algorithm, frames are superimposed onto a reference structure of the user’s choice (first frame of trajectory by default). A matrix of atomic coordinates can be diagonalised by either Eigenvalue Decomposition (EVD) or Singular Value Decomposition (SVD) to obtain the collective modes (eigenvectors) and associated eigenvalues which characterize the motion of proteins during the MD simulation. The magnitude of an eigenvalue represents the variance of the data covered by its eigenvector. In the case of EVD, the most important motions are extracted by calculating the modes from a covariance/correlation matrix constructed from atomic coordinates which are ranked based on their ability to explain the variance in the data. MODE-TASK retains all the modes by default with an option for the user to select a subset of the components. The input trajectory is projected onto the selected modes. These projections are called Principal Components (PCs), which represent the dynamics of a protein in terms of a reduced set of orthonormal modes.

Though computationally expensive in certain cases (David and Jacobs, 2014), the use of internal coordinates for PCA offers better qualitative insights, especially in protein folding (Sittel et al., 2014). Moreover, it is also suggested to use Kernel PCA with internal coordinates. MODE-TASK has the tools to perform the PCA and Kernel PCA on the internal coordinates such as pairwise distance, 1–3 angles of the backbone atoms and torsion angles. Choice of internal coordinates removes the necessity for the pre-alignment of frames (Sittel et al., 2014).

2.3.2 Kernel PCA

Standard PCA assumes that input data are linearly related. In cases where variables are not intrinsically linearly related, the user has an option to perform Kernel PCA, a nonlinear generalization of PCA, on an MD trajectory. MODE-TASK offers different choices for the kernel. In Kernel PCA, the input trajectory is raised to a higher dimension by a kernel function and PCA is performed on the elevated data. Kernel PCA should be used with caution as it is difficult to interpret the results, since the input trajectory is mapped to a different feature space than conformational space (David and Jacobs, 2014). Nevertheless, Kernel PCA could be an invaluable tool in studying structural mechanisms behind protein dynamics in cases where standard PCA is not helpful.

2.3.3 Incremental PCA

The speed of PCA calculation can be hindered by insufficient memory during loading of an MD trajectory. IPCA is a memory efficient variant of PCA that uses only the most substantial singular vectors to project the input data to a lower dimension. The IPCA algorithm uses a batch data loading approach and the incremental storage of various variables to achieve higher memory efficiency. MODE-TASK has implemented IPCA through scikit-learn Python library and the original algorithm (Pedregosa et al., 2011; Ross et al., 2008).

2.3.4 Assessment of extent of sampling

Assessment of the extent of sampling in an MD trajectory is crucial before performing PCA. One such measure of sampling is Kaiser–Meyer–Olkin (KMO) index (Sarmento and Costa, 2017), calculated by,

$$KMO=\frac{{\sum }_i{\sum }_{j\ne i}{r}_{ij}^2}{{\sum }_i{\sum }_{j\ne i}{r}_{ij}^2+{\sum }_i{\sum }_{j\ne i}{a}_{ij}^2}$$

The value of KMO ranges between 0 and 1, where 1 indicates a perfect sampling. MODE-TASK also calculates the cosine content of the top three PCs. The cosine content is the measure of correlation between the T values of a PC and cosine function (cos(2πt/bT)), where 0 < tT <, b = n/2 and n is the index of PC. Cosine content values near 1 are an indicator that the simulation did not converge (David and Jacobs, 2014).

2.4 Other dimensionality reduction techniques

MDS is a technique of dimensionality reduction where a measure of dissimilarity in a dataset is used. It places each input point in N-dimensional space while trying to preserve the original distance matrix. MODE-TASK implements metric and nonmetric types of MDS for the MD trajectory by using the scikit-learn library (Pedregosa et al., 2011). The Euclidean distance between internal coordinates and pairwise RMSD between the MD frames are used as dissimilarity measures.t-SNE is another dimensionality reduction for high dimensional data (van der Maaten and Hinton, 2008). t-SNE has been implemented for protein MD trajectory in MODE-TASK. The dissimilarity measures used are the same as for MDS.

2.5 Outputs

Essential outputs from the ANM tool set include a coarse-grained PDB structure. The complete set of eigenvalues and eigenvectors, correlations to conformational changes, and the mean square fluctuations for specific modes are written in text file format. For visualisation, eigenvectors are projected onto the structure as a set of frames in which the vectors are added to the original atomic coordinates in increasing steps and corresponding arrows are given in a Tcl script. Useful information about the input trajectory is printed on the terminal. In case of PCA, a 2D plot of the first three PCs is written in a grace formatted text file. Additionally, a .png format 2D plot is also written; with each point color coded per time of trajectory. A screen plot of variance explained by 100 PCs is also written for evaluation purposes. The contribution of each residue towards a PC is visualized in MODE-TASK through RMSD mode plots in a grace formatted text file. In the case of MDS and t-SNE, 2D grace plots and .png files are constructed by MODE-TASK.

2.6 User interface

The MODE-TASK tool kit can be downloaded and run through the command line. A PyMOL plugin (pyMODE-TASK) has also been developed to make the functionality of the tool accessible from a GUI. PyMOL is a community-run, mixed source (source code is freely available to build) and widely used molecular visualization program. Availability of the MODE-TASK functionality to the large base of PyMOL users is crucial for the widespread reach of the unique capabilities and novel coarse graining algorithm of MODE-TASK. The plugin (Supplementary Fig. S2) is designed to be intuitive and user friendly with separate tabs for each step in the analysis. To help guide the users, the buttons and text fields have roll over help texts and appropriate warning and error messages. For each analysis step, the user also has the option to set the output directory where all the plots and results files are saved. Additionally, help pages including theory, usage and tutorials are accessible from the “Help” menu.

3 Performance

	Main parameters	Time
NMA scripts
coarseGrain.py	5C4W full capsid; Coarse grain level 4; Cβ atoms starting atom 3	<1 s
ANM	5C4W coarse-grained; Cut off 50 Å; 2460 nodes	97 min
conformationMode.py	4JGY full capsid; 5C4W coarse-grained	26 s
combinationMode.py	4JGY full capsid; 5C4W coarse-grained	26 s
visualiseVector.py	5C4W coarse-grained; mode 7	1 s
assemblyCovariance.py	5C4W coarse-grained; mode 7	317 secs
meanSquareFluctuations.py	4JGY coarse-grain level 9; 5C4W coarse-grained; mode 7	275 s
Essential dynamics scripts
pca.py	SVD solver; 10 000 frames	26 s
pca.py	RBF kernel; 10 000 frames	40 min
internal_pca.py	Phi angles; 1 000 frames	10 s
mds.py	RMSD; 10 000 frames	88 m
tsne.py	10 000 frames	68 min

Tests were conducted on a PC running Ubuntu 16.04.2 LTS on an Intel Core i7-4790 CPU with a clock speed of 3.60 GHz with 32GB of physical memory.

4 Applications

4.1 NMA

Coarse graining (level 4, start at residue 3) was performed along the C_β atoms (C_α for glycine) of the CAV-16 viral capsid (PDB: 5C4W; diameter ≈ 300 Å). The ANM.cpp then obtained the eigenvalues and eigenvectors of the respective modes. The cutoff distance was increased to 50 Å (default 15 Å) because of the capsid’s internal cavity. During host cell infection, the capsid expands for RNA-release (PDB: 4JGY). We used conformationMode.py, getEigenVector.cpp and visualiseVector.py to identify normal modes associated with the structural change. The mode with the largest overlap (0.86) to the conformational change is presented as a radial expansion (Supplementary Fig. S3 and Movie S1). Instructions to generate similar images in VMD are given in the ANM Tutorial. A detailed analysis of the overlap across the respective asymmetric units and chains of the capsid has been included in Supplementary Figure S4.

4.2 Essential dynamics

P40L variation is disruptive to the stability of the renin-angiotensinogen system (RAS, 781 residues) (Brown et al., 2017a). We explored the essential dynamics of the complex using standard PCA for the wild type versus the mutant RAS MD trajectories. PCA was performed on two separate 100 ns MD simulations, only CA atoms were selected. SVD was used for decomposition, with a linear kernel. Figure 1 depicts the shifts in the energy landscape of the protein upon mutation.

Fig. 1.

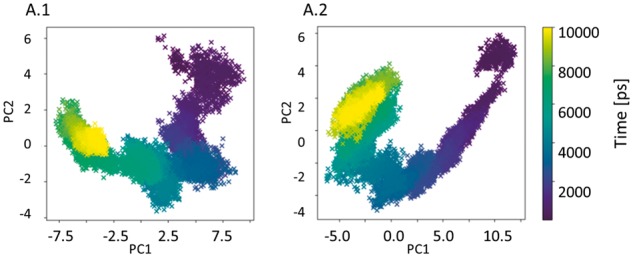
MODE-TASK visual outputs. Dimension reduction by PCA for WT (A.1) and mutant (A.2), presented per MD time point

5 Conclusion

Here, we present a novel and comprehensive downloadable software suite, MODE-TASK, which integrates a set of tools to analyse protein dynamics obtained from MD simulations as well as coarse grained elastic network models. Further, MODE-TASK is a sequel to MD-TASK (Brown et al., 2017b) and can be used side by side.

Funding

Research reported in this publication is supported by the National Research Foundation (NRF), South Africa, (grant number 93690) and the National Human Genome Research Institute (NHGRI), Office of the Director, National Institutes of Health (OD) under award number U24HG006941, and the Scientific and Technological Research Council of Turkey (grant number 116F229). The content is solely the responsibility of the authors and does not necessarily represent the official views of the funders.

Conflict of Interest: none declared.