A stochastic basis for neural inertia in emergence from general anaesthesia

Abstract

Background

Transitions into and out of the anaesthetised state exhibit resistance to state transitions known as neural inertia. As a consequence, emergence from anaesthesia occurs at a consistently lower anaesthetic concentration than induction. Motivated by stochastic switching between discrete activity patterns observed at constant anaesthetic concentration, we investigated the consequences of such switching for neural inertia.

Methods

We simulated stochastic switching in MATLAB as Brownian motion on an energy landscape or equivalently as a discrete Markov process. Effects of anaesthetics were modelled as changing stability of the awake and the anaesthetised states. Simulation results were compared with re-analysed neural inertia data from mice and Drosophila.

Results

Diffusion on a two-well energy landscape gives rise to hysteresis. With additive noise, hysteresis collapses. This collapse occurs over a mixing time that is independent from pharmacokinetics. The two-well potential gives rise to the leftward shift for the emergence dose-response curve. Yet, from in vivo data, $\Delta E{C}_{50}$ and Δ Hill slope are strongly negatively correlated (R²=0.45, P<1.7×10⁻¹⁵). This correlation is not explained by a two-well potential. The extension of the diffusion model to a Markov process with 10 states (three awake, seven unconscious) reproduces both the left shift and the shallower Hill slope for emergence.

Conclusions

Stochastic state switching accounts for all known features of neural inertia. More than two states are required to explain the consistent increase observed in variability of recovery from general anaesthesia. This model predicts that hysteresis should collapse with a time scale independent of anaesthetic drug pharmacokinetics.

Editor's key points.

• •The dose-response curve for emergence from general anaesthesia is shifted to lower concentrations relative to induction of general anaesthesia, known as neural inertia.
• •Using mathematical modelling, a bistable system can account for neural inertia, and more than two states are required to explain the variability of emergence for different anaesthetic agents and taxa.
• •As a consequence of resistance to state transitions, emergence from anaesthesia occurs at a consistently lower anaesthetic concentration than induction; this is independent of pharmacokinetic factors.

How does the brain recover after consciousness is disrupted by general anaesthesia? The brain is a complex non-linear dynamical system, which are generically multistable. Thus, even when all parameters are fixed, the brain can exhibit multiple, qualitatively distinct behaviours depending on initial conditions.¹ It therefore is not guaranteed that, after anaesthesia, the brain will ever return to its previous, conscious state. As a consequence of resistance to state transitions, emergence from anaesthesia occurs at a consistently lower anaesthetic concentration than induction, known as neural inertia.

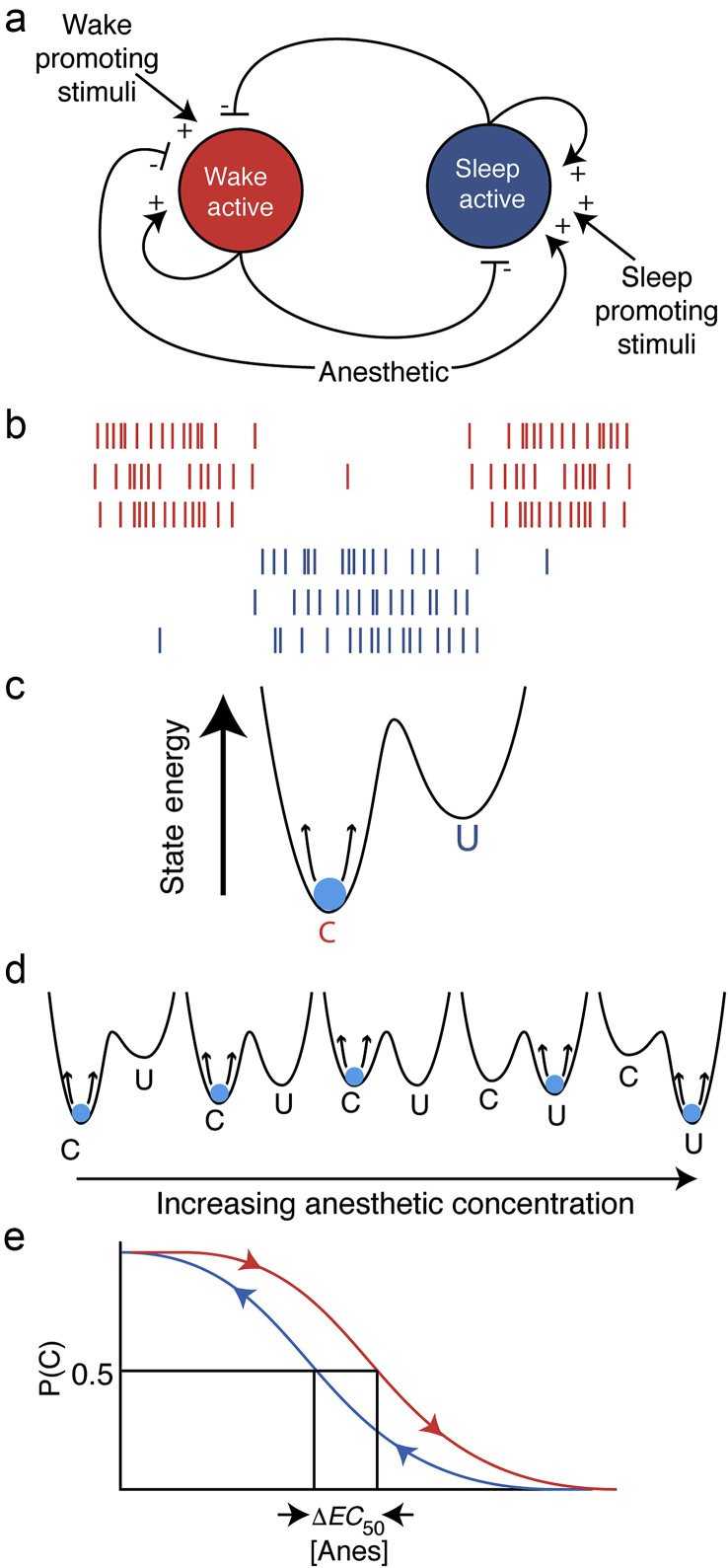
While sleep and anaesthesia are fundamentally distinct, there is overlap in the underlying neuronal mechanisms.2, 3, 4 Sleep and wakefulness activate mutually inhibitory sleep5, 6 and wake-active7, 8 neurone populations, respectively, suggesting that transitions between sleep and wakefulness could be thought of as a ‘flip-flop’ switch (Fig. 1a).6, 9 General anaesthetics inhibit wake-active and excite sleep-active neurones, biasing the flip-flop.2, 3, 5, 10, 11, 12, 13, 14, 15 The dynamics of flip-flop networks lead to just two stable patterns of neuronal activity¹⁶: either the wake-active neurones are active and sleep-active neurones are silent, or vice versa (Fig. 1b). Neuronal mechanisms of anaesthesia are not limited to sleep-wake circuitry. Nevertheless, dynamics similar to the flip-flop switch arise in a broad class of neuronal systems called attractor neural networks.17, 18, 19, 20

Fig 1.

(a) Anaesthesia (sleep) active and wake active neuronal populations are self-reinforcing and mutually inhibitory. This has been theorised to produce a flip-flop switch that prevents graded, intermediate responses but stabilises one of two all-or-none response patterns to reinforce conscious or unconscious behaviours. One possible model of anaesthetic effects could be to bias the system to favour the anaesthesia-active population. Bias could be either an additional inhibitory input to the wake-active side or an excitatory input to the anaesthesia-active side or both. (b) A cartoon of activity patterns expected from wake active (red) and anaesthesia active (blue) neurones with connectivity from panel A. Note that the network strongly favours one population or the other firing, but there is little overlap except when the system switches states. (c) This system can be abstracted as a two-well energy potential, with each local minimum representing one of the ‘attractors’ in this network structure: the wake-active dominant conscious state (C) or the anaesthesia-active dominant unconscious state (U). The brain, conceptualised as a particle that is being perturbed by noise (in this case wake-promoting and anaesthesia-promoting stimuli), spends most of its time near the basin of the attractor, but occasionally the noise will send the system over the energetic barrier into the neighbouring attractor. (d) By continuously varying the concentration of anaesthetic as a parameter, the system behaviour can be observed to infer the change in the underlying energy landscapes. (e) During induction of anaesthesia, after waiting long enough for pharmacokinetic equilibration to occur, the probability of being conscious P(C) at a given dose of anaesthetic ([Anes]) is higher than during emergence. That is, measured at the time of effect-site equilibrium, the $E{C}_{50}$ is higher during induction than during emergence, with $\Delta E{C}_{50}$ serving as a measure of the degree of hysteresis. This has been termed ‘neural inertia’.

Dynamics of attractor networks are well-approximated by diffusion on an energy landscape.²¹ This energy landscape typically has multiple wells representing distinct attractors (Fig. 1c). While meanfield models of anaesthesia18, 22, 23, 24 use a different formalism, their dynamics can also be thought of as diffusion on energy landscapes. These meanfield models of anaesthesia exhibit bistability—a special case of multistability where only two stable states (i.e. attractors) are observed. These stable states are typically interpreted as ‘awake’ or ‘anaesthetised’. More complex dynamics occur when multiple bistable networks are coupled.²⁰

In contrast to meanfield approaches, here we do not address how the shape of the energy landscape depends on the underlying neuronal architecture. Rather, we study the consequences of multistability for neuronal inertia.14, 25, 26 That is, how does the energy landscape shift with increasing anaesthetic drug concentrations (Fig. 1d)? What are the implications of these shifts for transitions between the awake and the anaesthetised state? What is the effect of noise on neural inertia? Are just two states sufficient to explain the phenomenology of neural inertia?

Experimental evidence argues that neural inertia—the hysteresis present between dose-response curves for induction and emergence (Fig. 1e)—is ubiquitous and not explainable by pharmacokinetic factors alone. Here, we show that a bistable system such as a flip-flop switch can account for the left shift of the dose-response curve for emergence relative to induction, but more than two states are required to explain the increased variability of emergence seen across different anaesthetic agents and taxa.

Methods

Energy landscape simulations

All simulations were performed in MATLAB 2014b (MathWorks, Natick, MA, USA). To simulate transitions between two distinct states, we used a ‘potential energy’ function adapted from Moreno-Bote and colleagues:²¹

$$E\left(x,a\right)=x^2\left(\frac{x^2}{2}-2\right)+a{\left(x-1\right)}^2+\left(1-a\right){\left(x+1\right)}^2$$ (1)

$E$ is a function of the state of the system denoted by $x$. $x=r_{\text{wake}}-r_{\text{sleep}}$ where $r$ could be thought of as the firing rate of a neuronal population in arbitrary units and $a$ is anaesthetic concentration in arbitrary units scaled between 0 and 1.

$E$ naturally describes an attractor network comprised of two mutually inhibitory populations of neurones. The two minima of $E$ are located at $x\approx \pm 1$. These minima could correspond, for example, to activated wake-active neurones or sleep-active neurones. Consistent with experimental evidence, this two-well potential function assures that the two populations of neurones are not likely to be co-activated. The analogy to sleep and wake active neurones is used for illustration only. The presence of more than one well in the potential energy produces the phenomena of interest, rather than any specific features of neuronal architecture.

For the sake of mathematical convenience, anaesthetic-induced activation of sleep-active and inhibition of wake-active neurones are assumed to have the same strength. This assumption does not change any conclusions appreciably, because the Boltzmann relationship assures that the energy landscape uniquely specifies the probability distribution of the system states $\pi \left(x\right)\propto e^{-E\left(x,a\right)}$ (i.e. the probability of being awake at each anaesthetic concentration). $\pi \left(x\right)$ is the limiting distribution at steady-state in a system perturbed by noise. Without noise, the system would drift down the energy gradient and stay at the minimum indefinitely. Thus, without noise, the behaviour of the system can be computed analytically (black line in Fig. 2a). Transitions between the awake and anaesthetised states in the noiseless case only occur when the starting state of the system loses stability at some critical anaesthetic concentration. This loss of stability for the awake and the anaesthetised state occurs at different anaesthetic concentrations. This difference in concentrations is a necessary consequence of multistability—if only one stable state exists for all anaesthetic concentrations, then the system is by definition not multistable. Thus, without noise, bistable systems generically give rise to hysteresis, as predicted by meanfield models.18, 24

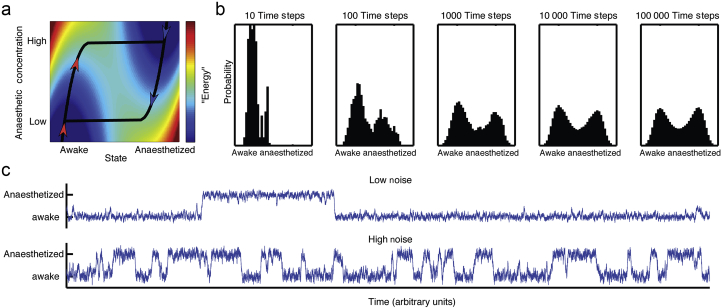
Fig 2.

(a) The system traces out the minimum contour on the energy surface, indicated by the heat map, where red indicates high energy and blue indicates low energy. The energy surface is a function of anaesthetic concentration and the state of the system as conscious or unconscious computed according to Equation (1). The red arrows indicate the trajectory the system will take as anaesthetic concentration is raised from zero, and the blue arrows indicate the trajectory when lowered from maximal. Note that the induction arm stays in the ‘awake’ minimum until the local minimum disappears, when the trajectory abruptly shifts to the ‘anaesthetised’ minimum. The converse happens when the system starts anaesthetised and the concentration decreases, producing hysteresis. (b) Once additive noise is included in the system, hysteresis collapses over time. For an intermediate anaesthetic concentration ($E{C}_{50}$ in this case), we simulate the behaviour of the system that starts out in the awake state for a progressively larger number of time steps. The number of steps is shown above each panel (100 simulations were used). The distribution of data eventually converges to the expected even split between the awake and. (c) The magnitude of the noise can affect perception of system state. Both traces represent the results of a simulation for a single brain flickering between the awake and anaesthetised states. In the upper trace, the noise term is much smaller than the lower trace, giving the impression that the upper trace is more ‘awake’. Yet the two systems have the same probability of being in the anaesthetised and awake states.

Our primary interest here is the non-trivial effect of noise superimposed on the potential function. Specifically, we are concerned with the dynamics of the system at a constant anaesthetic concentration. To model the effect of noise, we use Brownian motion on an energy landscape—the change in the state of the system over time is a sum of the gradient of the energy landscape (first term) and noise $\epsilon$:

$$\frac{dx}{dt}=-D\frac{\partial E\left(x,a\right)}{\partial x}+\epsilon$$ (2)

Together with $\epsilon$, the diffusion constant $D$ scales the noise relative to the energy barrier separating the two stable states. For the purposes of simulation, $D$ was held fixed while $\epsilon$ was varied. $\epsilon$ is modelled as Gaussian noise with mean 0 and variance $\sigma$. Equation (2) can be generalised to a broad class of reaction-diffusion systems which include both stochastic and deterministic components. Here, we assume the simplest model that only includes stochastic processes. For clarity we omit the normalisation constant $\sqrt{2}$ typically used to scale $\epsilon$. Increasing $\sigma$ makes the system more noise-driven. Simulations of Brownian motion were performed using the standard Euler method.

Markov processes

Equations (1), (2) allow both the state of the system $x$ and the anaesthetic concentration $a$ to vary continuously. Discretising the energy function over a set of bins in the plane spanned by $x$ and $a$ offers significant simplification. Using Equation (2) for every value of $x$ one can calculate the probability of transitioning to $x^{\prime }$ in the next time step. This process can be iterated for $N$ values of $x$. A transition probability matrix $\text{M}$, commonly referred to as the Markov matrix, describes the transition probabilities between each pair of states. Because the system is most likely to be near the energy minima, the potential energy function [Equation (1)] can be closely approximated by a 2×2 transition probability matrix $\text{M}$:

$$\text{M}=\left(\begin{array}{cc}w& 1-w\\ 1-s& s\end{array}\right)$$ (3)

The probabilistic state of the system at time $t$ can then be expressed as:

$${\text{x}}_{\text{t}}={\text{x}}_{\text{t}-1}\text{M}$$ (4)

Diagonal elements $w$ and $s$ express the probability that the system in the waking or sleeping, respectively, state will remain in the same state for one time step. Therefore, parameters $w$ and $s$ set the noise level in the system. The closer $w$ and $s$ are to 1, the less likely the system will switch its current state (i.e. the less noisy the system is). Equation (4) can be iterated to compute the probabilistic state of the system at any time. As a corollary to the Boltzmann relationship between $E$ and $\pi \left(x\right)$, one can use $\text{M}$ to compute the distribution of states as time goes to infinity starting from a distribution of states at time zero as $\underset{x\to \infty }{\lim }{\text{x}}_{\text{t}}={\text{x}}_0{\text{M}}^{\text{t}}$. The solution to this equation depends solely on the eigenvalues of $\text{M}$. Because rows of $\text{M}$ must add up to 1, it follows that the largest eigenvalue of $\text{M}$ is 1. Assuming that no elements of $\text{M}$ are zeros, and that $\text{M}$ is a 2×2 matrix, the steady-state distribution is the eigenvector of $\text{M}$ associated with the largest eigenvalue:

$$\text{P}=\left[\frac{1-s}{2-\left(w+s\right)}\frac{1-w}{2-\left(w+s\right)}\right]$$ (5)

The denominator for each element of $\text{P}$ is a normalisation factor, which assures that the two components of $\text{P}$ add to 1. The first component of $\text{P}$ is the steady-state probability of being awake, and the second component denotes the steady-state probability of being anaesthetised. The effect of anaesthetic is modelled by making components of $\text{M}$ a sigmoid function of the anaesthetic concentration, such that $\text{P}$ is entirely in the awake state when $a$ is zero and entirely in the anaesthetised state when $a$ is 10 (in arbitrary units). The specific choice of this sigmoid function does not affect any of our conclusions. The sigmoid function used for the simulations is a standard Hill equation:

$$F\left(a\right)=\frac{1}{{\left(\frac{a}{E{C}_{50}}\right)}^{-h}+1}$$ (6)

where $E{C}_{50}=5$ and $h=10$ is the Hill slope and $a$ is the anaesthetic concentration. The Hill slope was chosen such that the sigmoid comes very close to 1 at the highest anaesthetic concentration (10 in this case), so that the system is concentrated in the anaesthetised state at the highest anaesthetic concentration.

Using Equation (6), the transition probability matrix at any anaesthetic concentration $a$ can be constructed as follows:

$$\text{M}\left(a\right)=\left(\begin{array}{cc}1-F\left(a\right)& F\left(a\right)\\ 1-F\left(a\right)& F\left(a\right)\end{array}\right)$$ (7)

Akin to the case with the energy landscape, Equation (7) assumes that anaesthetics affect the stability of the awake and the anaesthetised states symmetrically. Recall that, because rows of $\text{M}$ must add up to 1, the largest eigenvalue has to be 1, and the associated eigenvector is the steady state distribution of the states of the system. Thus, simply changing how $F$ affects $w$ relative to $s$ by changing $E{C}_{50}$ or Hill slope would not result in hysteresis in the long time limit, because $\text{M}$ can only have one uniquely specified final distribution of states (assuming that no elements of $\text{M}$ are zeros, i.e. all states are connected). Therefore, the system must converge onto the same dose-response curve for induction and emergence in the long time limit. This is a well-known analytical result.

When $a=E{C}_{50}$, awake and anaesthetised states are equiprobable. This recapitulates the salient features of the energy landscape. Note that there is no unique solution to Equation (5)—while every $\text{M}$ has only one steady-state distribution, an infinite number of Markov matrices can be constructed with the same steady-state distribution of states. For instance, increasing $w$ and $s$ proportionally will maintain the same steady-state distribution but change the influence of noise. This allows us to separate the effect of noise from the effect of anaesthetics in a Markov process model.

Results

Figure 2a generalises Figure 1d into an energy surface by plotting Equation (1) as a function of the state of the system $x$ and anaesthetic concentration $a$. A brain obtained from the bottom left hand corner, awake with no anaesthetic, will, in the absence of noise always be in the local minimum of the energy surface, denoted by the black line. As anaesthetic concentration is raised (red arrowheads) and then lowered (blue arrowheads), the brain state traces a non-overlapping trajectory. The area between the curves indicates that this simple system can give rise to hysteresis. The difference between the induction and emergence curves necessarily follows from the fact that $E$ has multiple (two) stable states.

Yet biological systems are perturbed by noise such as external stimuli, thermal fluctuations, stochastic opening and closing of ion channels, and other variables. Even though a system starts out in the awake state at $E{C}_{50}$, with addition of noise, there is a non-zero probability that it will spontaneously transition into the unconscious state. A simulated evolution of the distribution of states of the system as a function of time at a fixed anaesthetic concentration ($E{C}_{50}$ in this case) is shown in Figure 2b. By the Boltzmann relationship (see Methods), in the long time limit the distribution of states is solely determined by the relative stability of the awake and the anaesthetised states. This implies that, for a broad class of systems that can be approximated by a multistable potential function and stochastic processes, over time hysteresis should disappear. After 100 time steps, the system begins to show hysteresis collapse, with a substantial fraction of simulated systems reaching unconsciousness. By 10 000 time steps, the system is nearly at steady-state (with minimal further change by 100 000 time steps) where the awake and anaesthetised states are equiprobable as predicted by the Boltzmann relationship.

To examine the impact of noise on system behaviour, we simulated the system while varying the magnitude of noise (Fig. 2c). When the noise magnitude is small, transitions between states are rare. When noise increases, transitions occur more frequently. From Figure 2c, the brain in the top trace is more awake than the one in the bottom. Indeed, during the interval shown, the top trace spends a greater fraction of time in the awake state. And yet, in the long time limit the two systems converge to the same probability of being awake (50% in this case). This illustrates how one can erroneously show differences in potency of an anaesthetic based on the amount of noise in the system. Note that the anaesthetic concentration is held fixed and collapse of hysteresis is entirely driven by noise rather than by anaesthetic effects.

The traces in Figure 2b also illustrate that the potential function in Figure 2a can be simplified as a two-state Markov process. In the long time limit, the probability of being awake (or anaesthetised) in a two-state Markov process is determined by the stability of the awake and the anaesthetised states. The time to converge on this long time limit is referred to as the system's state ‘mixing time’,²⁷ and is determined by the magnitude of the noise term relative to the energetic barrier between wells (or, in the two-state Markov model, the transition probability). More formally, the timescale of collapse to the steady-state distribution is related to the spectral gap of the transition probability matrix.²⁸ By construction, this mixing time is totally independent of pharmacokinetics, as the simulation holds $a$ fixed.

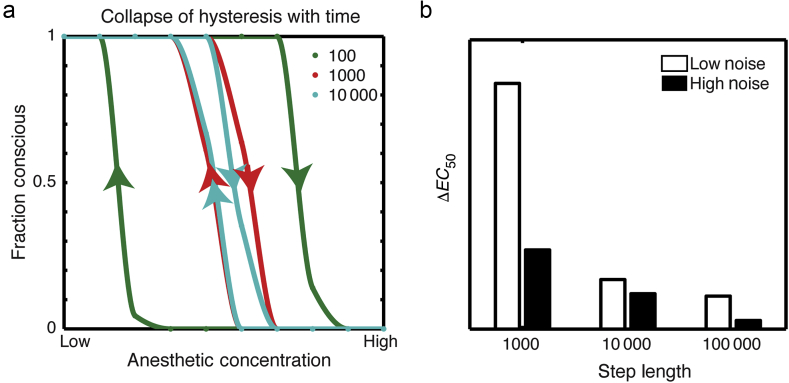
To explore the collapse of hysteresis over time as a result of noise, the same simulations as in Figure 2 were performed at multiple anaesthetic concentrations to construct concentration-response curves for induction and emergence after different time intervals (Fig. 3a). As expected, hysteresis collapses over time, and does so faster in a system with more noise (Fig. 3b). All curves have the same Hill slope, and the entire dose-response curve shifts as the simulation runs for longer times with a change in $E{C}_{50}$.

Fig 3.

(a) Hysteresis collapse over time in the presence of noise. A dose-response curve for the same two-well system with additive noise is constructed after varying numbers of time steps, 100 (green curve), 1000 (red curve), or 10 000 (blue curve). The only difference between these dose-response curves is the speed with which the ramps are performed; the model there has no pharmacokinetic equilibration time and concentrations can be changed instantaneously. (b) Effect of noise on hysteresis collapse over time. The same simulation was run for high (black) or low (white) levels of noise, and the resulting $\Delta E{C}_{50}$ estimates are plotted as a function of delay time. Higher levels of noise result in a shorter mixing time with faster collapse of hysteresis.

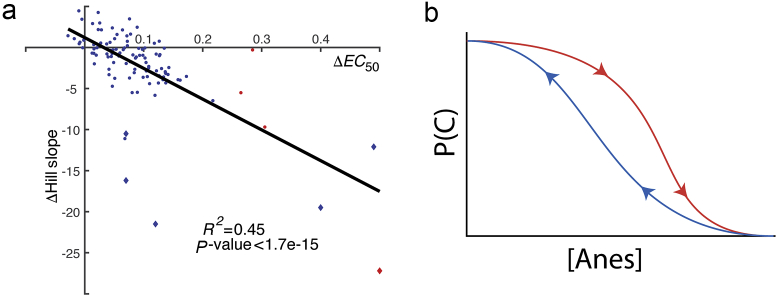
To compare our simulation against existing data for neural inertia, we obtained measures of $E{C}_{50}$ and Hill slope values for induction and emergence for more than 100 mutant strains of mice and Drosophila25, 26 (M. Kelz personal communication). Figure 4 plots $\Delta E{C}_{50}$ vs change in Hill slope between the induction and emergence arms of the hysteresis loop. There is a significant negative correlation between $\Delta E{C}_{50}$ and Δ Hill slope (Pearson's correlation coefficient R²=0.45; P<1.7×10⁻¹⁵, Student's t transformation of Pearson's correlation coefficient) (Fig. 4b). That is, the slopes of the curves on each arm of the hysteresis loop differ. Of note, this relationship holds true even with the rare mutants with negative hysteresis (those with a negative $\Delta E{C}_{50}$).²⁵

Fig 4.

(a) Degree of hysteresis is related to shift in the Hill slope. Each tested line for flies (circles) or mice (diamonds) tested for hysteresis with isoflurane (blue) or halothane (red) are plotted. (b) The generic shifts in the shape of the induction compared with emergence arms with neural inertia: the arm with the higher $E{C}_{50}$ has the steeper slope, and this difference increases with increasing magnitude of hysteresis $\Delta E{C}_{50}$.

The two-well potential model gives rise to a single Hill slope and cannot produce the shift in Hill slope seen in the real data. As the Hill slope reflects population variability, the steeper the Hill slope, the less variable the population response. The universally observed reduction of the Hill slope for the left-shifted curve implies that recovery from anaesthesia is consistently more variable than induction of anaesthesia. The two-state Markov process (or two-well potential system) cannot increase variability because dwell times in awake (and anaesthetised) states are exponential. The probability of leaving the state (the off diagonal elements in the transition probability matrix) determines the time constant for dwell times. Thus, in the two-potential well model, there is no way to adjust population variability separately for the induction and emergence arms of the hysteresis loop without affecting their equilibrium distribution.

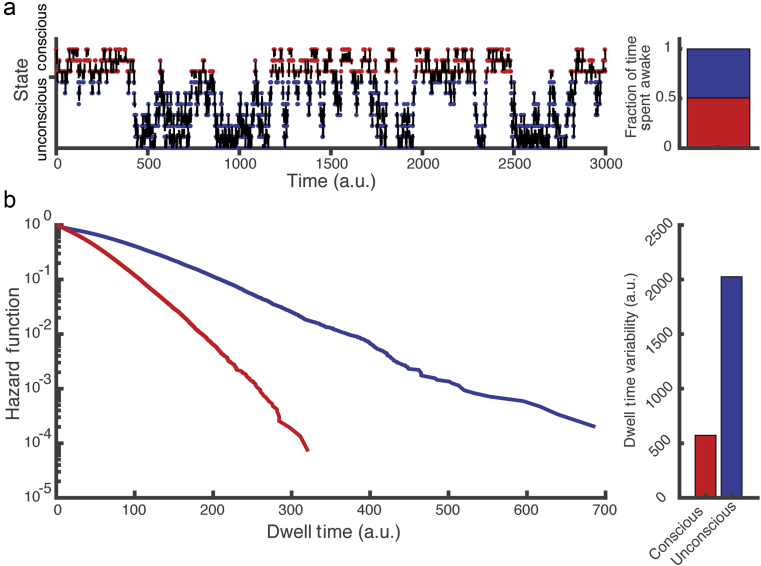
Experimental observations²⁹ suggest that multiple neurophysiological states can occur at a fixed anaesthetic concentration, and that some of the transition probabilities between states are essentially zero. All things held equal, sparse connectivity of the transition probability matrix increases the mixing time of the system.²⁷ Interestingly, sparse connectivity can also contribute to increased variability. To illustrate this, we generalised the Markov model to have multiple (e.g. 10) states. If the system is in States 1–3 it is ‘awake’ and otherwise ‘anaesthetised’. Both burst suppression and sustained delta waves in the EEG correspond to discrete brain activity patterns that are associated with being anaesthetised. The simplest case of this 10 state system is a random walk on a line—the state of the system can increase or decrease by 1 and the probability of transition is fixed. States 1 and 10 are reflective boundary conditions. A well-known result in theory of stochastic processes is that return times for a random walker on a real line have a power law distribution with an exponent of 3/2.³⁰ As a consequence, the mean, variance, and higher moments of the return times diverge, producing dramatic variation between seemingly identical experiments.

Transition probabilities were tuned to $E{C}_{50}$ —50% probability of conscious (States 1–3) and unconscious (States 4–10) behaviour (Fig. 5a). Unlike the two-state system, the multistate system allows control of both the overall probability of being awake and the variability. To show this, we plot the distribution of dwell times in the conscious and the unconscious states (Fig. 5b). Although the overall probability of being conscious is the same as being unconscious, the population variability is much higher in the unconscious states. This increase in variability is because of the right skew in the dwell-time distribution and matches the observed decrease in Hill slope of the emergence curve. A multistate Markov model will still produce hysteresis collapse over time. Thus, given a stochastic process, the parsimonious assumption that a random collection of neurones is unlikely to produce a conscious brain naturally leads to the observed features of neural inertia.

Fig 5.

(a) Simulating shifts between consciousness and unconsciousness as a discrete random walk on a line. Three states correspond to conscious states and seven states correspond to unconscious states, with system state shifting solely because of a stochastic process encoded in the transition probabilities between states. (b) This model produces a right skewed return time distribution, which generalises to power law behaviour in the continuous case. a.u., arbitrary units.

Discussion

We have shown that a simple model of the brain as a stochastic process on an energy landscape will generically produce hysteresis that dissipates after a mixing time determined by noise. To generalise the model while retaining tractability, we alternatively frame the two-potential well model as a Markov process, which allows us to generalise the model to incorporate multiple ‘conscious’ and ‘unconscious’ states, which has both empirical29, 31 and theoretical support.32, 33

This study attempted to identify a simple, abstract class of model capable of producing hysteresis with the features of neural inertia. Only the briefest characterisation of individual models within that class was performed to find simple choices capable of behaviour consistent with experimental observations. This is inherently limiting. For example, only a one-dimensional geometry of state space has been explored. As a result, no effects of sparseness or directedness of connectivity between Markov states were studied, so it is possible that a sparse or directed network with fewer than 10 states might produce behaviour similar to the multistate Markov model presented here. Furthermore, though this simple model captures the salient features of what is known currently about neural inertia, future experimental observations could invalidate this class of model. Yet the ability of such a simple class of dynamical models to reproduce neural inertia suggests that relatively simple dynamics can clarify several observations about the induction and recovery from anaesthesia.

While noise is unavoidable, the consequences of noise have not been explored in the context of mechanisms of anaesthesia. Noise is relevant for the basic definitions of minimum alveolar concentration (MAC),²⁷ which is defined as the concentration at which 50% of subjects do not respond to a painful stimulus. There are two paradigmatically different ways in which MAC can arise, however. The first is population variability: 50% of the population will not respond to any surgical stimulus, while the other 50% will remain responsive. Conversely, it is possible that the same subject will respond to 50% of repeated surgical stimuli. The latter possibility makes the effects of noise unavoidable. As we illustrate, state switching because of noise gives rise to mixing time—a time scale on which a stochastic system decays towards its final equilibrium distribution of states, which is completely independent of drug pharmacokinetics and can produce neural inertia. This neural inertia will be experimentally observed so long as the mixing time is longer than the pharmacokinetics of drug equilibration, which appears to be the case in both mice and Drosophila for volatile anaesthetics.25, 26 Mixing time may also be longer than pharmacokinetic equilibration for short34, 35 but not prolonged propofol infusions.³⁶

Using a simple Markov chain and the parsimonious assumption of more unconscious than conscious states, we were able to capture two essential features of neural inertia: the shift in $E{C}_{50}$ and the change in Hill slope. Fluctuations in behavioural responsiveness are because of stochastic dynamics of neuronal states themselves, and naturally raise questions about established measures of potency.³⁷ For example, if we attempt to measure MAC_Awake³⁸ before the mixing time has elapsed, the measure of potency will be confounded, even if the effect-site concentration of anaesthetic is at steady-state.

Our exploration of the experimental data for neural inertia in rodents and Drosophila revealed a consistent, previously unappreciated relationship between the degree of neural inertia (shift in the $E{C}_{50}$) and population variability (decrease in the Hill slope). The apparent increase in variability can be explained by generalising the stochastic model to include multiple unconscious states, which is consistent with fluctuations in local field potentials recorded in rats at a fixed anaesthetic concentration.²³ One implication of this model is that recovery times are inherently stochastic—any individual within a clonal population could have a highly variable recovery time. Furthermore, the same individual subjected to an identical anaesthetic could have dramatically different recovery times.

Ablation of orexinergic neurones¹⁴ in the hypothalamus or reduced catecholaminergic signalling²⁶ broadens hysteresis by shifting the emergence curve to the left. This might suggest that orexinergic and catecholaminergic systems are preferentially required for emergence from anaesthesia, an interpretation that implicitly assumes only two states: conscious and anaesthetised. Yet, multiple discrete stable39, 40 activity patterns occur in the anaesthetised rodent29, 41 or human.36, 42 Remarkably, not all transitions between these patterns are equally likely. A multistate Markov process with sparse connectivity produces hysteresis, capturing both the shift in the $E{C}_{50}$ and the decrease in Hill slope observed during emergence. Thus, in order to broaden hysteresis, orexinergic or noradrenergic neurones need not specifically act on emergence from unconscious to conscious states. An equally likely possibility is that these neurones change the transition probabilities between states of unconsciousness. The multistate Markov chain can also explain the hitherto puzzling observation of ‘negative hysteresis’ observed in some Drosophila mutants. Negative hysteresis arises if the mutation leads to a new connection from an unconscious to a conscious state. Thus, a multistate Markov process accounts for all known features of hysteresis, suggests an existence of a novel time scale that governs the collapse of hysteresis, and proposes a different interpretation of genetic experiments that specifically affect neural inertia.

Authors' contributions

Ran simulations: A.P.

Conceived the study, analysed and interpreted the results, and wrote and revised the manuscript: both authors.

Handling editor: H.C. Hemmings Jr

Editorial decision: March 5, 2018

Declaration of interest

None declared.

Funding

National Institute of General Medical Sciences (7K08GM106144 to A.P., 1K08GM121961 to A.E.H.)