DETECTING FEATURES OF EPILEPTOGENESIS IN EEG AFTER TBI USING UNSUPERVISED DIFFUSION COMPONENT ANALYSIS

Abstract

Epilepsy is among the most common serious disabling disorders of the brain, and the global burden of epilepsy exerts a tremendous cost to society. Most people with epilepsy have acquired forms, and the development of antiepileptogenic interventions could potentially prevent or cure these epilepsies [3, 13]. The discovery of potential antiepileptogenic treatments is currently a high research priority. Clinical validation would require a means to identify populations of patients at particular high risk for epilepsy after a potential epileptogenic insult to know when to treat and to document prevention or cure. We investigate the development of post-traumatic epilepsy (PTE) following traumatic brain injury (TBI), because this condition offers the best opportunity to know the time of onset of epileptogenesis in patients. Epileptogenesis is common after TBI, and because much is known about the physical history of PTE, it represents a near-ideal human model in which to study the process of developing seizures.

Using scalp and depth EEG recordings for six patients, the goal of our analysis is to find a way to quantitatively detect features in the EEG that could potentially help predict seizure onset post trauma. Unsupervised Diffusion Component Analysis [5], a novel approach based on the diffusion mapping framework [4], reduces data dimensionality and provides pattern recognition that can be used to distinguish different states of the patient, such as seizures and non-seizure spikes in the EEG. This method is also adapted to the data to enable the extraction of the underlying brain activity. Previous work has shown that such techniques can be useful for seizure prediction [6].

Some new results that demonstrate how this algorithm is used to detect spikes in the EEG data as well as other changes over time are shown. This nonlinear and local network approach has been used to determine if the early occurrences of specific electrical features of epileptogenesis, such as interictal epileptiform activity and morphologic changes in spikes and seizures, during the initial week after TBI predicts the development of PTE.

1. Background.

The mechanisms underlying human acquired epileptogenesis remain poorly understood, and an innovative approach to study the process from inception to manifest clinical epilepsy is needed. We have selected post-traumatic epilepsy (PTE) as a model to pursue this understanding because the timing of the potential epileptogenic insult is known, and the period of epileptogenesis can be determined. PTE is an important public health problem, accounting for 5% of all epilepsy [1, 2, 11, 15, 16]. Epileptogenesis is common after moderate-severe traumatic brain injury (TBI) [1] and begins early, offering a window of opportunity to test the efficacy of potential antiepileptogenic (AEG) drugs [10, 24, 25]. In order to design economically feasible antiepileptogenic clinical trials, however, it is necessary to identify reliable biomarkers that: 1) predict later PTE, to enrich the subject population; 2) stage the epileptogenic process, to determine the timing of intervention; and 3) diagnose epilepsy, to provide biomarkers. Our hypothesis is that early post-traumatic epileptic EEG activity indicates the presence of an epileptogenic process in patients after moderate-severe TBI. The secondary hypothesis is that epileptogenesis can be diagnosed during the latent period, prior to the establishment of PTE, creating a potential window for preventative or disease modifying therapies.

Development of prevention and disease modifying treatments for epilepsy requires understanding epileptogenic mechanisms, the timing of epileptogenesis, and biomarkers that accurately indicate the disease process. PTE is common, occurring in 15-55% of patients with severe TBI [1, 8, 18], but the latency from injury to the onset of recurrent seizures is short, usually less than 2 years. PTE is a significant public health burden, comprising 5% of patients referred for evaluation of drug resistant epilepsy. The literature is replete with putative predictors of PTE [1, 18], including markers of severity of injury such as intraparenchymal hemorrhage, skull fracture, and penetrating injury. PTE is associated with long term hippocampal disconnection, atrophy, cell loss and localized neocortical gliosis [26]. However, putative accurate biomarkers of epileptogenesis have not been validated in humans during the latent period, and prospective studies of anti-seizure drugs have failed to modify epileptogenesis after severe TBI or the resultant structural and functional deficits [9].

It is noteworthy that there have been no prospective comprehensive studies of the epileptogenic process starting immediately after human TBI, unlike recent animal studies on PTE [14, 7, 20, 12]. Since trauma is induced in the rats, it creates an easier model to identify potential biomarkers in the data that could lead to post-traumatic epilepsy, which several studies have found in either the EEG or MRI. Recent studies of continuous EEG (cEEG) in moderate-severe TBI demonstrate a high incidence of early seizures (25%) and interictal epileptiform activity (45-60%) [24, 25, 26]. The epileptiform activity begins within the first week after moderate-severe TBI and is associated with important physiologic changes in excitatory neurotransmitters [24, 26] and brain metabolism [25, 26]. The rate of early seizures is higher, over 60%, when depth EEG is used [26]. These EEG findings indicate early onset of epileptogenesis within the first week after TBI and suggest that EEG is an important and specific biomarker that can be used to identify those patients at high risk for PTE long before epilepsy is established. Human TBI is amendable to comprehensive study in the ICU using sophisticated disease biology research techniques, including phenotypic MRI imaging, cEEG and depth EEG, acute biomarker tracking, and long term cognitive follow up [11, 26].

2. Data.

Both scalp and depth EEG recordings were collected from patients at the University of California, Los Angeles (UCLA) with traumatic brain injuries. The standard 10-20 configuration was used for electrode placements. Data were collected on 9 females and 38 males who had sustained a TBI and were hospitalized between 1/2001 and 10/2011. Of these, 34 were white non-hispanic, 10 were white-Hispanic, 1 was Asian, 1 was Black, and 1 was mixed. Mean age was 36.9 years, with a range of 16-83. Glasgow Coma Scores showed a median of 7 with a range of 3-15. Mechanism of injury was fall in 13 cases, motor vehicle crash in 10, motorcycle crash in 7, auto vs pedestrian in 6, auto vs bicyclist in 4, blunt force in 4, and 3 others. Skull fracture was identified in 28 cases, with subdural hematoma in 30, extradural hematoma in 15, and diffuse axonal injury in 18. Urgent surgery was performed in 29 cases. Acute seizures were identified in 12 cases, elevated lactate/pyruvate ratios in 26, and elevated intracranial pressure in 20. Six months after discharge the Glasgow Outcome Scale - Extended scores showed a median of 5 and a range from 2 to 8; poor outcomes were evident in 28 cases and good outcomes in 13 cases, with 6 lost to follow-up. For our analysis, we focus on the 6 patients that had both scalp and depth EEG recordings.

3. Methods.

3.1. Principal components analysis.

One commonly used tool for neuroscience applications and EEG data, principal components analysis (PCA), is used for dimensionality reduction, in which the goal is to compute the most meaningful basis to re-express a large and noisy dataset. This new basis can reveal hidden patterns and structure in the data as well as remove the noise. An orthogonal linear transformation converts the data to a new coordinate system for more effective analysis. It is often a tool used for exploratory data analysis and for predictive models. The largest variance in the data is represented by the first coordinate or the first principal component [19]. A key difference between the algorithm that we propose in this paper and PCA is the use of nonlinear local analysis in the extension as opposed to PCA, which assumes the linear global information of the data. We perform PCA on temporally local regions of the EEG and then integrate the local information using a kernel and obtain a single model for all of the data. We use a data-driven adapted distance between windows of EEG to approximate the Euclidean distance between the features from the noisy EEG.

EEG data, including depth EEG, but particularly scalp EEG, are very noisy due to amplifier and impedance noise, technical artifacts (e.g., poor electrode location, electrode impedance, etc.), and physiological artifacts (e.g. eye movement), so we need to include steps in the algorithm that will ensure the highest level of extraction of the underlying brain activity from the noisy EEG.

3.2. Diffusion maps.

Diffusion mapping [4] is another method used to reduce the dimensionality of data and allow for pattern recognition and feature detection. Diffusion maps may detect special features in the data, so it can be used to identify abnormal EEG activity. Diffusion maps assume access to the process that they aim to classify. A recently developed algorithm based on diffusion maps assumes a stochastic mapping between the underlying processes and the measurements, so the mapping is inverted, and a kernel is used to recover the underlying activity [21, 23]. Thus it seems that this proposed algorithm is more appropriate than diffusion maps for our data. We have recently presented further improved results for noisy brain data using an adaptation of this algorithm [5]. That method, Unsupervised Diffusion Component Analysis, relies on the work by Talmon and Coifman [21] to extract the underlying brain structure from the MRI in both healthy individuals and patients with Alzheimer’s Disease. The algorithm is an extension of diffusion maps and uses local PCA. Our goal was to expand the use of this algorithm to different applications using data of various modalities. We have now modified Unsupervised Diffusion Component Analysis to be used for EEG data and identifying epileptogenic features. This is a more challenging application because of the amount of noise in such data and the subtleties of normal EEG activity, spikes, and epileptiform activity.

3.3. Unsupervised diffusion component analysis.

The EEG data are analyzed with either 3 or 4 electrode contacts (although more or fewer electrode contacts may be analyzed at one time) that are chosen based on highest spectral entropy and 5-second epochs, and these submatrices are overlapped by 50% for smoothing purposes and to account for the changes that occur temporally across different epochs. This overlapping is natural from the nonlinear assumptions in the approach [5]. These submatrices are then reshaped into vectors. Then these feature vectors are studied to analyze the slow variabilities and statistical changes over time that could help identify abnormal, epileptogenic activity and spikes in the data.

We analyze the data of each patient separately since each patient is expected to have epileptiform activity that cannot be generalized across all patients. For the set of feature vectors from one patient, we compute histograms using 20 bins to approximate the probability distributions, because the EEG data are assumed to be stochastic from various effects. We then calculate the Earth Mover’s Distance [17] rather than computing Euclidean distances between windows of data. This is a method to evaluate dissimilarity between multi-dimensional distributions in some feature space where a distance measure between single features is given. Using this method in our algorithm allows us to naturally extend the notion of a distance between elements to that of a distance between sets of elements, which is what we aim to do.

To reduce the chance of bias in the construction, we introduce a random shuffle in the columns of the matrix composed of feature vectors and apply a random projection as a method to reduce the large amount of data. Then we apply the Discrete Cosine Transform [22]. If the data are uncorrelated, we expect to obtain some approximation of a delta function with a spike at the origin after applying the Discrete Cosine Transform [5].

Given one of these feature vectors, S_y (m), we compute the empirical local covariance matrix Σ_mwithin a fixed interval, J,

$${\Sigma }_m=\frac{1}{J}{\displaystyle \sum _{m^{\prime }=m-J+1}^m({\mathbf{S}}_y(m^{\prime })-{\mu }_m){({\mathbf{S}}_y(m^{\prime })-{\mu }_m)}^T},$$ (1)

where μ_m is the empirical local mean of the feature vectors in the interval, and m describes the data that have been classified in cells by a histogram.

The dynamics of the controlling factors from the data are described by normalized independent Ito processes described in the stochastic differential equation below:

$$d{\theta }_i(t)=a_i({\theta }_i(t))dt+d{w}_i(t),$$ (2)

where i = 1, 2, …, d. (a1, …, a_d) in the above equation are (possibly nonlinear) unknown drift coefficients and w = (w₁, …, w_d) is a d—dimensional independent white noise. An n-dimensional process (Y(t), t ≥ 0) is the observation and a noisy measurement process Z arises as Z(t) = g(Y(t), V(t)), where V is a stationary noise process with unknown distribution.

We define a nonsymmetric distance known as the Mahalanobis distance using the covariance matrices, $a_{\Sigma }^2$, and a symmetric distance $d_{\Sigma }^2$. Mahalanobis distances between empirical distribution estimators (e.g., histogram vectors) are used to construct the affinity measure between segments in the series. Then anisotropic kernels are constructed and diffusion maps are applied to obtain a low-dimensional embedding, which uncovers the intrinsic representation. It has been shown in [4] that this distance approximates the Euclidean distance between the underlying factors in the data by local linearization of the nonlinear transformation. These distances, between points m and m′ in the dataset M, are defined as follows:

$$a_{\Sigma }^2(m,m^{\prime })={({\mathbf{S}}_y(m)-{\mathbf{S}}_y(m^{\prime }))}^T{\Sigma }_{m^{\prime }}^{-1}({\mathbf{S}}_y(m)-{\mathbf{S}}_y(m^{\prime })),$$ (3)

$$d_{\Sigma }^2(m,m^{\prime })=\frac{1}{2}(a_{\Sigma }^2({\mathbf{S}}_y(m),{\mathbf{S}}_y(m^{\prime }))+a_{\Sigma }^2({\mathbf{S}}_y(m^{\prime }),{\mathbf{S}}_y(m))).$$ (4)

We are able to recover these underlying factors using an eigendecomposition of an appropriate Laplace operator (kernel). A kernel is used to compare the underlying factors, and e is the kernel scale set according to the Mahalanobis distance. This kernel is used to define the local geometries of the graph between m and m′ from the dataset M.

We construct an NxN nonsymmetric affinity matrix A, whose (m, m′) element is given by

$$A^{m,m^{\prime }}=exp-\frac{a_{\Sigma }^2({\mathbf{S}}_y(m),{\mathbf{S}}_y(m^{\prime }))}{ϵ}$$ (5)

where ϵ > 0 is the kernel scale that is calculated by taking the median of all pairwise distances of the original data matrix.

The matrix formed from the elements with the above exponential converges to a low dimensional manifold and the eigenvectors parametrize the underlying structures in the data.

The kernel is normalized by a diagonal density matrix, which enables us to consider the sampling as uniform. The normalized matrix can be viewed as a Markov transition probability matrix for a jump process over the measurements. We then define an NxN symmetric matrix W as

$$W^{m,m^{\prime }}={\displaystyle \sum _{r\in R}{A}^{m,r}{A}^{m^{\prime },r}}.$$ (6)

Then an eigendecomposition is performed to address the nonuniform sampling of the data. The ℓ eigenvectors found from the eigendecomposition corresponding to the few largest eigenvalues provide a parametrization of the features, allowing for significant data dimensionality reduction and capturing the features that may be predictors of epileptogenesis after TBI.

$${\mathbf{S}}_y(m)\mapsto {[{\psi }_1(m),{\psi }_2(m),\mathrm{\dots },{\psi }_{\ell }(m)]}^T,$$ (7)

where ψ_i(m) is the i^th eigenvector. To determine which eigenvectors to use, we pick the optimal eigenvector embedding with a computable, reproducible criterion instead of visual inspection. All possible combinations of 3 or 4 eigenvectors are considered (not related to the choice of electrode channels). We compute the center of mass of the new embedded points. Then to choose which embedding provides the best separation of spikes and epileptiform activity, we calculate the variance of all points in the embedding to that center of mass. The eigenvectors and corresponding eigenvalues that produce the embedding with the largest spread and highest variability in embedded points is chosen to be the best embedding to identify abnormal, epileptiform EEG activity and spikes.

The details are summarized in the following table with algorithmic listing.

Algorithm
1:	Obtain EEG data of patient post TBI with n electrode contacts,
2:	Create m-second windows of data, overlapping by 50%,
3:	Reshape each small submatrix into a vector; place each vector side by side to form a matrix,
4:	Compute histograms (along matrix columns) using 20 bins,
5:	Calculate the Earth Mover’s Distance between consecutive feature vectors,
6:	To reduce the chance of bias, introduce a random shuffle in the columns of the matrix and apply a random projection,
7:	Apply the Discrete Cosine Transform,
8:	Calculate local covariance matrices for overlapping windows,
9:	Compute the eigenvalue decomposition to obtain eigenvalues and corresponding eigenvectors,
10:	Calculate inverse covariance matrices to calculate the Mahalanobis Distance,
11:	Use the median of all pairwise distances of the data matrix to choose epsilon, the Gaussian kernel scale,
12:	Compute the affinity matrix and build a Gaussian kernel according to (5),
13:	Normalize the kernel by a diagonal density matrix and employ eigenvalue decomposition to obtain the eigenvalues and eigenvectors,
14:	Consider all possible combinations of 3 or 4 eigenvectors for the embeddings; compute the center of mass for each embedding as well as the variance of the embedded points to determine the optimal embedding as the one with the largest spread among the embedded points.

4. Results.

We present a recently developed algorithm that we modify for EEG data to detect spikes that may be indicators of epileptogenesis after TBI. The challenge is to develop a robust tool to identify slow variabilities and subtle temporal changes in the underlying brain activity depicted in the EEG.

Figure 1 shows an example of raw EEG data containing abnormal spike activity at two time points. Figure 2 is the corresponding embedding using Unsupervised Diffusion Component Analysis where eigenvectors 2, 3, and 5 were found to provide the most variability among embedded points, so this embedding was chosen as the best of any combination of eigenvectors at accentuating the abnormal brain activity that may be used to predict epileptogenesis.

Figure 1.

Raw EEG data showing epileptiform spike activity at two time points

Figure 2.

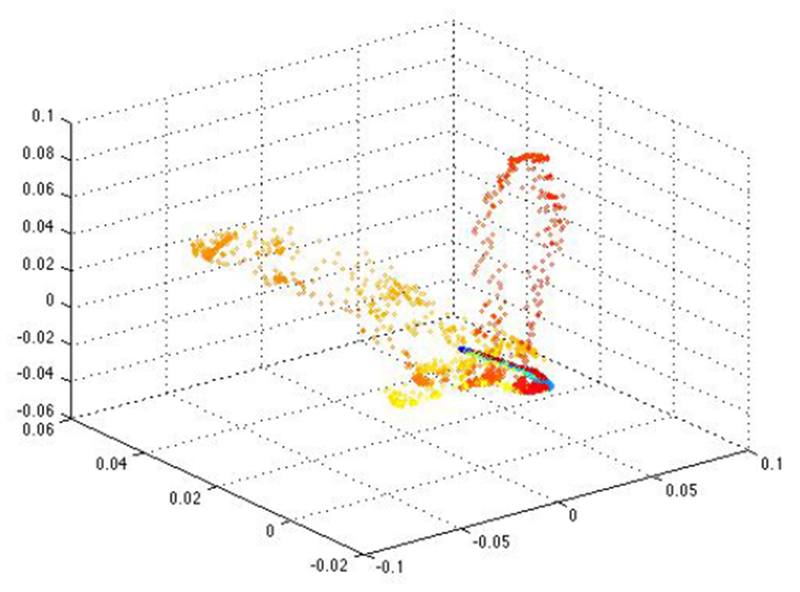
The corresponding embedding using Unsupervised Diffusion Component Analysis and eigenvectors 2, 3, and 5

Figure 3 shows the raw EEG data from four electrode contacts from another patient. We can see epileptiform activity at one time point and expect to see separation of the corresponding points in the embedding. Figure 4 is the corresponding embedding, and we can see that the yellow/orange points that correspond to the epileptogenic activity in the EEG is more variable and separated from the other points. It is interesting to note that we begin to see separation at an earlier time-point in the embedding than by looking at the raw data, so this could be an indicator of a useful tool for a predictive model of epileptogenesis after TBI.

Figure 3.

An example of raw EEG data from 4 electrode contacts from 1 patient with epileptiform activity at one time point

Figure 4.

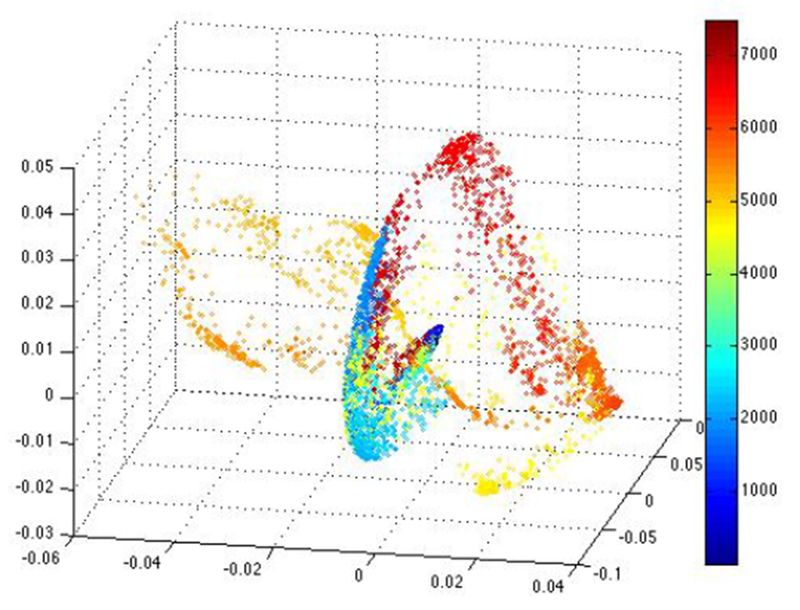
The corresponding embedding using Unsupervised Diffusion Component Analysis (color represents time), and the yellow/orange points are separated from the other embedded points

Figure 5 is the raw EEG data from three electrodes from another patient. Here it is unclear if the spike in the raw data is considered normal or epileptogenic. Figure 6 is the corresponding embedding. The teal/light blue points in the embedding separate some subtle epileptogenic activity in the EEG.

Figure 5.

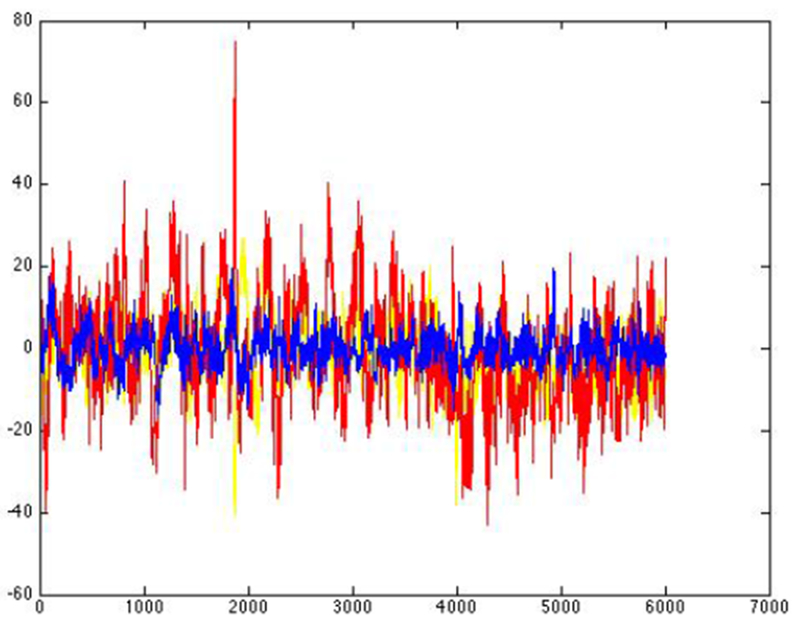
An example of EEG data from 3 electrode contacts from another patient with more subtle spikes that are not clear from examining the raw data

Figure 6.

The corresponding embedding using Unsupervised Diffusion Component Analysis

In comparison to these examples of epileptiform activity, Figure 7 shows the raw EEG data of normal spikes that are not considered epileptiform activity and the corresponding embedding using Unsupervised Diffusion Component Analysis in Figure 8. The points in the embedding tend to be a cloud of points scattered around the origin for all cases of “normal” EEG that we analyzed.

Figure 7.

An example of raw EEG data from 3 electrode contacts from 1 patient with no epileptiform activity

Figure 8.

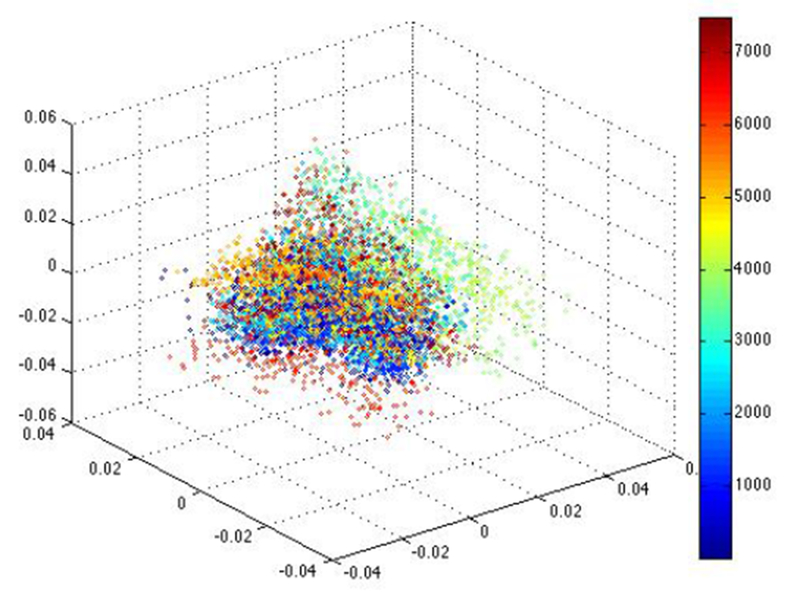
The corresponding embedding using Unsupervised Diffusion Component Analysis

5. Discussion.

This nonlinear and local network approach has been used to determine if the early occurrences of specific electrical features of epileptogenesis, such as interictal epileptiform activity and morphologic changes in spikes and seizures, during the initial week after TBI predict the development of PTE. The extensions lead to efficiency in use, in terms of reduced computational complexity, which have the potential to become useful techniques for practitioners in the field. Furthermore, the algorithm is completely automatic and unsupervised, which could potentially be a user-friendly and easy to use tool for doctors to identify early features of epileptogenesis after trauma. This method is also adapted to the data to enable the extraction of any underlying abnormal brain activity. The last step of choosing the embedding with the largest variability in embedded points did not always yield the embedding that we would have chosen by examining the embedding visually, so we plan to improve this step of the algorithm.

A method similar to the one proposed in this paper has already proved to be effective in identifying preseizure states in intracranial EEG data by providing a distinction between interictal (period between seizures) and preseizure states of a patient with epilepsy [6], and Unsupervised Diffusion Component Analysis has been successful in distinguishing Alzheimer’s disease and healthy brains using MRI data [5].

Unsupervised Diffusion Component Analysis combines diffusion maps and PCA with other techniques. The extensions lead to efficiency in use in terms of reduced computational complexity. The key difference between this method and others used for classification problems is the nonlinear and local network approach, which overcomes calibration differences and noisy data. Additionally, the algorithm is completely automatic and unsupervised.

6. Conclusions.

Unsupervised Diffusion Component Analysis has previously only been used on MRI data. In this paper, we adapt this algorithm to noisy EEG data and for the purpose of detecting atypical electrical activity in the brain after a TBI that may indicate the development of seizures. We were able to see unusual epileptiform activity that was not clear in the raw EEG data after TBI and before seizures across all six patients studied, providing promising results that could lead to a reliable predictor of the development of PTE. Our method was found to be very sensitive to distinguishing epileptiform activity leading to PTE and normal spiking activity in the EEG.

Future work will include statistical testing of the accuracy of the spikes that our algorithm identifies in predicting seizures. We plan to develop this into a robust tool that can predict epileptogenesis after TBI. To quantify the spike detection, we plan to set a threshold and calculate the Euclidean distance of points in the embeddings from the origin of the embeddings. We also plan to improve the algorithm to work as well on the noisier scalp EEG data as on the depth EEG data. If this tool can be used to accurately identify biomarkers of epileptogenesis after TBI, antiepileptogenic treatments can be used early on in an effort to prevent seizures from occurring in patients, which could have a truly significant positive impact on TBI patients.