Proton Relative Biological Effectiveness – Uncertainties and Opportunities

Abstract

Proton therapy treatments are prescribed using a biological effectiveness relative to photon therapy of 1.1, that is, proton beams are considered to be 10% more biologically effective. Debate is ongoing as to whether this practice needs to be revised. This short review summarizes current knowledge on relative biological effectiveness variations and uncertainties in vitro and in vivo. Clinical relevance is discussed and strategies toward biologically guided treatment planning are presented.

Introduction

Energy deposition events caused by radiation interactions with tissues can damage biological structures. While apoptosis or programmed cell death may also be initiated by damage to the cell membrane, for most cell types damage to the DNA molecules is decisive for mutation induction and killing. The type and spatial distribution of DNA damage and the properties of cell repair mechanisms determine the resulting biological effect.

The energy deposition pattern of a given radiation is determined by the particle's track structure. It is defined as a track core causing interactions of the primary particle and a surrounding halo generated by δ-electrons. Radiation of different linear energy transfer (LET) differs in track structure, which affects the type of damage and the capacity of the cell to repair it [1–3]. Clusters of strand breaks that are more concentrated in space and the associated damage is less likely to be repaired correctly [4–6]. For instance, even if photons and protons would cause the same number of DNA double-strand breaks per unit dose, their distribution may differ. In addition to differences in track structure for single tracks, the energy deposited per incident proton is significantly higher than the energy deposited per incident photon. For the same dose, the number of protons crossing a region of interest is typically lower than the corresponding number of photons. This further causes energy depositions in a cellular structure to be more heterogeneous for proton radiation compared with photon radiation [7].

Radiation therapy treatments are prescribed based on absorbed dose. Therefore, in order to account for differences in energy deposition patterns, a scaling parameter is needed when comparing different modalities such as photons and protons for the same physical absorbed dose. The proton relative biological effectiveness (RBE) is the ratio of the absorbed doses that produce the same biological effect between a reference radiation and a proton irradiation equation 1).

In addition to LET, the proton RBE varies with dose and the biological endpoint (as well as the intrinsic radiosensitivity of the tissue). Doses in proton therapy are prescribed as Gy(RBE) to reflect that the dose was multiplied with an RBE value [8]. The RBE is typically defined for a region of uniform absorbed dose. In a patient, variable RBE values would have to be assigned on a computer tomography voxel by voxel basis. Organ effect modeling would then be based on the RBE-weighted dose distribution. In the clinical use of RBE, fractionation effects are typically not considered in the RBE concept, that is, the RBE is considered for the dose per fraction [9, 10].

Cell survival curves measured in vitro are typically described using the linear quadratic dose-response curve with parameters α and β. Accordingly, one can deduce a relationship of RBE with the α_x and β_x values for the reference photon radiation, the α_p and β_p of the proton radiation, and the proton dose per fraction (D_p). Assuming α_p and β_p, depending on the dose-averaged LET (LET_d), this leads to equation 2.

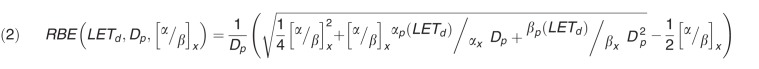Because the RBE depends on the photon reference radiation, the reference has to be stated when reporting RBE values. Clinically, one is interested in the RBE relative to 6-MV photons. However, cell experiments are often based on lower energy photons requiring RBE adjustment to account for differences among photon radiations.

Use of 1.1 as a Generic RBE in Proton Therapy

Because there is no simple relationship between dose and clinical endpoint, clinical prescription doses and dose constraints are assigned mostly empirically. For consistency and to benefit from the large pool of clinical results obtained with photon beams, prescription doses are defined as photon doses. Proton therapy tumor prescriptions and organ constraints are based on physical dose times a generic constant RBE of 1.1. This value is based on in vivo measurements relative to ⁶⁰Co reference radiation that were performed in the early days of proton therapy (eg [11–14]). It was initially reported for the center of the target volume, a 2 Gy(RBE) fraction size, and averaged over various endpoints, such as skin reaction or median lethal dose. Based on a more recent analysis of all published cell survival data in vitro, the estimated average RBE is about 1.15 in the center of a typical spread-out Bragg peak (SOBP) at 2 Gy(RBE) per fraction [15, 16]. Because one aims at a conservative RBE definition for tumor control, this is in line with the clinical use of 1.1.

RBE Variations in Laboratory Experiments

RBE Dependency on LET

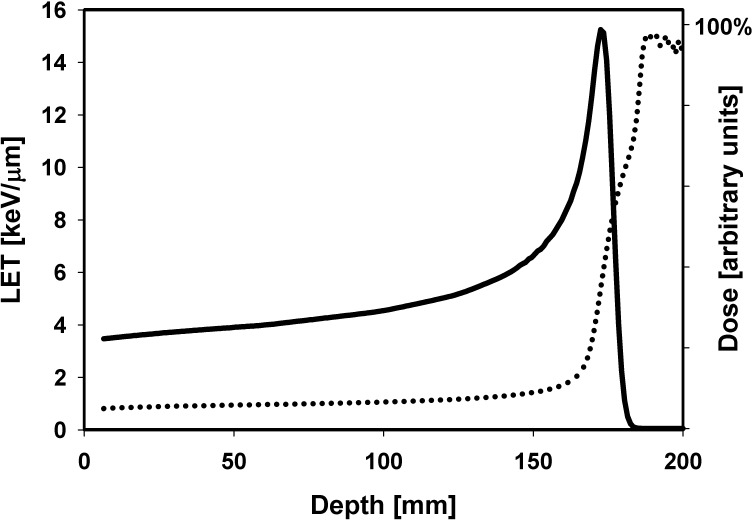
The slowing down of protons causes an LET increase resulting in an increasing RBE with depth in a pristine Bragg curve or SOBP (see, eg, [17–19]). The region of maximum LET is not at the Bragg peak position but downstream (Figure 1). The LET is a macroscopic dosimetric parameter and does not describe energy deposition in a biological target but, rather, the energy deposition per path length of a particle. Nevertheless, the use of LET to describe local energy depositions is a valid approximation for proton beams where the number of particle tracks crossing a subcellular structure is quite large [20].

Figure 1.

Dose (solid line; right axis scale) and dose-averaged LET (dotted line; left axis scale) as a function of depth in a water phantom for a 160 MeV beam. Abbreviation: LET, linear energy transfer.

For protons and heavier ions, the RBE increases with increasing LET up to a maximum and then decreases [21]. For protons, the maximum RBE occurs at very low proton energies that are dosimetrically negligible. Thus, one can safely assume that RBE increases with LET, with the slope depending on the biological endpoint.

When specifying RBE, one needs to consider the LET relative to the LET of the photon reference radiation. For instance, the LET caused by electrons of a ⁶⁰Co photon beam is ∼ 0.3 keV/μm [22]. Relative to this photon value_, the LET_d values in the entrance region of an SOBP up to the center of the SOBP are typically between 0 and 3 keV/μm; in the downstream half of an SOBP they are between 3 and 6 keV/μm, in distal edge region between 6 and 9 keV/μm, and in the dose fall-off region between 9 and 15 keV/μm. The LET_d in the central region of an SOBP is thus typically between ∼2 and ∼3 keV/μm.

Based on these typical LET_d values in an SOBP and based on the average of cell survival results obtained in vitro, the RBE for 2 Gy does increase with depth from ∼1.1 in the entrance region to ∼1.15 in the center, ∼1.35 at the distal edge, and ∼1.7 in the distal fall-off [16]. The rise in LET and RBE also results in an extension of the biologically effective range by 1 to 2 mm (see, eg, [19, 23–26]).

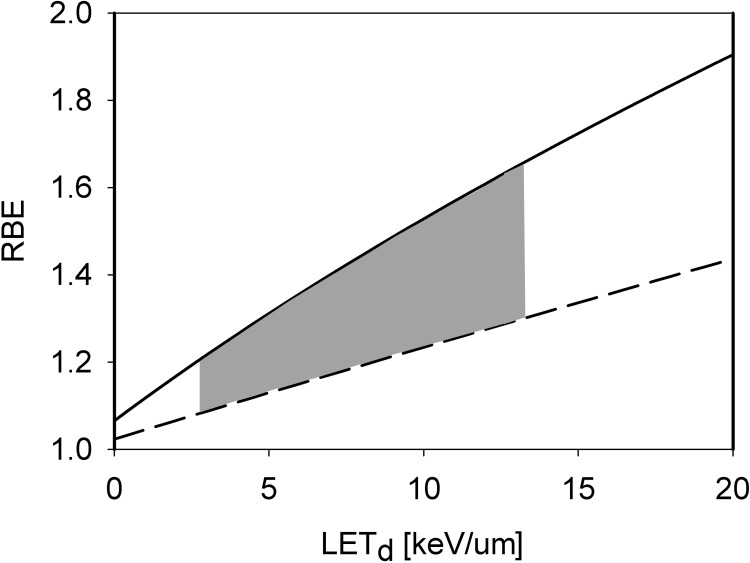
Phenomenologic models based on measured in vitro cell survival data predict a more or less linear relationship between RBE and LET_d (see Figure 2) [27]. The RBE also depends on the tissue (eg, the (α/β)_x) and models predict a steeper slope as (α/β)_x decreases. There is some evidence that the relationship becomes nonlinear at high LET values, with an increasing slope in RBE [28, 29].

Figure 2.

Proton RBE for clonogenic cell survival as a function of LET_d at 2 Gy photon dose for tissue (α/β)_x of 2 Gy (solid) and 10 Gy (dashed) as predicted by an empirical model [27]. The grey area shows the clinically and dosimetrically most relevant region as LET values are typically between 2.5 and 13 keV/μm [16]. Abbreviations: LET, linear energy transfer; LET_d, dose-averaged LET; RBE, relative biological effectiveness.

RBE Dependency on Dose

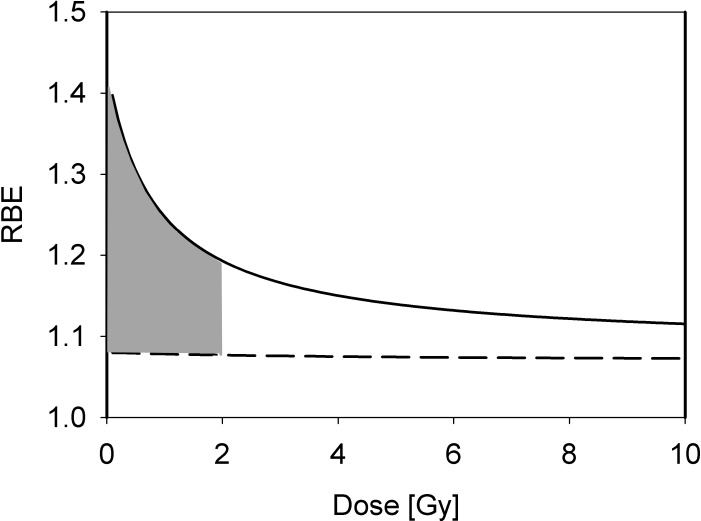
Due to the more pronounced shoulder in the photon dose response curve for cell survival compared with the proton dose response curve, the RBE increases with decreasing dose for cell survival [15, 16]. This trend is more pronounced for late-responding tissues (low α/β) compared with early responding tissues (high α/β) [19, 30–33]. Figure 3 shows the RBE as a function of dose for clonogenic cell survival in vitro as predicted by a phenomenologic model.

Figure 3.

Proton RBE for clonogenic cell survival as a function of dose for an LET_d of 2.5 keV/μm for tissue (α/β)_x of 2 Gy (solid) and 10 Gy (dashed) as predicted by an empirical model [27]. The grey area shows the clinically most relevant region for standard fractionation with doses at 2 Gy and doses to organs at risk <2Gy. Abbreviations: LET_d, dose-averaged linear energy transfer; RBE, relative biological effectiveness.

Experimental data on dose dependency of the RBE for clinically relevant doses are limited. Most in vitro studies do not report detailed cell survival data below 2 Gy. Furthermore, most experimental RBE studies in vivo have used large doses for which an RBE effect may be expected to be small.

RBE Dependency on Endpoint

Most in vitro experiments study cell survival, that is, colony formation. Furthermore, they have predominantly used CHO and V79 hamster cells, which exhibit large shoulders on their photon dose response curve, that is, low α/β. In studies with low energy beams, the data on human cells [34, 35] are significantly lower than the RBE values determined for hamster cells [36–41]. In contrast, most in vivo studies have used early reacting tissues having a high α/β. Also, the in vivo response reflects the more complex expression of radiation damage to 3-dimensional tissue systems and biological processes.

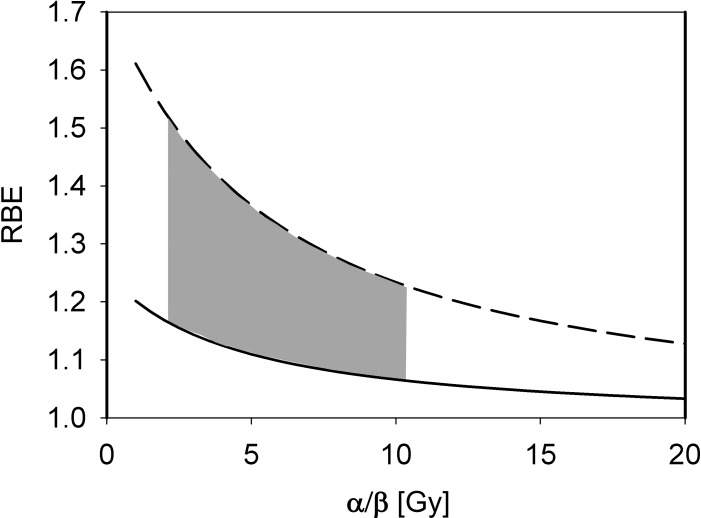
From the linear-quadratic model one expects a higher RBE for low (α/β)_x [26]. Studies have indicated that the increase of RBE with decreasing (α/β)_x is significant only at low (α/β)_x values (<∼5 Gy) [30, 42]. One would also expect the slope to be bigger for high LET_d values, which was not shown in a compilation of experimental data due to uncertainties in the experiments [16]. Figure 4 shows RBE values as a function of the tissues' (α/β)_x based on a phenomenologic model.

Figure 4.

Proton RBE for clonogenic cell survival as a function of (α/β)_x for a photon dose of 2 Gy and LET_d values of 2 keV/μm (solid) and 10 keV/μm (dashed) as predicted by an empirical model [27]. The grey area shows the clinically most relevant region as treatment planning considerations are typically based on (α/β)_x between 3 and 10 Gy. Abbreviations: LET_d, dose-averaged linear energy transfer; RBE, relative biological effectiveness.

Various RBE values for endpoints other than cell survival have been measured in vitro, for example, induction of reactive oxygen species leading to oxidative stress, which regulates a variety of response pathways, DNA single or double-strand breaks, foci formation, repair proteins, gene expression, chromosome aberrations, mutations, micronuclei formation, apoptosis, and cell cycle effects (see eg, [43–46]). The majority of data support an average RBE of ∼1.1. In vivo, the magnitude of RBE variation with physical or biological parameters is usually small relative to our abilities to determine RBE values. The required number of animals to measure a 5% RBE difference can be several hundred [15].

RBE Variations in Patients

RBE Dependency on LET

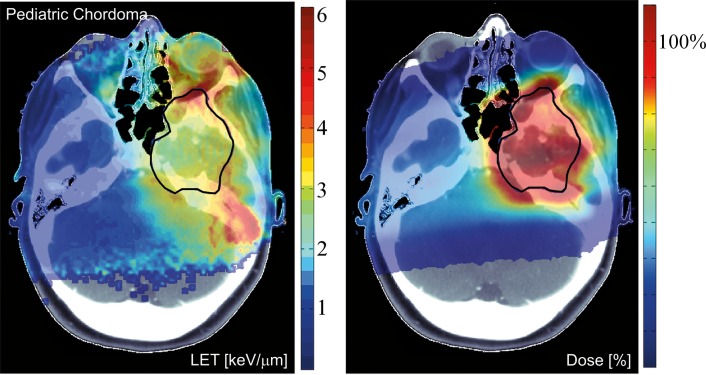
In patients, the increasing LET_d, (and RBE) with increasing depth is of concern for critical structures immediately downstream of the target area, particularly if single-field uniform dose (SOBP) fields are being delivered. It potentially causes an underestimation of the RBE-weighted dose. For multiple fields, and particularly in intensity-modulated proton therapy (IMPT) delivering inhomogeneous dose distributions per field, the LET distribution can be more inhomogeneous, although maximum values would still be mostly in the periphery of the target [47, 48]. Figure 5 illustrates the distributions of dose and LET_d in a patient. LET_d values in patients can typically be >10 keV/um in the distal fall-off, but only between 1.5 and 4 keV/um in the target for typical beam arrangements [48]. Due to margins added in treatment planning, high LET regions may extend well into normal tissues.

Figure 5.

Dose distribution and distribution of LET_d for an intensity-modulated proton therapy treatment plan. The contour for the clinical target volume is shown in black. Left: LET_d distribution in keV/μm. The LET distribution is a potential measure of biological effectiveness. Right: dose in percent of the prescribed dose. The figure uses dose and LET cut-offs at <0.1% of the maximum, respectively. See reference [48] for more details. Abbreviations: LET, linear energy transfer; LET_d, dose-averaged LET.

The clinical evidence that the use of 1.1 causes unexpected rates of toxicities in high LET regions is weak, perhaps due to interpatient variability and other cofounding factors. Even so, it seems clear from in vitro data that if regions of high LET_d are within organs at risk with a low (α/β)_x we most likely underestimate the RBE. Treatment planners have to keep potential RBE effects in mind. One example is the brainstem, which sometimes is located at the end of range of an SOBP field in patients with an ependymoma [49–52].

The clinical significance of RBE variability may become more apparent as other sources of uncertainty are reduced, leading to a reduction in margins, which in turn might expose RBE variations [26, 53]. Furthermore, the increasing use of IMPT could lead to variations in RBE as a function of delivery and/or planning parameters [48, 54–56].

RBE Dependency on Dose

An increase of RBE as dose decreases suggests higher RBE values in organs at risk compared with the target. Furthermore, it implies that hypofractionated regimens will result in lower RBE values [57]. Several theoretical studies have addressed the issue of RBE spatial variations in patients [57–59] and have analyzed the impact of RBE on fractionation [10, 60, 61].

RBE Dependency on Endpoint

In vitro data on cell survival suggest a tendency toward an increased RBE in cells with smaller (α/β)_x. Thus, in vivo, one might expect the biggest variation in RBE for late-responding normal tissues [62]. While most tumors types might on average show higher RBE values, there are also tumors with high (α/β)_x which would imply lower RBE values. It has been speculated that medulloblastoma, a tumor with a high (α/β)_x, could be underdosed when using protons because of an RBE below 1.1 [63–65]. However, when analyzing patients treated with protons no indication was found that the RBE was overestimated [65]. The trend with (α/β)_x does suggest an advantage of proton therapy when treating, for example, prostate carcinoma, which are expected to show low (α/β)_x [66]. For normal tissue toxicities, this trend might suggest an increased risk for low (α/β)_x tissues like the spinal cord that often have to be partially irradiated in order to achieve sufficient tumor coverage. For tumors and toxicities, the impact of (α/β)_x could affect the interpretation of clinical trials comparing photon and proton treatments.

We have not clearly identified toxicities or recurrences that were definitively a result of RBE effects [49, 65, 67]. However, it is difficult to assess RBE effects in patients because of patient variability in tissue radiosensitivity [68, 69].

A subset of human cancers may have defects in DNA repair pathways that influence the RBE. For example, homologous recombination is required for the repair of DSBs in late S- and G2-phases of the cell cycle. It has been shown that defective homologous recombination increases the RBE for cell survival [44, 68, 70–72]. There are research efforts toward identifying biomarkers to identify patients with RBE values either low or high compared with the overall patient population [44, 68, 70].

Tumor Control Probability

While cell survival might be a valid surrogate for tumor control, there are various pathways leading to cell death or to tumor regression. In terms of tumor control probability (TCP), clinically more relevant than cell survival studies might be measurements of tumor control dose 50% (the dose for 50% local control) using human tumor cells that have been implanted in immune-deficient animals. Studies on tumor growth delay in mice as well as recurrence of mouse mammary carcinoma found RBE values between 1.0 and 1.2 at doses >20 Gy [73–75].

In some TCP models radiosensitivity is parameterized with cell kill parameters. When analyzing the impact of (α/β)_x on TCP, one needs to consider that not only the RBE but also the TCP depends on (α/β)_x [69]. Assuming interpatient variability in linear-quadratic radiosensitivity parameters for a given tumor type, one might expect a lower TCP for patients with low average (α/β)_x. In proton therapy compared with photon therapy, the magnitude of such TCP variations in patients is potentially reduced because it is, in part, compensated by an increase in RBE as (α/β)_x decreases.

Normal Tissue Complication Probability

Considering typically lower (α/β)_x of healthy tissue for cell survival, as well as lower doses than in the target, one might expect larger RBE values for normal tissue. However, endpoints other than cell survival are presumably more relevant for most normal tissue complication probabilities (NTCP). Organ-specific effects of interest are early effects, such as erythema, and late effects, such as lung fibrosis, brain necrosis, or spinal cord injury. The relationship between cell kill and normal tissue effects is complex [46]. For instance, no relation has been found between fibroblast radiosensitivity and the development of late normal tissue effects such as fibrosis [76, 77].

Many endpoints have been studied in animal models, such as skin reactions or organ weight loss. The variety of endpoints does not allow a comprehensive analysis toward a clinical RBE for NTCP considerations. Organ effects are dependent on the dose distribution, and the mean dose is not necessarily a valid approximation. Thus, deducing RBE values for organs at risk based on clinical data is only meaningful if data analysis is done on a voxel-by-voxel basis because proton dose distributions in critical structures are typically more heterogeneous compared with photon therapy.

When considering NTCP models that parameterize radiosensitivity with (α/β)_x, patients with a lower (α/β)_x are predicted to have a lower complication probability, which is counteracted by an increase in RBE as (α/β)_x decreases. Consequently, toxicities in proton therapy would be more affected by variations in (α/β)_x compared with photon therapy [69]. While this does not imply an overall higher risk for side effects from proton therapy, it does suggest wider distribution of the severity of toxicities.

Modeling Cellular Radiation Effects

Modeling radiation action mechanistically is challenging because the radiation field can be complex—with primary and secondary particles—and because the biological target is highly structured. Most models are mechanistic when considering the underlying physics but take a phenomenologic approach toward biology.

For example, track structure models [78] are based on the physical details of a particle track, including its secondary particles. They ignore the actual mechanisms of damage initiation and repair. The key assumption is that the difference in biological efficacy, when comparing photons with protons, is caused by different microscopic dose deposition patterns. Other models consider radiation damage and repair more explicitly and are thus capable of describing a range of endpoints (eg, DNA repair, genetic aberration, and cellular survival) by incorporating the kinetics of different DNA repair processes, the spatial distribution of double-strand breaks and the resulting probability and severity of misrepair [79, 80].

In contrast to these more complex approaches, simple LET-based models, while entirely phenomenologic, can be a valuable approximation because they can be based on few parameters. LET-based models follow the linear-quadratic dose-response curve and parameterize the change in α and β with dose-averaged LET_d relative to the reference radiation according to Table 1.

Table 1.

Functional form and parameters of the most common linear energy transfer (LET)–based models to estimate relative biological effectiveness. Each model was fitted to a subset of available experimental data from the literature. The largest data set was used by McNamara et al [27].

Parameters
ϕ	ψ	A1	A2	B1	B2	Reference
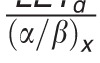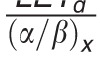		0.843	0.413644 Gy / (keV/μm)	1.09	0.01612 Gy / (keV/μm)	[26]
LETd	1	0.01 / αx, Gy−1	0.02 / αx Gy−1, (keV/μm)−1	1	0	[81]
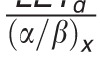	1	1	0.434 Gy / (keV/μm)	1	0	[82]
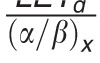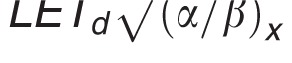		0.99064	0.35605 Gy / (keV/μm)	1.1012	–0.00387 Gy-1/2 / (keV/μm)	[27]

Equation for α_p: .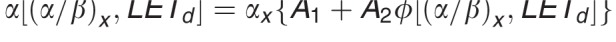

Equation for β_p: .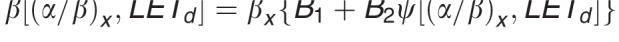

Biological Optimization

Due to the uncertainties in RBE, treatment plan optimization based on RBE models is currently not feasible with clinically acceptable accuracy [57, 83]. RBE variations are thus only taken into account intuitively (for instance by avoiding certain beam angles), but not quantitatively, during the planning process. The use of robust planning techniques has been suggested to consider RBE uncertainties [84, 85].

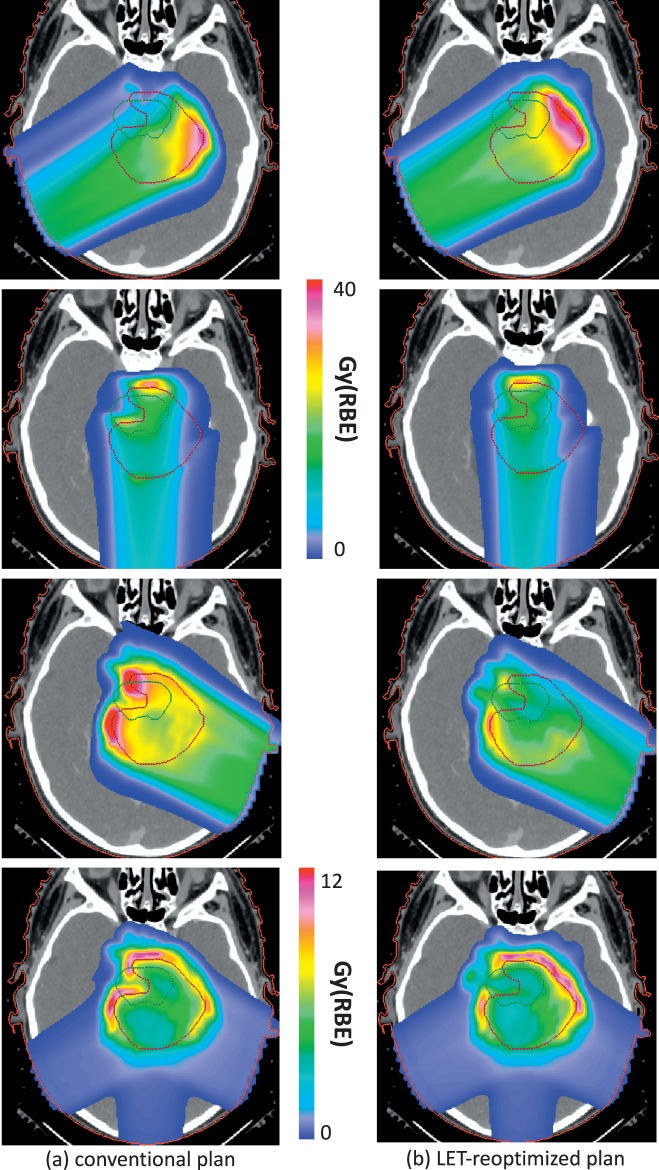
Even though RBE values are currently associated with large uncertainties, biological treatment optimization can be achieved. Algorithms have already been developed in the research setting or implemented in research versions of treatment planning systems. Because for a given dose and (α/β)_x, the RBE increases steadily with LET_d, the changes of the latter can be used as a surrogate for RBE changes. Interestingly, LET distributions can be influenced in IMPT without significantly altering the dose constraints, that is, dosimetrically equivalent plans can show differences in LET distributions (Figure 6) [48, 84, 86]. This can be utilized to increase the efficacy of proton therapy, thus turning the disadvantage of variable RBE values into a clinical opportunity. It allows biological dose optimization despite uncertainties in RBE values.

Figure 6.

Two intensity-modulated proton therapy plans for a patient with an ependymoma in whom the target volume involves parts of the brainstem. The patient was treated with 3 posterior oblique beams. The left panel shows the 3 fields as prescribed by the planning system (created based on a 2 mm clinical target volume to planning target volume expansion). The right panel shows the 3 fields as prescribed based on LET optimization obtained after minimizing (LET_d × dose × empirical constant (0.04 μm/keV)) in the brainstem while constraining the dose distribution to remain close to the conventional plan. The fourth row shows LET_d × dose × empirical constant (0.04 μm/keV) for all 3 fields clearly illustrating the reduction in biological effect in the brainstem. See reference [84] for more details. Abbreviation: LET_d, dose-averaged linear energy transfer.

The LET-based planning concept was demonstrated in a multicriteria optimization framework [47]. Significant differences in LET_d distributions were observed in different base plans, in particular for organs at risk, while preserving target coverage. Subsequently, optimization using a parameter proportional to (LET_d × dose) was proposed [87]. This parameter can, to first approximation, be interpreted as a measure of the biological extra dose that is caused by an elevated LET. From a mathematical perspective, (LET_d × dose) has the advantage that it is a linear function of pencil beam fluence. Therefore, the same optimization algorithms that are well established for physical dose optimization can be applied.

Summary and Conclusion

Experimental data in vivo and in vitro as well as biophysical models show clear trends in RBE as a function of physical and biological parameters. Nevertheless, other than assuming a 10% difference in required prescription doses and dose constraints, the biological difference between proton and photon therapy is not considered quantitatively in treatment planning. Treatment planning based on variable RBE values is not done clinically because of significant uncertainties, particularly for normal tissues. While the value of 1.1 is appropriate if a generic RBE is being applied, the proton therapy community will for sure move toward variable RBE values in the future after more research has been done. Ideally, this research would include in vivo experiments on normal tissue toxicities.

While RBE uncertainties might impact the efficacy of proton therapy and the interpretation of trials, RBE variations also offer an opportunity. It is important to identify biomarkers recognizing patients with RBE values either low or high compared with the general patient population for either tumor or normal tissue. Furthermore, biological optimization based on LET can lead to a decrease in patient-specific RBE values for organs at risk despite patient specific RBE uncertainties.