CUSTOMIZED TRAINING WITH AN APPLICATION TO MASS SPECTROMETRIC IMAGING OF CANCER TISSUE

Abstract

We introduce a simple, interpretable strategy for making predictions on test data when the features of the test data are available at the time of model fitting. Our proposal—customized training—clusters the data to find training points close to each test point and then fits an ℓ₁-regularized model (lasso) separately in each training cluster. This approach combines the local adaptivity of k-nearest neighbors with the interpretability of the lasso. Although we use the lasso for the model fitting, any supervised learning method can be applied to the customized training sets. We apply the method to a mass-spectrometric imaging data set from an ongoing collaboration in gastric cancer detection which demonstrates the power and interpretability of the technique. Our idea is simple but potentially useful in situations where the data have some underlying structure.

1. Introduction.

Recent advances in the field of personalized medicine have demonstrated the potential for improved patient outcomes through tailoring medical treatment to the characteristics of the patient [Hamburg and Collins (2010)]. While these characteristics most often come from genetic data, there exist other molecular data on which to distinguish patients. In this paper we propose customized training, a very general, simple and interpretable technique for local regression and classification on large amounts of data in high dimension. The method can be applied to any supervised learning or transductive learning task, and it demonstrates value in applications to real-life data sets.

This paper is motivated by a newly proposed medical technique for inspecting the edge of surgically resected tissue for the presence of gastric cancer [Eberlin et al. (2014)]. Gastric is the second most lethal form of cancer, behind lung cancer [World Health Organization (2013)], and the state-of-the-art treatment for gastric cancer is surgery to remove the malignant tissue. With this surgical procedure, removal of all diseased tissue is critical to the prognosis for the patient post-surgery. The new medical technique uses mass spectrometric imaging, rather than visual inspection by a pathologist, to more quickly and more accurately evaluate the surgical margin of the tissue for the presence of cancerous cells. This new technique replaces the procedure wherein the tissue samples are frozen until the pathologist is available to manually label the tissue as cancer or normal (see Figure 1).

Fig. 1.

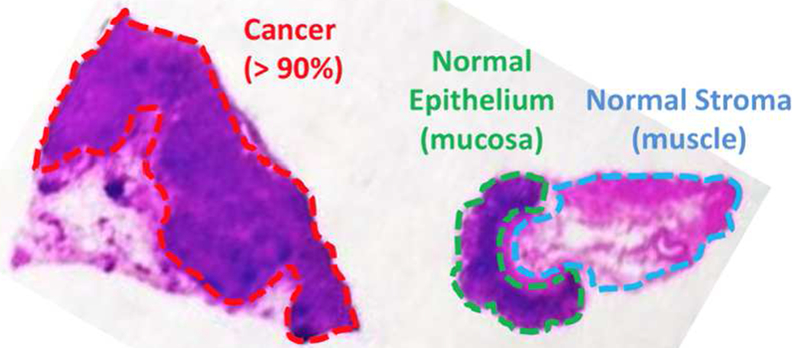
Histopathological assessment of a banked tissue example. This hematoxylin and eosin stain has been hand-labeled by a pathologist, marking three regions: gastric adenocarcinoma (cancer), epithelium (normal) and stroma (normal).

The data are images of surgical tissue from a desorption electrospray ionization (DESI) mass spectrometer, which records the abundance of ions at 13,320 mass-to-charge values at each of hundreds of pixels. Hence, each data observation is a mass spectrum for a pixel, as illustrated in Figure 2.

Fig. 2.

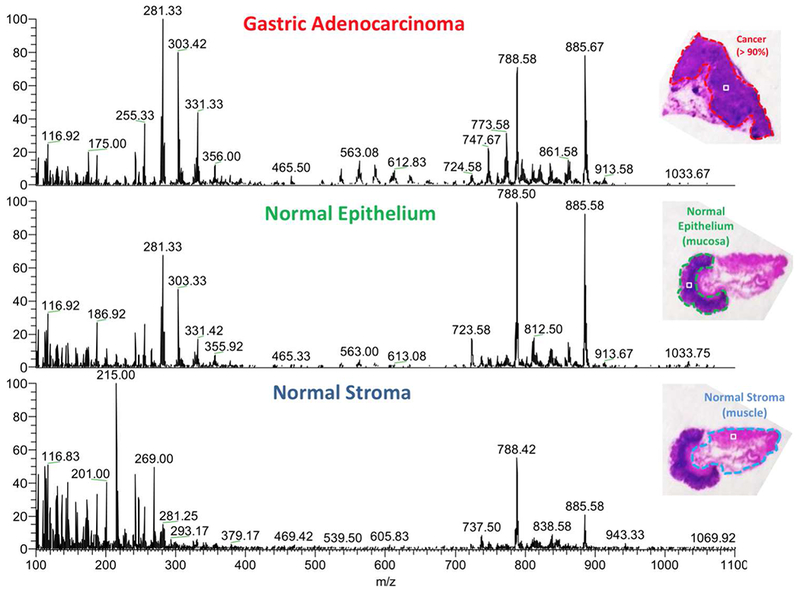
DESI mass spectra for one pixel taken from each region in the banked tissue example. The result of DESI mass spectrometric imaging is a 2D ion image with hundreds of pixels. Each pixel has an ion intensity measurement at each of thousands of mass-to-charge values, producing a mass spectrum. The three mass spectra in the image correspond to one pixel each. The objective is to classify a pixel as cancer or normal on the basis of its mass spectrum.

The 13,320 ion intensities from the mass spectrum for each pixel were averaged across bins of six⁴ to yield 2220 features. Each pixel has been labeled by a pathologist (after 2 weeks of sample testing) as epithelial, stromal or cancer, the first two being normal tissue. Each of 20 patients contributed up to three samples, from some or all of the three classes. The training set comprises 28 images from 14 patients, yielding 12,480 pixels, and the test set has 12 images from 6 different patients, for a total of 5696 pixels.

In Eberlin et al. (2014) the authors use the lasso (ℓ₁-regularized multinomial regression) to model the probability that a pixel belongs to each of the three classes on the basis of the ion intensity in each bin of six mass-to-charge values. In that study, the lasso performed favorably in comparison with support vector machines and principal component regression. For a detailed description of the lasso, see Section 2.2. For the purposes of the present paper, we collapse epithelial and stromal into one class, “Normal,” and we adopt a loss function that assigns twice the penalty to misclassifying a cancer cell as normal (false negative), relative to misclassifying a normal cell as cancer (false positive). This loss function reflects that missing a cancer cell is more harmful than making an error in the opposite direction. We collapse the two types of normal cells into one class because our collaborators are interested in identifying only the cancer cells for surgical resection. We find that treating epithelial and stromal as separate classes does not meaningfully change our results.

The lasso classifier fit to the data from the 12,480 pixels in the training set (with the regularization parameter λ selected via cross-validation; see Section 2.3) achieves a misclassification rate of 2.97% when used to predict the cancer/normal label of the 5696 pixels in the test set. Among cancer pixels the test error rate is 0.79%, and among normal pixels the test error rate is 4.16%. These results represent a significant improvement over the subjective classifications made by pathologists, which can be unreliable in up to 30% of patients [Eberlin et al. (2014)], but the present paper seeks to improve these results further. By using customized training sets, our method fits a separate classifier for each patient, creating a locally linear but globally nonlinear decision boundary. This rich classifier leads to more accurate classifications by using training data most relevant to each patient when modeling his or her outcome probabilities.

1.1. Transductive learning.

Customized training is best suited for the category of problems known in machine learning literature as transductive learning, in contrast with supervised learning or semi-supervised learning. In all of these problems, both the dependent and the independent variables are observed in the training data set (we say that the training set is “labeled”) and the objective is to predict the dependent variable in a test data set. The distinction between the three types of problems is as follows: in supervised learning, the learner does not have access to the independent variables in the test set at the time of model fitting, whereas in transductive learning the learner does have access to these data at model fitting. Semi-supervised learning is similar in that the learner has access to unlabeled data in addition to the training set, but these additional data do not belong to the test set on which the learner makes predictions. Customized training leverages information in the test data by choosing the most relevant training data on which to build a model to make better predictions. We have found no review of transductive learning techniques, but for a review of techniques for the related semi-supervised problem, see Zhu (2007).

In Section 2 we introduce customized training and discuss related methods. Section 3 investigates the performance of customized training and competing methods in a simulation study. Results on the motivating gastric cancer data set are presented, with their interpretation, in Section 4. We apply our method and others to a battery of real data sets from the UCI Machine Learning Repository in Section 5. The manuscript concludes with a discussion in Section 6.

2. Customized training.

First we introduce some notation. The data we are given are X_train, Y_train and X_test. X_train is an n × p matrix of predictor variables, and Y_train is an n-vector of response variables corresponding to the n observations represented by the rows of X_train. These response variables may be qualitative or quantitative. X_test is an m × p matrix of the same p predictor variables measured on m test observations. The goal is to predict the unobserved random m-vector Y_test of responses corresponding to the observations in X_test.

Let ${\widehat{f}}_{\Lambda }(\cdot )$ denote the prediction made by some learning algorithm, as a function of X_train, Y_train, X_test and an ordered set Λ of tuning parameters. So ${\widehat{f}}_{\Lambda }$ (X_train, Y_train, X_test) is an m-vector. For qualitative Y_train, ${\widehat{f}}_{\Lambda }$ is a classifier, while for quantitative Y_train, ${\widehat{f}}_{\Lambda }$fits a regression. We evaluate the performance of ${\widehat{f}}_{\Lambda }$ with L(${\widehat{f}}_{\Lambda }$(X_train, Y_train, X_test), Y_test), where the loss function L is often taken to be, for example, the number of misclassifications for a qualitative response, or squared error for a quantitative response.

The customized training method partitions the test set into G subsets and fits a separate model ${\widehat{f}}_{\Lambda }$ to make predictions for each subset. In particular, each subset of the test set uses only its own, “customized” subset of the training set to fit ${\widehat{f}}_{\Lambda }$. Identifying subsets of the training data in this way leads to a model that is locally linear but rich globally. Next, we propose two methods for partitioning the test set and specifying the customized training subsets.

2.1. Clustering.

Often test data have an inherent grouping structure, obviating the need to identify clusters in the data using unsupervised learning techniques. Avoiding clustering is especially advantageous on large data sets for which it would be very expensive computationally to cluster the data. For example, in the motivating application for the present manuscript, test data are grouped by patient, so we avoid clustering the 5696 test observations in 2220 dimensions by using patient identity as the cluster membership for each test point.

Given the G “clusters” identified by the grouping inherent to the test data, we identify the customized training set for each test cluster as follows: first, for each observation in the cluster, find the R nearest neighbors in the training set to that observation, thus defining many cardinality-R sets of training observations, one for each test point in the cluster. Second, take the union of these sets as the customized training set for the cluster. So the customized training set is the set of all training points that are one of the R nearest neighbors of any test point in the cluster. R is a tuning parameter that could in principle be chosen by cross-validation, but we have found that R = 10 works well in practice and that results are not particularly sensitive to this choice.

When the test data show no inherent grouping, customized training works by jointly clustering the training and test observations according to their predictor variables. Any clustering method can be used; here we apply hierarchical clustering with complete linkage to the data $(X_{\text{train}}^T,X_{\text{test}}^T{)}^T$. Then we cut the dendrogram at some height d_G, producing G clusters, as illustrated by Figure 3. In each cluster we train a classifier on the training observations within that cluster. This model is then used to make predictions for the test observations within the cluster. In this case, G is a tuning parameter to be chosen by cross-validation (see Section 2.3)

Fig. 3.

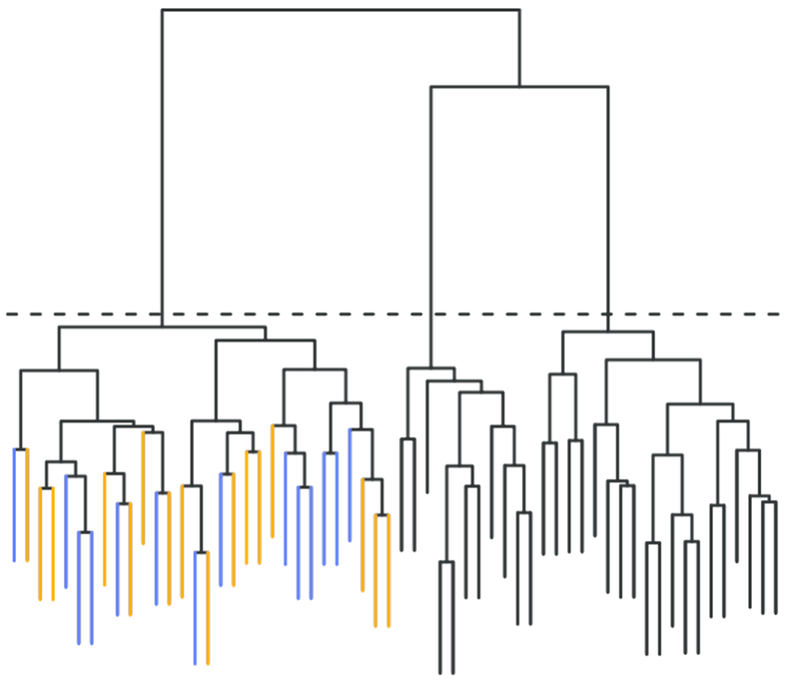
A dendrogram depicting joint clustering of training and test data, which is the method proposed for partitioning the test data and identifying customized training sets when the test data have no inherent grouping. Here the dendrogram is cut at a height to yield G = 3 clusters. Within the left cluster, the training data (blue leaves) are used to fit the model and make predictions for the test data (orange leaves).

2.2. Classification and regression.

The key idea behind our method is the selection of a customized training set for each group in the test set. Once these individualized training sets are identified, any supervised classification (or regression, in the case of quantitative outcomes) technique can be used to fit ${\widehat{f}}_{\Lambda }$ and make predictions for the test set. We suggest using ℓ₁-regularized generalized linear models because of their interpretability. Customized training complicates the model by expanding it into a compilation of G linear models instead of just one. But using ℓ₁ regularization to produce sparse linear models conserves interpretability. For an n × p predictor matrix X and corresponding response vector y, an ℓ₁-regularized generalized linear model solves the optimization problem

$$\underset{{\beta }_0,\beta \in {ℝ}^p}{\overset{\min }{}}-\frac{1}{n}\sum \ell ({\beta }_0,\beta \mid x_i,y_i)+\lambda \parallel \beta {\parallel }_1,$$ (2.1)

where ℓ(·) here is the log-likelihood function and depends on the assumed distribution of the response. For example, for linear regression (which we use for quantitative response variables),

$$y_i\mid x_i,{\beta }_0,\beta ~\text{Normal}({\beta }_0+{\beta }^T{x}_i,{\sigma }^2),$$

while for logistic regression (which we use for binary response variabes),

$$y_i\mid x_i,{\beta }_0,\beta ~\text{Binomial}\left(1,\frac{e^{{\beta }_0+{\beta }^T{x}_i}}{1+e^{{\beta }_0+{\beta }^T{x}_i}}\right).$$

For multiclass qualitative response variables we use the multinomial distribution in the same framework. The estimated regression coefficient vector $\widehat{\beta }$ that solves the optimization problem (2.1) can be interpreted as the contribution of each predictor to the distribution of the response, so by penalizing ||β||₁ in (2.1), we encourage solutions for which many entries in $\widehat{\beta }$ are zero, thus simplifying interpretation [Tibshirani (1996)].

Regardless of the ${\widehat{f}}_{\Lambda }$ chosen, for g = 1,…, G, let n_k denote the number of observations in the customized training set for the kth test cluster, and let $X_{\text{train}}^k$ denote the n_k × p submatrix of X_train corresponding to these observations, with $Y_{\text{train}}^k$ denoting the corresponding responses. Similarly, let m_k denote the number of test observations in the kth cluster, and let $X_{\text{test}}^k$ denote the m_k × p submatrix of X_test corresponding to these training observations, with $Y_{\text{test}}^k$ denoting the corresponding responses. Once we have a partition of the test set into G subsets (some of which may contain no test observations), with tuning parameter Λ our prediction for $Y_{\text{test}}^k$ is

$${\widehat{Y}}_{\text{test}}^k={\widehat{f}}_{\Lambda }(X_{\text{train}}^k,Y_{\text{train}}^k,X_{\text{test}}^k).$$ (2.2)

Note that if joint clustering is used to partition the test data, the customized training set for the kth test cluster may be empty, in which case ${\widehat{f}}_{\Lambda }(X_{\text{train}}^k,Y_{\text{train}}^k,X_{\text{test}}^k)$ is undefined. The problem is not frequent, but we offer in Section 2.4 one way (of several) to handle it. Once we have predictions for each subset, they are combined into the m-vector CT_G,Λ(X_train, Y_train, X_test), which we take as our prediction for Y_test.

2.3. Cross-validation.

Because customized training reduces the training set for each test observation, if the classification and regression models from Section 2.2 were not regularized, they would run the risk of overfitting the data. The regularization parameter λ in (2.1) must be large enough to prevent overfitting but not so large as to overly bias the model fit. This choice is known as the bias-variance trade-off in statistical learning literature [Hastie, Tibshirani and Friedman (2009)].

The number of clusters G is also a tuning parameter that controls the flexibility of the model. Increasing G reduces the bias of the model fit, while decreasing G reduces the variance of the model fit. To determine the optimal values of G and Λ, we use standard cross-validation to strike a balance between bias and variance. Because transductive methods have access to test features at training time, we explain carefully in this section what we mean by standard cross-validation.

The training data are randomly partitioned into J approximately equalsized folds (typically J = 10). For j = 1,…, J, $X_{\text{train}}^{(j)}$ denotes the submatrix of X_train corresponding to the data in the jth fold, and $X_{\text{train}}^{(-j)}$ denotes the submatrix of data not in the jth fold. Similarly, $Y_{\text{train}}^{(j)}$ denotes the responses corresponding to the data in the jth fold, and $Y_{\text{train}}^{(-j)}$ denotes responses not in the jth fold.

We consider $\mathcal{G}$ and A as the sets of possible values for G and Λ, respectively. In practice, we use $\mathcal{G}$ = {1,2,3,5,10}. We search over the grid $\mathcal{G}$ × A, and the CV-selected parameters G and Λ are

$$(G^{\ast },{\Lambda }^{\ast })=\underset{G\in \mathcal{G},\Lambda \in A}{\overset{\arg \min }{}}\sum _{j=1}^{J}L({\mathrm{CT}}_{G,\Lambda }(X_{\text{train}}^{(-j)},Y_{\text{train}}^{(-j)},X_{\text{train}}^{(j)}),Y_{\text{train}}^{(j)}).$$

In more detail, the G clusters for ${\mathrm{CT}}_{G,\Lambda }(X_{\text{train}}^{(-j)},Y_{\text{train}}^{(-j)},X_{\text{train}}^{(j)})$ are obtained as described in Section 2.1, and the loss for the jth fold is given by

$$L({\mathrm{CT}}_{G,\Lambda }(X_{\text{train}}^{(-j)},Y_{\text{train}}^{(-j)},X_{\text{train}}^{(j)}),Y_{\text{train}}^{(j)})=\sum _{k=1}^{G}L({\widehat{f}}_{\Lambda }(X_{\text{train}}^{(-j{)}^k},Y_{\text{train}}^{(-j{)}^k},X_{\text{train}}^{(j{)}^k}),Y_{\text{train}}^{(j{)}^k}).$$

2.4. Out-of-sample rejections.

As noted in Section 2, when joint clustering is used to partition the test data and identify customized training sets, predictions for a particular test subset may be undefined because the corresponding customized training subsets do not contain any observations. Using the convention of Bottou and Vapnik (1992), we refer to this event as a rejection (although it might be more naturally deemed an abstention). The number of rejections, then, is the number of test observations for which our procedure fails to make a prediction due to an insufficient number of observations in the customized training set.

Typically, in the machine learning literature, a rejection occurs when a classifier is not confident in a prediction, but that is not the case here. For customized training, a rejection occurs when there are no training observations close to the observations in the test set. This latter problem has not often been addressed in the literature [Bottou and Vapnik (1992)]. Because the test data lie in a region of the feature space poorly represented in the training data, a classifier might make a very confident, incorrect prediction.

We view the potential for rejections as a virtue of the method, identifying situations in which it is best to make no prediction at all because the test data are out-of-sample, a rare feature for machine learning algorithms. In practice, we observe that rejections are rare; Table 6 gives a summary of all rejections in the battery of machine learning data sets from Section 5.

Table 6.

A listing of all data sets from Section 5 for which K-CT_J makes a rejection for some K. The error rates in the last two columns refer to the error rate of standard training

Data set	Method	Rejections	Error rate on rejections	Error rate overall
First-order theorem proving	3-CTJ	3	1	0.518
	5-CTJ	3	1
	10-CTJ	3	1
LSVT Voice Rehabilitation	10-CTJ	2	0.5	0.142
Parkinsons	10-CTJ	4	0.25	0.154
Steel Plates Faults	3-CTJ	1	1	0.294
	5-CTJ	1	1
	10-CTJ	1	1

If a prediction must be made, there are many ways to get around rejections. We propose simply cutting the dendrogram at a greater height d′ > d_G so that the test cluster on which the rejections occurred is combined with another test cluster until the joint customized training set is large enough to make predictions. Specifically, we consider the smallest d′ for which the predictions are defined. Note that we update the predictions only for the test observations on which the method previously abstained.

2.5. Related work.

Local learning in the transductive setting has been proposed before [Zhou et al. (2004), Wu and SchÖlkopf (2007)]. There are other related methods as well, for example, transductive regression with elements of local learning [Cortes and Mohri (2007)] or local learning that could be adapted to the transductive setting [Yu, Zhang and Gong (2009)]. The main contribution of this paper relative to previous work is the simplicity and interpretability of customized training. By combining only a few sparse models, customized training leads to a much more parsimonious model than other local learning algorithms, easily explained and interpreted by subject-area scientists.

More recently, local learning has come into use in the transductive setting in applications related to personalized medicine. The most relevant example to this paper is evolving connectionist systems [Ma (2012)], but again our proposal for customized training leads to a more parsimonious and interpretable model. Personalized medicine is an exciting area of potential application for customized training.

Several methods [Gu and Han (2013), Ladicky and Torr (2011), Torgo and DaCosta (2003)] similarly partition the feature space and fit separate classification or regression models in each region. However, in addition to lacking the interpretability of our method, these techniques apply only to the supervised setting and do not leverage the additional information in the transductive setting. Others have approached a similar problem using mixture models [Fu, Robles-Kelly and Zhou (2010), Shahbaba and Neal (2009), Zhu, Chen and Xing (2011)], but these methods also come with a great computational burden, especially those which use Gibbs sampling to fit the model instead of an EM algorithm or variational methods.

Variants of customized training could also be applied in the supervised and semi-supervised setting. The method would be semi-supervised if instead of test data other unlabeled data were used for clustering and determining the customized training set for each cluster. The classifier or regression obtained could be used to make predictions for unseen test data by assigning each test point to a cluster and using the corresponding model. A supervised version of customized training would cluster only the training data and fit a model for each cluster using the training data in that cluster. Again, predictions for unseen test data could be made after assigning each test point to one of these clusters. This approach would be similar to Jordan and Jacobs (1994).

2.5.1. Alternative methods.

To compare customized training against the state of the art, we apply five other machine learning methods to the data sets in Sections 3, 4 and 5.

ST	Standard training. This method uses the ℓ1-penalized regression techniques outlined in Section 2.2, training one model on all of the Ttraining set. The regularization parameter λ is chosen through cross-validation.
SVM	Support vector machine. The cost-tuning parameter is chosen through cross-validation.
KSVM	K-means + SVM. We cluster the training data into K clusters via the K-means algorithm and fit an SVM to each training cluster. Test data are assigned to the nearest cluster centroid. This method is a simpler, special case of the clustered SVMs proposed by Gu and Han (2013), whose recommendation of K = 8 we use.
RF	Random forests. At each split we consider $\sqrt{p}$ of the p predictor variables (classification) or p/3 of the p predictor variables (regression).
KNN	k-nearest neighbors. This simple technique for classification and regression contrasts the performance of customized training with another “local” method. The parameter k is chosen via cross-validation.

3. Simulation study.

We designed a simulation to demonstrate that customized training improves substantially on standard training in situations where one would expect it to do so: when the data belong to several clusters, each with a different relationship between features and responses. We consider real-valued responses (a regression problem) for the sake of variety. We simulated n training observations and m test observations in p dimensions, each observation belonging to one of 3 classes. The frequency of the 3 classes was determined by a Dirichlet(2,2,2) random variable. The centers c₁, c₂, c₃ of the 3 classes were generated as i.i.d. p-dimensional normal random variables with covariance ${\sigma }_c^2{I}_p$.

Given the class membership z_i ∈ {1,2,3} of the ith observation, x_i was generated from a normal distribution with mean $({\beta }^{z_i}{)}^T{x}_i$ and covariance matrix I_p. The coefficient vector α^k corresponding to the kth class had p/10 entries equal to one, with the rest being zero, reflecting a sparse coefficient vector. The nonzero entries of α^k were sampled uniformly at random, independently for each class k. Given the class membership z_i and coefficient vector x_i of the ith observation, the response y_i had a normal distribution with mean $c_{z_i}$ and standard deviation one.

We conduct two simulations, the first with n = m = 300, p = 100 (the low-dimensional setting), and the second with n = m = 200, p = 300 (the high-dimensional setting). In each case, we vary σ_C from 0 to 10. Figure 4 shows the results. We observe that in both settings, customized training leads to significant improvement in test mean square error as the clusters separate (increasing σ_C). In the high-dimensional setting, the errors are expectedly much larger, but the same pattern is evident. For KSVM in this simulation we fix K = 3, thus cheating and giving the algorithm the number of clusters, whereas customized training learns the number of clusters from the data. For this reason, the performance of KSVM does not improve as the clusters separate. In fact, it is because none of the other methods make an attempt to identify the number of clusters that they do not improve as the clusters separate.

Fig. 4.

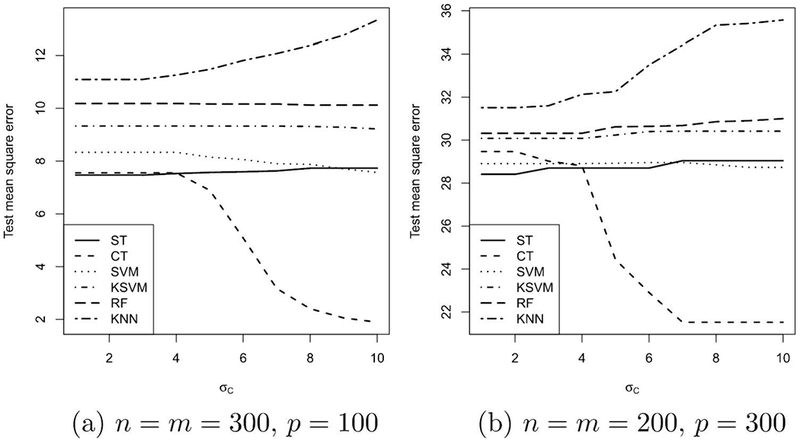
Simulation results. In (a), the low-dimensional setting, as σ_C increases and the clusters separate, the test error for customized training drops, while the test error for other-methods remains high. In (b), the test errors are much larger overall, but the same pattern persists: customized training leads to improved results as the clusters separate.

4. Results on gastric cancer data set.

We applied customized training to the mass-spectrometric imaging data set of gastric cancer surgical resection margins with the goal of improving on the results obtained by standard training. As described in Section 2.1, we obtained a customized training set for each test patient by finding the 10 nearest neighbors of each pixel in that patient’s images and using the union of these nearest-neighbor sets. Table 1 shows from which training patients the customized training set came, for each test patient. The patient labels have been ordered to make the structure in these data apparent: test patients 1–3 rely heavily on training patients 1–7 for their customized training sets, while test patients 4–6 rely heavily on training patients 9–14 for their customized training sets.

Table 1.

Source patients used in customized training sets for six test patients. Each column shows, for the corresponding test patient, what percentage of observations in that patient’s customized training set came from each of the training patients. Patient labels have been permuted to show the structure in the data: test patients 1–3 get most of their training sets from patients 1–7, while test patients 4–6 get most of their training sets from, patients 9–14

		Training patient
		1	2	3	4	5	6	7	8	9	10	11	12	13	14
Test patient	1	41.7	39.5	22.8	4.4	20.8	4.2	3.5	–	–	–	–	0.3	–	–
	2	46.2	50.2	40.1	59.6	39.1	44.3	33.7	–	–	1.3	–	0.6	–	0.9
	3	12.0	9.5	36.9	34.5	28.4	50.8	61.1	–	38.1	–	6.6	32.8	3.6	8.2
	4	–	0.2	–	1.2	–	–	0.7	38.1	55.8	73.7	20.4	21.2	6.6	25.4
	5	–	–	–	0.2	–	0.6	0.3	52.4	2.2	7.7	50.9	19.7	52.9	25.3
	6	−	0.7	0.2	0.2	11.6	−	0.7	9.5	3.9	17.3	22.2	25.3	36.9	40.1

In this setting it is more harmful to misclassify cancer tissue as normal than it is to make the opposite error, so we chose to use a loss function that penalizes a false negative (labeling a cancer pixel as normal) twice as much as it does a false positive (labeling a normal pixel as cancer). We observe that the results are not sensitive to the choice of the loss function (in the range of penalizing false negatives equally to five times as much as false positives) in terms of comparing customized training against standard training. We compare the results of customized training against the results of standard training for ℓ₁-regularized binomial regression—the method used by Eberlin et al. (2014)—in Table 2.

Table 2.

Error rates for customized training and standard training on the gastric cancer test data, split by patient and true label of the pixel (cancer or normal), with the lower overall error rate for each patient in bold. Each error rate is expressed by the percentage of pixels misclassified. Customized training leads to slightly higher errors for patients 3 and, 4 but much lower errors for all other patients and roughly half the error rate overall

Test patient		1	2	3	4	5	6	All
Standard training (lasso)	Cancer	–	2.67	0.21	–	–	2.70	1.54
	Normal	13.60	0.81	0.13	0.00	6.37	3.63	3.78
	Overall	13.60	1.61	0.18	0.00	6.37	3.14	2.98
Customized training (6-CT)	Cancer	–	1.07	0.11	–	–	1.80	0.74
	Normal	8.66	0.00	1.44	0.40	0.82	0.66	2.04
	Overall	8.66	0.46	0.71	0.40	0.82	1.26	1.58

We observe that customized training leads to a considerable improvement in results. For test patients 3 and 4, the test error is slightly higher for customized training than for standard training, but for all other patients, the test error for customized training is much lower. Overall, customized training cuts the number of misclassifications in half from the results of standard training. We focus on the comparison between customized and standard training because they are the fastest methods to apply to this large data set, but, indeed, the other methods described in Section 2.5.1 are also applicable. We report the overall test misclassification error and the run time for all methods in Table 3.

Table 3.

Overall test error rates and run times for customized training and the five other methods described in Section 2.5.1

Method	ST	CT	KSVM	KNN	RF	SVM
Misclassification rate	3.05%	1.58%	9.78%	9.18%	2.44%	2.07%
Run time (minutes)	2.1	2.4	6.0	7.6	21.9	197.8

4.1. Interpretation.

A key draw for customized training is that, although the decision boundary is more flexible than a linear one, interpretability of the fit is preserved because of the sparsity of the model. In this example, there are 2220 features in the data set, but the numbers of features selected for test patients 1 through 6 are, respectively, 42, 71, 62, 15, 21 and 54. Figure 5 shows which features are used in each patient’s model, along with the features used in the overall model with standard training.

Fig. 5.

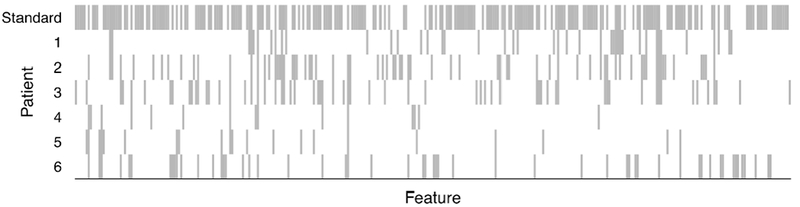
Features selected by customized training for each patient (variables not selected by any model are omitted from the x-axis). The first row shows features selected via standard training. Visual inspection suggests that patients 1, 2 and 3 have similar profiles of selected, variables, whereas patients 4 and 5 have selected-feature profiles that are more similar to each other than to other patients. Using hierarchical clustering with Jaccard distance between the sets of selected features to split the patients into two clusters, patients 1, 2 and 3 were in one cluster, with patients 4, 5 and 6 in the other.

We observe that some pairs of patients have more similar profiles of selected features than other pairs of patients. For example, about 36% of the features selected for test patient 1 are also selected for test patient 2. And about 39% of the features selected for test patient 3 are also selected for test patient 2. This result is not surprising because test patients 1 through 3 take much of their customized training sets from the same training patients, as observed above. Similarly, about 40% of the features selected for patient 4 are also selected for patient 6, and about 38% of the features selected for patient 5 are also selected for patient 6.

The third author’s subject-area collaborators have suggested that these data may actually suggest two subclasses of cancer; given that customized training identifies two different groups of models for predicting cancer presence, this subject-area knowledge leads to a potentially interesting interpretation of the results.

5. Additional applications.

To investigate the value of customized training in practice, we applied customized training (and the alternative methods from Section 2.5.1) to a battery of classification data sets from the UC Irvine Machine Learning Repository [Bache and Lichman (2013), Gil et al. (2012), Tsanas et al. (2014), Little et al. (2007), Mansouri et al. (2013), Kahraman, Sagiroglu and Colak (2013)]. The data sets, listed in Table 4, were selected not randomly but somewhat arbitrarily, covering a wide array of applications and values of n and p, with a bias toward recent data sets. In Table 5 we present results on all 16 data sets to which the methods were applied, not just those on which customized training performed well.

Table 4.

Data sets from UCI Machine Learning Repository [Bache and Lichman (2013)] used in Section 5

Abbrv.	Data set name	Abbrv.	Data set name
BS	Balance scale	BCW	Breast cancer Wisconsin (diagnostic)
C	Chess (king-rook vs king-pawn)	CMC	Contraceptive method choice
F	Fertility	FOTP	First-order theorem proving
LSVT	LSVT voice rehabilitation	M	Mushroom
ORHD	Optical recognition of handwritten digits	P	Parkinsons
QSAR	QSAR biodegration	S	Seeds
SPF	Steel plates faults	TAE	Teaching assistant evaluation
UKM	User knowledge modeling	V	Vowel

Table 5.

Test error of customized training and the five other methods described in Section 2.5.1 on 16 benchmark data sets. The bold text indicates the best performance for each data set. Customized training is competitive with the other methods and improves on standard training more often than not

			ST	CT		SVM	KSVM	RF	KNN
Data	n	p	Error	Error	G	Error	Error	Error	Error	k	%Imp*
BS	313	4	0.112	0.099	3	0.086	0.131	0.131	0.105	20	11.4
BCW	285	30	0.028	0.035	2	0.035	0.038	0.028	0.056	63	–25
C	1598	38	0.026	0.021	10	0.029	0.046	0.006	0.085	36	18.5
CMC	737	18	0.485	0.440	5	0.479	0.523	0.472	0.523	32	9.2
F	50	9	0.160	0.160	1	0.160	0.160	0.180	0.180	2	–
FTP	3059	51	0.557	0.530	5	0.489	0.444	0.427	0.508	47	4.7
LSVT	63	310	0.126	0.142	1	0.111	0.365	0.095	0.222	15	–12.5
M	4062	96	0.000	0.000	1	0.001	0.001	0.000	0.001	15	–
ORHD	3823	62	0.046	0.043	2	0.032	0.049	0.027	0.055	38	6.0
P	98	22	0.268	0.144	3	0.154	0.144	0.082	0.123	5	46.1
Q	528	41	0.176	0.134	5	0.146	0.148	0.140	0.144	19	23.6
S	105	7	0.047	0.047	2	0.066	0.114	0.104	0.066	9	–
SPF	971	27	0.321	0.278	5	0.273	0.281	0.246	0.357	57	13.3
TAE	76	53	0.720	0.470	10	0.653	0.613	0.506	0.493	1	34.6
UKM	258	5	0.041	0.013	1	0.103	0.213	0.068	0.565	79	66.6
V	528	10	0.610	0.491	2	0.387	0.480	0.409	0.508	1	19.5

^*%Imp: Percent relative improvement of customized training to standard training.

Random forests achieve the lowest error on 8 of the 16 data sets, the most of any method. But the method that achieves the lowest error secondmost often is customized training, on 7 of the 16 data sets, and customized training beats standard training on 11 data sets, with standard training coming out on top for only 2 data sets. We do not expect customized training to provide value on all data sets, but through cross-validation, we can often identify data sets for which standard training is better, meaning that G = 1 is chosen through cross-validation. The point of this exercise is not to show that customized training is superior to the other methods but rather to show that, despite its simplicity, it is at least competitive with the other methods.

Table 6 shows all of the rejections that customized training makes on the 16 data sets, for any value of G (not just the values of G chosen by cross-validation). For two of the data sets (LSVT Voice Rehabilitation and Parkinsons), it is clear that the rejections are just artifacts of using a G that is too large relative to the training sample size n. Such a G is not chosen by cross-validation. However, in the other data sets, Steel Plates Faults and First-order theorem proving, rejections occur for moderate values of G. It seems that this rejection is appropriate because the standard training method leads to an error for each test point which is rejected. Overall, we observe that rejections are rare.

6. Discussion.

The idea behind customized training is simple: for each subset of the test data, identify a customized subset of the training data that is close to this subset and use this data to train a customized model. We proposed two different clustering methods for finding the customized training sets and used ℓ₁-regularized methods for training the models. Local learning has been used in the transductive setting but not in such a parsimonious, interpretable way. Customized training has the potential to uncover hidden regimes in the data and leverage this discovery to make better predictions. It may be that some classes are over-represented in a cluster, and fitting a model in this cluster effectively customizes the prior to reflect this overrepresentation. Our results demonstrate superior performance of customized training over standard training on the mass-spectrometric imaging data set of gastric cancer surgical resection margins, in terms of discrimination between cancer and normal cells. Our approach also suggests the possibility of two subclasses of cancer, consistent with a speculation raised by our medical collaborators.

In this paper we focused on customized training with ℓ₁-regularized methods for the sake of interpretability, but, in principle, any supervised learning method may be used, which is an area for future work. Another area of future work is the use of different clustering techniques. We use hierarchical clustering, but there may be value in other methods, such as prototype clustering [Bien and Tibshirani (2011)]. Simulations in Section 3 show that the method can struggle in the high-dimensional setting, so it may be worthwhile to consider sparse clustering [Witten and Tibshirani (2010)].