Dual Energy CT with One Full Scan and a Second Sparse-View Scan using Structure Preserving Iterative Reconstruction (SPIR)

Abstract

Conventional dual-energy CT (DECT) reconstruction requires two full-size projection datasets with two different energy spectra. In this study, we propose an iterative algorithm to enable a new data acquisition scheme which requires one full scan and a second sparse-view scan for potential reduction in imaging dose and engineering cost of DECT. A bilateral filter is calculated as a similarity matrix from the first full-scan CT image to quantify the similarity between any two pixels, which is assumed unchanged on a second CT image since DECT scans are performed on the same object. The second CT image from reduced projections is reconstructed by an iterative algorithm which updates the image by minimizing the total variation of the difference between the image and its filtered image by the similarity matrix under data fidelity constraint. As the redundant structural information of the two CT images is contained in the similarity matrix for CT reconstruction, we refer to the algorithm as structure preserving iterative reconstruction (SPIR). The proposed method is evaluated on both digital and physical phantoms, and is compared with the filtered-backprojection (FBP) method, the conventional total-variation-regularization-based algorithm (TVR) and Prior-Image-Constrained-Compressed-Sensing (PICCS). SPIR with a second 10-view scan reduces the image noise STD by a factor of one order of magnitude with same spatial resolution as full-view FBP image. SPIR substantially improves over TVR on the reconstruction accuracy of a 10-view scan by decreasing the reconstruction error from 6.18% to 1.33%, and outperforms TVR at 50 and 20-view scans on spatial resolution with a higher frequency at the modulation transfer function value of 10% by an average factor of 4. Compared with the 20-view scan PICCS result, the SPIR image has 7 times lower noise STD with similar spatial resolution. The electron density map obtained from the SPIR-based DECT images with a second 10-view scan has an average error of less than 1%.

1 INTRODUCTION

Dual energy CT (DECT) has been increasingly used in different clinical applications, including direct angiography and bone removal,(Ruzsics et al., 2008; Tran et al., 2009; Watanabe et al., 2009; Kau et al., 2011) assessment of lung perfusion,(Thieme et al., 2012; Zhang et al., 2013a) characterization of renal calculi,(Primak et al., 2007; Graser et al., 2009) and generation of virtual unenhanced CT images.(De Cecco et al., 2010) Conventional DECT reconstruction theory requires two full-size projection datasets with two different energy spectra. In this paper, we aim to relax the data acquisition requirement of DECT for potential dose reduction and simplified imaging schemes by using an iterative reconstruction algorithm, which exploits the redundant structural information of the CT images acquired at two different x-ray energies.

The DECT theory assumes that the attenuation coefficient of any material in the diagnostic energy range can be approximated as a weighted summation of two universal energy-dependent functions mainly accounting for photoelectric and Compton interactions.(Alvarez and Macovski, 1976) In practice, the basis functions can be the energy-dependent linear attenuation coefficients of two different actual or even virtual materials.(Sidky et al., 2004) The weight distributions of the two basis functions, i.e., the decomposed material images, are reconstructed from the data acquired with two different x-ray energy spectra, which can be used to calculate electron density maps or effective Z images.(Alvarez and Macovski, 1976) The original concept of DECT requires acquisition of projection data with two different x-ray energies for each projection ray. Non-linear decomposition is then applied on the projection data to obtain the sinogram of two basis materials, from which decomposed materials are reconstructed via the same CT reconstruction principle. In practical implementations of DECT, dual-energy projection data can be acquired, for example, on advanced CT imaging systems, including dual-source CT(Petersilka et al., 2008) or fast kVp switching CT,(Hsieh, 2009; Xu et al., 2009) or using two sequential scans (so-called rotation-rotation mode) on a conventional diagnostic CT scanner. In these data acquisition schemes (except using a dual-layer detector as on the Philips IQon spectral CT system(Tanguay et al., 2010; Zhang et al., 1998; Murphy and Alaamri, 2015)), however, it is difficult or impossible to have dual-energy measurements on the same projection ray. The procedure of material decomposition is therefore more conveniently performed on CT images after the standard CT reconstruction, typically based on a linear model,(Dong et al., 2014; Szczykutowicz and Chen, 2010; Sukovic and Clinthorne, 2000; Yu et al., 2012) at the price of losing the beam-hardening correction capability. In the existing literatures,(Szczykutowicz and Chen, 2010; Yu et al., 2012) the terminology of DECT has extended from its original concept to include these imaging modalities based on image-domain decomposition. We follow the convention and refer to all imaging systems that acquire projection data with two effective x-ray spectra and perform material decomposition as DECT systems, although readers should be aware that DECT in the strict sense uses only non-linear decomposition in the projection domain.

DECT requires doubling the size of projection measurements. In current DECT implementations, this condition is satisfied by either scan time increase, as in the rotation-rotation mode on a conventional diagnostic CT scanner, or hardware advancements, as on the dual-source CT,(Petersilka et al., 2008) the fast kVp switching CT(Xu et al., 2009) and the dual-layer detector CT.(Tanguay et al., 2010; Zhang et al., 1998) In this work, we focus on a software-based improvement to reduce the requirement of data acquisition for DECT. We propose a new reconstruction algorithm using a full CT scan plus a second scan with very few projections for high-quality DECT, which potentially reduces imaging dose and allows for more flexible designs of data acquisition on clinical DECT systems. Our proof-of-concept investigations are performed on DECT using a rotation-rotation mode, i.e., two sequential CT scans at different x-ray energies, with image-domain decomposition. The proposed method is expandable to other DECT imaging modalities using either image-domain or projection-domain decomposition.

Iterative algorithms have demonstrated successes on CT reconstruction on sparse data.(Sidky et al., 2006; Emil and Xiaochuan, 2008; Junguo et al., 2010; Ludwig et al., 2011; Kudo et al., 2013; Zhang et al., 2013b; Li et al., 2002; Hansis et al., 2008; Niu and Zhu, 2012; Yan et al., 2014) The projection data for high-quality CT images are further reduced if the reconstruction is constrained by prior images, as shown in many recent applications, including 4D CBCT,(Leng et al., 2008) daily imaging CBCT,(Ho et al., 2012; Cho et al., 2009) and cardiac CT.(Chen et al., 2009; Tang et al., 2010) We propose an iterative algorithm to improve DECT on sparse data with a design strategy different from those of existing algorithms. In the proposed DECT reconstruction, we first use a full scan to obtain an estimated classification of object structures. A bilateral filter is calculated as a similarity matrix from the first full-scan CT image to quantify the similarity between any two pixels. This similarity matrix remains approximately unchanged on the same object in different CT scans, although the CT image pixel values may vary. In a second CT scan with different x-ray energy and significantly reduced projections, we reconstruct a high-quality CT image by an iterative method. In each iteration, we multiply the image vector to be reconstructed by the similarity matrix, a procedure equivalent to shift-variant low-pass filtering. To suppress noise and image artifacts on the reconstructed image, the algorithm updates the reconstructed CT image by minimizing the total variation (TV) of the difference between the image and its filtered image under the data fidelity constraint. Note that, the proposed algorithm for the second CT scan does not regularize on the TV of the image to be reconstructed as in the conventional TV based iterative CT reconstruction methods.(Emil and Xiaochuan, 2008; Sidky et al., 2006; Junguo et al., 2010; Kudo et al., 2013; Ludwig et al., 2011; Niu and Zhu, 2012; Yan et al., 2014) It is also distinct from other prior-image constrained iterative algorithms in that it does not rely on the matching of pixel values between the prior image and the image to be reconstructed. Instead, we improve the reconstruction accuracy from reduced projections based on an estimated classification of structures shared by the two images. The proposed iterative algorithm is therefore referred to as structure preserving iterative reconstruction (SPIR).

In this paper, we evaluate the DECT quality using SPIR on both digital and physical phantoms. In particular, we investigate the effects of structure classification errors on SPIR and the limit of data reduction for satisfactory DECT accuracy. Reconstruction error, spatial resolution, noise level and error of measured electron density are used as the image quality metrics in these DECT studies.

2 METHOD

2.1 Formulation of SPIR framework

In the presented studies, we choose to reconstruct a full-scan image at high kVp using the standard FBP algorithm, and aim to reconstruct a second sparse-view scan image at low kVp with the aid of structure preservation from the first CT image using SPIR. Similar to the optimization framework of other regularization-based iterative reconstruction algorithms,(Sidky et al., 2006; Chen et al., 2008; Dong et al., 2014) the proposed SPIR method is formulated as the following constrained minimization:

$$\overrightarrow{f_L^{*}}=\text{arg min}[\lambda ·R(\overrightarrow{f_L},\overrightarrow{f_H})+\frac{1}{2}{\Vert M\overrightarrow{f_L}-\overrightarrow{b}\Vert }_2^2],s.t.\overrightarrow{f_L}(i)\ge 0,$$ (1)

where $\overrightarrow{f_L}$ is the vectorized image at low kVp to be reconstructed, $\overrightarrow{f_H}$ is the vectorized image at high kVp reconstructed by FBP, $R(\overrightarrow{f_L},\overrightarrow{f_H})$ is the regularization term quantifying the extent of structure preservation. M is the system matrix modeling CT forward projection, vector b⃗ is the measured line integrals, and ${\Vert M\overrightarrow{f_L}-\overrightarrow{b}\Vert }_2$ calculates the L-2 norm of the difference between the estimated and the raw projections, i.e., the data fidelity error. λ is a user-defined penalty weight, which balances structure preservation and reconstruction accuracy. Each element of $\overrightarrow{f_L},\overrightarrow{f_L}(i)$ , is constrained by image non-negativity.

The design of the regularization term $R(\overrightarrow{f_L},\overrightarrow{f_H})$ is the key to the success of SPIR. We first extract the structural information from the full-scan FBP image via a procedure that we refer to as structure classification, which is inspired by the bilateral filtering method originated in imaging processing field.(Tomasi and Manduchi, 1998) Bilateral filtering combines two types of image filtering, domain filtering and range filtering. The domain filtering suppresses image noise via weighted averaging with domain weights that decrease as spatial distance between two pixels increases. The range filtering is performed in the same way with range weights that decay with pixel value differences. In the structure classification of our method, we use combined domain and range weights of bilateral filtering to quantify the similarity between any two pixels of the first full-scan CT image. These weights are organized in a matrix form and the bilateral filtering becomes similarity matrix multiplication.

In our implementation, the domain weight with respect to distance is set as a box function centered at 0 with a window size of X-by-X pixels, and the range weight with respect to the pixel value difference is set as Gaussian function centered at 0 with a kernel width h. The similarity between two pixels i and j, W_ij, on the full-scan CT image $\overrightarrow{f_H}$ is calculated by the following formula:

$$W_{ij}(\overrightarrow{f_H},X,h)=\{\begin{array}{c}\hfill \frac{\mathit{\text{exp}}(-\frac{{(\overrightarrow{f_H}(i)-\overrightarrow{f_H}(j))}^2}{h^2})}{{\sum }_{j\in {\Omega }_i^{(X)\mathit{\text{ exp}}}}(-\frac{{(\overrightarrow{f_H}(i)-\overrightarrow{f_H}(j))}^2}{h^2})}\hfill \\ \begin{array}{cc}\hfill 0\hfill & \hfill \mathit{\text{otherwise}}\hfill \end{array}\end{array}j\in {\Omega }_i^{(X)},$$ (2)

where X and h are user-defined parameters, ${\mathrm{\Omega }}_i^{(X)}$ is the X-by-X subset of the pixels in the neighborhood centered at pixel i. Note that the total similarity for one pixel is normalized to one.

To reduce errors of similarity calculation, we first generate a noise-suppressed $\overrightarrow{f_H}$ via bilateral filtering, i.e. multiplication by the similarity matrix W:

$$\overrightarrow{\widehat{f_H}}=W\overrightarrow{f_H},$$ (3)

where each element of W is calculated using Eq. (2) with X = 3 pixels and h = σ, the noise standard deviation (STD) measured on a uniform area in $\overrightarrow{f_H}$ . We then update the similarity matrix W on the noise suppressed CT image $\overrightarrow{\widehat{f_H}}$ using Eq. (2) again (i.e., $\overrightarrow{f_H}$ is replaced by $\overrightarrow{\widehat{f_H}}$ ) with h = σ and X = 41. In case that one pixel of interest does not have sufficient pixels with non-zero similarity, we adaptively increase the window X until the number of pixels with non-zero similarity exceeds 200 or the size of search window equals to that of the image.

The generation of similarity matrix W is a process of structure classification, because W contains the structural information of the image. For example, if the size of the high energy image is N by N, the kth row of W, W_ij, i = k, j = 1, 2, … N², can be reshaped as an N-by-N image, showing the relative similarity values of all pixels across the entire image compared with the kth pixel. In our method, we compute W on the high-kVp CT image (hereafter we refer to as W_H). Since the object structure remains unchanged in the low-kVp CT scan, the computed W_H is also an accurate estimate of the similarity matrix on the low-kVp CT image $\overrightarrow{f_L}$ , W_L, i.e.:

$$W_H\approx W_L.$$ (4)

As a process of bilateral filtering in nature, multiplication of an image vector by an accurate similarity matrix W yields a noise or error suppressed image. The reconstructed low kVp image, $\overrightarrow{f_L}$ , is expected to have a reduced quality due to insufficient projection data. As such, the similarity matrix calculated on $\overrightarrow{f_L}$ is inaccurate, and cannot be used to effectively reduce reconstruction errors. We therefore rely on Eq. (4) for improved reconstruction of $\overrightarrow{f_L}$ . If $\overrightarrow{f_L}$ is reconstructed accurately with low noise or small errors (e.g., from successful iterative reconstruction), multiplication of $\overrightarrow{f_L}$ by an accurately estimated similarity matrix (W_H based on Eq. (4)) should have small effects on $\overrightarrow{f_L}$ , i.e.:

$$\overrightarrow{f_L}\approx W_H\overrightarrow{f_L}$$ (5)

We use Eq. (5) as an additional data constraint in the design of the regularization term of the optimization framework. We notice that the difference between $W_H\overrightarrow{f_L}$ and $\overrightarrow{f_L}$ is relatively large at structure edges. To better preserve edge signals, we design the regularization term $R(\overrightarrow{f_L},\overrightarrow{f_H})$ to be the TV of the difference of $W_H\overrightarrow{f_L}$ and $\overrightarrow{f_L}$ as:

$$R(\overrightarrow{f_L},\overrightarrow{f_H})=\frac{1}{2}{\Vert \overrightarrow{f_L}-W_H\overrightarrow{f_L}\Vert }_{TV}=\frac{1}{2}{\Vert \nabla \left(A\overrightarrow{f_L}\right)\Vert }_1,$$ (6)

where = I − W_H, I is an identity matrix with the same size as that of W_H and ‖·‖₁ calculates the L1 norm. Note that, in Eq. (6), the matrix W_H is equivalent to a shift-variant low-pass filter computed from $\overrightarrow{f_H}$ , thus A = I − W_H is equivalent to a shift-variant high-pass filter. By plugging Eq. (6) into Eq. (1), we reformulate the SPIR method as the following constrained minimization problem:

$$\overrightarrow{f_L^{*}}=\text{arg min}[\frac{\lambda }{2}{\Vert \nabla \left(A\overrightarrow{f_L}\right)\Vert }_1+\frac{1}{2}{\Vert M\overrightarrow{f_L}-\overrightarrow{b}\Vert }_2^2],s.t.\overrightarrow{f_L}(i)\ge 0.$$ (7)

The contribution of our algorithm development is mainly two-fold. First, we reformulate bilateral filtering into similarity matrix multiplication, a form compatible with the framework of iterative CT reconstruction. Bilateral filtering, which is equivalent to shift-variant high-pass filtering, is included in the regularization term for improved CT reconstruction. Secondly, we propose to use SPIR to reduce the data acquisition of DECT since CT images at different energies on the same object share the same structures and therefore have almost identical similarity matrices. Only one high-quality CT image is needed to calculate an accurate similarity matrix, and thus we can reduce the projection data of a second CT scan and use SPIR to suppress reconstruction errors.

2.2 Implementation details of the SPIR algorithm

2.2.1 Summary of SPIR workflow

The DECT method using the SPIR algorithm implemented in this paper is summarized as follows:

1. Reconstruct a high kVp CT image $\overrightarrow{f_H}$ from a full scan using FBP reconstruction.

2. Generate noise-suppressed $\overrightarrow{\widehat{f_H}}$ by bilateral filtering via Eq. (2) and Eq. (3).

3. Calculate the similarity matrix W_H on $\overrightarrow{\widehat{f_H}}$ using Eq. (2).

4. Solve Eq. (7) and output $\overrightarrow{f_L}$ .

2.2.2 Solver to Eq. (7)

We efficiently solve the constrained minimization problem, i.e., Eq. (7), by gradient projection with an adaptive Barzilai–Borwein (GP-BB) step-size selection scheme. The implementation is similar to that presented in our previous work(Niu and Zhu, 2012), except that the gradient of the regularization term is included in the calculation of the descending direction of the objective function. Let $\overrightarrow{h}=A\overrightarrow{f_L}$ , and the regularization term (Eq. (6)) can be rewritten as

$$R=\frac{1}{2}{\Vert \nabla \overrightarrow{h}\Vert }_1=\frac{1}{2}{\sum }_{m,n}\sqrt{{(h_{m,n}-h_{m,n-1})}^2+{(h_{m,n}-h_{m-1,n})}^2},$$ (8)

where we reshape the vector h⃗ as a N_X × N_Y image matrix whose elements are h_m,n, 0 < m ≤ N_X, 0 < n ≤ N_Y. N_X × N_Y is the image size of reconstruction. Similarly, we reshape $\overrightarrow{f_L}$ as f_s,t and A as A_m,n,s,t, 0 < s, m ≤ N_X, 0 < t, n ≤ N_Y. Thus, we have h_m,n = Σ_s,t A_m,n,s,tf_s,t. Denoting the gradient of Eq. (8) with respect to $\overrightarrow{f_L}$ as ∇⃗R, we calculate its element via the following equation:

$${(\overrightarrow{\nabla }R)}_{i,j}=\frac{\partial R}{\partial f_{i,j}}={\sum }_{m,n}\frac{(h_{m,n}-h_{m,n-1})(A_{m,n,i,j}-A_{m,n-1,i,j})+(h_{m,n}-h_{m-1,n})(A_{m,n,i,j}-A_{m-1,n,i,j})}{\sqrt{{(h_{m,n}-h_{m,n-1})}^2+{(h_{m,n}-h_{m-1,n})}^2+\epsilon }},$$ (9)

where ε is a small positive number to avoid singularities in the derivative calculation and set as 10⁻⁸ in the algorithm.

ALGORITHM I shows the pseudo code of solver to Eq. (7) by the GP-BB method. Line 1 lists algorithm parameters with typical values controlling the optimization. The penalty weight λ in the optimization objectives balances the strength of noise suppression and data fidelity error. We empirically choose the value of λ to match the data fidelity error of image with those of other methods for a fair comparison in the studies presented later. A typical value range is also given in Line 1. The initial guess of low-kVp image in the optimization can be zero or generated by other iterative reconstruction algorithm (line 2). Note that, zero initial will give the same optimal solution but with more computation time. Line 3 to 16 is the main loop solving Eq. (7) using GP-BB method. When the L1 norm of the image difference between two adjacent iterations ${\Vert \overrightarrow{f_L}-\overrightarrow{f_{L,\mathit{\text{old}}}}\Vert }_1$ is less than the preset tolerance (line 15) or the number of iterations exceeds the upper limit N_iter, the iteration stops with a final result image $\overrightarrow{f_L}$ (line 17).

ALGORITHM I.

Pseudo code of solver to Eq. (7) by the GP-BB method (the comments are shown in italic).

1:	Niter ≔ 2000; κ ≔ 0.3; tol ≔ 10−10; λ ≔ 0.1~1;	empirical control parameters
2:	$\overrightarrow{f_L}≔0$ or result from other iterative reconstruction;	initial guess
3:	for t ≔ 1: Niter do	main loop
4:	$\overrightarrow{g}=\overrightarrow{\nabla }R+M^T(M\overrightarrow{f_L}-\overrightarrow{b}$;	gradient of objective function
5:	for i ≔ 1: N do	enforce gradient negativity and projection non-negativity
6:	if g⃗ (i) ≤ 0, or $\overrightarrow{f_L}(i)\ge 0$, then p⃗ (i): = g⃗ (i); else p⃗ (i): = 0 end if;
7:	end for;
8:	if t ≔ 1, then
9:	$\overrightarrow{f_{L,\mathit{\text{old}}}}≔0;\overrightarrow{p_{\mathit{\text{old}}}}≔0$; α ≔ 0;
10:	else	adaptive BB step size
11:	${\alpha }^{BB1}≔\frac{{(\overrightarrow{f_L}-\overrightarrow{f_{L,\mathit{\text{old}}}})}^T(\overrightarrow{f_L}-\overrightarrow{f_{L,\mathit{\text{old}}}})}{{(\overrightarrow{f_L}-\overrightarrow{f_{L,\mathit{\text{old}}}})}^T(\overrightarrow{p}-\overrightarrow{p_{\mathit{\text{old}}}})},{\alpha }^{BB2}≔\frac{{(\overrightarrow{f_L}-\overrightarrow{f_{L,\mathit{\text{old}}}})}^T(\overrightarrow{p}-\overrightarrow{p_{\mathit{\text{old}}}})}{{(\overrightarrow{p}-\overrightarrow{p_{\mathit{\text{old}}}})}^T(\overrightarrow{p}-\overrightarrow{p_{\mathit{\text{old}}}})}$;
	if αBB2/αBB1 < κ, then α: = αBB2; else α: = αBB1; end if;
12:	$\overrightarrow{f_{L,\mathit{\text{old}}}}≔\overrightarrow{f_L},\overrightarrow{p_{\mathit{\text{old}}}}≔\overrightarrow{p}$;
13:	end if;
14:	$\overrightarrow{f_L}≔\overrightarrow{f_L}-\alpha \overrightarrow{p}$;	update image
15:	if ${\Vert \overrightarrow{f_L}-\overrightarrow{f_{L,\mathit{\text{old}}}}\Vert }_1<\mathit{\text{tol}}$, then break; end if;	stopping criterion
16:	end for;
17:	return $\overrightarrow{f_L}$;

2.3 Evaluation

We demonstrate the feasibility of the proposed algorithm through both computer simulation and phantom experiments. In all the investigations, we use imaging parameters matching those of an On-Board Imager (OBI) cone-beam CT (CBCT) system on a Varian radiation therapy machine (e.g. Trilogy or Truebeam), except that we focus on fan-beam CT studies to avoid scatter errors. Each projection contains 1024 pixels with a pixel pitch of 0.388 mm. A full scan over 360° acquires 655 projections. The reconstructed CT images and the decomposed material images have a dimension of 512×512 with a pixel size of 0.5×0.5 mm². The CT images are converted to CT number in Hounsfield Unit (HU), and the decomposed material images are the relative weights (i.e., the effective volume fractions) of the basis materials. In simulation studies, we use a mono-energetic source at 47 keV and 61 keV. No scatter is simulated. Poisson noise is added on projections to simulate an image noise level close to that in experimental results. The phantom experiments are performed on our tabletop CBCT system at Georgia Institute of Technology, with two x-ray tube energies of 75 kVp and 125 kVp. A fan-beam geometry with a longitudinal beam width of 15 mm on the detector is used to acquire views with scatter contamination inherently suppressed.(Zhu et al., 2006) More details of the tabletop CBCT system can be found in Ref.(Niu and Zhu, 2011)

High-energy CT images are reconstructed from raw data by the FBP method with a Hamming filter and are used for structure classification in SPIR. Low-energy CT images are reconstructed using SPIR with different numbers of equi-angular views. A practical reason of using a full high kVp scan and a sparse-view low kVp scan is that compared with the CT image of a full low kVp scan, the CT image of a full high kVp scan is less noisy in our study and thus can generate a more accurate similarity matrix. A more accurate similarity matrix leads to a high-quality CT image of the second sparse-view scan reconstructed by our proposed method. The decomposed material images are generated from high-energy and low-energy CT images by an iterative image-domain decomposition method recently developed in our group.(Niu et al., 2014) CT images and decomposed material images by the conventional two-full-scan FBP method are used as the ground truths. The proposed algorithm is implemented in MATLAB. The majority of computation occurs in minimizing the objective function of SPIR, which typically takes about 10 minutes on a 2.67GHz CPU. The generation of similarity matrix W takes about 20 seconds with 8-thread parallel computation.

The performance of the proposed DECT heavily relies on the accuracy of structure classification. To investigate DECT image qualities when structure classification is challenging, we first evaluate our algorithm on a digital phantom with a water equivalent background containing 8 rods. On the high-energy CT image where structure classification is performed, we carefully design the attenuation coefficients of the 8 contrast rods to assess the proposed SPIR-based DECT for the following three scenarios:

Scenario I: Rods have sufficient contrasts compared with the background and each rod has a different CT value and therefore is identified as a different material.

Scenario II: Rods have sufficient contrasts compared with the background but have the same CT values on the high-energy CT image. These rods may be therefore falsely classified as the same material although they have different CT values on the low-energy CT image.

Scenario III: Rods have no contrasts compared with the background on the high-energy CT image. Structure classification therefore completely fails.

Scenario I represents the most common situation on clinical DECT images. Scenario II may happen in some cases such as angiography bone removal when the intensities of iodine and bone partially overlap. Scenario III is an extremely challenging case for assessment purposes only. We hypothesize that SPIR can accurately reconstruct the image of rods in Scenario I with a high overall image quality, and may have lower accuracy in Scenario II and III depending on the number of views. In addition, we include one small rod with a diameter of 1cm which contains a 0.5cm calcium rod surrounded by iodine solution. Similar to scenario II, the two materials in this rod have the same pixel value in the high energy image but different pixel values in the low energy image. We use this rod to simulate the scenario in angiography that a vessel contains calcium plaque and iodine contrast with similar HU values in the high kVp image, and to evaluate the preservation of the calcium/iodine boundary in the reconstructed image by our proposed method.

In the above studies, we focus on the evaluation of SPIR accuracy on the low-energy CT scan. The relative root-mean-square error (R-RMSE) is used as an image quality metric, which is calculated as

$$\mathrm{R}-\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\frac{\sqrt{\frac{1}{N}{\sum }_{i=1}^N{({\mu }_i-{\mu }_{i0})}^2}}{\frac{1}{N}{\sum }_{i=1}^N{\mu }_{i0}}\times 100\%,$$ (10)

where i is the index of the region of interest (ROI), μ_i is the mean reconstructed CT value inside the ROI, μ_i0 is the corresponding ground truth value, and N is the total number of the ROIs.

Measurements of line-spread function are used to evaluate the method performance on image spatial resolution. Besides rods, three 1-by-7-pixel lines with contrasts of 127 HU (line #1), 1017 HU (line #2) and 94 HU (line #3) corresponding to scenario I, II and III, respectively, are added in the digital phantom to further study the performance of the proposed method. For each line, 7 1D profiles pass through all the 7 pixels at the direction perpendicular to the line and are averaged along the direction of the line. The averaged profile is fitted by a Gaussian function and then converted to modulation transfer function (MTF). The frequency at 10% of maximum value of MTF is used to quantify the MTF function, and is referred as “10% MTF frequency” for conciseness in the presentation of our results. A larger value of 10% MTF frequency indicates a higher spatial resolution.

The overall performance of the proposed method is further evaluated on two physical phantoms, the Catphan©600 phantom and an anthropomorphic pediatric phantom. The slice of line pairs on the Catphan phantom is used to investigate the spatial resolution. Both CT images and decomposed material images are generated. A uniform ROI in CT image is also selected to measure the noise level. A similar study is performed on the anthropomorphic pediatric phantom to evaluate the method performance in the presence of complex object structures. A further evaluation is performed on head patient DECT images acquired at 140 kVp and 80 kVp. The full-scan CT image at 140 kVp is used for similarity matrix calculation. As we do not have access to raw projection data on the clinical CT scanner, the full-scan CT image at 80 kVp is forward-projected to generate a full-size sinogram. The projection views of the sinogram is then downsampled to simulate different sparse-view scans. This simulated sparse-view scan is reconstructed by the proposed method, and used in material decomposition of “iodine” and “tissue” images. In this paper, we focus on the evaluation of virtual unenhanced imaging using DECT, a common clinical technique that removes iodine from contrast-enhanced DECT images and reduces the need for an unenhanced CT scan.(Sahni et al., 2013) We generate virtual unenhanced images by weighted summation of the decomposed images, in the same way as shown in Ref (Kaza et al., 2012).

The contrast rod slice of the Catphan phantom is used to investigate the measurement accuracy of electron density using DECT, which is important in dose calculation for radiation therapy.(Hatton et al., 2009) The electron density map is generated as the summation of the decomposed basis material images weighted by their known electron densities. We use Teflon and polystyrene as the two basis materials of which electron densities can be found in the phantom manual. The contrast rods are selected as the ROIs. We calculate the measurement error of electron density as:

$$E_i=\frac{{\rho }_i-{\rho }_{i0}}{{\rho }_{i0}}\times 100\%,$$ (11)

where ρ_i is the mean electron density of the ith ROI and ρ_i0 is its ground truth obtained from the phantom manual. The absolute values of E_i of all ROIs are then averaged for comparison.

In above studies, we compare our SPIR approach with the FBP method as well as a conventional TV regularization-based iterative reconstruction method (TVR), which uses the TV of the image to be reconstructed as the regularization term.(Song et al., 2007; Niu and Zhu, 2012; Park et al., 2012). On the digital phantom, we also compare our approach with two iterative reconstruction method: Prior Image Constrained Compressed Sensing (PICCS), a state-of-the-art algorithm that uses a prior image to improve iterative CT reconstruction algorithm.(Chen et al., 2008) In PICCS, we set the strength parameter of prior image constraint the value recommended in Ref (Chen et al., 2008) (i.e., α = 0.91 in Eq.(3) of Ref (Chen et al., 2008)). In all the comparisons, we manually tune the parameters of different algorithms to have the same data fidelity errors on the reconstructed images.

In particular, we assess method performance on DECT data of a full scan and a second scan with different numbers of projection views. For conciseness, the following abbreviations are used in the presentations of our results. On the results of CT images, “Full-scan FBP” stands for the FBP reconstruction using a full scan dataset, “N-view SPIR/TVR/PICCS” stands for reconstruction by SPIR, TVR or PICCS using data of N views, and “high E/low E” stands for high energy CT image or low energy CT image. On the results of decomposed material images, electron density maps and virtual unenhanced images, “Full+Full FBP” refers to the conventional two-full-scan FBP method, and “Full+N SPIR” refers to the proposed DECT method using one full-scan FBP image and a second N-view SPIR image.

3 RESULTS

3.1 Digital phantom study

Fig. 1 shows the digital phantom setting at low energy and high energy. Both images are reconstructed by full-scan FBP as the ground truths. Fig. 2 shows the CT images of the digital phantom reconstructed by SPIR, TVR and PICCS with a sparse-view scan at the low energy level. In the comparison of TVR and PICCS with SPIR results, we tune the algorithm parameters to achieve the same data fidelity errors. The parameter α in PICCS, i.e., the strength of prior image constraint, is set as 0.91, the recommended value in Ref (Chen et al., 2008).

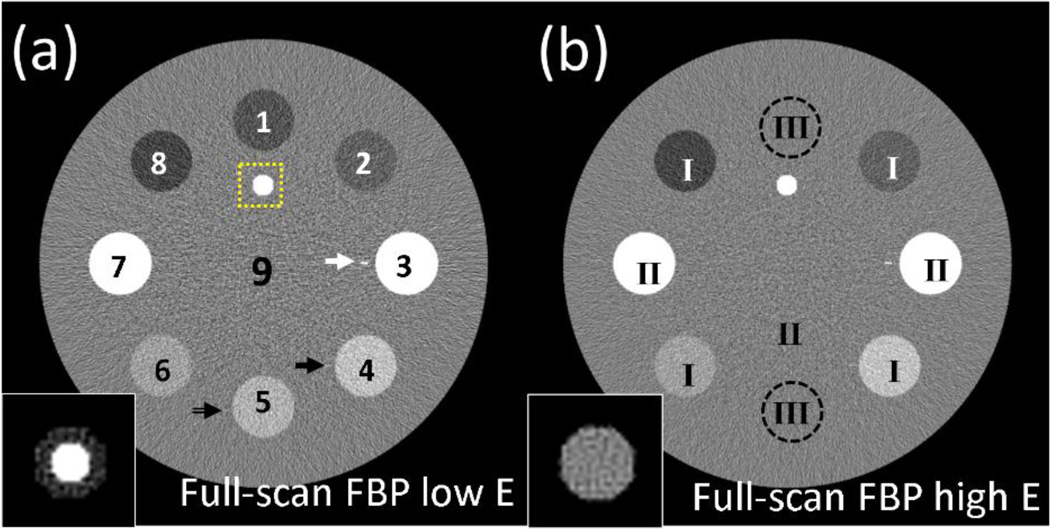
Figure 1.

CT images of a digital phantom reconstructed by full-scan FBP reconstructions at (a) low energy level, (b) high energy level. The labels in (a) are the indices of ROIs, and the labels in (b) indicate the different scenarios for each ROI. The dashed-line square in (a) indicates the region where the zoomed-in “vessel” at the bottom-left of each image is located. The black arrow, white arrow and double line arrow in (a) show the positions of line #1, line #2 and line #3 (corresponding to scenario I, II and III, respectively). Display window for full-FOV images is [−250 250] HU, and for zoomed-in “vessel” at bottom-left is $[\overline{HU}-80\overline{HU}+80]$ HU, where $\overline{HU}$ is the mean HU value of the “vessel” in each case.

Figure 2.

CT images of a digital phantom at low energy reconstructed by (a) SPIR, (b) TVR and (c) PICCS using (1) 50 views, (2) 20 views and (3) 10 views. The zoomed-in “vessel” at the bottom-left of each image is indicated by the dashed-line square in Fig. 1(a). The dashed circle shown in (c) is the ROI on which the noise STD in Table II is calculated. Display window for full-FOV images is [−250 250] HU, and for zoomed-in “vessel” at bottom-left is $[\overline{HU}-80\overline{HU}+80]$ HU, where $\overline{HU}$ is the mean HU value of the “vessel” in each case.

From Fig.2, it is seen that TVR and SPIR have similar reconstruction accuracy on a 50-view scan. The advantage of SPIR becomes prominent as the number of views further decreases. The images of SPIR on scans with 20 and 10 views show fewer patchy artifacts than those by TVR (see Figs. 2(a2), (a3), (b2) and (b3)). This finding is consistent with the measured reconstruction accuracies of CT numbers listed in Table I. SPIR with a 10-view scan has an R-RMSE of 1.33%, while TVR introduces large errors with the same number of views and increases R-RMSE to 6.18%. The CT images of SPIR shows sharper edges for rods with sufficient contrast in the high-quality CT image of the first scan (i.e., the scenario I and II rods) than the TVR images, which indicates a better spatial resolution on these objects. The result of PICCS shows a comparable accuracy and spatial resolution with that of SPIR, while it is much noisier. On the zoomed-in ROI of “vessel” simulating calcium plaque and iodine contrast which have the same pixel values in the high energy image, the boundaries between calcium and iodine are preserved in the low energy images of SPIR with scans of 20 views or more, a similar performance compared with TVR and PICCS (see Figs. 2(a2), (b2) and (c2)). However, TVR and PICCS fail to maintain the vessel shape, mainly because of their poor reconstruction accuracy for such a small object. On the scenario III rods with no sufficient contrast in the CT image of the first scan, the structure classification fails in SPIR. However, we find that SPIR still achieve similar image qualities with 10 views as TVR and PICCS. It is worth emphasizing again that the scenario III represents the most challenging case for SPIR and is considered rare in clinical practice.

Table I.

Measured CT number (in HU) of the ROIs and the background on CT images shown in Figure 1. The indices of ROIs are marked in Fig. 1(a). The indices of scenarios are marked in Fig. 1(b). The R-RMSEs are calculated by Eq. (10) with the ground truth obtained from the full-scan FBP images. The proposed SPIR method and TVR are applied on low-energy CT scans with different numbers of views. Note that, although the contrast rods have different linear attenuation coefficients at two different x-ray energies, their CT numbers in HU may be similar on the CT images of the two scans.

	ROI	High-E CT (First scan)	Low-E CT (Ground truth)	Low-E CT via SPIR				Low-E CT via TVR
Number of views		655	N/A	655	50	20	10	50	20	10
Scenario I	2	−58	−58	−59	−59	−60	−61	−59	−60	−46
	4	127	127	127	127	127	125	128	128	114
	6	62	63	63	63	63	65	63	61	51
	8	−113	−112	−113	−114	−114	−114	−114	−112	−95
II	3	508	1017	1017	1017	1016	1015	1018	1016	1004
	7	508	850	850	850	849	847	851	850	836
III	1	0	−87	−88	−88	−87	−83	−87	−85	−69
	5	1	94	96	96	96	92	95	95	87
Background	9	0	0	0	0	0	4	0	0	6
R-RMSE (%)				0.42	0.50	0.60	1.33	0.48	0.61	6.18

The measured 10% MTF frequency and noise STD are listed in Table II. On both line #1 and line #2 (i.e., scenario I and II, respectively), SPIR outperforms TVR on spatial resolution with the 10% MTF frequency higher by an average factor of 4, and maintains a similar noise STD. SPIR and PICCS show similar spatial resolution indicated by similar 10% MTF frequency. However, SPIR outperforms PICCS on noise suppression with a noise STD lower by a factor of 7. On line #3 (i.e., scenario III), SPIR, TVR and PICCS all fail to show observable contrast for this line. The above study reveals that the proposed SPIR is superior to TVR on spatial resolution with similar noise suppression, and superior to PICCS on noise reduction with similar spatial resolution.

Table II.

10% MTF frequency values and noise STD measured on Fig. 2.

	10% MTF frequency (lp/mm)
	50-view scan		20-view scan			Noise STD (HU)
	Line #1	Line #2	Line #1	Line #2	Average
SPIR	13.90	8.80	15.20	8.34	11.56	5
TVR	3.31	2.90	1.77	2.97	2.74	5
PICCS	6.76	11.43	6.29	11.48	8.99	34

3.2 Catphan phantom study

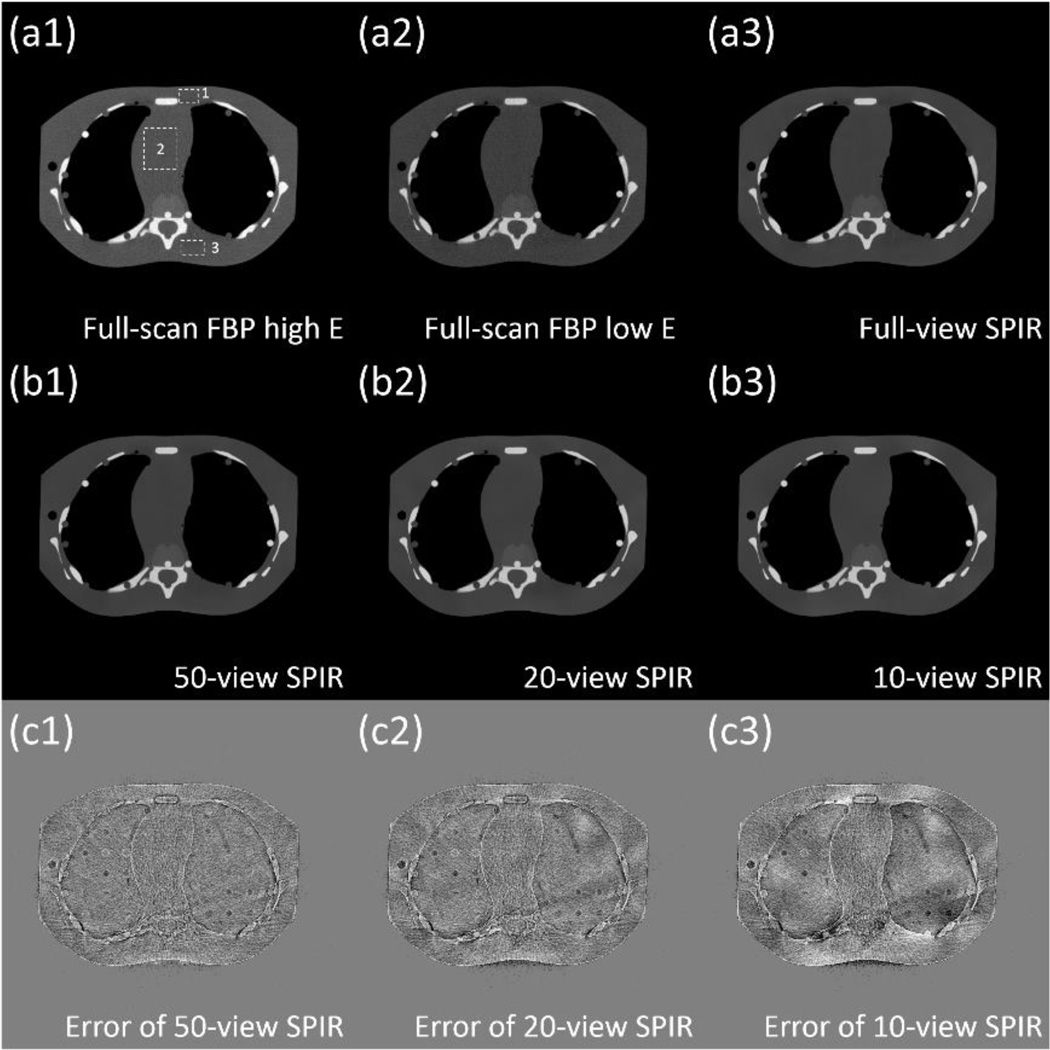
Fig. 3 shows the CT images of the Catphan phantom on the slice of line pairs, reconstructed by FBP, TVR and SPIR. The dotted circle area in Fig. 3(c) is selected as the ROI, of which the means and noise STDs are measured in Table III. SPIR achieves noise STD reduction by a factor of more than 10 compared with the full-scan FBP reconstruction. With the same data fidelity error, SPIR substantially outperforms the TVR method on image spatial resolution with half of the noise STD. As shown in the zoomed-in insert of each image on the ROI (indicated by the white rectangle in Fig. 3(a)), the TVR method has a spatial resolution of less than 5 pairs/cm when the view number is 50 (see Fig. 3(f)), while SPIR on even 10 views (see Fig. 3(e)) has a spatial resolution of 6 pairs/cm, comparable to that of the full-scan FBP image. The corresponding DECT decomposed images are shown in Fig. 4. The aluminum (the line-pair material) and the epoxy (the background) are chosen as the basis materials. It is seen that the high quality of CT images reconstructed by SPIR leads to high spatial resolution on the decomposed images.

Figure 3.

CT images of the Catphan phantom on the slice of resolution line pairs, reconstructed by FBP on full scan data at (a) low kVp and (b) high kVp, SPIR at low kVp using (c) 50 views, (d) 20 views and (e) 10 views, and (6) TVR at low kVp using 50 views. The dashed rectangle shown in (a) is the region where the zoom-in inserts of line pairs are located. The dotted circle shown in (c) is the ROI on which Table III is calculated. Labels in the bottom figure of (a) show the value of line pairs per cm for each line cluster. Display window: [−500 2500] HU.

Table III.

The means and the noise STDs of the CT number (in HU) in the ROIs indicated by the dotted circle shown in Figure 3(c).

Methods	Mean ± STD
Full scan FBP at 75kVp	−4±128
Full scan FBP at 125kVp	60±62
50-view SPIR at 75kVp	−4±9
20-view SPIR at 75kVp	−7±6
10-view SPIR at 75kVp	−4±7
50-view TVR at 75 kVp	−4±16

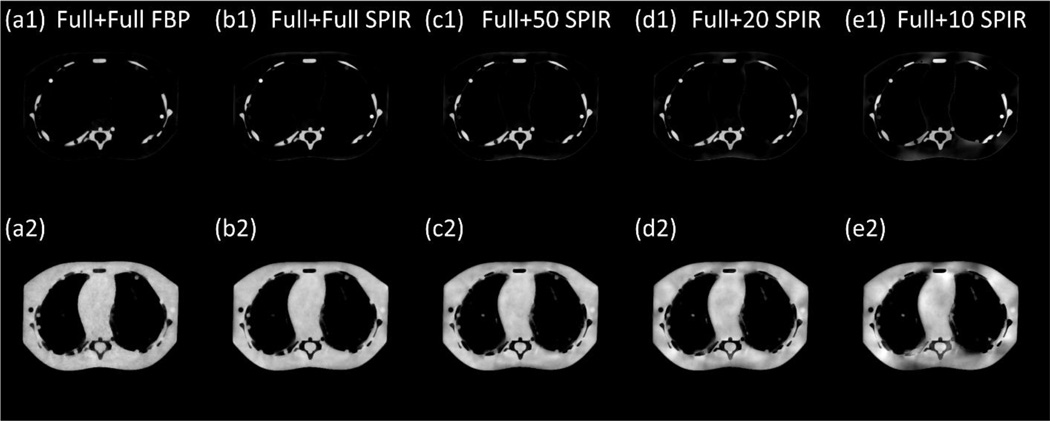
Figure 4.

The decomposed material images of line pair slice, based on the reconstruction images at low kVp and high kVp using (a) conventional two-full-scan FBP, SPIR-based DECT using one full scan and a second (b) 50-view, (c) 20-view and (d) 10-view scan. Row (1): “bone” images; row (2): “tissue” images; and row (3): magnified views of bone images in the ROI of dashed rectangle in Fig. 5(a). Display window: [0.1, 1.2].

We notice some low frequency artifacts in the decomposed images shown in Fig. 4(d2). Compared with simulation studies, phantom experiments contain larger projection errors mainly from beam-hardening and scatter. These errors propagate through both reconstruction and decomposition processes. In reconstruction, because of the very limited number of views in one scan, the error is non-uniformly distributed across the reconstructed image. This artifact is not obvious in CT images, but it is magnified and becomes noticeable after material decomposition, which is an error-sensitive process. (Niu et al., 2014)

A different slice of contrast rods of the Catphan phantom is used to evaluate the electron density measurement accuracy of SPIR-based DECT. Fig. 5 shows the electron density maps generated by the conventional two-full-scan FBP and SPIR-based DECT. The measurement errors of ROIs are listed in Table IV. The average errors on the results by SPIR-based DECT are comparable with those of the conventional two-full-scan FBP, which indicates the high accuracy of the decomposed images and electron density maps obtained by our method. As a side note, the measurement errors of electron densities shown in Table IV are different from those reported in the recent papers from our group.(Niu et al., 2014; Dong et al., 2014) It is mainly because of the different basis materials used in the DECT decomposition as well as the different phantom geometry.

Figure 5.

Electron density maps of contrast rods, based on the reconstruction images at low kVp and high kVp using (a) conventional two-full-scan FBP, SPIR-based DECT using one full scan and a second (b) 50-view, (c) 20-view and (d) 10-view scan. The labels in (a) indicate the ROIs on which Table IV is calculated. Display window: [2.5 6.5]× 10⁻²³ cm⁻³.

Table IV.

The percentage error of electron density measurement of contrast rods using conventional two-full-scan FBP and SPIR-based DECT with one full scan and a second N-view scan (“Full+ N”). The indices of the ROIs are marked in Fig. 5(a). The ground-truth electron density values are obtained from Catphan©600 phantom manual. The average absolute error is the average of the absolute values of error in all ROIs.

Scan scheme	1 Teflon	2 PMP	3 LDPE	4 Polystyrene	5 Delrin	Average absolute error
Conventional two- full scan FBP	0.64%	0.81%	−0.63%	−0.45%	−1.69%	0.84%
Full+Full	0.48%	0.95%	−0.60%	−0.18%	−1.71%	0.78%
Full+50	0.32%	0.98%	−0.57%	−0.75%	−1.65%	0.85%
Full+20	0.16%	1.01%	−0.57%	−0.95%	−1.80%	0.90%
Full+10	−0.18%	0.60%	−1.24%	−0.88%	−1.65%	0.91%

3.3 Pediatric phantom study

An anthropomorphic pediatric phantom with realistic vertebra structures is used to evaluate the performance of our method on objects with a complex geometry. The bone of the phantom is made of calcium and the soft tissue is composed of epoxy. Fig. 6 and 7 show the CT images and decomposed material images. Similar to our previous results, SPIR-based DECT generates accurate CT images and decomposed images with clearly separated bone and tissue structures. The error maps of CT image reconstructed by SPIR are shown in Fig. 6(c), with the full-scan FBP image considered as the ground truth. Three rectangles indicated by the dashed rectangle in Fig. 6(a1) are used as the ROIs for the measurement of the root-mean-square-error (RMSE) in HU, shown in Table V. Overall, SPIR maintains a low reconstruction error of less than 10 HU for scans with different number of views, except for the 10-view scan where the RMSE increases to 18 HU. A similar performance on image qualities for different numbers of views is observed on decomposed images shown in Fig. 7. We also notice similar low frequency artifacts shown in Fig. 7(e2) as those of Fig. 4(d2). These artifacts stem from the reconstruction error shown in Fig. 6(c), which is magnified in the error-prone procedure of material decomposition.(Niu et al., 2014)

Figure 6.

CT images of the pediatric phantom, reconstructed by full-view scan using (a1) FBP at high kVp, (a2) FBP at low kVp and (a3) SPIR at low kVp, and SPIR at low kVp using (b1) 50 views, (b2) 20 views and (b3) 10 views. The error maps of SPIR using (c1) 50 views, (c2) 20 views and (c3) 10 views compared with the full-scan FBP are also shown. The dashed rectangles in (a1) are the ROIs on which Table V is calculated. Display window is [−500 1500] HU for (a) and (b), and is [−150 150] HU for (c).

Figure 7.

The decomposed material images of the pediatric phantom, based on the reconstruction images at low kVp and high kVp using (a) the conventional two-full-scan FBP, the proposed SPIR-based DECT using one full scan and a second scan with (b) full views, (c) 50 views, (d) 20 views and (e) 10 views. Row (1) is the “bone” image and row (2) is the “tissue” image. Display window: [0.1 1.2].

Table V.

Measurements on error of mean pixel value and RMSE (both in HU) on CT images reconstructed by SPIR with different numbers of views. The ROIs are marked in Fig. 6(a1). The CT image of full-scan FBP at low kVp is chosen as the ground truth.

Number of views	Error of mean HU			RMSE
	ROI 1	ROI 2	ROI 3
655	5	−1	2	3
50	13	0	8	9
20	10	2	8	7
10	14	0	28	18

3.4 Clinical study

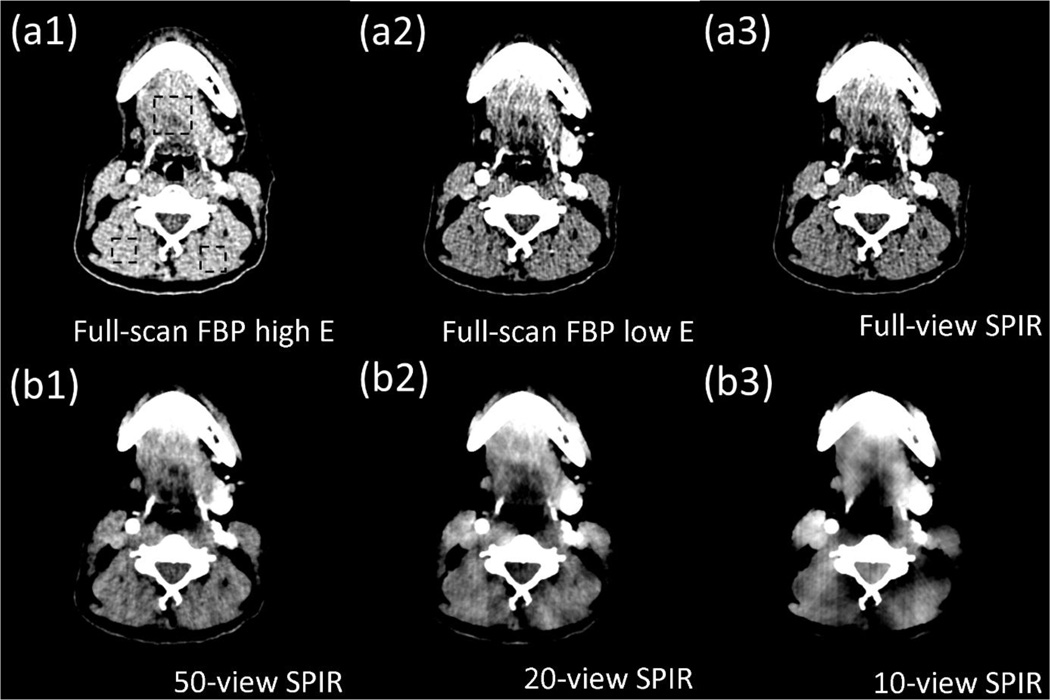
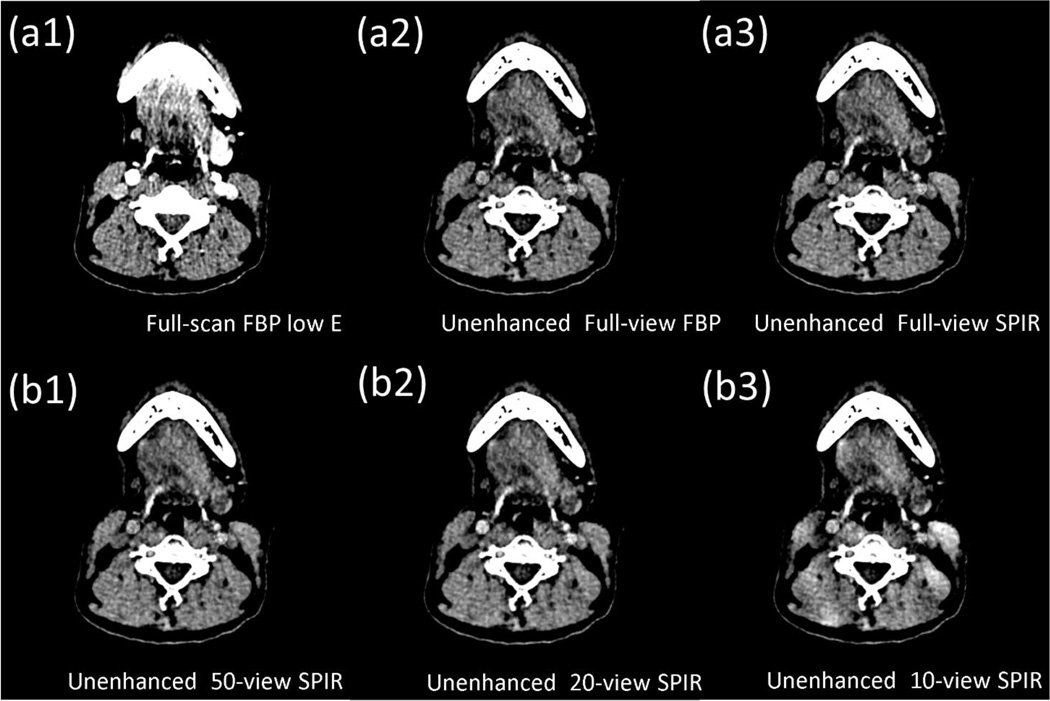
We use head patient DECT images acquired at 140 kVp and 80 kVp with full scans to further evaluate the performance of SPIR on a clinical dataset. Fig. 8 and 9 show the CT images and the virtual unenhanced images, with a narrow display window of 80 HU. To quantify the reconstruction accuracy by SPIR, RMSEs are measured on CT images in three uniform ROIs indicated by the dashed rectangles in Fig. 8(a1). The maximum RMSE is 7.2 HU when SPIR uses a second scan of only 10 views. As the number of projection views reduces, image non-uniformity and artifacts increase on the SPIR results. However, in the virtual unenhanced images of Fig. 9, it is seen that the vessels containing iodine contrast agency are successfully removed in the results using SPIR reconstructions on even 20 views, with an image quality similar to that using full-scan FBP.

Figure 8.

CT images of a head patient, reconstructed by (a1) full-view FBP at high kVp, (a2) full-view FBP at low kVp, (a3) full-view SPIR at low kVp, and SPIR at low kVp using (b1) 50 views, (b2) 20 views and (b3) 10 views. The dashed rectangles in (a1) are the ROIs on which RMSE is calculated. Display window is [0 80] HU.

Figure 9.

The original CT image and the virtual unenhanced CT images of a head patient. The virtual unenhanced CT images are generated from decomposed soft tissue and iodine images using (a2) the conventional two-full-scan FBP, the proposed SPIR-based DECT with one full scan and a second scan of (a3) full views, (b1) 50 views, (b2) 20 views and (b3) 10 views. The contrast-enhanced full-scan FBP image at low kVp is shown in (a1) for reference. Display window is [0 80] HU.

4 DISCUSSION AND CONCLUSIONS

In this work, we propose a new iterative CT reconstruction algorithm, SPIR, to reduce the data requirement for DECT. On a digital phantom, SPIR reduces the number of views in the second scan of DECT to as low as 10 with a reconstruction error of less than 1.5%. On physical phantoms, in addition to reduction of data acquisition in the second scan down to tens of views, SPIR achieves the same spatial resolution and an average error of less than 20 HU compared to the CT image reconstructed by the full-view FBP with image noise STD one order of magnitude less. Comparisons show that SPIR substantially improves over TVR on the reconstruction accuracy of a 10-view scan by decreasing the reconstruction error from 6.18% to 1.33%. SPIR also outperforms TVR at 50-view and 20-view scan in image spatial resolution with a higher 10% MTF frequency by an average factor of 4. Compared with the results by PICCS in 50-view and 20-view scan, the image reconstructed by SPIR has similar spatial resolution but with a noise STD 7 times lower. The high accuracy of SPIR leads to the high spatial resolution of decomposed material images and the high accuracy of electron density maps. The electron density map obtained from the SPIR-based DECT images with a second 10-view scan has an average error of less than 1%.

We demonstrate the performance of SPIR using a rotation-rotation mode of the broad-sense DECT technique with linear image-domain decomposition. Compared with the non-linear projection-domain decomposition of DECT in its original concept, such an implementation simplifies the signal processing of DECT at the price of lacking beam-hardening correction capability.(Yu et al., 2012) It should be noted, however, that our research presented in this paper is focused on the design of a new reconstruction algorithm for DECT independently of the decomposition process, and the use of SPIR does not require an image-domain decomposition. For example, we can first perform a non-linear decomposition on the dual-energy projection data using the same method as shown in our recent publication,(Petrongolo et al., 2015) and then carry out SPIR on the decomposed projections.

In this paper, we primarily focus on the development of a new reconstruction framework that reduces data acquisition for DECT without much degradation of image quality. In the presented proof-of-concept studies, we choose to evaluate the method performance using a rotation-rotation scan mode. It should be noted, however, that the rotation-rotation scan mode is not an ideal scheme of DECT imaging for our proposed method in clinical use. The involuntary patient movement might comprise the assumption that the second CT scan of DECT contains the same structural information as the first CT scan. The performance of the proposed algorithm is therefore expected to be more robust on advanced DECT scanners,(Xu et al., 2009; Petersilka et al., 2008) where patient motion is minimized via acquisition of dual-energy projections in a single scan.

We develop a new reconstruction framework that reduces data acquisition for DECT without much degradation of image quality. By reducing data acquisition for DECT, we can potentially reduce radiation dose on patients and hardware costs of the imaging system. For example, a “fast kVp switching” CT scanner (Xu et al., 2009) acquires dual-energy projections in one single rotation via switching the x-ray energy for neighboring projections. Since data acquisition is doubled without increasing scan time, the scanner is equipped with a fast detector and a fast-switching high-voltage generator, both of which significantly increase the system cost. The small number of projections in the low-kVp scan enabled by our method indicates that the switching rate can be significantly lowered on the kVp-switching CT scanner. A fast detector also becomes unnecessary as the total number of DECT projections only slightly increases compared with that of a single-energy CT scan. The manufacturing cost can therefore be substantially reduced on such a “slow kVp switching” DECT system.(Szczykutowicz and Chen, 2010) On a dual source CT,(Petersilka et al., 2008) The second sparse-view scan used by the proposed algorithm potentially leads to dose reduction on DECT imaging. In this paper, we have shown that a second scan with only 20 views (3% of a full scan, and thus negligible imaging dose) is sufficient for DECT imaging with a satisfactory image quality. In a clinical DECT protocol, it has been reported that, in order to maximize CNR, the optimal dose ratio between the low- and high-energy scans is approximately 1:2.(Richard and Siewerdsen, 2007; Sabol et al., 2001; Li et al., 2011) We can therefore roughly estimate the dose reduction achieved by the proposed method as about 30%, compared with the dose of DECT using two full scans. A thorough evaluation of dose reduction, however, entails comprehensive studies for different image quality metrics, clinical tasks and disease sites, and it is considered beyond the scope of this paper.

The parameters in similarity matrix generation are empirically chosen to yield results with satisfactory qualities. In the step of bilateral filtering for noise suppression, a small size of spatial window (i.e., X = 3) is used to ensure that each pixel is locally averaged by its neighboring pixels. In the step of similarity calculation step, a large window (i.e., X = 41) is used such that each pixel has a large number of pixels for similarity calculation. An over-large window includes too distant pixels that are less likely to be the same material, and also dramatically increases the memory burden. If the found similar pixels are less than a threshold value (200 in the presented implementations), the window size is adaptively enlarged until the threshold value is met. Otherwise the pixels with few similar pixels are less regularized and tend to be reconstructed poorly. In this paper, we find that the results obtained by the proposed algorithm are not sensitive to the above parameter values. As such, these parameters are fixed in all presented studies on different phantom data. For fair comparisons of SPIR, TVR and PICCS, we manually tune the regularization weighting of different algorithms to have the same data fidelity errors on the reconstructed images. Readers may notice that the results of TVR (see Figs. 1(c), (e), (g) and 6(f)) appear over-smoothed. It is because the data fidelity error is too large for TVR, while the same data fidelity error enables our proposed method to achieve a very high image quality with significantly reduced noise.

Future work is needed to further assess and improve the proposed SPIR algorithm. First, the method of generating similarity matrix W proposed in this paper is not the only solution of structure classification for SPIR. We will investigate more sophisticated image segmentation methods for improved calculation of the similarity matrix.

The success of SPIR mainly stems from the establishment of an additional data constraint shown in Eq. (5), where we use a similarity matrix W to exploit the redundant structural information of the CT images of the same object acquired at two different energies. By enforcing the new data constraint during the iterative reconstruction, SPIR shows promise on more accurate CT construction than TVR, a popular algorithm of iterative CT reconstruction. Studies have shown that TVR could over-smooth CT images and generate contouring artifacts because of its tendency to penalize the image gradient irrespective of the image structures.(Junguo et al., 2010; Yan et al., 2012; Tang et al., 2009; Liu et al., 2014) Instead of reducing signal variations only on adjacent pixels as done in TVR, SPIR reduces signal variations for all pixels of the same structure, which effectively avoids the image artifacts of a TVR reconstruction. As SPIR adopts an optimization framework with regularization, it is also possible to combine SPIR with TVR for unified benefits of these two algorithms.