Revisiting Models of Concurrent Vowel Identification: The Critical Case of No Pitch Differences

Summary

When presented with two vowels simultaneously, humans are often able to identify the constituent vowels. Computational models exist that simulate this ability, however they predict listener confusions poorly, particularly in the case where the two vowels have the same fundamental frequency. Presented here is a model that is uniquely able to predict the combined representation of concurrent vowels. The given model is able to predict listener’s systematic perceptual decisions to a high degree of accuracy.

1. Introduction

Humans demonstrate a significant ability to identify and concentrate on specific speakers within a complex auditory environment. Whilst this clearly relies on a multitude of cues, listeners can still identify both of a pair of steady-state vowels, presented simultaneously [1]. The concurrent vowel identification (CVI) task probes the effect that cues, such as pitch differences, have on this recognition [2].

Many models predicting human performance for CVI have been created [3, 4, 5, 6, 7]. The most widely accepted models generate segregated representations of each vowel by segregating information in different frequency regions according to fundamental frequencies (F0s) inferred from the model. The segregated representations are then compared to stored templates of individual vowels, to predict the concurrent vowel pair presented.

Meddis and Hewitt’s model [5] is widely cited as it is able to qualitatively predict human improvement in vowel identification when pitch differences are introduced between the vowel-pair. However, when no F0 differences are present, it under-predicts the correct identifications made by humans in their study (human: 57%, model: 37%). Recently, Chintanpalli and Heinz [8] further highlighted that although the model qualitatively reproduced the overall improvement with F0 differences, it very poorly accounted for the specific confusions made.

Even when the F0s of all vowels presented are identical, human CVI performance is greatly above chance [3]. This implies that identification cues beyond pitch differences are utilized that are not well accounted for in existing models. In this identical-F0 scenario, all existing models construct predictions of just individual vowels being identified by comparing unseparated representations of concurrent vowel pairs with internal templates of individual vowels. Furthermore, to construct predictions of concurrent vowel pairs being identified, either deterministic algorithms are used (e.g. [4, 5, 7, 8]), or probabilistic decisions are made following assumptions of independence (e.g. [3, 6]).

Here we explore the consequences of an alternative recognition process, for the important case where there is no F0 difference between vowel pairs. We hypothesize that predicting the complete internal representation of the presented stimulus would be an optimal solution to the CVI task, and might produce results in line with human behaviour. Therefore, internal representations should describe concurrent vowel pairs (i.e. retaining dependent information), as opposed to individual vowels. Our model simulates different variants of auditory processing, followed by a naive Bayesian classifier which allows for probabilistic predictions of human decisions and systematic comparison of different recognition strategies.

2. Concurrent Vowel Identification

2.1. Stimuli

Synthetic vowels (steady-state harmonic complexes) were created using a Klatt-synthesizer [9]. The formant frequencies and bandwidths matched those specified by Chintanpalli and Heinz [8]. The fundamental frequency of all vowels were 100 Hz, and all vowels were set to 65 dB SPL. All vowels had a duration of 400 ms (including 10ms onset/offset raised cosine ramps).

With a total of 5 individual synthetic vowels (/i/, /a/, /u/, /æ/, /ɝ/) there are a total of 15 unique pairwise combinations. The waveforms were added to one another to create concurrent vowel pairs.

2.2. Task

The CVI task and data are detailed in Chintanpalli and Heinz [8]. Five subjects were randomly presented one of the 15 concurrent vowel pairs and were required to identify two vowels from the set of five (different or identical). Each subject responded to 300 trials of concurrent vowels with identical F0s. Participants had considerable training with individual and concurrent vowel stimuli.

3. Computational Model

Our computational model generated ideal-observer based predictions of human decisions. For each concurrent vowel pair a probabilistic distribution of auditory activity was generated from a simulation of the auditory system. This was compared to distributions associated with all selectable concurrent vowel pairs, or individual vowels as in previous models.

3.1. Auditory System

Waveforms of concurrent vowel pairs (/ν_i, ν_j/ where ν_i, ν_j ∈ {i, a, u, æ, ɝ}) were bandpass filtered, simulating middle and outer ear effects, and then passed to a linear cochlear filter bank. This comprised 100 gammatone filters centred at logarithmically spaced frequencies from 80 to 4000 Hz. Different filter bandwidths could be implemented, determined from masking experiments in humans [10, 11] or guinea-pigs [12]. The outputs of each filter were then half-wave rectified. An auditory representation (μ_ij) followed from one of two processing pathways:

• Spectral processing. The logarithm of the RMS of each channel was calculated and standardised across channels (mean of 0, SD of 1).

• Temporal processing. An autocorrelation function was applied to each channel [6]. These were pooled across all channels and then standardised as above.

Independent, normal, zero-mean noise with identical variance was then added to each value of this representation. This resulted in a distribution of auditory activity $(\mathit{a}\sim \mathcal{N}({\mu }_{\mathit{ij}},{\sigma }^2\mathit{I}\left)\right)$The variance was the only free parameter in our model.

3.2. Classification

The task of the listeners, and our classifier, was to determine what stimulus had been presented for all instances of auditory activity (a). We did this using a naive Bayesian classifier, which determined regions of auditory activity (R_k) where a given stimulus class (C_k) was more probable than any other stimulus class to have produced said auditory activity (i.e. a ∈ R_k if k = arg max_i P(C_i|a)). Given the presentation of a concurrent vowel pair, the probability that our model predicted a certain stimulus class had been presented was

$$\mathit{P}(C_k\mid ∕v_i,v_j∕)={\int }_{\mathit{a}\in R_k}\mathit{P}(\mathit{a}\mid ∕v_i,v_j∕)\mathrm{d}\mathit{a}.$$ (1)

These high dimensional integrals were then evaluated numerically.

We modelled two approaches for classification which differed in the stimulus classes used, each producing a confusion matrix (P(/ν_x, ν_y/|ν_i, ν_j/) where ν_x, ν_y ∈ {i, a, u, æ, ɝ}):

• Combined Classes. Each class was a probabilistic template describing a combination of vowels. These were constructed by passing concurrent vowel pairs through our auditory model. Due to the equivalence of stimuli classes with the stimuli presented, calculating Equation (1) produced a suitable confusion matrix.

• Individual Classes. Each class was a probabilistic template describing an individual vowel (calculating Equation (1) resulted in P(/ν_z/|/ν_i, ν_j/) where ν_z ∈ {i, a, u, æ, ɝ}). To obtain predictions of concurrent vowel pair presentation probabilities, individual vowel presentation probabilities were multiplied together. This approach, assuming individual vowels are identified independently of one another, was initially proposed in [4].

For each model variant, we selected the variance of the internal noise (σ²; single free parameter) to predict the closest fit to the overall percent of concurrent vowels correctly identified by listeners.

4. Results

The model predicts the combined auditory response of presented concurrent vowels (Section 3.2: combined classes). Given this assumption it was able to match the mean number of concurrent vowels correctly identified by listeners in the absence of any F0 differences (73%). More importantly, however, the probabilities of individual decisions (i.e. the confusions) predicted by our model are acutely similar to those made by listeners (Figure 2, circles), despite the fact that no attempt was made to fit the confusions themselves. Spectral processing models were best at predicting human decision probabilities (r > 0.94, p < 0.01; r was calculated between sets of values, ignoring any matrix structure). Decisions predicted using temporal processing were less accurate (although in all cases r > 0.86, p < 0.01).

Figure 2.

A scatter plot comparing the probabilities with which humans predicted concurrent vowel pairs had been presented, against probabilities predicted from the combined-class (ο; σ² = 1.03) and individual-class (×; σ² = 1.20) variants of our spectral model. The probabilities of confusing /ɝ,ɝ/ for /u.ɝ/, and correctly identifying /a,æ/, are indicated.

We also considered a model which compared auditory responses of concurrent vowels to representations of individual vowels (Section 3.2: individual classes). Like similar previously published models, it fails to approach the mean number of concurrent vowels correctly identified by listeners for any amount of internal noise, predicting a maximum value of 42% when a temporal pathway was implemented. Additionally the probability of individual decisions were poorly correlated with human data (max r of 0.42, p <0.01).

The predictions from the best fitting of such models (Figure 2, crosses) are clustered close to 0% and 100% correct, suggesting that these errors are much more specific and confident than those of human listeners. Consistent with this, the entropy of the decision probabilities, corresponding to their randomness, was lower for models of individual-class recognition (<4.86 bits) than either the human data (5.11 bits) or the combined-class recognition model (>5.05 bits). Thus, the models of individual-class recognition make more errors than people because they make the wrong decisions consistently, and despite the probabilistic nature of the models.

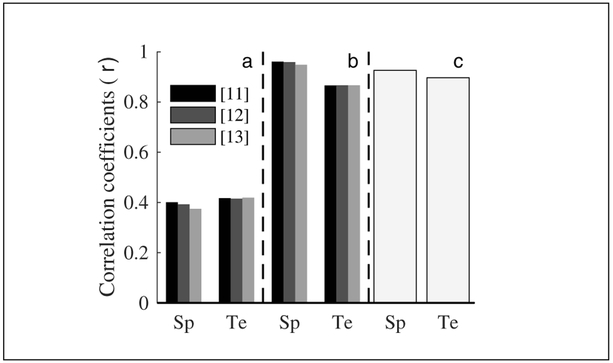
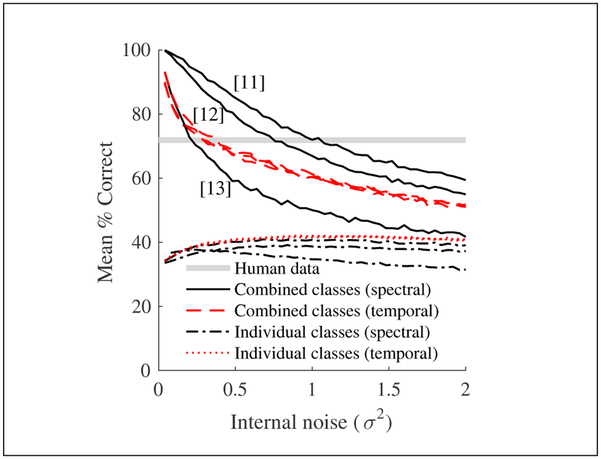
The combined-class model which predicted human decisions best used spectral processing, outperforming the temporal representation. Perhaps surprisingly, neither temporal nor spectral processing depended on whether filterbanks were based on human or guinea-pig bandwidth estimates (Figure 3b). Further investigation revealed that for spectral processing, filters with narrower bandwidths approached human like performance with more internal noise (Figure 4, solid lines). This was not the case when using a temporal pathway, in which frequency resolution is not such a constraint (Figure 4, dashed lines). In contrast, identification from individual classes (Figure 4, dotted and dash-dotted lines) did not converge on human performance for any amount of internal noise.

Figure 3.

Correlation coefficients (r) between predicted confusions for model variants, and listener confusions. ‘Sp’: Spectral pathway, ‘Te’: Temporal pathway. [11],[12],[13] are references to different cochlea filter-shapes. a) Individual classes, b) Combined classes, c) Combined classes with non-linear cochlear model [13].

Figure 4.

(Colour online) Average number of concurrent vowels correctly predicted as a function of internal noise, for variants of our model. [11],[ 12],[ 13] reference different cochlea filter-shapes.

Finally, we tested a more sophisticated model of the guinea-pig cochlea, which incorporated non-linear filtering and haircell transduction [13]. This produced the same qualitative relationships aforementioned (Figure 3c).

5. Discussion

The presented model demonstrated how predicting the complete internal representation of concurrent vowels produces decisions in line with listener behaviour, when no F0 differences are presented. However, instead assuming individual vowels are identified independently of one another (Section 3.2: individual classes) produced poor estimates of listener confusions. In fact fitting a confusion matrix in order to optimise the correlation coefficient between predicted and human confusions, under the constraint that individual vowels are identified independently of one another, results in a theoretical maximum r of 0.88.

Assmann and Summerfield [3] explored the effect of various transformations to auditory excitation patterns on predictions of listener CVI data, incorporating this assumption of independence. They achieved correlations with listener confusions between 0.42 and 0.71, over 0.25 lower than our best prediction. The authors found that emphasising spectral peaks best matched their listener data.

The work promotes the use of an ideal observer type model as an initial point to investigate cues beyond pitch for the CVI task. The model hints at a process that seeks to optimally predict which concurrent-vowel pair led to a corresponding auditory representation. Considering where listener behaviour deviates most from ‘ideal’ could represent a structured approach to extending, and improving the performance, of this model.

6. Conclusion

A novel computational model predicts human CVI behaviour, when vowels have identical pitches. It is better at predicting listener’s systematic perceptual confusions than existing models, when ideal representations of combined speech were implemented. The model’s simplicity allows potential extension to more complex scenarios with more identification cues (e.g. F0 differences), and to investigate the possible mechanisms underlying CVI.

Figure 1.

A diagram describing our model of CVI.