A threonine zipper that mediates protein–protein interactions: Structure and prediction

Abstract

We present the structure of an engineered protein–protein interface between two beta barrel proteins, which is mediated by interactions between threonine (Thr) residues. This Thr zipper structure suggests that the protein interface is stabilized by close‐packing of the Thr residues, with only one intermonomer hydrogen bond (H‐bond) between two of the Thr residues. This Thr‐rich interface provides a unique opportunity to study the behavior of Thr in the context of many other Thr residues. In previous work, we have shown that the side chain (χ ₁) dihedral angles of interface and core Thr residues can be predicted with high accuracy using a hard sphere plus stereochemical constraint (HS) model. Here, we demonstrate that in the Thr‐rich local environment of the Thr zipper structure, we are able to predict the χ ₁ dihedral angles of most of the Thr residues. Some, however, are not well predicted by the HS model. We therefore employed explicitly solvated molecular dynamics (MD) simulations to further investigate the side chain conformations of these residues. The MD simulations illustrate the role that transient H‐bonding to water, in combination with steric constraints, plays in determining the behavior of these Thr side chains.

Broader Audience Statement: Protein–protein interactions are critical to life and the search for ways to disrupt adverse protein–protein interactions involved in disease is an ongoing area of drug discovery. We must better understand protein–protein interfaces, both to be able to disrupt existing ones and to engineer new ones for a variety of biotechnological applications. We have discovered and characterized an artificial Thr‐rich protein–protein interface. This novel interface demonstrates a heretofore unknown property of Thr‐rich surfaces: mediating protein–protein interactions.

Short abstract

PDB Code(s): http://firstglance.jmol.org/fg.htm?mol=6CIU

Introduction

Protein–protein interactions are ubiquitous in biology and underlie virtually all cellular processes. Several analyses have studied the nature of protein–protein interactions and there have been some successful attempts to design new interactions.1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 We are still not, however, at the point where we can confidently predict whether or not a pair of proteins will interact. Here we present an interesting, and unexpected, Thr‐rich interface that mediates a novel interaction between protein subunits.

While studying the homotetrameric fluorescent protein Azami Green,13 we sought to decrease the strength of the subunit–subunit interaction. We also sought to maintain the overall β‐strand stability and structure of the dissociated subunits in addition to maintaining their solubility. Since Thr is a good β‐strand former,11 is hydrophilic, and a single mutation to Thr in Azami Green (V123T) has previously been shown to be disruptive to binding,13 we rationalized that multiple mutations to Thr at the interface would prove disruptive to binding. With this in mind, we introduced increasing numbers of Thr residues at one of the homodimer interfaces.

Introducing one and two Thr residues at this interface (V123T or V123T plus another mutation to Thr) had the desired effect. The protein interface was disrupted, as evidenced by the change in anisotropy of the observed fluorescence in Supporting Information, Figure S1, but the four subunits maintained their folded structures, as evidenced by their unchanged fluorescence excitation and emission spectra. We substituted yet another interface residue for Thr and found, unexpectedly, that the protein exhibited the fluorescence anisotropy properties consistent with it again being a tetramer [Fig. 1(B)].

Figure 1.

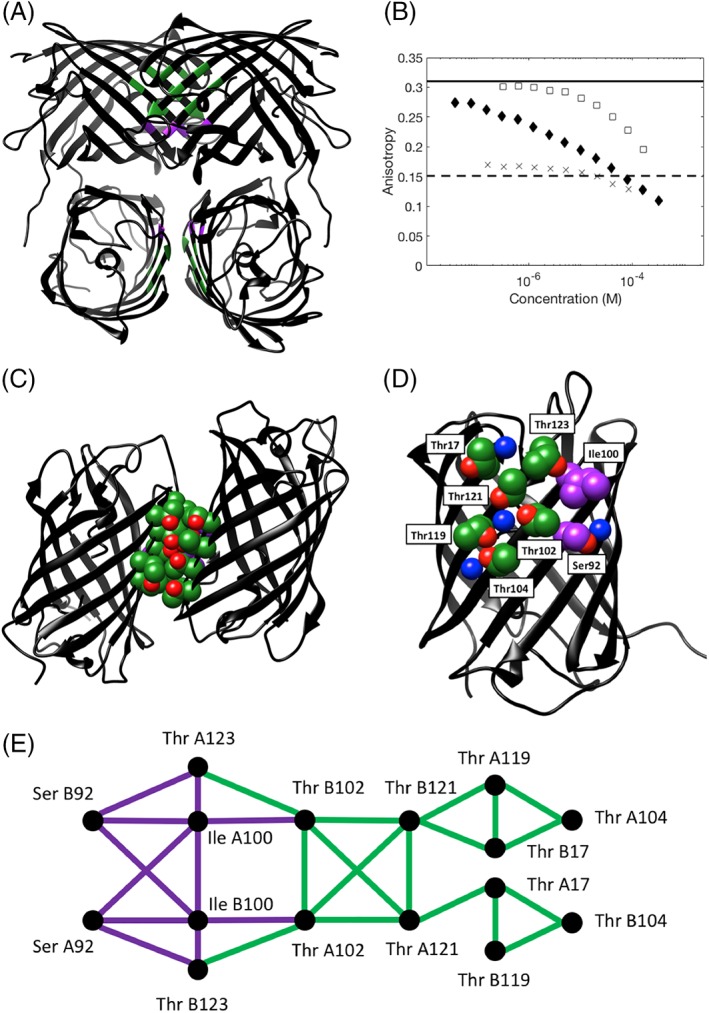
Crystal structure of the tetrameric Thr zipper protein, illustrating the positions of key interface residues and data for the oligomeric state from anisotropy experiments. (A) Ribbon representation of the Thr zipper tetramer structure with interface residues colored by residue type (green = Thr, purple = non‐Thr interface core residue). (B) Fluorescence anisotropy of Azami Green mutants, as a function of protein concentration. Each of the three mutants of Azami Green was serially diluted from its stock solution and then the anisotropy was measured: D121T (crosses), R119TD121TV123T (solid diamonds), and R119DD121TV123T (open squares). The solid line shows the expected anisotropy for an Azami Green monomer, the dashed line shows the expected anisotropy for an Azami Green tetramer. (C) Ribbon representation of the Thr zipper structure with two of the monomers shown to illustrate the dimer interface. (D) A view of the Thr zipper monomer, showing the positions of the key interface residues, and high occupancy water molecules. In both C and D, the side chains of interface residues are shown in space filling representation: green and red (oxygen) = Thr; purple = non‐Thr interface core residue, blue = a water molecule. (E) Interaction network of the key interface residues for chains A and B based on hard sphere interactions. Thr–Thr contacts are shown in green, other contacts in purple. The interaction graph for the interface residues on chains C and D has an identical network topology.

We were interested in determining how the Thr residues interact to form this new interface and, to this end, crystallized and solved a high‐resolution crystal structure of this protein [Fig. 1(A)]. For simplicity, we will refer to this as the Thr zipper protein. In addition to presenting this structure, we also show how computational studies using the hard sphere (HS) plus stereochemical constraint model and explicit solvent all‐atom molecular dynamics (MD) simulations give a more detailed understanding of the relative energetic contributions related to the positioning of each Thr side chain at the interface.

Results

Identification of Thr‐rich interface

We sought to manipulate the association properties of the naturally homotetrameric fluorescent protein, Azami Green.13 We made mutations at one of the two homodimer interfaces, with the goal of decreasing the affinity of the interaction at that interface, and thus causing the tetramer to dissociate into dimers [see Fig. 1(D) for the position of key interface residues]. We monitored the effects of the mutations by using fluorescence anisotropy to measure the dissociation constant of the dimer‐dimer interaction. The Azami Green monomer and tetramer have been previously reported to have fluorescence anisotropy values of ~0.31 and 0.15, respectively.13

We therefore measured the fluorescence anisotropy as a function of protein concentration for the wild‐type and all the mutant forms of Azami Green that we created. We found that wild‐type Azami Green has a fluorescence anisotropy value of ~0.15 over the entire concentration range we tested (2 pM to 10 μM). In contrast, the Azami Green mutant with the weakest binding that we studied (R119DD121TV123T) has a fluorescence anisotropy value of ~0.31 for all concentrations below 10 μM. This anisotropy value is consistent with previously reported anisotropy values for an Azami Green monomer.13

Mutant forms of Azami Green that have subunit–subunit binding affinities between those exhibited by tetrameric wild‐type Azami Green and monomeric Azami Green (R119DD121TV123T) are expected to show concentration‐dependent changes in fluorescence anisotropy. We therefore used fluorescence anisotropy to determine the effect of mutations on the subunit–subunit binding affinity.

Three exemplar plots of fluorescence anisotropy as a function of protein concentration are shown in Figure 1(B). A single mutation (D121T) was not noticeably disruptive to the interface and the protein harboring this mutation exhibits the same anisotropy as the wild‐type Azami Green tetramer. A mutant in which two of the interface residues are mutated to Thr and one is mutated to Asp (R119DD121TV123T) is the most disruptive. This protein displays a fluorescence anisotropy that is consistent with it being a monomer at all concentrations until high μM. The unexpected observation was that a triple mutant, in which residues 119, 121, and 123 are all mutated to Thr (R119TD121TV123T) showed much tighter binding than the R119DD121TV123T mutant, as evidenced by much higher anisotropy values for equivalent protein concentrations [Fig. 1(B)]. For the full set of Azami Green mutants tested, see Supporting Information, Table S1.

We followed up on this observation by determining the high‐resolution X‐ray crystal structure of the triple Thr mutant, to determine the molecular interactions that underlie the new, Thr‐rich interface (Fig. 1). Refinement statistics are presented in Supporting Information, Table S2.

The Thr zipper protein readily formed plate crystals under similar conditions used to crystallize monomeric Azami Green (PDB ID: http://firstglance.jmol.org/fg.htm?mol=3ADF). The structure of the Thr zipper protein was determined to a resolution of 1.7 Å, with four monomers forming a tetramer in the asymmetric unit. The Thr zipper protein monomer and wild‐type Azami Green monomer have similar backbone structures with root‐mean‐square deviations in the C _α positions on the order of ~0.5 Å between the wild‐type Azami Green monomer and each monomer of the Thr zipper protein. Although the four individual Thr zipper monomers are structurally similar to each other, they are not identical (Supporting Information, Table S3); we will note the instances in which they differ below.

In Figure 1(C,D), we show a close‐up of the Thr‐rich interface with the sidechains of the Thr introduced at positions 119, 121, and 123 indicated (see Supporting Information, Fig. S2 for a representation of the interacting Thr interface residues).

We explored the possibility that the stability of the Thr zipper interface derives from the removal of charged residues (R119 and D121) rather than from the introduction of new Thr residues. Considering the behavior of different combinations of mutations leads us to conclude that it is the introduction of Thr residues is important for formation of a stable interface, and not the removal of charged residues. Wild‐type Azami Green is a stable tetramer, whereas mutants R119DD121TV123T (Fig. 1) and R119TV123T and R119DV123T (Supporting Information, Fig. S1) are all monomeric below concentrations of ~10 μM.

To study the subunit–subunit interface of the Thr zipper protein, we first identified the interface residues by determining those with a solvent‐accessible surface area (SASA) that changes by more than 0.1 Ų upon complex formation (23 residues). We then determined which of these residues is core (or buried) at the interface, which we define as rSASA <0.3 (see Methods for calculations and definition of rSASA). We identified Thr 17, Ser 92, Ile 100, Thr 102, Thr 104, Thr 119, Thr 121, Thr 123, Val 152, and Thr 176 as core residues. We then identified the center of the interface by finding the center of mass of Thr 119, 121, and 123 on chain A and the corresponding residues on chain B of the Thr zipper protein, where chains A and B are those defined in the pdb file. We subsequently only considered residues with side‐chain atoms that are within 8 Å of the interface center, which was the smallest radius that included all of the Thr residues. As these residues presumably play a dominant role in determining the binding affinity of the subunit–subunit interface of the Thr zipper protein, we focused on the following eight residues: Thr 17, Ser 92, Ile 100, Thr 102, Thr 104, Thr 119, Thr 121, and Thr 123 (see Supporting Information, Table S4 for SASA values). These eight residues also form a cluster of mutually interacting hard spheres [Fig. 1(E)]. The cluster was determined by pairwise simultaneous rotation of each amino acid with a fixed backbone, where we define a hard sphere interaction as the overlap of the van der Waals surface of two atoms.

In previous work, we demonstrated that the positions of the side chains of residues in protein cores are dominated by steric interactions. To better understand how each residue contributes to the stability of the interface, we performed calculations to predict the χ ₁ dihedral angle conformations using the HS model that we developed previously.14, 15, 16 Specifically, we determined whether we are able to recover the conformation of the side chain of each interface residue that is observed in the crystal structure. Analysis of the results of these calculations provides insights into the forces that determine the side‐chain conformations of residues at the interface, and ultimately the stability of the interface. Below we discuss these results, residue by residue, for each of the eight interface residues.

In previous studies, we showed that we are able to recover the χ ₁ dihedral angles for the hydrophobic residues Ile, Leu, Phe, Trp, Tyr, and Val in the cores of soluble proteins, protein–protein interfaces, and transmembrane proteins.15 In particular, the HS model is able to recapitulate the side‐chain conformations of these residues in high‐resolution crystal structures to within 30° in more than 90% of cases. As shown in Table 1, we are able to repack the side chains of Ile 100 to within 17° of the crystal structure value of the χ ₁ dihedral angle in all four chains of the Thr zipper protein. We also predict Ser 92 within 4° of the side‐chain conformation observed in the crystal structure. The majority of the residues at the interface are Thr (six out of eight). In prior studies, we found that we could predict the χ ₁ dihedral angles of Thr in any high‐resolution crystal structure to within 30° in more than 90% of cases. Thus, statistically, we expect that the HS model should be able to recover five of the six Thr side‐chain conformations at the interface.

Table 1.

Side Chain Dihedral Angle Values for Interface Residues from the Thr Zipper Crystal Structure (Χ ₁ ^xtal), the HS Prediction (Χ ₁ ^pred), and from MD Simulations (Χ ₁ ^MD)

Residue	Χ 1 xtal (°)	Χ 1 pred (°)	Χ 1 MD (°)
			60° (%)	180° (%)	300° (%)
Thr 17	281	276	1	53	46
Ser 92	67	66	92.1	1.5	4.4
Ile 100	292	295	0	0	99.5
Thr 102	52	69	98.2	0	0
Thr 104	67	301	2.0	29.3	67.3
Thr 119	67	303	2.7	60.4	32.5
Thr 121	302	301	3.8	0	94.6
Thr 123	66	71	98.3	0	0

Each value is averaged over all four monomers. For Χ ₁ ^MD, we report the fraction of the simulation spent in each rotameric bin with width 30° centered around 60°, 180°, and 300°. See the Supporting Information for the Χ ₁ side chain dihedral angle data for each individual monomer.

In the crystal structure, Thr residues at the interface have nearly identical χ ₁ dihedral angles across all four monomers. For Thr 102, 104, 119, and 123, χ ₁ occupies the 60° side chain rotamer. For residues 17 and 121, χ ₁ occupies the 300° side chain rotamer. In Table 1, we show that the HS model is able to recover Thr 17, 102, 121, and 123 to within 30° of the χ ₁ dihedral angle conformations observed in the crystal structure. However, the HS model is not able to recapitulate the side chain dihedral angles of either Thr 104 or 119.

Thr 102 is H‐bonded to its pseudo‐symmetric partner Thr 102′ across the subunit–subunit interface. The HS prediction identifies the correct rotamer for this residue. The alternate rotamer is energetically unfavorable, presumably because this side chain is in a tightly packed environment. Thus, avoiding clashes of the side chain methyl group dominates the positioning of the side chain. Although the correct rotamer is predicted, the HS model predicts a value of χ ₁ that is on average 14° different from the observed χ ₁ value. We believe this is due to the fact the side chain is H‐bonded and recapitulating the exact χ ₁ observed in the crystal structure would result in an energetically unfavorable steric overlap when using the HS model. But, the close‐packing in the vicinity of this Thr residue does not allow an alternative rotamer, as that would be even more unfavorable.

The side chain of Thr 121 is predicted with a χ ₁ value <5° different from the value that is observed in the crystal structure. This result again indicates close‐packing of the side chain, so that an alternate rotamer conformation would result in a steric clash. Similarly, the side chain of Thr 123 is also well predicted, with a value of χ ₁ in close agreement with that observed in the crystal structure. Again, we interpret this result as indicating that this side chain is close‐packed and that positioning the side chain in an alternative rotamer would result in a steric clash. This side chain is H‐bonded to the backbone of Ile 100 in its own subunit, but the potential H‐bond is long enough that it is not identified as a steric overlap.

In contrast, the HS model does not predict the observed χ ₁ dihedral angle for either Thr 119 or Thr 104. These residues are H‐bonded to each other with a relatively short distance (2.7 Å). These residues are presumably not tightly packed. The alternate rotamer conformation does not result in a steric clash more energetically unfavorable than the H‐bond overlap. Even if we include crystallographically observed high‐occupancy water molecules at the interface, this area of the interface has sufficiently low packing density to allow these Thr side chains to adopt alternate rotamer conformations. In the HS model, the short Thr 104‐Thr 119 H‐bond is identified as a steric overlap, but there is space at the interface for these residues to be positioned in an alternate rotamer to avoid this apparent clash, while not moving the methyl group into a position where it overlaps with anything.

To better understand the instances where the HS model is not able to recapitulate the crystal structure χ ₁ dihedral angles, we used atomistic MD simulations to evaluate side chain positioning in the presence of hydrating water molecules. Such simulations also provide ensemble distributions of rotameric conformations that are sampled at room temperature, thereby providing complementary information to that obtained from the crystal structure and the HS model.

In the MD simulations, all side‐chain conformations are sampled while the protein backbone is harmonically constrained, but in most cases the most frequently populated χ ₁ dihedral angle is that observed in the crystal structure and predicted by the HS model. For some residues in the MD simulations, such as Thr 104 and Thr 119, the side chains move away from their experimentally determined positions. Initially, these amino acids orient their side chain hydroxyls toward one another to stabilize intramolecular hydrogen bonds. However, when experimentally determined high occupancy water molecules are removed, and the protein is “rehydrated,” new H‐bonds to water are allowed, therefore enabling new rotameric side chain conformations to become accessible (Fig. 2 and Supporting Information, Figs. S3 and S4). A movie showing this behavior is also included in the Supporting Information.

Figure 2.

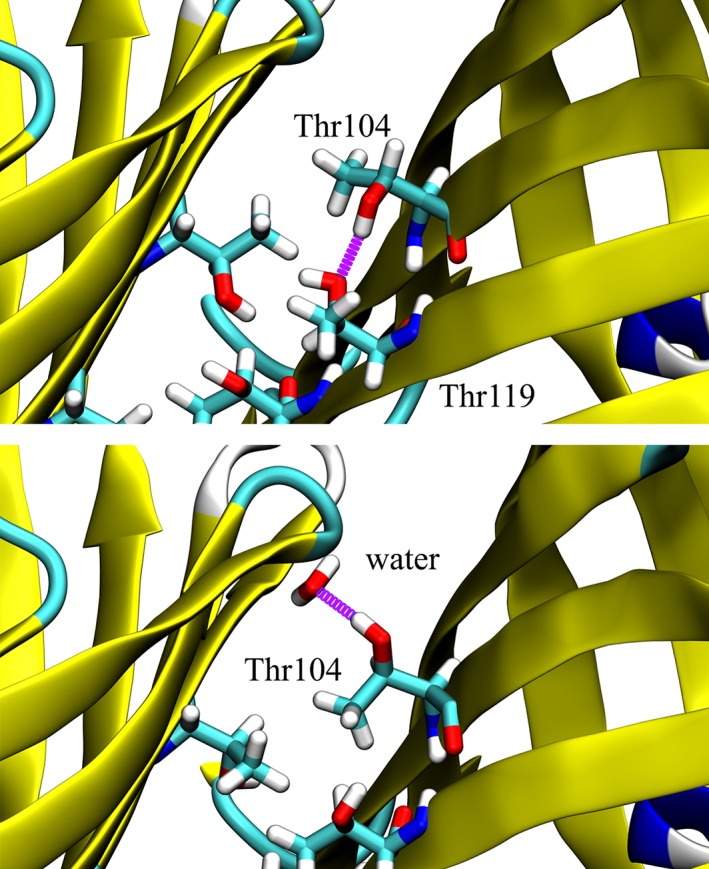
MD simulations of Azami Green reveal that Thr residues near the aqueous interface can either H‐bond to neighboring Thr (top) or to nearby water molecules (bottom). Many of the Thr hydroxyls that initially face inward (Χ ₁ ≈ 60) quickly rotate outwards toward water (Χ₁ ≈ 180, 300), though the rate of this transition depends strongly on the local hydration profiles and positions of stabilized water molecules. H‐bonds are shown in purple, carbon in cyan, oxygen in red, and hydrogen in white. Yellow, cyan, and white backbones indicate β‐sheet content, turns, and disordered regions, respectively.

Discussion

We describe the creation of a protein that adopts a new oligomeric state as a result of introducing multiple Thr residues clustered on its surface. By determining the structure of this protein, we showed how the Thr residues form the subunit‐subunit interface. We used the HS model, as well as all‐atom MD simulations with explicit solvent, to understand the factors that control the side chain conformations of buried interface residues and the resulting stability of the oligomer. In past work, we have shown that steric constraints are the dominant interactions that determine the positioning of Thr residues at buried positions in the core of proteins and at interfaces. Prior to this work, however, we had not investigated the ability of the HS model to predict the positioning of Thr side chains in such a Thr‐rich environment. We find that for many of the Thr residues, the HS model is able to predict their side‐chain conformations. For two residues, the HS model does not predict the value of χ ₁ observed in the crystal structure. However, MD simulations reveal that multiple side‐chain conformations are sampled, especially those stabilized by transient interactions with water molecules, suggesting alternative low energy conformations of certain Thr side chains.

Conclusions

In summary, we have shown how a cluster of Thr residues can form a new protein–protein interaction interface. We hypothesize that it is the ability of multiple, identical Thr residues to pack together when displayed on two relatively flat surfaces that is responsible for the stability of the interface. Neither the crystal structure nor the results of our MD simulations suggest that Thr–Thr H‐bonds play a significant role in stabilizing this interface. We consider such Thr‐rich surfaces as a new motif available to those who are interested in protein design.

Materials and Methods

Plasmid construction and mutagenesis

All cloning was performed in Escherichia coli strain DH10B using the pRSFDuet‐1 plasmid (Novagen). The wild‐type Azami Green sequence (ordered from Integrated DNA Technologies) was subcloned into the first of two multiple cloning sites, so that when expressed the resultant protein has an N‐terminal His₆ tag. Mutagenesis was performed using the QuikChange II method, according to manufacturer's instructions (Agilent).

Protein expression

Protein was expressed in Escherichia coli strain Rosetta (DE3) (Novagen). A 5 mL starter culture was grown from a single colony overnight at 37°C in LB medium supplemented with 50 μg/mL kanamycin. The 5 mL starter culture was used to inoculate 1 L LB supplemented with 50 μg/mL kanamycin. The culture was grown until it reached an optical density (A ₆₀₀) of 0.5. Overexpression of the protein was then induced using 0.1 mM β‐d‐thiogalactopyranoside. The protein was grown for 16 h at 22°C. The cells were harvested by centrifugation at 5000g for 20 min. The cell pellet was then resuspended in 20 mL of a lysis buffer (50 mM Tris pH 7.4, 150 mM NaCl, 20 mM imidazole, 2 mM 2‐mercaptoethanol, and 1 tablet of cOmplete Protease Inhibitor Cocktail (Roche). The cells were lysed by sonication and cell debris was removed by centrifugation at 35,000g for 40 min.

The supernatant was loaded onto an Ni‐NTA (Qiagen) column with a bed volume of 3 mL for purification by Ni‐affinity chromatography. After 1 h incubation at 4°C, six washes were performed: one wash with 50 mM Tris pH 7.4, 150 mM NaCl, 20 mM imidazole and fives washes with 50 mM Tris pH 8.0, 300 mM NaCl. The protein was eluted in 10 mL 50 mM Tris pH 8.0, 300 mM NaCl, and 250 mM imidazole. It was then dialyzed three times against 1 L 50 mM Tris pH 8.0, 300 mM NaCl, and 2 mM 2‐mercaptoethanol and flash frozen in liquid nitrogen for storage at −80°C.

Wild‐type Azami Green protein sequence (with mutated residues in bold):

MVSVIKPEMKIKLCMRGTVNGHNFVIEGEGKGNPYEGTQILDLNVTEGAPLPFAYDILTTVFQYGNRAFTKYPADIQDYFKQTFPEGYHWERSMTYEDQGICTATSNISMRGDCFFYDIRFDGVNFPPNGPVMQKKTLKWEPSTEKMYVRDGVLKGDVNMALLLEGGGHYRCDFKTTYKAKKDVRLPDYHFVDHRIEILKHDKDYNKVKLYENAVARYSMLPSQAK

Azami Green mutant triple threonine protein sequence (with mutated residues in bold):

MVSVIKPEMKIKLCMRGTVNGHNFVIEGEGKGNPYEGTQILDLNVTEGAPLPFAYDILTTVFQYGNRAFTKYPADIQDYFKQTFPEGYHWERSMTYEDQGICTATSNISMRGDCFFYDITFTGTNFPPNGPVMQKKTLKWEPSTEKMYVRDGVLKGDVNMALLLEGGGHYRCDFKTTYKAKKDVRLPDYHFVDHRIEILKHDKDYNKVKLYENAVARYSMLPSQAK

Crystallization

Crystals were obtained by sitting drop vapor diffusion: 1 μL of purified protein, concentrated to 5 mg/mL using Amicon centricon concentrators with a 10 kDa cutoff (Millipore) in 50 mM Tris pH 8.0, 300 mM NaCl, 2 mM 2‐mercaptoethanol, was mixed with 1 μL well solution (0.1 M magnesium chloride hexahydrate, 100 mM Tris pH 8.5, 25% w/v polyethylene glycol 3,350). This condition was identified as a hit in a sitting drop vapor diffusion screen of the PEG/ION HT kit (Hampton Research). Plate crystals were visible after 1 day at room temperature.

Data collection and structure solution

Crystals were frozen in liquid nitrogen with Parabar 10312 (patatone oil, Hampton Research HR2‐643) as the cryoprotectant. Diffraction data were collected at the NE‐CAT 24‐ID‐E beamline. Data were processed using HKL2000 (HKL Research). Molecular replacement was performed using the program Phaser17 with monomeric Azami Green (PDBID http://firstglance.jmol.org/fg.htm?mol=3ADF) as the search model. Initial rigid body refinement and then successive restrained refinement (including TLS refinement) was performed using Refmac5.18 Concurrent model building was carried out using the program Coot.19

Data availability

Coordinates and structural factors have been deposited in the Protein Data Bank under accession code 6CIU.

Fluorescence anisotropy

Fluorescence anisotropy measurements were performed using a PTI Quantamaster C‐61 two‐channel fluorescence spectrophotometer equipped with excitation and emission polarizers. Purified protein was concentrated to ~1 mM using Amicon centricon concentrators with a 10 kDa cutoff. The protein was excited off‐peak at 450 nm and emission was recorded at 505 nm. The anisotropy was calculated using the equation

$$r=\frac{I_{\parallel }-G{I}_{\perp }}{I_{\parallel }+2G{I}_{\perp }}$$

where r is the anisotropy, I _∥ and I _⊥ are the intensities of the emission with the polarizer oriented parallel and perpendicular to the excitation electric field, and G is the grating factor. The grating factor is calculated from

$$G=\frac{I_{\mathrm{HV}}}{I_{\mathrm{HH}}}$$

where I _HV is the emission intensity measured when the excitation polarizer is horizontal and the emission polarizer is vertical and I _HH is the emission intensity measured when both the excitation and emission polarizers are horizontal.

Solvent‐accessible surface area

To calculate the SASA of each residue, we used the software program Naccess20 with a probe size of 1.4 Å and z‐slice of 10⁻³ Å, which have been shown to give accurate results in previous work.15 Using this method, we identify residues on the interface of each monomer by first calculating SASA_protein, or the SASA of every residue in the Thr zipper protein, and then calculating SASA_mono, or the SASA for every residue in each monomer considered separately. We then calculate the change in SASA

$$\text{ΔSASA}=\mathrm{SAS}{\mathrm{A}}_{\text{protein}}-\mathrm{SAS}{\mathrm{A}}_{\text{mono}}$$

and define an interface residue as an amino acid with ΔSASA ≥ 0.1 Ų. We also compute the relative SASA of each residue using

$$\text{rSASA}=\frac{\mathrm{SAS}{\mathrm{A}}_{\text{protein}}}{\mathrm{SAS}{\mathrm{A}}_{\text{dipep}}},$$

where SASA_dipep is the SASA of the residue removed from the protein and modeled as a dipeptide mimetic with all bond length, bond angles, and side chain dihedral angles set to those in the crystal structure. rSASA gives a value between 0 and 1 and is inversely related to the packing fraction.

Hard sphere repacking

To predict the placement of amino acid side chains in the protein core, we use the hard‐sphere plus stereochemical constraint model.14 In this model, amino acids are treated as a union of spherical atoms that interact pairwise with nonbonded overlapping atoms via the repulsive Lennard–Jones potential:

$$U_{\mathrm{RLJ}}\left(r_{\mathit{ij}}\right)=\frac{\varepsilon }{72}{\left(1-{\left(\frac{{\sigma }_{\mathit{ij}}}{r_{\mathit{ij}}}\right)}^6\right)}^2\mathrm{\Theta }\left(1-\frac{r_{\mathit{ij}}}{{\sigma }_{\mathit{ij}}}\right),$$

where r _ij = ∣ r _j − r _i∣ is the distance between atoms i and j, σ _ij is their mean diameter, and the Heaviside step function Θ(x) enforces that the atoms do not interact when they are not in contact, with r _ij > σ _ij. Importantly, we use a hard sphere model with explicit hydrogen atoms, which has been shown16 to correctly predict the packing fraction of protein cores. Hydrogen atoms are added using the Reduce software21 and atomic radii are chosen to best predict the side‐chain dihedral angle distributions observed in high‐resolution protein crystal structures.

To predict a given side‐chain dihedral angle, we consider an amino acid with coordinates given by the crystal structure. While keeping the backbone atoms fixed, we rotate each dihedral angle χ ₁, …, χ _m individually in small increments, and calculate the total potential energy U(χ ₁, …, χ _m) = ∑_{i < j} U _RLJ(r _ij) for each value of χ. We find the side chain dihedral angle conformation $\left({\chi }_1^{*},\dots ,{\chi }_m^{*}\right)$that gives the minimum potential energy. We repeat this procedure over variations of the bond lengths and bond angles, and calculate the Boltzmann weight,

$$P\left({\chi }_1,\dots ,{\chi }_m\right)\propto exp\left(-\frac{U}{k_{\mathrm{B}}T}\right),$$

for each realization. We choose $\frac{k_{\mathrm{B}}T}{\varepsilon }={10}^{-2},$ which prevents large overlaps between nonbonded atoms. We then sum all probabilities for each unique χ over all bond length and bond angle fluctuations, and we normalize the resultant distribution such that ∫P(χ ₁, …, χ _m)dχ ₁…dχ _m = 1. The HS model's prediction is the side‐chain dihedral angle conformation that gives the highest probability $P\left({\chi }_1^p,\dots ,{\chi }_m^p\right)$.

MD simulations

Atomistic molecular dynamics simulations were carried out using the GROMACS 2018.3 integrator.22 The CHARMM36m force field23 with torsional CMAP corrections was used to parametrize topologies of Azami Green, while explicit TIP3P water24 was used to solvate the tetramer. Histidines were kept charge‐neutral, with a hydrogen atom attached to the ε nitrogen. Newton's equations of motion were integrated over a 2 fs time step using a leapfrog algorithm. Short‐range van der Waals and Coulomb potentials were truncated at 1.2 nm, while longer ranged electrostatics were tabulated with Particle Mesh Ewald summation.25 Cartesian periodic boundary conditions were implemented in all directions to minimize the effects from unit‐cell boundaries for the protein. All chemical bonds were harmonically constrained, except for bonds to hydrogens, which were rigidly constrained.

To prepare systems for MD, fluorophores in the interior of each monomer of the Thr zipper protein were first mutated to glycine residues. Then, after using GROMACS to generate topologies with the tool pdb2gmx, systems were energy‐minimized for 10 ps. Following this, systems were solvated with bulk water while the Azami Green backbone was harmonically constrained using a spring constant of 1000 kJ/mol nm². Then, systems were heated under an NVT ensemble at 300 K using the weakly coupled Berendsen thermostat. Finally, production MD was initiated by switching to an NPT ensemble and running for 100 ns under a Nose–Hoover thermostat26 and Parinnello–Rahman barostat,,27 which maintained 1 bar of isotropic pressure. Systems exhibited an isotropic compressibility of 4.5E‐5 bar⁻¹ and box dimensions around 10 × 10 × 10 nm³. The protein backbone was harmonically constrained throughout the production run, allowing only the amino acid side chains to move freely.

Supporting information

Supporting Information, Figure 1. Fluorescence anisotropy of Azami Green mutants, as a function of protein concentration. Each of the mutants of Azami Green was serially diluted from its stock solution and the anisotropy measured: wild‐type (solid circles), D121T (crosses), R119T (open diamonds), R119TD121TV123T (solid diamonds), V123T (pluses), R119DD121TV123T (open squares), R119TV123T (open circles), and R119DV123T (asterisks). The solid line shows the expected anisotropy for an Azami Green monomer, and the dashed line shows the expected anisotropy for an Azami Green tetramer.

Supporting Information, Figure 2. A detailed diagram of the Thr–zipper interface between Azami Green monomers shows densely interdigitated Thr flanked by two Asn residues. Only amino acids on the left monomer were labeled for simplicity; however, the right monomer is rotationally symmetric about the interface.

Supporting Information, Figure 3. Probability distributions for Χ ₁ from MD simulations indicate that the most difficult Thr residues to repack (Thr 104, 119, and 121) sample multiple side chain dihedral angles. Unlike what is observed experimentally, Thr in MD does not sample gauche⁻ states (Χ ₁ ~ 60°) as often as trans (Χ ₁ ~ 180°) or gauche⁺ states (Χ ₁ ~ 300°), which is consistent with the HS repacking calculations. However, these side chain dihedral angle conformations are likely highly dependent on the positions of water.

Supporting Information, Figure 4. Side‐chain dihedral angle Χ ₁ versus time from MD simulations reveal three types of interfacial Thr residues in the Thr zipper protein. The first type (top) tends to rotate between gauche⁺ (Χ ₁ ≈ 300°) and trans (Χ ₁ ≈ 180°) side chain conformations. The second type (middle) tends to rotate between all three side chain conformations. The third type (bottom) remains roughly fixed in a preferred side chain conformation, and infrequently samples other side chain conformations.

Supporting Information, Table 1. The predominant oligomeric state of Azami Green mutants as assayed by fluorescence anisotropy. Mutants are defined by which residues are present at locations 119, 121, and 123. The predominant oligomeric state was determined at 1 μM protein concentration. Positions mutated relative to the wild‐type Azami Green protein are in bold.

Supporting Information, Table 2. Crystallographic data collection and refinement statistics

Supporting Information, Table 3. Side‐chain dihedral angles for interface residues in the Thr zipper crystal structure (Χ ₁ ^xtal), the HS prediction (Χ ₁ ^pred), and from MD simulations (Χ ₁ ^MD). Each table corresponds to residues on an individual monomer in the Thr zipper protein. For ${\chi }_1^{\mathrm{MD}}$, we report the fraction of the simulation spent in each rotameric bin with width 30° centered around 60°, 180°, and 300°. When Χ ₁ ^xtal, Χ ₁ ^pred, and Χ ₁ ^MD all agree, the row is shaded green.

Supporting Information, Table 4. Solvent‐accessible surface area (SASA) values for core interface residues in both the monomeric and tetrameric cases for chains A & B. Data for these residues on chains C & D are similar. The change in SASA (delta SASA) is SASA_monomer − SASA_interface. Residues were determined to be part of the interface with delta SASA >0.1 Ų, and determined to be core if rSASA < 0.3. The definition of the relative SASA, or rSASA, is given in the Methods section.

Appendix S1: M1_thr119_movement_highres.mpg

Appendix S2: M2_thr119_water_highres.mpg