Value of inventory information in allocating a limited supply of influenza vaccine during a pandemic

Abstract

Objective

To understand the value of information on vaccine inventory levels during an influenza pandemic, we propose a simulation study to compare vaccine allocation strategies using: (i) only population information (pro-rata, or population-based, PB), (ii) both population and vaccine inventory information (population and inventory-based, PIB).

Methods

We adapt an agent-based simulation model to predict the spread of the disease both geographically and temporally. We study PB and PIB when uptake rates vary geographically. The simulation study is done from 2015 to 2017, using population and commuting data from the state of Georgia from the United States census.

Findings

Compared to PB under reasonable scenarios, PIB reduces the infection attack rate from 23.4% to 22.4%, decreases the amount of leftover inventory from 827 to 152 thousand, and maintains or increases the percentage of vaccinated population.

Conclusions

Our results indicate the need for greater vaccine inventory visibility in public health supply chains, especially when supply is limited, and uptake rates vary geographically. Such visibility has a potential to decrease the number of infections, help identify locations with low uptake rates and to motivate public awareness efforts.

Introduction

Influenza in the United States has led to thousands of deaths annually over the past decade [1], and historically, there has been a world-wide pandemic about every 30 to 40 years [2]. The last declared pandemic was due to the H1N1 virus in 2009, leading to an estimated average of 363,550 deaths world-wide [3]. Timely vaccination can prevent the spread and reduce the burden of the disease.

Influenza vaccine supply is often limited, especially during a pandemic [1]; hence, vaccine allocation decisions can play a significant role in the overall impact of vaccination on reducing the disease burden. In the United States, the most recent emergency vaccine distribution campaign (2009–2010) was coordinated by the Centers for Disease Control and Prevention (CDC). As new batches of vaccine became available, they were allocated to each state proportional to the state’s population (i.e., population-based or “pro-rata” allocation) [4]. The states then distributed the vaccine inventory locally, and providers administered vaccines to individuals.

During the 2009–2010 influenza pandemic, states were encouraged to collect and report data about the vaccines administered to the general population [5]. However, very few states collected detailed information on how many vaccines were administered in each location (e.g., a county or a census tract) [6]. As a result, states did not have a good visibility into the uptake rates and vaccine inventory levels geographically. This lack of visibility in the vaccine supply chain caused some areas to end the influenza season with excess inventory [7, 8] (i.e., leftover vaccine) while other areas (especially those with high uptake rates) experienced unmet demand [9, 10].

This study aims to quantify the value of information on (or visibility into) vaccine inventory, i.e., tracking inventory levels geographically and over time, and how the use of such information in vaccine allocation decisions can improve the overall impact of vaccination. Information on the quantity of vaccines administered versus leftover in inventory in different locations could inform the decision makers on how to allocate the next batch of vaccines geographically; it could also motivate initiatives to improve access to vaccines and inform decision makers about public awareness campaigns. Such visibility could be achieved in various ways, e.g., through vaccine registries.

Combining shipment and registry information would provide visibility into administered and leftover vaccine inventory. For example, the state of Oregon collects immunization data from both public and private health care providers to create vaccination records for individuals and reports immunization rates by county for the seasonal influenza vaccine [11]. Ultimately, it is expected that the value of inventory visibility is most important when the vaccine supply is limited, which is often the case during an influenza pandemic. Vaccine inventory information, updated geographically and over time, could help reduce the disease burden by decreasing the number of infections, reduce the leftover inventory (vaccine wastage) while meeting the demand of the population in a fair and equitable manner.

Relevant literature

Some of the literature on the allocation of limited vaccine supply focus on prioritizing certain sub-populations by age or other health risks and evaluating the benefits of targeting a limited vaccine supply [12–15], in line with the vaccine recommendations from the Advisory Committee for Immunization Practice (ACIP) in the United States, where the risk groups may be specific to an influenza strain. Some researchers have quantified the benefit from the availability and allocation of vaccines early in a pandemic [16, 17]. Prior work addressing the geographical allocation of a limited vaccine supply is scarce. Matrajt et al. propose a mathematical model to distribute vaccine in a network of cities in Southeast Asia connected by the airline transportation network; they find that a city-specific allocation strategy can reduce the attack rate substantially but at the expense of fairness [18]. Araz et al. consider the allocation of limited vaccine between and within the counties in the state of Arizona in the United States based on expected epidemic waves [19]. They find that a pro-rata strategy is effective when considering both the infection attack rate and the lead time for receiving vaccine inventory. Other authors consider shipping vaccines in two phases, where vaccines in the second phase may be sent to regions where the epidemic is not yet contained [20].

This paper proposes a modified pro-rata allocation strategy with respect to the “demand” for vaccine, by utilizing vaccine inventory information and allocating the available vaccine supply to any location where the individuals continue to request the vaccine. This is particularly important when uptake rates and vaccine coverage vary across population groups or geographically [11, 21–25]. The proposed population and inventory-based strategy thus maintains fairness with respect to the underlying demand from the population. Note that when the uptake rates are similar across geographical regions, the proposed strategy is equivalent to the traditional pro-rata (population-based) strategy; however, the proposed strategy is more effective (in terms of reducing the number of infections and leftover inventory, while maintaining fairness) when the uptake rates vary geographically.

Methods

Disease simulation

We adapt a simulation-based disease spread model and use data from the state of Georgia in the United States with heterogeneous population mixing to predict the spread pattern of the disease both geographically and temporally. We use a detailed Susceptible-Exposed-Infected-Recovered (SEIR) model that tracks the disease status of an individual as the disease spreads through a census-tract level contact network by interactions in households, workplaces, schools, and communities. The results presented in the main body of the paper are based on running scenarios with 10 million agents, i.e., one agent corresponding to one person in the population in the state of Georgia. (Additional results are presented in the Appendix based on running scenarios with 1 million agents, i.e., one agent corresponding to approximately 10 persons in the population.) The model is flexible and can be run with data from other locations. We consider vaccine uptake, vaccine inventory and its allocation, leftover vaccine, and total attack rate at the census tract level.

The method builds upon a previously-established agent-based simulation model [26–28]. Two main assumptions of the model are as follows (see S1 Appendix for details on how the contact network is generated):

1. Every individual is in one of following states at a given time: susceptible (S), exposed (E), pre-symptomatic (I_P), asymptomatic (I_A), symptomatic (I_S), hospitalized (H), recovered (R), or dead (D).

2. The entire population has three levels of mixing: (i) community (day and night), (ii) peer groups (day), and (iii) household (night).

At the start of a simulation run, the entire population contact network is generated and every individual is susceptible. An initial infection is introduced randomly to 10 agents from census tracts inside Fulton County (which is in the Metropolitan Atlanta Area). An infected individual’s disease status changes to exposed (E). With pre-defined probabilities, the disease progresses within infected individuals and spreads to previously healthy individuals across the network. Once recovered (R) from the disease, the individual remains in that state.

To assess the effect of vaccination under different vaccine allocation strategies, we expand this simulation model by adding the option of vaccination; within 14 days of vaccination, a person becomes immune to the disease (i.e., moves to the recovered state) with a positive probability [1].

The simulation outputs include the spatial and temporal estimates of the spread of the disease under different vaccine allocation strategies. The total infection attack rate (IAR) represents the cumulative percentage of the population who have been infected during the epidemic. The peak prevalence is the maximum percentage of the population infected at a given time.

An important parameter in the model is R₀, the reproductive number, which measures the transmission potential of the virus (i.e., the expected number of secondary infections caused by a typical infection). The analysis is presented for R₀ = 1.5; similar insights are obtained for R₀ = 1.8 and R₀ = 2.0.

Vaccine allocation and uptake

Since the capacity for the influenza vaccine is limited during a pandemic, vaccine supply becomes available in batches over time. Vaccine allocation begins in a “vaccination start week” and continues (e.g., on a weekly basis) until all the vaccine inventory is depleted or unmet demand reaches zero. Beginning with the vaccination start week, batches of vaccine arrive at each census tract in amounts that depend on the vaccine allocation strategy and the total vaccine availability.

The uptake rates often differ from one geographical location to another [1]. At the beginning of the simulation, we randomly select a subset of individuals (according to the uptake rate) in each census tract as willing to receive the vaccine. During each week, available vaccine is administered (randomly) to the individuals in that census tract who would like to be vaccinated, have not been infected previously, and are asymptomatic.

We consider two cases, where census tracts do and do not keep track of and report the remaining vaccine inventory levels on a weekly basis. When inventory levels are known geographically, they can inform the allocation strategy. The general principle is that areas with unused inventory could potentially receive less vaccine in the next allocation period.

We consider two strategies for allocating vaccine:

1. Population-Based (or pro-rata) Strategy (PB) delivers available vaccine in each period proportional to the population size of each census tract. This is similar to the practice followed by many states during 2009–2010 [4].

2. Population and Inventory-Based Strategy (PIB) allocates vaccine (in proportion to the remaining unvaccinated population in each census tract) only to those census tracts that have zero inventory, i.e., those that already administered all the vaccine that was shipped earlier.

PIB is motivated by a strategy used by organizations for allocating a limited supply of resources [29, 30]. When the uptake rates are equal in all census tracts, PB and PIB are equivalent. Detailed descriptions of both strategies are presented in S2 Appendix.

Each strategy is evaluated based on several criteria including the disease spread (e.g., IAR), operational aspects (e.g., vaccines shipped, administered, or leftover), and the “service level” (vaccine administered divided by the total number of susceptible individuals willing to receive the vaccine).

Experiments

We ran experiments simulating various scenarios with different parameters including vaccination start week (week 4 or 7), total vaccine supply (20%, 40%, 60%, or 80% of the population), vaccine distribution horizon over which the vaccine is delivered to census tracts (in 4, 8, or 12 weeks), and three different uptake rate settings:

1. UTR₁: half of the census tracts have uptake rate 25% and the other half 75%.

2. UTR₂: half of the census tracts have uptake rate 0% and the other half 100%.

3. UTR₃: the uptake rate of each census tract is randomly chosen from a uniform distribution between 0% and 100%.

We summarize all experimental parameters and provide justifications for their choice in Table A in S3 Appendix. To account for randomness, we generate five distinct contact networks and within each network we perform five simulation runs (replications) for each uptake rate setting (see S3 Appendix for the analysis of the number of replications needed) [31]. Hence, there are a total of 5×5 = 25 simulation runs for each of the 2×2×3×4 = 48 parameter combinations.

Results

We present results comparing the scenarios of no vaccination, and vaccine allocation under PB and PIB for R₀ = 1.5 and UTR₁, focusing on IAR and the percentage of leftover (i.e., allocated but not administered) vaccine inventory. Results on UTR₂ and UTR₃ are presented in S4 Appendix. Unless stated otherwise, the results presented in this section are the average for the instances where the vaccination start week is 4 and the vaccine distribution horizon is 8 weeks.

No vaccination versus vaccination under the population-based strategy

Without vaccination, the peak prevalence is 3.2%, which occurs around week 10, and the IAR is 52.0% (averaged over 25 simulation runs). The prevalence in every census tract is positive (i.e., no census tract remained free of the disease), and census tracts around the city of Atlanta have a higher IAR than rural census tracts.

When vaccine is available for 40% of the population and distributed under PB, the peak prevalence (1.6%) and IAR (26.8%) are lower and the peak occurs earlier compared to the no vaccination case (see S5 Appendix for further details). Vaccination under PB has a lower peak prevalence and IAR when vaccine is distributed earlier and over a shorter time horizon.

Selected comparisons on peak prevalence and IAR under various parameters of vaccination are presented in S6 Appendix. Detailed results for all combinations of vaccination start week, vaccine distribution horizon, and total available vaccine supply are presented in Tables A-I in S4 Appendix.

Vaccination under population-based versus population and inventory-based strategies (PB versus PIB)

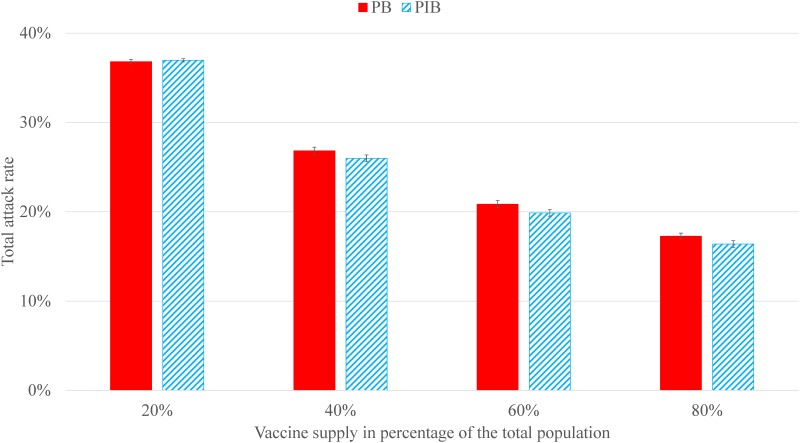
IAR relative to the total population under PIB is on average -0.1 to 0.9 percentage points lower than that under PB (Fig 1). These results, except for when the vaccine supply is 20% of the population, are significant under a two-sample t-test with a 95% confidence level. IAR under UTR₁ is generally lower than that under UTR₂ and UTR₃ for both PB and PIB, when all other parameters are the same. The average percentage points difference in IAR between PB and PIB (PB—PIB) ranges from 4.0 to 6.4 under UTR₂ and 0.9 to 1.6 under UTR₃. Detailed comparisons on IAR and t-test results are shown in S4 Appendix.

Fig 1. IAR under PB and PIB strategies, where the vaccination start week is 4 and the vaccine distribution horizon is 8 weeks.

Error bars are the standard errors over the 50 replications for each scenario.

Additional results (presented in S5 Appendix) indicate that an earlier vaccination start week and shorter vaccine distribution horizon reduce the IAR. The reductions are generally stronger for the PIB strategy.

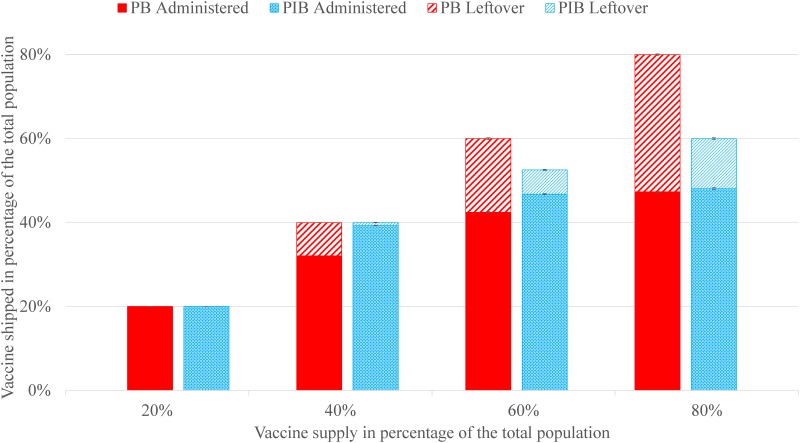
Fig 2 shows the number of vaccines shipped and administered under PB and PIB. The solid, striped, and combined columns represent the vaccines administered, leftover, and shipped during the entire vaccine distribution horizon, respectively.

Fig 2. The amount of vaccine shipped, administered, and leftover in inventory, as a percentage of the total population, where the vaccination start week is 4 and the vaccine distribution horizon is 8 weeks.

Error bars are the standard errors over the 50 replications for each scenario.

Under PIB, the total shipment is lower or the same, but the total amount of vaccine administered is higher compared to PB; hence, vaccine utilization (and service level) is higher, and the leftover inventory is lower under PIB. For example, when the vaccine supply is equal to 40% of the population, both PB and PIB ship all the available vaccine, but PIB administers 674 thousand more doses than PB. As a result, the leftover inventory is 20.7% of the total shipped under PB versus 3.8% of the total shipped under PIB.

The cost of the leftover vaccine inventory is estimated using information from a previous study in New York City [32, 33]. The (per dose) vaccine production cost is $5.0 to $10.0, distribution cost is $1.5 to $5.0, and disposal cost is $0.1 to $1.0. When the vaccine supply is enough to cover 40% of the population, PIB ships the same amount of vaccine and results in 667 thousand (95% CI on PIB-PB, 664 to 669, p < 0.0001) less doses of leftover vaccine (or equivalently, more doses of administered vaccine) compared to PB (Fig 1). Hence, the estimated cost savings under PIB versus PB range from $4.4 to $10.7 million dollars.

We also calculate the service levels under PB and PIB. “Demand” refers to the number of people who were willing to receive the vaccine (calculated by multiplying the population in an area with the uptake rate), and “Served” refers to the number of people who were vaccinated. Service level is defined as $\frac{Served}{Demand}\times 100\%.$ When the vaccine supply is sufficient to cover 40% of the population, the mean service levels under PB and PIB for census tracts with 75% uptake rate are 58.6% and 75.9% (95% CI of the percentage points difference on PIB-PB, 13.3 to 21.3, p < 0.0001), respectively. For census tracts with 25% uptake rate, the average service level for PB and PIB are 93.2% and 95.0% (-2.1 to 5.8, p = 0.3411), respectively. Additional results and details are presented in S6 Appendix.

Discussion

The results indicate that PIB dominates PB across multiple metrics. Given a fixed amount of vaccine supply, more vaccine is administered to the population (higher service levels), resulting in similar or lower IAR under PIB versus PB. Since PIB ships the vaccine (over time, as new batches become available) to those areas where there is still demand for the vaccine, versus shipping it to areas where the demand is saturated, it ships less vaccine, and hence, incurs a lower transportation cost and lower amount of leftover inventory, compared to PB. Note that the percentage of population vaccinated in any geographic area is higher under PIB versus PB; hence, the benefits of PIB are realized while maintaining fairness.

IAR under PIB is similar to or lower than that under PB. A 0.8% drop in IAR (with vaccine supply of 40% in Fig 2) implies approximately 100 thousand fewer influenza cases in the state of Georgia. In general, the reduction in IAR under PIB versus PB positively correlates with the variability in the uptake rates across locations (IAR reduction is the highest under UTR₂ and the lowest under UTR₁), i.e., the higher the variability in the uptake rates, the higher the benefits of PIB over PB. Additional results and discussions on the changes in IAR when the uptake rates are correlated geographically or when considering herd immunity can be found in S6 Appendix.

Leftover (unused, and potentially wasted) vaccine inventory often incurs extra cost (including storage and disposal), as experienced during the last phase of the H1N1 influenza vaccine campaign [34–36]. These costs are even higher if the leftover vaccine is treated as a hazardous waste, as was required in some states for vaccine containing thimerosal. Inventory visibility enables the implementation of allocation strategies such as PIB, reducing the amount and the cost of leftover vaccine inventory, and the potential negative environmental impact.

Visibility in inventory has additional benefits that have not been explored in this study. For example, inventory information can be used to learn the uptake rate in each census tract, and states could design policies or information campaigns for areas with low uptake rates to create awareness, which could result in an increase in vaccination rates across the population and greater reductions in IAR. The lower number of infections along with the cost savings enabled by PIB would free up valuable resources which could be invested elsewhere to improve the availability and access to public health services.

Overall, this study suggests that visibility of inventory information in public health supply chains can have many benefits. Some states have adopted systems and practices to increase visibility in supply chains [11], and others may want to consider the potential benefits and costs of such practices. Ultimately, investments towards increasing the visibility in public health supply chains could increase effectiveness (reducing the disease burden) and efficiency (saving cost), while promoting equity (fairness).

Limitations

We assume that the uptake rates, i.e., the willingness to receive the vaccine, are constant over time (but we allow the uptake rates to vary by location). In practice, uptake rates may vary over time, e.g., they may be lower towards the end of the epidemic. Since we limit the vaccine distribution horizon to several weeks around the peak (where one would expect the awareness about the epidemic to be high) it is reasonable to assume that the uptake rates would be somewhat stable during the vaccine distribution horizon. Uptake rates could lag behind the actual demand of the vaccine at the beginning of the pandemic. For example, poor logistics or limited vaccine availability could slow the distribution of vaccine to individual vaccine providers, or the public may not realize the availability of the vaccine due to inadequate marketing or public outreach. If the vaccine supply is very limited at the beginning, and people try to get vaccinated but are not able to do so after repeated tries, they may give up after a while and this could also reduce uptake rates. On the other hand, the severity of the epidemic could cause uptake rates to increase over time as the public becomes more informed about the spread and the danger of the disease. The benefits of inventory visibility could be even higher when the uptake rates vary over time. For example, a decreasing trend in uptake rates might prompt a local government to increase efforts in generating public awareness regarding the benefits of vaccination, and conversely, and increasing trend could be communicated to the upper levels of the vaccine supply chain to ensure inventory availability.

The current model considers a single type of influenza vaccine. In practice, there may be multiple types of vaccines, and there may be some overlap between the populations who are eligible to receive different types of vaccines. We expect that the PIB strategy would perform better than the PB strategy, even if the uptake rates differ among various vaccine types and geographical locations. In the models, we track the vaccine inventory in a semi-aggregate fashion for computational efficiency (e.g., vaccine inventory levels are computed for about 1,600 census tracts in the model vs. more than ten thousand providers in practice). There are well-known results in the supply chain management literature indicating that as the number of locations holding the inventory increases, stocking levels and costs increase (to meet a desired service level), or alternatively, service levels decrease for a given fixed amount of inventory. Hence, in practice, given a high number of inventory locations and potentially higher variability between uptake rates among different locations, we expect that PIB could be even more beneficial compared to PB.

Although we have demonstrated that PIB can reduce the cost associated with vaccine distribution and leftover inventory, it is still necessary to estimate the cost of implementing an information system that could track vaccine inventory at a local level to assess when PIB would be cost-saving compared to PB. Such a system may be relatively easy to implement, e.g., as an add-on to vaccine registries across the states.

Supporting information

S1 Appendix. Illustration of contact network generation and disease progression.

(DOCX)

S2 Appendix. Detailed description of vaccine inventory allocation strategies.

(DOCX)

S3 Appendix. Parameters of the simulation model.

(DOCX)

S4 Appendix. Detailed comparison between vaccine inventory allocation strategies under multiple scenarios.

(DOCX)

S5 Appendix. Detailed analysis on no vaccination vs. vaccination under PB (vaccine supply is 40% population).

(DOCX)

S6 Appendix. Additional analysis and discussion on PB vs. PIB.

(DOCX)

Data Availability

Most data relevant to this study is publicly available from census.gov. Additional data related to vaccine costs are from the literature and can be accessed directly from Reference 32 and 33. Census population/age data: https://factfinder.census.gov/faces/tableservices/jsf/pages/productview.xhtml?pid=DEC_00_SF1_DP1&prodType=table. Georgia county-to-county workflow data: https://www.census.gov/population/www/cen2000/commuting/#GA. Georgia education level data: https://factfinder.census.gov/faces/tableservices/jsf/pages/productview.xhtml?pid=DEC_00_SF3_DP2&prodType=table. Distances between Georgia census tracts were obtained from the longitude and latitude of the centroid of the census tract: https://www.census.gov/geo/maps-data/data/gazetteer2000.html.

Funding Statement

The study was supported by a seed grant from Georgia Institute of Technology and the Children’s Healthcare of Atlanta. This research was also supported in part by the Harold R. and Mary Anne Nash Junior Faculty Endowment Fund and the following Georgia Tech benefactors: William W. George, Andrea Laliberte, Joseph C. Mello, Richard “Rick” E. and Charlene Zalesky. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.