Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 May 15;57(26):3641–3649. doi: 10.1021/acs.biochem.8b00151

Cooperative Assembly of Hsp70 Subdomain Clusters

Maya A Wright †,∥, Francesco A Aprile †, Mathias M J Bellaiche †,‡, Thomas C T Michaels †,§, Thomas Müller †,∥, Paolo Arosio ⊥, Michele Vendruscolo †, Christopher M Dobson †, Tuomas P J Knowles †,#,*
PMCID: PMC6202011  PMID: 29763298

Abstract

graphic file with name bi-2018-00151t_0005.jpg

Many molecular chaperones exist as oligomeric complexes in their functional states, yet the physical determinants underlying such self-assembly behavior, as well as the role of oligomerization in the activity of molecular chaperones in inhibiting protein aggregation, have proven to be difficult to define. Here, we demonstrate direct measurements under native conditions of the changes in the average oligomer populations of a chaperone system as a function of concentration and time and thus determine the thermodynamic and kinetic parameters governing the self-assembly process. We access this self-assembly behavior in real time under native-like conditions by monitoring the changes in the micrometer-scale diffusion of the different complexes in time and space using a microfluidic platform. Using this approach, we find that the oligomerization mechanism of the Hsp70 subdomain occurs in a cooperative manner and involves structural constraints that limit the size of the species formed beyond the limits imposed by mass balance. These results illustrate the ability of microfluidic methods to probe polydisperse protein self-assembly in real time in solution and to shed light on the nature and dynamics of oligomerization processes.

Molecular chaperones play a crucial role in vivo not only in assisting in protein folding but also in regulating the formation of aberrant protein assemblies, including in particular those implicated in the onset and progression of neurodegenerative disorders such as Alzheimer’s and Parkinson’s diseases.1−9 Despite their important cellular roles, defining the microscopic mechanisms by which molecular chaperones can protect against pathogenic aggregation remains a substantial challenge to study as a result of the polydispersity of the systems involved.10−13 Indeed, many molecular chaperones, including the 70 kDa heat shock proteins (Hsp70s) and small heat shock proteins such as αB-crystallin, are known to have the propensity to self-assemble into various oligomeric forms, and it has been thought that this serves as a control mechanism for storage of chaperones when they are not exerting their cellular functions.12,14−29 Evaluating the intrinsic dynamics of molecular chaperones in the presence and absence of their interaction partners is therefore a key target in biophysical studies to begin to define the specific oligomeric species responsible for the suppression of protein aggregation.

A number of conventional biophysical techniques are currently available for probing the quaternary structure and oligomeric populations of proteins; these approaches, however, are typically more reliable for monodisperse solutions of isolated components.14,30−32 Moreover, many of the techniques involve the interaction of the protein of interest with a surface or a matrix, which may influence the self-assembly behavior. It has recently become apparent, however, that microfluidic techniques offer a fruitful avenue for the characterization of the dynamics, interactions, and physical properties of biomolecules in solution.8,9,16,33−39 These approaches include methods for the rapid sizing of biological complexes in solution by monitoring the spatiotemporal evolution of their diffusion through a microfluidic channel.39−41 In this work, we have applied microfluidic diffusional sizing (MDS) to the study of the oligomerization of SBD641, the substrate binding subdomain (residues 384–641) of human Hsp70. Construct SBD641 consists of the hydrophobic linker, the substrate binding subdomain itself, and the helical lid, which are the regions that have been found to be critical for oligomerization in full-length Hsp70.14 We show that the rapid nature of the microfluidic sizing measurements under native solution conditions makes this approach particularly important for quantitative studies of the kinetics as well as the thermodynamics of oligomerization processes. In particular, we demonstrate a robust method for determining the dissociation constant, oligomerization free energy, and association and dissociation rate constants of the self-assembly reaction and show that the assembly process is guided by specific structural constraints and is qualitatively different from unconstrained polymerization processes.

Materials and Methods

Protein Expression and Purification

SBD641 was purified according to a protocol outlined previously.42 In brief, N-hexa-His-tagged SBD641 was expressed recombinantly in Escherichia coli from the pET28b (Novagen) vector. The cells were then centrifuged, resuspended in buffer [50 mM Tris (pH 7.4)], and lysed using sonication. The expressed protein was collected using a Ni2+-NTA Superflow column (Qiagen, Manchester, U.K.) using standard washing procedures. The protein was further purified by size exclusion chromatography using a Superdex 75 26/60 column (GE Healthcare, Buckinghamshire, UK).

Labeling

Alexa Fluor 488 (Life Technologies, Paisley, UK) was added to SBD641 (10 mM Tris, pH 7.4) at a 1:2 Alexa:SBD641 molar ratio and degassed. The samples labeled at 1:2 and 1:5 ratios were used in the experiments for SBD641 concentrations below and above 3 μM, respectively. The mixture was left to incubate overnight in the dark at 4 °C. The excess dye was removed after 24 h of incubation using a Zeba Spin desalting column 7 kDa (Thermo Scientific, Cramlington, UK) followed by size exclusion chromatography with a Superdex 10/300 GL column (GE Healthcare Life Sciences, Amersham). The protein was then divided into aliquots, flash-frozen, and stored at −80 °C until further use.

Microfluidic Device Fabrication

The microfluidic devices used in this study were fabricated using standard soft-lithography techniques.43 SU-8 3025 photoresist (3 mL, MicroChemCorp, Westborough, MA) was spin-coated onto a silicon wafer at 3000 rpm to create 25 μm height channels. After being baked at 96 °C for 12 min, the wafers were covered with a photomask imprinted with a pattern of the device. The wafer was then exposed to ultraviolet (UV) radiation for 15 s at an intensity of 16 mW/cm2 (OAI Instruments, San Jose, CA) and baked at 96 °C for a further 5 min. This procedure allowed cross-linking of the photoresist in the regions exposed to UV light, and the residual photoresist was then removed with PGMEA (propylene glycol methyl ether acetate). The master was subsequently rinsed with IPA (isopropyl alcohol) and dried.

The PDMS (polydimethylsiloxane) curing agent and elastomer (Dow Corning) were thoroughly mixed in a 1:10 ratio. Carbon black nanopowder (Sigma-Aldrich, Dorset, U.K.) was added to the mixture, which was subsequently centrifuged for 5 min at 5000 rpm to spin down large clusters of carbon powder. The centrifuged black PDMS was then poured into a Petri dish containing the wafer, and the dish was placed in a vacuum desiccator for 30 min to eliminate air bubbles and then baked at 65 °C for 3 h.

Diffusion Measurements

The microfluidic devices were plasma bonded to glass microscope slides using an Electronic Femto Plasma Bonder (Diener, Ebhausen, Germany) directly before use. The channels in the bonded device were filled from the outlet with the relevant buffer using a 250 or 500 μL glass syringe (Hamilton Robotics, Bonaduz, GR, Switzerland), needles (25 gauge, 0.5 mm × 16 mm) (Neolus Terumo, Bagshot, U.K.), and polyethene tubing (inner diameter of 0.38 mm, outer diameter of 1.09 mm). The sample and buffers were loaded into their respective device inlets using gel loading pipet tips.

Fluid flow through the device was controlled using neMESYS syringe pumps (Cetoni GmbH, Korbussen, Germany) at a flow rate of 100 or 160 μL/h. Once the system had equilibrated, the diffusion profiles were imaged using an inverted fluorescence microscope (Zeiss Axio Observer.D1) fitted with broadband white LED illumination (Cairn Research, Faversham, U.K.) and a 49002 GFP filter (Chroma Technology, Bellows Falls, VT). The microfluidic diffusion channels were imaged at 12 points along the channels using an Evolve 512 CCD camera (Photometrics, Tuscon, AZ) with a 10× objective and exposure times ranging from 1 to 10 s depending on the sample concentration.

Numerical Simulations and Data Analysis for Microfluidic Sizing Experiments

Fitting of the basis functions to the experimental data was performed as described previously.39 The basis functions used in this analysis were simulated in the range of radii relevant to the samples, namely, 0.25–10 nm in 0.25 nm increments.44

Fluidity One Measurements

In addition, we used a Fluidity One (Fluidic Analytics Ltd., Cambridge, U.K.), which is a self-contained instrument that enables microfluidic diffusional sizing measurements with post separation labeling using injection moulded disposable plastic chips, rather than PDMS. Four repeats were taken on 10 μL of unlabeled SBD641 at 0.3 μM on a prototype instrument.

Thermodynamic Models of SBD641 Oligomerization

Model with No Cooperativity

Assuming a single equilibrium constant K for the association and dissociation of monomers, the equilibrium concentration [Aj] of j-mers is given by45

graphic file with name bi-2018-00151t_m001.jpg 1

where the equilibrium monomer concentration [A1] is linked to the total concentration of protein molecules [A]tot through mass conservation, yielding:

graphic file with name bi-2018-00151t_m002.jpg 2

Using eq 1, we obtain the average hydrodynamic radius at equilibrium

graphic file with name bi-2018-00151t_m003.jpg 3

where Lis(z) = ∑k=1∞zk/ks is the polylogarithm function of order s, Rm is the size of the pure monomer, and d is the fractal dimension governing the dependence of aggregate size on polymerization number Rj = jd−1Rm.

Negative Cooperativity

Assuming an association–dissociation equilibrium constant K = K0/j, we obtain the following expression for the concentration of filaments of size j at equilibrium

graphic file with name bi-2018-00151t_m004.jpg 4

where a relationship between the equilibrium monomer concentration and the total concentration of protein molecules is given in terms of the Lambert W-function K0[A1] = W(K0[A]tot). Thus, the dependence of the average hydrodynamic radius on the total protein concentration becomes

graphic file with name bi-2018-00151t_m005.jpg 5

Positive Cooperativity with a Size Limit

This model assumes a monomer–N equilibrium, with a very fast pre-equilibrium between intermediates. The overall equilibrium is a result of several distinct steps in a more detailed model in which monomers are sequentially added to N-mers. At low values of N, we note that intermediate populations can start to emerge. Using the equilibrium concentration of oligomers [AN] = K̃[A1]N, we obtain for the average hydrodynamic radius

graphic file with name bi-2018-00151t_m006.jpg 6

where the total concentration dependence of equilibrium monomer concentration [A1] is found by inverting the mass balance equation [Atot] = [A1] + NK̃[A1]N.

Kinetics

These rate laws assume that N-mers are the largest oligomers formed and that the time evolution is given by

graphic file with name bi-2018-00151t_m007.jpg 7
graphic file with name bi-2018-00151t_m008.jpg 8

where [A1](t) and [AN](t) are the monomer and N-mer concentrations at time t, respectively.

The time evolution of the hydrodynamic radius, then, is obtained from a mole-fraction weighted average of the radius of each species:

graphic file with name bi-2018-00151t_m009.jpg 9

Note that the kinetic equations (eqs 7 and 8) emerge from a steady-state approximation of a more detailed model that assumes N-mers to be formed by the addition of individual monomers in sequence with rate constant k+(i):

graphic file with name bi-2018-00151t_m010.jpg

The connection between association rate constant ka entering eqs 7 and 8 and the geometrically averaged elongation rate constant ⟨k+⟩ = [k+(1)k+k+(3)]1/3, assuming size-independent dissociation rate constants, is given by (for N = 4)

graphic file with name bi-2018-00151t_m011.jpg 10
graphic file with name bi-2018-00151t_m012.jpg 11

Using the measured values for ka and equilibrium constant K̃ = (⟨k+⟩/k–)3 = ka/k–, we could determine the elongation rate constant to be approximately ⟨k+⟩ = 2.0 ± 1.2 M–1 s–1. This elongation rate corresponds to an association reaction whose barrier is the arithmetic mean of those for dimer, trimer, and tetramer formation through monomer addition, assuming similar diffusive prefactors for all.

Data Fitting

We assumed in all cases that Rm = 1.7 nm, the Rh value obtained at the lowest concentration of SBD641 measured.

In the case of the fits to models without and with negative cooperativity, we minimized the χ2 = ∑iσi–2[yi – f(xi;p)]2 between the thermodynamic data and each model with respect to the parameters α = d–1 and the relevant equilibrium constant. Here yi is the measured hydrodynamic radius corresponding to initial concentration xi, and p is a vector of the parameters. We took as a constant estimate for the error σi the average non-zero standard deviation of hydrodynamic radii, averaged over all the initial concentrations.

For the two-state model, we performed a global fit to the thermodynamic and kinetic data simultaneously by minimizing the sum of kinetic and thermodynamic contributions to total χ2 with respect to the elements of parameter vector p = (α,K̃,ka). The errors in each kinetic data point were taken as 20% of the measured values. The derivation of the target function to minimize can be found in the Supporting Information. Note that off rate k– was constrained by ka and the association constant K̃ by applying detailed balance: K̃ = ka/k–. To sample rate constant space exponentially, the exponent (base 10) of the on rate constant ka was fitted.

In practice, all fits were performed by using the basinhopping algorithm of Python’s scipy module, which involves several minimization steps interspersed by random moves in parameter space and effectively samples glassy fitting landscapes by removing barriers between local and global minima.46 The minimization scheme was an L-BFGS-B algorithm implemented in Python’s scipy.minimize module.47 To avoid non-physical regimes, the parameters of the no- or negative-cooperativity models were constrained to the regions 0 ≤ α ≤ 1 and K ≥ 0. For the two-state fits, the imposed bounds were ka ≥ 0, K̃ ≥ 1, and 0 ≤ α ≤ 1 × 10–18.

Errors in the fitted parameters were estimated by building an approximate covariance matrix of χ2 and propagated to the fits as described in the Supporting Information.48 Following minimization, α was converted to scaling exponent d, using the equation d = α–1, with errors propagated in the standard way.

Results

Multidimensional Microfluidic Diffusion Measurements

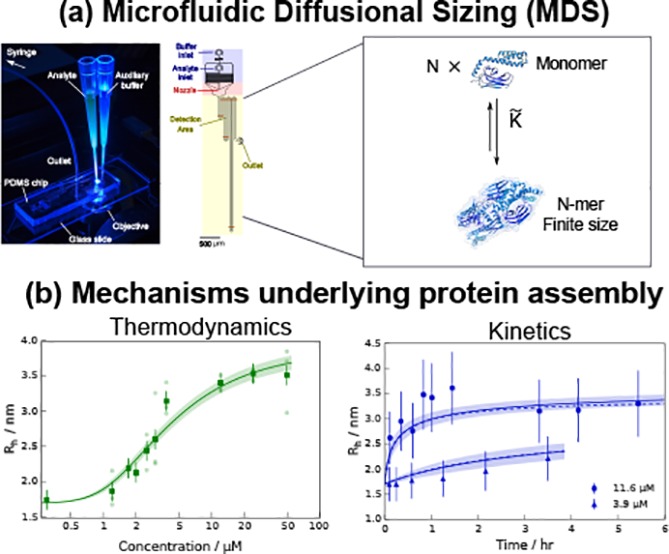
We measured the diffusion coefficients of SBD641 in solution by monitoring lateral diffusion under steady-state laminar flow in a microfluidic channel using a device shown schematically in Figure 1a.39 The cysteine residues of SBD641 were conjugated to an AlexaFluor488 dye for visualization of the sample diffusion profiles, and images were taken at 12 different positions under steady-state flow conditions using the experimental procedure shown in Figure 1b. The diffusion profiles acquired in this way were then fitted to a linear combination of simulated basis functions calculated for ideal monodisperse solutions44 (Figure 1c), yielding the average diffusion coefficients of the particles in the solution.37,39,49

Figure 1.

Figure 1

Open in a new tab

Overview of the approach for the rapid micrometer-scale diffusion measurements used for sizing biological complexes used in this work. (a) Schematic diagram of the microfluidic device, showing in brown the positions at which the mass distributions are measured. (b) Picture of a microfluidic diffusion device during measurement illuminated by blue light from an inverted fluorescence microscope. The tips connected to the device contain the analyte and an auxiliary buffer, which are drawn through the device by applying a low pressure at the outlet of the device by means of a syringe pump. (c) Diffusion profiles (left) of 24 μM SBD641 (in 10 mM Tris buffer at pH 7.4) at specific positions along the diffusion channel. The distances traveled by the analyte with respect to the nozzle are shown above each image. Lateral scans (right) of the diffusion profiles (dotted lines) fitted to a simulated set of basis functions (red lines). The extent of diffusion at each distance is dependent on the hydrodynamic radii of the molecular species present.

Thermodynamics of Oligomerization of the Hsp70 Substrate Binding Subdomain

To explore the thermodynamic determinants of SBD641 self-assembly, we determined the average hydrodynamic radius Rh of the SBD641 construct in solution at 12 different monomer concentrations between 0.3 and 50 μM using the microfluidic diffusion approach described above. Each measurement was repeated two to four times at flow rates of 100 and 160 μL/h in at least two devices fabricated independently. We found that the average Rh values increased significantly with concentration, from 1.8 ± 0.2 nm at 0.3 μM to 3.41 ± 0.15 nm at 12 μM, at which concentration the radius appeared to plateau (Figure 2a). The increase in the radius indicates an elevated population of higher-order oligomers with an increasing SBD641 concentration, in accordance with results from bulk experiments.14 In addition, to verify that the fluorescent label does not affect the measured hydrodynamic radii of SBD641, we performed sizing measurements at 0.3 μM unlabeled protein using a Fluidic Analytics Fluidity One instrument. This approach for microfluidic diffusional sizing is based on postseparation labeling.38 We found the radius of unlabeled SBD641 at 0.3 μM [10 mM sodium phosphate buffer (pH 7.4)] to be 1.89 ± 0.25 nm, in agreement with our labeled construct (Figure 2, blue data point).

Figure 2.

Figure 2

Open in a new tab

Analysis of the self-assembly behavior of the labeled SBD641 construct. In each case, the circles show the raw experimental data and the opaque green squares show the averaged data with error bars as the average standard deviations, averaged over all concentrations. The opaque blue squares show the average size of the unlabeled construct measured at 0.3 μM. Colored lines (red or green) show the fits to each model, and the shaded regions correspond to the error of each fit. (a) Oosawa model (no cooperativity),45 in which oligomers of infinite size are allowed to form. The fit yields an association constant K of 1.4 ± 0.6 μM–1 and a fractal dimension d of 3.2 ± 0.3. (b) Kinetic limit model (negative cooperativity),50 where the formation of larger oligomers is limited by the increasing rates of dissociation of the monomer from oligomeric clusters of increasing subunit numbers. The following parameters were obtained from the fit: K0 = 1.7 ± 0.6 μM–1, and d = 1.80 ± 0.13. (c) Positive cooperativity model, in which the largerst oligomer is capped to N = 4 subunits and a monomer–tetramer equilibrium is assumed (see Materials and Methods). The following parameters were obtained in the best fit: K̃ = 0.035 ± 0.011 μM–3, and d = 1.69 ± 0.06.

To evaluate the thermodynamic parameters governing the oligomerization process, we explored the extent to which the experimental data could be described by different equilibrium models with varying levels of cooperativity (details of each model can be found in Materials and Methods) (Figure 2). The average hydrodynamic radius obtained in the experimental measurements was converted to the number of monomers (j) in individual oligomeric species by means of the relationship 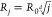Inline graphic, where Rj is the hydrodynamic radius of an oligomer with j subunits, R0 is the hydrodynamic radius of the monomeric species, and d indicates the dimensionality of the cluster (see the Supporting Information).

To understand the role of cooperativity in the assembly of these truncated Hsp70 clusters, we first considered the Oosawa model of equilibrium linear polymerization.45,51,52 This model does not display any cooperativity because the polymerization reaction is assumed to proceed through simple addition and removal of individual subunits to existing aggregates; moreover, a single equilibrium constant K describes monomer association and dissociation at each polymerization step. Figure 2a shows the best fit of our thermodynamic data to this simple model. Evidently, this model does not account for the key features of the experimental data set; in particular, the fit fails to capture the steep transition in oligomer size that occurs at the lowest concentrations measured (Figure 2a).

Because a simple polymerization model without cooperativity is unable to describe the data, we next investigated whether, at the next level of complexity, a polymerization model in which the formation of larger oligomers becomes increasingly less favorable as the size increases could result in a greater level of agreement between the simulation and the experimental data. We therefore examined a model for negative cooperativity in which the dissociation rate of larger clusters increases in proportion to their size,50 yielding a limit to oligomer size. As for the Oosawa model, the negative cooperativity model assumes that aggregation proceeds by the addition and removal of single subunits, but the equilibrium constant varies with the number of subunits (j) in an oligomer in proportion to Kj = K0/j for j > 1, thus making the formation of larger oligomers less favorable. Despite a slight improvement in the residuals of the fit, this model also fails to capture accurately the behavior of the experimental data under these conditions (Figure 2b).

Because the Oosawa and negative cooperativity models are incapable of capturing the sharp increase in the average Rh values observed in the experiments, we explored a positive cooperativity model by allowing for a higher-than-linear dependence of the rate of oligomer formation on monomer concentration. In the simplest scenario, this effect can be captured by assuming the formation of oligomers of a maximal size of N = 4 subunits, which is the largest oligomeric assembly reported in the literature,14 from the interaction of multiple monomers. Figure 2c shows that the best fit of the experimental data to this positive cooperativity model yields overall good agreement, demonstrating the necessity of a higher-than-linear monomer concentration dependence of oligomer formation to explain the observed sharp increase in Rh. Similar thermodynamic models in which the subunits demonstrate high positive cooperativity with a limiting oligomer size have been shown to describe protein self-assembly very well in systems that exhibit strong structural constraints, such as the assembly of viral capsids.53 The best fit to our data under our experimental conditions yields a value for the association constant K̃ of 0.035 ± 0.011 μM–3, i.e., an effective dissociation constant KD = K̃–1/3 = 3.1 ± 0.3 μM. The effective KD value determined in this study is broadly consistent with the value reported in the literature, 5–10 μM, for SBD641.14 We find, moreover, from the measurement of the equilibrium constants that the oligomerization process is thermodynamically favorable with a standard free energy change (ΔGassembly⊖) of −95.0 ± 0.8 kJ/mol under standard conditions. Our results show therefore that the assembly process of the SBD641 oligomers is highly cooperative with a limit to the maximum size. Moreover, our analysis shows that the limit in the oligomer size at high concentrations is unlikely to originate from purely kinetic constraints, as is the case for instance with linear protein aggregation,54 but rather appears to have an origin in structural constraints that counterbalance the thermodynamic driving force for forming larger aggregates at higher concentrations.

Kinetics of Oligomerization of the Hsp70 Substrate Binding Subdomain

We next demonstrate that the microfluidics-based strategy presented here allows us to probe directly the kinetics of self-assembly processes. To this effect, we probed SBD641 oligomerization by measuring the time taken for a purely monomeric sample to re-establish completely the dynamic equilibrium distributions of monomers and oligomers; an aliquot of the monomeric SBD641 was therefore purified by size exclusion chromatography, and the variation in average hydrodynamic radius as a function of time was monitored using MDS at different time points. The cooperativity of the oligomerization process meant that the reassembly started immediately after the fraction of monomers eluted from the column. We conducted measurements for monomeric SBD641 at concentrations of 3.9 and 11.6 μM in 10 mM Tris-HCl buffer (pH 7.4) and found that in both cases the average Rh value of SBD641 increases with time, indicating that the SBD641 oligomerization process is reversible on the time scales of this experiment and that the monomers are able to reassemble into higher-order oligomers (Figure 3), in accord with previous experiments performed in bulk.14

Figure 3.

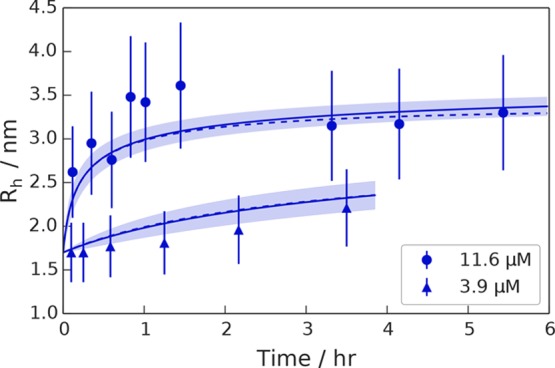
Figure 3

Open in a new tab

Microfluidic kinetic data obtained for SBD641 at two different concentrations [3.9 μM (triangles) and 11.6 μM (circles)]. The lines show fits of the data to the structural limit model in which the largest oligomer size present in the system is capped to Nmax = 4. Dashed and solid lines show the numerical and analytical approximate solutions to the kinetics, respectively, and shaded regions indicate the error in the fit (details of error analysis in the Supporting Information).

We fitted the microfluidic data obtained at two different initial chaperone concentrations (3.9 and 11.6 μM) to the integrated rate law that captures the kinetics of the positive cooperative aggregation model that was found to describe this system most effectively in our thermodynamic study. Details of the fitting can be found in Materials and Methods. Using this approach, for the self-assembly of the substrate binding subdomain of Hsp70, we obtained an association rate constant ka of (2.1 ± 1.2) × 1011 M–3 s–1 and a dissociation rate constant k– of (6 ± 4) × 10–6 s–1. The association rate constant can be further decomposed into an average elongation rate constant per monomer addition step of ⟨k+⟩ = 2.0 ± 1.2 M–1 s–1 (see Materials and Methods).

Discussion

Using the results of the kinetic fit, we compared the value of the average elongation rate constant ⟨k+⟩ obtained here for this truncated molecular chaperone system to that of a variety of self-assembling biomolecular systems, as shown in Figure 4 and Table S2. The self-assembly of the proteins shown in the graph has a variety of biological effects, including proteins such as actin and tubulin that have evolved to aggregate as a part of their function (magenta),55−57 the molecular chaperone αB-crystallin that is known to form native quaternary structures (green), and non-evolved proteins whose filamentous forms are associated with pathological aggregation such as Aβ40, Aβ42, α-synuclein, insulin, hemoglobin, and the yeast prion protein Ure2p (cyan).57−64 We find that the geometrically averaged elongation rate constant of the substrate binding subdomain of Hsp70 (red) is much lower than that of most other proteins of biological interest that are known to self-assemble, and that the average elongation rate obtained for our system compares well with that of αB-crystallin, another ubiquitous molecular chaperone, which also forms oligomers (Figure 4 and Table S2). This fits with the trend that is apparent from Figure 4, in which the aggregation rates of nonfilamentous (red and green) structures that form native quaternary assemblies do so more slowly than misfolded, filamentous proteins do (magenta and cyan). The slow average rate of monomer addition of the labeled subdomain of Hsp70 suggests that at least one of the reactions on pathway to aggregate formation is highly unfavorable, and that there is a high activation barrier in the self-assembly process.

Figure 4.

Figure 4

Open in a new tab

Comparison of the elongation rate constants of various proteins to that of SBD641 (red bar). Green bars indicate nonfilamentous structures, magenta bars evolved filamentous structures, and cyan bars pathological filamentous structures. The dashed line represents diffusion-limited aggregation, which is the limiting value that is physically possible to observe in solution.

Conclusions

In this study, we have developed a microfluidic approach for determining the values of the thermodynamic parameters governing the oligomerization of proteins under native solution conditions, in particular the dissociation constant and free energy of oligomerization, and have shown that these results can provide novel molecular insights into the mechanisms of the self-assembly process. For the system of truncated human Hsp70 studied here, the analysis of the thermodynamic data reveals that there are strong structural constraints on the size of the oligomers, which are most likely to be determined by specific molecular interaction modes at the oligomerization interface.

In addition, we took advantage of the short analysis times afforded by our microfluidic diffusion measurements, a feature that is crucial for determining the characteristic time scales associated with the rapid assembly of proteins, to show that this method can also be used to determine the overall association rate constant of oligomerization and extract the maximum assembly size. We have shown that the solution-state measurements ensure that we can observe the self-assembly behavior of proteins without compromising oligomer assembly by the interference of a surface as in many other techniques. We anticipate that the approach discussed in this work will provide the opportunity for further quantitative real-time studies of the structure and oligomerization of other self-assembling protein systems of key physiological relevance under native solution conditions.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.biochem.8b00151.

  • Integrated rate law for HSP70 assembly kinetics, maximum likelihood target function for simultaneous fitting, error analysis, and a summary of fit results and comparison of elongation rates of various proteins (PDF)

The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013) through ERC Grant PhysProt (Agreement 337969) (T.P.J.K., M.A.W., and T.C.T.M.). In addition, the authors are grateful for financial support from the Frances and Augustus Newman Foundation (T.P.J.K. and M.A.W.), the Marie Curie Fellowship scheme (P.A.), the Cambridge Commonwealth, European and International Trust (M.M.J.B.), the NIH-Oxford Cambridge Scholars Programme (M.M.J.B.), St John’s College Cambridge (T.C.T.M.), Peterhouse College Cambridge (T.C.T.M.), the Swiss National Science Foundation (T.C.T.M.), and the Biotechnology and Biological Sciences Research Council (T.M.). F.A.A. is supported by a Senior Research Fellowship award from the Alzheimer’s Society, UK (Grant 317, AS-SF-16-003). This work was supported in part by the Intramural Research Program of the National Institute of Diabetes and Digestive and Kidney Diseases at the National Institutes of Health (M.M.J.B.) and the Centre for Misfolding Diseases (Cambridge, U.K.).

The authors declare the following competing financial interest(s): Part of the work described here was done in collaboration with Fluidic Analytics Ltd., of which M.A.W. and T.M. are employees, P.A. is a share holder, C.M.D. is a scientific adviser, and T.P.J.K. is a board member.

Supplementary Material

bi8b00151_si_001.pdf (224.4KB, pdf)

References

  1. Hartl F. U.; Bracher A.; Hayer-Hartl M. (2011) Molecular chaperones in protein folding and proteostasis. Nature 475, 324–332. 10.1038/nature10317. [DOI] [PubMed] [Google Scholar]
  2. Hartl F. U.; Hayer-Hartl M. (2002) Molecular chaperones in the cytosol: from nascent chain to folded protein. Science 295, 1852–1858. 10.1126/science.1068408. [DOI] [PubMed] [Google Scholar]
  3. Evans C. G.; Wisén S.; Gestwicki J. E. (2006) Heat shock proteins 70 and 90 inhibit early stages of amyloid beta-(1–42) aggregation in vitro. J. Biol. Chem. 281, 33182–33191. 10.1074/jbc.M606192200. [DOI] [PubMed] [Google Scholar]
  4. Huang C.; Cheng H.; Hao S.; Zhou H.; Zhang X.; Gao J.; Sun Q.-H.; Hu H.; Wang C.-C. (2006) Heat shock protein 70 inhibits alpha-synuclein fibril formation via interactions with diverse intermediates. J. Mol. Biol. 364, 323–336. 10.1016/j.jmb.2006.08.062. [DOI] [PubMed] [Google Scholar]
  5. Klucken J.; Shin Y.; Masliah E.; Hyman B. T.; McLean P. J. (2004) Hsp70 Reduces alpha-Synuclein Aggregation and Toxicity. J. Biol. Chem. 279, 25497–25502. 10.1074/jbc.M400255200. [DOI] [PubMed] [Google Scholar]
  6. Luk K. C.; Mills I. P.; Trojanowski J. Q.; Lee V. M.-Y. (2008) Interactions between Hsp70 and the hydrophobic core of alpha-synuclein inhibit fibril assembly. Biochemistry 47, 12614–12625. 10.1021/bi801475r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Lashuel H. A.; Hartley D.; Petre B. M.; Walz T.; Lansbury P. T. (2002) Amyloid pores from pathogenic mutations. Nature 418, 291. 10.1038/418291a. [DOI] [PubMed] [Google Scholar]
  8. Arosio P.; Michaels T. C. T.; Linse S.; Månsson C.; Emanuelsson C.; Presto J.; Johansson J.; Vendruscolo M.; Dobson C. M.; Knowles T. P. J. (2016) Kinetic analysis reveals the diversity of microscopic mechanisms through which molecular chaperones suppress amyloid formation. Nat. Commun. 7, 10948. 10.1038/ncomms10948. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Aprile F. A.; Arosio P.; Fusco G.; Chen S. W.; Kumita J. R.; Dhulesia A.; Tortora P.; Knowles T. P. J.; Vendruscolo M.; Dobson C. M.; Cremades N. (2017) Inhibition of alpha-Synuclein Fibril Elongation by Hsp70 Is Governed by a Kinetic Binding Competition between alpha-Synuclein Species. Biochemistry 56, 1177–1180. 10.1021/acs.biochem.6b01178. [DOI] [PubMed] [Google Scholar]
  10. De Los Rios P.; Barducci A. (2014) Hsp70 chaperones are non-equilibrium machines that achieve ultra-affinity by energy consumption. eLife 3, e02218 10.7554/eLife.02218. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Freiden P. J.; Gaut J. R.; Hendershot L. M. (1992) Interconversion of three differentially modified and assembled forms of BiP. EMBO J. 11, 63–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Thompson A. D.; Bernard S. M.; Skiniotis G.; Gestwicki J. E. (2012) Visualization and functional analysis of the oligomeric states of Escherichia coli heat shock protein 70 (Hsp70/DnaK). Cell Stress Chaperones 17, 313–327. 10.1007/s12192-011-0307-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Preissler S.; Chambers J. E.; Crespillo-Casado A.; Avezov E.; Miranda E.; Perez J.; Hendershot L. M.; Harding H. P.; Ron D. (2015) Physiological modulation of BiP activity by trans-protomer engagement of the interdomain linker. eLife 4, e08961. 10.7554/eLife.08961. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Aprile F. A.; Dhulesia A.; Stengel F.; Roodveldt C.; Benesch J. L. P.; Tortora P.; Robinson C. V.; Salvatella X.; Dobson C. M.; Cremades N. (2013) Hsp70 oligomerization is mediated by an interaction between the interdomain linker and the substrate-binding domain. PLoS One 8, e67961 10.1371/journal.pone.0067961. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Gao B.; Eisenberg E.; Greene L. (1996) Enzymology: Effect of Constitutive 70-kDa Heat Shock Protein Polymerization on Its Interaction with Protein Substrate Effect of Constitutive 70-kDa Heat Shock Protein Polymerization on Its Interaction with Protein Substrate. J. Biol. Chem. 271, 16792–16797. 10.1074/jbc.271.28.16792. [DOI] [PubMed] [Google Scholar]
  16. Angelidis C. E.; Lazaridis I.; Pagoulatos G. N. (1999) Aggregation of hsp70 and hsc70 in vivo is distinct and temperature-dependent and their chaperone function is directly related to non-aggregated forms. Eur. J. Biochem. 259, 505–512. 10.1046/j.1432-1327.1999.00078.x. [DOI] [PubMed] [Google Scholar]
  17. Benaroudj N.; Batelier G.; Triniolles F.; Ladjimi M. M. (1995) Self-Association of the Molecular Chaperone HSC70t. Biochemistry 34, 15282–15290. 10.1021/bi00046a037. [DOI] [PubMed] [Google Scholar]
  18. Peschek J.; Braun N.; Franzmann T. M.; Georgalis Y.; Haslbeck M.; Weinkauf S.; Buchner J. (2009) The eye lens chaperone alpha-Crystallin forms defined globular assemblies. Proc. Natl. Acad. Sci. U. S. A. 106, 13272–13277. 10.1073/pnas.0902651106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Stengel F.; Baldwin A. J.; Painter A. J.; Jaya N.; Basha E.; Kay L. E.; Vierling E.; Robinson C. V.; Benesch J. L. P. (2010) Quaternary dynamics and plasticity underlie small heat shock protein chaperone function. Proc. Natl. Acad. Sci. U. S. A. 107, 2007–2012. 10.1073/pnas.0910126107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Stengel F.; Baldwin A. J.; Bush M. F.; Hilton G. R.; Lioe H.; Basha E.; Jaya N.; Vierling E.; Benesch J. L. P. (2012) Dissecting heterogeneous molecular chaperone complexes using a mass spectrum deconvolution approach. Chem. Biol. 19, 599–607. 10.1016/j.chembiol.2012.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Jacobs W. M.; Knowles T. P. J.; Frenkel D. (2016) Oligomers of Heat-Shock Proteins: Structures That Don’t Imply Function. PLoS Comput. Biol. 12, e1004756. 10.1371/journal.pcbi.1004756. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Smirnova E.; Chebotareva N.; Gurvits B. (2013) Transient transformation of oligomeric structure of alpha-Crystallin during its chaperone action. Int. J. Biol. Macromol. 55, 62–68. 10.1016/j.ijbiomac.2012.12.013. [DOI] [PubMed] [Google Scholar]
  23. Bova M. P.; Ding L.-L.; Fung B. K.; Horwitz J. (1997) Subunit Exchange of α A-Crystallin. J. Biol. Chem. 272, 29511–29517. 10.1074/jbc.272.47.29511. [DOI] [PubMed] [Google Scholar]
  24. Feil I. K.; Malfois M.; Hendle J.; van Der Zandt H.; Svergun D. I. (2001) A novel quaternary structure of the dimeric alpha-Crystallin domain with chaperone-like activity. J. Biol. Chem. 276, 12024–12029. 10.1074/jbc.M010856200. [DOI] [PubMed] [Google Scholar]
  25. Hochberg G. K. A.; Ecroyd H.; Liu C.; Cox D.; Cascio D.; Sawaya M. R.; Collier M. P.; Stroud J.; Carver J. A.; Baldwin A. J.; Robinson C. V.; Eisenberg D. S.; Benesch J. L. P.; Laganowsky A. (2014) The structured core domain of αB-Crystallin can prevent amyloid fibrillation and associated toxicity. Proc. Natl. Acad. Sci. U. S. A. 111, E1562–E1570. 10.1073/pnas.1322673111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Saha S.; Das K. P. (2004) Relationship between chaperone activity and oligomeric size of recombinant human alphaA- and alphaB-Crystallin: a tryptic digestion study. Proteins: Struct., Funct., Genet. 57, 610–617. 10.1002/prot.20230. [DOI] [PubMed] [Google Scholar]
  27. Horwitz J.; Huang Q.; Ding L. (2004) The native oligomeric organization of alpha-Crystallin, is it necessary for its chaperone function?. Exp. Eye Res. 79, 817–821. 10.1016/j.exer.2004.05.007. [DOI] [PubMed] [Google Scholar]
  28. Augusteyn R. C. (2004) Dissociation is not required for alpha-Crystallin’s chaperone function. Exp. Eye Res. 79, 781–784. 10.1016/j.exer.2004.08.010. [DOI] [PubMed] [Google Scholar]
  29. Hilton G. R.; Hochberg G. K. A.; Laganowsky A.; McGinnigle S. I.; Baldwin A. J.; Benesch J. L. P. (2013) C-terminal interactions mediate the quaternary dynamics of αB-Crystallin. Philos. Trans. R. Soc., B 368, 20110405. 10.1098/rstb.2011.0405. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Burmann B. M.; Hiller S. (2015) Chaperones and chaperone-substrate complexes: Dynamic playgrounds for NMR spectroscopists. Prog. Nucl. Magn. Reson. Spectrosc. 86–87, 41–64. 10.1016/j.pnmrs.2015.02.004. [DOI] [PubMed] [Google Scholar]
  31. Jehle S.; Rajagopal P.; Bardiaux B.; Markovic S.; Kühne R.; Stout J. R.; Higman V. A.; Klevit R. E.; van Rossum B.-J.; Oschkinat H. (2010) Solid-state NMR and SAXS studies provide a structural basis for the activation of alphaB-Crystallin oligomers. Nat. Struct. Mol. Biol. 17, 1037–1042. 10.1038/nsmb.1891. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Wright M. A.; Aprile F. A.; Arosio P.; Vendruscolo M.; Dobson C. M.; Knowles T. P. J. (2015) Biophysical approaches for the study of interactions between molecular chaperones and protein aggregates. Chem. Commun. 51, 14425–14434. 10.1039/C5CC03689E. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Sia S. K.; Whitesides G. M. (2003) Microfluidic devices fabricated in poly(dimethylsiloxane) for biological studies. Electrophoresis 24, 3563–3576. 10.1002/elps.200305584. [DOI] [PubMed] [Google Scholar]
  34. Herling T. W.; Arosio P.; Müller T.; Linse S.; Knowles T. P. J. (2015) A microfluidic platform for quantitative measurements of effective protein charges and single ion binding in solution. Phys. Chem. Chem. Phys. 17, 12161–12167. 10.1039/C5CP00746A. [DOI] [PubMed] [Google Scholar]
  35. Horrocks M. H.; Rajah L.; Jönsson P.; Kjaergaard M.; Vendruscolo M.; Knowles T. P. J.; Klenerman D. (2013) Single-Molecule Measurements of Transient Biomolecular Complexes through Microfluidic Dilution. Anal. Chem. 85, 6855–6859. 10.1021/ac4010875. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Srisa-art M.; Kang D.; Hong J.; Park H.; Leatherbarrow R. J.; Edel J. B.; Chang S. I.; DeMello A. J. (2009) Analysis of Protein - Protein Interactions by Using Droplet-Based Microfluidics. ChemBioChem 10, 1605–1611. 10.1002/cbic.200800841. [DOI] [PubMed] [Google Scholar]
  37. Kamholz A. E.; Yager P. (2001) Theoretical analysis of molecular diffusion in pressure-driven laminar flow in microfluidic channels. Biophys. J. 80, 155–160. 10.1016/S0006-3495(01)76003-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Yates E. V.; Müller T.; Rajah L.; De Genst E. J.; Arosio P.; Linse S.; Vendruscolo M.; Dobson C. M.; Knowles T. P. J. (2015) Latent analysis of unmodified biomolecules and their complexes in solution with attomole detection sensitivity. Nat. Chem. 7, 802–809. 10.1038/nchem.2344. [DOI] [PubMed] [Google Scholar]
  39. Arosio P.; Müller T.; Rajah L.; Yates E. V.; Aprile F. A.; Zhang Y.; Cohen S. I. A.; White D. A.; Herling T. W.; De Genst E. J.; Linse S.; Vendruscolo M.; Dobson C. M.; Knowles T. P. J. (2016) Microfluidic Diffusion Analysis of the Sizes and Interactions of Proteins under Native Solution Conditions. ACS Nano 10, 333–341. 10.1021/acsnano.5b04713. [DOI] [PubMed] [Google Scholar]
  40. Hatch A.; Kamholz A. E.; Hawkins K. R.; Munson M. S.; Schilling E. A.; Weigl B. H.; Yager P. (2001) A rapid diffusion immunoassay in a T-sensor. Nat. Biotechnol. 19, 461–465. 10.1038/88135. [DOI] [PubMed] [Google Scholar]
  41. Hatch A.; Garcia E.; Yager P. (2004) Diffusion-based analysis of molecular interactions in microfluidic devices. Proc. IEEE 92, 126–139. 10.1109/JPROC.2003.820547. [DOI] [Google Scholar]
  42. Roodveldt C.; Bertoncini C. W.; Andersson A.; van der Goot A. T.; Hsu S.-T.; Fernández-Montesinos R.; de Jong J.; van Ham T. J.; Nollen E. A.; Pozo D.; Christodoulou J.; Dobson C. M. (2009) Chaperone proteostasis in Parkinson’s disease: stabilization of the Hsp70/alpha-synuclein complex by Hip. EMBO J. 28, 3758–3770. 10.1038/emboj.2009.298. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Qin D.; Xia Y.; Whitesides G. M. (2010) Soft lithography for micro- and nanoscale patterning. Nat. Protoc. 5, 491–502. 10.1038/nprot.2009.234. [DOI] [PubMed] [Google Scholar]
  44. Müller T.; Arosio P.; Rajah L.; Cohen S. I.; Yates E. V.; Vendruscolo M.; Dobson C. M.; Knowles T. P. J. (2016) Particle-based simulations of steady-state mass transport at high Péclet numbers. Int. J. Nonlinear Sci. Numer. Simul. 17, 175–183. 10.1515/ijnsns-2015-0056. [DOI] [Google Scholar]
  45. Oosawa F., and Asakura S. (1975) Thermodynamics of the Polymerization of Protein, Academic Press. [Google Scholar]
  46. Wales D.; Doye J. P. K. (1997) Global Optimization by Basin-Hopping and the Lowest Energy Structures of Lennard-Jones Clusters Containing up to 110 Atoms. J. Phys. Chem. A 101, 5111–5116. 10.1021/jp970984n. [DOI] [Google Scholar]
  47. Zhu C.; Byrd R.; Lu P.; Nocedal J. (1997) L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization. ACM Transactions on Mathematical Software 23, 550–560. 10.1145/279232.279236. [DOI] [Google Scholar]
  48. Richter P. (1995) Estimating Errors in Least-Squares Fitting. TDA Progress Reports 42–122, 107–137. [Google Scholar]
  49. Culbertson C. T.; Jacobson S. C.; Ramsey M. J. (2002) Diffusion coefficient measurements in microfluidic devices. Talanta 56, 365–373. 10.1016/S0039-9140(01)00602-6. [DOI] [PubMed] [Google Scholar]
  50. Baldwin A. J.; Lioe H.; Robinson C. V.; Kay L. E.; Benesch J. L. P. (2011) αB-Crystallin polydispersity is a consequence of unbiased quaternary dynamics. J. Mol. Biol. 413, 297–309. 10.1016/j.jmb.2011.07.016. [DOI] [PubMed] [Google Scholar]
  51. Oosawa F.; Kasai M. (1962) A theory of linear and helical aggregations of macromolecules. J. Mol. Biol. 4, 10–21. 10.1016/S0022-2836(62)80112-0. [DOI] [PubMed] [Google Scholar]
  52. Cohen S. I. A.; Vendruscolo M.; Dobson C. M.; Knowles T. P. J. (2012) From Macroscopic Measurements to Microscopic Mechanisms of Protein Aggregation. J. Mol. Biol. 421, 160–171. 10.1016/j.jmb.2012.02.031. [DOI] [PubMed] [Google Scholar]
  53. Morozov A. Y.; Bruinsma R. F.; Rudnick J. (2009) Assembly of viruses and the pseudo-law of mass action. J. Chem. Phys. 131, 155101. 10.1063/1.3212694. [DOI] [PubMed] [Google Scholar]
  54. Michaels T. C. T.; Lazell H. W.; Arosio P.; Knowles T. P. J. (2015) Dynamics of protein aggregation and oligomer formation governed by secondary nucleation. J. Chem. Phys. 143, 054901. 10.1063/1.4927655. [DOI] [PubMed] [Google Scholar]
  55. Kuhn J. R.; Pollard T. D. (2005) Real-time measurements of actin filament polymerization by total internal reflection fluorescence microscopy. Biophys. J. 88, 1387–1402. 10.1529/biophysj.104.047399. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Engelborghs Y.; de Maeyer L. C.; Overbergh N. (1977) A kinetic analysis of the assembly of microtubules in vitro. FEBS Lett. 80, 81–85. 10.1016/0014-5793(77)80411-0. [DOI] [PubMed] [Google Scholar]
  57. Langelier E.; Suetterlin R.; Hoemann C. D.; Aebi U.; Buschmann M. D. (2000) The Chondrocyte Cytoskeleton in Mature Articular Cartilage: Structure and Distribution of Actin, Tubulin, and Vimentin Filaments. J. Histochem. Cytochem. 48, 1307–1320. 10.1177/002215540004801002. [DOI] [PubMed] [Google Scholar]
  58. Cohen S. I. A.; Linse S.; Luheshi L. M.; Hellstrand E.; White D. A.; Rajah L.; Otzen D. E.; Vendruscolo M.; Dobson C. M.; Knowles T. P. J. (2013) Proliferation of amyloid-β42 aggregates occurs through a secondary nucleation mechanism. Proc. Natl. Acad. Sci. U. S. A. 110, 9758–9763. 10.1073/pnas.1218402110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Knowles T. P. J.; Shu W.; Devlin G. L.; Meehan S.; Auer S.; Dobson C. M.; Welland M. E. (2007) Kinetics and thermodynamics of amyloid formation from direct measurements of fluctuations in fibril mass. Proc. Natl. Acad. Sci. U. S. A. 104, 10016–10021. 10.1073/pnas.0610659104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Buell A. K.; Galvagnion C.; Gaspar R.; Sparr E.; Vendruscolo M.; Knowles T. P. J.; Linse S.; Dobson C. M. (2014) Solution conditions determine the relative importance of nucleation and growth processes in α-synuclein aggregation. Proc. Natl. Acad. Sci. U. S. A. 111, 7671–7676. 10.1073/pnas.1315346111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Aprelev A.; Liu Z.; Ferrone F. A. (2011) The growth of sickle hemoglobin polymers. Biophys. J. 101, 885–891. 10.1016/j.bpj.2011.05.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Vekilov P. G. (2007) Sickle-cell haemoglobin polymerization: is it the primary pathogenic event of sickle-cell anaemia?. Br. J. Haematol. 139, 173–184. 10.1111/j.1365-2141.2007.06794.x. [DOI] [PubMed] [Google Scholar]
  63. Chiti F.; Dobson C. M. (2006) Protein Misfolding, Functional Amyloid, and Human Disease. Annu. Rev. Biochem. 75, 333–366. 10.1146/annurev.biochem.75.101304.123901. [DOI] [PubMed] [Google Scholar]
  64. Xu L. Q.; Wu S.; Buell A. K.; Cohen S. I. A.; Chen L. J.; Hu W.-H.; Cusack S. A.; Itzhaki L. S.; Zhang H.; Knowles T. P. J.; Dobson C. M.; Welland M. E.; Jones G. W.; Perrett S. (2013) Influence of specific HSP70 domains on fibril formation of the yeast prion protein Ure2. Philos. Trans. R. Soc., B 368, 20110410. 10.1098/rstb.2011.0410. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

bi8b00151_si_001.pdf (224.4KB, pdf)

Articles from Biochemistry are provided here courtesy of American Chemical Society

RESOURCES