Electron transfer characteristics of 2’-deoxy-2’-fluoro-arabinonucleic acid, a nucleic acid with enhanced chemical stability

The non-biological nucleic acid 2’-deoxy-2’-fluoro-arabinonucleic acid (2’F-ANA) may be of use because of its higher chemical stability than DNA in terms of resistance to hydrolysis and nuclease degradation. In order to investigate the charge transfer characteristics of 2’F-ANA, of relevance to applications in nucleic acid-based biosensors and chip technologies, we compare the electronic couplings for hole transfer between stacked nucleobase pairs in DNA and 2’F-ANA by carrying out density fuctional theory (DFT) calculations on geometries taken from molecular dynamics simulations. We find similar averages and distribution widths of the base-pair couplings in the two systems. On the basis of this result, 2’F-ANA is expected to have charge transfer properties similar to those of DNA, while offering the advantage of enhanced chemical stability. As such, 2’F-ANA may serve as a possible alternative to DNA for use in a broad range of nanobiotechnological applications. Furthermore, we show that the (experimentally observed) enhanced chemical stability resulting from the backbone modifications does not cause reduced fluctuations of the base-pair electronic couplings around the values found for “ideal” B-DNA (with standard step parameter values). Our study also supports the use of a DFT implementation, with the M11 functional, of the wave function overlap method to compute effective electronic couplings in nucleic acid systems.

DNA’s structural, biological, chemical and electronic properties make it of great interest in a wide range of fields, including nanobioelectronics,^{1, 2} biological sensing,^3–5 redox protein signaling,^{6, 7} and biomedicine.^{8, 9} Therefore, research aims to understand and to optimize DNA charge transport,^10–12 exploring its charge conduction mechanisms as a function of structure and sequence.^13–20 Fast DNA charge transport can be achieved through transient coherence (flickering resonance²¹) or ‘deep-hole transfer’.²²

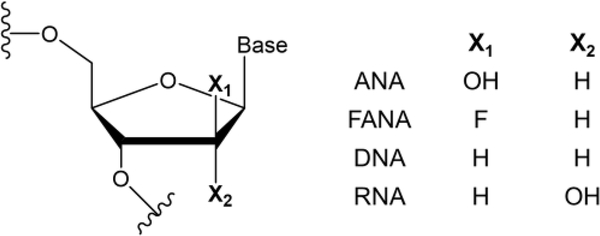
In contrast to the rich DNA literature, very little is known about hole transport through xeno-nucleic acids (XNA), although these chemically modified nucleic acids are known to also be capable of carrying out heredity and evolution functions (since genetic information can be stored in them and retrieved from them)²³ while having greater resistance to nuclease degradation compared to DNA/RNA. The XNA investigated in this study, 2’F-ANA (Fig. 1), has notable chemical properties including: (i) high resistance to acid hydrolysis;^{24, 25} (ii) a wider operating pH range than DNA and RNA;²⁴ (iii) the ability to form duplexes with DNA/RNA,^{26, 27} which can enable its use for the directed evolution of biopolymers; and (iv) the ability to induce the enzymatic degradation of target mRNA.²⁸ These properties make 2’F-ANA an attractive vehicle for oral absorption of oligonucleotides^{29, 30} and intracellular delivery (with relevance to cancer treatments, as exemplified by the gymnotic silencing of the androgen receptor in prostate cancer cells by 2’F-ANA³¹) and could enable increased durability in diagnostic applications.²⁴ For biosensing and chip technologies that rely on charge-transfer based signal transduction through a nucleic acid,^32–34 2’F-ANA probes can potentially be an improved alternative to DNA probes. In fact, probes using 2’F-ANA can be washed with acid or base to remove the analytes without compromising the structural integrity of the 2’F-ANA array. Furthermore, unlike DNA-inspired systems such as the peptide nucleic acids (PNAs) (in which a neutral backbone can destabilize hole states localized on the nucleobases that support charge migration³⁵), 2’F-ANA not only retains the negatively charged phosphate backbone but also contains a highly electronegative fluorine on the ribose moiety (Fig. 1) that increases the backbone charge compared to DNA.

Fig. 1.

Molecular Structures of 2’F-ANA and DNA, compared with ANA (arabinonucleic acid) and with RNA.

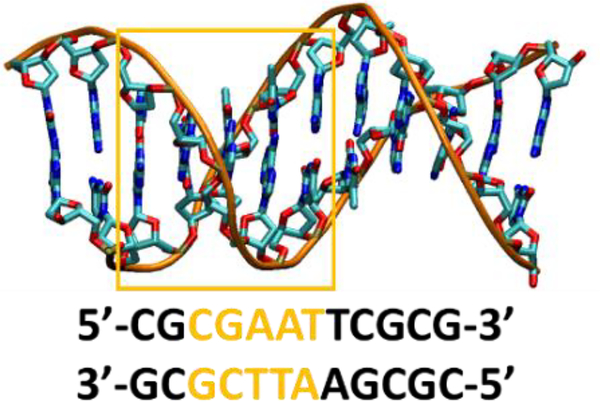
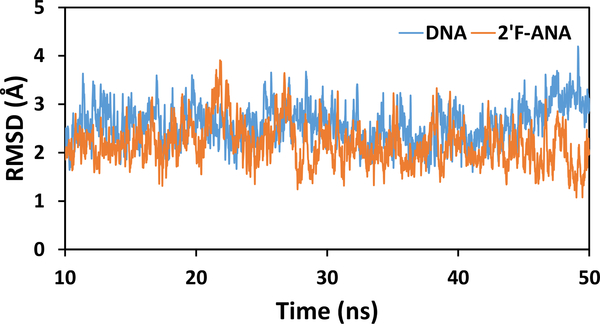
If charge transport in 2’F-ANA is at least as fast as in DNA, the 2’F-ANA’s enhanced structural properties favor its use in the nucleic acid applications mentioned above. Here, we compare the charge transfer properties of 2’F-ANA and DNA in terms of the effective³⁶ electronic couplings between nucleobase pairs as a function of the nuclear conformation. DNA and 2’F-ANA were modeled using the Dickerson-Drew dodecamers (that has a B-DNA structure) (Fig. 2), using the structures with PDB codes 4C64³⁷ and 2LSC,³⁸ respectively. To obtain the 2’F-ANA duplex from the 2’F-ANA/ANA structure in the 2LSC PDB file, the U bases of the ANA strand were modified to T bases and the sugar moieties were replaced with the corresponding ones in 2’F-ANA, as detailed in the Supporting Information. The two systems were solvated with TIP3P water³⁹ and simulated for 50 ns using classical molecular dynamics (MD), with the AMBER force field ff99 (see Supporting Information). In the 10–50 ns time window, the RMSDs of DNA and of 2’F-ANA fluctuate randomly around average values of 2.6 Å and 2.2 Å, with ranges of 1.6–4.2 Å and 1.1–3.9 Å, respectively (Fig. 3). The ranges of RMSD values suggest similar structural stability for 2’F-ANA and DNA, despite their different chemical stability. We selected MD snapshots for electronic coupling analysis each ns in the 10–50 ns time window of the MD production run.

Fig. 2.

Structure and base pair sequence of the Dickerson-Drew dodecamer (PDB 4C64³⁷). The base pairs used for V_IF calculations are highlighted in yellow.

Fig. 3.

RMSDs (excluding H atoms) along the MD production runs for DNA (blue) and 2’F-ANA (orange).

The (effective) electronic coupling V_IF (here, I and F denote the initial and final localized electronic states, respectively) is a crucial determinant of the charge-transfer rate constant.^{40, 41} In the nonadiabatic limit, at high temperatures (e.g., at room or physiological temperatures), and for slow modulation of the coupling by structural fluctuations,^{42, 43} the mean square electronic coupling $〈V_{IF}^2〉$ is used to compute the rate. The variance ${\sigma }^2=〈V_{IF}^2〉-{〈V_{IF}〉}^2$ of V_IF is used to calculate the coherence parameter⁴⁴ $C=1-{\sigma }^2/〈V_{IF}^2〉={〈V_{IF}〉}^2/〈V_{IF}^2〉$. C is a descriptor of coupling fluctuations. C = 1 occurs for rigid systems (σ = 0), while C ≅ 0 for very flexible systems with strong dependence of the coupling on the atomic conformation.

We calculated the effective electronic couplings with the formula (which is exact in the two-state approximation)^{45, 46}

$$V_{IF}=\left\{\begin{array}{ll}\left|\frac{ab}{a^2-b^2}\Delta E_{IF}\left(1+\frac{a^2+b^2}{2ab}{S}_{IF}\right)\frac{1}{1-{S_{IF}}^2}\right|& (\Delta E_{IF}\ne 0)\\ \frac{\Delta E_v}{2}& (\Delta E_{IF}=0)\end{array}\right.$$ (1)

In eqn (1), a and b denote the coefficients of the ground state expansion on the diabatic (localized) electronic states, S_IF is the overlap of such states and ΔE_IF is their energy difference; ΔE_v is the vertical energy difference between the adiabatic ground and first-excited states. The first expression in eqn 1 can also be used, with high accuracy,⁴⁶ near the transition state (where ΔE_IF ≪ 2V_IF), while it has a removable discontinuity exactly at the transition state coordinates (which, however, are always a zero-measure subspace of the conformational space), where the first expression is easily reduced to the second one. As shown previously,⁴⁶ eqn (1) enables CDFT states to be used as a suitable basis set to describe charge-transfer systems also in cases where the two CDFT states have a partial charge-transfer character⁴⁷ that is reflected in a large overlap, as long as the two state approximation is valid (see refs ^{45, 46} and Supporting Information). The DFT implementation of eqn (1) is also robust with respect to basis set superposition errors.⁴⁸

The quantities appearing in eqn (1) were obtained from DFT calculations. Constrained DFT^{49, 50} (as developed in refs. ^{51, 52} and implemented in the NWChem⁵³ and QChem⁵⁴ codes) was used to obtain the diabatic states. We used this theoretical approach on the selected MD structural snapshots. Since the Dickerson-Drew dodecamer has a palindromic sequence, we limited the coupling calculations to nearest-neighboring base pairs in the base set highlighted in Fig. 2. In the 5’-to-3’ direction, the base pairs are denoted CG-GC, GC-A₁T, A₁T-A₂T, and A₂T-TA. Our analysis first investigated the accuracy of different hybrid DFT approaches to calculate the GC-A₁T and A₁T-A₂T couplings in the DNA MD snapshot at 10 ns. CASSCF and CAS-PT2 calculations (with an active space of 11 electrons in 12 orbitals) provided benchmark values⁵⁵ in the range 36–46 meV for V_G–A (to be approximately compared with the values in the first column of Table 1, which were calculated for the base-pair dimers, that is, in the presence of the complementary bases) and in the range of 2–4 meV for V_A–A (cf. second column). Among the hybrid exchange-correlation (XC) functionals tested (Table 1), B3LYP⁵⁶ and PBE0⁵⁷ (with 20% and 25% of Hartree-Fock (HF) exchange, respectively) give the largest V_IF values because of excessive delocalization of the ground-state valence charge, as it was previously found with the double-zeta 6–31g* basis set⁴⁸. Although the value of an electronic coupling can depend on the nuclear coordinates,⁴⁸ the comparison with the benchmark coupling values and with the DFT values computed with XC functionals that have larger amounts of HF exchange (as well as a comparison with the ranges of values in Table S1) shows significant overestimation of the electronic couplings using B3LYP and PBE0. Although these XC functionals can produce appropriate optimized molecular geometries, their relatively small HF exchange components prevent accurate description of the ground-state tail on the acceptor nucleobase pair, which determines the value of the electronic coupling. The SOGGA11-X functional (with 40.15% HF exchange)⁵⁸ produces smaller electronic couplings. Further improvement is achieved by using the range-separated functional CAM-B3LYP (19% and 65% of HF exchange in the short and long range, respectively⁵⁹) and the Minnesota functionals M05–2X⁶⁰ (56% of HF exchange), M06–2X⁶¹ (54% HF), M08-HX⁶² (52.23% HF), and M08-SO⁶² (56.79% HF). The coupling values obtained using these density functionals correlate with the amount of HF-type exchange. The relatively short distance between adjacent nucleobase pairs may explain the suboptimal performance of the CAM-B3LYP functional despite its range separation with a relatively large HF exchange component at long range. The ωB97M-V functional⁶³ performs similarly to CAM-B3LYP for the GC-A₁T coupling, while providing an A₁T- A₂T coupling much closer to the benchmark post-Hartree-Fock value compared to CAM-B3LYP. The BHLYP^{56, 64} (50% HF) and range-separated LRC-ωPBEh⁶⁵ (20% and 100% of short and long range HF, respectively) XC functionals (which are suggested as the best performing XC functionals to describe charge transfer based on the error metric defined in ref. ⁶⁶) lead to a further decrease in the electronic coupling values. However, the best performance (in comparison with the multi-configurational methods) is achieved with the M06-HF⁶¹ (100% HF exchange) and range-separated M11⁶⁷ (42.8% short-range and 100% long-range HF exchange) XC functionals. M06-HF can underestimate the electronic couplings (as found recently by the combined use of constrained DFT and effective Hamiltonian approaches⁶⁸), although its behavior in the long-range limit is not affected by electron self-interaction errors.

Table 1.

Effective electronic couplings between B-DNA nearest-neighboring base pairs calculated using the 6–311G** basis set and the listed hybrid XC functionals. All values are in meV.

XC	$V_{GC-A_{1}T}$	$V_{A_{1}T-A_{2}T}$
B3LYP	604.7	197.2
PBE0	518.9	383.4
SOGGA11-X	272.4	25.1
ωB97M-V	150.4	7.6
CAM-B3LYP	147.6	33.1
LRC-ωPBEh	126.6	40.9
BHLYP	126.1	30.3
M05–2X	162.8	0.2
M06–2X	177.9	2.6
M06-HF	61.8	1.3
M08-HX	203.8	3.1
M08-SO	167.7	2.1
M11	78.9	4.1

Based on the analysis above, we used the M11 functional to calculate the electronic couplings between nearest-neighboring base pairs in the selected MD snapshots of DNA and 2’F-ANA at an affordable computational cost. Nonetheless, based on the values in Table 1, the differences among the results using the ωB97M-V, BHLYP, M06-HF and M11 approximations could be appreciably reduced by averaging the electronic couplings over the MD snapshots, due to considerable cancellation of errors. The values of mean-square electronic coupling and coherence parameter for the selected base pair dimers are reported in Table 2. The individual coupling values in all selected MD snapshots are given in the Supporting Information.

Table 2.

Mean square electronic coupling ⟨V_IF²⟩ (in meV²) and coherence parameter C for the indicated DNA and 2’F-ANA base pair dimers.

base pair dimer	DNA		2’F-ANA
	$〈{\mathit{V}}_{\mathit{I}\mathit{F}}^2〉$	C	$〈{\mathit{V}}_{\mathit{I}\mathit{F}}^2〉$	C
CG-GC	188	0.52	211	0.60
GC-A1T	8118	0.56	1242	0.70
A1T-A2T	1681	0.65	2661	0.43
A2T -TA	1087	0.46	3941	0.25

The mean-square electronic couplings for the corresponding base-pair dimers in the two dodecamers are of the same orders of magnitude. The intra-strand GC-A₁T coupling is stronger in DNA than in 2’F-ANA, while the converse holds for the inter-strand A₂T-TA coupling. Nevertheless, the electronic couplings in 2’F-ANA are larger than the corresponding couplings in DNA for three of the four nucleobase stacks studied. This result indicates enhanced conductivity of 2’F-ANA, compared to DNA, for sequential hole hopping mechanisms, if similar free energy parameters are associated with the charge hopping steps in the two structures. The average values of the coherence parameters for the DNA and 2’F-ANA systems are 0.55 and 0.50, respectively, thus suggesting similar fluctuations of the electronic couplings across their nucleobase π-stacks. Further RMSD analysis (Supporting Information, Fig. S1) finds that the backbones of DNA and 2’F-ANA undergo structural fluctuations of similar magnitude, in reasonable agreement with previous findings.³⁸ The nucleobase fluctuations span a slightly wider range in 2’F-ANA than in DNA and thus enable access to conformations with relatively large electronic coupling values (Figs. S2-S5).

While our current results show similar structural flexibility, and related similar electronic coupling fluctuations, for the DNA and 2’F-ANA duplexes, further theoretical studies need to investigate whether the more negative backbone of 2’F-ANA compared to DNA may lead to appreciable changes in the free energy parameters (reaction free energies and reorganization energies) associated with the hole transfer steps and to partial hole transfer to the backbone (namely, a partial transfer of electron charge to the positively charged bases).

From a methodological point of view, our study supports the use of eqn (1) in conjunction with the M11 Minnesota functional to compute electronic couplings in base-pair dimers (see Table 2). BHLYP and ωB97M-V are the next most accurate density functionals to compute nucleobase electronic couplings based on the results of this study (however, it was shown that the Becke half-and-half approximation can enable very accurate electronic coupling calculation by including diffuse functions in the basis set⁴⁶).

The computational results of Fig. 3 and Table 2 indicate that the modification of the DNA backbone leading to 2’F-ANA (which yields chemical protection against the external environment) does not enhance the intrinsic structural stability, with an appreciably increased charge transport efficiency of the π-stacking pattern, as quantified in terms of nucleobase pair electronic couplings. Nonetheless, our results indicate that 2’F-ANA combines its greater chemical stability with similar or slightly improved hole conduction compared to DNA (as quantified in Table 2), thereby promoting 2’F-ANA as a potentially better candidate than DNA for applications in (nano)biotechnology.