Semimechanistic Population Pharmacokinetic Model to Predict the Drug–Drug Interaction Between S‐ketamine and Ticlopidine in Healthy Human Volunteers

Abstract

Low‐dose oral S‐ketamine is increasingly used in chronic pain therapy, but extensive cytochrome P450 (CYP) mediated metabolism makes it prone to pharmacokinetic drug‐drug interactions (DDIs). In our study, concentration‐time data from five studies were used to develop a semimechanistic model that describes the ticlopidine‐mediated inhibition of S‐ketamine biotransformation. A mechanistic model was implemented to account for reversible and time‐dependent hepatic CYP2B6 inactivation by ticlopidine, which causes elevated S‐ketamine exposure in vivo. A pharmacokinetic model was developed with gut wall and hepatic clearances for S‐ketamine, its primary metabolite norketamine, and ticlopidine. Nonlinear mixed effects modeling approach was used (NONMEM version 7.3.0), and the final model was evaluated with visual predictive checks and the sampling‐importance‐resampling procedure. Our final model produces biologically plausible output and demonstrates that ticlopidine is a strong inhibitor of CYP2B6 mediated S‐ketamine metabolism. Simulations from our model may be used to evaluate chronic pain therapy with S‐ketamine.

Study Highlights.

What is the current knowledge on the topic?

 Ticlopidine is a potent mechanism‐based inhibitor of hepatic CYP2B6 in humans, which leads to an ~2.1‐fold rise in S‐ketamine exposure and may cause problems in pain therapy.

What question did this study address?

 How a semimechanistic approach could be used to predict mechanism‐based DDI between a CYP2B6‐substrate S‐ketamine and ticlopidine.

What does this study add to our knowledge?

 The complex interaction between S‐ketamine and ticlopidine can be accurately predicted with a mechanistic static model. In addition, the use of a semimechanistic nonlinear mixed effects modeling approach could accurately fit the pharmacokinetic profiles of S‐ketamine, norketamine, and ticlopidine.

How might this change drug discovery, development, and/or therapeutics?

 The mechanistic static model is a valuable resource for precisely predicting mechanism‐based DDIs in population modeling. The semimechanistic model developed in our study can be used to precisely dose S‐ketamine in patients simultaneously receiving ticlopidine.

Opioid receptor agonists are effective pain therapeutics,1 but their use is complicated by severe side effects. The so‐called “opioid crisis”2 emphasizes the need to reduce opioid use and to search for ways to improve multimodal analgesia in pain therapy. Activation of N‐methyl‐D‐aspartate (NMDA) receptors may play a crucial role in the pathogenesis of chronic pain,3 and, therefore, orally administered ketamine, a potent NMDA receptor antagonist, has been used to treat complex chronic pain.4 Orally administered ketamine undergoes extensive first‐pass metabolism, resulting in a bioavailability of ~17%.5 The N‐oxidation to norketamine by hepatic cytochrome P450 (CYP)2B6 is the primary metabolic pathway of ketamine biotransformation,6 whereas CYP3A has also been reported to contribute to ketamine metabolism in humans.7 A recent in vitro study has shown that the fraction of ketamine metabolized by hepatic CYP2B6 is around 60%,8 and, hence, CYP2B6‐inhibition can lead to a significant increase in S‐ketamine exposure.9

Ticlopidine is a mechanism‐based inhibitor of CYP2B6,10, 11 with a dissociation constant (K _i) of 0.031 μM, indicating a high potency of ticlopidine toward CYP2B6 inhibition. Ticlopidine has a complex nonlinear pharmacokinetic profile that has been recorded previously in several reports.12 Ticlopidine is metabolized to 2‐oxo‐ticlopidine primarily in the liver by CYP2B6 and CYP2C19,13, 14 and previous studies have indicated that ticlopidine half‐life is increased after multiple dosing, suggesting an auto‐inhibition of ticlopidine metabolism.12

Our previous drug‐drug interaction (DDI) study in healthy human volunteers demonstrated that ticlopidine causes a significant 2.1‐fold rise in systemic exposure of orally administered S‐ketamine after a 6‐day ticlopidine predosing (250 mg b.i.d.).9 Itraconazole, a CYP3A enzyme inhibitor, had no significant effect on plasma concentrations of orally administered S‐ketamine, indicating that the gut wall might not be a significant contributor in S‐ketamine first‐pass metabolism.

The information gained by a static approach of DDI modeling or a noncompartmental analysis (NCA) is limited.15 Time variant parameters, such as the full pharmacokinetic profile of the perpetrator and the respective metabolites, are ignored and the mechanistic description of the inhibition process is restricted. A semimechanistic population pharmacokinetic model provides an intuitive way to apply a dynamic approach to account for a time‐varying inhibition process and sources of unexplained interindividual variability (IIV) based on in vivo data, as highlighted previously.15, 16, 17

We have reanalyzed our S‐ketamine data with the aim of developing a population pharmacokinetic model that could: (1) account for the complex metabolic processes, which constitute the metabolism of S‐ketamine to norketamine; (2) adequately predict the concentration‐time course of S‐ketamine and its primary metabolite norketamine, and of ticlopidine; and (3) mechanistically account for the DDI between S‐ketamine and ticlopidine and accurately predict the rise in S‐ketamine plasma concentrations after ticlopidine predosing.

Methods

Concentration‐time data for S‐ketamine, norketamine, and ticlopidine were gathered from five previously conducted placebo controlled, blinded, randomized, crossover studies.7, 9, 18, 19, 20 For our analysis, we pooled the data from placebo phases of S‐ketamine administration. For the DDI model development, the complete dataset (i.e., placebo as well as inhibitor phase) was included from the study that investigated the DDI between S‐ketamine and ticlopidine.9 A summarized description of these studies with the study designs, sampling schemes, and the drug analysis are described in Supplementary Information S1 . The study protocols of all of these studies were approved by the ethics committee of the Hospital District of Southwest Finland and by the Finnish National Agency of Medicines, and were registered in the EudraCT clinical trials register.

Data analysis

Nonlinear mixed effects modeling was conducted with the NONMEM (version 7.3.0) software package (ICON Development Solutions, Ellicott City, MD21) aided with Perl‐Speaks‐NONMEM toolkit (PsN,22 version 4.6.0 or above), which was utilized to support the model development, execution, and evaluation. RStudio (version 1.0.153 or above) using R23 (R Foundation for Statistical Computing, 2018; version 3.4.0 or above) was used for model diagnostics and graphical visualization.

Model development

The first‐order conditional estimation with interaction method was applied to the data. Pharmacokinetic modeling was conducted in a sequential manner; first, a pharmacokinetic model for S‐ketamine was built, after which we incorporated a pharmacokinetic model for the major metabolite, norketamine. A pharmacokinetic model for ticlopidine was developed parallel to the S‐ketamine/norketamine model. These models were linked together with an interaction model and finally all parameters were estimated simultaneously using the full dataset.

Structural model

The structural model was built using a set of differential equations that were solved with the ADVAN13 subroutine. For all three substances, we commenced with a simple empirical one‐compartment model, and nested models were developed in a stepwise manner. The optimum number of compartments to account for drug disposition kinetics was optimized at first, after which the physiological compartments for gut wall, portal vein, and liver were added to the structural model.24, 25 Physiological parameters incorporated into the model were obtained from the previously published studies (Table 1).

Table 1.

Drug constants and physiological parameter values used in the final semiphysiologically based pharmacokinetic model

Parameter	Value	References
S‐ketamine (SK)
f u,SK	0.70	6
f u,GW,SK	1	41
BPRATIO	0.50	42
f m,CYP2B6	0.60a	8
Norketamine (NK)
f u,NK	0.50	37
f u,GW,NK	1	41
BPRATIO	1	41
Ticlopidine (TIC)
f u,TIC	0.02	43
f u,GW,TIC	1	41
BPRATIO	1	41
k inact	0.30 min−1	11
K I	0.57 μM	11
k i	0.031 μM	11
Physiological parameters
Q H	3.75aWTKG0.75	44
Q PV	0.75a Q H	45
Q HA	0.25a Q H	45
Q INT	0.40a Q H	45
Q MU	0.80a Q INT	41
Q VI	0.60a Q MU	41
V H	1
V GW	1
V PV	1
k deg	0.00026 min−1	43

BP_RATIO, blood to plasma ratio; CYP, cytochrome P450; f _u, unbound drug fraction in the blood; f _u,GW, unbound drug fraction in the gut wall; f _m,CYP2B6, fraction of drug metabolized by CYP2B6; k _deg, the de novo physiological rate of degradation of CYP2B6; k _i, the equilibrium dissociation constant of ticlopidine for CYP2B6; K _I, the inhibitor concentration half maximal inactivation rate; K _inact, maximum rate of inactivation of CYP2B6 at [I] = ∞; Q _H, Q _PV, Q _HA, Q_INT, Q _MU, and Q _VI, are the hepatic, portal vein, hepatic artery, intestinal, mucosal, and villous blood flow, respectively. V _H, V _GW, and V _PV are the hepatic, gut wall, and portal vein volumes.

^aCalculated as a parameter in the model, final value = 0.63.

Stochastic model

The IIV on the fixed effects parameters in the model was specified using an exponential model:

$${\mathrm{\Phi }}_i=\mathrm{\theta }\ast e^{{\mathrm{\eta }}_i}$$

where Φ_i represents the value of a fixed effect parameter for an individual, θ is the typical population value of the parameter, and η_i accounts for the IIV of the ith individual from the population typical value.

IIVs were first introduced with all model parameters stepwise in nested models, and addition of each IIV parameter was accepted only if it lead to a significant drop in the objective function value (OFV), ε‐shrinkage was <25%, and the model stability remained unaffected. The residual variability in predicted concentrations was specified with a proportional error model:

$$C_{\mathrm{ij},\mathrm{x}}={\widehat{C}}_{\mathrm{ij},\mathrm{x}}\ast (1+{\mathrm{\epsilon }}_{\mathrm{ij},\mathrm{x}})$$

where x is one of the three substances, C _ij,x is the jth observed concentration and ${\widehat{C}}_{\mathrm{ij},\mathrm{x}}$ is the model predicted concentration of the ith individual, and ε_ij,_x is a normally distributed random variable to quantify the residual variability in the concentrations. Both η and ε were assumed to be normally distributed random variables. Additive and constant coefficient of variation models were also tested.

Model evaluation

Among nested models, a difference in the OFV was used to discriminate between models. A significance level of 0.05 equaling to a drop of 3.84 points in the OFV was used. Standard goodness‐of‐fit plots26 were used to graphically visualize model performance. Model precision and parameter identifiability were determined by assessing relative SEs and evaluating covariance matrices.

Prediction‐corrected visual predictive checks27 (pcVPCs) were performed after key modeling steps by simulating 1,000 replicates of the original study design to evaluate the predictive performance and model appropriateness. For comparison, observed data were plotted against time and overlaid with the 95% predictive interval of the simulated data.

Because of extended model estimation times, the sampling importance resampling (SIR) procedure28 was used to evaluate parameter uncertainty and to calculate the 95% confidence intervals (CIs) for the parameter estimates of the final model. In order to get robust SIR results, the procedures were run with 20,000 final samples and 2,000 resamples (M/m = 10). A covariance matrix from the successful final model run was used as a proposal distribution. SIR results were evaluated with the graphical diagnostics methods in the sir‐package in PsN (differences in the OFV distribution plot, spatial, and temporal trends plots29).

Simulations

The ncappc‐package in PsN30 was used to compare model‐predicted maximum plasma concentration (C_max) and area under the curve (AUC) to the values from the NCA analysis from our previous report.9 Model‐based simulations were performed using the final parameter estimates for the fixed and random effects in 1,000 virtual subjects with NONMEM to assess the performance of the mechanism‐based and reversible components of the inhibition parameters in the mechanistic static model (MSM) model. These simulations were also used to evaluate the decrease in the intrinsic hepatic clearances of S‐ketamine during placebo and ticlopidine predosing phases and the apparent recovery over time during inhibitor washout, and to assess the time course of CYP2B6 inhibition after the administration of ticlopidine, and the temporal recovery of enzyme activity. Finally, we used the final DDI model to evaluate how ticlopidine administration affects the pharmacokinetics of intravenous (i.v.) S‐ketamine administration in comparison to an oral delivery route.

RESULTS

Model development

S‐ketamine model

A one‐compartment model was first tested but it did not capture the concentration‐time course of S‐ketamine properly. A three‐compartment mammillary model (∆OFV = −598) with a central and two peripheral compartments was observed to be superior to a two‐compartmental model (∆OFV = −578). This was consistent with a recent study,31 developing a population model for S‐ketamine and norketamine after oral and i.v. dosing. Physiological compartments for gut wall, portal vein, and liver were added in a sequential manner to account for the disposition kinetics of S‐ketamine (Figure 1) according to the simplified quasi‐steady‐state approximation approach25, 32 (Supplementary Information S2 ).

Figure 1.

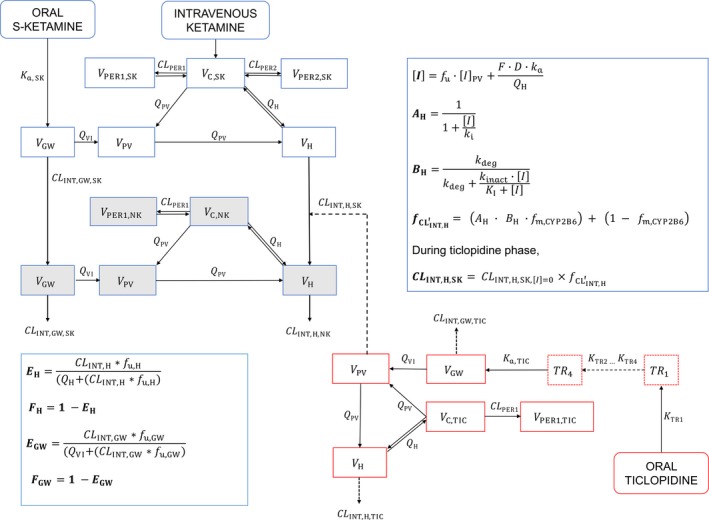
A diagrammatic representation of the final semiphysiologically based pharmacokinetic model that includes S‐ketamine model, norketamine model, ticlopidine model, and a dynamic drug‐drug interaction model. A _H, reversible component of CYP2B6 inhibition; B _H, the non‐reversible component of CYP2B6 inhibition; C, central compartment; CL_INT, intrinsic clearance; CYP, cytochrome P450; D, amount of inhibitor (ticlopidine) administered; F, bioavailability of ticlopidine into the first depot compartment; $f_{{{\mathrm{CL}}^{\prime }}_{\mathrm{INT},\mathrm{H}}}$, inhibition parameter signifying hepatic CYP2B6 degradation; f _m,CYP2B6, fraction of S‐ketamine metabolized by CYP2B6; f _u, fraction unbound of ticlopidine in the blood; GW, gut wall; H, hepatic; [I], ticlopidine concentration at the enzyme site; [I]_PV, ticlopidine concentration at the portal vein; k _a, absorption rate constant; k _deg, the physiological degradation rate of CYP2B6 at inhibitor concentration of [I] = 0; K _I, degradation rate of CYP2B6 at inhibitor concentration of [I]; k _i, the dissociation constant of ticlopidine for CYP2B6; k _inact, the maximal inhibition rate achieved at inhibitor concentration [I] = ∞; NK, norketamine; PER1, first peripheral compartment; PER2, second peripheral compartment; PV, portal vein; Q, blood flow; SK, S‐ketamine; TIC, ticlopidine; V, volume; VI, gut wall villous mucosa.

Absorption profile of S‐ketamine was best described with a simple first‐order absorption rate constant (k _a) model in comparison to a transit compartment model or a single Weibull absorption function. In addition, the use of single Weibull absorption function added a high level of uncertainty to the model parameters and was, therefore, discarded. An assumption was made that S‐ketamine is completely metabolized to norketamine and no other metabolites are involved. Thereafter, extraction at the gut wall and liver were used as direct inputs into the metabolite model.

The sum of metabolic processes at the gut wall and liver compartments was assumed to account for both the first pass as well as circulatory metabolism. Both of these processes were dependent on individually scaled blood flow levels that, in turn, used the body weight as a subject specific parameter (Table 1). Subsequently, a portal vein compartment was added to the model, and the central, hepatic, portal vein, and gut wall were linked by the relevant blood flows.

The simplified quasi‐steady‐state approximation approach was used in the specification of differential equations for model specifications.25 Based on the pcVPCs, the implementation of the well‐stirred model to describe the clearances in the gut wall and liver sites adequately captured S‐ketamine elimination. Our results suggest that the gut wall clearance of S‐ketamine is very low in comparison to hepatic clearance, and the ratio between these two clearances was ~1:253 (Table 2). Intestinal metabolism was implemented into the model assuming that the CYP‐mediated S‐ketamine metabolism takes place at the villous tips. This is supported by the results demonstrating the physiological distribution of CYP enzymes at this site.33, 34 The amount of CYP2B6 expressed in the gut wall compartment is negligible as compared to the liver,34 hence, the value of intrinsic clearance at the gut wall found in model estimations was attributable to the CYP3A‐based S‐ketamine metabolism. According to the output from our model, the gut wall contributes only fractionally to the total body clearance of S‐ketamine.

Table 2.

Pharmacokinetic parameter estimates from the final model, and median parameter estimates with 95% CIs from the PsN SIR package

Parameter (unit)	Description	NONMEM		SIR‐resultsa
		Mean θ estimate	%RSE	Median	95% CI
S‐ketamine
CLINT,H,SK (L/h)	Intrinsic hepatic clearance	301	14.2	304	[260, 352]
CLINT,GW,SK (L/h)	Intrinsic gut wall clearance	1.19	39.5	1.22	[0.66, 1.98]
K a,SK (/h)	Absorption rate constant	1.76	16.1	1.78	[1.47, 2.11]
V C,SK (L)	Volume of central compartment	14.4	43.1	14.4	[5.90, 22.5]
V PER1,SK (L)	Volume of first peripheral compartment	102	8.0	102	[92.5, 111]
Q PER1,SK (L/h)	Central to first peripheral compartment clearance	287	11.3	288	[250, 331]
V PER2,SK (L)	Volume of second peripheral compartment	180	3.8	180	[167, 190]
Q PER2,SK (L/h)	Central to second peripheral compartment clearance	22.4	6.0	22.3	[20.8, 24.1]
IIV on CLINT,H,SK	Interindividual variability on CLINT,H,SK	0.25	11.9	0.26	[0.17, 0.37]
IIV on CLINT,GW,SK	Interindividual variability on CLINT,GW,SK	2.1	22.4	2.0	[1.11, 3.67]
IIV on K a,SK	Interindividual variability on K a,SK	0.42	17.9	0.44	[0.29, 0.66]
IIV on  V PER1,SK	Interindividual variability on V PER1,SK	0.045	22.3	0.046	[0.022, 0.076]
RVSK,PLAC	Proportional residual error with placebo	0.086	2.1	0.086	[0.079, 0.093]
RVSK,TICLO	Proportional residual error with ticlopidine	0.065	33	0.065	[0.048, 0.09]
Norketamine
CLINT,H,NK (L/h)	Intrinsic hepatic clearanceb	73.5	7.8	73.4	[67.6, 79.9]
CLINT,GW,NK (L/h)	Intrinsic gut wall clearanceb	44.4	35.8	46.5	[29.7, 71.2]
V C,NK (L)	Volume of central compartmentb	88.4	4.8	88	[82.6, 93.5]
Q PER1,NK (L/h)	Central to first peripheral compartment clearanceb	19.9	12.3	20.1	[17.3, 22.8]
V PER1,NK (L)	Volume of first peripheral compartmentb	88.9	5.6	88.8	[81.7, 96.5]
IIV on CLINT,H,NK	Interindividual variability on CLINT,H,NK	0.10	15.1	0.10	[0.07, 0.15]
RVNK,PLAC	Proportional residual error with placebo	0.062	2.4	0.062	[0.057, 0.068]
RVNK,TICLO	Proportional residual error with ticlopidine	0.064	31	0.067	[0.050, 0.090]
Ticlopidine
CLINT,H,TIC (L/h)	Intrinsic hepatic clearance	1505	27.9	1490	[1148, 1820]
CLINT,GW,TIC (L/h)	Intrinsic gut wall clearance	0 (FIXED)	–	–	–
K a,TIC (/h)	Absorption rate constant	3.3 (FIXED)	–	–	–
V C,TIC (L)	Volume of central compartment	50.3	13.9	50.8	[43.9, 57.7]
V PER1,TIC (L)	Volume of first peripheral compartment	191	67	208.7	[130, 393]
Q PER1,TIC (L/h)	Central to first peripheral compartment clearance	26.3	24.4	25.8	[20.9, 32.0]
IIV on CLINT,H,TIC	Interindividual variability on CLINT,H,TIC	0.12	76.2	0.13	[0.06, 0.28]
RVTICLO	Proportional residual variability	0.066	9.5	0.067	[0.053, 0.083]

CI, confidence interval; GW, gut wall; H, hepatic; NK, S‐norketamine; PLAC, placebo; RSE, relative standard error; SK, S‐ketamine; TICLO, ticlopidine.

^aSIR procedure was executed with 20,000 final proposal samples and 2,000 resamples.

^bShould be considered as apparent rather than absolute values, as F _met was set to 1 but true value of F _met = 0.80 in humans for S‐ketamine to norketamine metabolism.

Norketamine model

The norketamine model included a physiological gut wall, portal vein, and liver compartments alongside a two‐compartment distributional model, which adequately described norketamine disposition kinetics (∆OFV = −734), compared to a one‐compartment model. A three‐compartment model was tested but it did not result in a significantly better fit (∆OFV = −1.5) and resulted in high uncertainty values in the added model parameters. The output from the well‐stirred clearance model for S‐ketamine at the gut wall and liver were used as input for the norketamine model and it led to a good model fit. Norketamine elimination was described with a well‐stirred clearance model and our results indicate that both gut wall and liver contribute significantly to the norketamine metabolism.

Ticlopidine model

The modeling of ticlopidine concentration‐time data was carried out alongside S‐ketamine/norketamine modeling. A two‐compartment disposition model described the ticlopidine data satisfactorily and, compared to the one‐compartment model, showed better model performance (∆OFV = −141). A three‐compartment model could not be estimated reasonably and was, thus, discarded. Gut wall, portal vein, and liver compartments were added sequentially in a similar manner as to the S‐ketamine model. Although a well‐stirred clearance model was initially implemented at the gut wall and liver compartments, it was noticed that a plausible estimate for the gut wall clearance could not be estimated because the timing for sample collection during the early absorption phase was scarce (see Supplementary Information S1 ), and was fixed to zero. Thus, the gut wall acted essentially as a physiological transit for ticlopidine with metabolism taking place at the liver site only. A considerable degree of sparsity in the ticlopidine data during the early absorption phase was challenging for ticlopidine model development. All efforts to calculate the absorption rate constant (k _a,TIC) freely in the model were unsuccessful and, therefore, k _a,TIC was fixed to a published value of 3.3/h.8 The absorption phase was adequately described by a transit compartmental model. Transit compartments were added to the preceding gut wall compartment in the model in a sequential manner to optimize the number of transits required. We observed that four transit compartments adequately described the sparse absorption phase among the nested models (∆OFV = −36).

Repeated dosing of ticlopidine may increase the elimination half‐life, indicating that ticlopidine may auto‐inhibit its metabolism in vivo.12 Because ticlopidine is a potent inhibitor of CYP2B6 enzyme, which is also the enzyme responsible for ticlopidine metabolism in humans, this hypothesis is biologically plausible. However, a potential auto‐inhibition could not be modeled in our study and ticlopidine metabolism was described as a first‐order process.

Drug‐drug interaction model

In vitro experiments indicate that ticlopidine causes both time‐dependent (mechanism based) and reversible (competitive) inhibition of CYP2B6‐mediated S‐ketamine metabolism.10, 14 We attempted to model the effective amount of CYP2B6 enzyme remaining after ticlopidine dosing while specifying intrinsic hepatic clearance as a function of the amount of CYP2B6 enzyme, but a high degree of uncertainty was noticeable in the model parameters. The use of a pseudo first‐order enzyme degradation model, whereby the degradation of CYP2B6 was a function of the inhibitor concentration, was also unsuccessful. The mechanistic static model (MSM)35 was then implemented as the drug interaction model to describe the complex DDI between S‐ketamine and ticlopidine. We assumed that ticlopidine administration leads to a complete cessation of CYP2B6‐mediated N‐demethylation by CYP2B6 due to a 100% loss of enzymatic activity. This equates to an ~60% fall in the intrinsic hepatic clearance during the ticlopidine phase (f _m,CYP2B6 = 0.60).8 An inhibition parameter describing the net effect of ticlopidine on the intrinsic hepatic clearance was calculated using a reversible and time‐dependent components (see Supplementary Information S2 ):

$$f_{{\mathrm{CL}}_{\mathrm{INT},\mathrm{H}}^{\prime }}=(A_{\mathrm{H}}·B_{\mathrm{H}}·f_{\mathrm{m},\mathrm{CYP}2\mathrm{B}6})+(1-f_{\mathrm{m},\mathrm{CYP}2\mathrm{B}6})$$

where $f_{{\mathrm{CL}}_{\mathrm{INT},\mathrm{H}}^{\prime }}$ is the inhibition parameter describing the fractional change in the intrinsic hepatic clearance of S‐ketamine during the ticlopidine predosing phase, A _H is the reversible part, B _H is the time‐dependent part of the of CYP2B6 inhibition, and f _m,CYP2B6 = 0.60 is the fraction of S‐ketamine metabolized by CYP2B6.

Next, the inhibition parameter $f_{{\mathrm{CL}}_{\mathrm{INT},\mathrm{H}}^{\prime }}$ was used to calculate the effect of ticlopidine‐mediated CYP2B6 inhibition on the intrinsic hepatic clearance of S‐ketamine as follows:

$${\text{CL}}_{\mathrm{INT},\mathrm{H},[\mathrm{I}]}={\text{CL}}_{\mathrm{INT},\mathrm{H},[\mathrm{I}]=0}·f_{{\mathrm{CL}}_{\mathrm{INT},\mathrm{H}}^{\prime }}$$

CL_INT,H,[I] and CL_INT,H,[I]=0 are the intrinsic hepatic clearance of S‐ketamine during the ticlopidine and placebo phases, respectively, and $f_{{\mathrm{CL}}_{\mathrm{INT},\mathrm{H}}^{\prime }}$ is the inhibition parameter that accounts for the inhibition of CYP2B6 by ticlopidine. Gut wall clearances of S‐ketamine and norketamine were fixed to the population values from placebo phase data assuming that these would remain unchanged during ticlopidine phase.

The MSM model resulted in a good fit and suggested a very strong inhibitory effect of ticlopidine on S‐ketamine metabolism. A 63% inhibition of S‐ketamine metabolism resulted in the lowest OFV, which is in accordance with the result from a recent in vitro study.8 Log likelihood‐profiling confirmed the results (Supplementary Information S2 ). The final model is depicted in Figure 1.

Model evaluation

The final drug interaction model resulted in a good fit for S‐ketamine at the ticlopidine predosing phase. The model converged with successful minimization and a functional covariance matrix, with plausible parameter estimates that had reasonably low SEs (Table 2). Goodness‐of‐fit plots showed an acceptable fit, although for norketamine there are slight trends visible during the ticlopidine phase (Figure S2 ). The pcVPCs indicate a good predictive performance and confirmed the model appropriateness (Figure 2), but some subjects showed obvious underprediction of norketamine during the inhibitor phase.

Figure 2.

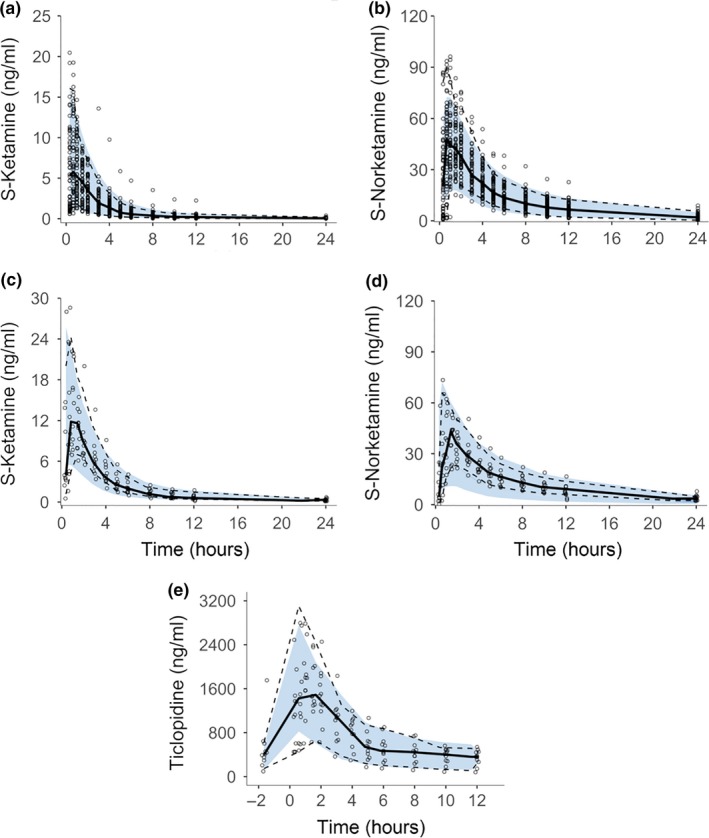
Prediction‐corrected visual predictive checks obtained from 1,000 simulations stratified on compound and study phase showing S‐ketamine and norketamine after oral administration of 0.2–0.3 mg/kg S‐ketamine during placebo phase (a and b, respectively), during ticlopidine predosing phase (c and d, respectively), and ticlopidine after oral ticlopidine administration of 250 mg/day b.i.d. for 6 days (e). Circles show the observed concentrations, solid lines the median and dashed lines the 2.5th and 97.5th percentiles of observed data. Blue area indicates simulation‐based 95% prediction interval of the final model.

Further evaluation of the model was performed with the SIR procedure. The final parameters were close to the median of SIR values (Table 2) and nonparametric 95% CIs obtained through the SIR procedure were also in good agreement with the CIs calculated from NONMEM produced SEs.

Simulations

The ncappc‐package was used to simulate AUC values during different phases of S‐ketamine dosing. Our results indicate that ticlopidine predosing can cause more than a twofold rise in S‐ketamine AUC in humans, which is consistent with previous NCA analysis and in vitro results9 (Table 3). Ticlopidine profoundly inhibited CYP2B6 activity and the final DDI model was used to simulate the effect of ticlopidine on the parameters describing the fractional inhibition of intrinsic hepatic clearance, the change in the intrinsic hepatic clearance during placebo and inhibitor phase, and the percentage of remaining CYP2B6 activity (%RA). The remaining CYP2B6 activity was calculated as follows:

$$\%\text{RA}=A_{\mathrm{H}}\ast B_{\mathrm{H}}\ast {\text{Activity}}_{[I]=0}$$

where A _H is the reversible and B _H is the time‐dependent part of inhibition, and Activity_[I] = 0 is the activity at placebo phase (i.e., numerically assumed to be 100%).

Table 3.

Comparison of the noncompartmental analysis (NCA) results from Peltoniemi et al.9 and the final semimechanistic pharmacokinetic model based on simulations with ncappc package in PsN30

Compound	PK parameter	S‐ketamine
		p.o. placebo‐phase	i.v. placebo‐phase	p.o. ticlopidine‐phase
NCA resultsa
S‐ketamine	AUC (ng h/mL)	21	76	54
	C max (ng/mL)	9.9	32	17
Norketamine	AUC (ng h/mL)	292	121	310
	Cmax (ng/mL)	61	14	46
Model predictionsb
S‐ketamine	AUC (ng h/mL)	22.4	70	53.2
	Cmax (ng/mL)	9.37	41	18.1
Norketamine	AUC (ng h/mL)	279	161	250
	Cmax (ng/mL)	56	22	45

AUC, area under the curve; C_max, peak plasma concentration; NCA, noncompartmental analysis.

AUC calculated by trapezoidal rule with extrapolation to infinity.

^aCalculated with ncappc package. Model prediction results were obtained simulating the original study design with the final model and 1,000 samples.

The results from these simulations show that the initial drop in the intrinsic hepatic clearance, which resembles an “on‐off” phenomenon is followed by a dynamic phase, which demonstrates the slow recovery of enzyme activity and consequently a rise in CL_INT,H (Figure 3 a). The recovery seems to level off as ticlopidine is dosed further during the predosing phase, until a steady state is reached near the last ticlopidine dose. After the final ticlopidine dose, the enzyme activity and intrinsic hepatic clearance start to recover quickly and reach the initial levels ~4–5 days after the final inhibitor challenge (Figure 3 b). Simulation of S‐ketamine plasma concentrations after oral dosing (25 mg, t.i.d.) after ticlopidine predosing demonstrated a high exposure of S‐ketamine immediately following the ticlopidine predosing (Figure 3 c). The exposure decreases slowly after ticlopidine has been washed out and intrinsic hepatic clearance recovers to the baseline levels. The effect of ticlopidine predosing is less pronounced on the i.v. S‐ketamine administration (5 mg t.i.d. after ticlopidine predosing 250 mg b.i.d. for 6 days). This can be attributed to the lack of first‐pass metabolism in this route of administration. However, an accumulation of S‐ketamine can be clearly seen, which wears off as ticlopidine is washed out (Figure 3 d).

Figure 3.

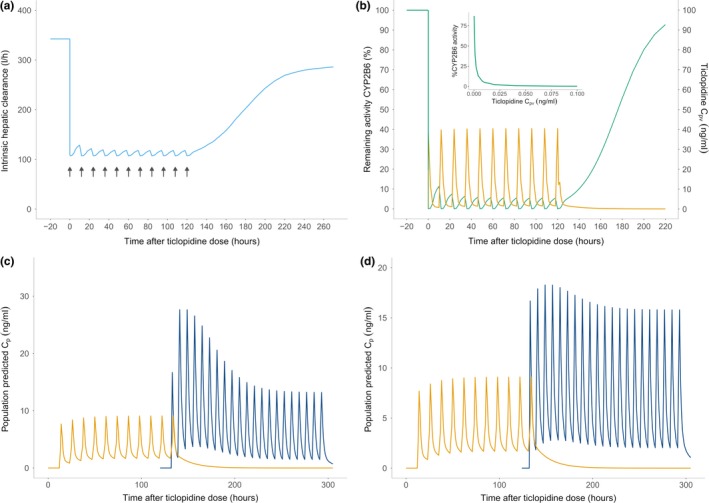
Simulation results. (a) The intrinsic hepatic clearance (sky‐blue) of S‐ketamine demonstrates the same pattern of a sudden drop, which attains a steady state during ticlopidine dosing, and then recovers quickly during the ticlopidine washout. The black arrows show ticlopidine dosing. (b) The percentage remaining activity (%RA) of cytochrome P450 (CYP)2B6 (green) immediately before, during and after ticlopidine dosing. Ticlopidine portal vein concentration is shown in orange. The %RA was calculated using the reversible and time‐dependent components of the mechanistic static drug‐drug interaction model. A sharp fall in %RA upon ticlopidine dosing resembles an “on‐off” phenomenon, however, the inset graph shows that the inhibition process is dynamically captured by the model during the inhibitor pretreatment and the inhibitor concentration required to cause a complete enzyme degradation is very low. The activity is completely recovered ~4–5 days after last ticlopidine dose. (c) The S‐ketamine plasma concentrations (blue) after oral dosing (25 mg, t.i.d.) after ticlopidine pre‐dosing (250 mg b.i.d. for 6 days). Ticlopidine plasma concentrations are shown in yellow. High exposure of S‐ketamine is noticeable immediately following the ticlopidine predosing, which drops slowly after ticlopidine has been washed out and intrinsic hepatic clearance recovers to the baseline levels. (d) S‐ketamine plasma concentrations (blue) after i.v. dosing (5 mg t.i.d.) after ticlopidine predosing (250 mg b.i.d. for 6 days). The effect of ticlopidine predosing is less pronounced on the i.v. S‐ketamine administration. This can be attributed to the lack of first‐pass metabolism in this route of administration. However, an accumulation of S‐ketamine can be clearly seen, which wears off as ticlopidine is washed out.

DISCUSSION

We have used previously collected in vivo data to develop a semimechanistic model to describe the pharmacokinetic profile of S‐ketamine and its metabolite norketamine simultaneously. Three‐compartment mammillary model and a two‐compartment model were successfully linked to physiological compartments representing the gut wall, portal vein, and liver for S‐ketamine and norketamine, respectively. A semimechanistic model for ticlopidine pharmacokinetics that included four transit compartments, and a two‐compartment distributional model in conjunction with the gut wall, portal vein, and liver compartments was built following the modeling strategy described earlier24 and added to the S‐ketamine/norketamine model. Finally, S‐ketamine and ticlopidine models were linked together with MSM describing the mechanism‐based inhibition of S‐ketamine metabolism by ticlopidine. Model evaluation with visual predictive checks and the sampling importance resampling‐procedure demonstrated that the model parameters were accurate and precise.

Our results indicate that the administration of ticlopidine led to a markedly low intrinsic hepatic clearance of S‐ketamine (from 304 L/hour at placebo phase to 113 L/hour), whereas the total hepatic clearance was much less affected (from 71 L/hour at placebo phase to 60 L/hour). This observation is typical for high extraction ratio drugs when using the well‐stirred clearance model.36 Another significant finding was the minor role of gut wall clearance in the overall S‐ketamine metabolism, as the ratio of gut wall to hepatic clearance was 1:253. Dense sampling after S‐ketamine dosing allowed us to model the gut wall clearance with a low uncertainty level. CYP3A4 has been proposed in the literature as the major enzyme responsible for S‐ketamine demethylation to norketamine,37 but our results demonstrate that the gut wall clearance is not an important player in S‐ketamine biotransformation, suggesting that CYP3A contribution to S‐ketamine metabolism is lesser than previously anticipated. Gut wall expression of CYP2B6 is negligible,33 therefore, the contribution of gut wall to total clearance can be attributed to the intestinal CYP3A4 reservoir only. These findings have been further emphasized by a recent study that showed that CYP2B6*6 allele in human liver microsomes and cos‐1 expressed CYP2B6 protein variants resulted in a considerable decrease of S‐ketamine metabolism.38 Although the gut wall has been documented to play a major role in the overall clearance of xenobiotics from the human body, it has to be noted that the role of gut‐wall CYP enzyme reservoirs is limited to first‐pass drug metabolism only, and do not impart a challenge to the unchanged drug fraction in the systemic circulation.39 Hence, the role of gut wall clearance is important only for the oral route of drug administration and is insignificant in vascular drug delivery.

Although S‐ketamine has several metabolites in vivo, norketamine accounts for 80% of the metabolites.3, 6 During the model development, we assumed that the extraction of S‐ketamine in the gut wall and liver compartments generates norketamine as the sole metabolite. The pharmacokinetic models for both of these substances demonstrated adequate precision and provided a good model fit. Our results indicate that the both gut wall and liver contribute significantly to norketamine metabolism to 6‐hydroxy‐norketamine (Table 2), which has been previously reported to take place rapidly.37 Norketamine elimination was described with a well‐stirred clearance model at both elimination sites. The assumption that S‐ketamine is metabolized only to norketamine is biologically plausible, because ~80% of S‐ketamine is metabolized to norketamine in vivo. The output from the well‐stirred clearance model for S‐ketamine could, therefore, be used as an input for the norketamine model, and it led to a good model fit.

A slight trend in the norketamine model fit at the inhibitor phase can be attributed to the fast metabolism to secondary metabolites, but also to the marked between‐subject variability in the S‐ketamine metabolism. Previous results indicate that norketamine is readily metabolized by CYP2B6 to a secondary metabolite.37 Although any significant change in norketamine profile after ticlopidine pretreatment was not documented,9 an inhibition of this metabolic pathway in vivo can cause an increase in norketamine AUC without affecting the maximum plasma concentrations, as shown by the model output. A metabolic inhibition model for the metabolite could not be implemented due to a lack of information about the metabolite parameters needed for the MSM. Furthermore, the mechanistic‐static model is formulated to be dependent only on the inhibitor concentration in the portal vein and not on the CYP‐enzyme levels, which are assumed constant across individuals. Therefore, the between‐subject variability could only be accounted for the portal vein inhibitor concentrations.

A well‐stirred clearance model for ticlopidine was initially implemented in the gut wall and liver compartments, but the resulting fit showed that a plausible estimate for gut wall clearance could not be estimated. This is most likely due to the scarce sampling during the early absorption phase after ticlopidine dosing. After testing several absorption models, we implemented a transit‐compartmental model, which provided an adequate fit. Some reports indicate that repeated ticlopidine dosing causes an increase in its half‐life suggesting an auto‐inhibition process.12 These findings are physiologically plausible due to the marked potential of ticlopidine to inhibit CYP2B6. We evaluated an auto‐inhibition of hepatic ticlopidine metabolism, but our attempts were unsuccessful, probably owing to the design of the original DDI study. Thus, the phenomena could not be supported with the current data.

The mechanistic‐static model35 allowed us to model the mechanism‐based DDI between S‐ketamine and ticlopidine. The MSM uses inhibitor concentration at the portal vein along with the enzyme inhibition constants (i.e., k _inact, K _I, and k _i) to dynamically account for the enzyme inhibition, resulting in a fractional parameter that describes the reduction in the S‐ketamine intrinsic hepatic clearance during the presence of an inhibitor. The enzyme parameters have been previously determined in in vitro studies,11 and, therefore, our model demonstrates an example of in vitro‐in vivo correlation models; a predictive mathematical model describing the relationship between in vitro property of an oral dosage form and relevant in vivo response.40

Ticlopidine is a strong mechanism‐based inhibitor of CYP2B6 in the liver and its enzyme constants imply that a very low ticlopidine concentration is required to cause a marked loss of CYP2B6 activity.11 Consistent with these findings, our model indicates a complete loss of CYP2B6 activity following the first dose, resembling an “on‐off” phenomena rather than a dynamic concentration‐dependent inhibition. However, our simulations indicate that ticlopidine shows a concentration‐dependent inhibition (Figure 3 b), but already a very low concentration of ticlopidine is capable of causing complete inactivation of the CYP2B6 pool in the liver. Our results suggest that a complete recovery of the CYP2B6 enzyme activity takes place only after ~4–5 days after the last ticlopidine challenge. As can be anticipated, the enzyme activity is linearly correlated with the intrinsic hepatic clearance, which is also seen to gradually rise back to the normal levels once ticlopidine has been washed out (Figure 3).

Our model has several limitations. Many assumptions of underlying processes had to be made and certain parameters were fixed during the model development phase. The models had to be developed in a way that would provide adequate fits while avoiding overparameterization at all stages. A number of limitations for model development came from the data at hand, which included a small sample size during the inhibitor phase, as well as sparsely sampled ticlopidine absorption. However, these limitations were successfully covered during model development and the final model shows clinically plausible parameter estimates.

In conclusion, our final model adequately predicts the DDI between S‐ketamine and ticlopidine, indicating a mechanistic basis of CYP2B6 inhibition by ticlopidine, and establishing the utility of “mechanistic‐static model” in DDI modeling. The use of in vitro results in population modeling in a semimechanistic system demonstrates a useful method to account for mechanism‐based DDIs in a dynamic concentration‐dependent manner. In comparison to a conventional NCA, this approach provides a dynamic framework with temporally varying inhibitor concentrations for driving DDI model equations, alongside enzyme inhibition constants previously reported in in vitro studies.

Funding

M.W. Ashraf was supported by a grant from Turku University Foundation, and personal research funding from the University of Turku Graduate School (University of Turku Drug Research Doctoral Program). T.I. Saari was supported by governmental research grant number 13821 from the Hospital District of South‐West Finland, Finland.

Conflict of Interest

The authors declared no competing interests for this work.

Author Contributions

M.W.A., M.A.P., K.T.O., P.J.N., and T.I.S. wrote the manuscript. M.A.P., K.T.O., and T.I.S. designed the research. M.W.A., M.A.P., K.T.O., and T.I.S. performed the research. M.W.A., M.A.P., K.T.O., T.I.S., and P.J.N. analyzed the data.

Supporting information

Supplementary Information S1 Description of the original drug‐drug interaction studies and drug analysis

Supplementary Information S2 Model development

Supplementary Information S3 Final model

Figure S2. Goodness‐of‐fit plots