PBPK Models for CYP3A4 and P‐gp DDI Prediction: A Modeling Network of Rifampicin, Itraconazole, Clarithromycin, Midazolam, Alfentanil, and Digoxin

Abstract

According to current US Food and Drug Administration (FDA) and European Medicines Agency (EMA) guidance documents, physiologically based pharmacokinetic (PBPK) modeling is a powerful tool to explore and quantitatively predict drug‐drug interactions (DDIs) and may offer an alternative to dedicated clinical trials. This study provides whole‐body PBPK models of rifampicin, itraconazole, clarithromycin, midazolam, alfentanil, and digoxin within the Open Systems Pharmacology (OSP) Suite. All models were built independently, coupled using reported interaction parameters, and mutually evaluated to verify their predictive performance by simulating published clinical DDI studies. In total, 112 studies were used for model development and 57 studies for DDI prediction. 93% of the predicted area under the plasma concentration‐time curve (AUC) ratios and 94% of the peak plasma concentration (C_max) ratios are within twofold of the observed values. This study lays a cornerstone for the qualification of the OSP platform with regard to reliable PBPK predictions of enzyme‐mediated and transporter‐mediated DDIs during model‐informed drug development. All presented models are provided open‐source and transparently documented.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

PBPK modeling is increasingly used for DDI analysis. To investigate and predict the DDI potential of new drugs with the help of PBPK, models of index perpetrator and victim drugs are needed.

WHAT QUESTION DID THIS STUDY ADDRESS?

The aim of this study was to provide whole‐body PBPK models of important CYP3A4 and P‐gp perpetrator and victim drugs that are all compatible, evaluated, and fit for use in PBPK DDI modeling.

WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

This study adds transparently built and evaluated PBPK models of rifampicin, itraconazole, clarithromycin, midazolam, alfentanil, and digoxin, integrating the current knowledge on the relevant pharmacokinetic mechanisms of these six drugs with insights gained during model development.

HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

A publicly available library, providing comprehensive PBPK models of the recommended DDI inhibitors, inducers, and substrates, evaluated and ready to use for their application in DDI modeling, has the potential to foster open collaboration and to accelerate the drug development process.

Physiologically based pharmacokinetic (PBPK) modeling is a powerful tool to explore and quantitatively predict the pharmacokinetic (PK) of drugs and the magnitude of drug‐drug interactions (DDIs). It is applied at increasingly early stages during drug development and is recommended by the US Food and Drug Administration (FDA) and the European Medicines Agency (EMA) for the design of clinical DDI trials and population PK studies. Furthermore, PBPK may even offer an alternative to dedicated clinical trials, to find dosing recommendations for the co‐administration of interacting substances, or the treatment of special populations.1, 2

To investigate and predict the DDI potential of new drugs with the help of PBPK, models of index perpetrator and victim drugs are needed. A library of PBPK models of recommended DDI inhibitors, inducers, and substrates, evaluated for their application in DDI modeling, has the potential to accelerate the drug development process.

The aim of the presented work was to develop and carefully evaluate whole‐body PBPK models of frequently used perpetrator and victim drugs and to provide them to the PBPK modeling community. Focusing on cytochrome P450 3A4 (CYP3A4) and P‐glycoprotein (P‐gp) as major interaction pathways affecting approximately half of all drugs in use,3, 4 models of rifampicin (most prominent CYP3A4 and P‐gp inducer), itraconazole (competitive CYP3A4 and P‐gp inhibitor), clarithromycin (mechanism‐based CYP3A4 inactivator and competitive P‐gp inhibitor), midazolam, alfentanil (specific CYP3A4 substrates), and digoxin (specific P‐gp substrate) have been established. All selected compounds are recommended by the FDA for application in clinical DDI trials.5

The perpetrator and victim drug models were developed independently of each other, without the use of data from clinical DDI studies for parameter optimization. With this approach, the prediction of co‐administration studies could be utilized as an additional means of model evaluation. Being recommended by the FDA for DDI potential assessment, the six selected compounds have been co‐administered in different combinations in many clinical trials, providing ample data for the evaluation of DDI predictions. Figure 1 shows the developed DDI modeling network of interacting perpetrator and victim drugs, assessing multiple combinations for mutual DDI evaluation.

Figure 1.

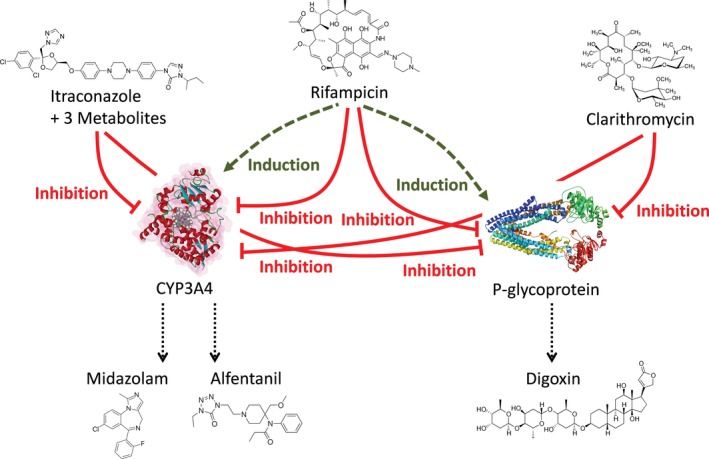
Physiologically based pharmacokinetic drug‐drug interaction network. Schematic illustration of the modeled interaction network of cytochrome P450 (CYP)3A4 and P‐glycoprotein perpetrator (upper level: itraconazole, rifampicin, and clarithromycin) and victim drugs (lower level: midazolam, alfentanil, and digoxin). Green dashed lines indicate induction; red solid lines indicate inhibition.

Clinical DDI studies, for example, the full inhibition of an important metabolizing enzyme, provide valuable information on the fraction of victim drug that is normally eliminated via this pathway (“fraction metabolized”). Therefore, victim drug plasma concentrations during co‐administration of perpetrators can serve as additional information for victim drug model evaluation. Furthermore, correct prediction of the impact of a perpetrator drug on the PK of a victim drug indicates that the model is able to describe the perpetrator concentrations at the sites of inhibition or induction. This is not trivial, as drug concentrations are generally measured in blood plasma, but the interactions take place in other compartments, such as the intracellular space of the liver or intestine. Taken together, DDI studies provide additional information on both, the perpetrator and the victim drug PKs, and their correct prediction is a challenge for both models and a valid means of model evaluation.

The aim of this study was to establish and thoroughly evaluate PBPK models of relevant DDI perpetrator and victim drugs. The presented models are whole‐body PBPK models, allowing for dynamic DDI assessment in all organs expressing the affected enzyme or transporter. Evaluations indicate that the models are fit for DDI prediction. The model files have been made publicly available as supplementary material to this paper (Data S1‐S6) and in the Open Systems Pharmacology (OSP) repository (http://www.open-systems-pharmacology.org), as tools for the drug development and clinical research community to assess the DDI potential of investigational drugs, to inform the design of clinical trials or to be expanded for predictions in special populations.

Methods

Software

PBPK modeling was performed with PK‐Sim and MoBi modeling software version 7.1.0 (part of the OSP Suite). The OSP Suite makes formerly commercial software tools PK‐Sim and MoBi available as freeware under the GPLv2 License. The software allows the modification of system parameters and the model structure by the (qualified) user and the source code is publicly available on GitHub (accessible via http://www.open-systems-pharmacology.org), together with published models and tutorials. Details on how to modify a PBPK model in PK‐Sim can be found, for example, in Kuepfer et al.,6 the PK‐Sim/MoBi user manual, and in the user forum. Parameter optimization was accomplished using the Monte Carlo algorithm of the “Parameter Identification Toolbox” in MATLAB version R2013b (The MathWorks, Natick, MA) or in PK‐Sim. Sensitivity analyses were performed within PK‐Sim. Plots and PK parameter analyses were compiled with MATLAB.

Model development

Models of rifampicin, itraconazole, clarithromycin, midazolam, alfentanil, and digoxin were built combining bottom‐up and top‐down techniques. To establish the models, an extensive literature search was conducted, collecting (i) physicochemical parameters, (ii) information on absorption, distribution, metabolism, and excretion processes, and (iii) clinical studies of intravenous and oral administration to healthy subjects in single‐dosing and multiple‐dosing regimens, covering the full dosing range published. All data used in this analysis has been taken from previously published human or preclinical studies.

The PBPK models were developed based on a healthy male European individual, 30 years of age, with a body weight of 73 kg, and a height of 176 cm. Physiological parameters, like organ volumes, blood flow rates, and surface permeabilities, are provided within the software.7 Absorption, distribution, metabolism, and excretion‐relevant proteins reported to govern the PK of a drug, such as metabolizing enzymes, transporters, or binding partners, were implemented into the models and tested. Whenever available and in accordance with literature protein expression, the PK‐Sim expression database reverse transcription‐polymerase chain reaction (RT‐PCR) profiles8 were used to define the relative tissue distribution of these proteins. For parameters that could not be informed from (in vitro) experimental data, parameter identification based on plasma concentration‐time profiles was performed using a subset of the available clinical studies (training dataset) for optimization. The decision of which studies to include into the training dataset was based on the number of studies available and the information contained in the different studies (dosing regimen, study size, sampling times, fraction excreted measurements, etc.).

Model selection was based on the ability of the model to describe (training dataset) and predict (test dataset) plasma concentration‐time profiles from all published clinical studies as well as fraction excreted unchanged to urine. Furthermore, physiological plausibility, precision and covariance of parameter estimates, and population predictions were assessed.

Model evaluation

The models were evaluated by comparison of concentration‐time profiles, area under the plasma concentration‐time curve (AUC), and peak plasma concentration (C_max) values resulting from our simulations to the values observed during clinical studies. As a quantitative measure of the descriptive and predictive performance of each model, the geometric mean fold error was calculated according to Eq. (1):

$$\text{GMFE}={10}^{(\mathrm{\Sigma }|{\log }_{10}(\mathrm{pred}\mathrm{PK}\mathrm{parameter}/\mathrm{obs}\mathrm{PK}\mathrm{parameter})|)/\mathrm{n}},$$ (1)

with GMFE = geometric mean fold error of all AUC or C_max predictions of the respective model, pred PK parameter = predicted AUC or C_max, obs PK parameter = observed AUC or C_max, and n = number of studies. Furthermore, models were evaluated by their ability to adequately predict the clinical data of all DDI studies available from literature. For this additional evaluation, the final perpetrator models were coupled to victim drug models using measured values (from literature) to inform the different interaction processes without further adjustment. Successful prediction of the victim drug plasma concentration‐time profiles during co‐administration is interpreted as indication of the correct simulation of the perpetrator drug concentration at the site where the DDI takes effect as well as of the appropriate implementation of the victim drugs’ affected disposition pathways.

DDI network development

Mathematical implementation of the induction and inhibition processes in general is specified in Section 1 of Appendix  S1. The final rifampicin model was coupled to models of midazolam, alfentanil, itraconazole, and digoxin, to assess its DDI performance with CYP3A4 and P‐gp substrates. To describe the influence of rifampicin on these victim drugs, induction and simultaneous competitive inhibition of CYP3A4 and P‐gp by rifampicin have been added. Furthermore, inhibition of midazolam and digoxin elimination by itraconazole and by clarithromycin were modeled and compared to observed clinical data, evaluating the performance of these two victim drug models with two different CYP3A4 and P‐gp inhibitors. Inhibition of alfentanil metabolism by itraconazole or clarithromycin was not tested, as there are no clinical studies available to compare to.

All induction and inhibition processes were modeled using interaction parameter values either identified during the development of the perpetrator models if no experimental values could be found to parameterize their auto‐induction or auto‐inhibition (using multiple‐dose perpetrator studies only, without co‐administration of victim drugs), or taken from literature without further adjustment or fitting, as a means of further evaluation of the perpetrator and victim drug models.

DDI network evaluation

The DDI modeling performance was assessed by comparison of predicted vs. observed victim drug plasma concentration‐time profiles during co‐administration, DDI AUC ratios (Eq. (2)), and DDI C_max ratios (Eq. (3)):

$$\text{DDI AUC ratio}=\frac{{\text{AUC}}_{\mathrm{victim}\mathrm{drug}\mathrm{during}\mathrm{co}-\mathrm{administration}}}{{\text{AUC}}_{\mathrm{victim}\mathrm{drug}}}$$ (2)

$$\text{DDI}{\mathrm{C}}_{\max }\mathrm{ratio}=\frac{{\mathrm{C}}_{\max \mathrm{victim}\mathrm{drug}\mathrm{during}\mathrm{co}-\mathrm{administration}}}{{\mathrm{C}}_{\max \mathrm{victim}\mathrm{drug}}}$$ (3)

As a quantitative measure of the prediction accuracy of each DDI interaction, GMFEs of the predicted DDI AUC ratios and DDI C_max ratios were calculated according to Eq. (1).

Sensitivity analysis

Sensitivity of the final models to single parameters (local sensitivity analysis) was calculated, measured as changes of the AUC extrapolated to infinity (for single‐dose administration drugs) or of the AUC of one dosing interval in steady‐state conditions (for multiple‐dose administration drugs) of a simulation with administration of the highest common dose. Parameters were included into the analysis if they have been optimized, if they might have a strong influence due to calculation methods used in the model (e.g., lipophilicity and fraction unbound), if they are related to optimized parameters, or if they had significant impact in other models (e.g., solubility and blood/plasma concentration ratio). Sensitivity to a parameter is calculated as the ratio of the relative change of the simulated AUC to the relative variation of the parameter around the value used in the final model (Eq. (4)):

$$S=\frac{\mathrm{\Delta }\text{AUC}}{\text{AUC}}·\frac{p}{\mathrm{\Delta }p},$$ (4)

with S = sensitivity of the AUC to the examined model parameter, ΔAUC = change of the AUC, AUC = simulated AUC with the original parameter value, Δp = change of the examined model parameter value, and p = original model parameter value. A sensitivity value of +1.0 signifies that a 10% increase of the examined parameter causes a 10% increase of the simulated AUC.

Virtual population characteristics

To quantitatively predict the variability of the simulated plasma concentration‐time profiles, virtual populations of 100 individuals within an age range of 20–50 years were generated. Weight, height, and many physiological parameters, such as organ volumes, blood flow rates, and gastrointestinal characteristics, were varied according to published data7 as implemented into the software.9 In addition to the variability in drug PK that results from these physiological differences within the virtual populations, the expression levels of the implemented drug metabolizing enzymes, transporters, and protein binding partners were varied around their reference values. If available, default population variabilities for enzyme expression in PK‐Sim were used. Otherwise, log‐normal distribution of the protein expression level in the population was assumed and variabilities were implemented as geometric SDs derived from literature reports. If no valid source could be found, log‐normal distributions with a moderate geometric SD of 1.4 (~35% coefficient of variation) were assumed. Please refer to Table S7 in Appendix S1 for an overview.

Population simulations were generated and compared with observed data. Observed data were most often reported in terms of arithmetic means and SDs. To allow comparison of observed and simulated variability, simulated 68% population prediction intervals were plotted that correspond to the range span of ±1 SD around the mean assuming normal distribution.

Results

Model development and evaluation

Of the total of 112 studies, in detail 16 studies of rifampicin, 27 studies of itraconazole, 17 studies of clarithromycin, 7 studies of midazolam, 7 studies of alfentanil, and 38 studies of digoxin administration, were used for model development. The respective modeling results are presented in Section 2 of Appendix  S1. This includes tables listing the clinical studies used for model development and evaluation, with administration protocols and study population details (Tables S1a, S2a, S3a, S4a, S5a, S6a in Appendix  S1), descriptions of the final models, and tables listing the respective drug‐dependent parameters (Tables S1b, S2b, S3b, S4b, S5b, S6b in Appendix S1).

All models show accurate and precise descriptive and predictive performance for intravenous and oral administration. Plots of population predicted compared with observed plasma concentration‐time profiles of all studies obtained from literature are shown as semilogarithmic (Figures S1c, S2c, S3c, S4c, S5c, S6c in Appendix S1) as well as linear plots (Figures S1d, S2d, S3d, S4d, S5d, S6d in Appendix  S1). In addition, predicted compared to observed AUC and C_max values with calculated GMFEs (also listed in Tables S1a, S2a, S3a, S4a, S5a, S6a in Appendix S1) and sensitivity analysis results (Figures S1e, S2e, S3e, S4e, S5e, S6e in Appendix S1) are presented. System‐dependent parameters are given in Table S7 in Appendix S1.

DDI network modeling

Of the total of 57 studies, in detail 18 clinical studies of rifampicin with midazolam, 12 studies of rifampicin with alfentanil, 1 study of rifampicin with itraconazole, 10 studies of itraconazole with midazolam, 4 studies of clarithromycin with midazolam, 7 studies of rifampicin with digoxin, 1 study of itraconazole with digoxin, and 4 studies of the interaction of clarithromycin with digoxin were predicted and compared with observed data. Table 1 lists all modeled clinical DDI studies, with administration protocols and study population details. The parameters to model the CYP3A4 and P‐gp induction and inhibition processes are described in Section 3 of Appendix S1.

Table 1.

DDI study dosing regimens, study population sizes, predicted and observed AUC ratios, and C_max ratios

Perpetrator (mg)	Victim (mg)	Dose gap (hours)	n	Males (%)	Predicted AUCratio	Observed AUCratio	Pred/Obs AUCratio	Predicted Cmax ratio	Observed Cmax ratio	Pred/Obs Cmax ratio	Reference
Rifampicin	Midazolam
600, q.d.	1.0, i.v. (bol)	24	9	100	0.460	0.378	1.22	–	–	–	Kharasch 199724
600, q.d.	1.0, i.v. (bol)	8	10	50	0.470	0.521	0.90	–	–	–	Kharasch 200425
600, q.d.	1.0, i.v. (bol)	8	6	50	0.470	0.481	0.98	–	–	–	Phimmasone 200126
600, q.d.	2.0, i.v. (–)	24	8	100	0.460	0.655	0.70	–	–	–	Link 200827
600, q.d.	0.05/kg, i.v. (bol)	12	3a	100	0.480	0.579	0.83	–	–	–	Szalat 200728
600, q.d.	0.05/kg, i.v. (0.5 hours)	12	14	100	0.510	0.512	1.00	–	–	–	Gorski 200329
600, q.d.	2.0, p.o. (syr)	0	11	100	0.220	0.123	1.78	0.300	0.162	1.85	Reitman 201112
600, q.d.	2.0, p.o. (syr)	168	11	100	0.370	0.383	0.97	0.470	0.403	1.17	Reitman 201112
600, q.d.	2.0, p.o. (syr)	336	11	100	0.910	0.815	1.12	0.940	0.731	1.29	Reitman 201112
600, q.d.	3.0, p.o. (syr)	8	10	50	0.040	0.053	0.76	0.070	0.110	0.64	Kharasch 200425
600, q.d.	4.0 control/6.0 DDI, p.o. (sol)	12	14	100	0.040	0.032	1.25	0.070	0.051	1.37	Gorski 200329
600, q.d.	0.075/kg, p.o. (syr)	22	18	50	0.040	0.124	0.32	0.060	0.170	0.35	Chung 200630
450, q.d.	7.5, p.o. (sol)	17	4	38	0.040	0.052	0.77	0.070	0.112	0.63	Eap 200431
600, q.d.	7.5, p.o. (–)	24	8	100	0.040	0.016	2.57	0.060	0.035	1.72	Link 200827
300, b.i.d.	8.0, p.o. (–)	2?	19	53	0.060	0.057	1.05	0.100	0.121	0.83	Gurley 200632
300, b.i.d.	8.0, p.o. (–)	2	16	50	0.060	0.060	0.99	0.100	0.108	0.93	Gurley 2008a33
600, q.d.	15.0, p.o. (tab)	17	10	50	0.050	0.041	1.21	0.050	0.064	0.79	Backman 199634
600, q.d.	15.0, p.o. (tab)	17	9	44	0.100	0.098	1.02	0.130	0.193	0.67	Backman 199835
					GMFE (range)		1.30 (1.00–3.11)			1.48 (1.08–2.83)
					Pred within twofold		16/18			11/12
Rifampicin	Alfentanil
5.0, q.d.	0.015/kg, i.v. (–)	10	12	67	0.750	0.791	0.95	–	–	–	Kharasch 201136
10.0, q.d.	0.015/kg, i.v. (–)	10	12	67	0.660	0.712	0.93	–	–	–	Kharasch 201136
25.0, q.d.	0.015/kg, i.v. (–)	10	12	67	0.560	0.564	0.99	–	–	–	Kharasch 201136
75.0, q.d.	0.015/kg, i.v. (–)	10	12	67	0.480	0.474	1.01	–	–	–	Kharasch 201136
600, q.d.	0.015/kg, i.v. (bol)	10	10	50	0.428	0.375	1.14	–	–	–	Kharasch 200425
600, q.d.	0.015/kg, i.v. (bol)	12	6	50	0.426	0.433	0.98	–	–	–	Phimmasone 200126
600, q.d.	0.02/kg, i.v. (bol)	24	9	100	0.425	0.362	1.17	–	–	–	Kharasch 199724
600, q.d.	0.06/kg, p.o. (sol)	10	10	50	0.084	0.046	1.84	0.139	0.111	1.25	Kharasch 200425
5.0, q.d.	0.075/kg, p.o. (sol)	10	12	67	0.519	0.692	0.75	0.606	0.863	0.70	Kharasch 201136
10.0, q.d.	0.075/kg, p.o. (sol)	10	12	67	0.399	0.555	0.72	0.498	0.863	0.58	Kharasch 201136
25.0, q.d.	0.075/kg, p.o. (sol)	10	12	67	0.270	0.295	0.92	0.365	0.490	0.75	Kharasch 201136
75.0, q.d.	0.075/kg, p.o. (sol)	10	12	67	0.170	0.123	1.38	0.246	0.255	0.96	Kharasch 201136
					GMFE (range)		1.19 (1.01–1.84)			1.34 (1.04–1.73)
					Pred within twofold		12/12			5/5
Rifampicin	Itraconazole
600, q.d.	200, b.i.d. (cap), fed	12	2b	100	0.015	0.018	0.83	–	–	–	Tucker 199237
					GMFE		1.20
					Pred within twofold		1/1
Itraconazole	Midazolam
200, q.d. (cap), fast	0.05/kg, i.v. (bol)	2	12	58	2.360	3.220	0.73	–	–	–	Olkkola 199638
50 (sol), fast	2.0, p.o. (sol)	4	6	83	2.780	2.000	1.39	–	–	–	Templeton 201039
200 (sol), fast	2.0, p.o. (sol)	4	6	83	7.390	4.700	1.57	–	–	–	Templeton 201039
400 (sol), fast	2.0, p.o. (sol)	4	6	83	9.700	5.400	1.80	–	–	–	Templeton 201039
100, q.d. (cap), fast	7.5, p.o. (tab)	2	12	33	3.780	5.745	0.66	2.730	2.559	1.07	Ahonen 199540
200 (cap), fast	7.5, p.o. (–)	2	12	58	4.680	3.423	1.37	3.080	1.750	1.76	Olkkola 199638
200, q.d. (cap), fast	7.5, p.o. (tab)	1	9	22	6.220	10.77	0.58	3.480	3.409	1.02	Olkkola 199441
200, q.d. (cap), fast	7.5, p.o. (–)	2	12	58	6.360	6.644	0.96	3.520	2.514	1.40	Olkkola 199638
200, q.d. (cap), fast	15.0, p.o. (tab)	2	9	44	4.730	7.970	0.59	2.650	3.120	0.85	Backman 199835
200, q.d. (cap), fast	15.0, p.o. (tab)	98	9	44	1.120	2.630	0.43	1.080	1.920	0.56	Backman 199835
					GMFE (range)		1.55 (1.04–2.35)			1.33 (1.02–1.78)
					Pred within twofold		9/10			6/6
Clarithromycin	Midazolam
500, b.i.d.	0.05/kg, i.v. (0.5 hours)	2	16	50	3.252	2.748	1.18	–	–	–	Gorski 199842
500, b.i.d.	3.0, p.o. (sol)	0.25	11	91	5.064	5.494	0.92	–	–	–	Markert 201343
500, b.i.d.	4.0, p.o. (sol)	2	16	50	8.676	7.000	1.24	3.130	2.765	1.13	Gorski 199842
250, b.i.d.	15.0, p.o. (tab)	1.5	12	33	2.336	3.572	0.65	1.653	2.440	0.68	Yeates 199644
					GMFE (range)		1.25 (1.08–1.53)			1.29 (1.13–1.48)
					Pred within twofold		4/4			2/2
Rifampicin	Digoxin
600, q.d.	1.0, i.v. (0.5 hours)	8c	8	100	0.780	0.905	0.86	–	–	–	Greiner 199945
300, b.i.d.	0.25, p.o. (–)	12	18	50	0.480	0.696	0.69	0.470	0.615	0.76	Gurley 2008b46
600, q.d.	0.5, p.o. (sol)	24d	10	50	0.510	0.817	0.62	–	–	–	Larsen 200747
600, q.d.	0.5, p.o. (–)	1	11	100	0.620	1.462	0.42	0.630	1.489	0.42	Reitman 201112
600, q.d.	0.5, p.o. (–)	169	11	100	0.950	0.683	1.39	0.920	0.693	1.33	Reitman 201112
600, q.d.	0.5, p.o. (–)	337	11	100	1.030	0.977	1.05	1.000	0.876	1.14	Reitman 201112
600, q.d.	1.0, p.o. (–)	8c	8	100	0.480	0.568	0.84	0.480	0.481	1.00	Greiner 199945
					GMFE (range)		1.41 (1.05–2.36)			1.36 (1.00–2.36)
					Pred within twofold		6/7			4/5
Itraconazole	Digoxin
200, q.d. (cap), fast	0.5, p.o. (tab)	1	10	10	1.399	1.610	0.87	1.465	1.340	1.09	Jalava 199748
					GMFE		1.15			1.09
					Pred within twofold		1/1			1/1
Clarithromycin	Digoxin
200, b.i.d.	0.5, i.v. (1 hours)	0	9	100	1.020	0.980	1.04	–	–	–	Tsutsumi 200249
250, b.i.d.	0.01/kg, i.v. (bol)	2	3	100	1.060	1.185	0.89	–	–	–	Rengelshausen 200350
500, b.i.d.	0.25, p.o. (–)	0	18	50	1.310	1.466	0.89	1.350	1.750	0.77	Gurley 2008b46
250, b.i.d.	0.75, p.o. (tab)	0.5	12	100	1.240	1.643	0.75	1.420	1.833	0.77	Rengelshausen 200350
					GMFE (range)		1.15 (1.04–1.32)			1.29 (1.29–1.30)
					Pred within twofold		4/4			2/2

AUC, area under the plasma concentration‐time curve; bol, bolus; cap, capsule; C_max, peak plasma concentration; DDI, drug‐drug interaction; fast, oral administration in fasted conditions; fed, oral administration with a meal; GMFE, geometric mean fold error; obs, observed; pred, predicted; sol, solution; syr, syrup; tab, tablet.

^aCerebrotendinous xanthomatosis (CTX) patients,

^bcoccidioidomycosis patients,

^csee Reitman et al.12,

^dpersonal communication, Rifampicin‐Midazolam: 0–∞ AUC_ratios, Rifampicin‐Alfentanil: 0–∞ AUC_ratios, Rifampicin‐Digoxin: 3 hours AUC_ratios, Rifampicin‐Itraconazole: 12 hours AUC_ratio, Itraconazole‐Midazolam: 0–∞ AUC_ratios, Itraconazole‐Digoxin: 12 hours AUC_ratio, Clarithromycin‐Midazolam: 0–∞ or 2–4 hours AUC_ratios, Clarithromycin‐Digoxin: 0–∞ or 24 hours AUC_ratios, matching reported observed values, –, not given.

Figure 2 presents a selection of the different modeled CYP3A4 DDIs, showing population predicted compared with observed victim drug plasma concentration‐time profiles of one study each of the rifampicin‐midazolam, rifampicin‐alfentanil, itraconazole‐midazolam, and clarithromycin‐midazolam DDIs, selected for their clinically relevant doses of perpetrator and victim drug. Figure 3 presents a selection of the different modeled P‐gp DDIs, showing population predicted compared with observed victim drug plasma concentration‐time profiles of one study each of the rifampicin‐digoxin, itraconazole‐digoxin, and clarithromycin‐digoxin DDIs, selected for their clinically relevant doses of perpetrator and victim drug. Please refer to Section 3 of Appendix S1 for the results of all 57 DDI studies, shown in Figures S8a, S9a, S11a, S12a, S13a, S14a, S15a in Appendix S1 (semilogarithmic), Figures S8b, S9b, S11b, S12b, S13b, S14b, S15b in Appendix S1 (linear), and Table S10 in Appendix S1, demonstrating the good predictive performance for all modeled DDIs.

Figure 2.

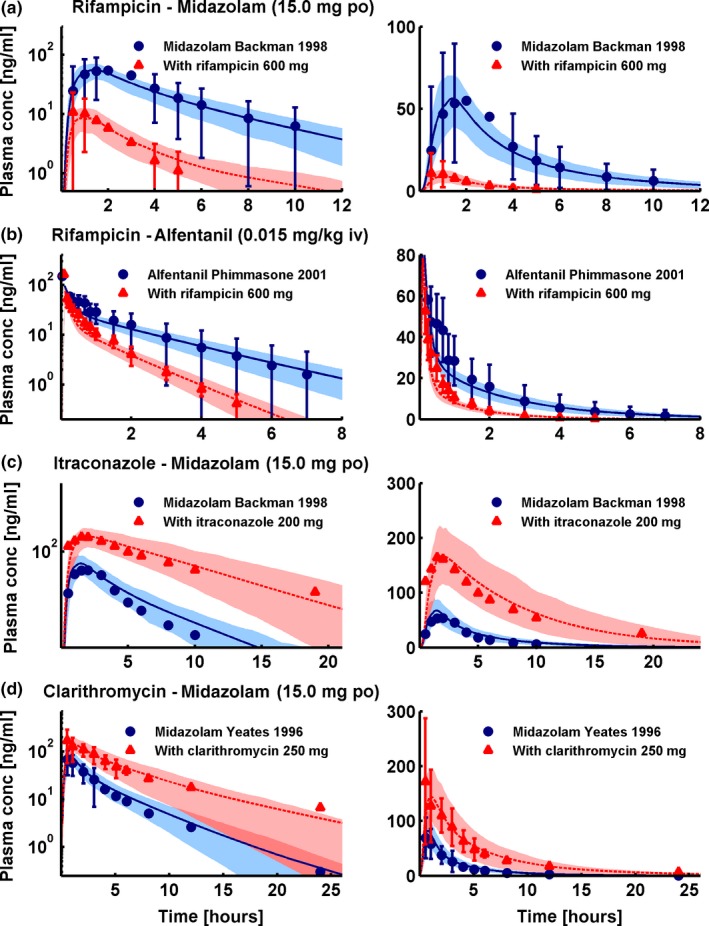
Cytochrome P450 3A4 drug‐drug interactions (DDIs). Selection of one study each of the rifampicin‐midazolam (a), rifampicin‐alfentanil (b), itraconazole‐midazolam (c), and clarithromycin‐midazolam (d) DDIs, presented in semilogarithmic (left panel) and linear plots (right panel). Shown are population predictions compared to observed victim drug concentration‐time profiles before and during perpetrator administration. Observed data are shown as blue dots (control) or red triangles (DDI) ± SD. Population simulation arithmetic means are shown as solid blue lines (control) or dashed red lines (DDI); the shaded areas illustrate the respective 68% population prediction intervals. Details on dosing regimens, study populations, predicted and observed DDI area under the plasma concentration‐time curve ratios and DDI peak plasma concentration ratios are summarized in Table 1.

Figure 3.

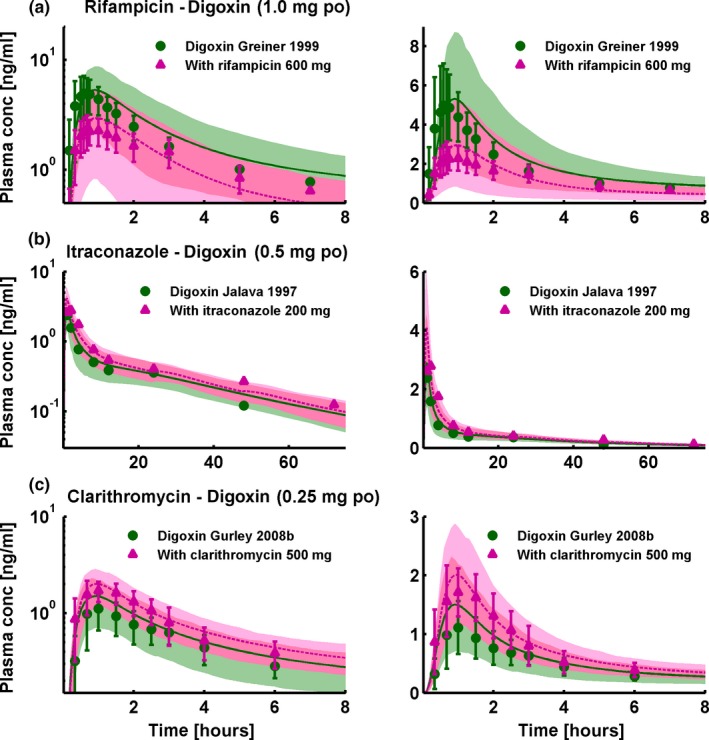
P‐glycoprotein drug‐drug interactions (DDIs). Selection of one study each of the rifampicin‐digoxin (a), itraconazole‐digoxin (b), and clarithromycin‐digoxin (c) DDIs, presented in semilogarithmic (left panel) and linear plots (right panel). Shown are population predictions compared to observed victim drug concentration‐time profiles before and during perpetrator administration. Observed data are shown as green dots (control) or pink triangles (DDI) ± SD. Population simulation arithmetic means are shown as solid green lines (control) or dashed pink lines (DDI); the shaded areas illustrate the respective 68% population prediction intervals. Details on dosing regimens, study populations, predicted and observed DDI area under the plasma concentration‐time curve ratios and DDI peak plasma concentration ratios are summarized in Table 1.

Modeled induction and de‐induction of CYP3A4 enzyme activity in the liver and duodenum is presented in Figure 4. The combination of simulated intracellular rifampicin concentrations and chosen induction parameters (half‐maximal effective concentration (EC₅₀) = 0.34 μmol/l, maximum effect (E_max) = 9) leads to CYP3A4 activity increases of 7.8‐fold in the liver and of 6.7‐fold in the duodenum with a 600 mg q.d. rifampicin regimen (Figure 4 a). De‐induction depends on the half‐lives of the perpetrator and the induced protein; we implemented CYP3A4 with protein half‐lives of 36 and 23 hours in the liver and intestine, respectively10, 11 (see Table S7 in Appendix S1). De‐induction kinetics were evaluated by prediction of midazolam PK when administered 1, 2, or 4 weeks after the last dose of rifampicin, as studied by Reitman et al.12 The rifampicin‐midazolam model successfully predicts the time course of CYP3A4 activity return to baseline after the last dose of rifampicin, shown by the correct simulation of the midazolam plasma concentration‐time profiles of this study (Figure 4 b).

Figure 4.

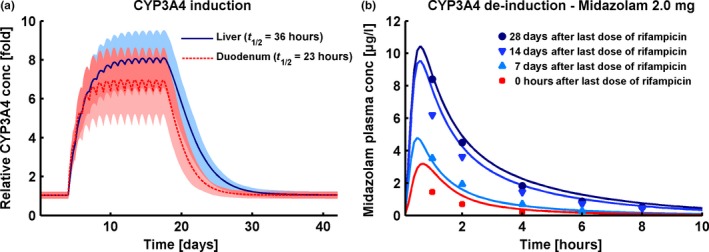
Cytochrome P450 (CYP)3A4 induction and de‐induction. (a) Fold change of predicted CYP3A4 concentrations in liver (solid blue line) and duodenum (dashed red line) before, during, and after a 600 mg q.d. rifampicin regimen. Shown are population prediction arithmetic means (lines) and 68% population prediction intervals (shaded areas). (b) Population simulation arithmetic means (lines) and observed (squares, triangles, and dots) midazolam plasma concentration‐time profiles during simultaneous administration of midazolam and rifampicin (red line and squares) or administration of midazolam 7 days (light blue line and triangles), 14 days (blue line and triangles) or 28 days (dark blue line and dots) after the last dose of a 600 mg q.d. rifampicin treatment. Observed data are from Reitman et al.12 Predicted and observed DDI area under the plasma concentration‐time curve ratios and DDI peak plasma concentration ratios are given in Table 1.

All victim drug plasma concentration‐time profiles before and during co‐administration with the different perpetrators are well predicted over the full range of administered doses and administration protocols. Predicted compared with observed DDI AUC ratios and C_max ratios with calculated GMFEs for each perpetrator‐victim pair are summarized in Table 1. Correlation of predicted to observed DDI AUC ratios and C_max ratios of all 57 modeled interaction studies, illustrating the performance of the entire DDI network, is presented in Figure 5.

Figure 5.

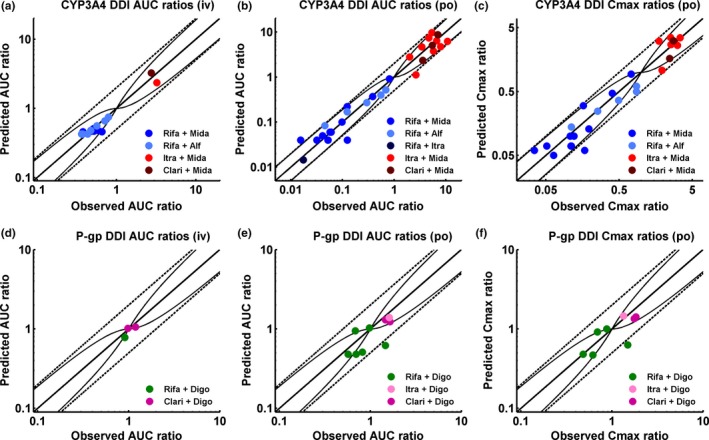
Correlation of predicted to observed DDI area under the plasma concentration‐time curve (AUC) ratios and DDI peak plasma concentration (C_max) ratios. The upper panel illustrates the cytochrome P450 (CYP)3A4 DDI prediction performance, the lower panel illustrates the P‐glycoprotein (P‐gp) DDI prediction performance of the network. (a, d) DDI AUC ratios of intravenously administered victim drugs, (b, e) DDI AUC ratios of orally administered victim drugs, and (c, f) DDI C_max ratios of orally administered victim drugs. The line of identity and the prediction acceptance limits proposed by Guest et al.23 are shown as solid lines. The 0.5‐fold to 2.0‐fold acceptance limits are shown as dashed lines. Induction of elimination pathways by rifampicin results in DDI ratios <1, inhibition of elimination pathways by itraconazole or clarithromycin results in DDI ratios >1. Study references and values of predicted and observed DDI AUC ratios and DDI C_max ratios are listed in Table 1.

Discussion

Comprehensive whole‐body PBPK models of rifampicin, itraconazole, clarithromycin, midazolam, alfentanil, and digoxin have been successfully developed, incorporating all current knowledge on the processes controlling the PKs of these drugs. All models were established using a large number of clinical studies and all models show a good performance over the full range of administered doses and administration protocols. Model evaluation comprised comparison of predicted with observed concentration‐time profiles, AUC, and C_max values, calculation of GMFEs as a measure of descriptive and predictive performance, and application of the independently developed models for DDI prediction.

Sensitivity analyses demonstrate that all models are sensitive to lipophilicity, fraction unbound, and the catalytic rate constants of influential eliminating enzymes or transporters. This result is expected, as the lipophilicity values are used for calculation of membrane permeabilities and partition coefficients, fraction unbound in plasma directly controls the concentration of drug available for passive distribution, transport, and metabolization from the blood, and the catalytic rate constants of the major eliminating enzymes or transporters naturally have a large impact on the predicted clearance and AUC. Experimental values were used for parameterization wherever possible. For example, fraction unbound was fixed to reported experimental values in five of the six models. For itraconazole, the attempts to set fraction unbound in plasma to one of the widely differing literature values (0.2–3.6%) did not result in a satisfactory model and, therefore, fraction unbound was optimized within the literature range (0.6%).

The presented rifampicin model accounts for metabolism by the arylacetamide deacetylase (AADAC), and transport by organic anion‐transporting polypeptide (OATP)1B1 and P‐gp, as described in the literature. Metabolism by CYP3A4 has not been implemented, as currently there is no conclusive evidence of rifampicin elimination via CYP3A4. Auto‐induction of rifampicin clearance was implemented via induction of AADAC, OATP1B1, and P‐gp expression. Furthermore, induction of CYP3A4 has been incorporated, without impact on the PK of rifampicin itself. In addition to these induction processes, the DDI application of the presented model is extended to simultaneous dynamic competitive inhibition of CYP3A4 and P‐gp. Several minimal or partial PBPK models of rifampicin13, 14, 15, 16 and one full PBPK model17 have been published to date, but many of them do not account for auto‐induction of rifampicin or lack the induction of P‐gp. Induction of further CYP isoforms and transporters by rifampicin as well as inhibition of OATP is not yet accounted for, as this requires evaluation of appropriate victim drug models and of the DDI predictions with clinical data, which is beyond the scope of this study. However, the implementation of additional interaction parameters is technically a simple and straight‐forward extension of the current model.

The presented itraconazole model accounts for competitive inhibition of CYP3A4 by itraconazole itself and its three sequentially generated main metabolites. Adhering to the reported competitive mechanism of CYP3A4 inhibition by itraconazole and hydroxy‐itraconazole,18 the strong observed nonlinearity and accumulation of itraconazole could not be adequately described using the inhibitory effects of parent drug and first metabolite, only. Therefore, the second and third metabolites were included, resulting in a model that slightly overpredicts the first dose of some studies, but accurately describes the steady‐state plasma concentrations of intravenous and oral multiple‐dose administration. The CYP3A4 inhibition constants of itraconazole and all three metabolites were fixed to literature values.18 Furthermore, the model correctly describes the strong food effects for both oral solution and capsule formulation, which is essential for modeling of the reported clinical studies.

The presented clarithromycin model is based on the PBPK model published by Moj et al.19 with small modifications. For DDI prediction, different compounds have to be coupled in one and the same individual with a specified expression of enzymes and transporters. Therefore, the clarithromycin model was adapted to the CYP3A4 expression profile reported by Nishimura et al.20 used in the other models (see Table S7 in Appendix S1). Furthermore, transport by OATP1B3 was removed, according to literature,21 and the values for pKa, lipophilicity, fraction unbound, and CYP3A4 K_M were fixed to literature values. The adapted model precisely captures the plasma concentration‐time profiles of all investigated studies with very low GMFEs (1.16 for AUC values and 1.11 for C_max values; n = 15).

The presented midazolam model is a simple, very robust, and reliable model that has been successfully applied for DDI simulations with many different perpetrator models, as demonstrated in detail in Section 3 of Appendix S1.

The presented alfentanil model has been established as a second CYP3A4 victim drug, to further evaluate the performance of the rifampicin model. It shows an accurate and precise performance in single compound simulations as well as in DDI predictions. Due to the lack of clinical studies with other perpetrator drugs it has only been coupled to the rifampicin model so far.

For the development of the presented digoxin model, a multitude of clinical studies (n = 38) was available in the literature, demonstrating the high interindividual variability in the PK of digoxin. A study measuring the P‐gp protein abundance in human duodenal biopsies found considerable variation of more than eightfold in a group of 25 patients.22 Considering the large interindividual differences in the observed digoxin PK, the presented digoxin model shows a good descriptive and predictive performance. This was accomplished by incorporation of the drug target Na⁺/K⁺‐ATPase as binding partner, and by increasing the relative P‐gp expression in the intestinal mucosa, to accurately describe the plasma concentrations following intravenous as well as oral administration. This altered expression profile has been evaluated by prediction of the digoxin DDIs with rifampicin, itraconazole, and clarithromycin. Especially the prediction of the rifampicin‐digoxin interaction was significantly improved applying the higher intestinal expression of P‐gp.

PBPK modeling is a rapidly evolving field, including continuously improved software capabilities and steadily increasing knowledge in systems pharmacology. There are many different models for the drugs investigated in this study, built with many different software platforms, and comparing their features and performance would take a study of its own.

The presented DDI modeling network demonstrates a very good performance of the models for DDI prediction over the full range of reported DDI administration protocols. This is illustrated by concentration‐time profiles, DDI AUC ratios, DDI C_max ratios, and corresponding GMFEs. In addition, some of the presented models have been applied for DDI prediction with currently unpublished models, which are either confidential or pending publication, also yielding good results and further increasing the confidence in their predictive capacity. Now that a core of mutually evaluated models has been established, further models can be added to this DDI network and evaluated via simulation of published clinical DDI studies utilizing the models provided in this study.

In summary, whole‐body PBPK models of rifampicin, itraconazole, clarithromycin, midazolam, alfentanil, and digoxin have been thoroughly built, and tested by DDI prediction within the presented network using different kinds of perpetrator (induction, competitive inhibition, and mechanism‐based inactivation) and victim drugs (CYP3A4, P‐gp), demonstrating that they reliably predict the observed data of all clinical DDI studies that have been reported for combinations of these drugs. The presented models are transparently documented and provided open‐source as supplementary material to this paper (Data S1‐S6) and in the OSP repository (http://www.open-systems-pharmacology.org) for the drug development community to help understand and characterize the DDI potential of investigational drugs and to inform the design of clinical trials. This study lays a cornerstone for the qualification of the OSP platform with regard to reliable PBPK predictions of enzyme‐mediated and transporter‐mediated DDIs during model‐informed drug development.

Funding

This study was sponsored by Bayer AG.

Conflict of Interest

S.F., T.E., and T.W. are employees of Bayer AG. T.L. has received research funding from Bayer AG. No potential conflicts of interest were disclosed by the other authors.

Author Contributions

N.H., S.F., T.E., T.W., and T.L. wrote the manuscript. N.H., S.F., T.E., T.W., and T.L. designed the research. N.H., S.F., D.M., H.B., T.W., and T.L. performed the research.

Supporting information

Supplementary information accompanies this paper on the CPT: Pharmacometrics & Systems Pharmacology website. (http://www.psp-journal.com)

Appendix S1. Model information and evaluation.

Data S1. Rifampicin model file.

Data S2. Itraconazole model file.

Data S3. Clarithromycin model file.

Data S4. Midazolam model file.

Data S5. Alfentanil model file.

Data S6. Digoxin model file.