The pathological brain is characterized by distributed structural alterations in grey matter, which tend to follow identifiable network-like patterns. Cauda et al. investigate how different types of brain connectivity – functional, anatomical, genetic – guide the spread of structural alterations, and show that co-alterations are distributed according to brain connectivity constraints.
Keywords: brain disorders, brain alterations, structural co-alteration, brain connectivity, functional connectivity, anatomical connectivity, genetic co-expressions
Abstract
The pathological brain is characterized by distributed morphological or structural alterations in the grey matter, which tend to follow identifiable network-like patterns. We analysed the patterns formed by these alterations (increased and decreased grey matter values detected with the voxel-based morphometry technique) conducting an extensive transdiagnostic search of voxel-based morphometry studies in a large variety of brain disorders. We devised an innovative method to construct the networks formed by the structurally co-altered brain areas, which can be considered as pathological structural co-alteration patterns, and to compare these patterns with three associated types of connectivity profiles (functional, anatomical, and genetic). Our study provides transdiagnostical evidence that structural co-alterations are influenced by connectivity constraints rather than being randomly distributed. Analyses show that although all the three types of connectivity taken together can account for and predict with good statistical accuracy, the shape and temporal development of the co-alteration patterns, functional connectivity offers the better account of the structural co-alteration, followed by anatomic and genetic connectivity. These results shed new light on the possible mechanisms at the root of neuropathological processes and open exciting prospects in the quest for a better understanding of brain disorders.
Introduction
Brain disorders are characterized by diffuse alterations of grey matter. Especially in neurodegenerative diseases, neuroanatomical abnormalities have been found to spread from one brain area to another according to distinctive network-like patterns (Yates, 2012; Pandya et al., 2017). These patterns of pathological structural co-alterations seem to develop along pathways that are influenced by the organization of brain connectivity (Raj et al., 2012; Zhou et al., 2012; Iturria-Medina and Evans, 2015; Oxtoby et al., 2017; Yuan et al., 2017; Cauda et al., 2018; Manuello et al., 2018; Tatu et al., 2018). Indeed, patterns of brain atrophy caused by neurodegenerative diseases appear to somewhat resemble the patterns of neuronal connections (Warren et al., 2013). Furthermore, brain disorders selectively target certain subpopulations of neurons that often lie at the centre of important functional networks (Saxena and Caroni, 2011). Arguably, their high topological centrality makes those areas brain hubs and, as a consequence, more likely to be affected by pathological processes (Crossley et al., 2014; Cope et al., 2018).
Thus far, at least four important mechanisms (not necessarily mutually exclusive) have been invoked to explain the spread of brain alterations: transneuronal spread, nodal stress, shared vulnerability, and trophic failure (Zhou et al., 2012; Fornito et al., 2015). The first mechanism is based on the involvement of certain toxic agents that propagate along neuronal connections (Soto and Estrada, 2008; Goedert et al., 2010; Korth, 2012; Jucker and Walker, 2013; Kraus et al., 2013; Walker et al., 2013; Clavaguera et al., 2014). A growing body of evidence indicates that misfolded proteins may spread in a prion-like way along brain axonal fibres (Chevalier-Larsen and Holzbaur, 2006) throughout a corruptive templating as a cascade phenomenon of misfolded protein propagation (Jucker and Walker, 2011; Hardy and Revesz, 2012; Warren et al., 2013). Borrowed from prion diseases (Aguzzi et al., 2007), this mechanism has been subsequently explored in neurodegenerative diseases such as Alzheimer’s disease, Parkinson’s disease, Huntington’s disease, amyotrophic lateral sclerosis and tauopathies (Clavaguera et al., 2013; Bourdenx et al., 2017), and more recently has been tentatively generalized to other brain disorders (Guest et al., 2011). However, the application of the prion-like mechanism to neurodegenerative diseases is still an open field of research.
The second mechanism (Zhou et al., 2012) is based on the hypothesis that the most active brain regions (i.e. network hubs) may also be the most functionally stressed (Crossley et al., 2014) and, as a result, susceptible to be structurally altered (Buckner et al., 2005; Saxena and Caroni, 2011). This phenomenon has been confirmed in humans by using in vivo neuroimaging techniques and voxel-based meta-analyses (Crossley et al., 2014). The third mechanism relies on the hypothesis that certain areas with shared gene or protein expressions may exhibit common vulnerability to neuropathology (Zhou et al., 2012). This phenomenon could be partially mediated by the relationship between expression of genes and patterns of brain connectivity (French and Pavlidis, 2011; Cioli et al., 2014). The fourth mechanism invokes a failure in the process of trophic factors production, which can lead to the pathological deterioration of neural wiring (Zhou et al., 2012; Fornito et al., 2015).
Studies analysing the networks formed by cerebral regions that appear to be co-altered in the pathological brain are guiding research to a new perspective, which claims a neurobiological and transdiagnostic approach for a better understanding of how the brain responds in a variety of both neurological and psychiatric conditions (Buckholtz and Meyer-Lindenberg, 2012; Raj et al., 2012; Zhou et al., 2012; Fornito et al., 2015; Goodkind et al., 2015; Iturria-Medina and Evans, 2015; McTeague et al., 2016; Sprooten et al., 2017; Cauda et al., 2018). This view may be counter-intuitive, as we are inclined to think that brain disorders have specific aetiological and pathogenetic mechanisms, which, in turn, produce peculiar patterns of neuronal alterations. However, a growing body of evidence points out that, apart from some pathology-specific alterations, a ‘core set’ of co-altered cerebral areas is frequently involved in the majority of brain diseases (Etkin and Wager, 2007; Ellison-Wright and Bullmore, 2010; Saxena and Caroni, 2011; Hamilton et al., 2012; Jagust, 2013; Menon, 2013; Baker et al., 2014; Douaud et al., 2014; Goodkind et al., 2015; Cauda et al., 2018).
This ‘core set’ is generally composed of areas that are related to important associative and cognitive functions, among which the insular and anterior cingulate cortices are the most prominent. These regions are essential parts of the cognitive control system, which is supposed to monitor a host of higher brain functions (Cauda et al., 2012b). Thus, for both its topological and functional features, the activity of the cognitive control system may be affected by a wide variety of brain disorders (McTeague et al., 2016). This would make it more difficult to differentiate neuropathological conditions solely based on structural or functional alterations exhibited by the areas constituting this system (Sprooten et al., 2017).
The contamination between neurodegenerative and psychiatric disorders may be highlighted by a number of studies. Genetic studies in neurodegenerative dementias show how brain abnormalities antedate the onset of symptoms by many years (Quiroz et al., 2015; Rohrer et al., 2015; Chhatwal et al., 2018), suggesting a less defined border between neurodegenerative and neurodevelopmental disorders (Zawia and Basha, 2005; Lahiri and Maloney, 2010; Warren et al., 2013). Moreover, a growing body of literature, demonstrating structural and functional brain changes in psychiatric illnesses, is bringing psychiatry and the study of neurological conditions together (Douaud et al., 2014; Gupta et al., 2015; Du et al., 2017).
The lack of direct correspondence between the development of neuropathological processes and the manifestation of brain alterations implies an overlap of symptoms that strictly depends on the disruption of large-scale networks. What is more, transdiagnostic symptoms are often produced by genetic and environmental risk factors that affect system-level circuits for many dimensions of cognitive functions. The impairment of these circuits brings about vulnerability to vast domains of psychopathology rather than distinct diseases (Buckholtz and Meyer-Lindenberg, 2012).
Given that the spread of brain alterations is likely to be non-random in both neurological and psychiatric diseases (Cauda et al., 2018; Tatu et al., 2018), an important and as yet unresolved issue is the prevalence of one or more mechanisms at the root of the propagation in different brain disorders. To our knowledge, thus far only one study (Cope et al., 2018) has tried to estimate, with the help of in vivo techniques, which mechanism is mostly associated with the distribution patterns of two neurodegenerative diseases (i.e. Alzheimer’s disease and progressive supranuclear palsy). Indeed, if neuronal alterations follow the patterns of brain connectivity, it should be possible to predict their spread based on brain connectivity profiles (Raj et al., 2012; Robinson, 2012; Zhou et al., 2012; Iturria-Medina et al., 2014). It should also be possible to simulate the temporal evolution of these alterations and to infer which of the different connectivity profiles (i.e. functional, anatomic, and genetic) can better explain the development of a certain structural co-alteration pattern. In light of this, it is reasonable to hypothesize that the different contributions of the aforementioned propagation mechanisms might lead to typical patterns of structural co-alterations (Cope et al., 2018). For instance, the prevalence of a pattern composed of anatomically connected areas may be better explained by the mechanism of the transneuronal spread, which implies a propagation across more contiguously and directly connected areas. By contrast, the prevalence of a pattern composed of functionally connected regions suggests that the mechanism of the nodal stress may be more effective in generating this network of co-alterations (Biswal, 2011, 2012; Buckner et al., 2013). In turn, the shared vulnerability hypothesis implies that structurally co-altered areas may be characterized by similar gene co-expression patterns (Stuart et al., 2003).
To address these important questions, we recently developed a methodology to estimate how each type of brain connectivity can predict the pattern formed by neuropathological co-alterations (Cauda et al., 2018). Herein, this methodology has been applied transdiagnostically so as to have a great deal of meta-analytical data to work on and, at the same time, to provide proof of concept. We would like to show that this method is applicable to every brain disorder and, in the future, we plan to use it for the analysis of specific neurological or psychiatric conditions.
To this aim, we began by examining the whole BrainMap (Fox and Lancaster, 2002; Fox et al., 2005; Laird et al., 2005b) voxel-based morphometry (VBM) database of brain MRI studies to construct the most comprehensive transdiagnostic map of pathological structural co-alterations. To do so we used the grey matter alterations detected by VBM as a proxy for the morphological brain abnormalities. Given a brain area (say, ‘A’) that is altered, our method was able to detect if other areas appeared to be altered together with ‘A’ (i.e. co-altered) (Cauda et al., 2018; Manuello et al., 2018; Tatu et al., 2018).
The result of this analysis was the creation of undirected co-alteration graphs showing the brain areas forming the structural co-alteration patterns. Then, to assess which of the three different connectivity profiles could account better for the structural co-alteration patterns, we calculated the anatomical, resting state functional, and genetic (i.e. the correlated gene expression pattern) connectivity networks using the brain most altered areas as starting points (i.e. nodes). The comparison of the different network matrices to the structural co-alteration patterns allowed us to find out the contribution of each connectivity profile to the co-alteration pattern and, consequently, to better understand its development through the spread of alterations [for the relationship between co-alteration patterns and the concept of propagation or spread, see Cauda et al. (2018)]. On these grounds, we also estimated—with simulation techniques—both the spatial and temporal progression of the distribution of alterations, so as to find out how the patterns of structural co-alterations could be predictable in terms of functional, anatomic, and genetic connectivity.
This method allowed us to address the following issues. How are structural co-alteration patterns distributed across the pathological brain? Since neuronal alterations seem to spread from one cerebral region to another, do these propagation patterns follow the routes of brain connectivity? Which type of connectivity (anatomic, functional, or genetic) is most involved in the generation of structural co-alterations? What is the temporal evolution of these co-alteration patterns?
Materials and methods
Selection of studies
We queried the VBM BrainMap database (Fox and Lancaster, 2002; Fox et al., 2005; Laird et al., 2005b; Vanasse et al., 2018) (December 2017) using the following search criteria: (i) decreases: Experiments Context is Disease AND Experiment Contrast is Gray Matter AND Experiments Observed Changes is Controls>Patients; and (ii) increases: Experiments Context is Disease AND Experiment Contrast is Gray Matter AND Experiments Observed Changes is Patients>Controls.
We retrieved 912 experiments and 350 experiments for the first and the second query, respectively. All the retrieved experiments with a sample size smaller than eight subjects were excluded. The identification of this lower bound is in accordance with the work of Scarpazza et al. (2015), which showed that VBM experiments based on an equivalent sample should not be biased by an increased false positive rate. We further decided to exclude all the experiments not clearly comparing pathological population with healthy controls, as well as considering subjects ‘at risk’. The remaining items were then coded according to the ICD-10 system. As a further criterion, all the experiments not coded with F (i.e. mental, behavioural and neurodevelopmental disorders) or G (i.e. diseases of the nervous system) labels were excluded. From the remaining records, we also expunged those related to codes that could not be considered as primary brain disorders (i.e. F10: Alcohol related disorders; F15: Other stimulant related disorders; F28: Other psychotic disorder not due to a substance or known physiological condition; F91: Conduct disorders; G11: Hereditary ataxia; G43: Migraine; G44: Other headache syndromes; G47: Sleep disorders; G50: Disorders of trigeminal nerve; and G71: Primary disorders of muscles). At the end of this procedure the 642 remaining experiments from the first query (for 15 820 subjects, and 7704 foci) and the 204 remaining experiments from the second query (for 4966 subjects, and 2244 foci) were used for the analyses.
For the first query, most studies explored F20: Schizophrenia (17.9%); F32-F33: Major depressive disorder, single episode/recurrent (9.8%); G40: Epilepsy and recurrent seizures (8.7%); G30: Alzheimer’s disease (8.3%) and G31: Other degenerative diseases of the nervous system (8.1%). For the second query, most studies explored F20: Schizophrenia (16.2%); G40: Epilepsy and recurrent seizures (12.7%); F84: Pervasive developmental disorders (11.3%); F31: Bipolar disorder (9.8%) and F32-F33: Major depressive disorder, single episode/recurrent (9.3%). The complete overview of the diagnostic spectra distribution is reported in Supplementary Table 1.
The overview of data search strategy and datasets is reported in the Supplementary material. A flow chart of key steps (used to generate the dataset of information, analyse data and obtain several levels of results) is also reported in Supplementary Fig. 1. The full list of the studies designated as suitable for meta-analysis, are reported in Supplementary Tables 2 and 3.
To calculate the pattern of structural co-alterations we used the same methodology previously applied in Cauda et al. (2018), Manuello et al. (2018) and Tatu et al. (2018).
Anatomical likelihood estimation and modelled alteration creation
First, we performed an anatomical likelihood estimation (ALE) (Eickhoff et al., 2009, 2012; Turkeltaub et al., 2012) to summarize the results of the retrieved experiments statistically using an in-house developed MATLABr script following both the algorithms used in Gingerale 2.3.6 (Eickhoff et al., 2009, 2012; Turkeltaub et al., 2012) and the recommendation of Eickhoff et al. (2017). Results are clustered at a level of P < 0.05, family-wise error (FWE)-corrected for multiple comparisons, with a cluster-forming threshold of P < 0.001 (Eickhoff et al., 2016).
The ALE is a quantitative voxel-based meta-analysis technique able to give information about the anatomical reliability of results through a comparison by using a sample of reference studies from the existing literature (Laird et al., 2005a). An ALE meta-analysis considers each focus of every experiment as a Gaussian probability distribution:
| (1) |
where d is the Euclidean distance between the voxels and the focus taken into account and σ is the spatial uncertainty.
A modelled alteration (MA) map was calculated for each experiment as the union of the Gaussian probability distribution of each focus present in the experiment itself. Then the ALE map was determined as the union of the MA maps.
The significance of alteration values within the ALE map was calculated by a permutation test, in which we redistributed the same number of foci across the brain and recalculated an ALE map as described before. The histogram of the obtained score was used to assign a threshold P-value.
Creation of nodes
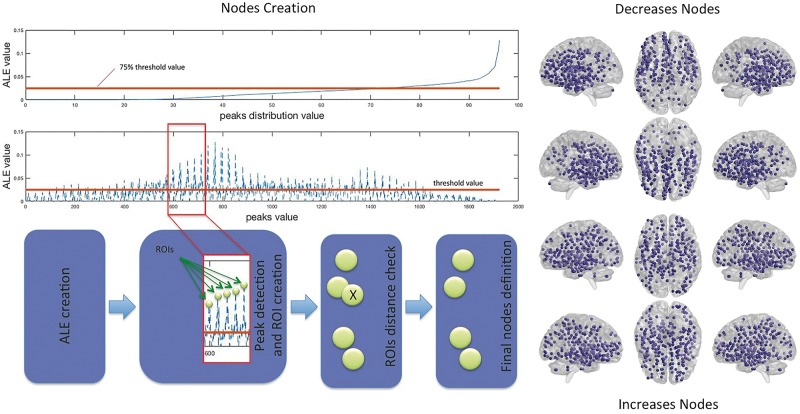
The creation of nodes was obtained from the ALE map using a peak detection algorithm that returns the set of local maxima. A local peak is a voxel whose ALE value is higher than the values of its neighbouring voxels. We selected the voxels with a peak value greater than a given threshold, which was set at the 75th percentiles of the peak values distribution. Then we created a distance matrix calculating the Euclidean distance between peaks. To avoid overlaps between regions of interest, we excluded all the peaks within a distance of 10 mm from the other peaks. Around each of those peaks we designed a 10 mm2 region of interest, which was used for the subsequent analysis (see Fig. 1 for a schema depicting the node detection pipeline; see Supplementary Tables 6 and 7 for the coordinates of nodes). For a detailed discussion of the rationales at the basis of our methodological choices, see Cauda et al. (2018).
Figure 1.
Node detection pipeline. Left: The schema illustrates the pipeline utilized for the detection of the regions of interest (i.e. nodes). Right: The obtained nodes for the decrease (top) and increase (bottom) conditions. See Supplementary Tables 6 and 7 for the node coordinates.
The structural co-alteration network
To trace the distribution of brain alterations we used a methodology aimed to characterize the structural co-alterations in the evolution of brain disorders (Cauda et al., 2015, 2018; Manuello et al., 2018; Tatu et al., 2018). This method can establish whether the alteration of a brain area statistically co-occurs with the alteration of one or more other brain areas. Specifically, we created a co-alteration matrix using the previously defined set of nodes. In the matrix of N × M dimension, the N rows represent experiments and the M columns the network nodes. For each pair of nodes of the co-alteration matrix, it is possible to obtain the strength of their co-alteration using the Jaccard index, which is defined as the number of experiments (rows) activating both the nodes divided by the union of the experiments activating the two nodes independently.
The obtained Jaccard matrix was thresholded at P < 0.01 using the method proposed by Toro et al. (2008). Given two nodes A and B, the null hypothesis states that the probability of B being altered does not depend on the value observed for A; by contrast, the alternative hypothesis states that a relationship of dependence between A and B exists. This can be expressed formally as:
| (2) |
| (3) |
| (4) |
| (5) |
We can obtain from the data an estimate under the null hypothesis as , where m is the number of experiments in which node B is altered and N the total number of experiments. Similarly, we can obtain the estimated probabilities under the alternative hypothesis as:
| (6) |
and
| (7) |
where n is the number of experiments in which the node A is altered and k is the number of experiments in which both nodes A and B are altered. The likelihood-ratio test is calculated with the following formula:
| (8) |
This formula is used to evaluate the alternative hypothesis H1 with respect to the null hypothesis H0.
The likelihood of the null hypothesis is defined as follows:
| (9) |
where B is the binomial distribution in which n is the number of contrasts that alters the second node, m is the number of contrasts that alters the first node, N is the total number of contrasts, and and k are the numbers of contrasts that alter both nodes.
The likelihood of the alternative hypothesis is defined as follows:
| (10) |
The λ distribution is shaped by a χ2 function with one degree of freedom. Connection at P < 0.01 corrected for false discovery rate (FDR) was maintained, otherwise discarded.
Functional connectivity matrix
For the same set of nodes considered in the previous analysis we calculated the functional connectivity matrix using resting state data (minimally preprocessed and ICA-FIX de-noised) from 200 healthy adult subjects in the 22–35 age range, obtained from the Human Connectome Project (2015 Q4, 900-subject release). For further details on the preprocessing of these data see Glasser et al. (2013) and Van Essen et al. (2012).
The matrix was constructed in the following manner. The previously determined nodes were used to create a spatial map and to generate subject-specific associated time series of the functional data, using the dual regression approach (Beckmann et al., 2009; Filippini et al., 2009). For each subject, the spatial map is regressed (as spatial regressors in a multiple regression) into the subject’s 4D space-time dataset. This results in a set of subject-specific time series. The output of the dual regression was a set of 200 matrices, one for each subject, where each column represents the time series of the corresponding node. Starting from these matrices we calculated the partial correlation between the nodes for each subject and then we mediated to obtain a final partial correlation matrix of the subjects’ group. This group connectivity matrix was then thresholded (α < 0.05) with a one sample permutation test (5000 permutation) using the FSL randomise program (Smith and Nichols, 2009; Winkler et al., 2014).
Anatomical connectivity matrix
The anatomical connectivity matrix was constructed using diffusion tensor imaging (DTI) data of 842 subjects in the 22–35 age range. These data were retrieved from the Human Connectome Project (2015 Q4, 900-subject release) (Van Essen et al., 2013). The diffusion images were acquired using a multishell diffusion scheme. The b-values were 1000, 2000 and 3000 s/mm2. The numbers of the diffusion sampling directions were 90, 90 and 90. The in-plane resolution was 1.25 mm. The slice thickness was 1.25 mm. The diffusion data were reconstructed in the MNI space using the q-space diffeomorphic reconstruction (Yeh and Tseng, 2011) to obtain the spin distribution function (Yeh et al., 2010). A diffusion sampling length ratio of 1.25 was used, and the output resolution was 1 mm. The atlas was constructed by averaging the spike density functions of the 842 subjects.
A deterministic fibre tracking algorithm (Yeh et al., 2013) was used to reveal the brain anatomical connections. The parameters were the following: whole brain seeding region method; angular threshold of 60°; step size of 0.5 mm; the anisotropy threshold was determined automatically by DSI Studio (Yeh et al., 2016). Tracks with length less than 30 mm were discarded. A total of 5000 seeds were placed in the brain. The nodes, obtained from the meta-analysis, were used to calculate the connectivity matrix by using the numbers of tracts passing between two nodes normalized by the median length of the connecting tracks.
Genetic co-expression matrix
Differently to the gene co-expression networks (Zhang and Horvath, 2005) that can quantify gene-to-gene relationships across different anatomical samples, the correlated ‘gene expression network’ proposed by Richiardi et al. (2015) is a form of genetic connectivity that quantifies anatomical region to anatomical region (i.e. region of interest to region of interest) across genes. This network has been obtained by using the complete microarray datasets of six brains, available for download from the Human Brian Atlas Project (Hawrylycz et al., 2012). The datasets contain values of gene expression that are normalized across all brains with an improved normalization process—for further information about the sample normalization see ALLEN Human Brain Atlas (2013). The downloaded files contain normalized microarray expression values as well as probe and sample metadata necessary for analysis.
It should be noted that the Allen Brain Atlas has some idiosyncrasies. For example, only two of the individuals whose data are stored in the database have bi-hemispheric samples. Moreover, the samples of brain areas were obtained with different stereotactic coordinates so that the variability among them is high. To address these issues, we used a method based on the Voronoi tessellation (Cauda et al., 2012a). Voronoi tessellation (Voronoi, 1907) is a specific decomposition of a metric space based on a finite set of points. In a 3D space, a given set of points S is a partition that associates a volume V(p) with every point so that all the points of the surface of V(p) are closer to p than to any other point in S. With this method, for each subject, we were able to create a parcellation of the brain based on the position of the samples, which are considered as the barycentres of the Voronoi polygons. We then assigned to all the voxels encompassed in a specific polygon the gene expression pattern of the sample located in the barycentre of that polygon.
Six parcellations were then constructed, one for each individual of the Allen project. In every parcellation, each voxel was characterized by a gene expression vector related to its closer sample. With regard to the four individuals with samples coming from one hemisphere, only one half brain was parcellated. Afterwards, we averaged the gene expressions of the six subjects voxel-wise. Gene expressions that are reported as non-statistically significant in the Allen database were excluded from the averaging process. This method made it possible to reduce the variance among the gene expression patterns of the six individuals, thus minimizing the weaknesses of the Allen database as much as possible.
The result was a tessellation of the brain in which every Voronoi polygon contains the mean gene expression of the six individuals (Cauda et al., 2012a). Subsequently, this information has been used to create the genetic co-expression matrix based on the set of nodes obtained from the meta-analysis. To every node we assigned the gene expression related to the Voronoi polygon associated with that node. We then constructed a matrix in which rows represent the gene expressions and columns represent the nodes. From this matrix we calculated the full and partial correlation of the mean gene expression between the nodes, so as to obtain a partial correlation matrix. This final matrix was probabilistically thresholded (α < 0.05) with a permutation test (5000 permutations).
Reliability measures
To assess the consistency of our measures (reliability) we used a Spearman-Brown split half methodology (or Spearman-Brown prediction formula) (Stanley, 1971; Allen and Yen, 2001). We divided each dataset (meta-analytic, functional, and genetic) into even and odd groups; for each group, we calculated the corresponding connectivity matrices. We then calculated the correlation between these connectivity matrices applying the Spearman-Brown correction (Allen and Yen, 2001) to get a better estimate of the reliability, as follows:
| (11) |
where r is the classical Spearman correlation.
Since DTI data were provided by the Human Connectome Project as ‘mean connectivity matrices’, we used a different approach to calculate the reliability of the anatomical connectivity measures. We used another mean DTI connectivity matrix obtained from a different dataset as a replication dataset. The replication dataset consisted of a different structural connectivity matrix that was constructed using a total of 842 subjects’ diffusion MRI data, in the 22–35 age range, obtained from the Human Connectome Project (2015 Q4, 900-subject release) (Van Essen et al., 2013). Finally, we calculated the correlation between the anatomical connectivity matrix derived from the primary dataset and the one derived from the replication dataset.
Comparison between connectivity matrices
The comparison between the different matrices (co-alteration, anatomical, functional, and genetic) was done using the Mantel test (Mantel, 1967; Glerean et al., 2016). In the Mantel test the correlation between two matrices was determined with a permutation test (5000 permutations). We calculated the correlation between the matrices by randomly permutating rows and columns. We subsequently obtained the distribution of the different correlations and calculated the P-value.
Diffusion connectivity matrix: spatial and temporal evolution
To assess the temporal evolution of the different types of connectivity, we developed a simple diffusion model. We considered the spread of neuronal alterations as a diffusion process by using a brain network-based model where nodes , which represents the cortical and subcortical structure as obtained from our meta-analysis, while edges , which represents the connection strength linking node i and node j. We used three types of connection strength for each model obtained from the anatomical, functional and genetic connectivity matrices.
Following Abdelnour et al. (2014) and Kondor and Lafferty (2002), we modelled the diffusion process using the heat equation, defined as:
| (12) |
where the matrix is the following Laplacian graph:
| (13) |
in which Δ is the diagonal matrix with δi = ∑j eij as the ith diagonal element. The heat Equation 12 can be solved explicitly as follows:
| (14) |
This formula defines the evolution of the initial configuration x0. We hypothesized an initial configuration in which the disease factor was uniform in all the nodes, thus obtaining the following equation:
| (15) |
which, having as free parameters the diffusion factor β and time t, can express the covariance of the system at each time of its evolution.
In our case we had the covariance matrix (the meta-analytic data) and the Laplacian matrices obtained from the resting state data, the anatomical data and genetic data, respectively. We estimated therefore the diffusion factor β and obtained the evolution of the diffusion for the functional, anatomical and genetic data. The best estimate of the parameter β and the time evolution of the diffusion were determined using a grid search on the parameter β, ranging between (0,1) with a step of 0.1. For each β-value, the matrix obtained from this simulation was correlated with the meta-analytic covariance matrix. With a Mantel test we assessed the significance of this correlation. Finally, the β-value that could maximize the correlation was chosen.
Contribution of the different kind of connectivity profiles to the structural co-alteration patterns
To find out the contribution of the different types of connectivity to the structural co-alteration patterns, we developed the following model:
| (16) |
where D is the structural co-alteration matrix and is the functional connectivity matrix, is the anatomical connectivity matrix, and is the genetic connectivity matrix, respectively.
Using an unconstrained non-linear optimization, we found the minimum of a scalar function of several variables. The algorithm was the simplex search method of Lagarias et al. (1998):
| (17) |
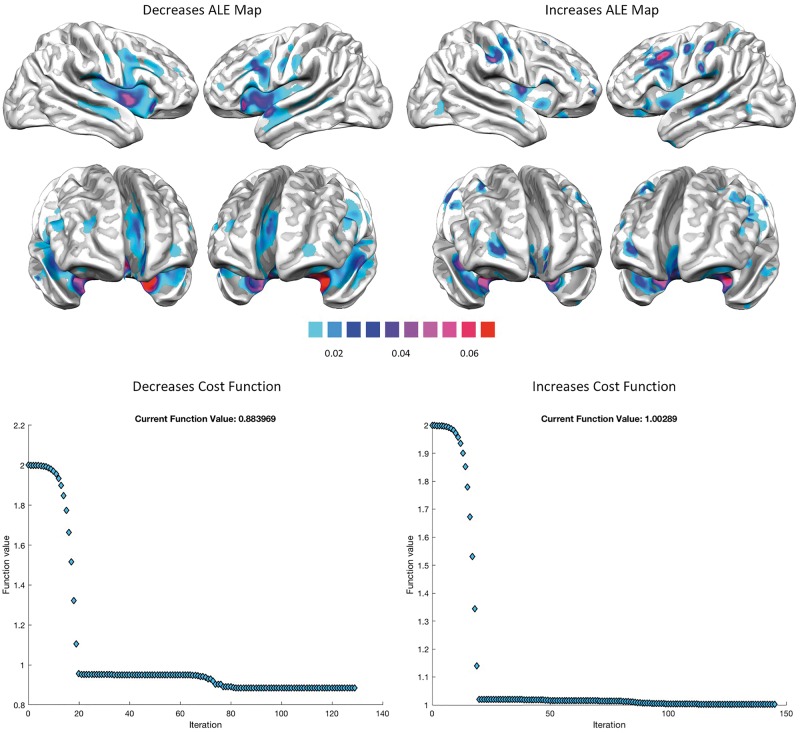
The final results are the coefficients that minimize the square difference norm between the structural co-alteration matrix and the other matrices. The algorithm was executed 1000 times with different initial conditions, each time to check the stability of the obtained minimum (Fig. 2, bottom).
Figure 2.
ALE results and cost functions. Top: ALE results for decreased (left) and increased foci (right). ALE results are clustered at the level of P < 0.05 and family-wise error-corrected for multiple comparisons, with a cluster-forming threshold of P < 0.001. Bottom: The schema illustrates the evolution of the cost function of the minimization algorithm for predicting the distribution of the structural co-alteration patterns.
Network analysis techniques
We analysed the co-alteration patterns further using a network-based analysis technique.
The node degree is the number of connections that the node has with the other nodes. We used the degree distribution to compare the node degree of the nodes of different networks. It was therefore possible to compare the structural co-alteration network with random networks. The degree distribution is the fraction of nodes with degree k, defined as follows:
| (18) |
The average shortest path length is defined as the average number of steps along the shortest paths for all pairs of nodes of the network under consideration. For an unweighted graph G with n vertices, the average path length is defined as follows:
| (19) |
where d is the shortest distance between node vi and node vj, with d = 0 if vj cannot be reached from vi.
This is one of the most robust measures in network topology and is inversely related to efficiency, which is a measure of how efficiently the network exchanges information. In particular, the local efficiency quantifies the network resistance when a failure occurs within it.
Data availability
The datasets we used in this study are from publicly available sources:
BrainMap (meta-analytic datasets) http://brainmap.org/.
Allen Brain Atlas (gene expression datasets) http://human.brain-map.org/static/download.
Human Connectome Project (resting state connectivity and DTI anatomical connectivity datasets) http://www.humanconnectomeproject.org/data/.
Above, we describe in detail which parts of these datasets were used or how we queried the BrainMap database.
A complete list of the literature involved in the meta-analytic analyses is provided in the Supplementary material.
Results
The ‘core set’ of altered brain areas
Figure 2 (top) shows the brain areas that appear to be altered in the VBM studies retrieved from our search. These areas form the ‘core set’ that is likely to be frequently affected by brain diseases. Areas showing significant statistical decreases are the insulae, anterior cingulate cortices, superior and middle temporal gyri, superior, middle and inferior frontal, pre- and postcentral gyri. Areas showing significant statistical increases are the right anterior and posterior insula, left middle insula, right pre- and postcentral gyri, right superior frontal gyrus, right superior temporal gyrus, left inferior temporal and inferior frontal gyri (see also Supplementary Tables 4 and 5).
Node creation and structural co-alteration network
Our automatic node creation procedure derived 277 nodes from the core set of decreased areas and 271 nodes from the core set of increased areas. These nodes are illustrated in the right panel of Fig. 1 (see also Supplementary Tables 6 and 7).
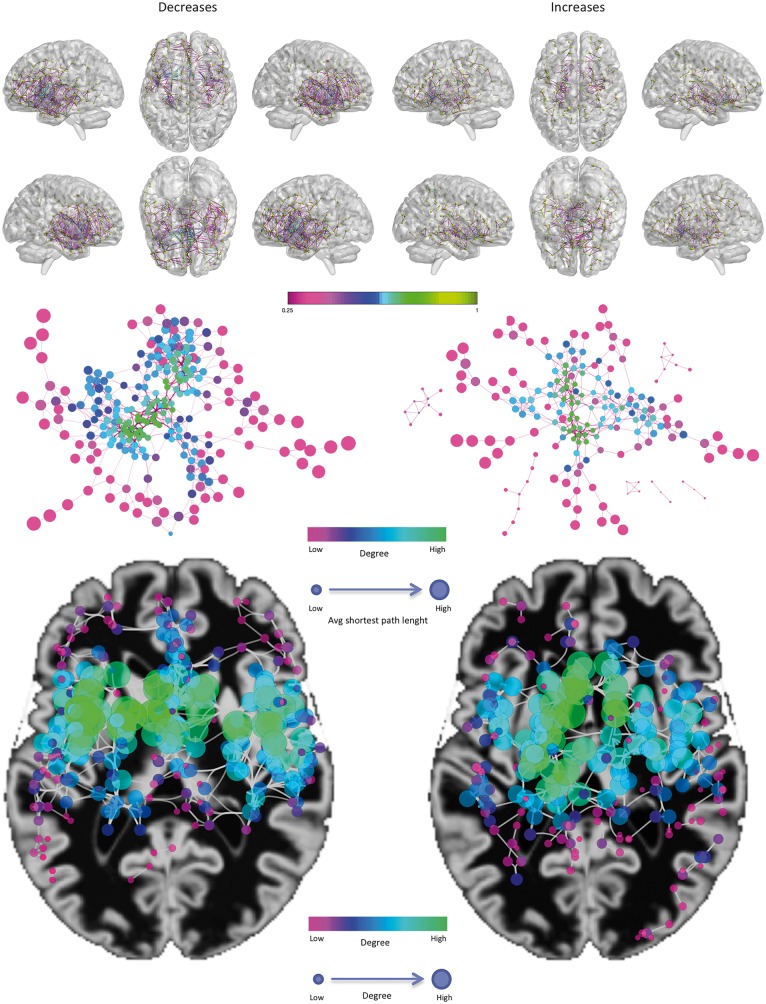
Given the nodes previously designed, we constructed the structural co-alteration networks for both the VBM datasets (decreases and increases). These networks are visualized in Fig. 3.
Figure 3.
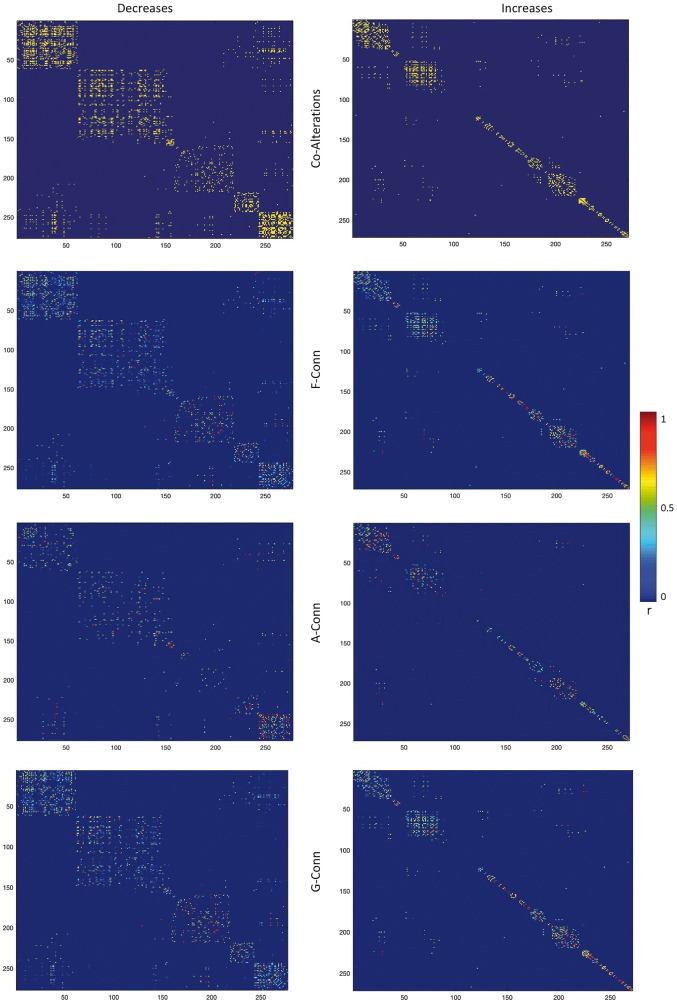
Co-alteration networks. Top: The decrease-related (left) and increase-related (right) structural co-alterations. Only for visualization purposes, the matrices were thresholded at the 95th percentile. Colours ranging from magenta to green represent lower to higher correlation values. Middle: Topological analysis of the structural co-alteration network, using a force directed spring embedded layout. Smaller nodes show lower average shortest path length. Colour tones from magenta to green indicate lower to greater degree values. Bottom: A geotagged layout of the networks. Node dimension and colour tones from green to red indicate lower to greater degree values.
Interestingly, the two structural co-alteration networks are topologically different (Fig. 3, middle and bottom). The one formed by decreased areas is more restricted and principally involves the insulae and the anterior cingulate cortices. These regions exhibit the nodes with the highest values of degree. In turn, the other network formed by increased areas is more widespread and less anatomically defined, albeit it includes parts of the insulae and is slightly prevalent in subcortical regions.
Anatomical, functional and genetic connectivity
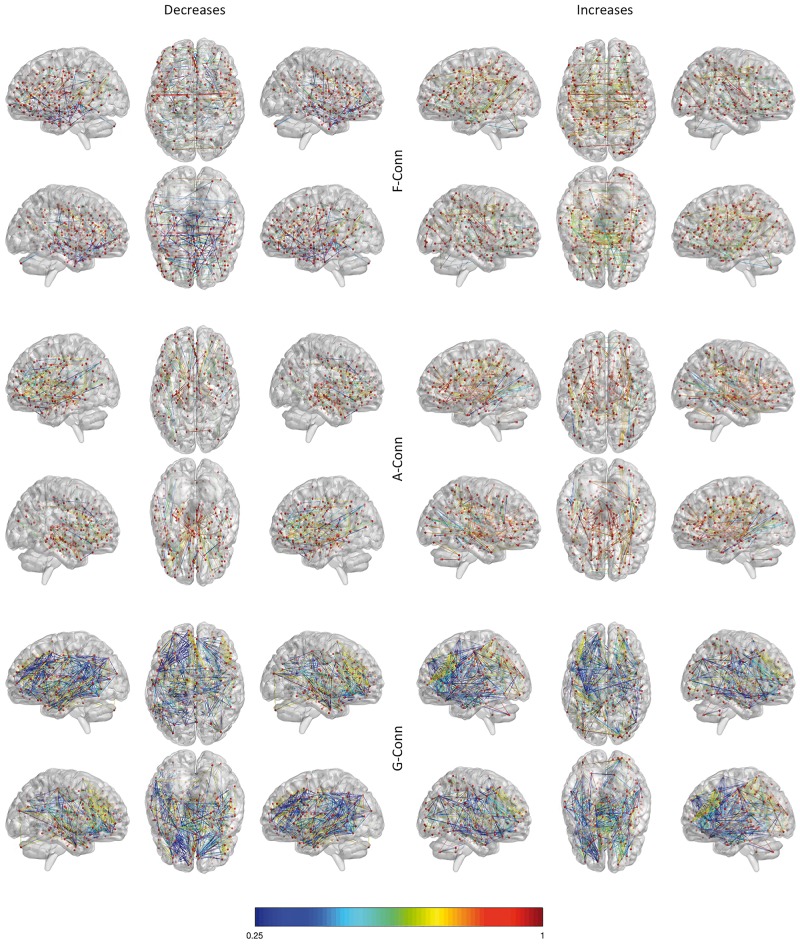
For the same sets of nodes, we calculated the resting state functional, anatomical and genetic networks. These networks are visualized in Figs 4 and 5. In line with the previous literature (Gong et al., 2014; Huang and Ding, 2016), functional and anatomical connectivity appear to be correlated (decreased nodes r = 0.14, P < 2.383 × 10−5; increased nodes r = 0.12, P < 2.421 × 10−5). Notably, the genetic connectivity also appears to correlate with both anatomical (decreased nodes r = 0.21, P < 2.195 × 10−5; increased nodes r = 0.18, P < 3.028 × 10−5) and functional connectivity (decreased nodes r = 0.18, P < 3.021 × 10−5; increased nodes r = 0.14, P < 2.359 × 10−5).
Figure 4.
Connectivity networks. The functional connectivity (F-Conn) network (top), the anatomical connectivity (A-Conn) network (middle), and the genetic connectivity (G-Conn) network or genetic co-expression network (bottom). Only for visualization purposes the matrices were thresholded at the 95th percentile. Colours ranging from blue to red represent lower to higher correlation values. For anatomical connectivity, colour ranging from blue to red represent lower to higher fibre density values.
Figure 5.
Distance matrices regarding the structural co-alteration, functional, anatomical and genetic connectivity. Colours ranging from blue to red represent lower to higher correlation values.
Reliability
Our connectivity matrices present a good reliability (Spearman-Brown split half test). Indeed, we have obtained mean values of 0.80, 0.72, 0.80, and 0.75 for the structural co-alteration, the functional, the gene co-expression and the anatomical connectivity matrices, respectively. These values indicate a good internal consistency of measures. In particular, the Spearman-Brown formula is related to the Cronbach’s alpha (Nunnally and Bernstein, 1994; Carlson et al., 2009); both formulas measure the ratio of the true-score and total-score variances. As suggested by Nunnally and Bernstein (1994), the rule of thumb for that measure usually considers a good internal consistency of data with values of >0.7.
Correlational analyses
As our experimental question is to investigate whether and how neuropathological co-alterations (independently related to both grey matter decreases and grey matter increases) are influenced by different types of normal brain connectivity (i.e. functional, anatomical, and genetic connectivity), we compared neuropathological co-alteration patterns with normal patterns of brain connectivity as they are measured in healthy individuals.
The statistical comparison between the structural co-alteration matrix and the other matrices (functional, anatomical, and genetic) shows that each of the three connectivity profiles is statistically correlated with the structural co-alteration patterns associated with grey matter decreases and grey matter increases, that is, each type of connectivity explains a statistically significant portion of those patterns.
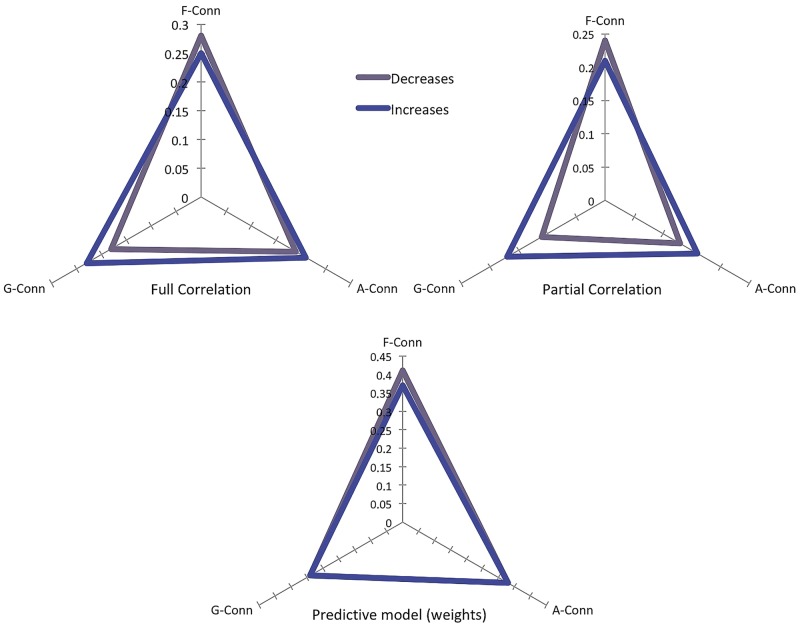
Figure 6 (top left) illustrates the correlation between the structural co-alteration matrix and the other three connectivity matrices. While the decrease-related structural co-alteration is better explained by functional connectivity (r = 0.28), followed by anatomical and genetic connectivity (r = 0.19 and r = 0.18, respectively), the increase-related structural co-alteration is better explained by functional connectivity (r = 0.26), followed by genetic and anatomical connectivity (r = 0.23 and r = 0.22, respectively).
Figure 6.
Results of the correlational and predictive tests. The top panel shows the correlational results (the left panel illustrates the full correlation, while the right panel illustrates the partial correlation). The bottom panel shows the predictive results.
However, as these three types of connectivity are known to be correlated with each other and exhibit a shared variance, as we previously mentioned, we decided to calculate the partial correlation between the three connectivity matrices and the structural co-alteration matrix with the aim to report how each type of connectivity correlates with the structural co-alteration pattern with the exclusion of their common shared variance. This analysis is described in Fig. 6 (top right), and provides further evidence that the decrease-related structural co-alteration correlates more with functional connectivity (r = 0.24), followed by anatomical (r = 0.14) and genetic (r = 0.11) connectivity. In turn, the increase-related structural co-alteration appears to correlate in a similar way with the three types of connectivity; it is slightly better explained by functional connectivity (r = 0.22), followed by genetic and anatomical connectivity (r = 0.17 and r = 0.16, respectively). Of note, all the partial and full correlation results are statistically significant: P-values < 2 × 10−7 for the partial correlation results, and P-values < 3 × 10−4 for the full correlation results. Overall, this indicates that structural co-alterations are in part explained by all these three types of connectivity.
Spatial and temporal progressions
Our model is able to predict the propagation patterns of neuronal alterations with good statistical confidence (all predictions survive the conservative statistic threshold of P < 10−5).
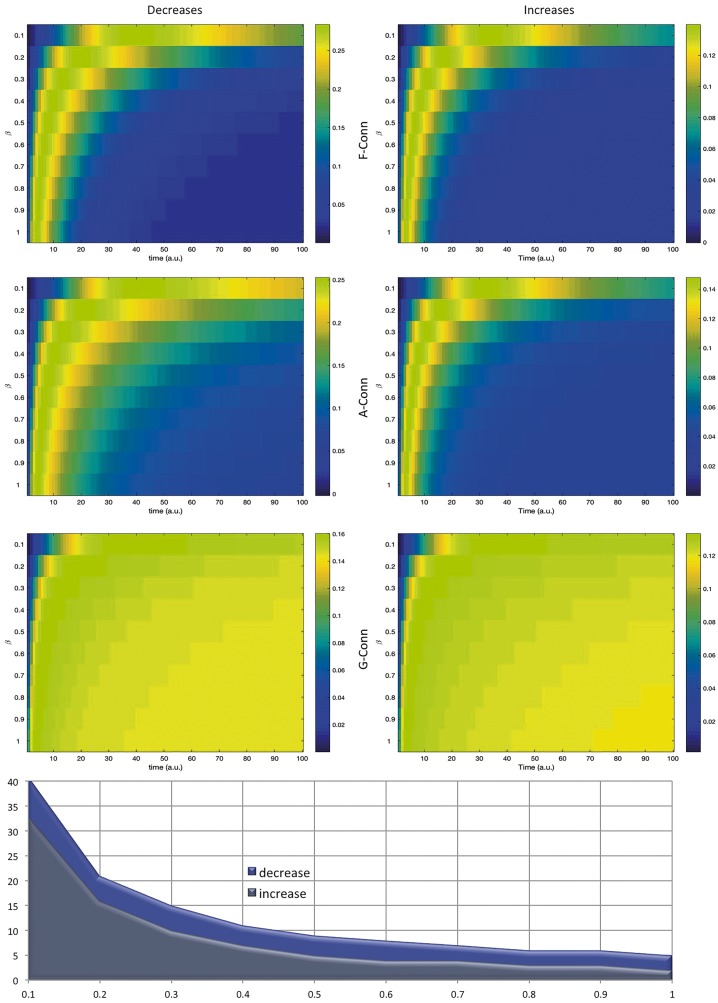
Figure 7 illustrates the temporal evolution of the structural co-alteration patterns (expressed in arbitrary units) as it is predicted by every β-value, used in the grid search, of the model. For each β-value we calculated the temporal evolution of the diffusion process and for each time we correlated the diffusion matrix derived from the distribution model of co-alterations and the co-alteration matrix obtained from the meta-analysis. What is clear is that around 30 temporal steps, all the connectivity models predict the complete diffusion of brain alterations. However, within the initial steps, only the genetic model can substantially show a prediction of how structural co-alterations are expected to develop. This result provides evidence that with the help of genetic connectivity, it is possible to predict a substantial portion of the pattern formed by neuropathological alterations in a variety of brain disorders just based on its initial manifestation. The chart in Fig. 7 illustrates how the average temporal evolution of structural co-alterations, calculated by the model based on grey matter increases, is characterized by a faster development compared with that calculated by the model based on grey matter decreases.
Figure 7.
Model's temporal evolution. Top: This series of maps shows the correlations of the functional, anatomical and genetic matrices with the structural co-alteration matrix for different beta values as a function of time (arbitrary units), as described in Equation 12. Colours ranging from blue to red represent lower to higher correlation values. Bottom: The chart summarizes the time in which the diffusion of brain alterations reaches the steady state as a function of the beta rate for the decrease and increase conditions. Note that the average temporal evolution of structural co-alterations calculated by the model based on grey matter increases is characterized by a faster development compared with that calculated by the model based on grey matter decreases.
The model of the distribution of the structural co-alteration patterns (D = αMF–Conn + βMA–Conn + γMG–Conn) shows that it is possible to describe the meta-analytic structural co-alteration matrix as a weighted sum of the functional, anatomical and genetic connectivity matrices. After the optimization procedure for the three parameters, we correlated the D matrix of the model with the co-alteration matrix obtained from the meta-analytical data and found a variance explained for the grey matter decreases of R2 = 0.77 (P < 0.0012) and for the grey matter increases of R2 = 0.72 (P < 0.0025). Furthermore, all the three matrices appear to contribute significantly to the description of the meta-analytic structural co-alteration matrix (Table 1 and Fig. 6, bottom). It is worth noting that, in our model, with regard to both grey matter decreases and increases the major contribution is made by the functional connectivity matrix, followed by anatomic and genetic connectivity.
Table 1.
Parametric values of correlation between the three connectivity matrices and the meta-analytic structural co-alteration matrix constructed with either grey matter increase or decrease data
| F-Conn R2 | A-Conn R2 | G-Conn R2 | Total R2 | |
|---|---|---|---|---|
| Decrease | 0.41 | 0.34 | 0.25 | 0.77 |
| Increase | 0.38 | 0.33 | 0.29 | 0.72 |
The total R2 value is the result of the correlation between the diffusion matrix obtained from the model and the co-alteration matrix obtained from the meta-analytic data. In this way we calculated the contribution of each connectivity profile to the variance explained, determining the R2 of each network profile with the diffusion matrix obtained from the model.
A-Conn = anatomical connectivity matrix; F-Conn = functional connectivity matrix; G-Conn = genetic connectivity matrix.
Discussion
The analyses carried out in this study provide support for the following points: (i) brain areas affected by neuropathological processes form typical patterns of structural co-alterations; (ii) the development of these transdiagnostic structural co-alterations is not random but preferentially follows the routes of brain connectivity; (iii) anatomical, functional and genetic connectivity are differently involved in shaping structural co-alterations; and (iv) starting from the brain connectivity matrices, it is possible to create a model that allows us to predict with relatively high accuracy the development of the structural co-alteration patterns and, based on this model, to estimate the evolution of how structural co-alterations are distributed across the brain in terms of the involvement of the type of brain connectivity. To the best of our knowledge, this is the first time that these issues have been addressed in humans using in vivo approaches.
Our results provide evidence that brain morphological alterations are distributed according to a statistically significant pattern: alterations are distributed across brain areas so as to form a network of pathological nodes. This pattern of structural co-alteration exhibits a topological definite structure and includes some regions (the insular and anterior cingulate cortices) that are thought to be important functional hubs of the brain.
We performed a predictive analysis of the structural co-alteration patterns by creating a model that, based on brain connectivity matrices, attempts to estimate the development of the co-alteration patterns; this model was able to explain the 77% and the 72% of the variance in the decrease and increase structural co-alteration patterns, respectively. This finding supports the idea that the two structural co-alteration patterns, as well as their temporal development (Cauda et al., 2018), are strictly associated with the brain connectivity patterns. Specifically, our model shows that, based on functional and anatomical connectivity, more consecutive steps are needed to completely predict the propagation of structural co-alterations. On the other hand, this is not the case for a model based on genetic connectivity, which is able to predict the propagation of structural co-alterations just at its early stages.
Our analysis proposes to take into consideration the contribution of three (i.e. transneuronal spread, nodal stress, and shared vulnerability) of the four possible mechanisms so far hypothesized for the spread of brain alterations (Saxena and Caroni, 2011; Zhou et al., 2012; Fornito et al., 2015), each of which with its typical temporal evolution. Future studies will be able to apply our model in order to better understand which mechanisms are more specifically involved in particular brain disorders.
With regard to both grey matter decreases and increases, the functional connectivity appears to be the best predictor of the pattern of structural co-alterations. Although a certain type of connectivity seems to play a prevalent role in both grey matter decreases and increases, it is worth noting that the other types of connectivity are also important factors in the generation of structural co-alterations; their contribution, however, is characterized by different timings. This result is consistent with the fact that we worked on a cross-diagnostic dataset (Goodkind et al., 2015), which includes a wide range of brain disorders. As recently demonstrated by Cope et al. (2018), certain brain disorders can be characterized by the prevalence of specific mechanisms.
The distribution of brain alterations
Our analysis of the VBM studies about a great variety of brain disorders, especially regarding grey matter decreases, shows that a core set of cerebral areas appears to be frequently altered in a large number of neuropathological conditions (for a review of this transdiagnostic approach see Buckholtz and Meyer-Lindenberg, 2012; McTeague et al., 2016). This finding confirms a similar result obtained by other meta-analyses, which, however, were only restricted to three (Cauda et al., 2017) or six psychiatric diseases (Goodkind et al., 2015).
The recurrence of this common alteration pattern is well illustrated by the ALE analysis (Fig. 2). Interestingly, this peculiar pattern overlaps to a great extent with those areas that have been proposed to be part of the cognitive control network (Cauda et al., 2012b, 2017; McTeague et al., 2016). It must be highlighted that the finding of a common alteration pattern in a vast number of brain diseases does not rule out the possibility that each disorder may be characterized by its own typical alterations (Crossley et al., 2015). However, here our aim was to investigate how alterations are generally spread across the pathological brain so as to achieve an overarching analysis supported by the most numerous sample of studies we could retrieve. Future studies will be needed to understand how the structural co-alteration patterns found in this meta-analysis differ with regard to each brain disorder independently considered.
A number of studies (Pearson et al., 1985; Saper et al., 1987; Braak and Braak, 1991; Brooks, 1991; Weintraub and Mesulam, 1996; Braak et al., 2011; Raj et al., 2012; Cauda et al., 2014; Iturria-Medina et al., 2014; Ravits, 2014; Fornito et al., 2015; Iturria-Medina and Evans, 2015) have proposed that the spread of neuronal alterations caused by neuropathological processes is not random but, rather, associated with typical network-like patterns. These data were already supported (Seeley et al., 2006, 2009; Zhou et al., 2012) and now receive further support from our study: brain alterations are distributed according to a statistically significant ‘neurodegenerative networking’ (Yates, 2012) or, as we have called it, ‘morphometric co-alteration network’ (Cauda et al., 2018); this broader term has the advantage to refer to all types of disorders capable of producing neuronal alterations, without committing to just the neurodegenerative factors, which consists of cerebral regions with pathologically grey matter increases or decreases.
Grey matter decreased areas are largely parts of the cognitive control network (Goodkind et al., 2015; McTeague et al., 2016) and include the insulae, anterior cingulate cortices, superior and middle temporal gyri, superior, middle and inferior frontal, pre- and postcentral gyri. In turn, grey matter increased areas include the right anterior and posterior insula, left middle insula, right pre- and postcentral gyri, right superior frontal gyrus, right superior temporal gyrus, left inferior temporal and inferior frontal gyri. The minor involvement of the precuneus in the co-alterations patterns may be viewed as counter-intuitive, given that this area is highly connected and is a central hub of the default mode network. Probably, because of the transdiagnostic approach of this study, similarities between brain disorders are likely to be highlighted and, though in some diseases the precuneus appears to be altered, the frequency of this alteration is not sufficient for being statistically relevant. Moreover, it must be considered that a high number of alterations in a certain brain area does not necessarily imply for this area to be co-altered with other ones. With regard to this point, a recent study by our group (Manuello et al., 2018) has investigated the co-alterations of Alzheimer’s disease and found out only a significant node of strong co-alterations within the precuneus. Even in the case of Alzheimer’s disease, therefore, the precuneus level of co-alteration appeared to be less significant than theoretically thought.
The structural co-alteration pattern differs significantly for decreased and increased VBM values. With regard to grey matter decreases, it appears to be more concentrated in insular, cingulate and prefrontal cortices (areas of the cognitive control/salience network) (Seeley et al., 2007; Cauda et al., 2011, 2012a, 2013), whereas with regard to grey matter increases it appears to be slightly more uniformly distributed, albeit with a little prevalence in subcortical regions (Fig. 3). This differentiation is likely to be because of the different factors at the root of the development of grey matter increases and decreases in brain density. In fact, grey matter decreased areas are generally associated with neurodegenerative processes, while grey matter increased areas are generally associated with compensatory mechanisms (Lin et al., 2013; Premi et al., 2014, 2016), which are supposed to occur at the initial phases of brain deterioration. This interpretation is consistent with the temporal evolution shown by our predictive model, according to which patterns of grey matter increased values present a faster temporal development than patterns of grey matter decreased values (Fig. 7, bottom).
From the viewpoint of the topological analysis, when altered, the brain areas showing a higher node degree and/or less average shortest path length are likely to play a central role in the spread of neuronal alterations. Their greater number of connections as well as their more intense activity may enhance the mechanisms hypothesized to be the causes of alterations, especially the nodal stress and the transneuronal spread mechanisms. As suggested by our predictive model, these two mechanisms are supposed to be more involved in the formation of the structural co-alterations (both increase-related and decrease-related), which seems to be more influenced by both functional and anatomical connectivity. However, as the hypothesized causal mechanisms are not mutually exclusive, they are all likely involved in the formation of structural co-alterations, each with distinctive temporal patterns.
The relationship between the spread of neuronal alterations and brain connectivity
All three types of connectivity taken into consideration in this meta-analysis (functional, anatomical, and genetic) account well for a substantial part of the variance of the development of structural co-alterations (see Supplementary Fig. 2 for an infographic).
In particular, functional connectivity is able to explain a greater part of the structural co-alteration patterns than the other matrices, followed by anatomic and genetic connectivity. This result has also been achieved by determining the partial correlation between the structural co-alteration matrix and each connectivity matrix excluding the contribution of the other connectivity matrices. This procedure was required because both functional and anatomical connectivity profiles are known to be partially correlated (Skudlarski et al., 2008; Honey et al., 2009; van den Heuvel et al., 2009; Misic et al., 2016) and because both these connectivity profiles have also been found to be associated with patterns of genetic co-expressions (Lichtman and Sanes, 2008; French and Pavlidis, 2011; French et al., 2011; Wolf et al., 2011; Cioli et al., 2014; Goel et al., 2014; Richiardi et al., 2015).
It is worth noting that the temporal evolution of the alterations’ spread predicted by our model, based on the functional and anatomical connectivity profiles, needs numerous steps (between 30 and 40, arbitrary units) before reaching completion. On the contrary, the prediction based on the genetic connectivity profile requires a shorter time: between 10 and 20 units. This interesting finding is consistent with the shared vulnerability hypothesis, according to which the spread of alterations caused by dysfunction in the co-expression of certain genes is supposed to need a shorter accretion time than when the other mechanisms are involved. Already at the early phases of neuropathological processes, many brain areas with similar genetic patterns can be altered. What is more, the genetic risk for brain disorders is pleiotropic and, thereby, can affect broad and transdiagnostic dimensions (Buckholtz and Meyer-Lindenberg, 2012) of symptomatically-related diseases (Gejman et al., 2011), thus disrupting brain connectivity patterns of core networks associated with fundamental cognitive functions (Cauda et al., 2012b). Our predictive model could therefore suggest that a chain of pathological factors is likely involved in a variety of neuropathological processes represented or better explained by different kinds of brain connectivity profiles (Supplementary Fig. 2). In other words, pathological patterns of gene co-expressions may lead to a neuronal shared vulnerability, which, in turn, may engender the alteration of important brain networks, with the subsequent involvement of abnormal functional and anatomical connectivity patterns. As highlighted by Buckholtz and Meyer-Lindenberg (2012), ‘genetic factors shape connectivity in networks linked to symptom domains, and imply that connectivity changes observed in mental disorders reflect a cause, rather than a consequence, of being ill’. The same authors remark that ‘the latent structure of psychopathology may reflect, in part, a genetically determined latent structure of brain connectivity’.
The result achieved by our predictive model—i.e. that functional and anatomical connectivity seem to better account for the development of structural co-alterations in a longer run than the genetic one—is consistent with the fact that the nodal stress and the transneuronal spread mechanisms need time to make their effects. The nodal stress implies a progressive intensification of excitotoxicity factors, whereas the transneuronal spread implies the transport of pathological substances through axons or the extracellular liquid. All these processes need time to exert disruption and this point is well illustrated by the temporal evolution of the structural co-alteration patterns (Fig. 7).
It is worth suggesting that the three mechanisms taken into consideration in the present work (transneuronal spread, nodal stress and shared vulnerability) may play a synergistic role not only in the pathogenesis of neurodegenerative diseases but also, to some extent, in psychiatric as well as in neurodevelopmental disorders. Although these conditions are not directly related to the presence of a defined brain proteinopathy, structural and functional alterations are not randomly distributed across the brain, following specific connectivity constraints that produce identifiable morphometric co-atrophy patterns, as already shown by our group in neurodevelopmental (autistic spectrum disorder) and psychiatric (schizophrenia spectrum disorder and obsessive-compulsive spectrum disorder) conditions (Cauda et al., 2018). Furthermore, from a speculative perspective, it has been proposed that it would be more appropriate to view schizophrenia as a failure of communication between critical nodes of large neuronal networks rather than a dysfunction of separate areas, thus suggesting the expression of ‘spatiotemporal psychopathology’ to describe this condition (Kasparek et al., 2010; Northoff and Duncan, 2016). In this sense, different pathogenic mechanisms (i.e. pathogenic proteins propagating preferentially based on intrinsic network vulnerabilities—molecular nexopathies—for neurodegenerative diseases, and genetic/environmental interactions for both psychiatric and autistic spectrum disorders) may be at play. Overall, these pathological mechanisms can ‘stress’ the brain networks and ‘shape’ the grey matter alterations in a network-based fashion, as described by the present work and others already cited. As defined for neurodegenerative proteinopathies (Warren et al., 2013), in other disorders (like psychiatric and autistic) the pathological and complex interaction between neurodevelopmental alterations and environmental/genetic modulators might trigger brain dysfunction (both functional and structural), even without a detectable proteinopathy (as in neurodegenerative diseases) but with a similar impact on brain connectivity and functioning, thus accounting for the good degree of concordance of the present findings.
Thus, given that the transneuronal spread mechanisms (Zhou et al., 2012; Fornito et al., 2015) implies a form of propagation along structural (axonal) pathways, that the nodal stress mechanism implies a form of common activity between altered brain areas, and that the shared vulnerability mechanism implies common gene expressions between cerebral regions, it is possible to advance the hypothesis that, based on our analysis, the decrease-related and increase-related structural co-alterations might be more shaped, in order, by nodal stress, transneuronal spread, and shared vulnerability mechanisms. Especially taking into consideration the transdiagnostic nature of our data, this finding suggests that the prevalence of a particular type of connectivity in the production and development of structural co-alterations leaves open the possibility that the other two types of connectivity could play a significant role as well. Indeed, this phenomenon may also be due to the fact that the data retrieved from BrainMap are about a great variety of brain disorders, which are likely to be originated by different combinations of the hypothesized factors underlying the formation of structural co-alterations.
Brain connectivity can predict the distribution of alterations
Taken together in a conjoint model, the three connectivity matrices are able to account for the development of structural co-alterations with good accuracy. This is a remarkable finding for the comprehension of how the pathological brain responds to diseases, as it allows one to predict the evolution of grey matter alterations from changes of the neurobiological substrate. Our result provides further support for the important role played by brain connectivity in the neuropathological processes and sheds new light on its involvement in their development and progression (Iturria-Medina and Evans, 2015). With the help of analyses based on brain connectivity profiles, we could achieve an in-depth understanding of the mechanisms at the root of brain disorders. Some suggestions along this line of research have already been proposed. For instance, in patients with Alzheimer’s disease, functional alterations and grey matter decreases within different brain areas reflect covariance patterns of part of the default mode network, thus indicating that these atrophic regions are not independently affected; rather, the primary deterioration in one of these areas might lead to a secondary deterioration in other connected areas (Wang et al., 2013, 2015). The cognitive decline would progress via sequential increases in connectivity, bringing about a functional overload. For example, in the case of Alzheimer’s disease increased connectivity in frontal areas (especially those associated with the salience network) seems to have a compensatory role, representing the other side of the coin. Interestingly, this pattern of complex functional alterations appears to largely mirror the one that can be highlighted in frontotemporal dementia, which involves primarily frontal regions and the salience network (Zhou et al., 2010).
Two important points need to be clarified. First, although brain connectivity profiles seem to guide the development of structural co-alterations, this does not imply that each brain disorder is expected to produce similar structural co-alterations, for as regards to each brain disorder, as well as to the particular patients involved, different network nodes can be altered. Moreover, given a final set of altered nodes, the foci from which alterations began to spread might have been different and, as a result, different temporal progressions might have occurred.
The second point is a methodological caveat and concerns the relationship between our co-alteration network analysis and the anatomical covariance (Mechelli et al., 2005). Anatomical covariations are defined as ‘the covariance of morphological metrics derived from morphological MRI’ (Evans, 2013). Apparently, then, the morphological co-alterations studied here may be thought of as a type of anatomical covariance. However, anatomical covariance is always derived from single-subject data, whereas our meta-analytic approach works on data originated from a statistical comparison between pathological and healthy subjects. Therefore, from the methodological point of view, the two approaches, albeit similar, are different and should not be confused (for a more detailed discussion about this similarity see Cauda et al., 2018).
Limitations and future directions
The pathological structural co-alterations have been studied with a method that uses meta-analytic data, which, compared to their original quality, are known to be affected, to some extent, by deterioration. This loss of quality increases the degree of spatial uncertainty and, therefore, can influence the detection of alterations by reducing the likelihood of statistical co-occurrences between the nodes. Therefore, future investigations with native data, possibly obtained from the same group of individuals, are needed.
VBM studies are at the basis of the methodology proposed here. Although being a widely used and well-validated technique, there are a number of procedural aspects that could influence the results of every single VBM experiment (e.g. field strength of the scanner, software used for the analysis, smoothing amount). However, since different combinations of these parameters had been used in the experiments considered for our research, it is unlikely that some of them can affect the results in a systematic way. Moreover, it has been recently suggested that possible false positive findings in VBM tend to be distributed randomly across the brain rather than accumulate in specific sites (Scarpazza et al., 2015); this aspect should prevent the spurious inclusion of nodes of alteration in the detected co-alteration networks. However, it is not possible to completely rule out this kind of inclusion.
To address the issue of heterogeneity due to studies with low sample sizes we decided to establish a lower bound of eight subjects for sample size and, consequently, all the retrieved experiments with a sample size smaller than eight subjects were excluded. As already mentioned, the identification of this lower bound is in line with the work of Scarpazza et al. (2015), which found that the use of balanced small samples in the VBM studies does not influence the false positive rate, even when considering only eight subjects. Thus, this suggests that our results should not be biased by the presence in our database of heterogeneous sample sizes. Moreover, since our methodology reveals the co-occurrences between alterations across the studies, experiments on small samples reporting different results from the others tend to bring about a sort of ‘random noise’ that is likely to increase the false negatives rather than the false positives (Acar et al., 2017). This consideration should lead us to think that, even though we cannot completely rule out the bias potentially caused by the inclusion of studies with a limited sample size, it is much more likely that we missed to detect real co-alterations rather than we identified false ones. However, to address this issue properly, future investigations on these data are needed as soon as larger and more controlled samples are available in the literature.
The ALE approach is one of the most used methods in the field of coordinate-based meta-analysis. One of the main concerns with this methodology is the possibility of the results to be driven by one, or a few, experiments, thus reflecting a specific case among the ones pooled for the meta-analysis rather that an overall representative effect. However, a minimum amount of 20 experiments is usually thought to be sufficient to resolve this issue (Eickhoff et al., 2016), so that analyses based on large databases, as the one used here, should not be so much biased as to produce invalid results.
The genetic matrix, too, is characterized by spatial uncertainty and other idiosyncrasies. First, the sample used for this analysis is made of six human brains only. So, the results obtained with this analysis can hardly be generalized to the whole population. Second, not all of the six brains were sampled completely. Third, the samples are not evenly spaced but have different stereotactic coordinates in each of the six brains. Although our methodology has tried to address these issues, especially the inhomogeneity of the samples, the results of the genetic analysis are to be interpreted cautiously and need to be supported by further evidence. However, to date the complex procedure and costs of the acquisition of gene expressions data do not allow better precision.
Spatial and temporal errors, related to specific aspects of the functional MRI and DTI procedures, may affect both functional and anatomical connectivity patterns. Still, it is worth noting that, with regard to correlation and prediction results, such errors are supposed to increase more the number of false negatives than the number of false positives, thus reducing the correlation values between matrices. Therefore, given the good statistical significance achieved by our model, we are inclined to think that the results are not caused by spatial or temporal errors but describe real phenomena. To support our findings further, the reliability values of the connectivity matrices are very good; this leads us to believe that the difficulties inherent in the neuroimaging procedures are not likely to undermine the conclusions reached in this study. However, we hope that future studies will be carried out with different statistical techniques and on wider and better samples so as to find out whether or not our results can be further supported.
Finally, this study focused on mixed data, coming transdiagnostically from a variety of brain disorders as well as from heterogeneous patients investigated in different time courses of their symptomatology. The aim was (i) to provide a proof of concept of our method; and (ii) to get the broadest retrievable sample to achieve a good statistical significance for the detection of structural co-alterations. We therefore obtained mean alteration patterns, which are not specifically related to one or another brain disorder, so as to study globally how neuronal alterations are distributed across the brain. Future investigations are needed to look into more specific patterns of structural co-alterations with regard to specific diseases. In particular, it would be interesting to calculate the co-alteration patterns starting from native single subject data stored in publicly available MRI datasets (e.g. ADNI) and to compare the results of this analysis with longitudinal data. It is also of primary importance to understand how each connectivity profile (functional, anatomical, and genetic) contributes in shaping the structural co-alterations of different brain disorders. An intriguing topic in this line of research could be the study of how structural co-alterations differ in patients’ population with fast or slow cognitive deterioration. Furthermore, it would be of great interest to understand which gene co-expressions play a major role in the developments of structural co-alterations associated with different brain disorders.
Conclusion
This study has investigated fundamental issues about how the brain is affected by pathological processes that were still unresolved in humans. Our research investigated which one among three types of connectivity profiles (functional, anatomical, and genetic) could shape and explain better the distribution of structural co-alterations. Intriguingly, our prediction model suggests that in our transdiagnostic sample, all three types of connectivity are involved and can statistically account for a very good portion of the pattern variance of structural co-alterations for both grey matter increases and grey matter decreases (72% and 77%, respectively) (Table 1). In addition, it shows that the three patterns of brain connectivity need different timings to play their role in the development of the co-alteration networks.
These results shed new light on the possible mechanisms at the root of neuropathological processes. Our analysis points out that three (i.e. nodal stress, shared vulnerability, and transneuronal spread) of the four mechanisms put forward so far (Saxena and Caroni, 2011; Zhou et al., 2012; Fornito et al., 2015) are likely to play a role with different temporal progressions in the formation and development of structural co-alterations. In particular, we found that functional connectivity offers the better account of the structural co-alteration patterns, followed by anatomic and genetic connectivity. Although one type of connectivity can be prevalent in the co-alteration patterns, it must be noted that all these three types are significantly involved in the progression of brain alterations. This is consistent with the cross-diagnostic nature of data used in this study (Goodkind et al., 2015).
Overall, the three different types of brain connectivity can account extremely well for the distribution and evolution of structural co-alterations across the human brain. This finding presents an exciting prospect for future research in the quest for a better understanding of brain disorders.
Supplementary Material
Acknowledgement
We thank Barbara Borroni for her valuable support and suggestions.
Glossary
Abbreviations
- ALE
anatomical likelihood estimation
- VBM
voxel-based morphometry
Funding
This study was supported by the Fondazione Carlo Molo (F.C., PI), Turin; NIH/NIMH grant MH074457 (P.T.F., PI) and CDMRP grant W81XWH-14-1-0316 (PT.F., PI).
Competing interests
The authors report no competing interests.
References
- Abdelnour F,, Voss HU,, Raj A. Network diffusion accurately models the relationship between structural and functional brain connectivity networks. Neuroimage 2014; 90: 335–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Acar F,, Seurinck R,, Eickhoff SB,, Moerkerke B. Assessing robustness against potential publication bias in coordinate based fMRI meta-analyses using the Fail-Safe N bioRxiv 2017, 189001. doi: 10.1101/189001. [Google Scholar]
- Aguzzi A,, Heikenwalder M,, Polymenidou M. Insights into prion strains and neurotoxicity. Nat Rev Mol Cell Biol 2007; 8: 552–61. [DOI] [PubMed] [Google Scholar]
- ALLEN Human Brain Atlas Technical white paper: microarray data normalization, v.1.Seattle, WA: Allen Institute; 2013. [Google Scholar]
- Allen MJ,, Yen WM. Introduction to measurement theory Long Grove, IL: Waveland Press; 2001. [Google Scholar]
- Baker JT,, Holmes AJ,, Masters GA,, Yeo BT,, Krienen F,, Buckner RL,, et al. Disruption of cortical association networks in schizophrenia and psychotic bipolar disorder. JAMA Psychiatry 2014; 71: 109–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckmann CF,, Mackay CE,, Filippini N,, Smith SM. Group comparison of resting-state FMRI data using multi-subject ICA and dual regression. Neuroimage 2009; S39–41. [Google Scholar]
- Biswal BB. Resting state functional connectivity In: Biological psychiatry New York, NY: Elsevier Science Inc; 2011. p. 200S. [Google Scholar]
- Biswal BB. Resting state fMRI: a personal history. Neuroimage 2012; 62: 938–44. [DOI] [PubMed] [Google Scholar]
- Bourdenx M,, Koulakiotis NS,, Sanoudou D,, Bezard E,, Dehay B,, Tsarbopoulos A. Protein aggregation and neurodegeneration in prototypical neurodegenerative diseases: examples of amyloidopathies, tauopathies and synucleinopathies. Prog Neurobiol 2017; 155: 171–93. [DOI] [PubMed] [Google Scholar]
- Braak H,, Braak E. Neuropathological stageing of Alzheimer-related changes. Acta Neuropathol 1991; 82: 239–59. [DOI] [PubMed] [Google Scholar]
- Braak H,, Thal DR,, Ghebremedhin E,, Del Tredici K. Stages of the pathologic process in Alzheimer disease: age categories from 1 to 100 years. J Neuropathol Exp Neurol 2011; 70: 960–9. [DOI] [PubMed] [Google Scholar]
- Brooks B. The role of axonal transport in neurodegenerative disease spread: a meta-analysis of experimental and clinical poliomyelitis compares with amyotrophic lateral sclerosis. Can J Neurol Sci 1991; 18 (3 Suppl): 435–8. [DOI] [PubMed] [Google Scholar]
- Buckholtz JW,, Meyer-Lindenberg A. Psychopathology and the human connectome: toward a transdiagnostic model of risk for mental illness. Neuron 2012; 74: 990–1004. [DOI] [PubMed] [Google Scholar]
- Buckner RL,, Krienen FM,, Yeo BT. Opportunities and limitations of intrinsic functional connectivity MRI. Nat Neurosci 2013; 16: 832–7. [DOI] [PubMed] [Google Scholar]
- Buckner RL,, Snyder AZ,, Shannon BJ,, LaRossa G,, Sachs R,, Fotenos AF,, et al. Molecular, structural, and functional characterization of Alzheimer’s disease: evidence for a relationship between default activity, amyloid, and memory. J Neurosci 2005; 25: 7709–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlson N,, Buskist W,, Heth CD,, Schmaltz R. Psychology: the science of behaviour. 4th Canadian edn. Toronto: Pearson Education Canada; 2009. [Google Scholar]
- Cauda F,, Costa T,, Fava L,, Palermo S,, Bianco F,, Duca S,, et al. Predictability of autism, schizophrenic and obsessive spectra diagnosis. toward a damage network approach bioRxiv 2015, 014563. doi: 10.1101/014563. [Google Scholar]
- Cauda F,, Costa T,, Nani A,, Fava L,, Palermo S,, Bianco F,, et al. Are schizophrenia, autistic, and obsessive spectrum disorders dissociable on the basis of neuroimaging morphological findings?. A voxel-based meta-analysis. Autism Res2017: 10: 1079–95. [DOI] [PubMed] [Google Scholar]
- Cauda F,, Costa T,, Palermo S,, D’Agata F,, Diano M,, Bianco F,, et al. Concordance of white matter and gray matter abnormalities in autism spectrum disorders: a voxel-based meta-analysis study. Hum Brain Mapp 2014; 35: 2073–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cauda F,, Costa T,, Torta DM,, Sacco K,, D’Agata F,, Duca S,, et al. Meta-analytic clustering of the insular cortex: characterizing the meta-analytic connectivity of the insula when involved in active tasks. Neuroimage 2012a; 62: 343–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cauda F,, D’Agata F,, Sacco K,, Duca S,, Geminiani G,, Vercelli A. Functional connectivity of the insula in the resting brain. Neuroimage 2011; 55: 8–23. [DOI] [PubMed] [Google Scholar]
- Cauda F,, Nani A,, Costa T,, Palermo S,, Tatu K,, Manuello J,, et al. The morphometric co-atrophy networking of schizophrenia, autistic and obsessive spectrum disorders. Hum Brain Mapp 2018; 39: 1898–928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cauda F,, Torta DM,, Sacco K,, D’Agata F,, Geda E,, Duca S,, et al. Functional anatomy of cortical areas characterized by Von Economo neurons. Brain Struct Funct 2013; 218: 1–20. [DOI] [PubMed] [Google Scholar]
- Cauda F,, Torta DM,, Sacco K,, Geda E,, D’Agata F,, Costa T,, et al. Shared “core” areas between the pain and other task-related networks. PLoS One 2012b; 7: e41929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chevalier-Larsen E,, Holzbaur EL. Axonal transport and neurodegenerative disease. Biochim Biophys Acta 2006; 1762: 1094–108. [DOI] [PubMed] [Google Scholar]
- Chhatwal JP,, Schultz AP,, Johnson KA,, Hedden T,, Jaimes S,, Benzinger TLS,, et al. Preferential degradation of cognitive networks differentiates Alzheimer’s disease from ageing. Brain 2018; 141: 1486–500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cioli C,, Abdi H,, Beaton D,, Burnod Y,, Mesmoudi S. Differences in human cortical gene expression match the temporal properties of large-scale functional networks. PLoS One 2014; 9: e115913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clavaguera F,, Grueninger F,, Tolnay M. Intercellular transfer of tau aggregates and spreading of tau pathology: implications for therapeutic strategies. Neuropharmacology 2014; 76 (Pt A): 9–15. [DOI] [PubMed] [Google Scholar]
- Clavaguera F,, Lavenir I,, Falcon B,, Frank S,, Goedert M,, Tolnay M. “Prion-like” templated misfolding in tauopathies. Brain Pathol 2013; 23: 342–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cope TE,, Rittman T,, Borchert RJ,, Jones PS,, Vatansever D,, Allinson K,, et al. Tau burden and the functional connectome in Alzheimer’s disease and progressive supranuclear palsy. Brain 2018; 141: 550–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crossley NA,, Mechelli A,, Scott J,, Carletti F,, Fox PT,, McGuire P,, et al. The hubs of the human connectome are generally implicated in the anatomy of brain disorders. Brain 2014; 137 (Pt 8): 2382–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crossley NA,, Scott J,, Ellison-Wright I,, Mechelli A. Neuroimaging distinction between neurological and psychiatric disorders. Br J Psychiatry 2015; 207: 429–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Douaud G,, Groves AR,, Tamnes CK,, Westlye LT,, Duff EP,, Engvig A,, et al. A common brain network links development, aging, and vulnerability to disease. Proc Natl Acad Sci USA 2014; 111: 17648–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du Y,, Fryer SL,, Fu Z,, Lin D,, Sui J,, Chen J,, et al. Dynamic functional connectivity impairments in early schizophrenia and clinical high-risk for psychosis. Neuroimage 2017; 180 (Pt B): 632–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eickhoff SB,, Bzdok D,, Laird AR,, Kurth F,, Fox PT. Activation likelihood estimation meta-analysis revisited. Neuroimage 2012; 59: 2349–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eickhoff SB,, Laird AR,, Fox PM,, Lancaster JL,, Fox PT. Implementation errors in the GingerALE software: description and recommendations. Hum Brain Mapp 2017; 38: 7–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eickhoff SB,, Laird AR,, Grefkes C,, Wang LE,, Zilles K,, Fox PT. Coordinate-based activation likelihood estimation meta-analysis of neuroimaging data: a random-effects approach based on empirical estimates of spatial uncertainty. Hum Brain Mapp 2009; 30: 2907–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eickhoff SB,, Nichols TE,, Laird AR,, Hoffstaedter F,, Amunts K,, Fox PT,, et al. Behavior, sensitivity, and power of activation likelihood estimation characterized by massive empirical simulation. Neuroimage 2016; 137: 70–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellison-Wright I,, Bullmore E. Anatomy of bipolar disorder and schizophrenia: a meta-analysis. Schizophr Res 2010; 117: 1–12. [DOI] [PubMed] [Google Scholar]
- Etkin A,, Wager TD. Functional neuroimaging of anxiety: a meta-analysis of emotional processing in PTSD, social anxiety disorder, and specific phobia. Am J Psychiatry 2007; 164: 1476–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans AC. Networks of anatomical covariance. Neuroimage 2013; 80: 489–504. [DOI] [PubMed] [Google Scholar]
- Filippini N,, MacIntosh BJ,, Hough MG,, Goodwin GM,, Frisoni GB,, Smith SM,, et al. Distinct patterns of brain activity in young carriers of the APOE-epsilon4 allele. Proc Natl Acad Sci USA 2009; 106: 7209–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fornito A,, Zalesky A,, Breakspear M. The connectomics of brain disorders. Nat Rev Neurosci 2015; 16: 159–72. [DOI] [PubMed] [Google Scholar]
- Fox PT,, Laird AR,, Fox SP,, Fox PM,, Uecker AM,, Crank M,, et al. BrainMap taxonomy of experimental design: description and evaluation. Hum Brain Mapp 2005; 25: 185–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox PT,, Lancaster JL. Opinion: mapping context and content: the brainmap model. Nat Rev Neurosci 2002; 3: 319–21. [DOI] [PubMed] [Google Scholar]
- French L,, Pavlidis P. Relationships between gene expression and brain wiring in the adult rodent brain. PLoS Comput Biol 2011; 7: e1001049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- French L,, Tan PP,, Pavlidis P. Large-scale analysis of gene expression and connectivity in the rodent brain: insights through data integration. Front Neuroinform 2011; 5: 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gejman PV,, Sanders AR,, Kendler KS. Genetics of schizophrenia: new findings and challenges. Annu Rev Genomics Hum Genet 2011; 12: 121–44. [DOI] [PubMed] [Google Scholar]
- Glasser MF,, Sotiropoulos SN,, Wilson JA,, Coalson TS,, Fischl B,, Andersson JL,, et al. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage 2013; 80: 105–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glerean E,, Pan RK,, Salmi J,, Kujala R,, Lahnakoski JM,, Roine U,, et al. Reorganization of functionally connected brain subnetworks in high-functioning autism. Hum Brain Mapp 2016; 37: 1066–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goedert M,, Clavaguera F,, Tolnay M. The propagation of prion-like protein inclusions in neurodegenerative diseases. Trends Neurosci 2010; 33: 317–25. [DOI] [PubMed] [Google Scholar]
- Goel P,, Kuceyeski A,, LoCastro E,, Raj A. Spatial patterns of genome-wide expression profiles reflect anatomic and fiber connectivity architecture of healthy human brain. Hum Brain Mapp 2014; 35: 4204–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong X,, Lu W,, Kendrick KM,, Pu W,, Wang C,, Jin L,, et al. A brain-wide association study of DISC1 genetic variants reveals a relationship with the structure and functional connectivity of the precuneus in schizophrenia. Hum Brain Mapp 2014; 35: 5414–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodkind M,, Eickhoff SB,, Oathes DJ,, Jiang Y,, Chang A,, Jones-Hagata LB,, et al. Identification of a common neurobiological substrate for mental illness. JAMA Psychiatry 2015; 72: 305–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guest WC,, Silverman JM,, Pokrishevsky E,, O’Neill MA,, Grad LI,, Cashman NR. Generalization of the prion hypothesis to other neurodegenerative diseases: an imperfect fit. J Toxicol Environ Health A 2011; 74: 1433–59. [DOI] [PubMed] [Google Scholar]
- Gupta CN,, Calhoun VD,, Rachakonda S,, Chen J,, Patel V,, Liu J,, et al. Patterns of gray matter abnormalities in schizophrenia based on an international mega-analysis. Schizophr Bull 2015; 41: 1133–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamilton JP,, Etkin A,, Furman DJ,, Lemus MG,, Johnson RF,, Gotlib IH. Functional neuroimaging of major depressive disorder: a meta-analysis and new integration of base line activation and neural response data. Am J Psychiatry 2012; 169: 693–703. [DOI] [PubMed] [Google Scholar]
- Hardy J,, Revesz T. The spread of Neurodegenerative disease. N Engl J Med 2012; 366: 2126–8. [DOI] [PubMed] [Google Scholar]
- Hawrylycz MJ,, Lein ES,, Guillozet-Bongaarts AL,, Shen EH,, Ng L,, Miller JA,, et al. An anatomically comprehensive atlas of the adult human brain transcriptome. Nature 2012; 489: 391–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honey CJ,, Sporns O,, Cammoun L,, Gigandet X,, Thiran JP,, Meuli R,, et al. Predicting human resting-state functional connectivity from structural connectivity. Proc Natl Acad Sci USA 2009; 106: 2035–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang H,, Ding M. Linking functional connectivity and structural connectivity quantitatively: a comparison of methods. Brain Connect 2016; 6: 99–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iturria-Medina Y,, Evans AC. On the central role of brain connectivity in neurodegenerative disease progression. Front Aging Neurosci 2015; 7: 90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iturria-Medina Y,, Sotero RC,, Toussaint PJ,, Evans AC. Epidemic spreading model to characterize misfolded proteins propagation in aging and associated neurodegenerative disorders. PLoS Comput Biol 2014; 10: e1003956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jagust W. Vulnerable neural systems and the borderland of brain aging and neurodegeneration. Neuron 2013; 77: 219–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jucker M,, Walker LC. Pathogenic protein seeding in Alzheimer disease and other neurodegenerative disorders. Ann Neurol 2011; 70: 532–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jucker M,, Walker LC. Self-propagation of pathogenic protein aggregates in neurodegenerative diseases. Nature 2013; 501: 45–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasparek T,, Marecek R,, Schwarz D,, Prikryl R,, Vanicek J,, Mikl M,, et al. Source-based morphometry of gray matter volume in men with first-episode schizophrenia. Hum Brain Mapp 2010; 31: 300–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondor RI,, Lafferty J. Diffusion kernels on graphs and other discrete input spaces. In: Proceedings of the nineteenth international conference on machine learning (ICML). Morgan Kaufmann Publishers Inc.; 2002. p. 315–22. [Google Scholar]
- Korth C. Aggregated proteins in schizophrenia and other chronic mental diseases: DISC1opathies. Prion 2012; 6: 134–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraus A,, Groveman BR,, Caughey B. Prions and the potential transmissibility of protein misfolding diseases. Annu Rev Microbiol 2013; 67: 543–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagarias JC,, Reeds JA,, Wright MH,, Wright PE. Convergence properties of the nelder–mead simplex method in low dimensions. SIAM J. Optim 1998; 9: 112–47. [Google Scholar]
- Lahiri DK,, Maloney B. The “LEARn” (Latent Early-life Associated Regulation) model integrates environmental risk factors and the developmental basis of Alzheimer’s disease, and proposes remedial steps. Exp Gerontol 2010; 45: 291–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird AR,, Fox PM,, Price CJ,, Glahn DC,, Uecker AM,, Lancaster JL,, et al. ALE meta-analysis: controlling the false discovery rate and performing statistical contrasts. Hum Brain Mapp 2005a; 25: 155–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird AR,, Lancaster JL,, Fox PT. BrainMap: the social evolution of a human brain mapping database. Neuroinformatics 2005b; 3: 65–78. [DOI] [PubMed] [Google Scholar]
- Lichtman JW,, Sanes JR. Ome sweet ome: what can the genome tell us about the connectome?. Curr Opin Neurobiol 2008; 18: 346–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin CH,, Chen CM,, Lu MK,, Tsai CH,, Chiou JC,, Liao JR,, et al. VBM reveals brain volume differences between Parkinson’s disease and essential tremor patients. Front Hum Neurosci 2013; 7: 247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mantel N. The detection of disease clustering and a generalized regression approach. Cancer Res 1967; 27: 209–20. [PubMed] [Google Scholar]
- Manuello J,, Nani A,, Premi E,, Borroni B,, Costa T,, Tatu K,, et al. The pathoconnectivity profile of alzheimer’s disease: a morphometric coalteration network analysis. Front Neurol 2018; 8: 739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McTeague LM,, Goodkind MS,, Etkin A. Transdiagnostic impairment of cognitive control in mental illness. J Psychiatr Res 2016; 83: 37–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mechelli A,, Friston KJ,, Frackowiak RS,, Price CJ. Structural covariance in the human cortex. J Neurosci 2005; 25: 8303–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menon V. Developmental pathways to functional brain networks: emerging principles. Trends Cogn Sci 2013; 17: 627–40. [DOI] [PubMed] [Google Scholar]
- Misic B,, Betzel RF,, de Reus MA,, van den Heuvel MP,, Berman MG,, McIntosh AR,, et al. Network-level structure-function relationships in human neocortex. Cereb Cortex 2016; 26: 3285–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Northoff G,, Duncan NW. How do abnormalities in the brain’s spontaneous activity translate into symptoms in schizophrenia? From an overview of resting state activity findings to a proposed spatiotemporal psychopathology. Prog Neurobiol 2016; 145–6: 26–45. [DOI] [PubMed] [Google Scholar]
- Nunnally JC,, Bernstein IH. Psychometric theory. 3rd edn.New York: McGraw-Hill; 1994. [Google Scholar]
- Oxtoby NP,, Garbarino S,, Firth NC,, Warren JD,, Schott JM,, Alexander DC. Data-driven sequence of changes to anatomical brain connectivity in sporadic Alzheimer’s disease. Front Neurol 2017; 8: 580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pandya S,, Mezias C,, Raj A. Predictive model of spread of progressive supranuclear palsy using directional network diffusion. Front Neurol 2017; 8: 692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearson RC,, Esiri MM,, Hiorns RW,, Wilcock GK,, Powell TP. Anatomical correlates of the distribution of the pathological changes in the neocortex in Alzheimer disease. Proc Natl Acad Sci USA 1985; 82: 4531–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Premi E,, Cauda F,, Costa T,, Diano M,, Gazzina S,, Gualeni V,, et al. Looking for neuroimaging markers in frontotemporal lobar degeneration clinical trials: a multi-voxel pattern analysis study in granulin disease. J Alzheimers Dis 2016; 51: 249–62. [DOI] [PubMed] [Google Scholar]
- Premi E,, Cauda F,, Gasparotti R,, Diano M,, Archetti S,, Padovani A,, et al. Multimodal FMRI resting-state functional connectivity in granulin mutations: the case of fronto-parietal dementia PLoS One2014; 9: e106500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quiroz YT,, Schultz AP,, Chen K,, Protas HD,, Brickhouse M,, Fleisher AS,, et al. Brain imaging and blood biomarker abnormalities in children with autosomal dominant Alzheimer disease: a cross-sectional study. JAMA Neurol 2015; 72: 912–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raj A,, Kuceyeski A,, Weiner M. A network diffusion model of disease progression in dementia. Neuron 2012; 73: 1204–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ravits J. Focality, stochasticity and neuroanatomic propagation in ALS pathogenesis. Exp Neurol 2014; 262 (Pt B): 121–6. [DOI] [PubMed] [Google Scholar]
- Richiardi J,, Altmann A,, Milazzo AC,, Chang C,, Chakravarty MM,, Banaschewski T,, et al. Brain networks. correlated gene expression supports synchronous activity in brain networks. Science 2015; 348: 1241–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson PA. Interrelating anatomical, effective, and functional brain connectivity using propagators and neural field theory. Phys Rev E Stat Nonlin Soft Matter Phys 2012; 85 (1 Pt 1): 011912. [DOI] [PubMed] [Google Scholar]
- Rohrer JD,, Nicholas JM,, Cash DM,, van Swieten J,, Dopper E,, Jiskoot L,, et al. Presymptomatic cognitive and neuroanatomical changes in genetic frontotemporal dementia in the genetic frontotemporal dementia initiative (GENFI) study: a cross-sectional analysis. Lancet Neurol 2015; 14: 253–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saper CB,, Wainer BH,, German DC. Axonal and transneuronal transport in the transmission of neurological disease: potential role in system degenerations, including Alzheimer’s disease. Neuroscience 1987; 23: 389–98. [DOI] [PubMed] [Google Scholar]
- Saxena S,, Caroni P. Selective neuronal vulnerability in neurodegenerative diseases: from stressor thresholds to degeneration. Neuron 2011; 71: 35–48. [DOI] [PubMed] [Google Scholar]
- Scarpazza C,, Tognin S,, Frisciata S,, Sartori G,, Mechelli A. False positive rates in voxel-based morphometry studies of the human brain: should we be worried?. Neurosci Biobehav Rev 2015; 52: 49–55. [DOI] [PubMed] [Google Scholar]
- Seeley WW,, Carlin DA,, Allman JM,, Macedo MN,, Bush C,, Miller BL,, et al. Early frontotemporal dementia targets neurons unique to apes and humans. Ann Neurol 2006; 60: 660–7. [DOI] [PubMed] [Google Scholar]
- Seeley WW,, Crawford RK,, Zhou J,, Miller BL,, Greicius MD. Neurodegenerative diseases target large-scale human brain networks. Neuron 2009; 62: 42–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seeley WW,, Menon V,, Schatzberg AF,, Keller J,, Glover GH,, Kenna H,, et al. Dissociable intrinsic connectivity networks for salience processing and executive control. J Neurosci 2007; 27: 2349–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skudlarski P,, Jagannathan K,, Calhoun VD,, Hampson M,, Skudlarska BA,, Pearlson G. Measuring brain connectivity: diffusion tensor imaging validates resting state temporal correlations. Neuroimage 2008; 43: 554–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM,, Nichols TE. Threshold-free cluster enhancement: addressing problems of smoothing, threshold dependence and localisation in cluster inference. Neuroimage 2009; 44: 83–98. [DOI] [PubMed] [Google Scholar]
- Soto C,, Estrada LD. Protein misfolding and neurodegeneration. Arch Neurol 2008; 65: 184–9. [DOI] [PubMed] [Google Scholar]
- Sprooten E,, Rasgon A,, Goodman M,, Carlin A,, Leibu E,, Lee WH,, et al. Addressing reverse inference in psychiatric neuroimaging: meta-analyses of task-related brain activation in common mental disorders. Hum Brain Mapp 2017; 38: 1846–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanley J. Educational measurement Washington, DC: American Council on Education; 1971. [Google Scholar]
- Stuart JM,, Segal E,, Koller D,, Kim SK. A gene-coexpression network for global discovery of conserved genetic modules. Science 2003; 302: 249–55. [DOI] [PubMed] [Google Scholar]
- Tatu K,, Costa T,, Nani A,, Diano M,, Quarta DG,, Duca S,, et al. How do morphological alterations caused by chronic pain distribute across the brain? A meta-analytic co-alteration study. Neuroimage 2018; 18: 15–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toro R,, Fox PT,, Paus T. Functional coactivation map of the human brain. Cereb Cortex 2008; 18: 2553–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turkeltaub PE,, Eickhoff SB,, Laird AR,, Fox M,, Wiener M,, Fox P. Minimizing within-experiment and within-group effects in activation likelihood estimation meta-analyses. Hum Brain Mapp 2012; 33: 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Heuvel MP,, Mandl RC,, Kahn RS,, Hulshoff Pol HE. Functionally linked resting-state networks reflect the underlying structural connectivity architecture of the human brain. Hum Brain Mapp 2009; 30: 3127–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC,, Smith SM,, Barch DM,, Behrens TE,, Yacoub E,, Ugurbil K. The wu-minn human connectome project: an overview. Neuroimage 2013; 80: 62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC,, Ugurbil K,, Auerbach E,, Barch D,, Behrens TE,, Bucholz R,, et al. The human connectome project: a data acquisition perspective. Neuroimage 2012; 62: 2222–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanasse TJ,, Fox PM,, Barron DS,, Robertson M,, Eickhoff SB,, Lancaster JL,, et al. BrainMap VBM: an environment for structural meta-analysis. Hum Brain Mapp 2018; 39: 3308–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voronoi G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. J Reine Angew Math 1907: 97–178. [Google Scholar]
- Walker LC,, Diamond MI,, Duff KE,, Hyman BT. Mechanisms of protein seeding in neurodegenerative diseases. JAMA Neurol 2013; 70: 304–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang WY,, Yu JT,, Liu Y,, Yin RH,, Wang HF,, Wang J,, et al. Voxel-based meta-analysis of grey matter changes in Alzheimer’s disease. Transl Neurodegener 2015; 4: 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y,, Chen K,, Yao L,, Jin Z,, Guo X. Structural interactions within the default mode network identified by bayesian network analysis in Alzheimer’s disease. PLoS One 2013; 8: e74070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren JD,, Rohrer JD,, Schott JM,, Fox NC,, Hardy J,, Rossor MN. Molecular nexopathies: a new paradigm of neurodegenerative disease. Trends Neurosci 2013; 36: 561–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weintraub S,, Mesulam MM. From neuronal networks to dementia: four clinical profiles In: La Demence: Pourquoi? Paris: Foundation Nationale de Gerontologie; 1996. [Google Scholar]
- Winkler AM,, Ridgway GR,, Webster MA,, Smith SM,, Nichols TE. Permutation inference for the general linear model. Neuroimage 2014; 92: 381–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf L,, Goldberg C,, Manor N,, Sharan R,, Ruppin E. Gene expression in the rodent brain is associated with its regional connectivity. PLoS Comput Biol 2011; 7: e1002040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yates D. Neurodegenerative networking. Nat Rev Neurosci 2012; 13: 288. [DOI] [PubMed] [Google Scholar]
- Yeh FC,, Badre D,, Verstynen T. Connectometry: a statistical approach harnessing the analytical potential of the local connectome. Neuroimage 2016; 125: 162–71. [DOI] [PubMed] [Google Scholar]
- Yeh FC,, Tseng WY. NTU-90: a high angular resolution brain atlas constructed by q-space diffeomorphic reconstruction. Neuroimage 2011; 58: 91–9. [DOI] [PubMed] [Google Scholar]
- Yeh FC,, Verstynen TD,, Wang Y,, Fernandez-Miranda JC,, Tseng WY. Deterministic diffusion fiber tracking improved by quantitative anisotropy. PLoS One 2013; 8: e80713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeh FC,, Wedeen VJ,, Tseng WY. Generalized q-sampling imaging. IEEE Trans Med Imaging 2010; 29: 1626–35. [DOI] [PubMed] [Google Scholar]
- Yuan B,, Fang Y,, Han Z,, Song L,, He Y,, Bi Y. Brain hubs in lesion models: predicting functional network topology with lesion patterns in patients. Sci Rep 2017; 7: 17908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zawia NH,, Basha MR. Environmental risk factors and the developmental basis for Alzheimer’s disease. Rev Neurosci 2005; 16: 325–37. [DOI] [PubMed] [Google Scholar]
- Zhang B,, Horvath S. A general framework for weighted gene co-expression network analysis. Stat Appl Genet Mol Biol 2005; 4: Article 17. [DOI] [PubMed] [Google Scholar]
- Zhou J,, Gennatas ED,, Kramer JH,, Miller BL,, Seeley WW. Predicting regional neurodegeneration from the healthy brain functional connectome. Neuron 2012; 73: 1216–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou J,, Greicius MD,, Gennatas ED,, Growdon ME,, Jang JY,, Rabinovici GD,, et al. Divergent network connectivity changes in behavioural variant frontotemporal dementia and Alzheimer’s disease. Brain 2010; 133 (Pt 5): 1352–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets we used in this study are from publicly available sources:
BrainMap (meta-analytic datasets) http://brainmap.org/.
Allen Brain Atlas (gene expression datasets) http://human.brain-map.org/static/download.
Human Connectome Project (resting state connectivity and DTI anatomical connectivity datasets) http://www.humanconnectomeproject.org/data/.
Above, we describe in detail which parts of these datasets were used or how we queried the BrainMap database.
A complete list of the literature involved in the meta-analytic analyses is provided in the Supplementary material.