Prediction of Hot Spots at Myeloid Cell Leukemia-1–Inhibitor Interface Using Energy Estimation and Alanine Scanning Mutagenesis

Abstract

Myeloid cell leukemia 1 (Mcl1) is an antiapoptotic protein that plays central role in apoptosis regulation. Also, Mcl1 has the potency to resist apoptotic cues resulting in up-regulation and cancer cell protection. A molecular probe that has the potential to specifically target Mcl1 and thereby provoke its down-regulatory activity is very essential. The aim of the current study is to probe the internal conformational dynamics of protein motions and potential binding mechanism in response to a series of picomolar range Mcl1 inhibitors using explicit-solvent molecular dynamics (MD) simulations. Subsequently, domain cross-correlation and principal component analysis was performed on the snapshots obtained from the MD simulations. Our results showed significant differences in the internal conformational dynamics of Mcl1 with respect to binding affinity values of inhibitors. Further, the binding free energy estimation, using three different samples, was performed on the MD simulations and revealed that the predicted energies (ΔG_mmgbsa) were in good correlation with the experimental values (ΔG_expt). Also, the energies obtained using all sampling models were efficiently ranked. Subsequently, the decomposition energy analysis highlighted the major energy-contributing residues at the Mcl1 binding pocket. Computational alanine scanning performed on high energy-contributing residues predicted the hot spot residues. The dihedral angle analysis using MD snapshots on the predicted hot spot residue exhibited consistency in side chain conformational motion that ultimately led to strong binding affinity values. The findings from the present study might provide valuable guidelines for the design of novel Mcl1 inhibitors that might significantly improve the specificity for new-generation chemotherapeutic agents.

Bcl-2 family proteins are the central regulators of apoptosis involved in removal of unwanted, injured, or infected cells.¹ Three major categories of Bcl-2 family members are (i) antiapoptotic proteins (AAP; Bcl2, Bcl-xL, Bfl-1/A1, Bcl-w, and Mcl1) containing four BH (Bcl-2 homologue) domains, (ii) proapoptotic proteins (PAP; Bax, Bak, and Bok) comprising BH domains, and (iii) BH3-only proteins (Noxa, Puma, Bid, and Bad) constituting only BH3 domain.² The BH domains are short segments involved in the interactions between proteins through homo- or heterodimerization, which ultimately determine the lifetime of a cell. Also, they facilitate the release of apoptotic factors by controlling the mitochondrial membrane permeabilization.³

Among the Bcl2 family proteins, Mcl1 amino-terminal PEST domain affects the most frequently amplified cancer genes and selectivity with its binding partners.⁴⁻⁷ Although, Mcl1 and Bcl-xL share common biological function, they exhibit distinct interaction profiles, expression patterns, and regulation. Mcl1 sequesters Bak and thereby affects cytochrome c release. Likewise, Mcl1 can bind selectively to Noxa and Bik.⁸ Mcl1 is important due to its emergence in resistance to chemotherapeutic agents. The up-regulation of Mcl1 leads to cancer, while the down-regulation causes apoptosis.⁹ Thus, Mcl1 is a key member of the family and an ideal cancer therapeutic target.

Mcl1 comprises ∼350 residues and shares common structural topology with Bcl2 family proteins.^10,11 The presence of a C-terminal transmembrane domain in Mcl1 helps to anchor the protein to various intracellular membranes.¹⁰ The surface of Mcl1 is highly conserved where it engages the α-helical BH3 domain of PAPs or chemotherapeutic agents.¹²⁻¹⁴

Several studies have been carried out for the development of selective Mcl1 inhibitors.^13,15 In order to develop inhibitors that specifically target Mcl1, the interaction pattern with its existing binding partners, such as BH3 peptides or available synthetic chemical compounds, should be explored extensively to predict the binding free energies and rank the ligands based on the estimated binding energies using docking and molecular dynamics (MD) simulation techniques.

In recent years, MD simulations have evolved to the level of predicting the binding affinities for novel lead compounds, which helps in accessing the quality of identified lead compounds, and mutants,¹⁶ intramolecular conformational change in pro-apoptotic Bax,¹⁷ the molecular basis of heterodimerization of Bak peptide with multiple antiapoptotic proteins,² and the molecular properties of series of chemical compounds to Bcl-xL.¹⁸ Based on this background, the current investigation is focused on highlighting the crucial interactions and hot spot residues for recently discovered high affinity 2-indole amide inhibitors that have a broad range binding affinity values.¹⁹ Here, we subject Mcl1–inhibitor complexes to explicit solvent molecular dynamics (MD) simulations and binding free energy estimation approach by molecular mechanics, generalized Born and solvent-accessible surface area (MMGBSA) techniques. The accuracy of this powerful computational method is high, providing valuable insights on the binding mode of Mcl1 inhibitors and helping to identify hot spot residues responsible for binding.

Materials and Methods

Starting Structure Preparation

Five recently discovered Mcl1 inhibitors (Figure 1) and their bioactivity values were obtained from the literature.¹⁹ The X-ray crystal structures of Mcl1 complexed with compounds 2 (PDB ID 5IEZ; 2.6 Å; Chain A) and 5 (PDB ID 5IF4; 2.39 Å; Chain A)¹⁹ were retrieved from Protein Data Bank (https://www.rcsb.org/pdb/home/home.do). Further, compounds 1, 3, and 4 were sketched in 2D representation using ChemDraw.²⁰ To maintain consistency, the crystal structure of Mcl1 complexed with compound 2 was used to build other complexes. In the current study, docking calculations were performed using AutoDock4.2.²¹ Initially, to test the reproducibility of the binding poses by the docking algorithm, compound 2 was “redocked” by manual removal of compound 2 from the crystal structure and docked using cocrystallized ligand as the grid center. Subsequently, the coordinates of Mcl1 and compound 2 were prepared using MGL Tools.²¹ Gasteiger-Marsili partial charges were added to all polar hydrogen atoms. One hundred docking cycles were performed using AutoDock 4.2 with 500 000 evaluation steps. Consequently, three independent docking calculations were performed for compounds 1, 3, and 4 with the redocking parameters used previously.

Figure 1.

2D-chemical structures of high affinity 2-indole amide inhibitor series.¹⁹

Molecular Dynamics Simulations on Mcl1–Inhibitor Complexes

The MD parameters used for the current investigation was adapted from our previous studies^2,18,22,23 and are summarized here. Six (Mcl1 protein in ligand free (apo) form and Mcl1 protein complexed with five different 2-indole amide inhibitors (holo)) independent systems were used as the starting structures for MD simulations. All MD simulations were carried out using NAMD²⁴ with standard Amber-ff03 force field.²⁵ The ligand topologies for all five different compounds were generated using the antechamber program, available in Ambertools 17.²⁵ Subsequently, five independent systems were built using the following steps for MD simulations: addition of (i) force field parameters for Mcl1 and inhibitors, (ii) hydrogen atoms, (iii) counterions to neutralize the system, and (iv) approximately 30 000 transferable intramolecular potential three-point (TIP3P) water molecules. Then, the system was placed in a cubic periodic box extended by 10 Å in every dimension from the surface of the solute. Subsequently, a step-by-step equilibration was carried out as follows. Initially, the water molecules, counterions, and amino acid side chains were subjected to 50 000 steps of minimization, while the Cα atoms were restrained by the harmonic force of 5 kcal/mol Ų. This permits the solvent and counterions to move freely and also removes the clash within the system. Next, a constraint-free minimization was carried out for 250 000 steps, which removes plausible remaining bad contacts. Further, the complete setup was subjected to 25 ns equilibration under constant pressure. Subsequently, a 100 ns unrestrained production run was carried out with time step integration set to 2 fs. The system temperature was maintained at 300 K. The system pressure was maintained using Nose–Hoover Langevin piston²⁶ for 1 atm, while the oscillation and damping time scale was set to 200 and 100 fs, respectively. The Langevin damping coefficient of 5 ps^–1 of simulation time was set to all non-hydrogen atoms. The SHAKE algorithm²⁷ was applied for bond constraints. The long-range electrostatics was computed using the particle mesh Ewald (PME) approach,^28,29 while the short-range electrostatics was calculated using 12 Å cutoff. The periodic boundary conditions were applied to all dimensions.

Trajectory Analysis

The trajectories obtained from the MD simulations on Mcl1–inhibitor complexes were analyzed using the cpptraj script available in Amber. Initially, the structural stability of the simulation was analyzed by calculating the root-mean-squared-deviation (rmsd) and root-mean-squared fluctuation (rmsf, thermal fluctuation calculated using B = 8π²/3⟨Δr²⟩) values. The Cα atoms of all five different Mcl1–inhibitor complexes were used to calculate the rmsd and rmsf values with reference to the starting structure.

Domain Cross-Correlation Analysis (DCCA)

The structural correlation motion of Mcl1 due to inhibitor binding was investigated by domain cross-correlation [C_(i,j)] analysis using all pairs of Cα atoms. The cross-correlation analysis was computed using 500 snapshots obtained from the last 20 ns of the MD trajectory with an even interval of 40 ps with the following formula:

1

where C_(i,j) represents the cross correlation values. The Δr_i correspond to the deviation of Cα atoms estimated from the mean position of the ith residue, while the values of C_(i,j) range between −1 and +1. The negative and positive values of the C_(i,j) represent the anticorrelated and correlated motion of the ith and jth residue of Mcl1, respectively. Higher C_(i,j) values highlight more correlated (lower values anticorrelated) motion between two Cα atoms of Mcl1.

Principal Component Analysis (PCA)

The conformational transition of Mcl1 due to inhibitor binding was generally estimated using PCA. Here, PCA was calculated using 500 snapshots obtained from the last 20 ns of the MD trajectory with an even interval of 40 ps. The covariance matrix, C_i,j, of atomic coordinates was constructed as follows;

2

where x_i is a Cartesian coordinate of the ith Cα atom, ⟨x_i⟩ represents the average time over all the configurations selected in the simulations, and N is the number of Cα atoms. The diagonalization of C yields the eigenvalues λ_i and the corresponding eigenvectors V_i, that is, the principle components.

Binding Free Energy (BFE) Estimation (in kcal/mol) for Mcl1–Inhibitors

The postprocessing trajectory analysis technique, BFE estimation, was carried out on all the simulated Mcl1–inhibitor complexes using the MMPBSA.py³⁰ script available in Amber 16.²⁵ Three different GB models, developed by Tsui and Case (igb = 1)³¹ and Onufriev et al. (igb = 2 (α = 0.8, β = 0.0, γ = 2.909) and igb = 5 (α = 1.0, β = 0.8, γ = 4.85),^32,33 were used to compute BFEs for all five Mcl1–inhibitor complexes using molecular mechanics generalized Born and solvent-accessible surface area approach (MMGBSA).^30,33,34 The α, β, and γ correspond to rescaling parameters used to represent solvation effects. The BFEs were computed for 500 snapshots obtained from the last 20 ns of the MD trajectory with an even interval of 40 ps.

For all Mcl1–inhibitor complexes, the BFEs were calculated as follows:

3

where ΔG_bind is the BFE and G_complex, G_protein, and G_inhibitors represents the energies of the Mcl1–inhibitor complex, Mcl1, and inhibitors, respectively.

Further, the BFEs were calculated using the following equation,

4

where ΔE_MM is the gas phase interaction energy for Mcl1–inhibitor complexes and was estimated using the sander program, ΔG_GB and ΔG_nonpolar correspond to polar and nonpolar components of BFE, and −TΔS corresponds to the change of conformational entropy due to inhibitor binding. Generally, the entropy is estimated with normal-mode analysis (NMA) or quasi-harmonic analysis (QHA)³⁵ of the vibration frequencies. Here, the conformational entropy calculation was ignored due to (i) high computational costs,^22,23 (ii) overestimation of entropy values by NMA,³⁶ (iii) a good convergence of the entropy being hardly reached by QHA,³⁷⁻³⁹ and (iv) the main goal of the current investigation being to obtain relative BFE comparisons with the experimental values and not to compute the absolute BFE value. The ΔG_GB/PB corresponds to the polar solvation free energy calculated using GB/PB equations embedded in Amber, while the ΔG_nonpolar corresponds to the nonpolar contribution to the solvation free energy.

Further, the nonpolar component was calculated using the following equation:

5

where γ represents the surface tension and is set to 0.0072 kcal/(mol·Å²), β is set to 0.92 kcal/mol, and SASA is the solvent-accessible surface area. The default dielectric parameters were set to 1 and 80 for interior solute and exterior solvent, respectively.

Free Energy Decomposition (FED) for Mcl1–Inhibitor Complexes

The FED analysis was performed using the same snapshots obtained from the last 20 ns of the MD trajectory used for the BFE calculations. To clearly highlight the BFEs of crucial residues involved in the complex formation, the decomp(30) module available in the Amber suite was used to calculate FED analysis for each residue in Mcl1–inhibitor complexes. Four important energy components, van der Waals contribution (ΔG_vdW), electrostatic contribution (ΔG_ele), polar solvation contribution (ΔG_ele,sol), and nonpolar solvation contribution (ΔG_nonpol, sol), were involved in calculating BFEs of each residues in Mcl1–inhibitor complexes.

6

Here, MMPBSA.py^30,33,34 script in Amber was used to calculate vdW and electrostatic interactions between Mcl1–inhibitor complexes, where as the contribution of polar solvation energy (ΔG_ele,sol) was calculated using generalized Born (GB) parameters and was computed based on SASA. Potential energy contributing residues were selected based on energy value greater than −1 kcal/mol.

Alanine Scanning

Computational alanine scanning was performed on the higher energy contributing residues in the Mcl1 binding pocket obtained from decomposition analysis. Here, the compounds with higher binding affinity values (compounds 3, 4, and 5) were alone considered as appropriate for the analysis. Consequently, each potential residue that exhibited higher energy was mutated to alanine using Maestro 9.6v suite (Schrödinger Inc. NY), and saved individually as “mutated Mcl1–inhibitor complex”, respectively. Furthermore, every mutated complex were subjected to 100 ns MD simulations, using same parameters used previously. The BFE values for the mutational complexes were obtained using the MMPBSA.py script.^25,30 The energy differences between the wild-type and mutated complexes were calculated using the following equation:

7

where ΔG_mmgbsa^ala-scan corresponds to total BFE calculated for the alanine mutational complex, ΔG_ala corresponds to Mcl1–inhibitor complexes mutated with single alanine residue, and ΔG_wild corresponds to wild-type Mcl1–inhibitor complex. Total BFEs with negative values were considered as favorable effects due to mutation, whereas the energies with positive values were considered as unfavorable effects due to mutation. Subsequently, the representative hot spot residues were categorized based on the residue contributing differences in BFE greater than −1 kcal/mol.

Results and Discussion

Molecular Docking

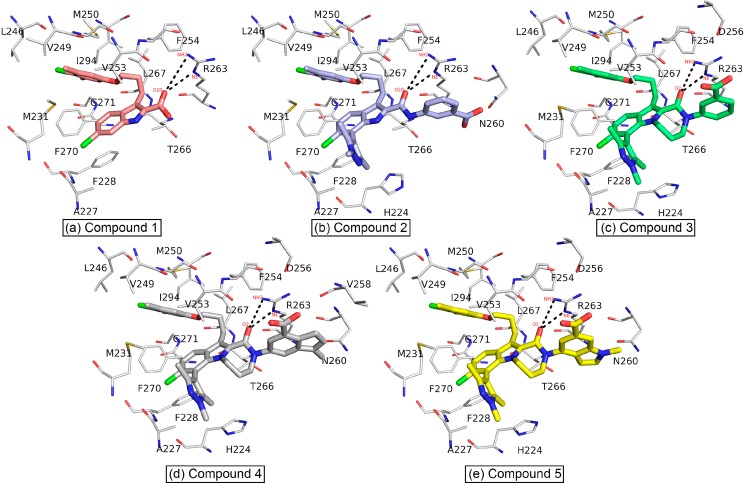
In order to gain structural insight on the plausible binding mode of potential inhibitors interacting with Mcl1, docking studies were performed. Initially, to ensure reproducibility of the binding poses from the docking algorithm, compound 2 was redocked to the X-ray crystal structure of Mcl1 (PDB ID 5IEZ), which produced 100 conformational poses. The ensemble of docked poses was examined closely, and the best conformation was selected based on (i) docking score (−9.48 kcal/mol), (ii) graphical inspection, and (iii) potential polar contacts between binding site residues and the inhibitors. Interestingly, docking reproduced all desirable residue interactions that were observed in X-ray coordinates (Figure 2). The final redocked compound 2 was surrounded by residues H224, A227, F228, M231, L246, V249, M250, V253, F254, N260, T266, L267, and F270 with favorable hydrophobic interaction at the binding site of Mcl1. Additionally, the comparison of the binding pose of redocked compound 2 and the X-ray coordinates showed 0.22 Å rmsd. Moreover, closer inspection of the binding pocket revealed potential charge–charge interactions between polar atoms of the carboxylate of compound 2 and the guanidinium of R263 from Mcl1. Particularly, the O20 atom of compound 2 forms a potential hydrogen bond interaction with NE and NH₂ atoms of the guanidinium side chain from R263. Additionally, the complex stability was improved by the formation of cation−π stacking between the guanidinium of R263 and the phenyl group of compound 2. Thus, the structural stability was maintained through the hydrophobic and polar interactions between compound 2 and Mcl1. Overall, these crucial interactions are well conserved between X-ray and redocked complexes. Therefore, the redocking result provided good confidence to use the same parameters to dock other compounds 1, 3, and 4 to the binding pocket of Mcl1.

Figure 2.

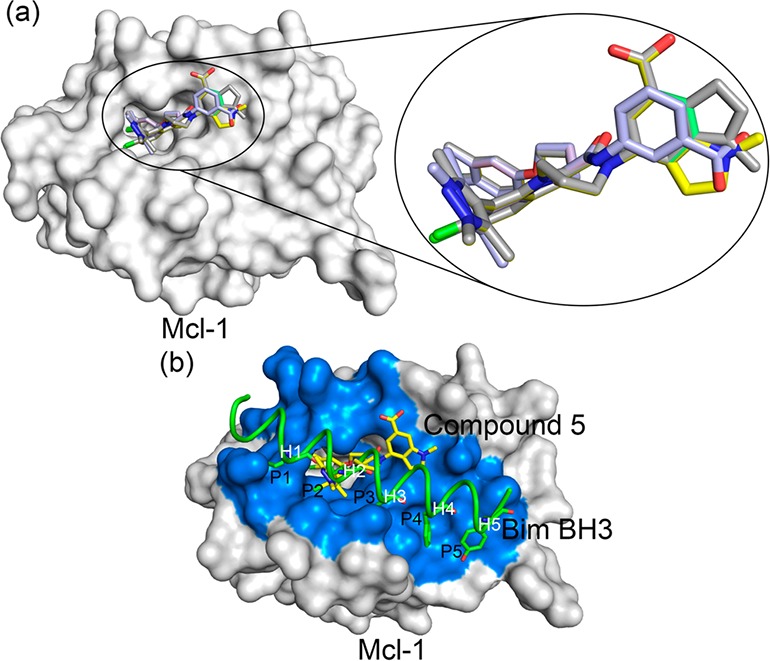
(a) The overlay of low energy poses of 2-indole amide inhibitor series¹⁹ bound to the hydrophobic binding pocket of Mcl1 (left) obtained from docking studies. The magnified image shows the docking cluster of 2-indole amide inhibitor series (right). (b) Relative binding position of compound 5 to BimBH3 peptide (2PQK) at the hydrophobic binding pocket (blue) of Mcl1 (light gray). The compound 5 interacts to the P2 subpocket present in the hydrophobic groove of Mcl1.

Next, three independent docking calculations were performed with compounds 1, 3, and 4 at the binding pocket of Mcl1, which produced 100 conformations each. The best-docked pose was selected using the same criteria described previously (compound 1 = −8.73; 3 = −10.11, and 4 = −10.53 kcal/mol). The docking results showed that compounds 1, 3, and 4 (i) occupied the hydrophobic binding pocket, (ii) covered a large area of surrounding residues similar to the crystal structure, and (iii) conserved the charge–charge interactions from the crystal structure (Figure 2). Particularly, the NE atom from the guanidinium side chain of R263 forms hydrogen bonds with the oxygen atom from the carboxylate of compounds 1, 3, and 4, respectively. To compare the docked conformation of compounds 1, 3, and 4, the selected final docked poses were clustered with the X-ray crystal structure of Mcl1 (PDB ID 5IEZ) (Figure 3). Based on these results, the selected docked pose and crystal structure conformations were subjected to MD simulations.

Figure 3.

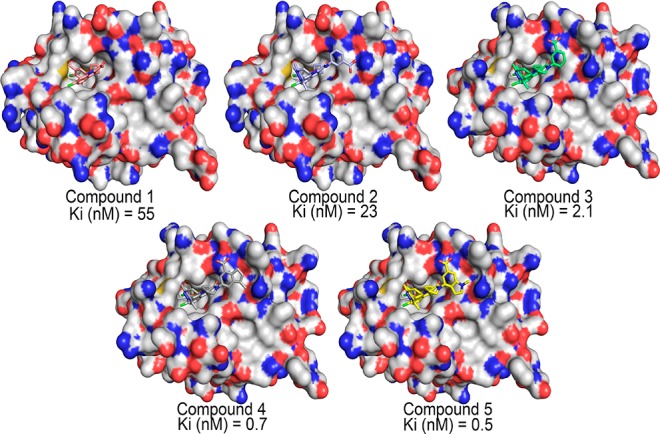
Binding mode of 2-indole amide inhibitor series (stick representation) interacting with the hydrophobic groove of Mcl1 (molecular surface representation).¹⁹ All five inhibitors occupied the shallow P2 subpocket present in the hydrophobic groove of Mcl1. The charged region over Mcl1 surface is highlighted by blue (positive) and red (negative) color.

MD Simulations

To gain insights on the stability of the docked complexes and the contributions of different inhibitors to binding free energy of Mcl1 over a period of time, six (one apo (ligand free) and five ligand bound (holo) conformations) MD simulations were performed for 100 ns, individually.

Structural Stability Analysis of Mcl1–Inhibitor Complexes

Root Mean Squared Deviation (rmsd)

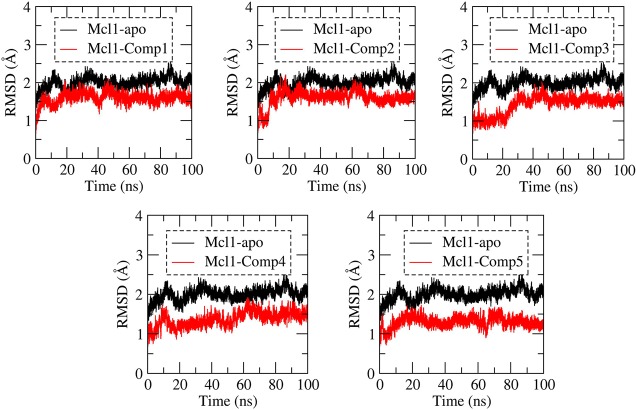
The structural deviation of Cα atoms during the MD simulation for Mcl1 in apo (ligand free) and five Mcl1–inhibitor (holo) complexes were calculated for each time point throughout the simulations by rmsd analysis (Figure 4). The rmsd values for the apo system showed higher deviation as expected, due to absence of inhibitor at the binding site. Contrastingly, the simulation reached equilibrium after 40 ns for Mcl1 complexed with compounds 1 and 3; whereas the simulation reached equilibrium after 50 ns for Mcl1 complexed with compound 4. Conversely, for Mcl1 complexed with compounds 2 and 5, simulation reached equilibrium after 20 ns, provided that these coordinates are crystal structures. The rmsd graph show that all Mcl1–inhibitor complexes rapidly reached the equilibrium phase after the initial relaxation period, approximately between 1.25–1.5 Å deviations from its starting structure. Particularly, the rmsd values for compounds 1 and 2 were ∼1.6 Å, whereas those for 3 and 4 were ∼1.5 Å, and that for 5 was 1.25 Å during the last 20 ns of the MD simulations. This suggested that the trajectory obtained from the last 20 ns of the MD simulations was reliable and could be used for further energy estimation analysis. Additionally, the diameter of the binding pocket for initial and the average structure was measured using EBI-PDBSum server⁴⁰ and its volume is tabulated (Table 1) for compounds 1–5. The dimensions of the binding pocket for compounds 1–5 after MD simulation showed converging variations in the volume in comparison with the initial structure.

Figure 4.

Root-mean-square deviation (rmsd) values obtained for the Cα atoms of ligand free and ligand bound states of Mcl1 relative to its initial coordinates during MD simulations.

Table 1. Comparison of the Dimension of the Mcl1 Binding Pocket Using the Initial and the Average Structure of Compounds 1–5 Using EBI-PDBSum⁴⁰.

compd	initial coordinates (Å3)	MD average structure (Å3)
1	1192.22	1065.23
2	1192.22	1273.22
3	1258.88	1179.98
4	1258.88	1201.50
5	1258.88	1348.31

Root Mean Squared Fluctuations (rmsf)

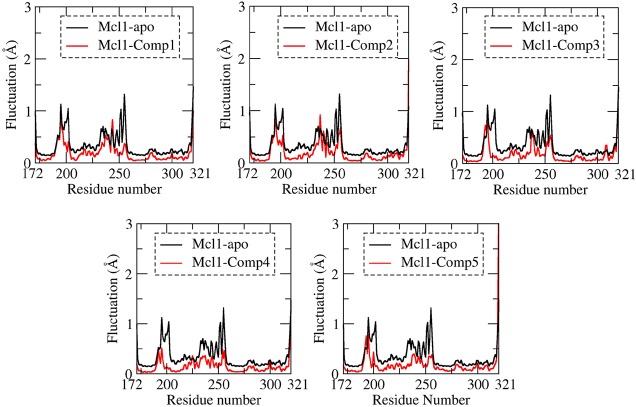
The structural flexibility for all Cα atoms of apo and holo complexes was calculated during the MD simulation by rmsf analysis (Figure 5). The apo form showed higher fluctuation, due to absence of inhibitor. Contrastingly, the rmsf graphs of holo forms showed (i) higher fluctuations at the loop and termini regions, as expected, and (ii) clear variations in backbone fluctuations among the inhibitors, particularly at the binding site region of Mcl1. Additionally, the residue range ∼230 to 260 showed higher to lower levels of fluctuations from compound 1 to 5, which is in agreement with the binding energy values. This clearly explains that the inhibitors with weak binding affinity values showed moderate or weak interaction to the binding site residues, which resulted in more fluctuation. Contrastingly, the inhibitors with strong binding affinity showed tight and stable interaction to binding site residues, which resulted in reduced or less fluctuation of Mcl1.

Figure 5.

Root-mean-squared fluctuation (rmsf) values obtained for the Cα atoms of ligand free and ligand bound states of Mcl1 relative to its initial coordinates during MD simulations.

Domain Cross Correlation Analysis (DCCA)

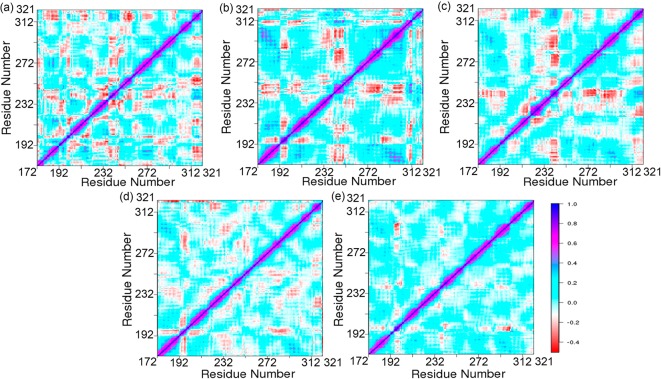
To calculate the internal dynamics of Mcl1 due to inhibitor binding, cross-correlated matrices were computed from the equilibrated snapshots obtained from the last 20 ns of the MD simulations rendered using the cpptraj(41) program in Amber. The cross-correlated matrices have the ability to clearly highlight the internal dynamics of the residues involved in interaction with the binding partners using highly positive (+1) and negative (−1) values, which in turn explains the strong correlated and anticorrelated motions (Figure 6). Different colors can be used to highlight the variations in the correlated motions that correspond to the positive or negative values. Here, strong correlated and anticorrelated regions are depicted using blue and red colors, respectively. Overall, Figure 6 explains two key features: (i) the global dynamics of the simulated system exhibited similar patterns, and (ii) the overall secondary structure of Mcl1 remains unchanged due to inhibitor binding in all cases.

Figure 6.

Domain cross correlation analysis performed on all Cα atom pairs of Mcl1 complexed with 2-indole amide inhibitor series of compound 1 to 5 (a–e).

Further, closer investigation of the cross correlation maps clearly exhibited major differences between the complexes due to inhibitor binding. In each DCCA map, the diagonal region showed strong correlation (blue color) for each residue relative to itself. Conversely, distinct red spots highlighting strong anticorrelated regions were also observed. Particularly, the DCCA maps displayed more anticorrelated regions for binding site residues (Figure 6) for the inhibitor with weak binding affinity, compound 1, K_i = 55 nM,¹⁹ whereas reduced or no anticorrelated regions were observed for the inhibitor with strong binding affinity (compound 5; K_i = 0.5 nM). This explains that the inhibitor with weak binding affinity values (compound 1) exhibited moderate or unstable binding with Mcl1 and favored more conformational flexibility for binding site residues, whereas the inhibitor with strong binding affinity (compound 5) showed tight and stable binding with Mcl1, thereby permitting less conformational flexibility. This result was in agreement with rmsf results.

Principle Components Analysis (PCA)

PCA is a powerful MD analysis technique, which is widely used to probe the internal conformational changes of protein.^16,23,42 Therefore, in the current study PCA was carried out to investigate the internal conformational motion of Mcl1 due to inhibitor binding using the snapshots collected from the last 20 ns of the MD simulations. A two-dimensional PCA plot and its corresponding fluctuation are depicted for all Mcl1–inhibitor complexes (Figure 7). The PCA plot displays eigenvalues versus eigenvector indices obtained from the diagonalization of the covariance matrices for all the atomic coordinates (Figure 7a). Figure 7a shows first that few eigenvalues alone project the concerted motion of atomic coordinates of Mcl1 due to inhibitor binding. Particularly, the first 14 PCs accounted for 76.25%, 70.71%, 63.58%, 62.67%, and 60.63% of the total concerted motions observed in the last 20 ns of the MD trajectories for compounds 1, 2, 3, 4, and 5, respectively. The subsequent concerted motions showed a rapid decrease in amplitude and reached more localized fluctuation and were thus ignored. Also, significant variations were observed for these concerted motions between the five Mcl1–inhibitor complexes. However, it is important to point out that the magnitude of PC1 is significant for the inhibitor with strong binding affinity (compound 5) in comparison with the inhibitor with weak binding affinity (compound 1).

Figure 7.

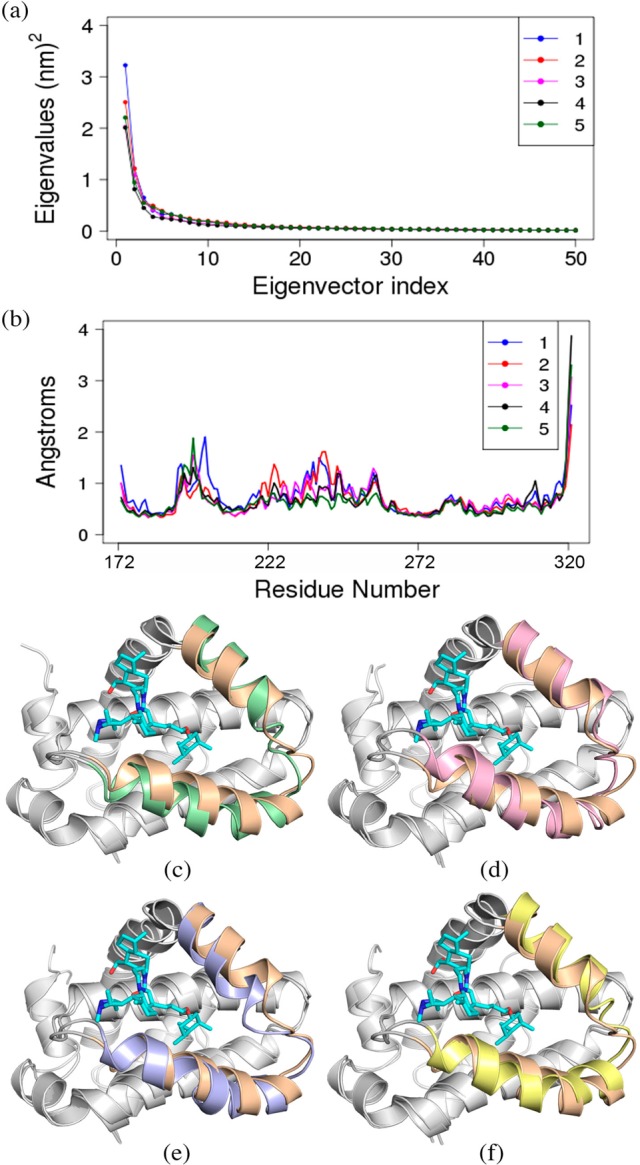
Principle Component Analysis for Mcl1–inhibitor complexes. (a) The eigenvalues plotted against eigenvector indices from the Cα covariance matrices. (b) Internal fluctuation obtained for first eigenvector obtained for Mcl1–inhibitor complexes. Superposition of Mcl1 (light brown) complexed with compound 5 (cyan color) over (c) Mcl1 (green) with compound 1, (d) Mcl1 (pink) with compound 2, (e) Mcl1 (purple) with compound 3 and (f) Mcl1 (yellow) with compound 4.

To understand how inhibitor binding influences the internal fluctuations of Mcl1 protein, the displacement of PC1 was separately depicted in Figure 7b. The result revealed that (i) the loop and (ii) the N′ and C′ terminal regions of Mcl1 experienced conformational fluctuations as expected. Additionally, Figure 7b clearly depicts significant fluctuation at residues ∼215 and 260 of Mcl1 due to inhibitor binding. Particularly, the inhibitors with weak binding affinity values (1 in blue color and 2 in red color) showed higher fluctuation, whereas the inhibitor with strong binding affinity (5 in green color) values showed low or reduced fluctuation. This result indicates that the inhibitors with strong binding affinity values can influence the conformational motion of binding site residues in terms of tight binding. These results were consistent with rmsf analysis.

Mechanism of Interaction Based on BFE Calculation

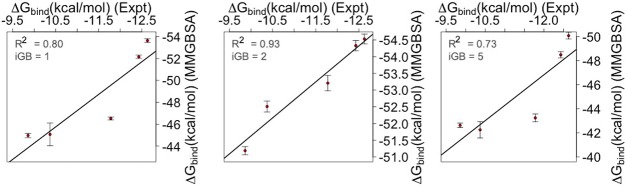
In order to predict the binding strength between protein and its binding partners, BFE can be computed using the MMGBSA approach available in the Amber program.²⁵ In the present investigation, relative BFE values have been estimated for five different Mcl1–inhibitor complexes. Three different GB parameters were used to calculate BFE with snapshots obtained from last 20 ns of the MD trajectories. The predicted BFEs were then compared with experimental values (Table 2 and Figure 8). The BFEs obtained by predicted (ΔG_mmgbsa) and experimental (ΔG_expt) values were negative for all Mcl1–inhibitor complexes. Figure 8 exhibits the magnitude of the predicted energy value increases with increase in experimental binding affinity values for all three GB sampling parameters. The igb = 1 model exhibited correlation coefficient (R² = 0.80) for predicted versus and experimental ΔG value. Additionally, to explore more conformational space for the simulated complexes two more igb parameters, developed by Onufriev et al.³² (igb = 2 and igb = 5) were also considered. The correlation coefficient values obtained for igb = 2 and igb = 5 models were R² = 0.93 and R² = 0.73, respectively. Nevertheless, the magnitude of the energy values showed sequential increase; reduced R² values were observed for igb = 1 and igb = 5 models in comparison with igb = 2 model. This might be due to significant intervals observed between the predicted BFE values (ΔG_mmgbsa) obtained for compounds 4 and 5 using igb = 1 and igb = 5 models, in comparison with igb2 model, respectively.

Table 2. BFE (*ΔG_mmgbsa in kcal/mol) Values Calculated for Mcl1–Inhibitor Complexes Obtained from Last 20 ns of the MD Simulations^a.

method	compd 1	compd 2	compd 3	compd 4	compd 5
ΔGmmgbsa(igb=1)	–44.97 ± 0.20	–45.07 ± 1.05	–46.52 ± 0.14	–52.16 ± 0.15	–53.64 ± 0.16
ΔGmmgbsa(igb=2)	–51.19 ± 0.12	–52.51 ± 0.16	–53.21 ± 0.23	–54.33 ± 0.15	–54.53 ± 0.15
ΔGmmgbsa(igb=5)	–42.63 ± 0.19	–42.26 ± 0.98	–43.25 ± 0.13	–48.49 ± 0.15	–50.08 ± 0.17
ΔGexpt	–9.863	–10.377	–11.789	–12.438	–12.636
Ki (nM)	55	23	2.1	0.7 ± 0.1	0.5 ± 0.09

^aThe experimental binding free energies (ΔG_expt) were converted using −RT ln(K_i).¹⁹

Figure 8.

Correlation coefficient (R²) values plotted for experimental (ΔG_bind = −RT ln(K_i)) versus predicted (ΔG_mmgbsa in kcal/mol) BFE values. The predicted BFE values were produced using three different igb parameters.

In general, the energy values obtained by MD based MMGBSA approach fail to converge consistently. Therefore, it is suggested that several repeated simulations could obtain reliable BFE values.²² In the current study, the MD simulations were repeated five times to obtain good estimate of BFE values for Mcl1–inhibitor complexes.

In summary, the BFE values obtained by MD based MMGBSA approach were in good agreement with experimental values. In general, the correlation coefficient (R²) values are used as a primary measure to quantify the consistency of the computed BFE values from the MD trajectories. In the current study, good correlation values were observed for first two igb models. Additionally, the correlation coefficient approach was used to rank the binding affinity values. Overall, this clearly indicates that first two igb models can be preferred for further evaluation, as there are studies reporting a similar trend.²²

Identification of the Key Residues Responsible for the Complex Formation

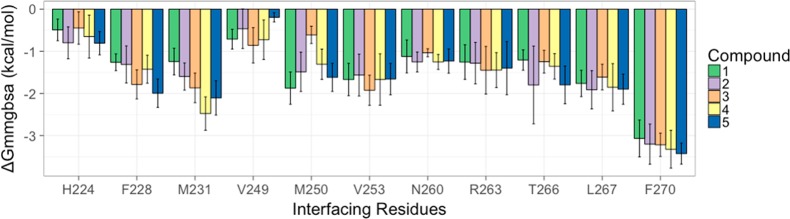
Per-residue decomposition analysis was performed to probe the energy differences among the interface residue due to inhibitor binding using the MMPBSA.py³⁰ script with 500 snapshots obtained from the last 20 ns of the MD trajectory with an even interval of 40 ps (Figure 9). The decomposition analysis provided valuable insight on the major energy contributing residues that were in contact with inhibitor. Closer investigation at the binding site of Mcl1 revealed that an ensemble of hydrophobic and polar residues exhibited significant variations in energy profiles (Figure 10).

Figure 9.

Comparison of BFEs (kcal/mol) for Mcl1 interfacing residues with 2-indole amide series of inhibitor.¹⁹ Mean values ± SD from decomposition analysis of MD simulations.

Figure 10.

Binding site residues of Mcl1 complexed with 2-indole amide inhibitor series.¹⁹

The decomposition analysis revealed an ensemble of 11 residues, H224, F228, M231, V249, M250, V253, N260, R263, T266, L267, and F270, that contributed approximately greater than −1 kcal/mol to the free energy of binding. To gain more insight on the relative energy contribution among the contact residues, the BFEs obtained for all five inhibitor complexes were compared (Figure 9 and Table 3). The predicted BFEs for all the complexes showed that the core indole acid group of the inhibitors acts as the central stabilizing factor, anchored to the interior of hydrophobic binding pocket of Mcl1 very well.

Table 3. BFE (kcal/mol) Values Obtained for the Key Residues in Contact with 2-Indole Amide Series of Inhibitor from Decomposition Analysis.

residues	compd 1	compd 2	compd 3	compd 4	compd 5
H224	–0.49 ± 0.3	–0.79 ± 0.4	–0.44 ± 0.1	–0.65 ± 0.2	–0.81 ± 0.1
F228	–1.26 ± 0.0	–1.31 ± 0.2	–1.79 ± 0.1	–1.43 ± 0.0	–1.99 ± 0.1
M231	–1.24 ± 0.4	–1.60 ± 0.1	–1.87 ± 0.4	–2.48 ± 0.4	–2.11 ± 0.4
V249	–0.71 ± 0.3	–0.46 ± 0.1	–0.85 ± 0.3	–0.72 ± 0.2	–0.19 ± 0.1
M250	–1.87 ± 0.4	–1.48 ± 0.2	–0.61 ± 0.4	–1.30 ± 0.4	–1.61 ± 0.4
V253	–1.67 ± 0.2	–1.56 ± 0.0	–1.92 ± 0.1	–1.66 ± 0.1	–1.65 ± 0.3
N260	–1.12 ± 0.0	–1.25 ± 0.4	–1.04 ± 0.2	–1.25 ± 0.3	–1.23 ± 0.0
R263	–1.26 ± 0.1	–1.28 ± 0.1	–1.45 ± 0.4	–1.45 ± 0.1	–1.40 ± 0.1
T266	–1.21 ± 0.4	–1.80 ± 0.2	–1.25 ± 0.1	–1.36 ± 0.1	–1.80 ± 0.2
L267	–1.76 ± 0.3	–1.91 ± 0.3	–1.61 ± 0.4	–1.85 ± 0.0	–1.90 ± 0.4
F270	–3.07 ± 0.1	–3.20 ± 0.1	–3.22 ± 0.3	–3.32 ± 0.1	–3.43 ± 0.1

From Figure 10, one can observe that the residue F270 located proximal to the parent indole acid group of the inhibitor contributed predominantly to the binding free energy with −3.07, −3.2, −3.22, −3.32, and −3.43 kcal/mol, for complex 1 to 5, respectively (Figure 9 and 11). In addition, three hydrophobic residues, M231, V253, and L267, provided large energy contributions. The cumulative energies for these residues were −4.68, −5.07, −5.40, −6.00, and −5.66 kcal/mol for complex 1 to 5, respectively. Furthermore, F228, M250, and T266 generated moderate energies. The combined energies for these residues were −4.34, −4.6, −3.64, −4.09, and −5.41 kcal/mol for complex 1 to 5, respectively. Similarly, N260 and R263, residues highly conserved among the Bcl2 family members, also contributed moderate energies. Particularly, N260 contributed −1.12, −1.25, −1.04, −1.25, and −1.26 kcal/mol for complex 1 to 5, respectively. Closer investigation revealed that N260 of complex 5 produced higher energy in comparison to the other complexes. To probe the reason behind this higher energy contribution by N260, the binding pocket of Mcl1 was inspected. The result showed that N260 interacts with the methyl-pyrrazole group of the inhibitor improving the binding affinity in complex 5. This is in agreement with the experimental results.¹⁹ Likewise, R263 forms polar interactions with inhibitors contributing −1.26, −1.28, −1.45, −1.45, and −1.4 kcal/mol, for complex 1 to 5, respectively. Closer inspection at the binding site revealed that the complex stability was further strengthened by a cation−π interaction between the guanidinium group of R263 and the 3-benzoic acid of inhibitors. H224 and V249 provided only meager energy contributions. Their combined energies were −1.2, −1.26, −1.31, −1.38, and −1 kcal/mol for complex 1 to 5, respectively (Figures 9–11). This suggests that H224 and V249 play less important roles in complex formation. Likewise, M250 shows less energy for compound 3 in comparison with other compounds, which implies less importance. Overall, the decomposition analysis suggests that F270 is the major energy-contributing residue for the 2-indole amide Mcl1 inhibitor series.

Figure 11.

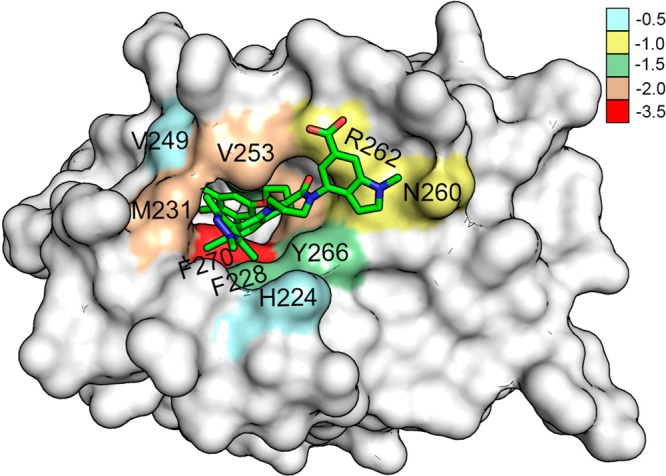
Distribution of BFE (kcal/mol) values depicted over the residues at the P2 binding pocket of Mcl1 (molecular surface representation) complexed with compound 5.

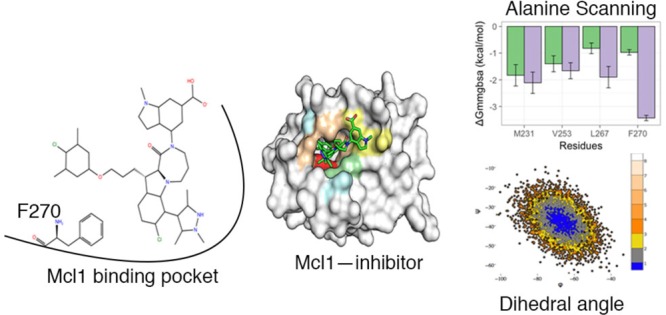
Computational Alanine Scanning

To validate the predicted energy values of the crucial residues obtained from per residue decomposition analysis, computational alanine scanning was performed. According to decomposition analysis, the residues M231, V253, L267, and F270 produced more energy contributions with inhibitors (Figure 9). To further substantiate these high energy residues, computational alanine scanning (ΔG_ala) was performed (Table 4). Consecutively, residues were mutated to alanine for compounds 3, 4, and 5, which exhibited high experimental values (ΔG_expt). The selected three complexes were subjected to 100 ns MD simulations. Furthermore, decomposition analysis was performed for residues in the complex (ΔG_ala), and the energies were compared with residues in the wild-type complex (ΔG_wild). Subsequently, the differences in the BFE (ΔG_mmgbsa^ala-scan) obtained between wild-type (ΔG_wild) and the mutant complex (ΔG_ala) were used to determine the hot spot residues.

Table 4. The BFE (kcal/mol) Values Obtained from Computational Alanine Scanning (ΔG_mmgbsa^ala-scan) Approach for Major Energy Contributing Residues.

	compd 3			compd 4			compd 5
residue	ΔGwild	ΔGala	ΔGmmgbsaala-scan	ΔGwild	ΔGala	ΔGmmgbsaala-scan	ΔGwild	ΔGala	ΔGmmgbsaala-scan
M231	–1.87 ± 0.4	–1.25 ± 0.2	–0.62 ± 0.2	–2.48 ± 0.4	–0.89 ± 0.3	–1.59 ± 0.1	–2.11 ± 0.4	–1.83 ± 0.4	–0.28 ± 0.0
V253	–1.92 ± 0.1	–0.89 ± 0.3	–1.03 ± 0.0	–1.67 ± 0.1	–1.24 ± 0.2	–0.43 ± 0.0	–1.66 ± 0.3	–1.40 ± 0.3	–0.26 ± 0.0
L267	–1.61 ± 0.4	–0.74 ± 0.2	–0.87 ± 0.2	–1.85 ± 0.0	–1.18 ± 0.2	–0.67 ± 0.0	–1.90 ± 0.4	–0.82 ± 0.2	–1.08 ± 0.2
F270	–3.22 ± 0.3	–0.98 ± 0.3	–2.24 ± 0.0	–3.32 ± 0.1	–1.05 ± 0.3	–2.27 ± 0.0	–3.43 ± 0.1	–0.97 ± 0.1	–2.46 ± 0.0

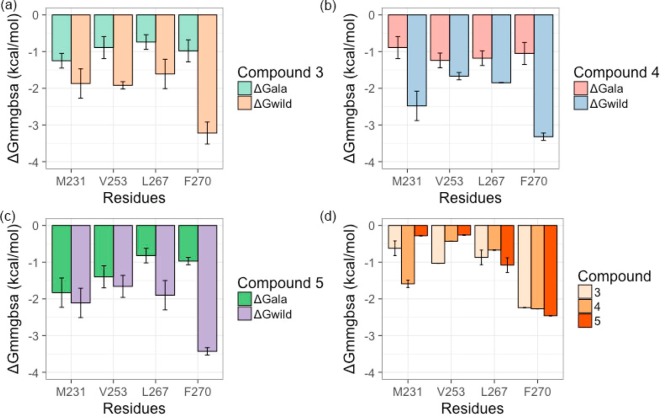
The BFEs obtained for all the complexes were negative (Figure 12). For compound 3, the BFEs for the four mutated residues, ΔG_M231A, ΔG_V253A, ΔG_L267A, and ΔG_F270A, were −1.35, −0.89, −0.74, and −0.93 kcal/mol, respectively (Figure 12a). Consequently, the differences in BFE (ΔG_mmgbsa^ala-scan) between wild-type (ΔG_wild) and the mutant complex (ΔG_ala) were −0.62, −1.03, −0.87, and −2.29 kcal/mol (Figure 12d). For compound 4, the BFEs for the mutated residues were −0.89, −1.24, −1.18, and −1.05 kcal/mol (Figure 12b), and the energy differences with wild-type residues were −1.59, −0.43, −0.67, and −2.27 kcal/mol (Figure 12d). Similarly, for compound 5, the BFEs for mutated residues were −1.83, −1.40, −0.82, and −0.97 kcal/mol (Figure 12c), and their change in energies from wild-type residues were −0.28, −0.26, −1.08, and −2.46 kcal/mol (Figure 12d).

Figure 12.

In silico alanine screening performed on major energy contributing residues (a–c). The bar graph plotted for BFEs (kcal/mol) obtained for wild-type and the in silico mutants. (d) Comparison of energy difference between wild-type and in silico mutants. Consistency in energy pattern, high energy, observed for F270 in all three complexes, in comparison with other three mutants. Mean values ± SD from decomposition analysis of MD simulations.

As the current study comprises the same series of chemical compounds that bind to the hydrophobic binding pocket of Mcl1 (Figure 10) and exhibit a conserved binding pattern of interactions, we assume that the energies exhibited by the potential residues can be on a similar scale. Considering these factors, results from the Table 4 and Figure 12d reveal that the BFEs (ΔG_mmgbsa^ala-scan) obtained for the in silico mutants (M231A, V253A, and L267A) failed to display consistency. Therefore, the feasibility of the obtained energies is somewhat doubtful. Despite the fact that the compounds 3–5 interact with the common residue pattern, M231A (helix 3), V253A (helix 4), and L267A (helix 5) residues in the Mcl1 binding pocket, inconsistency in BFEs could plausibly be due to the following reasons: a crucial portion of the chemical compound (a) is prevented from important surrounding interactions or (b) exhibits weak interactions with the surrounding residues in the binding pocket leading to negligible energy contributions, or (c) there is a cooperative interacting effect of this residue pattern with the inhibitors that might tend to exhibit strong energies, while the point mutations on these residues affected the BFEs. This prediction can be further validated by experimental approaches.

Contrastingly, the differences in BFE (ΔG_mmgbsa^ala-scan) obtained for the mutant F270A were as high as −2.2, −2.27, and −2.46 kcal/mol for compounds 3, 4, and 5, respectively. From this strong evidence, we were able to make a plausible assumption that F270 might serve as a hot spot residue for 2-indole amide inhibitor series.

Conformational Mobility Analysis

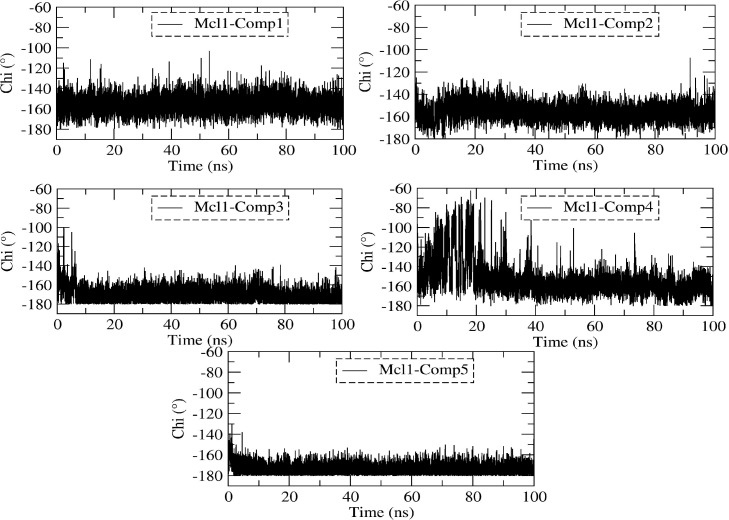
To explore the reason behind the tight binding, the evolution of the χ₁ dihedral angle of the F270 side chain was measured for all five complexes over time (Figure 13). According to decomposition and in silico alanine scanning analysis, F270 contributed stronger binding energy values in comparison with other interacting binding site residues. Figure 13 show that the side chain mobility of F270 is much stronger in all five complexes over the time. Likewise, the χ₁ dihedral angle of F270 is located in the range ∼162° to 167° in all complexes.

Figure 13.

Dihedral angle (chi (χ₁), deg) measured for the side chain residue F270 in complex 1–5 during MD simulation.

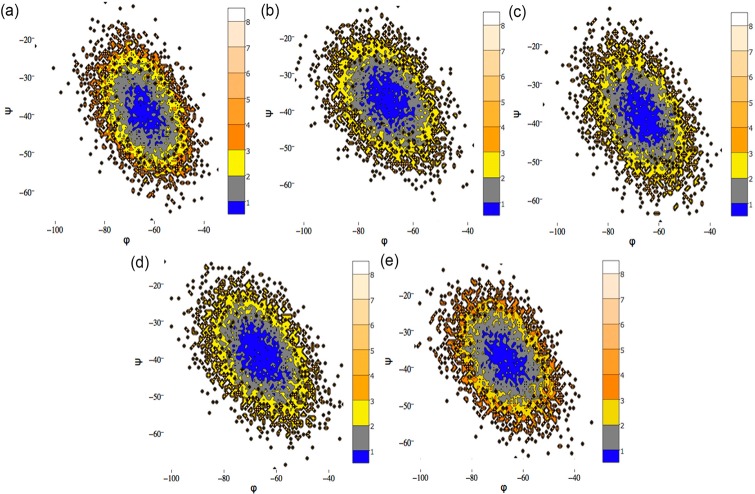
Energy landscape maps generated using the ψ and φ angle values of a particular residue can clearly emphasize the differences in conformational change between the complexes. Therefore, to further probe the conformational change of F270 residue the free energy landscape maps were plotted using ψ and φ angle values (Figure 14). The result shows that the ψ and φ angles of F270 exhibited similar conformational orientation for all complexes. The ψ and φ angles of F270 are −39.98° and −63.83° for complex 1, −37.13° and −68.86° for complex 2, −39.39° and −65.18° for complex 3, −38.45° and −65.51° for complex 4, and −38.85° and −65.04° for complex 5. The above results suggest that the F270 exhibited strong interaction to the core indole acid group of the inhibitors by maintaining the similar side chain conformational orientation, which significantly contributed to the tight binding over time. This result was in agreement with decomposition and in silico alanine scanning mutation analysis.

Figure 14.

Energy landscape contour map depicted using the backbone angle ψ and φ for F270 in complex 1–5 (a–e) during MD simulation.

Conclusion

In the current study, binding poses were predicted for 2-indole amide Mcl1 inhibitors using docking and MD simulations. The major differences between the inhibitors on Mcl1 were studied extensively by (i) domain cross-correlation analysis highlighting the differences by correlated and anticorrelated regions and (ii) principle components analysis highlighting the observable variations by concerted motions on the atomic coordinates. Subsequently, multiple sampling models of MMGBSA technique were used to compute the BFEs between the compounds. The calculated energies confirm that the binding energies predicted by igb-2 model were in good agreement with experimental values (R² = 0.93). Additionally, the per-residue decomposition analysis revealed that M231, V253, L267, and F270 contributed more energy in all complexes. This further suggests that these might be crucial residues involved in the origin of binding for 2-indole amide inhibitors to Mcl1. Furthermore, F228, M231, M250, V253, T266, L267, and F270 residues provided considerable contributions to the complex formation. Conversely, we were able to predict the hot spot residue using computational alanine scanning and decomposition analysis. The predicted hot spot residue might be used as a guideline to improve the binding quality from nanomolar to picomolar range for 2-indole amide inhibitor. Also, the overall results obtained from the current study might serve as valuable insights for the discovery of new generation Mcl1 inhibitors.

Glossary

Abbreviations

AAP

antiapoptotic proteins

BFE

binding free energy

FED

free energy decomposition

Bcl-2

B cell leukemia

Mcl1

myeloid cell leukemia

BH

BH3 homologue

MD

molecular dynamics simulations

MMGBSA

molecular mechanics-generalized Born solvent accessibility

The authors declare no competing financial interest.