Biophysical Characterization of Supported Lipid Bilayers Using Parallel Dual-Wavelength Surface Plasmon Resonance and Quartz Crystal Microbalance Measurements

Abstract

Supported lipid bilayers (SLBs) have been used extensively as an effective model of biological membranes, in the context of in vitro biophysics research, and the membranes of liposomes, in the context of the development of nanoscale drug delivery devices. Despite numerous surface-sensitive techniques having been applied to their study, the comprehensive optical characterization of SLBs using surface plasmon resonance (SPR) has not been conducted. In this study, Fresnel multilayer analysis is utilized to effectively calculate layer parameters (thickness and refractive indices) with the aid of dual-wavelength and dispersion coefficient analysis, in which the linear change in the refractive index as a function of wavelength is assumed. Using complementary information from impedance-based quartz crystal microbalance experiments, biophysical properties, for example, area-per-lipid-molecule and the quantity of lipid-associated water molecules, are calculated for different lipid types and mixtures, one of which is representative of a raft-forming lipid mixture. It is proposed that the hydration layer beneath the bilayer is, in fact, an integral part of the measured optical signal. Also, the traditional Jung model analysis and the ratio of SPR responses are investigated in terms of assessing the structure of the lipid layer that is formed.

1. Introduction

Biomimetic membrane models are the leading platforms to complement in vitro cell-screening assays in the analysis of biochemical and physical interactions involving biomembranes.^1,2 The design and study of these platforms is not only important with respect to advancements in cell biology but also from a pharmaceutical perspective; individualized drug therapies and selective targeting of membrane proteins require information regarding the complex catalytic biochemical processes performed by membrane proteins with a resolution far beyond the diffraction limit of visual optics. Understanding the functionality of membrane proteins, in turn, will require insight into the biophysical properties of the membrane. Moreover, the use of fluorescence in drug screening is problematic: the introduction of exogenous fluorescent tags to the molecules of interest can lead to prominent changes in system morphology. Also, intrinsic autofluorescence of the compound libraries themselves can result in false positives through interference effects. These factors increase the need for label-free alternatives resilient to autofluorescence.³ Furthermore, membrane models are a key tool for the in vitro investigation of the surface properties of nanoscale drug delivery devices, for example, drug delivery liposomes.⁴

One particular type of membrane model, supported lipid bilayers (SLBs), is known for its relative ease of preparation. Since the pioneering work of Tamm and McConnell,⁵ using monolayer transfer from a Langmuir trough to an oxidized silicon wafer, and the later studies of Kasemo and co-workers, using quartz crystal microbalance (QCM),⁶ SLBs have been successfully characterized using a myriad of surface-sensitive techniques. These include conventional surface plasmon resonance (SPR),⁶ dual polarization interferometry (DPI),⁷ coupled plasmon-waveguide resonance,⁸ ellipsometry,⁹ and atomic force microscopy.¹⁰ In many cases, the combined use of these techniques has proven to be effective.¹¹⁻¹⁴ Despite this, the extent to which SLB morphology and the mechanism of its formation via vesicle fusion have been characterized remains limited. Regarding the use of one promising technique, SPR, this can be seen to be, at least partly, due to the lack of the development of suitable computational algorithms to accurately calculate optical properties of ultrathin layers. Now that these algorithms that make use of the Fresnel-layer formalism are available, we have utilized what we believe to be the most effective protocols for these calculations.

In contrast to conventional SPR devices with fixed optical configurations, where the incident laser angle is confined to a very limited scanning range, the angular range of the SPR instrument used in our study is much broader, spanning 38–78°. This facilitates the measurement of reflection spectra in both air and liquid media. A broad angular range of scanning also allows for the determination of the refractive index of the bulk medium above the sensor surface from a measurement of the angle of total internal reflection (TIR) that can be extracted from the data contained within the reflectance spectrum.

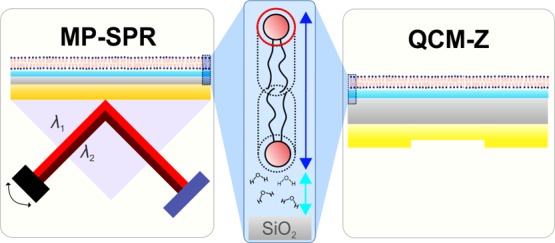
In our study, we used QCM as a complementary technique to investigate the SLB. So far, two varieties of QCM instruments have been developed: QCM with dissipation monitoring (QCM-D) and impedance-based QCM (QCM-Z); we have used QCM-Z in our study. While QCM-D calculates the energy dissipation via decay in the ring-down effect of the voltage between the QCM electrodes, QCM-Z calculates the same parameter using equivalent-circuit modeling of the QCM quartz crystal.

SLBs are typically formed on the interior surface of the sensor or the transducer-forming part of the microfluidic flow channel systems. This is achieved using the well-established approach of vesicle fusion and adsorption onto a silicon dioxide (SiO₂) sensor surface.¹⁵ Typically, small unilamellar vesicles (SUVs), prepared via thin-film hydration using either extrusion or sonication resizing techniques, are introduced into the flow channel. The vesicles adsorb onto the surface and subsequently rupture to form an SLB, promoted through substrate–vesicle interactions. It is now recognized that many variables affect this process and impact the final quality of the SLB that is formed, for example, vesicle size, lipid concentration, pH, and flow speed. Furthermore, osmotic pressure difference¹⁶ and α-helical peptide-mediated vesicle fusion^17,18 have both been used as supplementary approaches to induce vesicle rupture of systems where SLB formation is more challenging. Such cases include lipid systems in possession of a more stable structure that is difficult to disrupt, or the deposition of an SLB onto a surface with less favorable surface chemistry for SLB formation, for example, gold or titanium dioxide, as opposed to the standard SiO₂ surface, optimal for SLB formation. Even when these advanced techniques are used to enhance SLB formation, the resulting SLB may still be imperfect, and patches of supported vesicular layers (SVLs) may remain within the SLB. In some cases, it is possible to determine the extent to which SVLs remain within the SLB.¹⁹ However, even if this is the case, interactions between analytes and the SVLs cannot be differentiated from those with the uncorrupted regions of the SLB that is to be studied. Therefore, enhanced control of the SLB structure and morphology of the SVLs that remain within it is required.²⁰ While a fully formed SLB is characterized by the overlap of multiple frequency overtones and low values of energy dissipation when both the QCM-Z and QCM-D techniques are used, no reliable parameters allowing for the differentiation between SLB and SVL morphologies have yet been found for optical techniques.

In general, biophysical analysis of SLBs using purely optical methods, for example, SPR, is burdened by two key factors: (1) the relation between the surface mass of the bilayer to the recorded SPR sensorgram and (2) the contribution of the hydration layer between the sensor surface and the bilayer to the measured signal. In this study, we delve into both problems, using a combination of dual-wavelength SPR and QCM-Z techniques. This type of multi-technique analysis, however, is not new: Reimhult et al.,^11,21 using conventional SPR and QCM-D, have previously developed the foundations for theoretical analysis of time-dependent hydration of simple SLBs composed of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC). In recognition of their work performed on this subject, we intend to complement the established techniques using dual-wavelength Fresnel-layer modeling.

The aim of this study is to provide a complete optical characterization of SLBs with different lipid compositions, along with their formation processes, using Fresnel-layer modeling of the SPR reflectance data. The analysis is complemented with QCM-Z experiments conducted in parallel, to extract the properties of the hydration layer between the SLB and the sensor surface, that is not possible to discern using SPR alone. It should be noted that while the current manuscript will focus on the SPR protocol, such measurements and analyses are also relevant to ellipsometry experiments. We present the theoretical framework for the calculation of hydration-layer thickness and biophysical parameters of SLBs and a procedure for the extraction of Fresnel-layer parameters for the SLB formation. Last, we investigate the prospects of SLB–SVL differentiation concerning the recent work of Rupert et al.²² regarding the ratio of SPR responses. Five lipids or lipid compositions were investigated, namely, 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC); POPC; DOPC together with negatively-charged 1,2-dioleoyl-sn-glycero-3-phospho-l-serine (DOPS) in a molar ratio of 7:3; 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC); and a ternary mixture of DOPC, sphingomyelin (Sm), and cholesterol (Chol) in a molar ratio of 1:1:1. A lipid with a serine headgroup was chosen to induce a net negative surface charge to the lipid headgroup region. DPPC was chosen as a saturated lipid with a high phase transition temperature to promote formation of an SVL. The last composition (DOPC–Sm–Chol) is particularly interesting from a biological perspective, as it is known to form liquid-ordered domains that consist of Sm and Chol.²³ Such domains are believed to be the main constituent of lipid “raft” structures in biological membranes.²⁴

2. Experimental Section

2.1. Materials

DOPC, POPC, DOPS, DPPC, and egg Sm were obtained from Avanti Polar Lipids (Alabaster, USA) and dissolved in chloroform (25 mg/mL in CHCl₃). Chol was obtained from Northern Lipids (Burnaby, Canada). NaCl (sodium chloride), CaCl₂ (calcium chloride), HEPES (4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid), and CHAPS (3-[(3-)cholamidopropyl) dimethylammonio]-1-propanesulfonate) were obtained from Sigma-Aldrich (Helsinki, Finland). Ion-exchanged ultrapure water with a resistivity of 18 MΩ·cm and a TOC level of <5 ppm from a Milli-Q purification system was used for the preparation of water-based solutions.

2.2. Sensor Surface Preparation

Silica-coated SPR sensor slides and QCM-Z crystals were obtained from BioNavis Ltd (Tampere, Finland) and Q-Sense Inc./Biolin Scientific (Västra Frölunda, Sweden), respectively. It should be noted that while both silica-coated surfaces are similar in nature, they are not identical. Both the slides and crystals were first flushed with a sufficient volume of 70% (v/v) ethanol and ultrapure water and then dried under a steady stream of nitrogen. They were then treated with oxygen plasma (PDC-002, Harrick Plasma, Ithaca, USA) for 5 min at 29.6 W and 133–173 Pa to remove any organic contaminants. Between individual QCM-Z measurements, all crystals were washed in situ with sequential injections of 20 mM CHAPS, 2% (v/v) Hellmanex, 70% (v/v) ethanol, and ultrapure H₂O. Because of the differences in the fabrication techniques, the silica layer of the SPR sensor slides is more prone to structural degradation in comparison to the silica layer on QCM sensors. Therefore, between individual SPR measurements, SPR sensor slides were cleaned following removal from the measurement chamber by first rinsing the sensors with CHAPS, to remove any lipids from the surface, and then by the plasma cleaning protocol described above. If it seemed that the flush sequence for the QCM-Z crystals was not enough to regenerate the surface, the ex situ procedure was also repeated for the QCM-Z crystals.

2.3. Fabrication of Small Unilamellar Vesicles

SUVs were prepared using the thin-film hydration method followed by extrusion. Chloroform was first evaporated from the lipid solution (1 mL of 10 mg/mL lipids) using a rotary vacuum evaporation system at 60 °C for the DOPC, POPC, DOPC–DOPS, and DPPC, or under a steady nitrogen stream and vacuum desiccator for DOPC–Sm–Chol. Afterward, hydration was performed either at room temperature (SLB-forming vesicles) or at 60 °C (DPPC vesicles) by first dissolving the lipids into a standard HEPES buffered saline (HBS)-buffer (20 mM HEPES, 150 mM NaCl at pH 7.4) and then vigorously shaking the tube for 5 min. The multilamellar ternary lipid suspension (DOPC–Sm–Chol) was first extruded through a 400 nm pore-size polycarbonate filter membrane at 60 °C, followed by extrusion through 200, 100, and 50 nm filter membranes at 60 °C, 11 times for each membrane. Other multilamellar vesicle suspensions were extruded 11 times through a 50 nm pore-size polycarbonate filter membrane at 60 °C. After extrusion, all the vesicle solutions used for the SLB formation experiments had a mean particle-size (number average) of less than 70 nm and a polydispersity index of <0.2 (see the Supporting Information, Table S1 for individual size distributions), as determined using dynamic light scattering (Zetasizer APS instrument, Malvern Instruments Ltd, Worcestershire, UK). Vesicles were stored at 4 °C until use. Before experiments, vesicles were diluted in a HBS buffer containing 5 mM CaCl₂. The final lipid concentration in each experiment was 0.15 mg/mL.

2.4. Experimental Procedure for Dual-Wavelength SPR and QCM-Z

A dual-wavelength (670 and 785 nm lasers) multiparametric SPR (MP-SPR) instrument (BioNavis 220A, BioNavis Ltd, Tampere, Finland) was used to record SPR reflectance spectra over the range of 57.5°–78° as a function of time. For clarity, the plot of the change in the angular position of the SPR peak minimum as a function of time is referred to as an “SPR sensorgram” throughout the present work. The impedance-based QCM Z-500 instrument (KSV Instruments Ltd, Helsinki, Finland) was used as a complementary measurement technique. A peristaltic pump system (Ismatec/Cole-Parmer GmbH, Wertheim, Germany) was used for both SPR and QCM-Z experiments to ensure similar hydrodynamic flow conditions. To approximately match the flow conditions between the two systems, flow speeds of 30 and 250 μL/min were used for SPR and QCM, respectively.¹² Three measurements were performed using SPR and QCM-Z for each lipid composition: DOPC; POPC; DOPC–DOPS (7:3); DPPC; and DOPC–Sm–Chol (1:1:1). Both SPR and QCM-Z measurements were performed at 20 °C. Data analysis was performed with BioNavis LayerSolver (v. 1.2.1, BioNavis Ltd, Tampere, Finland), OriginPro (v. 8.6, OriginLab Corp., Northampton, MA, USA), and MATLAB (R2016a, The MathWorks Inc., Natick, MA, USA) software.

3. Theory and Data Analysis

3.1. Fresnel-Layer Analysis

The Fresnel-layer matrix formalism, as employed within the proprietary LayerSolver (BioNavis) program, has proven to be effective as a technique to determine the optical properties of layers with thicknesses in the nanometer range for a variety of biological applications.²⁵⁻²⁸ In the analysis software, Fresnel multilayer equations for p-polarized light are fitted to the SPR reflection spectra, treating every layer as an optically homogenous layer. Basically, there are four options to calculate optical properties of layers using LayerSolver software provided with the SPR instrument, as detailed below. Three of these methods of analysis have been described in previous studies (methods 1, 2, and 3). The fourth (4), that we have developed, is a new methodology that we have combined with method (3) for our study. Each of these approaches will be described in greater detail below. For clarity, all of the SPR studies described in this manuscript involve simultaneous SPR reflectance measurements at two different wavelengths, namely, 670 and 785 nm, as shown in the Supporting Information, Figure S1.

3.1.1. Two-Media Method²⁵

If the optical properties of the layer do not change between different bulk media (e.g., no layer swelling in response to the liquid), thickness values may be solved in two media (typically, air and water) as a function of n, where n is the refractive index of the layer. The procedure is repeated for all recorded wavelengths separately, using a range of refractive index values (n) to derive a continuum plot for each media. The continuum plot for each media is then drawn on a common graph, with the intersection of the obtained continuum solutions for each media indicating the exact thickness and the refractive index of the layer.

3.1.2. Dual-Wavelength Method

This method has been the standard dual-wavelength analysis method since its introduction by Peterlinz and Georgiadis.²⁹ The method is based on the assumption of a linear dispersion coefficient relative to wavelength change, which approximates the derivative of the refractive index as a function of the wavelength according to equation

1

where the two wavelengths are abbreviated as λ₁ = 670 nm and λ₂ = 785 nm, in our case. A disadvantage of this method is that this coefficient must be known beforehand. Because the change in the angular position of the SPR peak minimum is a continuum solution of changes in both adsorbing layer thickness and the refractive index, a change of variables according to eq 1 allows the resolution of a unique solution of (d, n₁, n₂), given that dn/dλ is known. Possible values of d are calculated for a wide range of n₁ and n₂ values and, by horizontally shifting the second refractive index continuum solution, d(n₂), by the amount Δ(dn/dλ), d and n₁ can be solved from the cross-section of the two data sets. While this can be done manually, as described, the analysis can also be performed automatically in the LayerSolver software by setting the parameters (d, n) as dependent variables between the two wavelengths and dn/dλ as a fixed value using the “linear” simulation mode. Since the thickness, d, is not expected to have dependence on wavelength and both wavelength measurements are performed in the same buffer, it is a real dependent variable between the two data sets which are to be modeled. However, setting the refractive index as a dependent parameter is merely a software-specific feature and does not mean that the refractive indices for the two wavelengths are equal. To obtain the refractive index for the second wavelength, eq 1 can be used afterward.

3.1.3. Algorithm-Based Dual-Wavelength Method

An algorithm-based dual-wavelength method was used to calculate optical parameters during the vesicle rupture process because of the fact that the inverse dual-wavelength method (4) was not found to be sensitive in the low refractive-index, high-thickness regime. The method has been used before by Granqvist et al.²⁰ and has the advantage that the precise value of the dispersion coefficient does not need to be known.

In contrast to method (2), all the parameters (d, n, dn/dλ) are linked as dependent variables between the two wavelengths in this method, and the LayerSolver software attempts to find the best fit values of d, n, and dn/dλ using dedicated fitting algorithms. Therefore, the only difference between methods (2) and (3) is that the dispersion coefficient is a variable in method (3), while it is fixed in method (2). Ultimately, the refractive index of the layer for the second wavelength, n₂, can be calculated using eq 1 as previously.

In contrast to method (4), this algorithm-based method was not very sensitive to the values of bulk refractive indices and, hence, nearly the same thickness and refractive index values (with different dispersion coefficients of the layer) can be obtained even with slight differences in the bulk refractive indices. This method was not found to be suitable for determining the hydration-layer thicknesses because of its lower precision in comparison with method (4), but instead, was implemented to analyze the evolution of the optical parameters during the formation of SLBs.

3.1.4. Inverse Dual-Wavelength Method

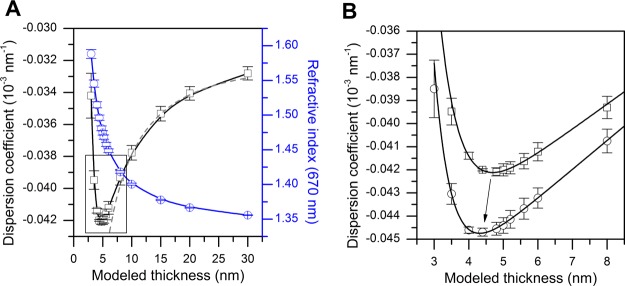
Instead of finding d for each pair of n₁ and n₂ values separately, as utilized in method (2), refractive indices can be calculated simultaneously for each fixed thickness value (hence the term “inverse”). In this case, the linear dispersion coefficients can be calculated for each value of d via eq 1 and plotted as a function of layer thickness. In a thin-film regime, the plot tends to form a minimum at certain values of d and dn/dλ, which is likely due to the specific properties of the software’s algorithms. In Figure 1A, the entire range of modeled thickness values and the corresponding dispersion coefficients and refractive indices at 670 nm are presented for a DOPC bilayer.

Figure 1.

Principle of inverse dispersion coefficient modeling, demonstrated for DOPC bilayers. (A) Dispersion coefficient (black squares) and refractive index at 670 nm (blue circles) modeled in the thickness range of 3–30 nm. Solid lines are Bezier curves connecting the data points. The dashed line depicts the fit of the Jung model to the data as a combination of eqs 1 and 3. (B) Framed area of the dispersion coefficient is highlighted, with hydration-layer thickness d_H2O = 0 (squares). The dispersion coefficient with hydration-layer thickness d_H2O = 0.5 nm (circles) is also shown. Solid lines show the best fits of an asymmetric parabola (Shah) function which were used to determine the exact minima of the dispersion coefficient curves.

The values of the dispersion coefficients are heavily dependent on the refractive indices of the bulk liquid media used in the measurements, which are nearly impossible to determine with a high degree of precision. While the initial bulk indices were obtained from the data collection software (calculated from the TIR angle via Snell’s law), it was discovered that even the smallest possible changes in the bulk refractive indices (and hence the change in the dispersion coefficient of the bulk) induce a change in the minimum position (see the Supporting Information, Figure S2). The consequences of this bulk index effect to the determination of the optical parameters of the layer have not been discussed in detail in previous SPR studies. We found that by changing the refractive index of the bulk liquid at 785 nm from its initial value with the smallest possible increments, one can find the value where the minimum position first shifts below 6 nm, which is an approximate dimension of where the layer thickness is to be expected. In a few cases, there was a second bulk index value which was equally likely to correspond to the correct minimum position. In these instances, the bulk index value which provided the best resolution near the minimum was selected, that is, the other value was discarded because the dispersion coefficient near the theoretical minimum did not change as much with 0.1 nm incremental changes in thickness. A more detailed description of the analysis method can be found in the Supporting Information.

3.2. Hydration-Layer Analysis

Biophysical characterization of model membranes requires defined universal quantities which allow effective comparisons between different types of measurements. The surface-area-per-lipid-molecule (a), which can be calculated from the lipid mass per unit surface (Γ, surface-mass density), describing lateral packing of the lipids in the bilayer, is well-suited for this purpose. However, calculation of this value using purely optical methods is challenging because of the discrepancies regarding the influence of the hydration layer located between the bilayer and the sensor surface, previously estimated to be ∼0.5–1 nm in thickness.^11,30 In QCM-Z or QCM-D, the mass of this layer is coupled with the quartz crystal resonator and cannot be distinguished from the mass of the “dry” bilayer, making the use of complementary methodologies necessary to resolve the characteristics of these co-existing layers. The surface-mass density of the hydration layer can be written as a difference of surface-mass densities obtained by QCM and SPR

2

While Γ_QCM is readily available from Sauerbrey analysis of the QCM-Z data (Supporting Information eq S3), mass density and thickness of the bilayer are needed to calculate Γ_SPR. These parameters can be calculated from an approximation of the angular shift in SPR peak minimum using the well-established Jung model.³¹ The model states that the angular position of the SPR peak minimum (in absolute degrees) of an optically homogenous layer is proportional to d and n via equation

3

where S is the bulk sensitivity constant in degrees per refractive index unit (deg), δ is the decay length of the intensity of the evanescent electric field, and n_b is the bulk refractive index. The best fit of the Jung model to the dispersion coefficient (combinations of eqs 1 and 3) as a function of the modeled thickness for a DOPC bilayer is presented in Figure 1A (dashed gray line). Using mass density of the layer provided by the de Feijter formula

4

and assuming a linear approximation at small layer thicknesses (d ≪ δ), eq 3 can be used to solve the surface-mass density as follows

5

In the abovementioned equations, dn/dC is the derivative of the refractive index with respect to the lipid concentration in the measured volume, signified by the capital letter “C”. Unfortunately, the dn/dC value has not yet been properly established for lipid bilayers. While the commonly accepted average for proteins is 0.185 mL/g,³² the choice of values for bilayers varies between 0.135 mL/g to as high as 0.25 mL/g.^7,11,33 In addition, all the sensor-specific parameters (R, S, δ) are expected to vary between different sensor batches, making the analysis even more challenging. Reimhult et al.¹¹ acknowledged the limitations of the de Feijter formula in their study and used a more complicated two-component Lorenz–Lorentz formula to calculate surface-mass densities from the refractive index values obtained from the Jung model. Therefore, eq 5 is not needed if the refractive index of the layer is known. However, calculation of the refractive index using the Jung model is not as accurate as Fresnel-layer modeling because of the variations in S and δ in eq 3. Therefore, instead of using the Jung model in our analysis, we use a combination of Fresnel-layer modeling and the Lorenz–Lorentz equation to calculate surface-mass densities from the SPR experiments.

The two-component Lorenz–Lorentz equation gives the (isotropic) mass density of the bilayer from an optical measurement as follows

6

where r = A/M is the ratio of molar refractivity and the molecular weight of the lipids (r = 0.2859 mL/g for DOPC) and ν is the partial specific volume of lipids (a reasonable value of ν = 1.05^–1 mL/g ≈ 0.952 mL/g is assumed).^7,34 Isotropic refractive indices were estimated according to n_iso = ((n² + 2(n – ϕ)²)/3)^1/2, where values of n were calculated from Fresnel-layer modeling at 670 nm wavelength as discussed previously, and anisotropy values (ϕ) were obtained from the studies of Mashaghi et al.⁷ It should be noted that because the Lorenz–Lorentz formula is very sensitive to changes in the isotropic refractive index, the choice of anisotropy values obviously affects the results. However, we found it more reasonable to make this correction to our data because using the refractive index values for the p-polarized field can lead to a vast overestimation of surface-mass density of the bilayer. Isotropic refractive indices are used only to calculate surface-mass densities. For the exact choice of parameters for different lipid compositions, see the Supporting Information, Table S3.

By changing the thickness of the hydration layer between the SiO₂ layer and the lipid bilayer in the Fresnel-layer modeling (d_H2O = 0, 0.5, 1.0 and 1.5 nm), values of d and n for the bilayer were calculated for each hydration-layer thickness value and, finally, c_iso was calculated for each value of n. Because the surface-mass density of the hydration layer can be calculated as Γ_H2O = c_H2O·d_H2O, eqs 2 and 6 can be used to solve the average surface-mass density of the “dry” unsolvated lipid bilayer as a cross-section of two data sets obtained with the two measurement methodologies, Γ_QCM – Γ_H2O = Γ_QCM – c_H2O·d_H2O (from QCM-Z) and Γ_SPR = c_iso·d (from SPR), when plotted as a function of modeled hydration-layer thickness.

The data obtained using only the 670 nm wavelength SPR data were used in the hydration-layer modeling (n = n₁ in the preceding equations), and the dispersion coefficient “inverse” method (4) was used to extract d and n₁ for each d_H2O value, as described previously. As demonstrated in Figure 1B, the minimum of the dispersion coefficient curve shifts to lower thickness values along with increasing d_H2O. The thickness of the nonhydrated bilayer was calculated as d = νΓ, where Γ is the cross-section value of the surface-mass density and ν ≈ 0.952 mL/g. Hydration-layer analysis was not performed for DPPC SVLs because the lipid-associated water cannot be treated as one homogenous layer.

3.3. Optical Layer Modeling of the SLB Formation

We use, to our knowledge, dispersion coefficient modeling for the first time to characterize SLB formation via the vesicle rupture process. While the aforementioned method (3) is not new, its application to optical layer modeling of the SLB formation is, as far as we are aware, novel. For this procedure, six time points were selected for each SLB formation experiment: four time points during the steep rise phase of the response at the beginning of the injection (adsorption of vesicles to the surface), one time point just before the end of the injection, and one time point after the end of the injection, once the signal had stabilized. Because the fitting algorithm is very sensitive to the initial values of the fit, a specific and defined approach to exclude unrealistic fitting results was established. First, it was assumed that the refractive index of the lipid system will increase with time, and the initial values of the refractive index n₁ were chosen accordingly as 1.35, 1.40, and 1.48 depending on the time point. Second, thickness values were varied between 5 and 20 nm. Third, the initial value of the dispersion coefficient was always kept at dn/dλ = −0.035 × 10^–3 nm^–1 to minimize variability in fitting conditions between different measurements. For clarity, the list of initial values used for each time point is presented in the Supporting Information, Table S4. Finally, unrealistic fits, as defined by improbable thickness values for the calculated layer, were discarded, and three fits were chosen at each time point which had the most similar dispersion coefficient values. For all cases where this was not possible, the fits that had the most similar thickness values were chosen. The averages of those fit values were selected as the final result of that experiment at that time point.

In addition, quantification of coupled water mass during the rupture process was investigated. The mass of the lipid system in the QCM-Z studies was calculated using the simple Sauerbrey equation (Supporting Information eq S3). Because the adsorbing vesicular layer and the bilayer are treated as homogenous optical layers in the analysis, the two-component Lorenz–Lorentz formula (eq 6) could be used first to calculate the Γ_SPR for each six time points. These values were then used in the linear fitting of Γ_SPR as a function of R (average sensorgrams for each lipid composition) at the same time points to obtain the correlation factor ΔΓ/ΔR for each composition. After transforming the average SPR sensorgrams for each lipid composition to the surface-mass densities, as a function of time via multiplication with the corresponding correlation factor, Γ_H2O could be calculated via eq 2, as a function of time. However, in this approach, the coupled water beneath the bilayer is not treated as a separate layer in the analysis.

In addition, packing densities of vesicles at the point of maximal associated water for SLB-forming vesicles and DPPC vesicles were calculated. Following the recent work of Rupert et al.,²² we define the relative packing density of vesicles as follows

7

where the subscript l refers to the vesicular layer over the sensor surface and f corresponds to the lipid bilayer which forms the vesicle. Values of d_f and n_f were obtained from Fresnel-layer modeling of the bilayers via the algorithm-based method (3), and d_f = 5 nm and n_f = 1.48 were used for analysis involving DPPC vesicles, for which bilayer parameters were not available from experiments. The factor 0.74048 in the equation takes into account the fact that the relative packing density is calculated in relation to the full hexagonal packing of vesicles as a single layer. The vesicle deformation is not taken into account in the analysis. For DPPC vesicles, at least, the effect is not expected to be prominent because of the high transition temperature of DPPC (T_m = 41 °C).

4. Results and Discussion

4.1. Single-Layer Analysis of SLBs

First, SLBs were modeled through Fresnel-layer analysis of the SPR data, treating a bilayer and hydration layer as a single optically homogenous layer. According to the results of the modeling (Table 1), the dispersion coefficient values, excluding the ternary lipid mixture, are close to the value of −0.042 × 10^–3 nm^–1. For the ternary DOPC–Sm–Chol bilayer, the magnitude of the dispersion coefficient is slightly higher (dn/dλ ≈ −0.046 × 10^–3 nm^–1) probably because of the presence of liquid-ordered domains in the bilayer. The two methods (3 and 4) used in the analysis yield very similar results: refractive index values at 670 nm wavelength for different lipid bilayer compositions are in the range of 1.4776–1.4889, using method (3) and 1.4774–1.4855, using method (4). DOPC and ternary DOPC–Sm–Chol vesicles form the most optically dense bilayers (highest n), followed by DOPC–DOPS and POPC, respectively. Mashaghi et al.,⁷ using dual-polarization interferometry, found the opposite ranking in the values of refractive indices. In contrast to our analysis, they modeled the data in both “TM” and “TE” polarization modes using constant isotropic thickness (4.7 nm). Despite the differences in methodology and order of ranking, the refractive index values obtained in our study for the p-polarized electric field are within the same range as their values for isotropic modeling of the refractive index (∼1.46–1.49).

Table 1. Optical Parameters of the SLBs Obtained with Fresnel-Layer Modeling of the Reflectance Spectra from SPR Measurements, Averaged over Three Individual Measurements with Standard Errors of the Mean (See the Supporting Information for Calculation of SEMs).

lipid	d (nm)	n1	n2	dn/dλ (10–3 nm–1)
Method 3:Algorithm-BasedDual-WavelengthModeling
DOPC	4.90 ± 0.06	1.4776 ± 0.0013	1.4728 ± 0.0013	–0.0420 ± 0.0006
DOPC–DOPS	4.89 ± 0.10	1.4827 ± 0.0018	1.4778 ± 0.0018	–0.0427 ± 0.0007
POPC	4.96 ± 0.03	1.4776 ± 0.0017	1.4728 ± 0.0017	–0.0423 ± 0.0003
DOPC–Sm–Chol	6.04 ± 0.33	1.4889 ± 0.0069	1.4835 ± 0.0069	–0.0463 ± 0.0009
DPPC	76.13 ± 3.34	1.3614 ± 0.0016	1.3567 ± 0.0014	–0.0410 ± 0.0020
Method 4: InverseDual-WavelengthModeling
DOPC	4.70 ± 0.16	1.4845 ± 0.0025	1.4797 ± 0.0025	–0.0421 ± 0.0001
DOPC–DOPS	5.04 ± 0.15	1.4781 ± 0.0062	1.4732 ± 0.0061	–0.0428 ± 0.0009
POPC	4.96 ± 0.04	1.4774 ± 0.0016	1.4725 ± 0.0016	–0.0421 ± 0.0001
DOPC–Sm–Chol	6.13 ± 0.06	1.4855 ± 0.0033	1.4800 ± 0.0032	–0.0459 ± 0.0003
DPPCa	37.36 ± 1.26	1.3829 ± 0.0019	1.3792 ± 0.0016	–0.0320 ± 0.0031

^aThe average thickness of the DPPC vesicle layer was first calculated from Sauerbrey analysis of the QCM-Z data by using an adlayer mass density of c = 1.05 g/mL. Subsequently, the refractive indices were calculated by Fresnel-layer modeling of SPR measurements, with the thickness value derived from the QCM-Z measurements used as a fixed value in the Fresnel modeling. All other values in the table were determined from modeling of the SPR reflectance spectra.

Granqvist et al.²⁰ have previously calculated refractive indices for Egg-PC bilayers using dual-wavelength SPR with Fresnel-layer modeling. However, Granqvist et al. quote a drastically lower refractive index value (n₁ = 1.4421) for Egg-PC, compared to our results for synthetic lipids. This disparity may indicate differences between the analytical procedures between the two studies. Particularly, the determination of the optical properties of the substrate layers of the sensor slides themselves and the choice of initial values for the fits may have an impact on the final results. Theoretical calculations by Huang and Levitt³⁵ (n = 1.486 for a bilayer lipid membrane in a field perpendicular to the long lipid tails—with length N = 37) further support our findings of higher refractive indices for SLBs, rather than the lower values suggested by Granqvist et al.

4.2. Hydration-Layer Analysis of SLBs

Next, the hydration layer was modeled as a separate optical layer in the Fresnel-layer analysis, and QCM-Z was used as a complementary technique to extract the thickness of the “dry” bilayer. The average area-per-lipid-molecule and thickness values calculated from hydration-layer modeling are shown in Table 2, and the calculation principle of finding the cross-section of surface-mass densities is presented in graphical form for DOPC in Figure 2. Our results are in agreement with those published using X-ray and neutron scattering techniques: Kučerka et al. obtained the values of d = 3.98 nm and a = 0.627 nm² for POPC bilayers at 20 °C and d = 3.68 nm and a = 0.669 nm² for DOPC at 30 °C.³⁶⁻³⁸ Measurements in our study were performed at 20 °C, while theirs for DOPC were executed at 30 °C; if the temperature difference is taken into account, our results are in good agreement. While no similar data are available for the DOPC–Sm–Chol lipid mixture, this exact system has been investigated previously using molecular dynamics simulations: Pandit et al. calculated a thickness difference of 0.74 nm near the center of the “raft-like” domains and 0.45 nm at the domain boundaries.³⁹ Assuming constant bilayer density, our results predict the averaged thickness difference between the DOPC and DOPC–Sm–Chol bilayers to be ∼0.73 nm. Finally, introducing negative-charged DOPS to the bilayer results in a slight increase in bilayer thickness (from 3.83 to 3.93 nm) and a tighter packing of the lipids (a decrease in area-per-lipid-molecule of pure DOPC from 0.649 to 0.638 nm²). The effect is probably due to the increase in hydrogen-bonding between the PS headgroups.⁴⁰

Table 2. Hydration-Layer Modeling of Data from SPR and QCM-Z Measurements^a.

lipid	d (nm)	a (nm2)	dH2O (nm)	NH2O
DOPC	3.83 ± 0.08	0.649 ± 0.013	0.336 ± 0.167	7 ± 4
DOPC–DOPS	3.93 ± 0.06	0.638 ± 0.010	0.526 ± 0.168	11 ± 4
POPC	3.90 ± 0.03	0.617 ± 0.005	0.597 ± 0.127	12 ± 3
DOPC–Sm–Chol	4.56 ± 0.15	0.421 ± 0.013	0.561 ± 0.234	8 ± 4

^aThickness d corresponds to the thickness of a nonhydrated bilayer calculated assuming a constant density (c = 1.05 g/mL).

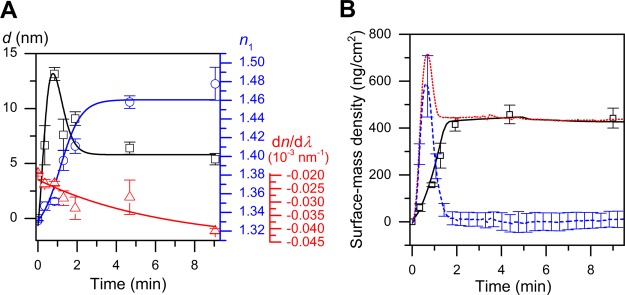
Figure 2.

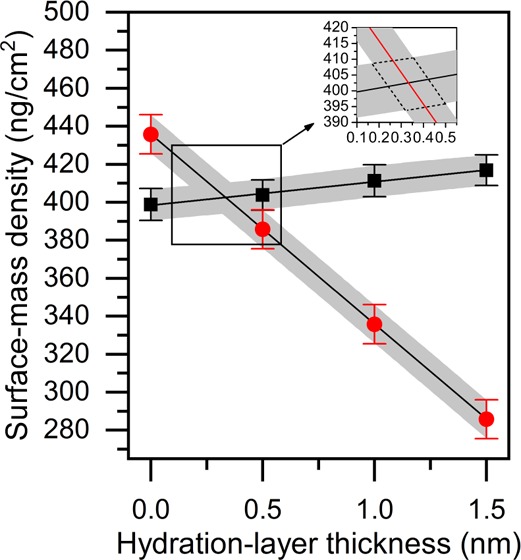
Hydration-layer modeling (surface-mass density, ng/cm², as a function of hydration-layer thickness, nm) of the SPR (black squares) and QCM-Z data (red circles) for a DOPC bilayer. Gray areas depict the standard errors of the mean for both measurement techniques. The inset shows more closely the cross-section of the two data sets. Dotted lines surrounding the cross-section in the inset were used as error boundaries for surface-mass density, hydration-layer thickness, and the other measured parameters derived from these two (presented in Table 2).

In addition to the area-per-lipid-molecule and thickness values of the “dry” bilayer, we calculated the number of water molecules (N_H2O) associated with each lipid headgroup using the thickness values for the hydration layer (d_H2O) beneath the bilayer (Table 2). On average, the thickness of the hydration layer varies between 0.34 and 0.60 nm, and the number of water molecules in the hydration layer ranges from 7 to 12. These values are close to those calculated by Reimhult et al.¹¹ (d_H2O = 0.6 nm and N_H2O = 13 for POPC), despite the fact that our method for calculating the optical parameters of the bilayer differ from their simpler iterative approach. Zwang et al.,³⁰ on the other hand, using a combination of DPI and QCM-D, have claimed that the thickness of the hydration layer between the DOPC bilayer and SiO₂ surface is even higher (d_H2O = 1.02 nm). Their method of mass conversion for the DPI methodology, however, was not explained in detail. Therefore, the “dry” mass of the bilayer in their study may have been underestimated.

In the hydration-layer analysis, the hydration layer is treated as a separate layer in the Fresnel-layer analysis. When the modeled thickness of the hydration layer is increased, the refractive index of the “dry” bilayer must increase accordingly, to compensate. In this study, these refractive index values were transformed into surface-mass density values of the “dry” bilayer using the Lorenz–Lorentz equation (eq 6). As shown in Figure 2 (black squares), the resulting data, when plotted against the hydration-layer thickness, depict almost a horizontal line. The relationship indicates that analyzing the hydration layer as a separate layer has no significant effect on the “dry” surface-mass density when using the Lorenz–Lorentz equation as a method of mass conversion. Thus, if only the conversion from SPR data to surface-mass density is desired, resolving the thickness of the hydration layer is not necessary.

Even if the hydration layer and the “dry” bilayer are treated as a single layer in the analysis, a component of the angular shift in the SPR peak minimum still belongs to the hydration layer. This is reasoned by the fact that the hydration layer is in direct contact with the sensor surface and not the bulk liquid. Therefore, the optical parameters derived from the single-layer analysis (Table 1) are for the “wet” bilayer. If the thickness of the hydration layer is to be resolved, SPR data alone is not sufficient, and complementary techniques are required. It may be argued, however, that the amount of coupled water does not match between the two complementary techniques used. For SPR and QCM-Z, the differences in surface roughness of the sensor surfaces and the possibility of dynamically coupled water being partly included in the QCM-Z baseline cannot be ruled out.

4.3. Kinetics of SLB Formation

As a last step in the modeling of the SPR and QCM-Z data obtained in this study, the formation kinetics of the SLBs were investigated. The adsorbing and rupturing SUVs forming the SLBs were treated as homogenous optical layers, as per the argument in the previous section, namely, that the hydration layer has a negligible effect in SPR signal-to-mass conversion. The formation of an SLB in SPR is characterized by a rapid increase in layer thickness during the first phase of vesicle adsorption (shown for DOPC in Figure 3A), behaving much like energy dissipation observable via QCM-Z and birefringence in dual-polarization interferometry studies. At the same time, the amount of dynamically coupled water increases (Figure 3B). The average refractive index value of 1.352 ± 0.003 and a layer thickness of 13.2 ± 0.7 nm for DOPC at critical coverage indicate the presence of a loosely packed SVL (Table 3). Beyond that point, the system enters into a “state of uncertainty,” and it is likely that vesicles and patches of recently formed SLBs coexist. The heterogeneity of the system is demonstrated by the high uncertainty of the parameters at the fourth time point.

Figure 3.

(A) Time-evolution of DOPC bilayer thickness (black squares), refractive index (blue circles), and dispersion coefficient (red triangles) calculated using algorithm-based Fresnel-layer modeling of the SPR data. Squares represent the calculated values, and solid lines are the fits using appropriate functions showing the trend of the data. (B) Time-evolution of different surface-mass densities for the DOPC bilayer: Γ_SPR (black solid line), Γ_QCM (red dotted line), and Γ_H2O (blue dashed line, calculated via eq 2 using SPR and QCM-Z data). Square data points are the calculated values from Fresnel-layer modeling which were used to transform SPR sensorgrams into surface-mass densities as a function of time.

Table 3. Maximum Surface Coverage (% of Full Hexagonal Packing) for Different Lipid Compositions along with Maximum Vesicle Thickness (Calculated from SPR Fresnel-Layer Modeling), Maximum Coupled Water Mass and Water-to-Lipid ratio at the Point of Maximum Coupled Water Mass (Calculated from Eq 2 Using SPR and QCM-Z Data)^a.

lipid	αmax(%)	dmax (nm)	Γmax,H2O (ng/cm2)	water-to-lipid ratio at Γmax,H2O
DOPC	8.7 ± 1.0	13.2 ± 0.6	588 ± 81	5.05 ± 1.17
DOPC–DOPS	13.3 ± 0.3	15.3 ± 2.3	726 ± 7	4.86 ± 0.08
POPC	12.3 ± 0.2	21.2 ± 2.3	754 ± 46	4.00 ± 0.56
DOPC–Sm–Chol	11.1 ± 1.8	16.7 ± 3.8	817 ± 22	4.07 ± 0.13
DPPC	71.2 ± 2.2	81.9 ± 3.3	2644 ± 188	1.96 ± 0.16

^aQCM-Z frequency values used in the analysis were calculated using the Sauerbrey equation (Supporting Information eq S3).

The calculated critical coverage for DOPC is only ∼9% of the full hexagonal packing (Table 3). Because of the charge repulsions that exist between the negatively charged SiO₂ surface and DOPS headgroups, higher surface coverage of vesicles (∼13%) is needed for vesicle rupture of DOPS compared to other lipid compositions. The calculated degrees of lateral packing, however, do not consider the possibility of vesicle deformation, a crucial step in vesicle-bilayer transformation.⁴¹ Therefore, the results presented here should only be taken as relative values between the different lipid types.

Vesicles consisting of DPPC do not spread to form SLBs at 20 °C and, instead, form a rigid layer of SVLs on the SiO₂ surface, with a high packing density (71 ± 2%). Sauerbrey analysis (Supporting Information eq S3) of the QCM-Z measurement data resulted in an average layer thickness of 37.36 ± 1.26 nm (using a constant surface density of c = 1.05 g/mL in the calculation). The modeled thickness is indeed low, but defects in the SVL and the uncertainty in the amount of coupled water (and surface concentration of the lipids) make it difficult to model the SVL as a homogenous layer. On the other hand, SPR modeling resulted in a much higher layer thickness (76.1 nm) for the SVLs than the average vesicle diameter calculated using dynamic light scattering (56 nm). One explanation for this discrepancy is the limitations of the modeling using method (3) as described previously.

4.4. Jung Model Parameters

Parameters in the Jung model may be useful for assessing the quality of the formed SLB. The Jung model (eq 3) was first fitted to the individual continuum solution curves for the two wavelengths which yielded the decay lengths for each SPR experiment. Refractive index increments were then calculated with two different methods: (1) with the aid of correlation factors from the linear fitting of Γ(R)curves and the Jung-model approximation of the surface-mass density (eq 5), and (2) with the mass conversion by the Jung-model approximation (eq 5) and the two-component Lorentz–Lorenz equation (eq 6, using the values in Table 1 method 4). The average correlation factors were calculated as 595.6 ± 20.6 (ng·cm^–2)/° (670 nm) and 1070.0 ± 30.0 (ng·cm^–2)/° (785 nm) for SLBs. The calculated refractive index increments using the first method were (dn/dC)_λ,1 = 0.155 ± 0.002 mL/g and (dn/dC)_λ,2 = 0.153 ± 0.002 mL/g, while the values calculated by the second method were (dn/dC)_λ,1 = 0.159 ± 0.002 mL/g and (dn/dC)_λ,2 = 0.162 ± 0.003 mL/g. In contrast to these values, Konradi et al.³³ used a significantly higher refractive index increment in their study (0.25 mL/g). They claimed to have derived this value from the study of Salamon and Tollin⁸ who calculated unusually high optical parameters for a POPC bilayer (n_p = 1.526 and d = 5.3 nm at λ = 632.8 nm). While the principle of calculation for dn/dC = 0.25 mL/g was not made clear by Konradi et al., a completely different method of SLB formation by Salamon and Tollin is suspected to be the origin of the difference between that value of Konradi et al. and our results. One should remember, however, that the values of refractive index increment for a lipid bilayer were determined using the Jung model for SLBs and not by conventional measurement of the refractive index as a function of the bulk concentration.

For SVLs composed of DPPC, using the average thickness and refractive index values from the modeling of SVL formation kinetics resulted in SPR correlation factors of 711.0 (ng·cm^–2)/° (670 nm) and 1227.2 (ng·cm^–2)/° (785 nm) and refractive index increments of (dn/dC)_λ,1 = 0.127 mL/g and (dn/dC)_λ,2 = 0.133 mL/g using the first method and (dn/dC)_λ,1 = 0.141 ± 0.002 mL/g, (dn/dC)_λ,2 = 0.153 ± 0.001 mL/g using the second method. The results agree with previously published turbidity and light-scattering measurements on lipid vesicle dispersions.⁴² The surface-mass density values calculated from optical modeling of the SPR data follow closely the trend of the actual measured SPR sensorgram (Figure 3B), even with the slight differences between correlation factors calculated for SLBs and SVLs. Also, refractive index increments are similar: the average of the (dn/dC)_λ,1 values calculated using the two methods are 0.157 mL/g for the SLBs and 0.134 mL/g for the SVLs. Hence, the similarity of mass conversion for SLBs and SVLs is expected, given the uncertainties in the experimental methodology and measurements.

4.5. Ratio of SPR Responses and Peak Widths as Potential Tools for SLB–SVL Differentiation

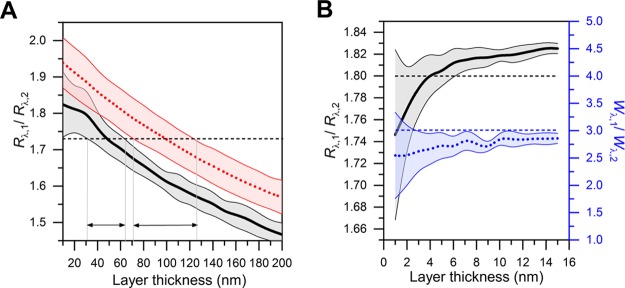
Rupert et al.²² have suggested use of the ratio between SPR responses at two separate wavelengths as a tool to determine nanoparticle size along with the bulk concentrations under diffusion-limited conditions. Here, we review the method in relation to our experiments. As per the analysis of the previous section, the dispersion coefficient of the adsorbing layer is expected to increase gradually from the value of pure buffer (dn/dλ ≈ −0.02 × 10^–3 nm^–1) as the surface-coverage of vesicles increases. This is regardless of whether a true SLB is formed or not. Choosing the ratio of refractive index increments for the two wavelengths as 1.02, as used by Rupert et al., is equivalent to choosing a dn/dλ value of −0.023 × 10^–3 nm^–1 in the refractive index range 1.34–1.35 (670 nm). Figure 4A illustrates the fact that thickness determination using the ratio of responses should only be applied in the case of low surface coverages of nanoparticles in a narrow refractive index range near to the value of the bulk liquid. With low surface coverage, using an average ratio of responses for vesicles results in a thickness estimate of 31–64 nm (black, solid thick line in Figure 4A). However, with higher surface coverage (n = 1.35–1.37 and dn/dλ ≈ −0.04 × 10^–3 nm^–1, red, dotted line in Figure 4A), the thickness estimate will change considerably (i.e., 71–126 nm). In contrast, using a high refractive index range (n = 1.47–1.49 and dn/dλ ≈ −0.04 × 10^–3 nm^–1, Figure 4B), corresponding to the properties of SLBs, no estimates can be made. Therefore, the amount of error arising from the errors of individual parameters is too high to make conclusions about layer thicknesses of neither vesicles nor SLBs at higher surface coverages of adsorbing lipid material; this is in line with the analysis of Rupert et al.²² Because the dynamic light scattering studies revealed that the extruded vesicles had a diameter less than 70 nm, however, SVLs in this study may have been formed in the lower range of surface coverage corresponding to the refractive index range of 1.34–1.35.

Figure 4.

(A) Calculated ratio of SPR responses for SVLs at a low coverage (thick black solid line, n = 1.34–1.35, dn/dλ = −0.024 × 10^–3 nm^–1) and at higher coverage (thick red dotted line, n = 1.35–1.37, dn/dλ = −0.04 × 10^–3 nm^–1). Horizontal dashed line corresponds to the experimental average for SVLs, while the regions defined by the arrowheads correspond to the possible ranges of layer thickness values at that experimental value (1.73). (B) Ratio of SPR responses (thick black solid line) and the ratio of shifts in SPR peak width (thick blue dashed line), n = 1.47–1.49, dn/dλ = −0.04 × 10^–3 nm^–1). Horizontal dashed lines represent the experimental average values for SLBs. Solid thin lines show the error boundaries of the calculation averaged over the described refractive index range.

In addition to the ratio of response values, we analyzed the ratio of changes in the SPR peak width between the two wavelengths. Peak width was calculated as the 25% intensity value between the angular peak minimum intensity and the maximum intensity of the SPR angular spectrum. Average ratios of responses were R_λ,1/R_λ,2 = 1.80 ± 0.01 for SLBs (total of 12 measurements) and 1.73 ± 0.01 for SVLs (three measurements). The corresponding average ratios of the change in peak widths were W_λ,1/W_λ,2 = 3.01 ± 0.14 (SLBs) and 2.61 ± 0.45 (SVLs). Because the dispersion coefficients of the two types of layers (SLBs and SVLs) are similar, some qualitative assessments about the nature of the layer can be made. The results indicate that regardless of the layer parameters of individual sensors, the ratio of response and peak width values well below 1.8 and 3.0 may indicate incomplete SLB formation and the presence of unruptured vesicles. This suggests that these parameters may be used as tools to assess the quality of SLB formation. However, the reader is reminded that these guiding values are only applicable to the SiO₂ sensors used in this study and, in any case, complete characterization of the layer with Fresnel-layer modeling is preferable.

In addition to the dispersion coefficients of the bulk liquid and the bilayer, decay lengths of the evanescent electric field will also affect the variation in the measured response ratios. Using experimentally determined bulk sensitivity parameters (S_λ,1 = 116.68° and S_λ,2 = 98.75°) in the Jung model (eq 3), which is demonstrated in Figure 1A, yielded decay-length values of δ_λ,1 = 107.2 ± 1.4 nm and δ_λ,2 = 161.6 ± 1.6 nm on the SPR SiO₂ substrate. These values were calculated by fitting the Jung model to the continuum solutions obtained with the Fresnel-layer analysis. In the study of Rupert et al.,²² an uncertainty range of 5% was used for the individual decay lengths when keeping the ratio δ_λ,2/δ_λ,1 fixed. However, this uncertainty depends on the way that the error is calculated. In this study, the uncertainty for the ratio δ_λ,2/δ_λ,1 was 2.5%, using the standard error of the mean, and 9.5%, using standard deviation, the average ratio being 1.507.

Our results agree conclusively with the previous work of Reimhult et al.¹¹ with regards to the degree of hydration beneath the POPC lipid bilayer. Also, the values obtained for the refractive indices in the p-polarized field are in line with the study of Mashaghi et al.⁷ When Fresnel-layer analysis of SPR reflectance spectra was combined with Sauerbrey analysis of the QCM-Z technique, it was possible to extract the thicknesses of the hydration layer and the overlying “dry” lipid bilayer itself. The thickness values obtained were surprisingly close to those obtained in a number of previously published X-ray and neutron scattering studies.³⁶⁻³⁸ In addition, simplified tools for characterizing SLBs and SVLs without the usage of Fresnel-layer analysis have been provided. Similar values for both SLBs and SVLs can be used when converting the measured SPR signal responses to mass density by using dn/dC values and linear mass conversion coefficients. For example, using the average parameters obtained in this study with the angular shift in SPR peak minimum of 0.7° at 670 nm wavelength would yield Γ_SPR = 410 ng/cm² using the Jung model and Γ_SPR = 417 ng/cm² using linear mass conversion coefficient. Finally, the ratio of responses (∼1.80 for SLBs vs ∼1.73 for SVLs) was investigated, as previously proposed by Rupert et al.²² Despite the fact that the exact values for these ratios are greatly sensor substrate-dependent, lower values of the ratio (≪1.80) may indicate defects in the formed SLB.

5. Conclusions

Previously, calculation of optical properties of nanometer-scale films using SPR has been hindered by the lack of accurate analysis methods. In this study, we have provided advanced methodology for thin-layer characterization utilizing Fresnel-layer analysis, enabling the accurate determination of the thickness, refractive indices, and linear dispersion coefficient of the layer. Also, following the work of Reimhult et al.,¹¹ we further investigated the combination of dual-wavelength SPR and QCM-Z in revealing critical biophysical details of hydrated thin films that are not possible to evaluate using either of the techniques alone. This was readily demonstrated using SLBs, important biomimetic systems, formed on silicon dioxide surfaces.

The analysis in this work revealed that once the optical effect of the bulk liquid on the measured signal is carefully taken into account, dispersion coefficients of different SLB compositions are very similar. The difference between the liquid-disordered bilayers (DOPC, DOPC–DOPS, and POPC) and the bilayers forming liquid-ordered domains (DOPC–Sm–Chol) indicates that the dispersion coefficient may directly reflect the degree of the molecular order within a layer. While inverse dispersion coefficient modeling (4), complemented with the algorithm-based method (3), is superior for in-depth optical modeling, the conventional dispersion coefficient analysis (2) using a fixed dispersion coefficient of approximately −0.042 × 10^–3 nm^–1 for SLBs can be less time-consuming, especially because this method is implemented in the proprietary LayerSolver software and does not need to be performed manually. For other ultrathin films, for which the thickness is only approximately known, method (4) can provide more control over which continuum solutions should be chosen. Also, while the additional use of the algorithm-based method (3), with different initial values of the layer parameters, is recommended, it must be recognized that the choice of these initial values has a drastic influence on the final results.

Looking ahead, we intend to focus toward systems that exhibit greater complexity, for example, bioactive compounds expressing nonspecific binding to SLBs and other biologically relevant thin films. These systems have proved problematic to investigate because of the lack of measurement and analysis methodologies of sufficient accuracy. Differences in adsorbed mass between the SPR and QCM techniques would indicate hydration-related changes in the bilayer morphology. Therefore, the parallel use of these techniques would be particularly beneficial. While the approaches presented in this study form a basis for studying biomimetic platforms using SPR, appropriate analysis methodology for these more novel applications remains to be clarified in further studies.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.8b01259.

• Definition of the error parameters; size distributions of the vesicles; calculation of SPR sensor parameters; inverse dual-wavelength analysis; SPR experimental details; and QCM-Z experimental details (PDF)

The authors declare no competing financial interest.