Prioritized memory access explains planning and hippocampal replay

Abstract

To make decisions, animals must evaluate candidate choices by accessing memories of relevant experiences. Yet little is known about which experiences are considered or ignored during deliberation, which ultimately governs choice. We propose a normative theory predicting which memories should be accessed at each moment to optimize future decisions. Using nonlocal “replay” of spatial locations in hippocampus as a window into memory access, we simulate a spatial navigation task where an agent accesses memories of locations sequentially, ordered by utility: how much extra reward would be earned due to better choices. This prioritization balances two desiderata: the need to evaluate imminent choices, vs. the gain from propagating newly encountered information to preceding locations. Our theory offers a simple explanation for numerous findings about place cells; unifies seemingly disparate proposed functions of replay including planning, learning, and consolidation; and posits a mechanism whose dysfunction may underlie pathologies like rumination and craving.

1. Introduction

A hallmark of adaptive behavior is the effective use of experience to maximize reward [1]. In sequential decision tasks such as spatial navigation, actions can be separated from their consequences in space and time. Anticipating these consequences, so as to choose the best actions, thus often requires integrating multiple intermediate experiences from pieces potentially never experienced together [2, 3]. For instance, planning may involve sequentially retrieving experiences to compose a series of possible future situations [4, 5]. Recent theories suggest that humans and animals selectively engage in such prospective planning as appropriate to the circumstances, and that omitting such computations could underlie habits and compulsion [6, 7, 8]. However, by focusing only on whether or not to deliberate about the immediate future, these theories largely fail to address which of the many possible experiences to consider in this evaluation process, which ultimately governs which decisions are made.

In addition to prospective planning, behavioral and neuroimaging data suggest that actions can also be evaluated by integrating experiences long before decisions are needed. Indeed, future decisions can be predicted not only from prospective neural activity [5], but also from neural reinstatement when relevant information is first learned [9] and during subsequent rest [10, 11] (Fig. 1a). Yet, this further highlights the selection problem: If actions can be evaluated long before they are needed, which experiences should the brain consider at each moment to set the stage for the most rewarding future decisions? Addressing this question requires a more granular theory of memory access for evaluation, which takes forward planning as a special case of general value computation.

Figure 1: A rational model of prioritized memory access.

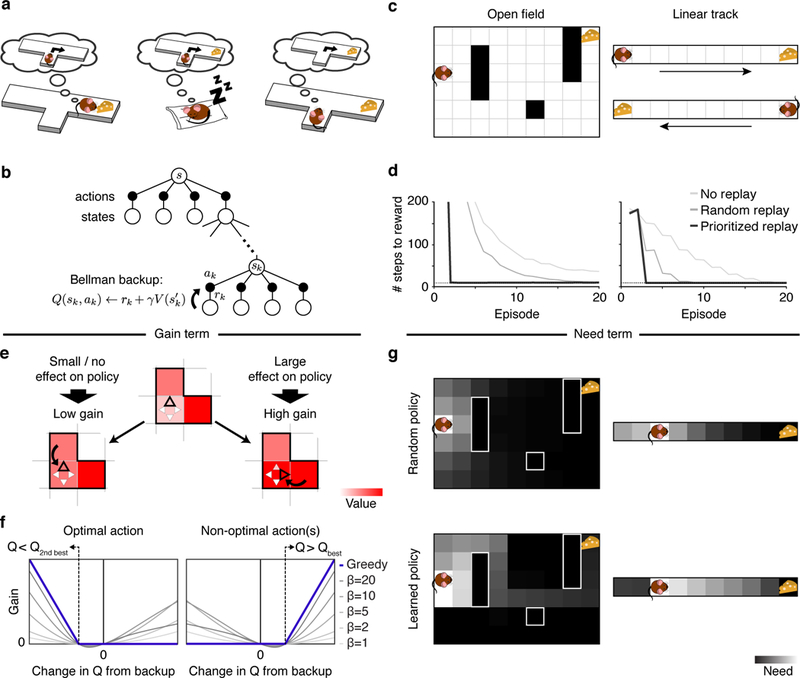
(a) Three ways an agent might learn, through sequential memory access, the relationship between actions and rewards: Left: when reward is first encountered, through reverse reactivation; Center: during sleep or rest through “offline” reactivation of the sequence; Right: prior to choice, by prospective (forward) activation. The latter case is the most commonly envisioned in theories of model-based deliberation, but replay of all three sorts exist, and human neuroimaging evidence suggests that all can support decisions. (b) A schematic of a Bellman backup where the reactivation of a nonlocal experience e_k = (s_k,a_k,r_k,s´_k) propagates the one-step reward r_k and the discounted value of s^´_k to the state-action pair (s_k,a_k). (c) Grid-world environments simulated. Left: A two-dimensional maze (Sutton’s DYNA maze [26]) with obstacles. Right: a linear track simulated as two disjoint segments (to reflect the unidirectionality of the hippocampal place code in linear tracks) with rewards in opposite ends. (d) Performance of a greedy agent in the two simulated environments. Replaying experiences according to the proposed prioritization scheme speeds learning compared to learning without replay or with replay of randomly ordered experiences. Left: Open field; Right: linear track. Dotted lines represent optimal performance. (e) The gain term for updating the value of a target action in a target state quantifies the expected increase in reward following a visit to the target state. Left: if the best action is updated with a higher value, the policy changes little/nothing, resulting in a small/zero gain. Right: if a non-optimal action is updated with value higher than the best action’s value, the policy in the corresponding state changes, resulting in a large gain. Here, squares represent states, triangles represent actions, and the arrow represents a Bellman backup which updates the value of an action. The highlighted triangle represents the action with highest estimated value. (f) For a greedy agent (one who always chooses the best action; blue line), the gain is positive either when the best action is found to be worse than the second best action (left, changing the policy to disfavor it) or when a suboptimal action is found to be the best action (right, changing the policy to favor it). In both cases, the gain increases depending how much better the new policy is. Otherwise, the gain is zero, reflecting no effect in the policy. For a non-greedy agent (one who sometimes chooses random exploratory actions; thin gray lines), changes in Q-values that do not change the best action can nonetheless affect the degree of exploration, leading to nonzero gain (β: softmax inverse temperature parameter). Notice that a perfectly symmetric gain around zero amounts to prediction error. (g) The need term for a particular target state corresponds to its expected future occupancy, measuring how imminently and how often reward gains will be harvested there. This is shown as a heat map over states, and also depends on the agent’s future action choice policy, e.g. Top: Random policy (initially). Bottom: Learned policy (following training).

A window into patterns of memory access is offered by the hippocampus [12]. During spatial navigation, hippocampal place cells typically represent an animal’s spatial position, though it can also represent locations ahead of the animal during movement pauses [13, 14, 15]. For instance, during “sharp wave ripple” events, activity might progress sequentially from the animal’s current location toward a goal location [14, 15]. These “forward replay” sequences predict subsequent behavior and have been suggested to support a planning mechanism that links actions to their consequences along a spatial trajectory [15]. However, this pattern is also not unique: Activity in the hippocampus can also represent locations behind the animal [16, 14, 17, 18, 19], and even altogether disjoint, remote locations (especially during sleep [20, 21]; Fig. 1a). Collectively, these three patterns (forward, reverse, and offline replay) parallel the circumstances, discussed above, in which reinstatement in humans predict choice. The various patterns of hippocampal replay have been suggested to support a range of distinct functions such as planning [13, 15], learning through credit assignment [22, 16, 19], memory retrieval [23, 24], consolidation [25, 23], and forming and maintaining a cognitive map [18]. Yet, we still lack a theory describing how these various functions of replay come together to promote adaptive behavior, and predicting which memories are replayed at each time and in which order.

To address this gap, we develop a normative theory to predict not just whether but which memories should be accessed at each time to enable the most rewarding future decisions. Our framework, based on the DYNA reinforcement learning (RL) architecture [26], views planning as learning about values from remembered experiences, generalizing and reconceptualizing work on tradeoffs between model-based and model-free controllers [6, 7]. We derive, from first principles, the utility of retrieving each individual experience at each moment to predict which memories a rational agent ought to access to lay the groundwork for the most rewarding future decisions. This utility is formalized as the increase in future reward resulting from such memory access and is shown to be the product of two terms: a gain term that prioritizes states behind the agent when an unexpected outcome is encountered; and a need term that prioritizes states ahead of the agent that are imminently relevant. Importantly, this theory at present investigates which experience among all would be most favorable in principle; it is not intended as (but may help point the way toward) a mechanistic or process-level account of how the agent might efficiently find them.

To test the implications of our theory, we simulate a spatial navigation task in which an agent generates and stores experiences which can be later retrieved. We show that an agent that accesses memories in order of utility produces patterns of sequential state reactivation that resemble place cell replay, reproducing qualitatively and with no parameter fitting a wealth of empirical findings in this literature including (i) the existence and balance between forward and reverse replay; (ii) the content of replay; and (iii) effects of experience. We propose the unifying view that all patterns of replay during behavior, rest, and sleep reflect different instances of a general state retrieval operation that integrates experiences across space and time to propagate value and guide decisions. This framework formalizes and unifies aspects of the various putatively distinct functions of replay previously proposed, and may shed light onto related psychiatric disorders including craving, hallucinations, and rumination.

2. Results

We address how best to order individual steps of computation, known as Bellman backups (Fig. 1b-d), for estimating an action’s value. A Bellman backup updates an estimate of the future value of taking a particular “target” action in some state, by summing the immediate payoff received for the action with the estimated future value of the successor state that follows it. Stringing together multiple backup operations over a sequence of states and actions computes aggregate value over a trajectory.

To analyze the optimal scheduling of individual steps of value computation, we derive the instantaneous utility of every possible individual Bellman backup: the expected increase in future reward that will result if the backup is executed (see Methods for formal derivation). The intuition is that a backup, by changing an action’s value, can improve the choice preferred at the target state, leading to better rewards if that state is ever visited. Thus, the utility of a backup can be intuitively understood as the increase in reward following the target state multiplied by the expected number of times the target state will be visited: the product of a gain and a need term, respectively. The gain term quantifies the increase in discounted future reward expected from a policy change at the target state— that is, it measures how much more reward the agent can expect to harvest following any visit to the target state, due to what it learns from the update (Fig. 1e). Importantly, this value depends on whether the update changes the agent’s policy, meaning that (in contrast to other prioritization heuristics considered in AI; [27, 28, 29]), the theory predicts asymmetric effects of positive and negative prediction errors due to their differential effect on behavior (Fig. 1f). To determine priority, the gain term is multiplied by the need term, which quantifies the number of times the agent is expected to harvest the gain by visiting the target state in the future. Here, earlier visits are weighted more heavily than later visits due to temporal discounting. This weighting implies that the need term prioritizes the agent’s current state, and others likely to be visited soon (Fig. 1g).

To explore the implications of this theory, we simulate an agent’s behavior in two spatial navigation tasks (Fig. 1c). First, we simulate a linear track where the agent shuttles back and forth to collect rewards at the ends, a task widely used in studies of hippocampal replay (Fig. 1c, right). Second, we simulate a two-dimensional field with obstacles (walls) where the agent needs to move toward a reward placed at a fixed location, a task used extensively in previous RL studies [28, 1] (Fig. 1c, left). In both, the agent learns which actions lead to reward by propagating value information through Bellman backups. We assume that when the agent is paused (here, before starting a run and upon receiving a reward), it may access nonlocal memories, and that it does so in order of utility. By reactivating memories sequentially, value information can be propagated along spatial trajectories that may have never been traversed continuously by the agent. In particular, value information can be propagated backward by chaining successive backups in the reverse direction, or forward by chaining successive backups in the forward direction. The latter case is achieved by allowing the agent to look one step deeper into the value of an action — i.e., we consider the utility of all individual backups and, in particular, one that extends the previous backup with one extra state and updates the values of all actions along a trajectory. This approach allows for symmetric forward and reverse updates that have comparable effects along all the states of a trajectory. To connect the theory to hippocampal recordings, we assume that this local operation is accompanied by place cell activity at the target location.

2.1. Memory access and learning

We first predicted that prioritized memory access speeds learning. In both environments, we contrasted an agent that accesses memories in prioritized order with a model-free agent that learns only by direct experience, and an agent that replays experiences drawn at random (original DYNA [26]). In all cases, the number of steps to complete an trial (find the reward) gradually declines as the agent learns the task. Learning with prioritized experience replay progresses faster due to rapid propagation of value information along relevant trajectories (Fig. 1d). Notice that our theory predicts that a model-free agent is nonetheless able to learn this type of task, albeit in a slower fashion, in line with empirical demonstrations that disrupting replay slows learning without abolishing it [24].

2.2. Context-dependent balance between forward and reverse sequences

A major prediction of our theory is that patterns of memory access are not random, but often involve patterned trajectories. In our simulations, as in hippocampal recordings, replayed locations typically followed continuous sequences in either forward or reverse order (Fig. 2). In the model, this is because backups tend to produce situations that favor adjacent backups. In particular, our theory predicts two predominant patterns of backup, driven by the two terms of the prioritization equation.

Figure 2: Replay produce extended trajectories in forward and reverse directions.

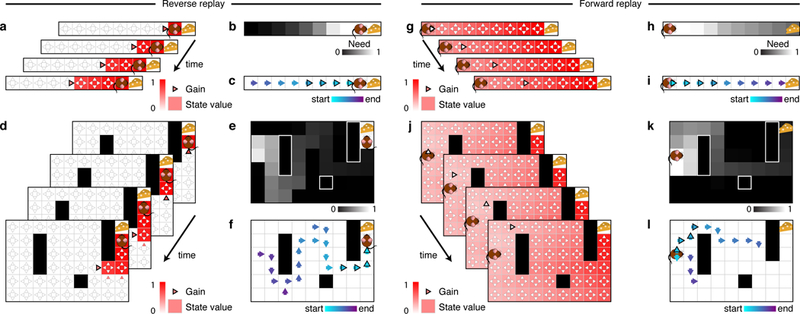
(a-f) Example of reverse replay. (g-l) Example of forward replay. (a,d) Gain term and state values. Notice that the gain term is specific for each action (triangles), and that it may change after each backup due to its dependence on the current state values. Replay of the last action executed before finding an unexpected reward often has a positive gain because the corresponding backup will cause the agent to more likely repeat that action in the future. Once this backup is executed, the value of the preceding state is updated and replaying actions leading to this updated state will have a positive gain. Repeated iterations of this procedure lead to a pattern of replay that extends in the reverse direction. The highlighted triangle indicates the action selected for value updating. (g,j) If gain differences are smaller than need differences, the need term dominates and sequences will tend to extend in the forward direction. (b,e,h,k) Need term. Notice that the need term is specific for each state and does not change after each backup due to being fully determined by the current state of the agent. The need term prioritizes backups near the agent and extends forwards through states the agent is expected to visit in the future. In the field, the need term is also responsible for sequences expanding in a depth-first manner as opposed to breadth-first. (c,f) Example reverse sequences obtained in the linear track (c) and open field (f). (i,l) Example forward sequences obtained in the linear track (i) and open field (l). Notice that forward sequences tend to follow agent’s previous behavior but may also find new paths towards the goal.

First, when an agent encounters a prediction error, this produces a large gain behind the agent (Fig. 2a-f), reflecting the value of propagating the new information to predecessor states where it is relevant to choice. Following this backup, gain now favors, recursively, propagating the information toward that state’s predecessors, and so on. Thus, following an unexpected reward, sequences tend to start at the agent’s location and move backwards toward the start state (Fig. 2c,f). Because the need term is largest for states the agent expects to visit next (Fig. 2e), and since following reward the agent returns to the start for a new trial, prioritized backups often extend backwards, depth-first, even in a 2D environment (Fig. 2f, S1). The depth-first pattern reflects the agent’s expectation that it will return to the reward in the future following a trajectory similar to that followed in the past, in contrast to a breadth-first pattern observed in alternative prioritization heuristics that do not include a need term [27, 28, 29].

The need term, instead, tends to be largest in front of the agent (Fig. 2g-l). When it dominates, sequences tend to start at the agent’s location and move forward toward the goal (Fig. 2i,l). They tend to iterate forward because following a forward sequence of n steps, an adjacent step can extend it to an n+1-step backup that carries information about each preceding action. This pattern is observed whenever the utility of looking one step deeper into the value of the actions along the route is sufficiently high.

The model thus predicts when different patterns of backup (driven by fluctuating gain and need) are likely to occur. To quantify this in simulation, we classified each backup as forward or reverse (see Methods). In line with rodent hippocampal recordings on the linear track, we observed that replay (driven by need) extended forward before a run (Fig. 3a, left), providing information relevant for evaluating future trajectories. In contrast, replay extended backward upon completing a run (driven by gain, Fig. 3a, right), providing a link between behavioral trajectories and their outcomes. Very few reverse sequences were observed prior to a run, or vice versa, in line with previous findings [14] (Fig. 3b). Note that the need term must be positive for either pattern to occur (Fig. S2).

Figure 3: Forward and reverse sequences happen at different times and are modulated asymmetrically by reward.

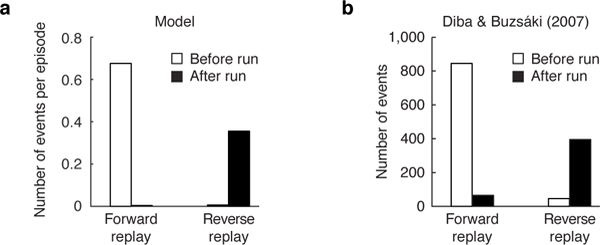
(a) Forward sequences tend to take place before the onset of a run while reverse sequences tend to take place after the completion of a run, upon receipt of reward. (b) Data from Diba & Buzsa´ki (2007) (their Fig. 1c) showing that the majority (841 out of 887) of forward sequences occurred at the start end of the track before running, while the majority (395 out of 464) of reverse sequences occurred at the other end following the run [14].

2.3. Statistics of replayed locations: current position, goals, and paths

In addition to directionality, the theory predicts which particular routes should be considered, which ultimately determines the locations of behavioral change. Coarsely, replay should be biased toward relevant locations such as the agent’s position (due to high need) and reward sites (due to high gain). Such general biases arise from the average over individual replay trajectories, which are patterned due to the influence of locations like reward sites on both the need and gain terms.

In our simulations, most significant events start in locations at or immediately behind the agent and extend in either direction (Fig. 4a). Empirical results on the linear track support this prediction: hippocampal events display an “initiation bias,” a tendency to begin at the animal’s location [16, 17, 14] (Fig. 4b).

Figure 4: Replay over-represents agent and reward locations and predicts subsequent and past behavior.

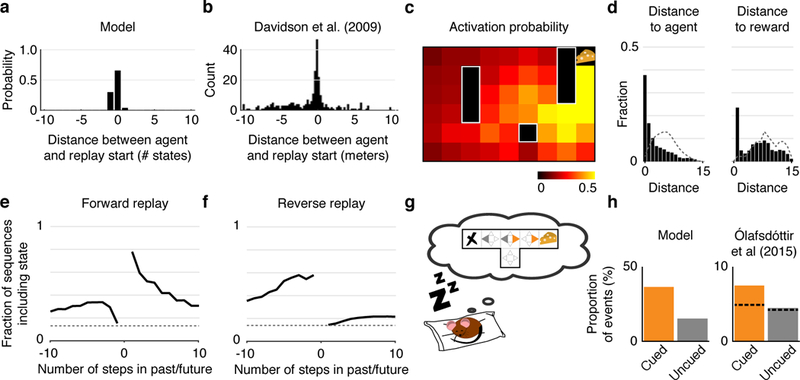
(a) Distribution of start locations of significant replay events relative to the agent’s position and heading on the linear track. Negative distances indicate that the replayed trajectory starts behind the agent. Most significant replay events in the linear track start at or immediately behind the agent’s location. (b) Data from Davidson et al (2009) (their Fig. 3F), showing the distribution of start locations of replay trajectories relative to the animal’s position and heading on the track (n = 136 cells; four rats) [17]. (c) Activation probability across all backups within an episode. Colors represent the probability of a backup happening at each location within a given episode. Notice that backups are more likely to occur in locations near the reward. (d) Probability that a given backup happens at various distances from the agent (left) and from the reward (right) in the open field. Dotted lines represent chance levels. Notice that backups are substantially more likely to happen near the agent and/or near the reward than chance. (e,f) How forward and reverse replay predict future and previous steps in the open field. The lines indicate the probability that the first 5 backups of any significant forward or reverse sequence contains the state the agent will/have occupied a given number of steps in the future/past. Dotted lines represent chance levels. Notice that forward replay is more likely to represent future states than past states, while the opposite is true for reverse replay. (g) We simulated an agent in an offline setting (e.g. sleep) after exploring a T-maze and receiving a reward on the right (cued) arm. (h) Left: The proportion of backups corresponding to actions leading to the cued arm (orange) is much greater than the proportion of backups corresponding to actions leading to the uncued arm (gray). Right: Data replotted from Olafsd´ottir et al (2015) (their Fig. 2D, used under CC BY), showing the´ proportion of spiking events categorized as “preplay” events for the cued and uncued arms (n = 212 cells; four rats). The dashed line indicates the proportion of events expected by chance [31].

Sequences that start at the animal’s location can, nonetheless, extend in any direction, especially in open field environments where trajectories are less constrained. Yet, gain and need in the model both favor important locations like reward sites. Empirically, sequential replay in open environments is also biased toward these locations [30, 15]. We simulated navigation in an open field (Fig. 1c, left), and examined these content biases by calculating the activation probability of a backup occurring at each location. Visualized over space (Fig. 4c), backups tended to concentrate near the reward (goal) locations, in line with rodent recordings [15, 31]. Quantified as a function of distance (Fig. 4d), backups were again more likely than chance to happen near the reward or the agent [32, 15].

Results like these have been taken to reflect replay’s involvement in planning future routes. Indeed, the bias toward locations near the goal was seen even for forward replay considered separately (Fig. S3). (This cannot simply reflect initiation bias because our simulations randomized starting locations were randomized.) Locations at the final turn toward the reward were emphasized even more than locations nearer the reward itself, a consequence of the gain term being higher where there is a greater effect on behavior. The over-representation of turning points is a consequence of the barriers in the simulated environment, and is consistent with reports that reactivated place fields congregate around relevant cues [33].

The hypothesized involvement of replay (both forward and reverse) in evaluating potential routes can also be assessed by comparing replayed trajectories to recent or future paths. In the model, these tend to coincide, both because backups tend to occur in locations favored by the need term, and additionally, for forward trajectories, by the definition of valid n-step sampling, which measures rewards expected along the agent’s predicted future trajectory. However, the correspondence is not perfect; in fact backups can sometimes construct trajectories not previously traversed continuously by the agent [18]. (Although our model as implemented only replays individual transitions that have previously been made in real experience, these can be recombined, and the same framework would work equally with transitions whose availability and future need can be inferred, as by vision.) We measured the probability that the first 5 backups of a forward or reverse event would include locations visited by the agent in the future or past. In the open field, forward replay correlated with the agent’s future trajectory much more than its past (Fig. 4e). In contrast, reverse replay showed the opposite pattern (Fig. 4f). That replayed trajectories tend to correspond to the trajectories followed by the agent in either the past (reverse replay) or future (forward replay) is again in line with rodent recordings [33, 15].

Last, we address remote replay, where sequences correspond to spatial locations away from the animal [17] or remote environments [21]. Even during sleep (where replay rarely corresponds to the location where the animal is sleeping) replay tends to represent rewarding areas of the environment, in comparison to similar but unrewarding areas [31]. In our model, biases in reactivation during rest can again be understood in terms of the same needand gain-based prioritization (with need defined as expected future occupancy subsequently). We tested these predictions of sleep replay by simulating a T-maze with a reward placed at the end of one of the two arms (Fig. 4g), with the agent absent from the environment (see Methods). The proportion of backups corresponding to actions leading to the rewarded arm was much greater than the proportion of backups corresponding to actions leading to the unrewarded arm (Fig. 4h), reproducing equivalent empirical results [31].

2.4. Asymmetric effect of prediction errors

We have shown that prioritized memory access for action evaluation applied in different conditions may give rise to forward and reverse sequences. However, our claim that both sorts of replay may arise from the same prioritized operation may seem at odds with the general view that forward and reverse sequences have distinct functions (e.g., planning and learning, respectively [14, 19]). One observation that has been argued to support this distinction is that reverse and forward replay are differently sensitive to reward context. In rodents navigating a linear track, the rate of reverse replay increases when the animal encounters an increased reward, but decreases when the animal encounters a decreased reward. In contrast, the rate of forward replay is similar despite either change in reward [33, 19].

Our hypothesis is instead that planning and learning are better understood as different variants of the same operation: using backups (in different orders) to propagate reward information over space and time. In our model, asymmetric effects of increases vs. decreases in reward are a hallmark of the gain term, arising from its definition in terms of policy change (Fig. 1e,f), and distinguishing our prioritization hypothesis from others that simply trigger update on any surprise [27, 28, 29]).

Because gain is accrued when an update changes the agent’s choices toward a better one, it depends both on whether the news is good or bad, and also what alternative actions are available (Fig. 1e,f). Fig. 5a,b demonstrates this predicted interaction by plotting gain for different types of feedback about the action previously believed to be better (Fig. 5a) or worse (Fig. 5b) in a two-action situation. Gain is large for learning that the seemingly worse action is actually better than the alternative, or that the seemingly better action is worse — either result teaches the agent a better choice. There is a second, subtler asymmetry when (as in our model due to “softmax” choice) how reliably an action is executed depends on its relative advantage over alternatives. Learning that the best action is even more rewarding makes the agent more likely than previously to choose it, so there is small positive gain; learning it is somewhat worse (but still the best option) carries zero or negative gain since it makes choice sloppier. All these effects arise only for reverse replay occurring at the end of a run, when the gain term is large and, therefore, dominates the utility of the backup.

Figure 5: Forward and reverse sequences happen at different times and are modulated asymmetrically by reward.

(a) Gain term for an example case where two actions are available and the agent learns a new value (Q_new) for the best action. (b) Gain term for an example case where two actions are available and the agent learns a new value (Q_new) for the worst action. (c) We simulated a task where, in half of the episodes, the reward received was 4x larger than baseline. Left: The number of forward events was approximately equal in every lap both when the rewards were equal (gray bar), as well as when the rewards were 4x larger (red bar). Right: In contrast, the number of reverse events was approximately equal when the rewards were equal (gray bar), but much larger upon receiving a larger reward in the unequal reward condition (red bar). (d) Data from Ambrose et al (2016) (their Fig. 3E,H) showing percent difference in replay rate from unchanged to increased reward end of track in the equal (gray bars) and unequal (red bars) reward conditions (n = maximum of 467 stopping periods in the equal reward condition and 217 in the unequal reward condition; five rats; mean ± 95% confidence interval; significance assessed with a Wald’s z test). Note that, forward replay (left), the effects on the two ends of the track are not significantly different (n.s.) [19]. (e) We simulated a task where, in half of the episodes, the reward received was zero. Left: The number of forward events was approximately equal in every lap both when the rewards were equal (gray bar), as well as when the rewards were removed (blue bar). Right: In contrast, the number of reverse events was approximately equal when the rewards were equal (gray bar), but almost completely abolished upon receiving no reward in the unequal reward condition (blue bar). (f) Data replotted from Ambrose et al (2016) (their Fig. 5C,F) showing percent difference in replay rate from unchanged to decreased reward end of track in the equal (gray bars) and unequal (blue bars) reward conditions (n = maximum of 580 stopping periods in the equal reward condition and 230 in the unequal reward condition; five rats; mean ± 95% confidence interval; significance assessed with a Wald’s z test). Note that, forward replay (left), the effects on the two ends of the track are not significantly different (n.s.) [19]. (g) Activation probability at the end of a linear track during random exploration without rewards or punishments (left) and after shock delivery at the end of a track (right). Dots represent mean activation probability across simulations. (h) Data from Wu et al (2017) (their Fig. 3e) showing the activation probability during population burst events of cells with place fields at a light zone before shock delivery (left) and similarly for cells with place fields at a shock zone after shock delivery (right). (n = 30 cells with place fields at a light zone; n = 26 cells with place fields at a shock zone; four rats; horizontal lines in box plots are the median and the 25% and 75% range values; whiskers indicate the most extreme data points ≤ 1 interquartile range from box edges; significance assessed with a two-sided Wilcoxon rank-sum test [34]).

We investigated the asymmetric effects of positive or negative prediction errors on replay by simulating two conditions on a linear track task similar to that studied by Ambrose et al. (2016) [19]: (i) an increased reward condition where the reward encountered by the agent was four times larger in half of the episodes, and (ii) a decreased reward condition where the reward encountered by the agent was zero in half of the episodes. The number of forward events was approximately equal in all cases. In contrast, the number of reverse events was larger upon receiving a larger reward than upon receiving a conventional reward (Fig. 5c,d). This effect was driven both by an increase in reverse replay for larger rewards, and a decrease for conventional (1x) rewards (Fig. S4), as observed experimentally [19]. In contrast, the number of reverse events was smaller upon receiving no reward than upon receiving a conventional reward (Fig. 5e,f). This effect was driven both by a decrease in reverse replay when the reward was 0, and an increase when the reward was conventional (1x) (Fig. S4), again replicating empirical findings [19].

Another crucial prediction of the model is that propagating negative prediction error is unhelpful if no better action is available, but advantageous if alternative actions become preferred. Above, reduced reward produces no replay because no better option is available. If negative reward (e.g., electric shock) is encountered, propagating it has positive gain (Fig. 5a), as it enables omitting the action altogether. Staying still or moving backwards is better than moving toward a shock zone. Indeed, in simulation, backup occurs at the shock zone after shock delivery (to propagate this information and prevent the agent’s return), but not prior to shock delivery (Fig. 5g). This prediction has also been confirmed: In a conditioned place avoidance task, replays were observed extending from the animal’s position toward the end of a track previously paired with shock, despite the fact that the animals did not then enter the shock zone [34] (Fig. 5h). These results not only provide direct support to our theory’s notion of gain, but also illustrate how the notion of planning embodied by our model differs from a narrower, colloquial sense of planning. Evaluating candidate actions by simulation does not just find paths to goals, it also helps agents figure out what not to do.

2.5. Effects of familiarity and specific experiences

As a learning model, our theory also predicts effects of experience on the prevalence and location of replay. In particular, change in the need vs. gain terms predicts countervailing effects of experience. As a task is learned, prediction errors decrease, policies stabilize, and the gain expected due to replay decreases, causing a reduction in significant replay events. At the same time, as behavior crystallizes, need becomes more focused along the routes learned by the agent (e.g., compare Fig. 1g, top and bottom). This predicts that, conditional on replay occurring, particular states are increasingly likely to participate.

These countervailing effects may help to explain apparent inconsistencies in the replay literature, as both increases and decreases in replay have been reported, albeit using a range of dependent measures and designs [32, 35, 36, 33, 37, 16]. Specifically, the more time an animal spends between two place fields, the more the corresponding place cell pair is reactivated during sleep. This is consistent with focusing of need on these states [35]. In contrast, replay is more easily observed in novel than in familiar tracks (consistent with a decrease in gain overall [16]), and the average activation probability is highest in novel environments [36]. It has been suggested that replay tends to increase within session with exposure, but decrease across sessions as the animal becomes familiar with a novel environment [37]. This may reflect the additional effect of experience vs. computation on learning in our model. In particular, both need (favoring focused replay) and gain (opposing overall replay) are affected by actual experience in an environment, but only gain is affected by replay (e.g. during rest between sessions). This is because only experience can teach an agent about the situations it is likely to encounter (i.e. need), but value learning from replayed experience reduces subsequent gain.

We examined the effect of familiarity and specific experience on replay by calculating the number of significant replay events as a function of experience (episode number). In line with previous reports [16], we observed that the number of significant events decays steadily with experience. This effect was due to a decrease in both forward and reverse replay. Similarly, activation probability decayed steadily with experience (Fig. 6a), in line with empirical findings (Fig. 6b) [36], and this decay occurred for both forward and reverse sequences (Fig. 6a, insets). In contrast, when events occurred, the probability they included a specific state increased with number of visits (Fig. 6c), also in line with previous reports (Fig. 6d) [35]. These two effects reflect the effect of experience on the two terms governing priority: while the gain term decreases with exposure, the need term increases as the agent’s trajectory becomes more predictable.

Figure 6: Replay frequency decays with familiarity and increases with experience.

(a) In the linear track, the probability that significant replay events include a state in the linear track decays across episodes, peaking when the environment is novel. Insets show that the number of both forward (top) and reverse (bottom) replay events decay with experience. (b) Data replotted from Cheng & Frank (2008) (their Fig. 4A), showing the activation probability per high-frequency event (n = 41,43,34,34,31,28 cells, respectively for each bar; four rats; error bars represent standard errors; significance assessed with a Wilcoxon rank-sum test) [36]. (c) Probability that significant replay events include a state in the linear track as a function of the number of visits in an episode. Analogously to the effect reported in Fig. 1g, driven by the need term, the probability of a state being replayed increases with experience in that state. (d) Data replotted from O’Neil et al (2008) (their Fig. 3c), showing that the more time rats spent in the cofiring field during exploration, the larger is the increase in probability that these cell pairs fire together during sleep SWRs (n = 613 cells and 19,054 cell pairs recorded over 33 sessions in the novel (Nov) environment; n = 309 cells and 4,865 cell pairs recorded over 15 sessions in the familiar (Fam) conditions; 14 rats; error bars represent standard errors) [35].

2.6. Effect of replay on choice behavior

The preceding simulations demonstrate that a range of properties of place cell replay can be predicted if replay is optimized for planning involving the reactivated locations. This implies a complementary set of behavioral predictions about replay’s involvement guiding choices. Behavioral effects are most characteristically expected for acquiring tasks (like shortcuts) that exercise the ability of replay to compose novel trajectories from separate experiences [3], and which cannot be solved by simple model-free learning from experience.

Hippocampal replay can follow novel paths or shortcuts [18], though there is less direct evidence for its behavioral consequences. In one report [31], activation of a path not yet explored was followed by rats subsequently being able to choose that path, correctly, over another, consistent with planning. Forward hippocampal replay predicts future paths even when the goal location is novel [15]. Finally, blocking sharp wave ripples selectively impairs learning and performance of a spatial working memory task [24]. Though our model would require elaboration to simulate that task (because it is non-Markovian), it demonstrates that awake replay is required for associating events over space and time [24].

Our theory also emphasizes that several different patterns of replay (Fig. 1a) can solve decision tasks requiring integrating multiple experiences, which have largely been assumed to reflect forward planning at choice time. Apart from forward replay, reverse replay allows connecting an experienced outcome with potential predecessor actions, and nonlocal replay can compose sequences of experiences during rest. Although these behavioral consequences have not been examined in hippocampal spatial research, research with humans using non-spatial versions of revaluation tasks (and activity of category-specific regions of visual cortex to index state reinstatement) verifies that forward replay [5], reverse replay [9], and nonlocal replay [11] all predict subjects’ ability to solve these tasks. The present theory’s account of which replay events are prioritized might provide a basis for explaining why different task variants in different studies have evoked different solution strategies.

3. Discussion

Given all the experience accumulated in a lifetime, which memories should one access to plan the most rewarding decisions? We offer a rational account for the prioritization of memory access to support action evaluation. We propose that various nonlocal place cell phenomena reflect a single evaluation operation, which has different utility in different circumstances. This utility, derived from first principles, amounts to the product of two terms, gain and need. Simulations qualitatively reproduced a range of results about hippocampal replay without parameter fitting. This theory draws new connections between hippocampus and decision making, with implications for both areas. It has long been recognized that place cell activity (including forward and reverse replay) likely supports choice [13, 16]; we render this idea experimentally testable by specifying a hypothesis about what the brain learns from any particular replay event.

Hippocampal researchers typically envision that replay serves disjoint functions in different circumstances, including learning [16], planning [13, 14, 15, 38], spatial memory retrieval [24], and consolidation [25, 23]. By focusing on a specific operation (long-run value computation), we sharpen these suggestions and expose their relationships. In RL, learning amounts to propagating value between adjacent states for temporal credit assignment. This perspective unifies the proposed role of forward replay in planning with that of reverse replay in learning (both linking sequences to their outcome [16]), and attributes a similar role to nonlocal replay. Though serving a common goal, these patterns are appropriate in different circumstances, explaining differential regulation (such as asymmetric effects of prediction errors on forward vs. reverse replay), which has previously been taken as evidence for distinct functions [19]. As for consolidation, our perspective echoes other work [25] in viewing it not merely as strengthening existing memories, but more actively computing new summaries from the replayed content. As with other systems consolidation theories, the summaries (here, value) are likely stored elsewhere in the brain (here, cortico-striatal synapses), and replay presumably evokes coordinated activity throughout the brain, especially the dopaminergic-striatal reward networks [39, 40].

While we explore a specific role for replay in computing long-run action value, we do not exclude other computations over replayed experiences [25]. One variant of our theory uses replay to learn a successor representation(SR): a model of the long-run locations expected to follow some action, instead of the reward consequences alone. The SR can be used as an intermediate representation for computing action values [41], and has been proposed to be learned within hippocampal recurrents [42]. Like value, it can be learned from replayed experience [43], connecting learning from replay more directly with building a type of cognitive map [18]. Our account extends fully to this case. Indeed, our prioritization computation is the same whether replay updates an SR or action values, because an SR update has the same utility (under our myopic approximation) as the corresponding action value update: both implement the same Bellman backup.

A key insight in decision neuroscience is that how decision variables are computed governs what is ultimately chosen. Thus, the view that the brain contains separate systems for “model-based” vs. “model-free” value computation (which differ in whether they recompute values at decision time) may explain phenomena such as habits and compulsion. We extend this to a more granular view, addressing which branches are considered during recomputation [44]. Dysfunction in such selection may explain symptoms involving biased (e.g., craving, obsession) and abnormal patterns of thought (e.g., rumination, hallucination). Our theory goes beyond planning about the immediate future, to consider value computation at nonlocal states: offline replay [26, 22]. This systematizes several instances where tasks thought to index model-based planning at choice time are instead apparently solved by computations occurring earlier [9, 10, 11], and links them (hypothetically) to different patterns of replay. Finally, reinterpreting planning as learning from remembered experience suggests this operation might be subserved by the same dopaminergic machinery as learning from direct experience — driving it with replayed experiences instead. Indeed, trajectory replay in the hippocampus drives activation and plasticity throughout this system [39, 40]. Such shared machinery would explain the otherwise puzzling involvement of dopamine in model-based evaluation [45, 46, 47, 48].

The AI literature suggests one alternative approach for prioritizing backups: Prioritized Sweeping (PS) [28, 27, 29]. PS triggers backups on large prediction errors (whether negative or positive), to propagate unexpected information to predecessor states. Our approach adds the need term, to focus backups on states likely to be visited again. Also, our gain term considers the effect of a backup on an agent’s policy, propagating information only when it has behavioral consequences. Data support both features of our model over PS. Positive and negative prediction errors have asymmetric effects, consistent with gain but not PS [19] (Fig. 5c-f). Also, due to need, our model also searches forward from the current state, in addition to PS’s largely backward propagation. The need term also channels activity along recently or frequently observed trajectories. This may help to explain why nonlocal place cell activity follows extended sequences even though straightforward error propagation is often more breadth-first [28, 27].

Our model has a number of limitations, which are opportunities for future work. We have omitted many model features to construct the simplest instantiation that exposes the key intuition behind the theory: the roles of gain and need driving, respectively, reverse and forward replay. For instance, we restricted our simulations to simple spatial environments, though the framework applies generally to sequential tasks. Because these environments are stationary and deterministic, we omitted uncertainty from the model. Both stochasticity and nonstationarity would give rise to uncertainty about action values, which would be crucial to a fuller account of prioritized deliberation. This will require, in future, re-introducing these features from previous accounts of online deliberation [6, 7]; with these features restored, the current theory should inherit its predecessors’ account of habits, such as how they arise with overtraining.

The most important limitation of our work is that to investigate the decision theoretic considerations governing replay, we define priority abstractly, and do not offer a mechanism for how the brain would realistically compute it. Although the need term is straightforward (it is the SR [41], which the brain has been proposed to track for other reasons [49, 42]), the calculation of gain, as we define it, requires that the agent knows the effect of a backup on its policy prior to deciding whether to perform it. We use this admittedly unrealistic rule to investigate the characteristics of efficient backup, but a process-level model will require heuristics or approximations to the gain term, whose form might be motivated by our simulations.

To highlight the role of sequencing computations, we constructed the theory at a single spatial and temporal scale, with a Bellman backup as the elementary unit of computation. We build both forward and reverse replay trajectories recursively, step by step. Of course, research in both hippocampus and decision making (separately) stresses the multiscale nature of task representations. A fuller account of planning would include temporally extended actions (“options”) [50, 44] or similarly extended state predictions [41]. In this case, the principles of prioritization would carry over directly, but over a set of extended trajectories rather than individual locations.

The key experimental opportunities suggested by our theory involve monitoring or manipulating nonlocal place cell activity during trial-by-trial RL tasks, especially those that defeat alternative, model-free mechanisms[45, 5]. Fundamentally, the theory predicts a series of relationships spanning experience to choice: The statistics of experience (via need and gain) influence the likelihood of particular trajectories replaying; these events update action values (and their neural signatures, as in striatum) at the replayed locations; finally, this impacts choice behavior. Each of these associations could be monitored or intervened upon. Furthermore, they are all detailed event-by-event, so for instance we predict not just that replay promote better integrative learning overall, but what computation is subserved by any particular nonlocal event. Thus, conditional on an event (or interrupting one), the theory predicts specific, localized changes in neural value representations and choice behavior. Similarly, by manipulating experience to affect need or gain, the theory predicts one can affect not just whether forward or reverse replay is favored, but on which trajectories.

4. Online Methods

4.1. Formal setting

We consider a class of sequential decision tasks where an agent must decide in each situation (state; e.g. a location in a spatial task) which action to perform with the goal of maximizing its expected future reward. The optimal course of action (policy) consists of selecting the actions with highest expected value. The value of an action (Q-value) is defined as the expected discounted future reward from taking that action and following the optimal policy thereafter. Optimal decision making, therefore, requires the agent to estimate action values as accurately as possible for maximizing total reward.

We address how best to order individual steps of computation, known as Bellman backups (Fig. 1b), for estimating an action’s value. A single Bellman backup updates the estimate of the future value of taking a particular “target” action in some state, by summing the immediate payoff received for the action with the estimated future value of the successor state that follows it. This backup operation is fundamental for predicting future reward in RL, because it propagates information about reward to states and actions that precede it. Bellman backups can be applied action-by-action during ongoing behavior to allow the agent to learn from experienced states and rewards; this corresponds the standard update rule for “model-free” temporal difference (TD) learning, as thought to be implemented in the brain by dopaminergic prediction errors [51]. Our account includes this sort of learning from experienced events as a special case, but also allows for additional Bellman backups to be performed to update estimates for target states and actions that are not currently being experienced (Fig. 1a,b). In these cases, the resulting reward and successor state are given by remembered or simulated experiences, but the learning rule is otherwise the same. In computer science, this approach is known as the DYNA framework [26]. We refer to the information processed in a nonlocal backup as a “memory” — a target state and action, and the resulting reward and successor state. However, the same approach applies regardless of whether this information is a retrieved record of an individual event (like an episodic memory), or instead a simulated experience (a sample drawn from a learned “world model” of the overall statistics of state transitions and rewards, more like a semantic memory). These two representations are largely the same in the present work because we simulate only fixed, deterministic tasks (Fig. 1c). Importantly, because this process can compose behavioral sequences of simulated experience from pieces not experienced together, it can discover consequences missed by TD learning, which evaluate actions only in terms of their directly experienced outcomes [1, 51].

Stringing together multiple backup operations over a sequence of states and actions computes expected value over a trajectory. Thus, the value of an action — the expected cumulative discounted reward that will follow its execution — can be sampled by adding up expected immediate rewards over a trajectory of one or more forward steps, plus any additional value expected forward from the last state considered. This is known as an n-step Bellman backup or a rollout, and can be composed from a series of one-step backups using a learning mechanism called eligibility traces [1]. Similarly, value information can be propagated backwards along a trajectory (i.e. from a destination state to each of a series of predecessors) by chaining successive one-step backups in the reverse direction. Both of these patterns (forward and reverse value propagation) have precedent in different computer science methods (e.g. Monte Carlo tree search [52] and Prioritized Sweeping [27]). Indeed, various existing “model-based” algorithms for computing values from a world model amount to a batch of many such backup operations, performed in different orders [1, 2]. A major goal of our theory is to provide a principled account of when each pattern is most useful.

4.2. Model description

The framework of reinforcement learning [1] formalizes how an agent interacting with an environment through a sequence of states should select its actions so as to maximize some notion of cumulative reward. The agent’s policy π assigns a probability π(a|s) to each action a ∈ A in state s ∈ S. Upon executing an action A_t at time t, the agent transitions from state S_t to state S_t+1 and receives a reward R_t. The goal of the agent is to learn a policy that maximizes the discounted return G_t following time t defined as:

$$G_t=R_t+\gamma R_{t+1}+{\gamma }^2{R}_{t+2}+\dots ={\displaystyle \sum _{i=0}^{\infty }{\gamma }^i}{R}_{t+i,}$$ (1)

where γ ∈ (0,1] is the discount factor that determines the present value of future rewards.

The expected return obtained upon performing action a in state s and subsequently following policy π is denoted q_π(s,a) and is given by:

$$q_{\pi }(s,a)=\underset{\pi }{\mathbb{E}}\left[{\displaystyle \sum _{i=0}^{\infty }{\gamma }^i}{R}_{t+i}|S_t=s,A_t=a\right].$$ (2)

The policy that maximizes the expected return is the optimal policy and denoted q_∗. Following Q-learning [53], the agent can learn an action-value function Q that approximates q_∗ through iteratively performing Bellman backups:

$$Q\left(S_t,A_t\right)\to Q\left(S_t,A_t\right)+\alpha \left[R_t+\gamma \underset{{}_{a\in \mathcal{A}}}{\max }Q\left(S_{t+1},a\right)-Q\left(S_t,A_t\right)\right],$$ (3)

where α ∈ [0,1] is a learning rate parameter. Bellman backups are performed automatically after each transition in real experience and may also be performed nonlocally during simulated experience, as in the DYNA architecture [26].

The following framework provides a rational account for prioritizing Bellman backups according to the improvement in cumulative reward expected to result. Let the agent be in state S_t = s at time t. We represent an experience e_k by the 4-tuple e_k = (s_k,a_k,r_k,s^´_k), and we consider that accessing experience e_k amounts to a Bellman backup which updates Q(s_k,a_k) with the target value r_k + γ max_a∈A Q(s^´_k,a). We also denote by π_old the current (old) policy, prior to executing the backup, and π_new the resulting (new) policy after the backup.

The utility of accessing experience e_k to update the value of Q(s_k,a_k), or Expected Value of Backup, is denoted by EV B(s_k,a_k) and is defined as:

$$EVB\left(s_k,a_k\right)=\underset{{\pi }_{new}}{\mathbb{E}}\left[{\displaystyle \sum _{i=0}^{\infty }{\gamma }^i}{R}_{t+i}|S_t=s\right]-\underset{{\pi }_{old}}{\mathbb{E}}\left[{\displaystyle \sum _{i=0}^{\infty }{\gamma }^i}{R}_{t+i}|S_t=s\right],$$ (4)

i.e., EVB is theimprovement in expected return due to a policy change. A key point about this definition is that although it sums rewards over all future timesteps, it can be rewritten in terms of a sum over expected visits to the updated state s_k (the full derivation is given below.) This is because accessing e_k can only affect the policy in state s_k (i.e., π_new and π_old differs only in state s_k); and we can then separately consider the gain accrued each time the agent visits that state s_k, and the expected number of times s_k will be visited. In other words, by conditioning EV B(s_k,a_k) on S_t = s_k, this expression can be separated into the product of two terms: EV B(s_k,a_k) = Gain(s_k,a_k) × Need(s_k).

4.2.1. Gain term

The gain term quantifies the expected improvement in return accrued at the target state, s_k:

$$Gain\left(s_k,a_k\right)={\displaystyle \sum _{a\in \mathcal{A}}{Q}_{{\pi }_{new}}}\left(s_k,a\right){\pi }_{new}(a|s_k)-{\displaystyle \sum _{a\in \mathcal{A}}{Q}_{{\pi }_{new}}}\left(s_k,a\right){\pi }_{old}(a|s_k),$$ (5)

where π_new(a|s_k) represents the probability of selecting action a in state s_k after the Bellman backup, and π_old(a|s_k) is the same quantity before the Bellman backup.

4.2.2. Need term

The need term measures the discounted number of times the agent is expected to visit the target state, a proxy for the current relevance of each state:

$$\mathrm{Need}\left(s_k\right)={\mu }_{\pi }\left(s_k\right)={\displaystyle \sum _{i=0}^{\infty }{\gamma }^i}{\delta }_{S_{t+i},s_k,}$$ (6)

where δ_·,· is the Kronecker delta function. Notice that, for γ = 1, the need term is the exact count of how many visits to state s_k are expected in the future, starting from current state S_t = s.

The need term can be estimated by the Successor Representation [41], which can be learned directly by the agent or computed from a model. Here, we assume that the agent learns a state-state transition probability model T for the purpose of computing the need term. The need term is thus obtained directly from the n-th row of the SR matrix, (I − γT )⁻¹, where n is the index of the agent’s current state S_t. An alternative option is to use the stationary distribution of the MDP, which estimates the asymptotic fraction of time spent in each state (i.e., after convergence). This formulation is particularly useful when the transition probability from the agent’s current state is unavailable (e.g., during sleep). The need term bears close resemblance to the concept of need probability from rational models of human memory [54] — the probability that an item needs to be retrieved from memory because of its relevance to the current situation.

Note that the utility of a backup depends simultaneously on gain and need. Thus, a backup that has no effect on behavior has zero utility even if the target state is expected to be visited in the future (because it has zero gain, despite high need). Similarly, the utility of a backup is zero if a state is never expected to be visited again, even if this backup would greatly impact behavior at the that state (because it has zero need, despite high gain). Crucially, utility is computed separately for each individual backup. This “myopic” view neglects the possibility that a backup may harvest additional gains by setting the stage for other, later backups.

4.3. Simulation details

We simulated two “grid-world” environments (Fig. 1c) where an agent can move in any of the four cardinal directions – i.e. A = {up,down,right,left}. At each state, the agent selects an action according to a softmax decision rule over the estimated Q-values, π(a|s) ∝ e^β·Q(s,a), where β is the inverse temperature parameter which sets the balance between exploration versus exploitation. In our simulations, β = 5. Upon selecting action A_t = a in state S_t = s, the agent observes a reward R_t = r and is transported to an adjacent state S_t+1 = s^’. The value of Q(s,a) is then updated according to (3) using α = 1.0 and γ = 0.9. We used a learning rate of α = 1 due to it being both maximally simple and optimal when the world’s dynamics are deterministic.

The first environment — a linear track (Fig. 1c, right) — was simulated as two disjoint 1 × 10 segments. (The motivation for this was for the state space to differentiate both location and direction of travel, as do hippocampal place cells in this sort of environment; this also clearly disambiguates forward from reverse replay.) The agent started in location (1,1) of the first segment. Upon reaching the state (1,10), the agent received a unit reward with Gaussian noise added with standard deviation of σ = 0.1 (noise is added to each encountered reward to promote continuous learning). The agent was then transported to state (1,10) of the second segment. Upon reaching state (1,1) in the second segment, the agent received a new unit reward (plus independent Gaussian noise with σ = 0.1) and was transported back to state (1,1) of the first segment. Each simulation comprised of 50 episodes (i.e. sequence of steps from starting location to reward). The second environment was a 6 × 9 field with obstacles (Fig. 1c, left), with a unit reward (σ = 0.1) placed at coordinate (1,9). Each simulation comprised of 50 episodes with the start location randomized at each episode.

Our theory assumes that the memory access leads to more accurate Q-values. Improved estimates of action values can be obtained from samples of experience in which that action is used (whether by single or multiple-step sample backups). Thus, at every planning step we compute the need and gain for activating each possible one-step experience $e_k=(s_k,a_k,r_k,s_k^{\text{'}})$; these correspond to one-step updates given by (3). However, one of these experiences has special properties that permit additional learning if it is selected (which corresponds to a so-called n-step backup, from a version of the Bellman equation that sums n rewards before the recursive step, and must be accounted for with different need and gain). In particular, if the target state action (s_k,a_k) is an optimal continuation of the sequence replayed immediately previously (i.e. if s_k was the end state considered previously, and a_k is the optimal action there), then this replay can extend a previous one-step backup to a two-step backup, updating the values of both a_k and the action replayed previously in light of the value at the next end state. Similarly, following an n-step backup, one experience corresponds to an optimal n + 1st-step, updating the values of all intermediate actions. Note that only the optimal action is allowed as a continuation of the sequence replayed previously. This is because n-step backups are only valid estimators of the target function if the choices, after the first, are on-policy with respect to the target function Q^∗.

Such sequence-extending experience activations permit a special learning step, and a corresponding special case of need/gain computation. If a sequence-extending experience is activated, the corresponding learning rule applies an n-step Bellman update at each of the preceding states in the sequences (i.e. it updates the value of all n preceding state/actions according to their subsequent cumulative, discounted rewards over the whole trajectory, plus the Q-value of the best action a at the added state s^’_k.) Implementationally, this can be accomplished using a Q(1) update rule over eligibility traces that are cleared whenever a sequence is not continued. The gain for this update, then, accumulates the gain over each of these state updates according to any policy changes at each, and this sum is multiplied by the need for the last state s^’_k (looking one step deeper at the value of an action only makes sense if the additional state is actually likely to be visited). Thus, a sequence-extending experience is only activated if the need is sufficiently large along the entire trajectory.

Thus, the utility of a multi-step backup is computed as follows:

• Need is computed from the last (appended) state;

• Gain is summed for all actions along the trajectory (to reflect the fact that all actions are updated);

• EV B ties are broken in favor of shorter sequences.

The inclusion of this case is important because it allows the model to choose to construct either forward or backward replay sequences in parallel fashion by appending or prepending successive individual steps. Whether built forward or backward, these sequences are also equivalent in the sense that they ultimately update the values of all the state/actions along the trajectory with n-step returns. Note that the requirement that sampled forward trajectories follow what is currently believed to be the greedy policy does not mean they are uninformative; values updated along the path can change behavior (and also potentially the path sampled on subsequent rollouts). Conversely, a sequence-extending experience does not necessarily have a higher utility simply because it considers the cumulative gain over all intermediate states; if the value of the subsequent state is unsurprising (leading to small summed gains), or if the subsequent state is not expected to be visited (leading to a small need), the activation of a new, one-step experience elsewhere will be favored.

The agent was allowed 20 planning steps at the beginning and at the end of each episode. Because the gain term is a function of the current set of Q-values, the utilities EV B were re-computed for all experiences after each planning step. In order to ensure that all 20 planning steps were used, a minimum gain of 10⁻¹⁰ was used for all experiences. This small, nonzero minimal value is meant to capture an assumption of persistent uncertainty due to the possibility of environmental change.

Prior to the first episode, the agent was initialized with a full set of experiences corresponding to executing every action in every state (equivalent to a full state-action-state transition model, which in sparse environments like these can be inferred directly from visual inspection when the agent first encounters the maze), including transitions from goal states to starting states. The state-state transition probability model T (for the need term) was initialized from this model under a random action selection policy, and thereafter updated after each transition using a delta rule with learning rate α_T = 0.9. In all simulations in the online setting, the need term was then estimated from the SR matrix, (I − γT )⁻¹. In the only simulation of sleep replay (Fig. 4g,h), where the agent is not located in the environment where need is computed, we estimated the need term as the stationary distribution of the MDP, i.e., the vector μ such that μT = μ.

4.4. Identification of significant replay events

We classified each individual backup as forward or reverse by examining the next backup in the sequence. When a backed-up action was followed by a backup in that action’s resulting state, it was classified as a forward. In contrast, when the state of a backup corresponded to the outcome of the following backed-up action, it was classified as reverse. Backups that did not follow either pattern were not classified in either category. To identify significant replay events, we followed standard empirical methods and assessed, with a permutation test, the significance of all consecutive segments of forward/reverse backups of length five or greater [16, 14, 17].

4.5. Formal derivation

Below is a formal derivation of EVB for the general case of stochastic environments. Let the agent be in state S_t = s at time t. The expected return from following policy π is defined as $v_{\pi }(s)={\mathbb{E}}_{\pi }\left[{\sum }_{i=0}^{\infty }{\gamma }^k{R}_{t+i}|S_t=s\right],$ and the true (yet unknown) value of taking action a in state s and following policy π thereafter is denoted by q_π(s,a). The utility of updating the agent’s policy from π_old to π_new is:

$$v_{{\pi }_{new}}(s)-v_{{\pi }_{old}}(s)={\displaystyle \sum _a{\pi }_{new}}(a|s)q_{{\pi }_{new}}(s,a)-{\displaystyle \sum _a{\pi }_{old}}(a|s)q_{{\pi }_{old}}(s,a)={\displaystyle \sum _a\left[{\pi }_{new}(a|s)q_{{\pi }_{new}}(s,a)-{\pi }_{old}(a|s)q_{{\pi }_{new}}(s,a)+{\pi }_{old}(a|s)q_{{\pi }_{new}}(s,a)-{\pi }_{old}(a|s)q_{{\pi }_{old}}(s,a)\right]}={\displaystyle \sum _a\left[\left({\pi }_{new}(a|s)-{\pi }_{old}(a|s)\right)q_{{\pi }_{new}}(s,a)+{\pi }_{\text{ old }}(a|s)\left(q_{{\pi }_{new}}(s,a)-q_{{\pi }_{old}}(s,a)\right)\right],}$$ (7)

where we have both added and subtracted the term π_old(a|s)q_πnew(s,a) on the second line.

We then write q(s,a) in terms of v(s) using the definition of the MDP dynamics, p(s^’,r|s,a) =^. Pr(S_t+1 = s^’,R_t = r|S_t = s,A_t = a):

$$q_{\pi }(s,a)=\underset{\pi }{\mathbb{E}}\left[R_t+\gamma v_{\pi }\left(S_{t+1}\right)\right]={\displaystyle \sum _{s^{\prime },r}p}\left(s^{\prime },r|s,a\right)\left[r+\gamma v_{\pi }\left(s^{\prime }\right)\right]$$ (8)

Since the MDP dynamics does not depend on π, we can write:

$$q_{{\pi }_{new}}(s,a)-q_{{\pi }_{old}}(s,a)={\displaystyle \sum _{s^{\prime },r}p}\left(s^{\prime },r|s,a\right)\left[r+\gamma v_{{\pi }_{new}}\left(s^{\prime }\right)\right]-{\displaystyle \sum _{s^{\prime },r}p}\left(s^{\prime },r|s,a\right)\left[r+\gamma v_{{\pi }_{old}}\left(s^{\prime }\right)\right]=\gamma {\displaystyle \sum _{s^{\prime }}p}\left(s^{\prime }|s,a\right)[v_{{\pi }_{new}}\left(s^{\prime }\right)-v_{{\pi }_{old}}\left(s^{\prime }\right)].$$ (9)

Substituting this result on (7):

$$v_{{\pi }_{new}}(s)-v_{{\pi }_{old}}(s)={\displaystyle \sum _a\left[\left({\pi }_{new}(a|s)-{\pi }_{old}(a|s)\right)q_{{\pi }_{new}}(s,a)+{\pi }_{old}(a|s)\left(q_{{\pi }_{new}}(s,a)-q_{{\pi }_{old}}(s,a)\right)\right]}={\displaystyle \sum _a\left[\left({\pi }_{new}(a|s)-{\pi }_{old}(a|s)\right)q_{{\pi }_{new}}(s,a)+{\pi }_{old}(a|s)\left(\gamma {\displaystyle \sum _{s^{\prime }}p}\left(s^{\prime }|s,a\right)\left[v_{{\pi }_{new}}\left(s^{\prime }\right)-v_{{\pi }_{old}}\left(s^{\prime }\right)\right]\right)\right]}$$ (10)

Notice that (10) contains an expression for v_πnew(s) − v_πold(s) in terms of v_πnew(s^’) − v_πold(s^’). We can use this to ‘unroll’ the expression and write v_πnew(s’) − v_πold(s^’) in terms of v_πnew(s^”) − v_πold(s^”). After repeated unrolling we obtain:

$$v_{{\pi }_{new}}(s)-v_{{\pi }_{old}}(s)={\displaystyle \sum _{x\in \mathcal{S}}{\displaystyle \sum _{i=0}^{\infty }{\gamma }^i}}Pr\left(s\to x,i,{\pi }_{old}\right){\displaystyle \sum _a\left({\pi }_{new}(a|x)-{\pi }_{old}(a|x)\right)}{q}_{{\pi }_{new}}(x,a),$$ (11)

where Pr(s → x,i,π_old) is the probability of transitioning from state s to state x in i steps under policy π_old.

Since the effect of a backup on state-action pair (s_k,a_k) is localized at a single state for punctate representations, ${\pi }_{new}(a|s_i)={\pi }_{old}(a|s_j)$ , ∀i,j k, and thus there is only one non zero term on the first summation:

$$v_{{\pi }_{new}}(s)-v_{{\pi }_{old}}(s)={\displaystyle \sum _{i=0}^{\infty }{\gamma }^i}Pr\left(s\to s_k,i,{\pi }_{old}\right){\displaystyle \sum _a\left({\pi }_{new}(a|s_k)-{\pi }_{old}(a|s_k)\right)}{q}_{{\pi }_{new}}(s_k,a),$$ (12)

Denoting ${\mu }_{\pi }\left(s_k\right)={\displaystyle \sum _{i=0}^{\infty }{\gamma }^i}Pr\left(s\to s_k,i,\pi \right)$ as the discounted number of time steps in which S_t = s_k in a randomly generated episode starting in S_t = s and following π, we have:

$$EVB\left(s_k,a_k\right)={\mu }_{{\pi }_{old}}\left(s_k\right){\displaystyle \sum _a\left({\pi }_{new}(a|s_k)-{\pi }_{old}(a|s_k)\right)}{q}_{{\pi }_{new}}\left(s_k,a\right)=Need\left(s_k\right)\times Gain(s_k,a_k),$$ (13)

where $Need\left(s_k\right)={\mu }_{\pi }{}_{old}\left(s_k\right)$ and $Gain\left(s_k,a_k\right)={\sum }_a\left({\pi }_{new}\left(a|s_k\right)-{\pi }_{old}\left(a|s_k\right)\right)q_{\pi }{}_{new}\left(s_k,a\right).$

We note that the same framework can be readily extended to the function approximation case and to policy gradient methods — i.e., computing the utility of a policy change even when the policies differ in multiple states (by using equation (11)). In this more general case, the above derivation corresponds to a discrete version of the Policy Gradient Theorem [55].