A novel anthropomorphic flow phantom for the quantitative evaluation of prostate DCE-MRI acquisition techniques

Abstract

A novel anthropomorphic flow phantom device has been developed which can be used for quantitatively assessing the ability of MRI scanners to accurately measure signal / concentration time-intensity curves (CTCs) associated with dynamic contrast-enhanced (DCE) MRI. Modelling of the complex pharmacokinetics of contrast agents as they perfuse through the tumour capillary network has shown great promise for cancer diagnosis and therapy monitoring. However, clinical adoption has been hindered by methodological problems, resulting in a lack of consensus regarding the most appropriate acquisition and modelling methodology to use and a consequent wide discrepancy in published data. A heretofore overlooked source of such discrepancy may arise from measurement errors of tumour CTCs deriving from the imaging pulse sequence itself, while the effects on the fidelity of CTC measurement of using rapidly-accelerated sequences such as parallel imaging and compressed sensing remain unknown. The present work aimed to investigate these features by developing a test device in which ‘ground truth’ CTCs were generated and presented to the MRI scanner for measurement, thereby allowing for an assessment of the DCE-MRI protocol to accurately measure this curve-shape. The device comprised of a 4-pump flow system wherein CTCs derived from prior patient prostate data were produced in measurement chambers placed within the imaged volume. The ground truth was determined as the mean of repeat measurements using an MRI-independent, custom-built optical imaging system. In DCE-MRI experiments, significant discrepancies between the ground truth and measured CTCs were found for both tumorous and healthy tissue-mimicking curve shapes. Pharmacokinetic modelling revealed errors in measured K^trans, v_e and k_ep values of up to 42%, 31%, and 50% respectively, following a simple variation of the parallel imaging factor and number of signal averages in the acquisition protocol The device allows for the quantitative assessment and standardisation of DCE-MRI protocols (both existing and emerging).

Introduction

The technique of dynamic contrast-enhanced (DCE) MRI with pharmacokinetic (PK) modelling of the contrast agent uptake curves has shown considerable potential as a quantitative marker of tumour malignancy and also for monitoring of therapy. However, its adoption into routine clinical practice has been hindered by uncertainties surrounding the most appropriate or optimum acquisition protocol and also the choice of PK model to use to analyse the measured uptake curves. This has resulted in a plethora of protocols and processing methodologies being used in the published literature, with a commensurate wide divergence in published data which has diminished the discriminative potential of the technique.

In DCE-MRI a sequence of consecutive T₁-weighted MR images are acquired as a bolus of gadolinium-based contrast agent (CA) is administered to a patient, producing a signal time-intensity curve (STC) for each voxel, from which contrast time-intensity curves (CTCs) can be derived (see Appendix 1 for more details). The shape of CTCs is related to the microvascular structure of the tissue being imaged. Tumour microvasculature has been demonstrated to be important for prostate cancer (PCa) diagnosis, response assessment, and treatment planning (Yang and Knopp, 2011). Generally, when a tumour grows to 200 μm or greater, it induces angiogenesis (the formation of new blood vessels) through the sprouting of capillaries from pre-existing micro-vessels (Battegay, 1995), which causes an increase in microvasculature (Folkman, 1990). This microvasculature tends to be more heterogeneously distributed and have higher permeability when compared to the microvasculature of healthy tissue (Passe et al., 1997). However, a challenge for DCE-MRI relates to the relatively low spatial resolution (millimetre scale) at which MR images are acquired, whereas micro-vessels in the capillary bed have an average internal diameter of approximately 8 μm (Martini, 2012). This discrepancy in scale means that the signal measured from a single voxel is not actually a direct measure of microvasculature, but rather a measure of bulk concentration, which is influenced by several physiological factors, such as micro-vessel density, cellular density, and the volume of the extravascular extracellular space.

Semi-quantitative phenomenological parameters can be extracted directly from the STCs, such as the onset to enhancement, wash-in gradient, maximum intensity, wash-out gradient, and integral area under gadolinium contrast concentration after 60 seconds. These parameters have shown efficacy for differentiating malignant from healthy prostate tissue.

For example, using the wash-in rate Kim et al. reported an increase in sensitivity and specificity from 65% to 96% and 60% to 82% respectively in the detection and localisation of PCa, compared to T₂-weighted imaging alone (Kim et al., 2005). Although useful in differentiating normal from malignant prostate tissue, the functional information provided by this type of model free analysis is limited, since the enhancement curve is dependent on multiple physiological factors. On the other hand PK modelling of CTC data offers the prospect of extracting and quantifying sub-voxel functional physiological information, such as the volume-transfer constant (K^trans) and the fractional volume of the extravascular extracellular space (v_e), allowing for a more accurate elucidation of tumour biology. In the literature, several models have been proposed for use in the PK analysis of prostate DCEMRI data, most commonly conventional compartmental models such as the Standard and Extended Tofts models (Tofts and Kermode, 1991, Tofts et al., 1999), as well as more complex models such as the Shutter Speed (Li et al., 2005) and Adiabatic Approximation of Tissue Homogeneity (St Lawrence and Lee, 1998); however, to date, there is no consensus as to which is most appropriate for modelling sub-voxel CA behaviour in prostate tissue.

The temporal resolution of data acquisition has been shown to affect the accuracy of derived PK parameters, with some of the more complex models requiring very rapid acquisition (Henderson et al., 1998); however, in previous DCE studies of the prostate that used PK modelling, temporal resolutions varied widely from 2 to 30 s (Rosenkrantz et al., 2015). The arterial input function (AIF), the concentration of CA as it enters the tissue of interest, is also a vital component of most PK models, and any error in measuring or estimating the AIF will result in an error in the derived PK parameters. Measurement of the AIF is particularly sensitive to temporal resolution, since it is a rapidly-varying CTC, and as such its accurate measurement requires fast acquisition, of the order of 1 s (Henderson et al., 1998). Advances in phased array detector technology, which implement various forms of accelerated imaging, such as k-t SENSitivity Encoding (SENSE) (Pruessmann et al., 1999), SiMultaneous Acquisition of Spatial Harmonics (SMASH) (Sodickson and Manning, 1997), and GeneRalized Autocalibrating Partially Parallel Acquisitions (GRAPPA) (Griswold et al., 2002), faster gradient coils, coupled with novel acquisition techniques, such as compressed sensing (Lustig et al., 2007), show potential to greatly improve temporal resolution without sacrificing image quality, allowing for the use of more complete and accurate PK models. However, there is always a trade-off between acquisition speed and image quality, and to date a gold standard method to quantitatively evaluate this ‘trade-off’ is lacking. This is mainly related to difficulties associated with determining the accuracy of measured parameters, since the actual parameters in the object of interest are generally unknown. There is thus a need for a physical device to quantitatively and prospectively test these new DCE techniques in situ in the scanner, and various phantom designs have been proposed to this end.

One such design type utilises the hollow fibres found commonly in commercial haemodialysis cartridges to produce ‘leaky’ phantom devices, which physically mimic permeable microvasculature. Heilmann et al. demonstrated the usefulness of this type of phantom design in the classification of the permeability characteristics for CAs with different molecular weights (Heilmann et al., 2009). In a study by Mehrabian et al., a similar phantom design was used to test an independent component analysis technique for separating the AIF and extravascular space signals using the signal that is measured in the target tissue (Mehrabian et al., 2011). However, since these phantom designs physically mimic the behaviour of blood vessels, the CTCs produced are dependent on the porosity and perfusion conditions of the system and hence it is not possible to theoretically calculate actual parameter values against which to check the accuracy of the PK modelling. Furthermore, the inevitable retention of CA in the gel space surrounding the hollow fibres limits the use of such devices for multiple experiments. Other designs include ‘lesion’ phantoms, which produce an enhancement curve within single or multiple compartmentalised spaces. In a study by Freed et al., a single 10 mm spherical measurement chamber was mounted into a breast phantom, and the phantom’s ability to produce measurable CTCs was demonstrated (Freed et al., 2011). The behaviour of the system was characterised using a high spatial resolution X-ray system, although its temporal resolution was poor (2.6 – 24.7 s). Additionally, the MR data was acquired at a very low temporal resolution (79 s), making it difficult to access the CTCs measured using MRI. Ledger et al. presented a phantom which consisted of a 40 mm spherical object divided into four inter-linking compartments, for use in quality assurance and the development of DCE-MRI breast protocols (Ledger et al., 2014). Good repeatability was reported for MR measurements made in the phantom, however the curves produced by the system were not independently verified or characterised by a modality other than MRI, meaning that the system’s utility was limited to the relative comparison between MR measurements. A further limitation of the above-described studies was that none allowed for measurements to be made in an environment which realistically challenges prostate DCE-MR imaging by closely emulating conditions observed in vivo, in terms of physical size, image complexity, and sparsity.

The aim of the current work was to develop an anthropomorphic phantom device in which precisely and accurately known ‘ground truth’ CTCs were generated and thus could be presented to the MRI scanner for measurement, thereby allowing for a quantitative assessment of the scanner’s ability to accurately measure the contrast agent wash-in and wash-out curve-shapes. The hypothesis under investigation was that measurement inaccuracies in these curves-shapes, whether slowly or rapidly-varying, deriving from features of the DCE imaging pulse sequence themselves, may contribute significantly to the wide divergence in DCE PK modelling output parameter values in the published literature.

Methods

Phantom design

The phantom contained two measurement chambers, the geometry of which (illustrated in Figure 1(a)) was optimised in a previous study using computational fluid dynamical modelling to allow for optimal uniform distribution of liquids at low flow rates (Hariharan et al., 2013). The 12 mm diameter of these chambers was selected specifically so that several DCE imaging voxels, of a size typically used in prostate DCE, could be positioned within, minimising any partial volume effects due to the chamber walls. These two measurement chambers were set within a larger prostate-sized object (manufactured using a rapid prototyping system) containing a further arrangement of chambers, as shown in Figure 1(b). Liquid containing the Gd-DTPA CA (Multihance, Bracco, USA) was pumped into each measurement chamber through the two inputs and subsequently flowed out through the central output (Figure 1(a)) and then through the larger prostate ‘volume’, before leaving via a single waste output, as shown in Figure 1(b). This larger volume was designed to mimic the enhancement profile typical of the entire prostate, imitating the reduction in sparsity in the temporal domain observed in in vivo scans, which should facilitate the robust validation of certain emerging techniques, such as compressed sensing (Lustig et al., 2007).

Figure 1:

(a) Schematic representation of the geometry of the one measurement chamber’s input/output configuration, and (b) photographs of the final prostate-mimicking object (left: complete, and right: sectioned) containing the two measurement chambers, with inputs into chambers 1 (red) and 2 (blue) highlighted.

This prostate was set into a large custom-built anthropomorphic phantom device (shown in various stages of construction in Figure 2; phantom size = 280(w) × 390(l) × 200(h) mm³). Agar-based tissue mimic materials (TMMs) were used to mimic the T₁ and T₂ properties of bone, muscle, fat, and bladder tissue (details of TMM composition are presented in Table 1). Latex moulds were produced and used to shape certain components, such as the femur bones and bladder.

Figure 2:

(a–d) Photographs showing various stages during construction of the large anthropomorphic phantom, with: (a) an initial layer of fat TMM; (b) a layer of muscle TMM (red dye used to differentiate from other TMMs); (c) the prostate mimicking object in situ prior to surrounding TMM being deposited, as well as two ‘femur bones’ composed of bone TMM; (d) deposition of a heterogeneously distributed fat / muscle layer; and (e) the final phantom device. Dimensions: 280(w) × 390(l) × 200(h) mm³.

Table 1:

Composition of TMMs used in construction of anthropomorphic phantom

	Agar [wt. %]	Gd-DTPA [mM]	MnCl2 [mM]	NaCl [wt. %]	Benzalkonium Chloride [wt. %]
Bone	2.5	-	0.085	0.5	0.046
Muscle	4.0	-	0.026	0.5	0.046
Fat	2.7	0.35	-	0.5	0.046
Bladder	3.0	-	-	0.5	0.046

Fluid pump system design and operation

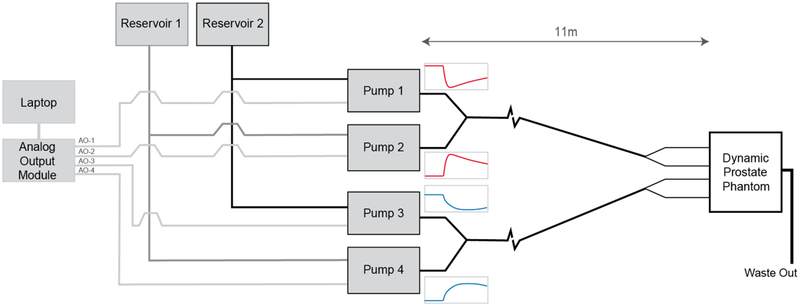
A computer-controlled multi-pump system was designed to produce two simultaneous CTCs within the two separate measurement chambers. The pump system consisted of four gear pumps (Reglo-Z, ISMATEC, Switzerland), and was designed to produce CTCs by varying the relative flow rates of two pumps feeding a given measurement chamber in parallel over time, one pumping a lower baseline concentration, the other a higher concentration of the CA (pumps 1 and 2 feeding measurement chamber 1, and pumps 3 and 4 feeding measurement chamber 2, as illustrated in Figure 3). This configuration ensured a constant volumetric flow rate so that any potential flow-related artefacts would be constant across the concentration range. The inlet tubing placement within the phantom was designed such that, for imaging fields of view typical of DCE protocols, the inflowing liquid was driven to a steady-state prior to entering the measurement chambers, thereby eliminating inflow artefacts. Concentrations of CA (0.15mM and 1.5mM) were selected to give a similar relative peak enhancement to that observed in vivo. The flow rate produced by the pumps was controlled by a time-varying voltage signal produced via a 12-bit analog output module (USB-DA12–8A, ACCES, USA), controlled using custom-written in-house software. The fluid from both pumps flowed through 8 m of 6.4 mm internal diameter (i.d.) tubing (Tygon-R, Saint-Gobain, France) before mixing together via a ‘Y’ connection, following which the fluid travelled a further 1.2 m down a single 6.4 mm i.d. tube before bifurcating to two 3.2 mm i.d. tubes and traveling into the phantom. After passing through the mixing chambers and prostate object the liquid is output to a waste container through a single 6.4 mm i.d. tube.

Figure 3:

Schematic diagram of complete pump system (red and blue traces are representative of the change in flow rate at each pump over time, with the overall flow-rate kept constant).

Contrast time-intensity curves

The physiological curves used in this study, mimicking tumour and healthy tissue, were generated via the Tofts-Kety model based on PK parameters (K^trans = 0.126 min⁻¹ (healthy) and 0.273 min⁻¹ (tumorous) and v_e = 0.292 (healthy) and 0.412 (tumorous)) taken from patient prostate data from a previous study (Alonzi et al., 2010), as well as a model AIF generated using the method and model parameter values reported by Parker et al. (Parker et al., 2006), using code developed in MatLab (R2015b, MathWorks Inc., USA). For each experiment, the CTCs consisted of a 10 s flush, 120 s of baseline flow, and a 300 s physiological curve (representing either tumorous or healthy tissue).

Characterising CTCs and establishing the optimal flow rate for the system

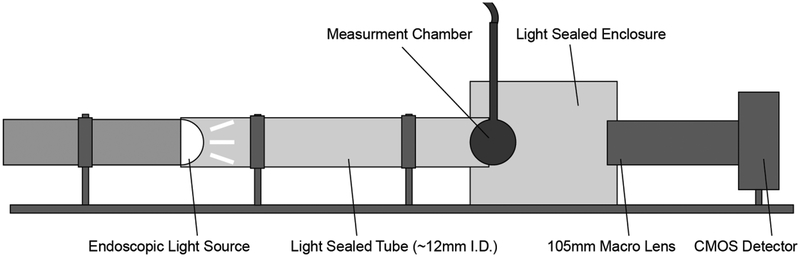
In order to characterise the response of the phantom system, and hence the actual shape of the CTCs produced in the measurement chamber (the ‘ground truth’) after the fluid has been pumped through 11 m of tubing and several tubing connectors, an optical imaging system was designed and set-up as shown in Figure 4. This optical imaging system was also used to establish the threshold minimum flow rate, above which CTC curve-shape distortions were minimised and uniform distribution of dye within the measurement chambers was achieved.

Figure 4:

Schematic diagram of optical imaging system setup used to establish minimum flow rates and ground truth measurements for the CTCs produced by the system.

In this system, a single measurement chamber was connected to two pumps, with the same tubing configuration and lengths as for the main phantom device, and set within a custom-built light-sealed enclosure. An endoscopic light source (Fujinon Eve Σ400, Fujifilm Corp, Japan) was used in conjunction with a high resolution CMOS camera (Canon 50D, Canon Inc, Japan) with a 4752 × 3168 array for detection, giving 4 × 4 μm² pixels, and a temporal resolution of 1 s. An ROI was defined across approximately the same spherical region of the measurement chamber as used in the ROI analysis of the MR data. The temporal stability of measurements made using the optical scanner was measured over a thirty-minute period by imaging the chamber without liquid flow every second and calculating the variation in mean signal over that period. Black dye was used as a CA surrogate in the system, which caused a change in the measured intensity at different concentrations due to the attenuation of incident photons. Imaging known concentrations of dye in the chamber across a range of concentrations used for the CTC runs produced a calibration curve. The calibration curve was fitted using a least squares method with a model adapted from the Lambert–Beer equation, given as:

$$y=a{e}^{bx}+c$$ (1)

where: y = dye concentration, x = average intensity measured over a region of interest (ROI), and a, b, and c are constants derived from fitting the model to the calibration curve data. Very good agreement was observed between the model and the calibration data (R² = 0.998). The calibration curve was used to derive the black dye CTCs from the optical STCs, which were subsequently converted to Gd CTCs (for comparison against the DCE-MRI data) using:

$$C_{\text{Gd}}=\frac{C_{\text{HGd}}-C_{\text{LGd}}}{C_{\text{Hdye}}-C_{\text{Ldye}}}{C}_{\text{dye}}+\frac{C_{\text{LGd}}{C}_{\text{Hdye}}-C_{\text{HGd}}{C}_{\text{Ldye}}}{C_{\text{Hdye}}-C_{\text{Ldye}}}$$ (2)

where C_dye is the total concentration of dye, and C_Gd the total concentration of Gd, in the measurement chamber, comprising of a proportional contribution from each reservoir, which in turn depends on the relative flow rates of the pumps. C_Hdye and C_HGd are respectively the concentrations of dye and Gd used in reservoir one, the higher CA concentration reservoir; and C_Ldye and C_LGd are respectively the concentrations of dye and Gd used in reservoir two, the lower CA concentration reservoir (see Appendix II for the full derivation of Equation [2]). In order to establish the minimum flow rate for the system, full CTC runs of the tumorous curve were measured at flow rates from 0.5 to 3.5 ml s⁻¹, in 0.5 ml s⁻¹ increments. Two criteria were accessed when selecting the minimum threshold flow rate, namely: (i) how well the measured curves fit those expected based on the pump voltage input (programmed), assessed by calculating the percentage root mean square error (%RMSE) between the programmed and measured CTCs (RMSE reported as a percentage of the overall enhancement of the tumorous CTC); and (ii) the uniformity of CA distribution measured within the chamber, calculated by subtracting a static image with no-flow from several images with flow, taken from different experimental runs during the most rapidly changing portion of the CTC (i.e. ‘wash-in’ region on tumorous curve), with percentage uniformity across the resultant images calculated. Once a minimum flow rate had been established, five full CTC runs were measured for each curve (tumorous and healthy). Intraclass correlation coefficient (ICC) analysis was performed on the data in order to access the repeatability of CTCs produced by the system, and the mean CTCs values taken as the measured ground truth, for comparison with the MR data.

MRI measurements

To demonstrate the operation of the phantom, DCE-MRI data were acquired using a 3T scanner (Achieva, Philips, Netherlands) and 32-channel phased array cardiac detector coil (Philips, The Netherlands). A 3D spoiled gradient echo imaging sequence with multi-transmit was used, with the following scan parameters: repetition time = 3.8 ms, echo time = 1.4 ms, flip angle (FA) = 10°, matrix size = 224 × 224 × 80 mm³, spatial resolution = 1 × 1 × 4 mm³, and number of slices = 20. The parallel imaging factor (SENSE) and number of signal averages (NSA) were varied to give temporal resolutions from 1.9 s to 21.4 s, as shown in Table 2. Two manually-selected ROIs were used in the analysis of the data, each containing 24 voxels and set within the respective measurement chamber. The relaxivity (r₁) of the CA in aqueous solution was calculated using a multi-FA approach (FA = 2° to 20° in increments of 2°) by imaging a phantom containing vials with known concentrations of CA. This phantom was deliberately kept small (60 × 60 × 120 mm³), and positioned at the centre of the bore in order to minimise any effects of B₁ inhomogeneity on the measurements.

Table 2:

MRI scan parameters, adjusted to achieve temporal resolutions from 1.9 s to 21.4 s.

Scan Number	R-factor (AP / FH)	NSA	Temporal Resolution [s]
1	1.8 / 2	1	1.9
2	1.4 / 1.6	1	3.4
3	1.2 / 1.4	1	5
4	1	1	7.1
5	1	2	14.3
6	1	3	21.4

Data analysis

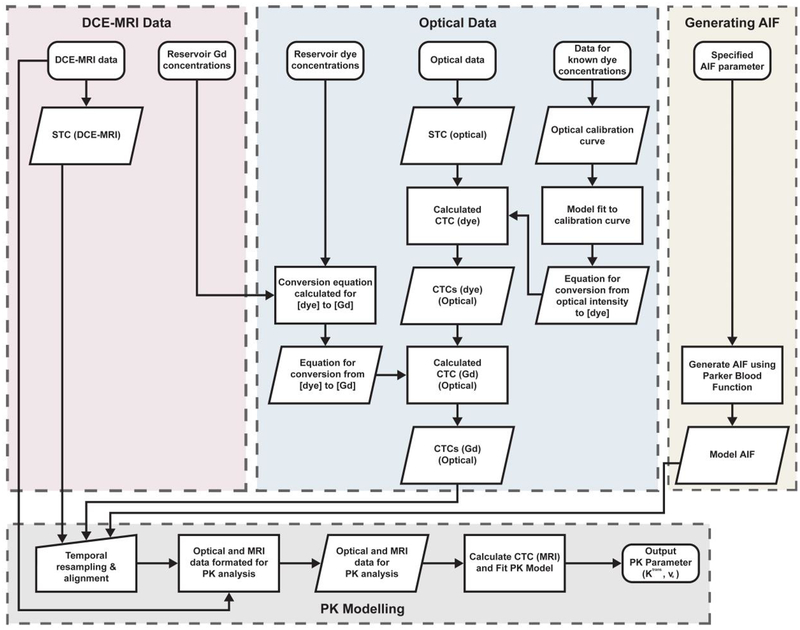
The AIF was generated using the method proposed by Parker et al. (Parker et al., 2006) with code developed in MatLab at temporal resolutions matching those used in the optical and MR studies, to simulate measurement of the AIF, and was then subsequently used in the analysis of all optical and MR data. All PK modelling was performed using the DCEMRI.jl toolkit (Smith et al., 2015). The standard Tofts-Kety model was used to derive K^trans, v_e, and k_ep values for the ground truth CTCs (i.e. as measured in the optical experiments) and the MRI-measured CTCs, and the percentage differences calculated. The optical data were analysed using a ROI approach (i.e. PK parameters were derived from single mean CTCs, averaged from multiple pixel measurements), and the MR data using both ROI and voxel-wise methods (i.e. PK parameters calculated for multiple CTCs taken from each voxel within the ROI, and mean PK parameter values and standard deviations calculated). The flow diagram presented in Figure 5 visually illustrates the steps that were implemented in the acquisition and analysis of the data.

Figure 5:

Flow diagram illustrating the steps implemented in the analysis of the DCE-MRI and optical data.

Results

Phantom construction

Measurement chambers with a wall thickness of 0.3 mm were produced using an Eden 250 3D-printing system (Stratasys, USA) and VeroClear polymer (FullCure-GD810, Stratasys, USA). Agar-based tissue mimic materials were produced which closely approximated the T₁ and T₂ properties of bone, muscle, fat, and bladder tissue (de Bazelaire et al., 2004).

Optical experiments

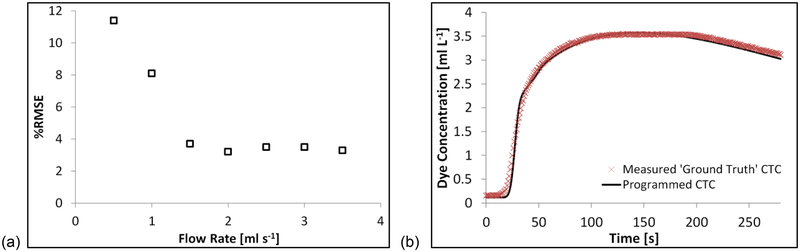
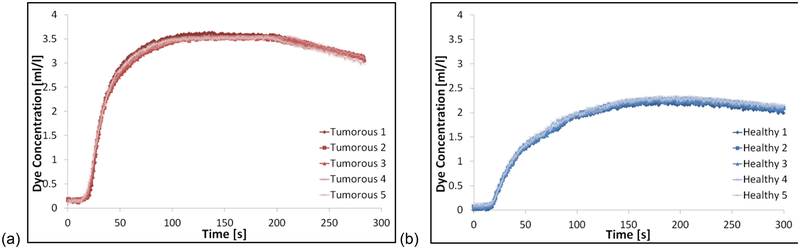
The temporal stability of measurements made using the optical scanner was found to vary by ±0.4% over a 30-minute period. The %RMSE values between the optically-measured and programmed CTCs were lowest (< 4%) with flow rates ≥ 1.5 ml s⁻¹, with no further decrease in the %RMSE values observed at flow rates greater than 1.5 ml s⁻¹, as shown in Figure 6. At a flow rate of 1.5 ml s⁻¹ the uniformity of CA distribution across the chambers was measured to be 96%, with uniformity decreasing at lower flow rates, and not changing significantly at flow rates higher than this. This analysis revealed a clear threshold minimum flow rate for the phantom setup of 1.5 ml s⁻¹, and as such this flow rate was used for all subsequent experiments. Very good correlation was observed between the five consecutively measured CTCs for both curve shapes (tumorous and healthy) as illustrated in Figure 7, with high ICC values of 0.996 and 0.998 for healthy and tumorous CTCs respectively. Average values from each of the five measured CTCs were converted to Gd-DTPA concentration, and used as the measured ground truth CTCs in subsequent MRI experiments. PK parameters values were also calculated from each of the optically-measured CTCs, with the mean values taken as the ground truths. Ground truth K^trans values were measured to be 0.123 ± 0.001 min⁻¹ and 0.233 ± 0.002 min⁻¹, and v_e 0.355 ± 0.001 and 0.461 ± 0.002, for healthy and tumorous CTCs respectively (errors are given by the standard deviation across repeated optical-measurements).

Figure 6:

Plots showing: (a) the % root mean square error (%RMSE) values calculated between the programmed and optically-measured CTCs at different flow rates (presented as a percentage of the overall programmed CTCs amplitude); and (b) the programmed and optically-measured ground truth tumorous CTCs (measured with 1.5 ml s⁻¹ flow rate).

Figure 7:

Plots showing five repeated measurements of the (a) tumorous and (b) healthy CTCs used in this study, using the optical imaging system at 1.5 ml s⁻¹ flow rate.

MRI Experiments

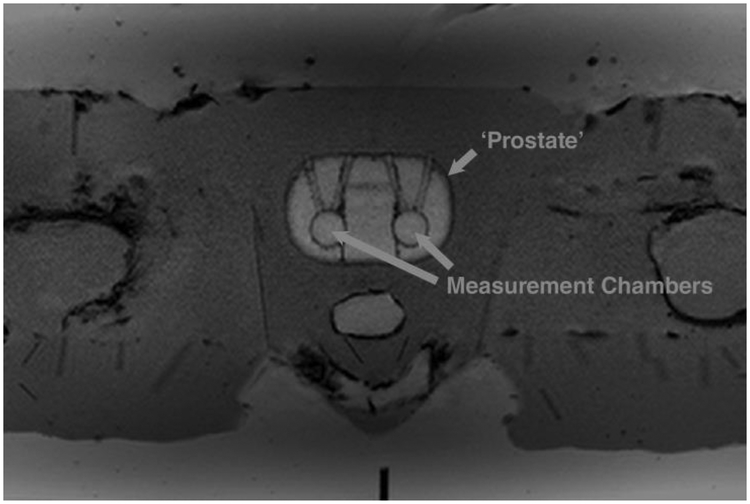
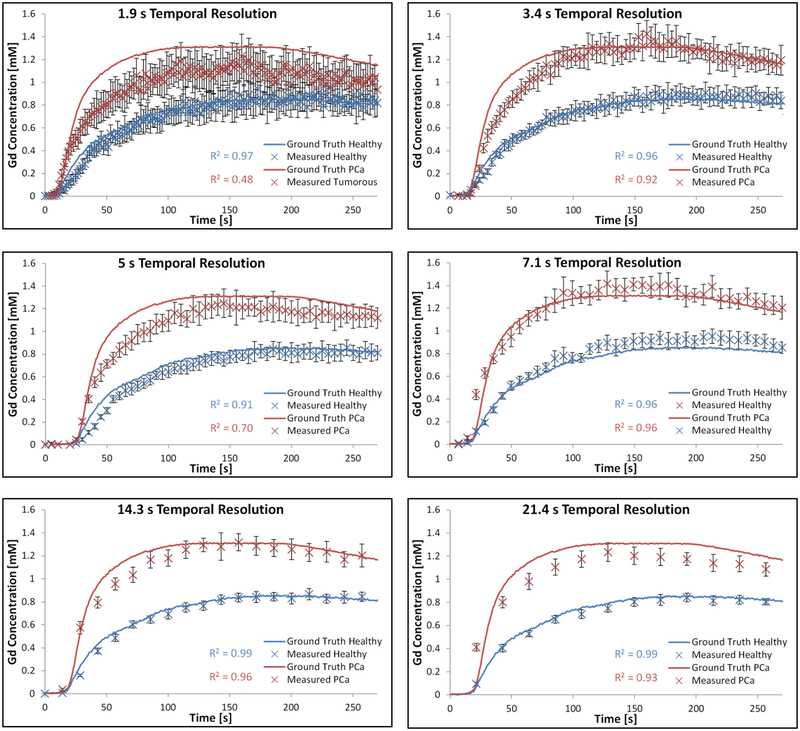
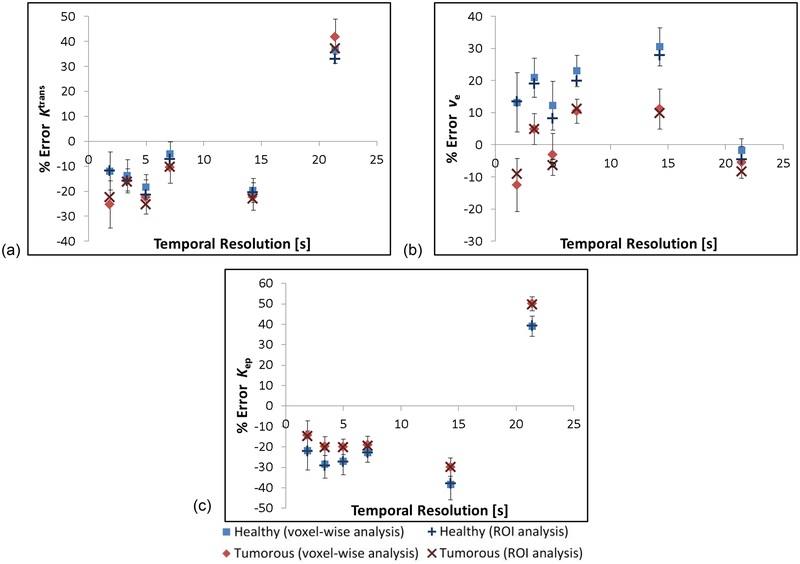
Initial scans of the large anthropomorphic phantom show similar visual appearance to in vivo patient prostate scans, as shown in Figure 8. Figure 9 shows preliminary data comparing the CTCs derived from the MR data with those from the ground truths. All protocols (with the exception of the 5 s temporal resolution protocol) measured the healthy-shaped CTC with R² > 0.95, however only two protocols measured the tumorous-shaped CTC with an R² > 0.95 (7.1 and 14.3 s). K^trans, v_e and k_ep values derived from the MR data were found to differ from the ground truths by up to 42%, 31%, and 50% respectively; details of the specific PK parameter errors as a function of the temporal resolution used for the DCE acquisitions are presented in Figure 10, for both a voxel-wise and ROI analysis of the data. PK parameters derived using these two different methods (voxel-wise versus ROI) differed by < 4%, with all PK parameter values derived using the ROI method within the standard deviations of those derived using the voxel-wise approach. The lowest errors in the measurement of both tumorous and healthy K^trans, v_e and k_ep values occurred using the 7.1-, 21.4-, and 1.9-second temporal resolution protocols respectively.

Figure 8:

Axial T₁-weighted image of the anthropomorphic phantom with the ‘prostate’ and measurement chambers highlighted. Regions mimicking subcutaneous fat, muscle, and bone are visible

Figure 9:

Plots presenting tumorous and healthy CTCs derived from DCE-MRI data at 1.9 to 21.4 s temporal resolutions, compared with the ground truths derived from optical scanner data.

Figure 10:

Percentage errors in (a) K^trans, (b) V_e, and (c) k_ep values derived from the DCE-MRI data using the Tofts-Kety model. Values shown for both a voxel-wise and ROI analysis of the data. Error bars shown for voxel-wise results taken from the standard deviation in the data.

Discussion

There is currently a lack of standardisation of prostate DCE-MRI image acquisition protocols, particularly in relation to the trade-off which must be made between spatial and temporal resolution, with studies in the prostate alternatively giving preference to either spatial resolution (McClure et al., 2012, Costa et al., 2013) or temporal resolution (Vos et al., 2013, Chen et al., 2012). The European Society of Urogenital Radiology presented guidelines (Barentsz et al., 2012) which recommend a temporal resolution of ≤ 15 s and spatial resolution of ≤ 0.7 × 0.7 × 4 mm³; however, there is growing consensus that temporal resolutions much lower than 15 s are required when more complex PK models are used to analyse the data (Henderson et al., 1998). However, the effect on measurement accuracy of pushing the temporal resolution to these values remains unclear, and to date it has not been possible to quantitatively assess measurement errors deriving from acquisition protocol-related factors. It has rather been assumed that such protocols accurately measure slowly-changing CTCs, such as those in healthy tissue and most tumours, whereas only rapidly-changing tumour CTCs, and AIFs in particular, pose a problem for MRI measurement. However, the results presented herein using the novel phantom design demonstrate the significant influence the acquisition protocol has on the measured shape of even slowly-changing CTCs. Given the ability to generate and characterise any arbitrary CTC-shape, it was possible to quantify errors in PK output parameter estimation deriving exclusively from the DCE acquisition protocol. Using specific K^trans and v_e values (taken from prior prostate patient studies) to generate CTCs, using the optical imaging system to determine the actual CTCs arriving in the phantom, and finally performing a PK analysis on the optically-measured CTCs (and hence re-deriving the actual ‘ground truth’ K^trans and v_e values that would give rise to this curve-shape); differences between the ground truth PK parameter values and those derived from the MR-measured CTCs could be used to quantify errors in the DCE acquisition protocol.

Key to this determination of accuracy was a precise and accurate knowledge of the ground truth CTC presented to the MRI scanner for measurement. In attempts to characterise the CTCs produced by their phantom systems, previous studies have used repeated MR measurements (Casas et al., 2014), prediction models (Driscoll et al., 2011, Ebrahimi et al., 2010), and X-ray measurements (Freed et al., 2011); however, these system designs do not allow for a determination of the ground truth against which DCE-MRI measurements can be compared. In the current study the ground truth CTCs were independently determined using a high spatial and temporal resolution, calibrated optical imaging system. The use of a ‘ground truth’ descriptor for the CTCs in this context was considered reasonable due to the low measurement error associated with the optical imaging system (±0.4% measurement accuracy; ICC > 0.996 for consecutive runs, both tumorous and healthy CTCs). Concentration values were derived via a calibration curve, the data for which was acquired by imaging known concentrations of black dye with no flow; however, the same known concentrations were also imaged with flow of 1.5ml s⁻¹, with no measurable differences observed between the two datasets. Differences between the programmed and optically-measured CTCs translated to an 18% maximum difference between the programmed and optically-measured ground truth PK parameters values, for the CTCs used in the study. However, the resultant ground truth PK parameters values were still well within the range of patient-derived values for tumorous and healthy prostate tissue reported in the literature (Alonzi et al., 2010). Furthermore, repeat optical experiments demonstrated the ability of the phantom system to precisely reproduce contrast curves with these PK parameter values, with low standard deviations of <1.2% recorded for all optically-measured ground truth PK parameter values.

The choice of flow rate used in the phantom device struck a balance between minimising discrepancies between the programmed and optically-measured CTCs (which imposed a lower limit on the flow rate that could be used) and reducing the potential for flow artefacts in the MR images (which mitigated against using very high flow rates). Discrepancies between the programmed and measured CTCs occur at lower flow rates due to two principal factors: (i) excessive longitudinal mixing along the length of the tubing caused by diffusional and turbulent flow effects which adversely affected the shape of the CTCs produced; and (ii) an incomplete flushing of the solution within the entire volume of the measurement chamber at each time-point within a DCE run, resulting in undesired dye (and hence MR contrast agent) concentration variations within the chambers. This latter effect was noted in an earlier study involving computational fluid dynamics of flow profiles in measurement chambers of similar design to that used herein (Hariharan et al., 2013). In the current study, a flow rate of 1.5 ml s⁻¹ was found to be sufficient to eliminate this effect, as determined by the highly-uniform (> 96%) dye distribution measured within the measurement chambers. This flow rate also marked the threshold at which the %RMSE between the programmed and measured CTCs was minimised (< 4%).

There were minor differences between the two modalities (optical and MRI) in where and how the signal was measured; for example, the ROI used for the optical experiments encompassed data from approximately 90% of the measurement chamber’s volume, whereas with the MRI experiments the ROI analysis was performed on voxels measured in a 4 mm slice taken through the centre of the chambers. However, since the phantom system provided highly-uniform distribution of CA within the measurement chambers at the flow rate used, one may assume that the concentration measured at a particular voxel in the MR data is representative of the overall concentration within the chamber, and since the optical experiments also provide a measure of the overall CA concentration within the measurement chamber, direct comparison between the two modalities was possible.

An anthropomorphic phantom design was used with an internal complexity and physical dimensions sufficient to present a clinically-realistic challenge to the image acquisition protocols under test, with a specific emphasis herein on prostate imaging although the principal is valid for other body areas. Thus, protocols developed and validated using the phantom can be easily translated to patient studies in the clinic. A visual comparison of the CTCs presented in Figure 9 shows discrepancies between the measured and ground truth curve-shapes, and this is reflected in the calculated R² values. An apparent bias was observed in the MR-measured curves in the form of an underestimation of the concentration values in the ~ 20 – 100 s time range (see Figure 9), the source of which remains the subject of future work. Of the acquisition protocols tested, it was found that K^trans was most accurately measured using a protocol with a temporal resolution of 7.1 s. As the parallel-imaging factor was increased with resultant improvement in temporal resolution, the accuracy of K^trans measurements decreased by up to 15%, which may be related to decreased SNR in the images, although other parallel imaging-related factors may also have contributed to these increased errors. Furthermore, as the NSA was increased in subsequent experiments, causing a deterioration in temporal resolution, the accuracy of the measured K^trans values also decreased by up to 31%, as one would expect due to the reduced number of sampling points leading to a loss of fidelity in the shape of the measured CTCs, particularly rapidly changing portions of the curves such as the initial wash-in (on which K^trans is strongly dependant), as well as the resampled AIF used for the PK modelling. v_e was measured with the lowest error at 21.4 s temporal resolution, possibly due to more accurate measurement of the CTCs’ wash-out section for which v_e is most sensitive. Errors in measured k_ep were lowest using the 1.9 s temporal resolution protocol, and increased at temporal resolutions > 1.9 s. These preliminary data highlight the need to further refine acquisition protocols to identify the source of and hence to reduce these errors

These data demonstrate the critical dependence of the accuracy of PK output parameter values on the quality of the data inputted to the models, whether that be adequate temporal sampling of the uptake curves, or adequate data quality to ensure faithful fitting of the model. It should be noted that the use of inappropriate PK models for specific tissue and tumour types also likely contributes to discrepancies in the published literature (Sourbron and Buckley, 2012), and here again the current phantom device could be of use, for example in exploring the relationship between SNR and temporal resolution on the modelling accuracy for increasingly complex PK models.

In the preliminary data presented in this study, no B₁ corrections were made, however it is likely that any inhomogeneity present may have contributed to errors. Other issues, such as inadequate spoiling, B₀ inhomogeneity, and off-resonance effects, may also have contributed to the errors in the MR-measurements. The anthropomorphic nature of the phantom will facilitate further investigation of these deviations in ideal performance of the spoiled gradient echo imaging sequence, and are the focus of future work. Potential further errors arising from the use of rapidly-accelerated techniques such as parallel imaging, zoom imaging, and compressed sensing remain to be tested, and are the current focus of on-going work in this area. This work nevertheless further demonstrates the difficulties in performing quantitative measurements using what is substantially a qualitative instrument, that is, a clinical MRI scanner. Precise and accurate knowledge of the ground truth CTC values in the phantom design presented herein, absent in other phantom designs, facilitates a more quantitative approach to DCE-MRI by providing a test-bed on which new and existing acquisition protocols can be quantitatively assessed.

Conclusions

The development of a novel dynamic anthropomorphic prostate phantom test device is described, and its use in quantitatively determining the measurement accuracy of several DCE-MRI acquisition protocols is demonstrated. The device is capable of simultaneously producing two distinct, accurate, and reproducible CTCs representative of those observed in DCE-MRI data of the prostate within two separate measurable regions. The programmed shape of the CTCs produced by the system can easily be modified to simulate any shape CTC, including tumour-mimicking and AIFs. Ground truth CTCs produced within the phantom’s measurement chambers were precisely and accurately determined using a custom-built calibrated optical imaging system, which had high temporal and spatial resolution. Errors in K^trans, v_e and k_ep values of up to 42%, 31%, and 50% respectively were recorded with varying temporal resolution. These results demonstrate heretofore unappreciated yet significant errors introduced by standard DCE acquisition protocols into derived PK output parameter values. The phantom device provides a system on which new DCE acquisition protocols can be accurately validated, for example those using highly accelerated acquisition schemes such as compressed sensing.

Appendix I: Conversion of DCE-MRI STCs to CTCs

DCE-MRI STCs can be converted from signal to T₁ values using the signal equation for a spoiled gradient echo sequence:

$$S\left(x,t\right)=S\left(x,0\right)\text{sin}\theta \frac{1-\text{exp}\left[-\frac{1}{T_1}\left(x,t\right)TR\right]}{1-\text{cos}\theta \text{exp}\left[-\frac{1}{T_1}\left(x,t\right)TR\right]}$$ (A.1.)

where S(x,t) is the signal as a function of space x and time t, θ is the flip angle, and TR is the repetition time. $T_2^{*}$ decay was ignored in our study, on the assumption that the echo time was much shorter than $T_2^{*}$. T₁ values can then subsequently be converted into [CA] via:

$$\left[\text{CA}\right]=\frac{\frac{1}{T_1}-\frac{1}{T_{10}}}{r_1}$$ (A.2.)

where [CA] is the concentration of CA (mM), T₁ is the measured T₁ value at a given time-point, T₁₀ is the native T₁ (i.e. the T₁ of water in the case of our study), and r₁ is the relaxivity of the CA (mM⁻¹s⁻¹).

Appendix II: Derivation of relationship between dye and Gd concentrations

Below we derive a linear relationship between the dye and Gd concentrations. We assume that the pumps perform the same across all experiments. Since the concentration of dye in the chamber is controlled by varying the relative flow rates of two pumps in parallel, one pumping the higher concentration of CA, the other the lower, we can model the contribution from each pump to the overall concentration of CA in the chamber using the following:

$$C_{\text{dye}}=C_{\text{Hdye}}{F}_1+C_{\text{Ldye}}{F}_2$$ (B.1.)

$$C_{\text{Gd}}=C_{\text{HGd}}{F}_1+C_{\text{LGd}}{F}_2$$ (B.2.)

where C_dye is the concentration of dye in the measurement chamber and C_Gd is the concentration of Gd in measurement chamber. C_Hdye and C_HGd are respectively the concentrations of dye and Gd used in reservoir one, the higher CA concentration; and C_Ldye and C_LGd are respectively the concentrations of dye and Gd used in reservoir two, the lower CA concentrations. F₁ and F₂ give the normalised flow rate for pumps one and two respectively. Since F₁ and F₂ are varied relative to one another across the full dynamic range of the pumps, we have

$$F_1+F_2=1$$ (B.3.)

Substituting Equation (B.3.) into Equations (B.1.) and (B.2.) and rearranging gives

$$C_{\text{dye}}=\left(C_{\text{Hdye}}-C_{\text{Ldye}}\right)F_1+C_{\text{Ldye}}$$ (B.4.)

$$C_{\text{Gd}}=\left(C_{\text{HGd}}-C_{\text{LGd}}\right)F_1+C_{\text{LGd}}$$ (B.5.)

Combining Equations (B.4.) and (B.5.), one can then easily derive

$$C_{\text{Gd}}=\frac{C_{\text{HGd}}-C_{\text{LGd}}}{C_{\text{Hdye}}-C_{\text{Ldye}}}{C}_{\text{dye}}+\frac{C_{\text{LGd}}{C}_{\text{Hdye}}-C_{\text{HGd}}{C}_{\text{Ldye}}}{C_{\text{Hdye}}-C_{\text{Ldye}}}$$ (B.6.)

Equation (B.6.) provides a general model for the conversion of measured dye concentration to Gd concentration, which is only dependent on the reservoir concentrations used, which are constant.