An Adaptive Seismocardiography (SCG)-ECG Multimodal Framework for Cardiac Gating Using Artificial Neural Networks

Abstract

To more accurately trigger data acquisition and reduce radiation exposure of coronary computed tomography angiography (CCTA), a multimodal framework utilizing both electrocardiography (ECG) and seismocardiography (SCG) for CCTA prospective gating is presented. Relying upon a three-layer artificial neural network that adaptively fuses individual ECG- and SCG-based quiescence predictions on a beat-by-beat basis, this framework yields a personalized quiescence prediction for each cardiac cycle. This framework was tested on seven healthy subjects (age: 22-48; m/f: 4/3) and eleven cardiac patients (age: 31-78; m/f: 6/5). Seventeen out of 18 benefited from the fusion-based prediction as compared to the ECG-only-based prediction, the traditional prospective gating method. Only one patient whose SCG was compromised by noise was more suitable for ECG-only-based prediction. On average, our fused ECG-SCG-based method improves cardiac quiescence prediction by 47% over ECG-only-based method; with both compared against the gold standard, B-mode echocardiography. Fusion-based prediction is also more resistant to heart rate variability than ECG-only- or SCG-only-based prediction. To assess the clinical value, the diagnostic quality of the CCTA reconstructed volumes from the quiescence derived from ECG-, SCG- and fusion-based predictions were graded by a board-certified radiologist using a Likert response format. Grading results indicated the fusion-based prediction improved diagnostic quality. ECG may be a sub-optimal modality for quiescence prediction and can be enhanced by the multimodal framework. The combination of ECG and SCG signals for quiescence prediction bears promise for a more personalized and reliable approach than ECG-only-based method to predict cardiac quiescence for prospective CCTA gating.

ECG-Seismocardiography (SCG) Multimodal Framework for Coronary Computed Tomography (CCTA).

I. Introduction

According to the World Health Organization, cardiovascular disease (CVD) is the leading cause of death globally. In 2015, approximately 17.7 million people died from CVDs, comprising 31% of global death [1]. Coronary artery disease (CAD) is the most common type of CVD that relates to the heart’s major blood vessels. Catheter coronary angiography (CCA) [2] is considered the gold standard for assessing coronary blood vessels to evaluate and manage CADs. However, CCA is invasive in that it requires insertion of a catheter and intraarterial injection of contrast agent to visualize arterial blockage via X-Ray imaging. Computed tomography angiography (CTA) [3] is an attractive alternative since it is a less invasive, less expensive and faster technology than CCA [4], [5]. Yet, coronary CTA (CCTA) is limited by temporal resolution, and cardiac motion artifacts can compromise image quality. To improve the diagnostic quality of CCTA, it is crucial to obtain CCTA images within the quiescent period¹ of the cardiac cycle.

Currently, clinical quiescence prediction relies almost exclusively on the real-time electrocardiography (ECG) signal. CCTA data acquisition is triggered by either a prospective gating signal derived from that ECG signal, or by retrospective selection of CCTA data from ECG-selected phases. In either case, quiescence prediction based on ECG is not always reliable since ECG is a proxy of heart motion and has been demonstrated to be an imprecise marker of the instantaneous cardiac mechanical motion [6], [7]. On the other hand, seismocardiography (SCG) directly records the cardiac vibration via an accelerometer placed on the chest wall and reflects the mechanical state of the heart more accurately and could potentially provide a better gating signal for CCTA.

The effectiveness of SCG in facilitating diagnosis for CADs have been demonstrated by multiple studies. An early research compared the diagnostic accuracy of ECG with SCG and suggested that SCG can significantly improve the accuracy for detection of anatomic and physiologic CADs [10]. A recent study evaluated the potential of tri-axis acceleration-based signal as a gating signal for positron emission tomography (PET) [11]. In addition, a more recent study presented a dual-sensor quiescence detection method using both a tri-axial chest accelerometer and gyroscope for PET [12], reporting an improvement in diagnostic accuracy on both reconstructed phantom images and two atherosclerosis patients. With respect to at-home monitoring and remote cardiovascular disease follow-up system, SCG-based measurement modality was emphasized due to its robustness, feasibility and capability in detecting cardiac vibrations [13].

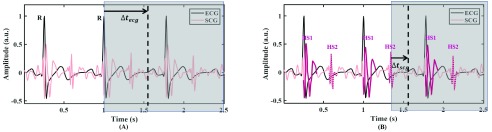
This paper builds upon our earlier work [14] where we developed an SCG-based quiescence detection and prediction method. In the SCG-based method, we focused on the frequency component (10-45 Hz) of SCG associated with cardiac sounds.² Personalized heart sound associated waveforms, denoted in Fig. 1 as HS1 and HS2, can be extracted from pre-recorded SCG signals and then correlated to streaming SCG signals for detecting the heart sound features. The predicted quiescence, measured as a delay , is in reference to a cardiac feature within the upcoming cardiac cycle. In the SCG-based prediction, we used the heart sound associated waveform since it is a more proximal reference than the R-peak of ECG and thus can provide more accurate predictions.

Fig. 1.

Quiescence prediction methods. (A) The traditionally ECG-based prediction method; (B) Developed SCG-based prediction method. HS1 and HS2 are heart sound associated waveforms in systole and diastole, respectively [8], [9]. The vertical dotted line is the quiescence derived from echocardiography which is considered as the baseline for quiescence in this study. Areas covered in grey contain succeeding unknown signals. The predicted quiescence, measured as a time , is in reference to a cardiac feature within the upcoming cardiac cycle. As a demonstration we review predicting quiescence in diastole. Predicting from HS2 involves less uncertainty than that from using R-peak of ECG, therefore SCG-based prediction can potentially predict quiescence more accurately.

In this study we expand our foundational work through a multimodal approach for prospective CCTA that adaptively yields a corrected quiescence by fusing individual predictions derived from ECG and SCG on a beat-by-beat basis. Fusion of predictions from two sensing modalities are implemented via an artificial neural network (ANN). Using quiescence derived from echocardiography as a baseline, the performance of SCG- and fusion-based predictions are compared with the ECG-based prediction, which is the traditional approach for CCTA gating.

We base our rationale for selecting an ANN approach upon the wide application of ANNs in classifying physiological signals [15], [16]. In addition, extensive studies have demonstrated the competence of ANNs in capturing associations among vaguely understood variables [17]. Furthermore, the use of an ANN does not impose constraints upon the input data structure [18]. In particular to our study, we use personalized features to construct input to an ANN. More specifically, the selected features include heart rate, heart rate variability [19], waveform correlation [20], HS associated waveform power intensity [21] and wavelet-based time-frequency coefficients [22], [23]. To obtain the corrected quiescence, we employ a linear combination of predicted quiescence from ECG and SCG whereby weights are outputs from the ANN.

The paper is organized as follows. The next section describes methods and procedures of the ANN implementation followed by ANN classification results and quiescence prediction performance in Section III. In addition, the diagnostic quality of CCTA images reconstructed at predicted quiescence derived from different gating modalities are evaluated and analyzed. Lastly, Section IV delivers a discussion and conclusions.

II. Methods and Procedures

A. Subjects and Data Acquisition

Cardiac signals were acquired from seven healthy subjects (mean age: 31; age range: 22-48; males: 4) and eleven cardiac patients³ (mean age: 56; age range: 31-78; males: 6). Written, informed consent was obtained from each participant and the study was conducted under the approval of the Emory University Institutional Review Board. Cardiac signals including ECG, SCG and echocardiography were acquired simultaneously using a trimodal data acquisition system consisting of a custom SCG-ECG device and a commercial ultrasound machine SonixTOUCH Research Scanner (Analogic, Peabody, MA, USA) [25].

The ECG-SCG custom device acquired ECG and SCG signals at the rate of 1.2 kHz. Both signals were pre-filtered and amplified by the analog end before feeding to a 16 bit analog-to-digital converter (ADC). The accelerometer (ADXL327, Analog Devices, Inc., Norwood, MA) weighs approximately 5 g and and has an RMS noise of 250 . The accelerometer was tuned to have a passband of 50 Hz [25].

Simultaneously, B-mode echocardiography data, specifically apical four-chamber view, were obtained at a rate of 50 Hz/frame, and the associated ECG was recorded at 200 Hz. The redundant ECG signals from the two machines were used to align SCG and echocardiography signals, as well as to segment heartbeats.

During data acquisition, each participant was resting in a supine position for approximately 30 minutes, with a single-axis linear accelerometer placed against the sternum recording dorso-ventral vibrations transmitted to the chest wall.⁴ While many studies used the tri-axis accelerometer to measure the mechanical movement of the heart, the tri-axis SCG signals have not yet been quantified with a widely acknowledged standardization in terms of cardiac events, particularly with the heart sound in the lateral-medial and superior-inferior directions for this study. A potential reason for this is the intersubject variability observed in the tri-axis SCG signals [26], [27].

B. Pre-Processing

Raw signals were pre-processed to remove the noise and baseline drift [28]. By analyzing the frequency spectrum, the ECG signal and SCG signal were conditioned by a -order FIR low-pass filter with a Hamming window configuration and cutoff frequency 50 Hz [29]. For ECG signal, this was to ensure to retain the sharp R peaks of ECG. For SCG signal, this was to keep the high frequency components related to heart sounds. Following the low-pass filter was a notch filter centered at 0 Hz with a cutoff of 1 Hz to remove the DC component and remaining respiratory baseline drift in ECG and SCG signals [25], [30].

The magnitude of the cardiac interventricular septal (IVS) motion velocity from B-mode sequences was derived by applying the phase-to-phase deviation measure elaborated in [31]. For each subject, quiescence was identified from the velocity magnitude using a voting mechanism, which can be modeled as a linear function of heart rate [14]. Quiescence derived using the modeled linear function was considered as the baseline when comparing quiescence derived from ECG and SCG.

C. Artificial Neural Network Configuration

The ANN configuration was selected since it outputs both a classification decision and Bayesian probability estimates, which were used as assigned weights, and , for fusion-based prediction.⁵ Furthermore, the weights also indicate how likely a specific cardiac cycle is to be gated using one modality, either ECG or SCG. Gating with solely ECG or SCG are special cases of weighted fusion where one of the weights takes the value of 0 and the other one takes 1. Let be the quiescent phase derived from the ECG-based prediction and from the SCG-based prediction. The fusion-based prediction is a linear combination of the individual predictions from ECG () and SCG () and are expressed as where .

A two-layer ANN is able to represent any arbitrary continuous function, and an ANN with greater than two layers is able to represent any function [32]. Thus, a three-layer ANN configuration is a good fit for this study in which the associated data structure is unknown. Figure 2 illustrates the feedforward ANN configuration used in this study. The ANN consists of three layers: two hidden layers with hyperbolic tangent-sigmoid and log-sigmoid as threshold functions [33], respectively, and an output layer with softmax threshold function [24]. The hyperbolic tangent-sigmoid function ranges from −1 to 1 and it is zero centered, making the gradient update faster and easier. The log-sigmoid function restricts any input value within 0 and 1 which is especially helpful for models that predict the probability as an output. The number of neurons in each layer was set heuristically. The network was trained with scaled conjugate gradient back-propagation [34]. The number of nodes in each layer was determined by using the trial-and-error method.

Fig. 2.

Three-layer ANN configuration [24]. The input is a set of features consisting of 11 single-valued entries linked with two hidden layers with threshold functions tansig and logsig, each consisting of 10 neurons. are configuration parameters representing the weights and bias. Two softmax output neurons in the output layer generate 2 values corresponding to the predicted probabilities, referred to as weights, of ECG- and SCG-based gating in the weighted fusion, WF.

D. Feature Selection

The rationale for choosing ANN features is three-fold. First, the feature set should contain as much information of the original dataset as possible. Second, the features are expected to be invariant to irrelevant transformations of the data. Third, features are expected to be distinguishing. More specifically, a new feature is only worth adding when it serves to increase information in the current feature set.

In this study, subject-specific features were selected from each cardiac cycle of the ECG and SCG signals. Cardiac cycles were each re-sampled into 1000 sample length for computational simplicity before extracting features on a beat-by-beat basis. The re-sampling was made on a beat-by-beat basis since the quiescence prediction for cardiac gating needs to be done on a beat-by-beat-basis. Consequently, the sampling frequency after re-sampling varies with different instantaneous heart rates.

Feature selection involve two stages. The first stage is constructing an original feature set that contains a broad coverage of features. The original features and their corresponding numbers are summarized in Table 1. The second stage selects a subset of the original feature set to form a more concentrated and computational efficient feature set.

TABLE 1. Original features.

Original ECG Features					Original SCG Features				Total
HR	HRV
1	1	1	1	4	1	1	1	3	14

ECG features in the original feature set are:

• 1)HR: Heart rate. Reciprocal of the interval between two consecutive R-peaks.
• 2)HRV: Heart rate variability [19], [35]. The HRV is defined as the deviation to the mean of the most recent eight R-R intervals, measured by the absolute difference [36]. Hence, the first eight cardiac cycles are for initialization.
• 3)C_ecg: Waveform correlation [20], [37]. An ensemble averaged template waveform is generated by averaging the re-sampled time-series beat cycles. The correlation of a cardiac cycle to the template is an indication of morphological distortion level and thus the noise contamination level.
• 4)SNR_ecg: Signal-to-noise ratio. The difference between the aforementioned ensemble averaged template waveform and an individual re-sampled cardiac cycle, labeled as the difference time-series, is a measurement of magnitude distortion due to noise. Thus, for each cardiac cycle, the root-mean-square (RMS) power of the difference time-series quantitatively represents the relative noise power of that cardiac cycle. The estimated signal-to-noise ratio is the ratio of template waveform power (summation of squared sample values) to the noise power within a beat.
• 5.DWT_ecg: Wavelet-based time-frequency coefficients [22], [38], [39]. For ECG, Daubechies four (Db4) was tested to be a suitable mother wavelet and a decomposition level of 8 was found to be suitable [38], [40]. Four wavelet levels (2-5) were used, corresponding to the frequency band spanning approximately 2-20 Hz. The mean coefficient of each scale was then used as an original feature.

SCG features in the original feature set are:

• 1){PSD_output, PSD_HS1, PSD_HS2}: Heart sound waveform intensity [21]. The power spectrum based on Fourier transform of the conditioned SCG can be divided into three frequency ranges: 0-10 Hz which is related to the cardiac output, 10-30 Hz related to the first heart sound (HS1), and 30-50 Hz related to the second heart sound (HS2) [41]–[43]. Periodogram estimate of the power spectrum density (PSD) was used as an estimated spectrum density of a time series obtained by squaring the magnitude components of the discrete Fourier transform of the signal. The aggregate power within each 10 Hz bin was calculated by summing the power within the aforementioned three spectrum ranges providing a periodogram estimate of the PSD.
• 2)DWT_scg: Wavelet-based time-frequency representation. Previous work demonstrated the superiority of ‘Coif5’ mother wavelet in heart sound signals decomposition [42]. Similar to ECG, a decomposition level of 8 was applied to SCG. Three wavelet levels (1-3) were used, corresponding to the frequency band spanning approximately 10-45 Hz. The mean coefficient of each scale was then used as an original feature.

The choices of frequency range for the DWT are based on the frequency spectrums of the cardiac events of interest. Based on the Fourier transform of the human ECG signal, it was found that the QRS complex frequency ranges within 4 Hz and 20 Hz, the heart rate component is within 0.67 Hz and 5 Hz (corresponds to 40-300 bpm), and P and T wave frequencies generally lie between 0.5 and 10 Hz [29]. The wavelet decomposition of the SCG was intended to extract information from the high-frequency accelerometric waveforms associated with the first (10-30 Hz) and second heart sound (30-45 Hz).

It is important to note that not all cardiac cycles are good candidates for feature selection. Before feature selection, a cardiac cycle is evaluated by its ECG and SCG HS waveform. Cardiac cycles with C_ecg < 0.3 and HS not identified by the waveform template detection approach [14] are considered to be severely contaminated by noise, and thus are eliminated. Cardiac cycles with C_ecg > 0.3 but with no HS identified are suitable for ECG-based prediction, and cycles with HS identified but C_ecg < 0.3 use SCG-based prediction. The threshold criterion is set based on empirical statistics of C_ecg and the HS identification is based on template matching conditions in [14]. Only those cardiac cycles whose ECG and SCG waveforms are clean enough are valid for fusion-based prediction by the ANN. On average, 72% of the cardiac cycles were good candidates for feature selection.

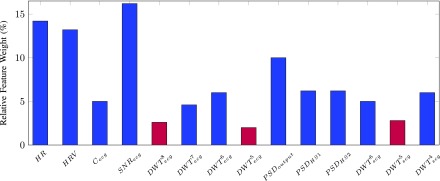
The original feature set has 14 single-value features which can be reduced by identifying the importance of each feature and construct a more concentrated feature set. The neighborhood component analysis [44] was applied to each subject’s original feature set along with the corresponding real labels elaborated in Section II-F. The average relative weight of each original feature was presented in Fig. 3 where the 3 low-weight features were excluded.

Fig. 3.

Relative feature weight (%) evaluated by the neighborhood component analysis. The three features in plum bars demonstrated less importance in distinguishing ECG and SCG signals and consequently were discarded.

E. Dimensionality Reduction

To reduce the dimensionality of the feature dataset, principal component analysis (PCA) was applied in which eigenvalues less than 20% of the largest eigenvalue were abandoned. Lastly, features were normalized by calculating their Z-scores [45], [46] to eliminate the bias of mean and variance before inputting into an ANN.

F. Training, Testing and Cross-Validation

We have two cohorts of subjects, one consists of all healthy subjects and the other one all cardiac patients. Fusion-based prediction was applied on each subject in such as way that the testing dataset was formed by the designated subject’s cardiac data. The corresponding training dataset was formed using cardiac data from the rest of participants who belong to the same cohort. The cohort-based leave-one-out method allows us to evaluate the fusion-based prediction on all participants. To avoid over-training by the excessive number of cardiac data contributed by the rest of participants in the cohort, we blindly selected a subset of size four times of that of the testing dataset. Consequently, the evaluation for each participant involves an average number of 6336 for training and 1584 for testing.

Labels in the dataset were obtained by comparing the ECG- and SCG-based predictions with the quiescence derived from the baseline subject-specific echocardiography, respectively. The modality that led to a smaller prediction error was considered to be an optimal modality for this cardiac cycle. The prediction error, in milliseconds, was calculated as the absolute difference between the predicted quiescent timing and the time derived from baseline subject-specific echocardiography. The ECG-based prediction was obtained from a pre-defined piece-wise linear gating function elaborated in [47]. This gating function is dependent on a predicted heart rate which is generated from a linear regression formed by using the previous six heart beats. SCG-based prediction was obtained using the patient-specific HS waveform detection method [14].

Different from the training dataset, features {HR, HRV} from the testing dataset were unknown since the upcoming cardiac cycle of this particular subject is unknown. To predict the upcoming instantaneous heart rate, a linear regression method with previous six heartbeats [14] was used. To predict the instantaneous heart rate variability, the predicted instantaneous heart rate was used to calculate its deviation from the mean of the most recent eight heart rates [36].

The training dataset was further divided into four uniform parts randomly, one of which was used for cross-validation [48]. This 4-fold cross-validation was repeated 10 times with random partition of the training dataset to make the whole process as 10x4-fold cross-validation. The output from ANN, including classification accuracy and modality probability, were the average results over 10 iterations.

G. Radiology Reader Evaluation

A board certified cardiothoracic radiologist, with over 7 years of experience, evaluated the images and scored the quality of the coronary artery image quality using a 4 point Likert response format: 1 = excellent, 2 = good, 3 = adequate, 4 = non-diagnostic. The radiologist was blind to the modality that selected the phase for the reconstruction. Significance was tested using the Wilcoxon signed-rank test. The diagnostic quality of the left main (LM), left anterior descending (LAD), left circumflex (LCX) and right coronary arteries (RCA) from the origin to the first branch was graded.

III. Results

The effectiveness of the multimodal framework is evaluated by the ANN prediction accuracy and precision, and the quiescence prediction error. The cardiac phase, normalized over a cardiac cycle for HRV, is effective in mathematical modeling. However, the evaluation of temporal error (in milliseconds) is what essentially results in the degradation of CCTA image quality, since the sensitivity to mistiming varies among individuals and their predicted HR. Results⁶ presented in this section were from cardiac cycles that meet the feature selection criteria for ANN classification in Section II-D.

A. Artificial Neural Network Classification Accuracy

In TABLE 2, two cohorts of subjects are listed in an order of increasing heart rate. Subjects H1 to H7 are the cohort of healthy subjects and P1 to P11 are the cardiac patients. For each subject, a threshold for decision-making related to classification accuracy for testing/prediction is set according to the subject-specific data in the training dataset: and , where is the total number of ECG-labeled and SCG-labeled cycles. By comparing the classification output, and , with and , respectively, classified/predicted labels are decided. A correct ANN prediction leads to a value close to 1 for the weight associated with the correct gating type and close to 0 for the other, thus a reasonable threshold to distinguish gating type is 0.5. However, we set up thresholds and to take into account the bias observed in the labels of training dataset where SCG is dominant over cardiac cycles.

TABLE 2. Three-Layer ANN Binary Classification.

Healthy Subjects
Subject	HR (bpm)	HRV (ms)	Accuracy (%)	Precision (%)
H1	58	41	90.1	95.4
H2	60	48	89.4	92.7
H3	68	28	90.4	93.8
H4	73	50	92.2	94.7
H5	77	50	87.1	91.0
H6	84	19	90.2	93.7
H7	92	58	89.9	92.9
Avg	72	42	89.9	93.5
Cardiac Patients
P1	52	20	80.6	82.8
P2	54	65	80.7	83.5
P3	54	208	77.3	81.3
P4	63	63	80.7	83.1
P5	64	38	81.3	84.1
P6	65	60	82.8	84.1
P7	73	57	83.3	86.5
P8	81	170	79.5	84.3
P9	84	147	81.3	85.8
P10	87	29	78.8	82.7
P11	102	3	79.9	83.3
Avg	70	78	80.6	83.8

The classification accuracy is the percentage of correct labels being identified. Precision is the percentage of correctly predicted SCG-labeled cycles over the total number of cycles predicted as SCG-labeled cycles. The values of accuracy and precision from the three-layer ANN are 89.9% and 93.5% on average for the healthy cohort, and 80.6% and 83.8% for the cardiac patients, respectively, indicating that the selected features are fair representatives of the cardiac information from acquired signals.

Factors that may affect the classification accuracy:

• 1)Acquired data: Outliers in the data may cause overlapping patterns. The training dataset is expected to have adequate number of instances for an effective learning for the ANN.
• 2)Selected features: The presence of irrelevant features or an inadequate number of effective features.
• 3)Modality selection algorithm: In general, this factor does not significantly impact the classification accuracy when the dataset is large and the selected features for modality selection are salient representatives of the cardiac information of the raw signal. Therefore, other classification algorithms are very likely to give similar results as the ANN in this study [48].

B. Quiescence Prediction Errors

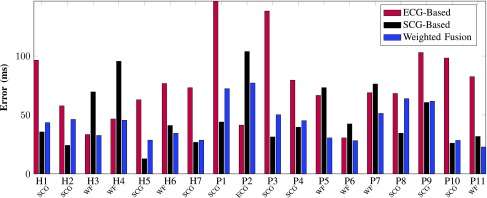
Figure 4 reveals the individual average prediction error (in milliseconds) calculated over all cardiac cycles in the testing dataset that belongs to that individual. The overall prediction error across all subjects associated with ECG-, SCG- and WF-based method are 76.15 ms, 48.30 ms and 43.95 ms, respectively. Out of the 18 subjects, only one subject (P2) would actually benefit from using ECG-based gating solely. It is also observed that subjects H3 and H4 are potential candidates for ECG-based prediction, but fusion-based prediction works as well for them.

Fig. 4.

Quiescence prediction error (milliseconds) of different cardiac gating modalities. The overall prediction error across all subjects associated with ECG-, SCG- and WF-based method are 76.15 ms, 48.30 ms and 43.95 ms, respectively. For each subject, the optimal gating modality, either ECG, SCG or WF, is selected based on the least error (ms). Except for subject P2, all subjects demonstrate less prediction error using the WF- or SCG-based prediction for cardiac gating.

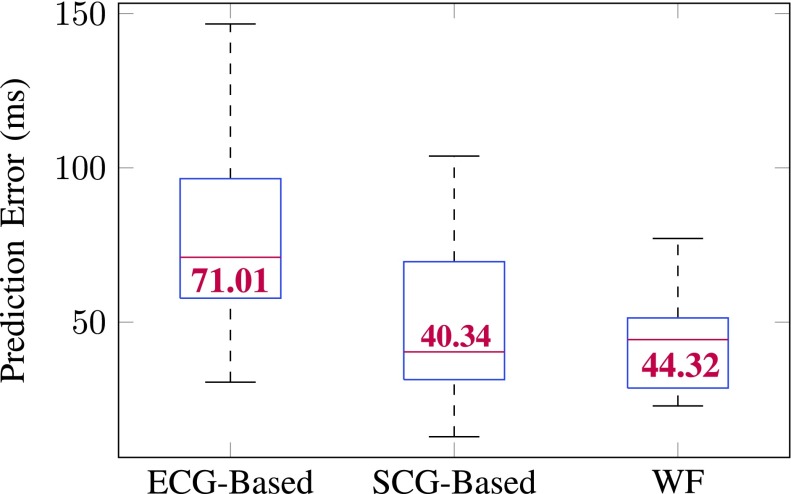
Figure 5 reports the quiescence prediction error from different prediction methods. WF- and SCG-based prediction elicited comparable low errors than that from ECG, but WF caused less variability among all methods.

Fig. 5.

Box plot of quiescence prediction error (milliseconds) of all 18 subjects. On each box, the central mark indicates the median (value in red), and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. No outlier was observed. ECG-based prediction resulted in the most error. WF and SCG-based predictions are comparable. The smallest variability is seen in the prediction error associated with WF.

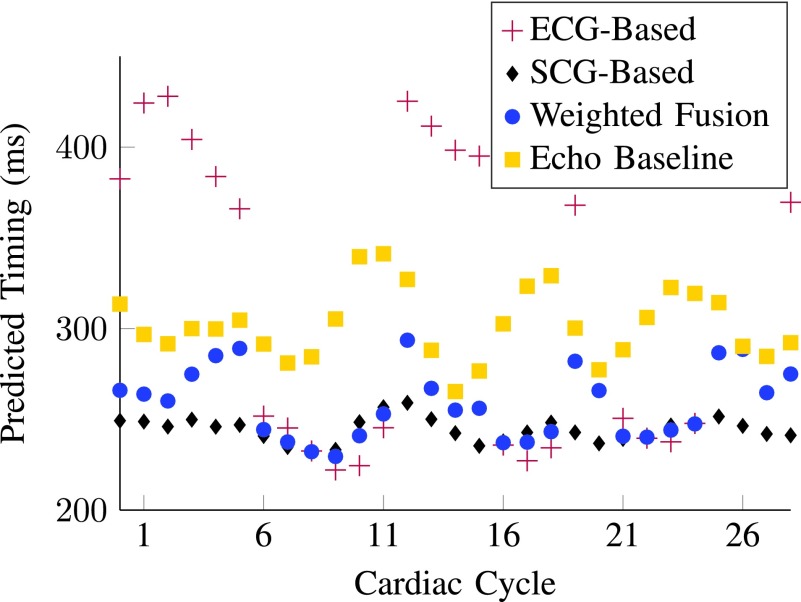
Although the absolute prediction improvement in milliseconds by using WF- or SCG-based prediction may not seem very prominent for all individuals, it is noticeable that for some patients whose ECG-based predictions give large prediction errors, such as subjects P3 and P11, their SCG- and WF-based predictions are able to reduce the error significantly. For such patients, SCG- or WF-based prediction of quiescent periods could potentially lead to improved diagnostic quality of CCTA. Figure 6 illustrates a subset of cardiac cycles from subject P11 with predicted temporal quiescence (time of quiescence occurrence within a cardiac cycle w.r.t. the ECG R-peak) derived from multiple modalities. SCG-based prediction is closer to the baseline echocardiography than ECG-based prediction. Fusion-based prediction fuses predictions from ECG and SCG, and performs better than ECG-based prediction. This is consistent with results in Fig. 4 where WF-based quiescence prediction is the most effective for patient P11.

Fig. 6.

A subset of predicted temporal quiescence derived from different gating modalities for patient P11. Overall, WF gating is the optimal gating modality for P11 according to the average error presented in Fig. 4.

Denoting the quiescence prediction error (from either WF-or SCG-based method), the error reduction is calculated by

where could be or .

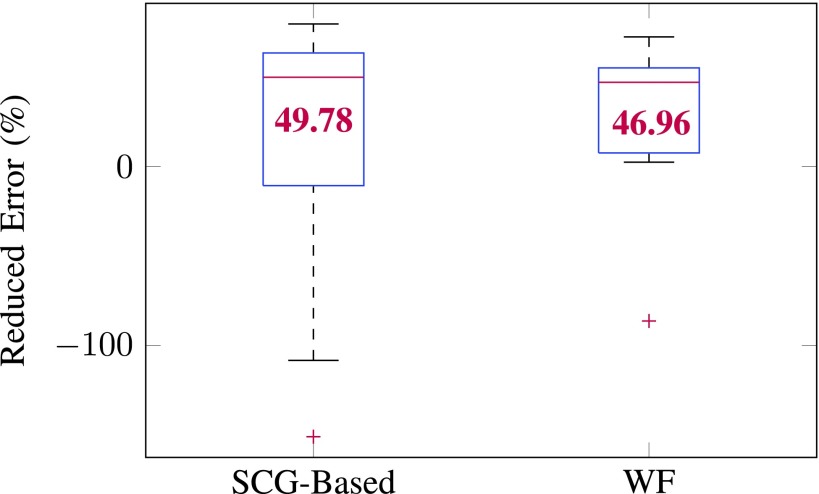
This error reduction measures the percentage of average errors that can be reduced from ECG-only-based gating. The average error reduction of the 18 subjects using SCG- and WF-based method is 49.78% and 46.96%, respectively. Fig. 7 reports error reduction from different prediction methods. WF- and SCG-based methods reduced comparable percent of prediction error, but WF resulted in less variability in the reduced error.

Fig. 7.

Box plot of percentage of error reduction (%) against quiescence prediction error from ECG-based prediction across the 18 subjects. On each box, the central mark indicates the median (value in red), and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The outliers are plotted individually using the ‘+’ symbol. WF and SCG-based predictions are comparable and can reduce more percent of prediction errors than cohort-specific echocardiography. But the variability in the reduced error associated with WF is smaller than SCG.

C. CCTA Reconstructed Image Quality

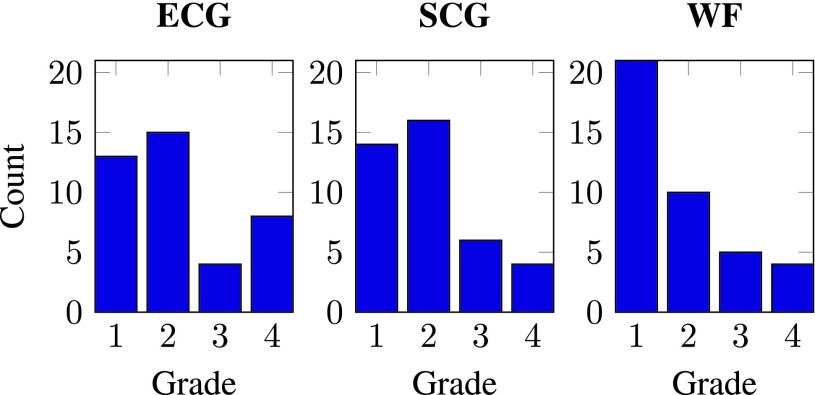
To quantify the accuracy with which the gating modality can predict the cardiac quiescence, reconstructed CT volumes are generated at phases derived from ECG-, SCG- and WF-based prediction methods. Histograms that summarize the grade distribution of diagnostic quality associated with different prediction methods are shown in Fig. 8.

Fig. 8.

Histograms of the diagnostic quality grades. Four point Likert response scale: 1 = excellent, 2 = good, 3 = adequate, 4 = non-diagnostic.

The histograms in Fig. 8 showed a higher count of lower Likert format grade (1 = excellent, 2 = good, 3 = adequate, 4 = non-diagnostic) using the WF quiescence prediction, indicating that WF yielded the best diagnostic quality. SCG-based prediction achieved better diagnostic quality than ECG-based method since SCG has slightly higher frequency in achieving the lower Likert format grade. The WF prediction consistently achieves the best diagnostic quality for all patients, whereas ECG achieves the least for all. The average grade over all the reconstructed volumes and segments for ECG, SCG and WF are 2.18, 2.00 () and 1.80 (), respectively, assuming there is no correlation among tests performed in left main (LM), left anterior descending (LAD), left circumflex (LCX) and right coronary arteries (RCA). The p-values were derived from the two-sided Wilcoxon signed-rank test (). Among the four segments, RCA, which is generally degraded most by motion artifacts of the coronary vessels, achieves the highest improvement in diagnostic quality using WF as compared to ECG.

Due to configuration limitations from the clinical CT scanner, reconstructed CT volumes for an individual are retrospectively generated at a constant phase throughout all cardiac cycles, rather than on a beat-by-beat basis. This constant phase is the average of the beat-by-beat quiescent phases derived from a specific gating modality. If the reconstruction is made on a beat-by-beat basis, the diagnostic quality associated with SCG- and WF-based quiescence prediction could potentially provide a more substantial improvement over the ECG-based prediction.

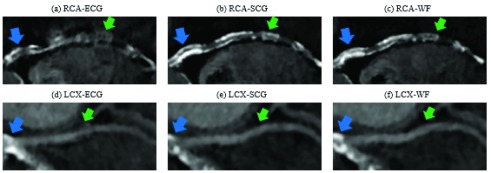
The selection of gating during cardiac systole or diastole within a cardiac cycle is based on the HR. For higher HR (> 70 bpm) the systolic quiescent period is better. However, a more comprehensive consideration would include both HR and HRV as variables of a function that dynamically selects the period in which gating achieves the best diagnostic quality. Example RCA and LCX segments from cardiac CCTA reconstructions of cardiac patient P11 are shown in Fig. 9. Reconstructions associated with the WF-based prediction resulted in the best diagnostic quality, while ECG-based prediction resulted in the worst.

Fig. 9.

Comparison of the diagnostic quality of CCTA images reconstructed at quiescent phases derived from different gating modalities. CCTA data presented are from patient P11. Blue arrows point to one example of calcification. Green arrows point to motion artifacts. Compared to ECG-phases, the SCG-selected phases in (b) and (e), and WF-selected phases in (c) and (f) demonstrate sharper outline of the RCA and LCX. Calcification in the RCA is also more sharply defined by SCG- and WF-selected phases. Significant motion artifacts rendered the pointed (green arrows) regions of the RCA and LCX non-diagnostic for ECG-selected quiescent phases.

IV. Conclusion and Discussion

A. Conclusion

To more accurately predict cardiac quiescence, we developed a multimodal framework by fusing individual quiescence predicted from ECG and SCG. Results from a pilot group of seven healthy people and eleven cardiac patients demonstrated that our proposed framework is effective and robust. Our major findings showed that the multimodal framework achieved 47% improvement in prediction error and resulted in better diagnostic quality of CCTA coronary vessels, as compared with the current ECG-based method. In addition, the fusion-based prediction method was more robust. The significance is the potential for a more reliable approach than ECG only-based gating to predict cardiac quiescence for prospective CCTA.

B. Discussion

CCTA as an emerging alternative is not only less invasive and less costly, but is also associated with fewer complications while still providing adequate resolution for assessing the coronary artery. When considering radiation dose, it is noteworthy to compare our fusion-based prospective CCTA triggering with retrospective CCTA gating. The method proposed in this work can possibly reduce dose to approximately 4mSv, while a 64 slice retrospective CCTA exposes an individual to 12mSv. Another consideration is the low yield of obstructive coronary disease found at CCA [49], which raises the concern of undergoing unnecessary invasive tests for people at low to intermediate risk of coronary artery disease [50].

This study ultimately aims to improve the diagnostic quality of cardiac images while maintaining or reducing the radiation dose during prospective CCTA exam. Enhancing and broadening the application of prospective cardiac CCTA is of importance. This improvement would tremendously mitigate risks for congenital cardiac patients who are repeatedly exposed to radiation throughout their lives and for patients presenting repeatedly to different emergency room for chest pain.

C. Limitations

The primary limitation of this study is that interventricular septal motion derived from echocardiography is used as the baseline for coronary vessel motion. Ultimately, we need to correlate our fusion-based quiescence prediction with the motion of coronary arteries derived from CCTA. However, because of radiation dose, it is not desirable to obtain CCTA data for a large number of cardiac cycles. On the other hand, it has been shown that IVS septal motion is a very good marker of coronary arterial motion [51]. Therefore, echocardiography-derived motion serves as an excellent, and ethically acceptable, surrogate marker of coronary vessel motion. A superior marker closer to coronary vessel motion such as angiogram has yet to be explored for future work.

The next limitation lies in the features used in ANN of this study. The selected features were individually demonstrated to be effective representations of cardiac signals based on findings of previous research [37]–[39], [41], [42]. However, the applied feature set may be sub-optimal and a superior feature set can be established by investigating other features and attempting different combination of features.

With respect to the sample size, we are currently recruiting more participants, particularly coronary cardiac patients, to enlarge the subject population. The inclusion of additional subjects would enhance the statistical significance of improvement in diagnostic quality associated with WF-based prediction. In addition, this can lead to a more generalized training dataset. The ANN depends highly on the properties of the training dataset. Thus, the more generalized a training dataset, the more comprehensive the extracted features are, and thus the less biased the trained ANN becomes. In a complementary fashion, we will also recruit additional readers to explore the effect of inter-reader variability.

Another limitation is that this study is part of the cascaded pipeline for improving CCTA gating accuracy wherein the prediction from the first stage is the input of the next stage. The individual quiescence predictions from ECG and SCG are input of the trained ANN to be fused to generate a corrected prediction. Thus, prediction errors in the ECG- and SCG-based quiescence predictions can be amplified as prediction stages ascend.

Lastly, both the training and testing datasets are usually from observation. However, in this study the training dataset of ANN comes from observation but the testing dataset is partly by prediction. Therefore, the distribution of training and testing datasets are not exactly the same based on the way the two datasets are constructed.

D. Future Work

Implementation of the proposed framework in real-time with relevant hardware integration is the natural next step. This requires a rigorous consideration of computational complexity and time delay occurring in different phases of signal transmission and processing. In addition, the co-investigation and enhancement of both hardware and software makes it highly possible to achieve a better diagnostic image quality and reduced radiation exposure in cardiac imaging.

Looking more broadly, our multimodal approach to improving cardiac gating bears promise in being applied to other cardiac imaging modalities. For example, impedence cardiography could be used together with ECG to trigger MRI.

Funding Statement

This work was supported in part by the National Science Foundation under Grant CAREER ECCS-1055801 and the National Center for Advancing Translational Sciences of the National Institutes of Health under Grant UL1TR000454. The work of S. Tridandapani and C. A. Wick was supported by the National Institute of Biomedical Imaging and Bioengineering under Grant K23EB013221.