Time-varying coefficient of determination to quantify the explanatory power of biomarkers on longitudinal GFR among children with chronic kidney disease

Abstract

Purpose:

Coefficients of determination (R²) for continuous longitudinal data are typically reported as time-constant, if they are reported at all. The widely used mixed model with random intercepts and slopes yields the total outcome variance as a time-varying function. We propose a generalized and intuitive approach based on this variance function to estimate the time-varying predictive power (R²) of a variable on outcome levels and changes.

Methods:

Using longitudinal estimated glomerular filtration rate (eGFR) from the Chronic Kidney Disease in Children Study, linear mixed models characterized the R² for two chronic kidney disease (CKD) risk factors measured at baseline: a traditional marker (proteinuria) and a novel marker (fibroblast growth factor 23; FGF23).

Results:

Time-varying R² divulged different disease processes by risk factor and diagnoses. Among children with glomerular CKD, time-varying R² for proteinuria had significant upward trends, suggesting increasing power to predict eGFR change, but crossed with FGF23, which was higher up to 2.5 years from baseline. In contrast, among those with non-glomerular CKD, proteinuria explained more than FGF23 at all times, and time-varying R² for each risk factor was not substantially different from time-constant estimates.

Conclusions:

Proteinuria and FGF23 explained substantial eGFR variability over time. Time-varying R² can characterize predictive roles of risk factors on disease progression, overcome limitations of time-constant estimates and are easily derived from mixed effects models.

BACKGROUND

Clinical epidemiologists are often interested in the prospective predictive power of biomarkers. Determining how much variability of an outcome is explained by the level of a predictive biomarker over time provides an important epidemiological characterization of disease progression. Several methods have been proposed that summarize predictive power by the coefficient of determination (referred to as R²) in the setting of longitudinal data: typically this is a single fixed value that describes the proportion of variability of the outcome of interest over time explained by an exposure [1–8]. However, there is a reasonable biological expectation that in some settings, the predictive power of a biomarker on an outcome is time-varying and the assumption that R² is constant over time may not be appropriate. To our knowledge, few studies have quantified this type of dynamic relationship.

Linear mixed effects models are commonly used as conventional tools to parametrically characterize longitudinal changes of a continuous outcome and how these are modified by an exposure [9–14]. In addition to providing estimates of outcome levels and changes, the variance components serve to characterize the behavior of the outcome variance over time, enabling the calculation of R². For the simpler case of random intercepts only, it is well known that the variance of the outcome is simply the sum of the between individuals’ variance and the within individuals’ variance. Hence, the associated R² is time-constant [2,5,7]. In contrast, in the more common case of allowing random intercepts and slopes, the variance of the outcome is time-varying and so is the associated R².

The purpose of the present study was to construct and compare time-fixed and time-varying R² values in the context of pediatric chronic kidney disease (CKD) progression. Methodologically, we show cases where the time-constant R² oversimplifies the behavior of the data and discuss the need to enrich models to ensure that the proposed model of random intercepts and slopes suffice. Epidemiologically, we aimed to compare separately and combined the baseline levels of urine protein (a marker of kidney injury [15–20]), and baseline levels of fibroblast growth factor 23 (FGF23; a bone-derived hormone and a novel CKD risk factor associated with mineral metabolism [21–23]). Urine protein is a ubiquitous clinical measurement; in contrast, FGF23 is currently not a clinical biomarker. Lastly, we sought to demonstrate how heterogeneity of effects by underlying CKD diagnoses can improve epidemiologic understanding of these conditions. This applied example seeks to highlight the utility of time-varying explained variability, the parameters of which are easily obtained in widely used linear mixed models.

METHODS

Study population

The Chronic Kidney Disease in Children (CKiD) Cohort

The CKiD study is an ongoing pediatric cohort study of CKD who were enrolled between 1 to 16 years of age at 54 pediatric nephrology centers from the United States and Canada. Eligibility included a diagnosis of CKD and an estimated glomerular filtration rate (eGFR) between 30 and 90 ml/min|1.73m² [24] with 891 children were enrolled prior to April 2014. Briefly, clinical and demographic information, including biological specimens for immediate analysis and for repository storage, were collected at annual study visits. All biological specimens were analyzed at the CKiD central laboratory, with the exception of plasma C-terminal FGF23, which was measured using repository specimens at the University of California, San Francisco [23]. Full details of the study protocol have been previously published [25].

Outcome

At annual study visits, the primary outcome was eGFR based on the 2012 CKiD equation which utilized serum creatinine, cystatin c, blood urea nitrogen, as well as sex and height data [24]. Participants who contributed at least two visits with eGFR data were included.

Exposures

The time origin for this analysis was the first visit when the two predictors of interest were measured: proteinuria (i.e., urine protein to creatinine ratio, mgP/mgCr) and plasma FGF23 (RU/ml). This first visit was considered the baseline, or index visit and the primary objective was to determine how these two markers explained the variability of eGFR at the index visit and variability of trajectories. The inter- and-intra assay coefficients of variation (CVs) for creatinine was 2.1% and 0.8%, respectively; and for proteinuria was 3.8% and 5.2% (Roche Diagnostics, Indianapolis, IN). For FGF23, the inter- and intra-assay CVs were 11.5% and 5.7%, respectively (Immutopics Int., San Clemente, CA).

All analyses were stratified by underlying CKD diagnosis, classified as either non-glomerular (largely congenital kidney abnormalities) or glomerular (mostly non-congenital diseases) [26]. Previous studies have described the heterogeneity of disease progression by the glomerular and non-glomerular classifications [11,14,19,27–29]. In addition, those with glomerular diagnoses were enrolled with higher eGFR than children with non-glomerular CKD.

Statistical methods

Four linear mixed models (random intercepts and slopes) were fit: the null (or reference) model included only time as the independent variable; the second model included baseline proteinuria as the independent variable; the third model included baseline FGF23 as the independent variable; and the fourth model included both baseline proteinuria and FGF23 as independent variables, allowing both to modify the intercepts and the effects of time. To make the outcome closer to a Gaussian distribution, eGFR was converted to the natural log scale while proteinuria and FGF23 were log₂ transformed so that the regression coefficients could be interpreted as the effect of doubling the levels of each of the predictors.

At the j^th visit of the i^th participant occurring t_ij years from baseline, the mixed models were of the form:

$$\log \left(eGF{R}_{ij}\right)=\alpha Z+a_i+\left(\beta Z+b_i\right)t_{ij}+e_{ij}$$ [1]

where Z = [1], [1, log₂(proteinuria_i0)], Z = [1, log₂(FGF23_i0)] , and Z = [1, log₂(protenuria_i0), log(FGF23_i0)] for models 1 to 4, respectively, and the number of α and β coefficients for each corresponding model were 2, 4, 4 and 6.

The between-subject deviations from the population intercept and slope were distributed as:

$$\left(\begin{array}{c}{a}_i\\ b_i\end{array}\right)~N\left[\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\sigma }_1^2& {\sigma }_{12}\\ {\sigma }_{12}& {\sigma }_2^2\end{array}\right)\right]$$

The within-subject deviations were assumed to be independent from the between-subject deviations and distributed as:

$$e_{ij}~N(0,\mathrm{ }{\sigma }^2)$$

Therefore, the total variance of eGFR (in the log scale) at t years from baseline is determined by:

$$Var\left(\log \left(eGFR\right)\right)={\sigma }_1^2+2{\sigma }_{12}t+{\sigma }_2^2{t}^2+{\sigma }^2$$ [2]

Biomarkers as independent variables may explain (reduce) any of the components of the total variance (from the between individual variability of initial values, ${\sigma }_1^2$, and slopes, ${\sigma }_2^2$, to the within individual variance, σ²). Separate comparisons of the three components of variance may yield the inadmissible result of negative R² and fails to incorporate the expected covariance between the random intercepts and slopes (σ₁₂). Combining the components to describe the total variance of the outcome over time overcomes these limitations.

The R² corresponds to the ratios of total variance from models 2 to 4 to that of model 1 (i.e., null). In particular, for the fourth model with the two biomarkers, this is formally expressed as:

$$R^2=\left[1-\frac{Var{\left[\log \left(GFR\right)\right]}_{Z=(1,{log}_2\left(proteinuria\right),{log}_2\left(FGF23\right))}}{{Var\left[\log \left(GFR\right)\right]}_{Z=\left(1\right)}}\right]\times 100$$ [3]

The R² values are the proportions of total eGFR variability explained by a risk factor(s) that is not explained by passage of time alone.

For biomarkers that only slightly modify ${\sigma }_2^2$ and σ₁₂, the R² may be described by a constant value and conforms to the R² from a linear mixed model with random intercepts only [5,7] (i.e., ${\sigma }_2^2=0$ and σ₁₂ = 0). Indeed, a mixed model with random intercepts only yields the total variance as simply ${\sigma }_1^2+{\sigma }^2$. The time-constant R² is simply one minus the ratio of the constant variances from the explanatory and null models. To determine whether the 95% confidence interval for the time-constant R² contained the dynamic nature of the time-varying R², bootstrap methods were used.

All analyses were performed using PROC MIXED in SAS, version 9.3 (SAS Institute, Inc., Cary, North Carolina). Graphical figures were conducted in S-PLUS version 8.2. All statistical significance was evaluated at the 5% level.

RESULTS

A total of 679 children contributed an index study visit with measurements of proteinuria and FGF23, and at least one measurement of eGFR after the index visit. Table 1 displays clinical and demographic characteristics of these 679 children stratified by glomerular (n= 186) and non-glomerular (n= 493) diagnoses. Duration of CKD at the time of study entry was much longer among those with a non-glomerular diagnosis, consistent with kidney diseases primarily caused by congenital abnormalities. Table 2 summarizes the dates of enrollment and the longitudinal eGFR data used in the analysis. Based on the study recruitment design, children with a non-glomerular diagnosis were enrolled earlier and thus, were followed longer than those with a glomerular diagnosis, who were enrolled later.

Table 1.

Baseline Characteristics of Children with Underlying Glomerular (n= 186) and Non-Glomerular (n= 493) Chronic Kidney Disease. % (N) or Median [25^th percentile, 75^th percentile]

	Glomerular CKD n= 186 (27%)	Non-glomerular CKD n= 493 (73%)
Age, years	15 [12, 17]	11 [8, 15]
Female sex	48.4% (90)	35.1% (173)
Race
Caucasian	55.9% (104)	73.2% (361)
Black	28.5% ( 53)	16.6% ( 82)
Other	15.6% ( 29)	10.1% ( 50)
Hispanic ethnicity	15.8% ( 29)	13.9% ( 68)
Duration of CKD, years	4.5 [2.5, 8.8]	10.4 [7.2, 14.2]
SBP z-score
Proteinuria, mg/mgCr	0.45 [0.20, 1.17]	0.25 [0.10, 0.61]
FGF23, RU/mL	106 [76, 169]	112 [78, 171]
eGFR level, ml/min|1.73m2	63 [48, 82]	52 [38, 64]

Table 2.

Description of longitudinal GFR data available. Median [interquartile range] and % (n).

	Glomerular CKD n= 186 (27%)	Non-glomerular CKD n= 493 (73%)
Year of study entry	September 2012 [July 2008, January 2014]	August 2008 [August 2007, June 2012]
Number of eGFR measurements
2 to 3	56.5% (105)	29.8% (147)
4 to 5	27.4% ( 51)	34.9% (172)
6 to 7	8.1% ( 15)	17.4% ( 86)
8 or more	8.1% ( 15)	17.8% ( 88)
Years of follow-up	2.2 [1.2, 3.3]	3.5 [2.2, 6.0]

Table 3 presents the results from the four models (Table 3a for children with glomerular CKD and Table 3b for children with non-glomerular CKD). The parameter estimates for the coefficients for the fixed effects are presented in the upper portion of the table; in the lower portion of the table, the variance parameters corresponding to the random effects are presented as standard deviations and correlations.

Table 3a.

Results from Linear Mixed Effects Models for Log-Transformed eGFR with Random Intercepts and Slopes among Children with a Glomerular CKD Diagnosis.

	Model
Parameter	Null	Proteinuria only	FGF23 only	Proteinuria and FGF23
Fixed effect level
Constant (Proteinuria= 0.45, FGF23= 110)	4.113 ± 0.029	4.117 ± 0.027	4.14 ± 0.025	4.138 ± 0.024
log2(Proteinuria/0.45)	0	−0.074 ± 0.014	0	−0.039 ± 0.013
log2(FGF23 / 110)	0	0	−0.219 ± 0.026	−0.187 ± 0.027
Fixed effect slope (years from baseline)
Constant (Proteinuria= 0.45, FGF23= 110)	−0.087 ± 0.010	−0.082 ± 0.009	−0.082 ± 0.010	−0.080 ± 0.009
log2(Proteinuria/0.45)	0	−0.033 ± 0.005	0	−0.029 ± 0.005
log2(FGF23 / 110)	0	0	−0.044 ± 0.011	−0.022 ± 0.010
Random effects
S.D. (level) [σ1]	0.379	0.349	0.316	0.308
S.D. (slope) [σ2]	0.111	0.084	0.103	0.082
Correlation [$\frac{{\sigma }_{12}}{{\sigma }_1{\sigma }_2}$]	0.377	0.262	0.221	0.173
S.D. residual [σ]	0.139	0.141	0.139	0.141
AIC	91.109	39.553	32.108	5.383

Bold indicates p<0.05 for fixed effects. Estimates ± Standard errors. Corresponding 95% confidence intervals may be calculated as ± 1.96 × Standard errors.

Abbreviations: S.D., standard deviation; SBP z-score, systolic blood pressure z-scores based on the normal population adjusted for age, gender and height; FGF23, fibroblast growth factor 23; AIC, Akaike’s information criterion

The coefficient parameters are presented in the log scale and can be re-expressed on the natural scale by taking antilogs of the parameter estimates for a more meaningful interpretation. For example, in Table 3a, the mean eGFR level at entry (approximately 4.5 years after disease onset) was 61.1 ml/min|1.73m² (= exp(4.113)). For the slope in this model, the average change per year can be expressed as −8.3% (= (exp(−0.087))-1 × 100). The parameters for log₂(Proteinuria/0.45) and log₂(FGF23/110) refer to the difference in GFR levels or slope (in the log scale) corresponding to a doubling of the level of the biomarker. In Table 3a, for the proteinuria only model, children with twice the level of proteinuria as a reference group (e.g., 0.90 vs. 0.45 mgP/mgCr) would have a 7.1% lower GFR at study entry (= [exp(−0.074) – 1] × 100). Likewise, the average GFR decline for children with proteinuria levels of 0.90 mgP/mgCr is estimated as −10.8% per year (= [exp(−0.082 – 0.033) – 1] × 100) compared to children with a level of 0.45 mgP/mgCr whose decline is estimated as −7.9% (= [exp(−0.082) – 1] × 100).

Among those with glomerular CKD (Table 3a) and relative to the reference model, for the proteinuria only model, the standard deviations of levels and slope and the correlation decreased. For the FGF23 only model, the standard deviation of level decreased more than the proteinuria only model, while the standard deviation of slopes was higher than the proteinuria only model. Lastly, when both proteinuria and FGF23 were included in the model, the standard deviations were lowest for both the level and slope and the correlation was also diminished. The AIC of the model including both baseline proteinuria and FGF23 was substantially lower than each of the two models containing one predictor.

For children with non-glomerular CKD (Table 3b) and relative to those with glomerular disease, there was less variability in the random slopes, suggesting a more homogeneous behavior of disease progression. While including both biomarkers as predictors offered the best model fit by AIC; in univariate models, baseline proteinuria had more predictive value than FGF23, in contrast to those with a glomerular diagnosis.

Table 4 presents the variance parameters from random intercepts only models. The residual (or error) term variability was consistent across the null, proteinuria only, FGF23 only and proteinuria and FGF23 combined models. The standard deviations of the random intercepts decreased with the inclusion of the biomarkers for both children with glomerular and non-glomerular CKD diagnoses. For children with glomerular CKD, the FGF23 only model had lower total variance (which is equal to the sum of the between and within individuals variances; Equation 2) compared to the proteinuria only model (0.153 vs. 0.172). In contrast, for children with non-glomerular CKD, the proteinuria only model had lower total variance compared with the FGF23 only model (0.138 vs. 0.153).

Table 3b.

Results from Linear Mixed Effects Models for Log-Transformed eGFR with Random Intercepts and Slopes among Children with a Non-Glomerular CKD diagnosis.

	Model
Parameter	Null	Proteinuria only	FGF23 only	Proteinuria and FGF23
Level
Constant (Proteinuria= 0.45, FGF23= 110)	3.892 ± 0.017	3.906 ± 0.014	3.920 ± 0.015	3.926 ± 0.013
log2(Proteinuria/0.45)	0	−0.113 ± 0.008	0	−0.093 ± 0.008
log2(FGF23 / 110)	0	0	−0.188 ± 0.015	−0.149 ± 0.013
Slope (years from baseline)
Constant (Proteinuria= 0.45, FGF23= 110)	−0.051 ± 0.003	−0.048 ± 0.003	−0.049 ± 0.003	−0.048 ± 0.003
log2(Proteinuria/0.45)	0	−0.016 ± 0.002	0	−0.015 ± 0.002
log2(FGF23 / 110)	0	0	−0.015 ± 0.004	−0.008 ± 0.003
Random effects
S.D. (level) [σ1]	0.368	0.310	0.317	0.274
S.D. (slope) [σ2]	0.061	0.054	0.060	0.054
Correlation [$\frac{{\sigma }_{12}}{{\sigma }_1{\sigma }_2}$]	0.477	0.310	0.427	0.283
S.D. residual [σ]	0.111	0.111	0.111	0.111
AIC	−1239.604	−1418.868	−1363.118	−1513.796

Bold indicates p<0.05 for fixed effects. Estimates ± Standard errors. Corresponding 95% confidence intervals may be calculated as ±1.96 × Standard errors.

Abbreviations: S.D., standard deviation; FGF23, fibroblast growth factor 23; AIC, Akaike’s information criterion.

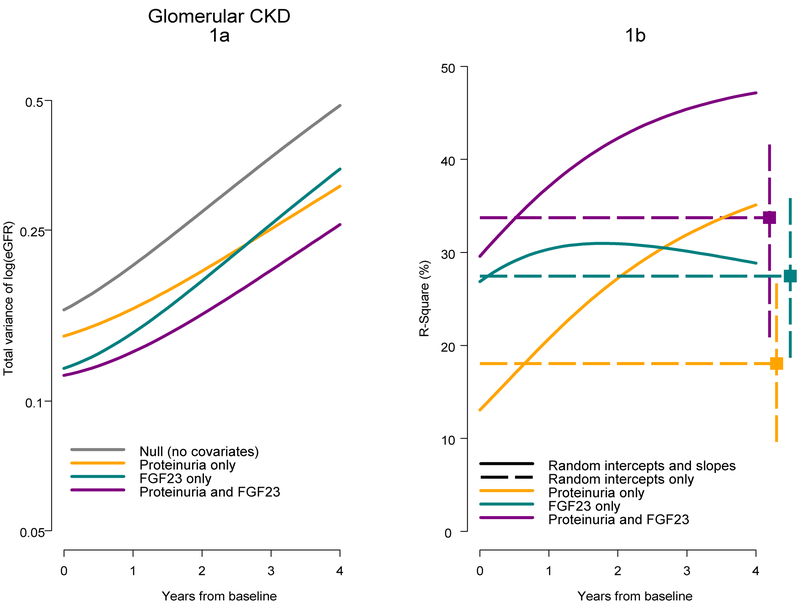
For children with glomerular CKD diagnoses and using Equation 2 (Methods), Figure 1a presents the total variance of eGFR (in the log scale) as a function of the model parameters of variability and correlation in Table 2a with time 0 corresponding to about 4.5 years after disease onset. When comparing the proteinuria only and FGF23 only models, the lines cross at about 2.5 years. In the combined model, the estimated total variance was lowest and incorporated the short-term explanatory power of FGF23 with the longer-term lower variability related to proteinuria. Figure 1b presents the R² over time based on the estimates of variance in Figure 1a and Equation 3. The R² for the FGF23 only model was relatively stable over time, while the R² for the proteinuria only model increased from about 13% at baseline to 35% by 4 years after baseline. The R² for the proteinuria only model surpassed the R² for the FGF23 only model at about 2.7 years. This underscores the influence of baseline proteinuria on longer term levels of eGFR compared to the stronger short-term influences of FGF23. For the combined model, the baseline R² was close to the R² from the FGF23 only model (30% vs. 27%) and the shape of this function was more similar to the R² from the proteinuria only model. At 4 years, the R² from this combined model was 47%.

Figure 1.

Total variance and R-square as a function of time for mixed effects models for children with a glomerular CKD diagnosis. Figure 1a presents estimates of total eGFR variance for four mixed models in Table 2a. Figure 1b presents time-varying R-square values for mixed models (random intercepts and slopes; Table 2a) and time-constant R-square values based on mixed models with random intercepts only in Table 3.

The points on the right-most part of Figure 1b, depict the R² derived from the parameters described in Table 3 based on the models with random intercepts only. Dashed horizontal lines reflect the assumption of constant R² over time. Bootstrapped 95% confidence intervals are depicted by the vertical bounds. For FGF23, the estimated time-constant R² was very similar to the time-varying R² for the same model. However, for the proteinuria only and combined models, the time-constant R² values were substantially different from the time-varying R² values.

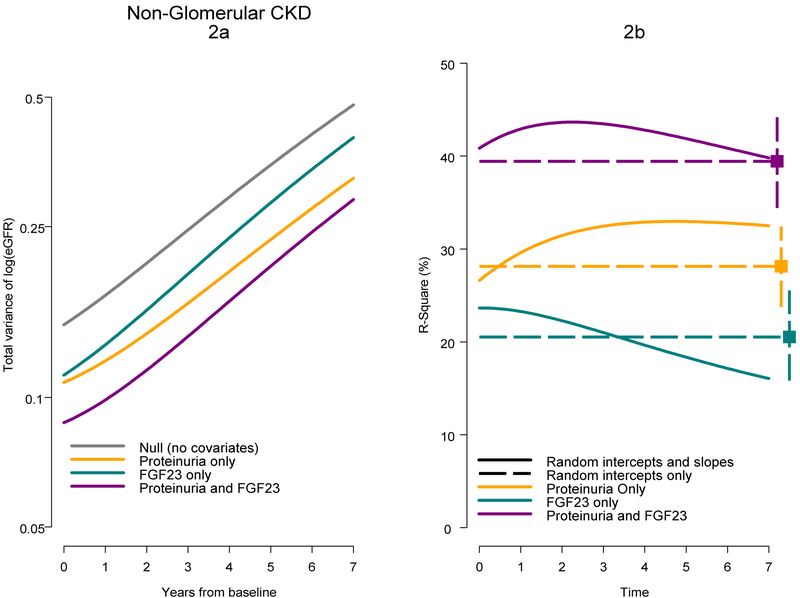
Figure 2 presents the corresponding total variance and R² over time for children with a non-glomerular CKD, and based on parameters presented in Tables 2b and bottom of Table 3, with time 0 corresponding to approximately 10.5 years after disease onset. The R² for the FGF23 only model diminished over time, while the R² for the proteinuria only model increased slightly over 3 years and then plateaued. The combined model offered the highest R² value and increased from 41% at baseline to 44% about 2.5 years after baseline and diminished thereafter (40% at 7 years). All curves in this group were reasonably summarized by the time-constant R² values from models based on random intercepts only and were contained in the bootstrapped 95% confidence intervals.

Figure 2.

Total variance and R-square as a function of time for mixed effects models for children with a non-glomerular CKD diagnosis. Figure 2a presents estimates of total eGFR variance for four mixed models in Table 3a. Figure 2b presents time-varying R-square values for mixed models (random intercepts and slopes; Table 2b) and time-constant R-square values based on mixed models with random intercepts only in Table 3.

As an additional analysis, SBP z-score (based on the normal population) was investigated as another predictive biomarker. The main effects were minimal and this was consistent with previous publications [30]; the variance components were not different than the null model and it offered no additional predictive power (results not shown). This was likely explained by the close relationship between blood pressure and proteinuria.

DISCUSSION

Linear mixed effect models are commonly used in epidemiologic studies to quantify the effect of an exposure on a continuous outcome over time. While these models offer an appropriate approach to account for within-person repeated measurements to validly estimate population levels and changes, the variance and covariance parameters are likely overlooked in favor of reporting only coefficient estimates of fixed effects.

Characterizing time-varying variance has utility in describing different disease processes related to different risk factors. In our application, for children with glomerular CKD, baseline levels of FGF23 were more strongly associated with short-term variability (i.e., within 2 years of index visit) in eGFR compared to proteinuria. However, proteinuria measured at the same time was more strongly related to longer term outcomes (i.e., after 3 years) than FGF23. There is biological support for these findings as proteinuria is a marker of and contributor to kidney injury. FGF23, a novel marker of CKD risk and kidney function, reflects dysregulation of phosphorus and vitamin D metabolism that is more related to concurrent CKD severity and eGFR level. Among those with a non-glomerular CKD diagnosis, proteinuria was more predictive of short-term and long-term eGFR outcomes than FGF23, but there was substantial benefit to including both in the model.

Clinically, these results underscore the importance of proteinuria and FGF23 as therapeutic targets for both diagnosis groups. The use of an angiotensin converting enzyme inhibitor or an angiotensin receptor blocker is an effective intervention to reduce proteinuria [31] and a standard approach to pediatric CKD management. There is currently no therapy approved for FGF23 management in pediatric CKD; thus, there is a need for clinical trials to investigate potential interventions targeting dietary phosphorus management [32] or bone disorders or growth retardation [33]. Interestingly, the effect of FGF23 on eGFR level at entry and change was much stronger among those with glomerular diagnoses compared to the non-glomerular group (−0.219 vs. −0.049 for level, respectively; −0.044 vs. −0.016 for change, respectively; Tables 3a and 3b). These results suggest that children with glomerular CKD are an important target population for exploring FGF23 therapies.

Zheng et al. [1] proposed a simple and intuitive method to calculate R² values from generalized linear mixed models (with random intercepts and slopes) as the square of the correlation of observed and predicted outcomes. This model assumes a time-constant R² and the results were inferentially similar to the R² values determined by the random intercept only models. Specifically, among the children with glomerular CKD, the proteinuria only, FGF23 only and combined model R² values were 16%, 28% and 32%. Among the children with non-glomerular CKD, these R² values were 23%, 16% and 31%, respectively. While this method offered consistent inferences and an appealing intuitive approach, it lacks a depiction of the dynamic nature of the exposure-outcome relationship.

There are limitations in deriving time-varying R² from these models. First, a characterization of total variance and R² values (time-varying or time-constant) is not an indicator of correct model specification or model fit. Indeed, these parameters assume correct specification and have the same assumption when linear mixed models are used to summarize longitudinal data. Second, the estimate of time-varying total variance is influenced by non-sparse data. It is common for longitudinal cohort studies to have more data in the early years of the study, with less later on due to delayed enrollment or drop out, and confidence in the estimated total variance should be commensurate to the presence of data (i.e., the confidence intervals of the time-varying R² will increase over time, in general). Third, longitudinal measurement of predictive biomarkers are ideal for characterizing disease progression, however, longitudinal FGF23 was not available. Therefore, these models may be interpreted from a clinically meaningful perspective as the predictive power after biomarker measurements.

It should be noted that in four of the six instances in our application, time-varying R² values (from random intercepts and slopes) were reasonably similar to their corresponding time-constant R² (from random intercepts only). While the best model fit by AIC in all cases included random intercepts and slopes (compared to random intercepts only), these results show that for coefficients of determination, there may not be substantial departures from the time-constant R² of the random intercepts only model. The time-constant R² assumption was sufficient in four instances, but there was important information obtained in the other two when allowing the R² to vary by time.

It is also possible that the relationship between the outcome and time is not linear (as was assumed in the present analysis). Indeed, eGFR decline in CKD populations, particularly those with glomerular CKD, is often not linear. If so, then time-varying R² as based on a quadratic polynomial of the total variance may oversimplify the heterogeneity over time. To address this, we explored a quadratic random effect of time as a sensitivity analysis. Using the same general approach, the total variance for this model is a quartic polynomial. In our application, for the two instances in which time-varying R² was identified, we fit models with a quadratic random effect of time. For the quadratic term in each model, the fixed effect was not significant, the variance of the random effect was negligible (i.e., no randomness) and the model AIC values were higher than the models specifying a linear effect of time. While we did not find evidence of non-linear effects of time, we recommend investigating more complex models of the outcome over time for a complete assessment of different potential shapes of time-varying R² functions with consideration of model fit parameters (e.g., AIC values).

The correlation between the intercept and the slope was positive indicating that lower eGFR at baseline was associated with faster eGFR decline (Tables 3a and 3b). The square of this correlation provided an estimate of the proportion of variability in the random (individual) slopes that was explained by the baseline eGFR level (random intercept). For the children with glomerular CKD, these R² values ranged from 14% in the null model to 3% in the model including proteinuria and FGF23. For the non-glomerular group, this ranged from 22% and 11%, respectively. It is intuitive that the predictive power of baseline eGFR on changes over time diminishes as biomarkers of risk are included in the model. However, within the non-glomerular group, there remained substantial explanatory power of baseline eGFR on slopes (11%) in the presence of both proteinuria and FGF23.

In the present analysis, children with glomerular CKD had shorter follow-up time than children with non-glomerular CKD. These differences in observed study time were largely due to the recruitment design of CKiD. It is possible that with longer duration of follow-up time among the glomerular CKD group, the disposition of the time-varying R² may differ. If differential drop-out were an issue, implementation of joint longitudinal and survival models with random intercepts and slopes is one method to control for this bias [34]. Furthermore, the variance-covariance estimates of the random effects in a joint model can determine the R² measure proposed here. Indeed, our approach can be readily applied to this setting as well.

In summary, linear mixed models are commonly used in epidemiologic analyses to describe the effect of an exposure on an outcome in a longitudinal setting. While interpretation of fixed effect coefficients from these models are likely to provide primary inferences, we believe that investigation of variance parameters can provide important epidemiologic insight into disease processes or novel risk factors. Importantly, these parameters and the assumptions of time-varying variance are explicitly embedded within this commonly used model structure. This approach extends these assumptions to calculate R² values that can demonstrate heterogeneity over time. Deriving these estimates is simple and accessible and uses parameters that are standard output in statistical software. These results should encourage epidemiologists to explore time-varying coefficients of determination in these settings as these may yield important insights.

Table 3.

Random Effects Parameters from Linear Mixed Effects Models with Random Intercepts Only Stratified by Glomerular and Non-Glomerular CKD Diagnoses.

	Among children with glomerular CKD
Parameter	Null	Proteinuria only	FGF23 only	Proteinuria and FGF23
S.D. (level) [σ1]	0.417	0.374	0.343	0.328
S.D. (slope) [σ2]	0	0	0	0
Correlation [$\frac{{\sigma }_{12}}{{\sigma }_1{\sigma }_2}$]	NA	NA	NA	NA
S.D. residual [σ]	0.192	0.180	0.188	0.179
AIC	221.760	132.725	145.526	90.566
	Among children with non-glomerular CKD
	Null	Proteinuria only	FGF23 only	Proteinuria and FGF23
S.D. (level) [σ1]	0.412	0.342	0.361	0.308
S.D. (slope) [σ2]	0	0	0	0
Correlation [$\frac{\sigma 12}{{\sigma }_1{\sigma }_2}$]	NA	NA	NA	NA
S.D. residual [σ]	0.150	0.146	0.150	0.146
AIC	−589.712	−854.061	−710.660	−936.368

Abbreviations: S.D., standard deviation; AIC, Akaike’s information criterion.