Interferometric near-infrared spectroscopy directly quantifies optical field dynamics in turbid media

Abstract

Sensing and imaging methods based on the dynamic scattering of coherent light (including laser speckle, laser Doppler, diffuse correlation spectroscopy, dynamic light scattering, and diffusing wave spectroscopy) quantify scatterer motion using light intensity fluctuations. The underlying optical field autocorrelation, rather than being measured directly, is typically inferred from the intensity autocorrelation through the Siegert relationship, assuming that the scattered field obeys Gaussian statistics. Here, we demonstrate interferometric near-infrared spectroscopy for measuring the time-of-flight (TOF) resolved field and intensity autocorrelations in turbid media. We find that the Siegert relationship breaks down for short TOFs due to static paths whose optical field does not decorrelate over experimental time scales. We also show that eliminating such paths by polarization gating restores the validity of the Siegert relationship. The unique capability of measuring optical field autocorrelations, as demonstrated here, enables the study of non-Gaussian and non-ergodic light scattering processes. Moreover, direct measurements of field autocorrelations are more efficient than indirect measurements based on intensity autocorrelations. Thus, optical field measurements may improve the quantiffcation of scatterer dynamics with coherent light.

1. INTRODUCTION

Coherent light scattered from a turbid medium generates a random intensity distribution or speckle pattern [1,2], which fluctuates in time as the scatterers move. This effect serves as the basis for sensing and imaging methods based on dynamic scattering of coherent light (DSCL). In dynamic light scattering (DLS), the time scale of fluctuations of single scattered light, quantified using the intensity autocorrelation [3,4] or power spectrum [5,6], is used to determine scatterer dynamics. Assuming the time-dependent field U_s(t_d) obeys zero-mean Gaussian statistics, the field autocorrelation g₁(τ_d), which encodes scatterer dynamics, can be obtained from the intensity autocorrelation g₂(τ_d) via the Siegert relationship [7–11],

$$g_2\left({\tau }_d\right)=1+\beta {\left|g_1\left({\tau }_d\right)\right|}^2,$$ (1)

where

$$g_1\left({\tau }_d\right)=\frac{\langle U_s^{\ast }\left(t_d\right)U_s\left(t_d+{\tau }_d\right)\rangle }{\langle I_s\left(t_d\right)\rangle },$$ (2)

I_s(t_d) = |U_s(t_d)|² denotes the instantaneous intensity, and

$$g_2\left({\tau }_d\right)=\frac{\langle I_s\left(t_d\right)I_s\left(t_d+{\tau }_d\right)\rangle }{{\langle I_s\left(t_d\right)\rangle }^2},$$ (3)

where τ_d denotes the time lag for correlation, the brackets indicate ensemble averaging, and β ∈ [0, 1] is a parameter accounting for the number of measured speckles. If coherent detection is used (as in this work), β = 1.

The extension of DLS to the multiple scattering regime [10,12–16], diffusing wave spectroscopy (DWS) [13], was first demonstrated for the analysis of colloids, and similar methods have been applied to study blood flow in biological tissue [17,18]. These methods use the Siegert relationship to estimate blood dynamics from intensity autocorrelations [12,13,16,19,20]. A key assumption in DSCL, and more broadly, in stochastic transport [21,22], is ergodicity, or the equivalence of the ensemble [Eqs. (2) and (3)] and parametric (e.g., temporal) averages within a sample.

DSCL techniques have two main limitations. Firstly, the photon time-of-flight (TOF) is not measured. Accurate determination of particle dynamics from multiply scattered light is challenging if the TOF distribution is unknown. Secondly, conventional intensity-based DSCL methods are limited to systems in which the Siegert relation holds [3]. If the number of scattering paths are few or correlated, Gaussian statistics do not hold, invalidating the Siegert relation [23]. Additionally, the Siegert relationship cannot be applied to non-ergodic media [24], including samples with static components [10,25].

When the field reemitted by a turbid medium contains a static, time-independent, additive component U_c, U_s (t_d) is written as

$$U_s\left(t_d\right)=U_f\left(t_d\right)+U_c,$$ (4)

where U_f(t_d) is a zero-mean Gaussian process. The interpretation of Eq. (4) is that U_c does not change over experimental time scales, whereas U_f(t_d) does. After substituting Eq. (4) into Eq. (2), g₁(τ_d) takes the form [10,11,26]

$$g_1\left({\tau }_d\right)=\eta +\left(1-\eta \right){\gamma }_1\left({\tau }_d\right),$$ (5)

where η = I_c/Ī_s, γ₁(τ_d) = G₁,_f(τ_d)/Ī_f, and $G_{1,f}\left({\tau }_d\right)=\langle U_f^{\ast }\left(t_d\right)U_f\left(t_d+{\tau }_d\right)\rangle$ is the autocorrelation of the dynamic term, while $I_c=U_c^{\ast }{U}_c$, Ī_f = G₁,_f(0) and ${\overline{I}}_s={\langle I_s\left(t_d\right)\rangle }_{t_d}=I_c+{\overline{I}}_f$. Assuming ergodicity of U_f, ensemble averaging to determine G₁,_f is equivalent to temporal averaging with respect to t_d.

If β = 1, the intensity autocorrelation is [10,11,26]

$$g_2\left({\tau }_d\right)=1+2\eta \left(1-\eta \right)\mathrm{Re}\left[{\gamma }_1\left({\tau }_d\right)\right]+{\left(1-\eta \right)}^2{\left|{\gamma }_1\left({\tau }_d\right)\right|}^2.$$ (6)

By solving Eq. (6) for γ₁(τ_d) and assuming it is real and non-negative, one obtains

$${\gamma }_1\left({\tau }_d\right)=\frac{\sqrt{{\eta }^2+g_2\left({\tau }_d\right)-1}-\eta }{1-\eta },$$ (7)

which yields a different estimation for the field autocorrelation than the Siegert relationship with β = 1; nevertheless, both agree for η = 0. Assuming coherent detection (β = 1), $\eta =\sqrt{2-g_2\left(0\right)}$, since γ₁ (0) = 1. However, unless β is known a priori or fixed at a known value (e.g., 1) through careful experimental design [27], η cannot usually be estimated independently of β.

Approaches to address non-ergodicity include the use of higher-order intensity autocorrelations [11,28], ensemble averaging of independent speckles [24,26] by inducing sample motion [29], spatial diversity [10,16,30], insertion of an additional ergodic medium [31], or fitting based on an assumed functional form of γ₁(τ_d) [25]. However, these approaches entail either added complexity or extra measurements. Yet another approach is to deliberately introduce a strong static component to increase η, such that the central term in Eq. (6) dominates and Reined)] can be assessed [24]. However, in this “heterodyne” approach, the relative fluctuation size is reduced [11] and η is artificially modified. Here, we present a straightforward approach to directly measure g₁(τ_d) from a single time series and obtain both η and γ₁(τ_d) from Eq. (5) (see Eq. (S9) of Supplement 1).

To accomplish this, we demonstrate interferometric near-infrared spectroscopy (iNIRS) [32] for direct determination of TOF-resolved field and intensity autocorrelations. This is achieved through the analysis of the spectral interference between light traversing the sample and reference paths. This work extends beyond the intensity autocorrelations [32] demonstrated previously and determines field autocorrelations directly from the phase of the spectral interference.

2. MEASUREMENT OF FIELD AUTOCORRELATIONS

The spectral density is measured as a function of optical frequency, ν, over time, t_d, by a Mach–Zehnder interferometer (MZI) with a narrow-linewidth tunable laser. The time for one laser sweep is assumed to be rapid compared to the time scale of the field fluctuations. The registered signal is then given by

$$\mathcal{S}\left(\nu ,t_d\right)={\mathcal{S}}_{\text{DC}}\left(\nu ,t_d\right)+2\mathrm{Re}\left[{\mathcal{W}}_{rs}\left(\nu ,t_d\right)\right],$$

where ${\mathcal{S}}_{\text{DC}}\left(\nu ,t_d\right)$ is the DC component, assumed to be dominated by the reference arm, and ${\mathcal{W}}_{rs}\left(\nu ,t_d\right)$ is the crossspectral density between complex spectral amplitudes of the two paths [33]. By the Wiener–Khintchine theorem, ${\mathcal{W}}_{rs}\left(\nu ,t_d\right)$ can be used to recover information about the sample field. Namely, after suppressing ${\mathcal{S}}_{\text{DC}}\left(\nu ,t_d\right)$, and inverse Fourier transforming the resulting signal, one obtains

$$\begin{gathered} {\mathcal{F}}^{-1}\left\{2\mathrm{Re}\left[{\mathcal{W}}_{rs}\left(\nu ,t_d\right)\right]\right\} \\ ={\mathcal{F}}^{-1}\left\{{\mathcal{W}}_{rs}\left(\nu ,t_d\right)\right\}+{\mathcal{F}}^{-1}\left\{{\mathcal{W}}_{rs}^{\ast }\left(\nu ,t_d\right)\right\} \\ ={\mathrm{\Gamma }}_{rs}\left({\tau }_s,t_d\right)+{\mathrm{\Gamma }}_{rs}^{\ast }\left(-{\tau }_s,t_d\right), \end{gathered}$$ (8)

where ${\mathcal{F}}^{-1}$ denotes the inverse Fourier transform, Γ_rs is the mutual coherence function,

$$\begin{gathered} {\mathrm{\Gamma }}_{rs}\left({\tau }_s,t_d\right)={\langle U_r^{\ast }\left(t_s,t_d\right)U_s\left(t_s+{\tau }_s,t_d\right)\rangle }_{t_s} \\ =\underset{T\to \mathrm{\infty }}{\lim }\frac{1}{2T}{\displaystyle {\int }_{-T}^T{U}_r^{\ast }\left(t_s,t_d\right)U_s\left(t_s+{\tau }_s,{\tau }_d\right)\mathrm{d}{t}_s,} \end{gathered}$$ (9)

and τ_s is the conjugate variable to ν, representing the TOF delay between interferometer arms. U_r and U_s are hypothetical, not measured, reference and sample fields whose complex mutual coherence function, Γ_rs(τ_s, t_d) [inverse Fourier transform of W_rs(ν, t_d)], relates to the complex transmitted sample field. We assume that the complex conjugate term $\left[{\mathrm{\Gamma }}_{rs}^{\ast }\left(-{\tau }_s,t_d\right)\right]$ can be excluded. This, in practice, is achieved by adjusting the optical path mismatch between interferometer arms so the two terms in the last line of Eq. (8) do not overlap.

By repeatedly measuring Γ_rs(τ_s, t_d) over time t_d (distinct and separable from τ_s), the TOF-resolved first-order iNIRS autocorrelation is determined using

$$g_1^{\left(\text{iNIRS}\right)}\left({\tau }_s,{\tau }_d\right)=\frac{G_1^{\left(\text{iNIRS}\right)}\left({\tau }_s,{\tau }_d\right)}{G_1^{\left(\text{iNIRS}\right)}\left({\tau }_s,0\right)},$$ (10)

where $G_1^{\left(\text{iNIRS}\right)}\left({\tau }_s,{\tau }_d\right)={\langle {\mathrm{\Gamma }}_{rs}^{\ast }\left({\tau }_s,t_d\right){\mathrm{\Gamma }}_{rs}\left({\tau }_s,t_d+{\tau }_d\right)\rangle }_{t_d}$. This experimental measurement is related to the TOF-resolved field autocorrelation,

$$G_1\left({\tau }_s,{\tau }_d\right)={\langle U_s^{\ast }\left({\tau }_s,t_d\right)U_s\left({\tau }_s,t_d+{\tau }_d\right)\rangle }_{t_d},$$ (11)

by a convolution integral,

$$G_1^{\left(\text{iNIRS}\right)}\left({\tau }_s,{\tau }_d\right)={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{G}_1\left({\tau }_s^{\prime },{\tau }_d\right){\mathcal{I}}_0\left({\tau }_s-{\tau }_s^{\prime }\right)\mathrm{d}{\tau }_s^{\prime },}$$ (12)

where ${\mathcal{I}}_0\left({\tau }_s\right)$ denotes the instrument response function (IRF), which depends on the spectral range over which ${\mathcal{W}}_{rs}$ is measured [32]: $\Delta \nu \approx c\Delta \lambda /{\lambda }_0^2$ (c is the speed of light, Δλ denotes the wavelength bandwidth, and λ₀ stands for the center wavelength in free space). Hence, iNIRS measures the convolution of the TOF-resolved autocorrelation G₁ with the IRF. For large Δλ, the IRF approaches a delta function. Therefore, $G_1^{\left(\text{iNIRS}\right)}$ extracts TOF-resolved dynamics. In addition,

$$\begin{gathered} {\overline{I}}_s^{\left(\text{iNIRS}\right)}\left({\tau }_s\right)=G_1^{\left(\text{iNIRS}\right)}\left({\tau }_s,0\right)={\langle {\mathcal{I}}_s\left({\tau }_s,t_d\right)\rangle }_{t_d} \\ ={\langle I_s\left({\tau }_s,t_d\right)\rangle }_{t_d}\ast {\mathcal{I}}_0\left({\tau }_s\right), \end{gathered}$$ (13)

where ${\mathcal{I}}_s\left({\tau }_s,t_d\right)={\left|{\mathrm{\Gamma }}_{rs}\left({\tau }_s,t_d\right)\right|}^2$ and * denotes convolution with respect to τ_s. Thus, ${\overline{I}}_s^{\left(\text{iNIRS}\right)}\left({\tau }_s\right)$, the measured temporal point spread function (TPSF), is equal to the true photon TOF distribution, ${\langle I_s\left({\tau }_s,t_d\right)\rangle }_{t_d}$, convolved with the IRF.

In the presence of a static component, I_c, Eq. (11) can be written as

$$G_1\left({\tau }_s,{\tau }_d\right)=I_c\left({\tau }_s\right)+G_{1,f}\left({\tau }_s,{\tau }_d\right).$$

After convolving with the IRF, one obtains [cf. Eq. (12)]

$$\begin{gathered} G_1^{\left(\text{iNIRS}\right)}\left({\tau }_s,{\tau }_d\right)=\left[I_c\left({\tau }_s\right)+G_{1,f}\left({\tau }_s,{\tau }_d\right)\right]\ast {\mathcal{I}}_0\left({\tau }_s\right) \\ =I_c^{\left(\text{iNIRS}\right)}\left({\tau }_s\right)G_{1,f}^{\left(\text{iNIRS}\right)}\left({\tau }_s,{\tau }_d\right), \end{gathered}$$ (14)

where $G_{1,f}^{\left(\text{iNIRS}\right)}$ is the component of $G_1^{\left(\text{iNIRS}\right)}$ that decorrelates over time. Accordingly, Eq. (13) now reads as

$${\overline{I}}_s^{\left(\text{iNIRS}\right)}\left({\tau }_s\right)=I_c^{\left(\text{iNIRS}\right)}\left({\tau }_s\right)+{\overline{I}}_f^{\left(\text{iNIRS}\right)}\left({\tau }_s\right)$$

with ${\overline{I}}_f^{\left(\text{iNIRS}\right)}\left({\tau }_s\right)=G_{1,f}^{\left(\text{iNIRS}\right)}\left({\tau }_s,0\right)$. Therefore, by using temporal field autocorrelations, iNIRS distinguishes static and dynamic contributions. Finally, the TOF-resolved intensity autocorrelation can also be determined experimentally using iNIRS:

$$g_2^{\left(\text{iNIRS}\right)}\left({\tau }_s,{\tau }_d\right)=\frac{{\langle {\mathcal{I}}_s\left({\tau }_s,t_d\right){\mathcal{I}}_s\left({\tau }_s,t_d+{\tau }_d\right)\rangle }_{t_d}}{{\langle {\mathcal{I}}_s\left({\tau }_s,t_d\right)\rangle }_{t_d}^2}$$ (15)

Consequently, iNIRS measures both the TPSF and TOF-resolved field and intensity autocorrelations, overcoming ambiguities inherent in intensity-based DSCL techniques. This allows verification of the Siegert relation, and potentially, the study of non-Gaussian and non-ergodic light scattering where Eq. (1) does not hold.

The iNIRS experimental setup is depicted in Fig. 1(a). The frequency-swept light is divided into reference and sample arms. The collimated beam from the sample arm irradiates the turbid medium, which attenuates, broadens, and delays the incident light distribution. The light paths are finally combined by a fiber coupler and detected by a differential detector. The digitized electronic signal approximates $2\mathrm{Re}\left[{\mathcal{W}}_{rs}\left(\nu ,t_d\right)\right]$. Since the laser is swept in frequency, short photon paths through the sample produce smaller electronic beat frequencies than longer paths, provided that the reference arm TOF is shorter than the ballistic sample arm TOF [Fig. 1(b)]. By converting $2\mathrm{Re}\left[{\mathcal{W}}_{rs}\left(\nu ,t_d\right)\right]$ to Γ_rs(τ_s, t_d) through Fourier analysis [Eq. (8)], the beat frequency, amplitude, and phase of the electronic signal [Fig. 1(b)] yield the sample TOF, field magnitude, and field phase, respectively. This novel feature enables plotting TOF-resolved analytic field time courses [Fig. 1(c)] based on Γ_rs. As the field is complex, consisting of real and imaginary parts, these plots are naturally three-dimensional.

Fig. 1.

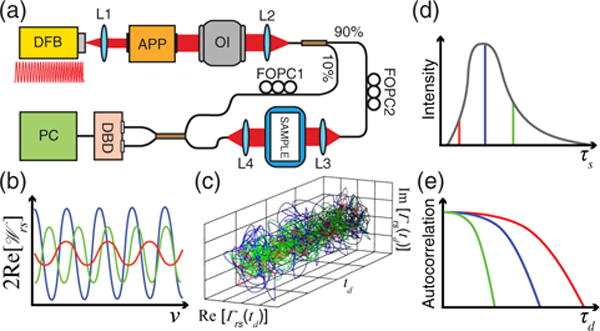
(a) A Mach–Zehnder interferometer with a tunable, temporally coherent light source (DFB, distributed feedback laser centered at 855 nm; APP—anamorphic prism pair; OI—optical isolator; FOPC, fiber optical polarization controller; DBD—dual balanced detector; L1, L2, L3, L4—lenses; PC—personal computer). (b) Idealized visualization of the real part of the cross-spectral density for different photon paths. (c) Coherent light scattering from moving particles causes fluctuations in the mutual coherence function, Γ_rs. Fluctuation dynamics increase with photon TOF due to increasing momentum transfer. (d) TPSF is obtained by temporally averaging consecutive measurements of |Γ_rs|² [see Eq. (13)]. (e) Field and intensity autocorrelations are determined from Γ_rs and |Γ_rs|², respectively.

The coherent addition of multiple light paths within the TOF range defined by the IRF [Eq. (13)] leads to fluctuations in $\left|{\mathrm{\Gamma }}_{rs}\left({\tau }_s,t_d\right)\right|=\sqrt{{\mathcal{I}}_s\left({\tau }_s,t_d\right)}$ and. φ_s(τ_s, t_d) = arg[Γ_rs(τ_s, t_d)] as the phases of these light paths change over time [Fig. 1(c)]. The TPSF can be determined by incoherent averaging over t_d at each value of τ_s [Fig. 1(d) and Eq. (12)]. The field of ballistic photons does not decorrelate (although not present in this work, the field of photons with purely static scattering also does not decorrelate). The field of late photons decorrelates faster than that of early photons, as more scattering events lead to increased momentum transfer [Fig. 1(e)]. In the DWS limit [13], the field decorrelation rate linearly depends on the number of reduced scattering events, ${\mu }_s^{\prime }\upsilon {\tau }_s$ (with υ denoting the speed of light in the medium and ${\mu }_s^{\prime }$ standing for the reduced scattering coefficient).

3. RESULTS

To compare the TOF-resolved field and intensity autocorrelations under ergodic and non-ergodic conditions, Intralipid 20% (IL20) with ${\mu }_s^{\prime }=17{\text{mm}}^{-1}$ [34] was diluted in a 10 mm thick cuvette with deionized water to achieve phantom concentrations of c_p = 5.2% ( ${\mu }_s^{\prime }=0.89{\text{mm}}^{-1}$), c_p = 5.5% ( ${\mu }_s^{\prime }=0.94{\text{mm}}^{-1}$), and c_p = 5.8% ( ${\mu }_s^{\prime }=0.99{\text{mm}}^{-1}$). Then, both MZI arms were co-polarized using two polarization controllers [FOPC in Fig. 1(a)]. For each sample, N = 40, 000 consecutive interference signals were acquired with a laser sweep duration of ~10 μs at a sweep repetition rate of 50 kHz and an incident power of 25 mW. Each signal was processed to estimate Γ_rs(τ_s, t_d), and temporal averages of ${\mathcal{I}}_s\left({\tau }_s,t_d\right)$ were calculated to obtain the TPSFs [first column of Fig. 2]. As c_p increases, $I_c^{\left(\text{iNIRS}\right)}\left({\tau }_s\right)$ decreases rapidly due to ballistic attenuation, while ${\overline{I}}_f^{\left(\text{iNIRS}\right)}\left({\tau }_s\right)$ decreases more gradually. Therefore, with increasing c_p, the relative contribution of the dynamic intensity, ${\overline{I}}_f^{\left(\text{iNIRS}\right)}\left({\tau }_s\right)$, increases. Note that $I_c^{\left(\text{iNIRS}\right)}\left({\tau }_s\right)$ has the same width as the IRF due to the convolution in Eq. (14). The static and dynamic intensities are analogous to the prompt and equilibrated components, respectively, from wave scattering in complex systems [21,35].

Fig. 2.

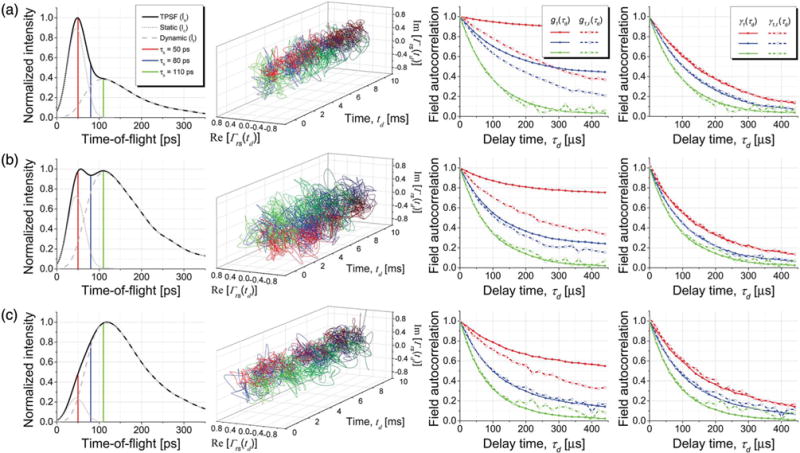
Transmitted field and intensity dynamics as a function of TOF and scatterer concentration for parallel polarization: (a) c_p = 5.2%, (b) c_p = 5.5%, and (c) c_p = 5.8%. The first column shows the TPSFs, with constituent static and dynamic components, and the second column shows complex field time courses for three τ_s values, marked on the TPSF plots. The third column shows that the directly estimated field autocorrelations, $g_1^{\left(\text{iNIRS}\right)}$, calculated using Eq. (10), disagree with $g_{1,I}^{\left(\text{iNIRS}\right)}$, the field autocorrelations inferred from the intensity autocorrelations using the Siegert relation [Eq. (1)] with variable β. Discrepancies are most notable for short paths and low scattering. However, as shown in the fourth column, both the field-based and intensity-based dynamic-component autocorrelation estimates ( ${\gamma }_1^{\left(\text{iNIRS}\right)}$ and ${\gamma }_{1,I}^{\left(\text{iNIRS}\right)}$, respectively) agree better if the non-ergodic component is accounted for [cf. Eqs. (5) and (7)]. In this figure, the superscript (iNIRS) was omitted to improve readability.

The fluctuating complex field time courses (second column of Fig. 2) were used to estimate $g_1^{\left(\text{iNIRS}\right)}$ [Eq. (10)] and $g_2^{\left(\text{iNIRS}\right)}$ [Eq. (15)]. All autocorrelation estimates were corrected for biases caused by additive noise (see Supplement 1). The resulting intensity-based estimate, denoted as $g_{1,I}^{\left(\text{iNIRS}\right)}$ is compared to the direct, field-based estimate, $g_1^{\left(\text{iNIRS}\right)}$, in the third column of Fig. 2. For short TOFs, $g_{1,I}^{\left(\text{iNIRS}\right)}$ decays faster than $g_1^{\left(\text{iNIRS}\right)}$, and $g_1^{\left(\text{iNIRS}\right)}$ decorrelates to a constant value η instead of zero. This indicates that the Siegert relationship breaks down due to the non-ergodicity of the reemitted light.

Since the dynamic component decorrelates, the static contribution can be estimated as $\eta ={\lim }_{{\tau }_d\to \mathrm{\infty }}{g}_1^{\left(\text{iNIRS}\right)}\left({\tau }_s,{\tau }_d\right)$ and used, in turn, to determine ${\gamma }_1^{\left(\text{iNIRS}\right)}$, the dynamic (ergodic) component autocorrelation [Eq. (5)]. This is compared, in the fourth column of Fig. 2, to ${\gamma }_{1,I}^{\left(\text{iNIRS}\right)}$, calculated from $g_2^{\left(\text{iNIRS}\right)}$ using Eq. (7). Evidently, both ${\gamma }_1^{\left(\text{iNIRS}\right)}$ and ${\gamma }_{1,I}^{\left(\text{iNIRS}\right)}$ now agree. However, the intensity-based estimate is noisier, particularly for long-photon TOFs [see Fig. 2(c)]. As suggested by our simulations, the additional phase information in the optical field reduces the autocorrelation estimation error and bias (see Supplement 1).

The non-ergodicity, which invalidates the Siegert relationship, was confirmed through a statistical analysis. The intensity and phase distributions for a complex Gaussian field with a static background of zero phase angle [Eq. (4)] are given by [2]

$$p_I\left({\mathcal{I}}_s\right)=\xi \exp \left[-\xi \left({\mathcal{I}}_s+I_c\right)\right]I_0\left(\alpha \right),{\mathcal{I}}_s\ge 0,$$ (16)

$$\begin{gathered} p_{\phi }\left({\phi }_s\right)=\frac{\xi }{2\pi }{e}^{-\xi I_c}{\displaystyle {\int }_0^{\mathrm{\infty }}\exp \left[\alpha \cos \left({\phi }_s\right)-\xi {\mathcal{I}}_s\right]\mathrm{d}{\mathcal{I}}_s,} \\ -\pi \le \phi <\pi , \end{gathered}$$ (17)

where $\xi ={\overline{I}}_f^{-1}$, $\alpha =2\xi \sqrt{{\mathcal{I}}_s{I}_c}$, I₀(α) is a modified Bessel function of the first kind, and I_c is the static intensity. Equation (16) is the modified Rician distribution. For I_c = 0, Eq. (16) reduces to the negative exponential distribution, $p_I\left({\mathcal{I}}_s\right)=\xi \exp \left[-\xi {\mathcal{I}}_s\right]$, while Eq. (17) becomes $p_{\phi }\left({\phi }_s\right)=\frac{1}{2\pi }$.

Figure 5 depicts the intensity and phase distributions obtained for the c_p = 5.2% IL20 phantom at three fixed values of τ_s. The intensity distributions were also fitted with modified Rician and negative exponential distributions using a maximum likelihood approach. For short paths, the intensity distribution obeys modified Rician statistics, and the negative exponential fit is poor. However, as the static contribution decreases with the increasing path length, the phases become more uniform [Fig. 3(d)], the intensities approach the negative exponential distribution, and zero-mean Gaussian statistics describe the field. Thus, the statistical distributions in Fig. 3 confirm the autocorrelations in Fig. 2.

Fig. 5.

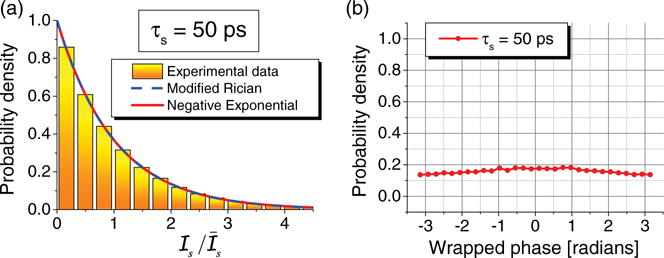
Transmitted intensity and phase distributions for c_p = 5.2% phantom and perpendicular polarizations [Fig. 4]. (a) Intensity histogram for a short path (τ_s = 50 ps) is fitted with negative exponential and modified Rician distributions, which overlap. (b) Optical field phases are uniform for even the shortest paths [cf. Fig. 3].

Fig. 3.

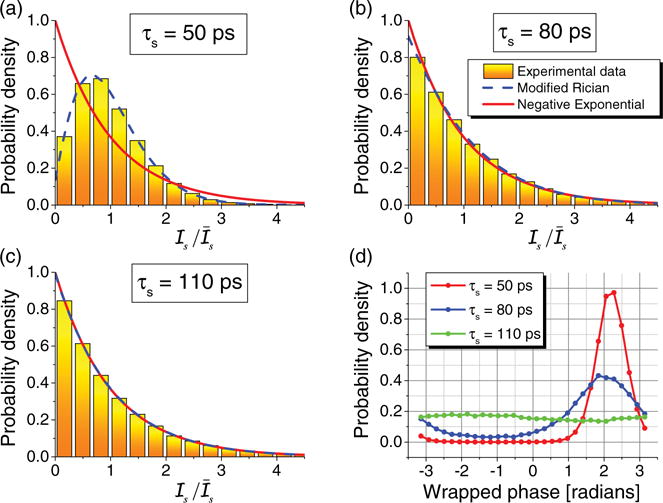
Transmitted intensity and phase distributions for a c_p = 5.2% phantom and parallel polarizations [Fig. 2(a)]. Intensity histograms for: (a) τ_s = 50 ps, (b) τ_s = 80 ps, and (c) τ_s = 110 ps are fitted with modified Rician [Eq. (16)] and negative exponential distributions. Both fits overlap for long paths. ${\overline{\mathcal{I}}}_s$ denotes the mean value of ${\mathcal{I}}_s$. (d) Optical field phases are uniform for long paths.

To further confirm that the static field component invalidates the Siegert relationship, the detection path was cross-polarized, suppressing ballistic paths. Figure 4 depicts the TPSF, complex field time courses, and autocorrelation estimates for c_p = 5.2%, where the invalidity of the Siegert relation was previously most apparent. Comparing cross- to co-polarization results [Fig. 2(a)], the TPSF now comprises only a dynamic component [Fig. 4(a)]. Consequently, the transmitted field does not contain a constant term [Fig. 4(b)]. As a result, the validity of Eq. (1) is restored for all paths [see Figs. 4(c) and 4(d)]. Exclusion of the static component by polarization gating is also confirmed by statistical distributions in Fig. 5. Here, the measured light intensities, even for short paths, are exponentially distributed and the phases are uniform.

Fig. 4.

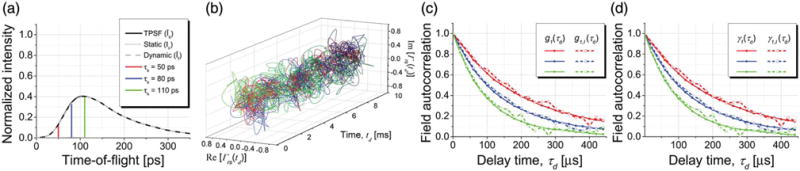
Transmitted field and intensity dynamics as a function of TOF for perpendicular polarization and c_p = 5.2% [same concentration as in Fig. 2(a)]. (a) TPSF overlaps with I_f(τ_s) due to the absence of the static component. Note that normalization was performed to the TPSF maximum for parallel polarization [cf. Fig. 2(a)]. (a) Complex field time courses. (c, d) Directly estimated field autocorrelations agree with those inferred from intensity autocorrelations.

4. DISCUSSION

In iNIRS, as in other DSCL methods, multiple speckles must be observed in order to estimate the autocorrelations, with improved precision being achieved with more temporal speckle evolutions or “lifetimes” [36]. However, our simulations (Supplement 1) suggest that fewer speckle lifetimes are required with field-based measurements to achieve the same precision as intensity-based measurements. Though results were obtained with a measurement time of 0.8 s in the main text and 0.2 s in Supplement 1, these times could be further reduced by employing improved estimators or utilizing both forward and backward laser sweeps.

It is important to note that the interferometer must be more stable for field-based than intensity-based measurements. As a rule of thumb, the phase of the interferometer must be stable over the decorrelation time scale of interest. In the present study, this criterion was satisfied without taking special measures to stabilize the interferometer. The advantages of field-based DSCL, including statistical efficiency and freedom from constraints of the Siegert relationship and ergodicity, are expected even if alternative methods (e.g., phase shifting) are used to determine the optical field. Importantly, iNIRS yields TOF-resolved field autocorrelations, from which sample dynamics can be derived through DWS [13] without explicit knowledge of the absorption.

In summary, we demonstrated iNIRS for the measurement of the intensity and field autocorrelations simultaneously with the TOF resolution. This approach to address non-ergodicity uses a single set ofmeasurements on the light naturally reemitted from an intact sample. We used this unique capability to directly examine the Siegert relationship, assumed in many DSCL techniques. We found a breakdown of this relationship for small scatterer concentrations and short photon TOFs. Methods to measure the optical field will improve the efficiency and quantitative capabilities of DSCL techniques.