MRI-based assessment of function and dysfunction in myelinated axons

Significance

Blood-oxygen-level-dependent (BOLD) fMRI has proven to be extremely powerful for studying brain function, but is essentially limited to applications in gray matter. This work investigates the underlying mechanisms responsible for MRI-based signal changes in myelinated axonal fibers of perfused bullfrog sciatic nerves. Simultaneous in-magnet recording of compound action potentials (CAPs) and MRI data acquisition reveal that the diffusion fMRI response is linearly proportional to the number of electrical impulses. Increased restricted diffusion fraction (from diffusion basis spectrum imaging) could be related to submyelinic vacuole formation observed by electron microscopy of perfused nerves fixed resting or undergoing stimulation. Microstructural changes and osmotically driven redistribution of tissue water play a crucial role in the observed diffusion fMRI response in myelinated fibers.

Abstract

Repetitive electrical activity produces microstructural alteration in myelinated axons, which may afford the opportunity to noninvasively monitor function of myelinated fibers in peripheral nervous system (PNS)/CNS pathways. Microstructural changes were assessed via two different magnetic-resonance-based approaches: diffusion fMRI and dynamic T₂ spectroscopy in the ex vivo perfused bullfrog sciatic nerves. Using this robust, classical model as a platform for testing, we demonstrate that noninvasive diffusion fMRI, based on standard diffusion tensor imaging (DTI), can clearly localize the sites of axonal conduction blockage as might be encountered in neurotrauma or other lesion types. It is also shown that the diffusion fMRI response is graded in proportion to the total number of electrical impulses carried through a given locus. Dynamic T₂ spectroscopy of the perfused frog nerves point to an electrical-activity-induced redistribution of tissue water and myelin structural changes. Diffusion basis spectrum imaging (DBSI) reveals a reversible shift of tissue water into a restricted isotropic diffusion signal component. Submyelinic vacuoles are observed in electron-microscopy images of tissue fixed during electrical stimulation. A slowing of the compound action potential conduction velocity accompanies repetitive electrical activity. Correlations between electrophysiology and MRI parameters during and immediately after stimulation are presented. Potential mechanisms and interpretations of these results are discussed.

Blood-oxygen-level-dependent (BOLD) functional magnetic resonance imaging (fMRI) has revolutionized our ability to study human brain function (1, 2). Because gray matter (GM) is relatively well vascularized, the BOLD effect works exceptionally well as a means to indirectly monitor neuronal activity. Further improvement of BOLD fMRI measurement of GM neural activity is achieved by accounting for regional variation in local vascular (especially venous) structure (3). By comparison, successful studies with white matter (WM) BOLD fMRI are limited because both blood volume and the tissue’s capacity for physiologic modulation of blood flow are considerably less than in GM (4), although there have been some recent gains toward that aim (5, 6).

It should be noted that BOLD measurements are not the only MRI approach to detect neuronal function. Le Bihan has suggested that diffusion fMRI may offer a more direct measure of brain activation and points to cell swelling as a cause for the observed decrease in activity-induced water apparent diffusion coefficient (ADC), as evidenced in diffusion fMRI studies carried out by his group (7, 8) and others (9, 10). Those studies utilized a single-direction diffusion measurement, assuming isotropic water diffusion within GM. A point of contention was raised subsequently by investigators who showed experimentally that ADC changes similar to the task-evoked diffusion fMRI response—a decrease in human visual cortex ADC with visual stimulation (8)—could be elicited by hypercapnia-induced modulation of brain blood flow in the absence of functional activation (11) or that the observed ΔADC of diffusion fMRI in the visual cortex of cats was largely dominated by vascular contributions (12).

Regardless of any such controversies, a sizeable body of work supports the notion that cell swelling and concomitant shrinkage of the extracellular space (ECS) regularly accompanies neuronal activity both in vivo and ex vivo (for examples, see refs. 13–18). A survey of this literature indicates that the extent and temporal dynamics of the activity-induced ECS shrinkage depend upon both the amount of stimulation/electrical activity and the cellular and even subcellular composition of the tissue under study. Bearing in mind these caveats, a modulation of ECS volume is expected to produce ADC changes observable via diffusion MRI since the direction (19) and time-dependent water diffusivity in tissue (20) is dictated by the distribution of intracellular and extracellular water segregated by cellular membranes.

In the case of WM, differences exist in water diffusivity along vs. perpendicular to the fiber axis. Thus, diffusion tensor imaging (DTI; models random thermal displacement of water as a tensor) has been employed extensively to investigate the direction-dependent behavior of water diffusion, reflecting fiber orientations in ordered tissues (21).

WM diffusion fMRI investigations have applied DTI, or variants thereof, to monitor short-term structural alterations with WM electrical activity (22–24). For example, functional DTI was performed to measure task-related changes in fractional anisotropy along the thalamocortical tract and optic radiation upon tactile and visual stimulation, respectively (24). In our own WM diffusion fMRI work with healthy mice, a flashing-light visual stimulus led to a reversible decrease in the ADC of water perpendicular to the optic nerve fibers (ADC_⊥, also denoted as λ_⊥) of the stimulated eye (22). Diffusion changes were absent in the optic nerve of the contralateral, nonstimulated eye, and no modulation of λ_⊥ was observed with hypercapnia (i.e., blood flow change does not reproduce activity-induced ADC_⊥ change in this case). Moreover, the ADC_⊥ decrease was found to be attenuated in mice with acute optic neuritis. The magnitude of the WM diffusion fMRI response was correlated with visual acuity in the affected eye (23).

In the present work, we turn our attention to a model system consisting of coherently oriented myelinated axons without the potential confounds of blood flow—ex vivo perfused nerves of the jumbo bullfrog. As they are exceptionally robust (25), ex vivo frog sciatic nerves have been the subject of numerous electrophysiology (26, 27) and MRI studies over the years (28–31). MRI studies of frog sciatic and other nonmammalian nerves have provided useful insight into our understanding of the diffusion MRI signal behavior observed in human WM (32).

Using perfused bullfrog sciatic nerves, we demonstrate that repetitive electrical activity produces dynamic changes in diffusion MRI and nerve tissue T₂ spectra [which provide information about water distribution in the peripheral nervous system (PNS) between intracellular, extracellular, and myelin compartments and are used to assess myelin water fraction (MWF) in CNS demyelination (28–34)]. This report demonstrates dynamic changes in water T₂ spectral components with electrical activity in WM. These changes are observable on the timescale of minutes. Taken altogether, the MRI, electrophysiology, and microscopy data (poststimulation- or quiescent-fixed tissues), a consistent picture emerges—repetitive electrical activity leads to osmotically driven microstructural modification of the myelinated fibers. Lastly, it will be demonstrated, in principle, that WM diffusion fMRI can noninvasively localize foci of electrical conduction blockage in axonal pathways as might be present in cases of neurodegeneration or neurotrauma.

Results

Diffusion Functional DTI Time Course.

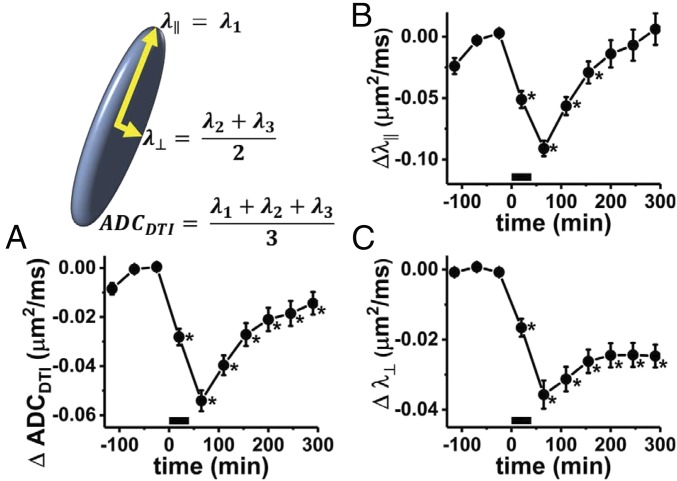
The time course of the DTI parameters following a 40-min period of stimulation at 100 Hz shows different responses for diffusion parallel vs. perpendicular to the axonal fibers. The DTI-derived mean ADC (ADC_DTI) shows a maximum decrease from baseline, ΔADC_DTI = −0.054 ± 0.004 μm²/ms (mean ± SEM, n = 6), at the time point immediately poststimulus (Fig. 1A). This amounts to a 6.2% decrease, recovering toward baseline over the next several hours.

Fig. 1.

Perfused frog sciatic nerve diffusion fMRI time course from DTI modeling. The period of electrical stimulation is depicted by the black bar along the x axis (0–40 min). The principal eigenvalue of the diffusion tensor represents axial diffusivity (λ_║) of the diffusion ellipsoid. With the assumption of cylindrical symmetry, the radial diffusivity is taken as the average of the other two eigenvectors. Three time points were acquired before stimulation, with the prestimulus baseline of each parameter determined by the average parameter values in the final two baseline time points. (A) Time-course change of the ADC (ADC_DTI), compared with the average of the ADC measured at the two time points before stimulation (n = 6, error bars represent sample SEM). In absolute terms, prestimulus ADC_DTI = 0.88 ± 0.02 μm²/ms (mean ± SEM), which falls to a nadir value (0.83 ± 0.02 μm²/ms) at the poststimulation time point. (B) The prestimulus λ_║ = 1.68 ± 0.06 μm²/ms decreases to a minimum of 1.59 ± 0.06 μm²/ms before rebounding to 1.69 ± 0.06 μm²/ms at the last time point. (C) The initial λ_⊥ = 0.48 ± 0.01 μm²/ms decreases to 0.44 ± 0.01 μm²/ms, before achieving a poststimulus plateau at 0.45 ± 0.01 μm²/ms. Time points which were statistically significantly different from the prestimulus measurement, as determined via repeated-measures ANOVA/Tukey post hoc testing, are indicated by an asterisk.

The recovery in ADC_DTI is largely driven by the parallel diffusivity (λ_||), which shows a large decrease from baseline at the poststimulus time point (Δλ_|| = −0.091 ± 0.006 μm²/ms, −5.4 ± 0.4%) and recovers fully to baseline over the course of 4 h poststimulation (Fig. 1B). Radial diffusivity, λ_⊥, exhibits a smaller absolute drop (Δλ_⊥ = −0.036 ± 0.004 μm²/ms), which is, however, larger as a percentage of its initial value (−7.4 ± 0.8%). The radial diffusivity, which shows some tendency to recover over the course of 3 h poststimulation, appears to finally stabilize at a level decreased from the prestimulus value (Fig. 1C).

In summary, while the decrease in λ_|| appears transient, recovering to baseline values, decreases in λ_⊥, and ADC_DTI are more sustained over ∼5 h poststimulation.

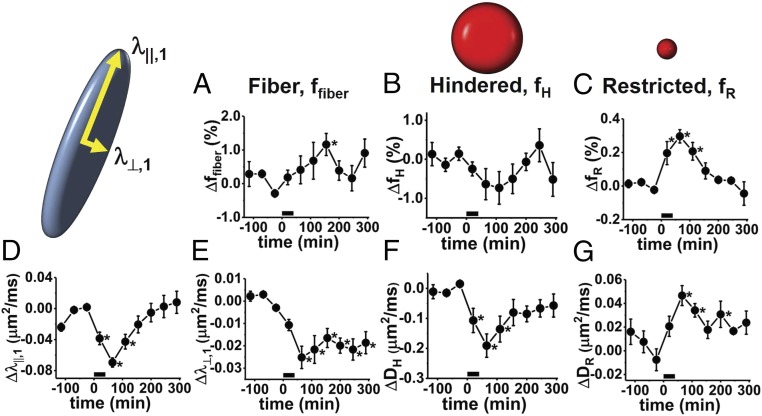
Diffusion Functional Diffusion Basis Spectrum Imaging Time Course.

Not surprisingly, the readouts on fiber-component axial (λ_||,1) and radial (λ_⊥,1) diffusivities from diffusion basis spectrum imaging (DBSI) are similar to those provided by DTI modeling (Fig. 2 D and E, respectively), the DBSI fiber component (f_fiber) accounting for >70% of the total diffusion signal. In Fig. 2, changes in the various DBSI diffusion signal components (f_fiber, fiber fraction; f_H, hindered isotropic diffusion fraction; and f_R, restricted isotropic diffusion fraction) are presented as a percent of the total sciatic nerve signal. Repetitive electrical stimulation results in a mild increase in f_fiber, on the order of 1%, that only achieves statistical significance at the time point 155 min poststimulus (Fig. 2A). At the same time, a decrease in the hindered fraction, f_H, is seen, along with a simultaneous decrease in the hindered component’s apparent diffusivity, D_H. A transient increase occurs for the signal component associated with the most restricted diffusivity, f_R, for which D_R < 0.3 μm²/ms. In all cases studied here, the restricted diffusion fraction accounts for <1% of the total sciatic nerve water. On average, 0.3% of the water transiently shifts into this restricted DBSI signal component after 40 min × 100-Hz electrical stimulation. The increase in f_R achieves statistical significance for the three time points poststimulus, before returning to baseline values (Fig. 2C).

Fig. 2.

Time-course changes in DBSI model diffusion parameters from initial value (n = 6). (A) Fiber fraction exhibits an increase (f_fiber,init = 0.778 ± 0.009) to a maximum of 0.789 ± 0.008. This difference is only statistically significant at the fourth time point after the start of stimulation. This suggests a shift of 1.1% (Δf_fiber = 1.1 ± 0.3) into the fiber signal component of the DBSI model. (B) The hindered component (f_H) of the isotropic ADC spectrum indicates a maximum poststimulus shift of 0.7 ± 0.3% of tissue water out of the hindered. More pronounced is the decrease in the ADC of this component (D_H), shown in F. (C) A small portion of the water in the perfused nerve, Δf_R = 0.30 ± 0.03% of the total, transiently shifts into a compartment with restricted isotropic diffusion. Prestimulation, the restricted diffusion component accounts for 0.2 ± 0.1% of the total signal in the nerve. In relative terms, f_R transiently increases by 230%. (D and E) Changes in the axial (D) and radial (E) diffusivities of the fiber component, f_fiber. (F) Poststimulus, ΔD_H = −0.19 ± 0.04 μm²/ms, from an initial prestimulus D_H of 1.30 ± 0.06 μm²/ms. (G) The prestimulus restricted diffusivity, D_R, increases from 0.11 ± 0.02 to 0.15 ± 0.02 μm²/ms. The finding that D_R appears to remain elevated while f_R returns nearly to baseline suggests that it is the largest of the submyelinic vacuoles that are the least transient in nature. Time points that are statistically significantly different from the prestimulus value via repeated-measures ANOVA/Tukey test are indicated by an asterisk.

While some of the DBSI signal components show only transient changes (f_R, D_H, D_R, and λ_||,1), the induced change in DBSI fiber radial diffusivity (λ_⊥,1) is sustained over the poststimulus observation period.

Cross-Validation of Diffusion Data Modeling.

We performed cross-validation (CV) to evaluate the DTI and DBSI model fits of the data, a summary of which is presented in SI Appendix, Fig. S3. CV analyses were carried out on data from two of the prestimulus time points (the second and third time points in Figs. 1 and 2) for a 3 × 3 voxel region of interest (ROI) placed at the center of the nerve. These points were chosen because the diffusion signal was not evolving in time, as was the case poststimulation. The reproducibility of signal intensity in repeat measurements was found to be quite high (R²_repeat = 0.99933 ± 0.00009, mean ± SD). In the CV assessment, using the DBSI model of the first dataset to predict the second dataset was comparable to the measurement reproducibility (R²_CV,DBSI = 0.99926 ± 0.00044, mean ± SD). In four of the six cases, the DBSI model made a better prediction of the repeat measure data than when the first dataset was used to predict signal intensities in the second dataset. For all time points across the serial measurements, the DBSI model of the multidirection/multi-b-value diffusion data provided excellent fits to the data (R² ≥ 0.99859). Reproducibility in repeat measurements is very high due to high signal-to-noise ratio (SNR) and the absence of bulk physiological motion.

Not surprisingly, the DTI model, with fewer parameters, did not fit the data as well as the DBSI model, nor did it do as well in the CV assessment, but the DTI model still provided very good fits to the data presented herein. For instance, across the time series of measurements the DTI model produces very high-quality fits to the data (0.99696 ≤ R² ≤ 0.99868).

Electron Microscopy.

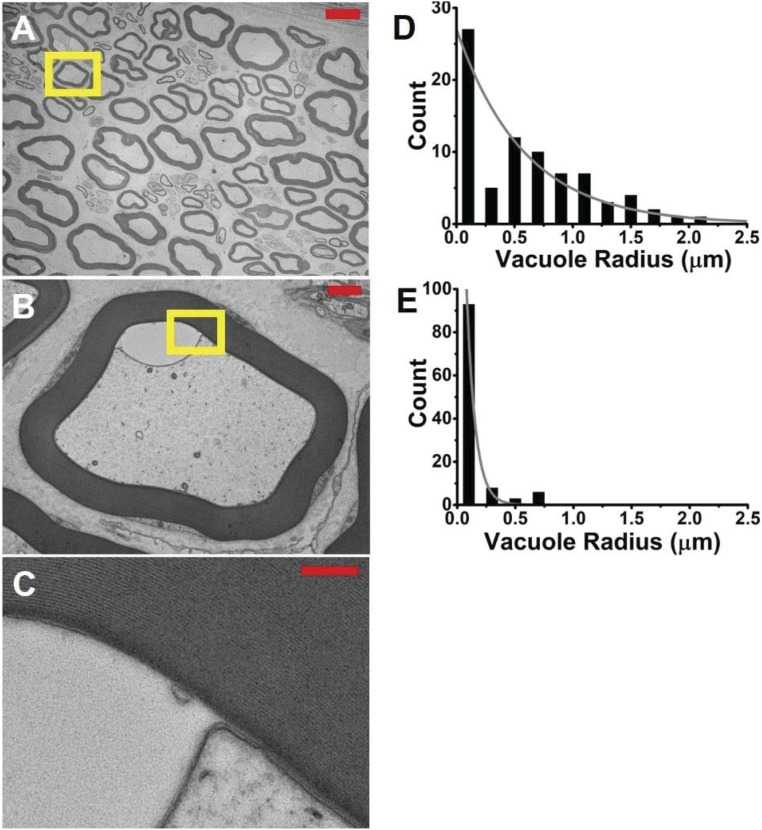
The aim of the electron microscopy (EM) measurements was to verify whether or not, in the current perfused nerve preparation, we could observe any phenomenon similar to that reported by Wurtz and Ellisman (35). In frog sciatic nerves, they observed transient paranodal intramyelinic vacuoles resulting from repetitive in situ electrical stimulation. Transverse EM images of the two sciatic nerves (one stimulation-fixed, the other rested and fixed) showed clear microstructural differences. At relatively low magnification, it can be appreciated that the myelin in the stimulation-fixed and rested nerve sample was well-preserved and intact. A low-magnification image of the stimulation-fixed nerve is shown in Fig. 3A. However, closer examination revealed the presence of numerous, fluid-filled vacuoles in the periaxonal space or, occasionally, confined within the first few layers of myelin (Fig. 3 B and C). In the stimulation-fixed axons, the submyelinic vacuoles were both more prevalent and larger in size than in the rest-fixed axons (Fig. 3 D and E). Vacuole sizes estimated by the semiautomatic method and manual segmentation were in high concordance (>95% agreement).

Fig. 3.

Electron micrographs reveal large submyelinic vacuoles in stimulation-fixed perfused frog sciatic nerves. (A) Low-magnification EM (600×), axial image of a stimulation-fixed perfused frog sciatic nerve. Overall, the myelin appears well preserved. (Scale bar: 10 μm.) (B) Close-up (6,000×) of the region indicated by the yellow box in A. The example shown here depicts the submyelinic vacuoles that are larger and more prevalent than in the rest-fixed perfused frog sciatic nerve. The vacuole region is clear, devoid of the microtubules, present in axoplasm. (Scale bar: 1 μm.) (C) Further magnification (30,000×) of the outlined region in B reveals that this particular fluid-filled vacuole has opened up between the innermost wraps of the myelin. (Scale bar: 200 nm.) (D and E) Histograms of the equivalent radius of vacuoles in sampled axons from stimulation-fixed (D) and rest-fixed (E) perfused frog sciatic nerves. The difference between these exponentially distributed histograms was found to be highly statistically significant via the Cox–Mantel test (P < 10⁻⁶).

Electrophysiology of the Frog Sciatic Nerve.

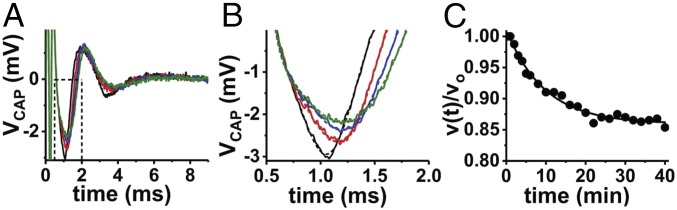
A universal observation in the perfused nerve experiments was that sustained, repetitive electrical stimulation produced a decrease in the compound action potential (CAP) conduction velocity during the stimulation period. In concert with the conduction velocity decrease, the CAP waveform was observed to broaden with a concomitant decrease in peak-to-peak amplitude (Fig. 4).

Fig. 4.

An example of the decrease in CAP conduction velocity exhibited during repetitive electrical stimulation of a perfused bullfrog sciatic nerve at 100 Hz × 40 min. (A) Individual CAP recordings are shown at selected times during the stimulation period: black, 1 min; red, 10 min; blue, 20 min; green, 30 min. (B) Zoomed-in view of the data from A. Solid curves show the recorded data, and dashed lines show the model fit of the CAP. The CAP fitting was used to reduce variations in the estimated waveform peak amplitude and latency. (C) Normalized conduction velocities are plotted vs. time during the stimulation period. Since it is not possible to record the exact conduction length (l) in the suction electrode experiment (54), this quantity is removed by normalization—v(t) = l/τ_latency(t) and v_o = l/τ_latency,init, then v(t)/v_o = τ_latency,init/τ_latency(t). The broadening (decreased V_pk-pk) and slowing of the CAP is well represented by exponential kinetics. In the example shown, the conduction velocity slows to 84% of its initial value over the course of 40 min. The quantity v_CAP,40min/v_CAP,o is used to describe slowing of the CAP conduction velocity in subsequent analyses.

T₂ Spectral Changes.

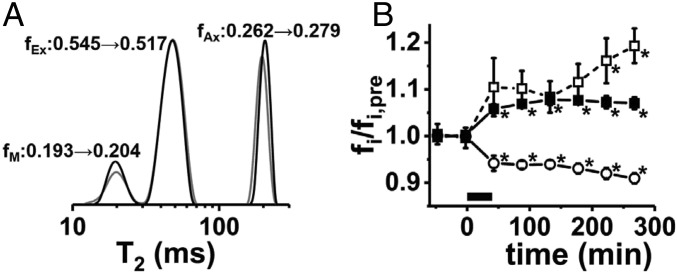
We sought to determine whether dynamic T₂ spectroscopy could noninvasively detect structural changes accompanying repetitive electrical activity. Dynamic T₂ spectra were successfully acquired from five perfused nerves. The prestimulus T₂-spectroscopy-based signal fractions [f_M = 0.173 ± 0.009 (myelin), f_Ex = 0.568 ± 0.011 (extracellular), f_Ax = 0.259 ± 0.011 (axonal), mean ± SEM] are in reasonably good agreement with existing literature reports for in vivo and ex vivo sciatic nerves of various frog species (28–31). Fig. 5A shows prestimulation and poststimulation T₂ spectra for a perfused bullfrog sciatic nerve. A general feature in the T₂ spectral measurements (Fig. 5B) was that repetitive electrical stimulation produced an increase in the myelin–water fraction (+8.7 ± 1.2%, prestimulus vs. poststimulus) and the intraaxonal water fraction (+7.3 ± 1.0%, prestimulus vs. poststimulus) with a shrinkage of the extracellular water fraction (−5.9 ± 0.7%, prestimulus vs. poststimulus). For the T₂ time-course analysis, only five of the six nerves were included, with one of the datasets exhibiting 60 Hz interference (signal oscillations) superimposed upon the T₂ decay envelope.

Fig. 5.

(A) An example of prestimulation (gray) and poststimulation (black) T₂ spectra acquired from a perfused frog sciatic nerve. The CPMG echo-trains acquisitions (4,096 echoes spaced by 1 ms, TR = 20 s, 16 averages, 5 min and 20 s per measurement) were interleaved between the diffusion fMRI time points. T₂-based signal fractions f_M (myelin), f_Ex (extracellular), and f_Ax (axonal) are shown. (B) Group-averaged evolution of the T₂ signal components vs. time revealed by dynamic T₂ spectroscopy (n = 5, error bars represent SEM). Here, the nerve T₂ signal fractions, f_i, are normalized such that their prestimulus average is 1, so the dynamics of the three signal components can be displayed in a single plot (f_M/f_M,pre, open squares; f_Ax/f_Ax,pre, filled squares; f_Ex/f_Ex,pre, open circles). The period of applied electrical stimulation (100 Hz × 40 min) is represented by the black bar from 0 to 40 min along the x axis. Statistically significant differences from the prestimulus measurement (repeated-measures ANOVA/Tukey post hoc testing) are indicated by an asterisk.

Induced changes in intraaxonal and extracellular signal components showed statistically significant alterations from baseline and appeared relatively stable in the extended time course after stimulation. After an initial increase, the MWF appeared to tail upward, especially at later time points during the serial measurements.

Diffusion fMRI Dose–Response.

The applied electrical stimulus in the experiments presented so far were quite vigorous. This was partially to assure maximal observable response. However, it is worth assessing the diffusion fMRI response with stimuli of lower intensity—that is, reduced duration and/or frequency of applied supermaximal electrical stimulation.

In Fig. 6, the diffusion fMRI response in terms of the prestimulus to poststimulus changes in radial and axial diffusivity are presented for three different intensities of electrical stimulation—50 Hz × 24 min, 100 Hz × 24 min, and 100 Hz × 40 min. Stimuli of 50 Hz × 24 min and 100 Hz × 24 min were applied to the same set of nerves in series, separated by a 3-h rest period (n = 6). A separate set of nerves, described in the preceding sections, underwent the more vigorous 100 Hz × 40 min stimulation regimen (n = 6). Time-course data for the twice-stimulated nerves are presented in the SI Appendix, Figs. S4 and S5.

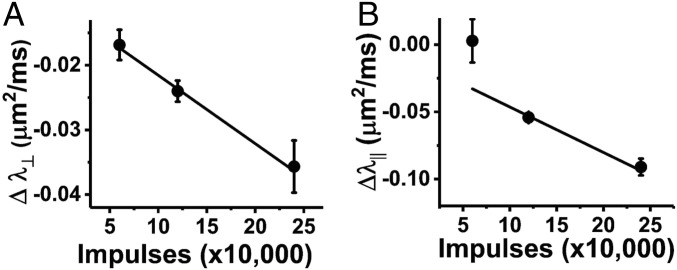
Fig. 6.

Electrical stimulus dose–response. (A) The magnitude of the diffusion fMRI response, Δλ_⊥, increases in proportion to the number of electrical impulses carried by the nerve fibers during periods of sustained electrical activity (error bars represent SEM). (B) For Δλ_||, the trend is similar; however, presumably due to increased scatter in the lower spatial resolution imaging data, the correlation between impulse count and Δλ_|| diffusion fMRI response is not as robust.

It should be noted that the diffusion MRI data for the set of nerves that underwent two rounds of electrical stimulation (50 Hz × 24 min and 100 Hz × 24 min, separated by 3-h rest) was acquired with a smaller imaging matrix (32 × 32). The raw k-space data were filtered (Materials and Methods); however, the smaller matrix size introduced shifts in the estimated diffusion eigenvalues (SI Appendix, Table S2) and larger uncertainty/data scatter in the parameter estimates (SI Appendix, Figs. S4 and S5), presumably as a result of more pronounced Gibb’s ringing phenomenon (36). The dependence of individual DTI-estimated eigenvectors has been shown to depend in a complex way upon matrix size, diffusion-weighted signal-intensity differences between adjacent tissues, and filtering employed (36). SI Appendix, Fig. S4 suggests that λ_⊥ is the most stable (smallest data scatter) for the data acquired on a 32 × 32 image matrix.

The magnitude of the Δλ_⊥ diffusion fMRI response appeared to be proportional to the overall electrical activity (total number of impulses carried by the nerve) during sustained repetitive stimulation (Fig. 6A). For Δλ_|| the trend was similar; however, presumably due to increased scatter in the lower spatial resolution imaging data, the correlation between impulse count and Δλ_|| diffusion fMRI response was not as robust or at least did not display a linear response (Fig. 6B).

Correlations Among Electrophysiology, T₂, and Diffusion fMRI Changes.

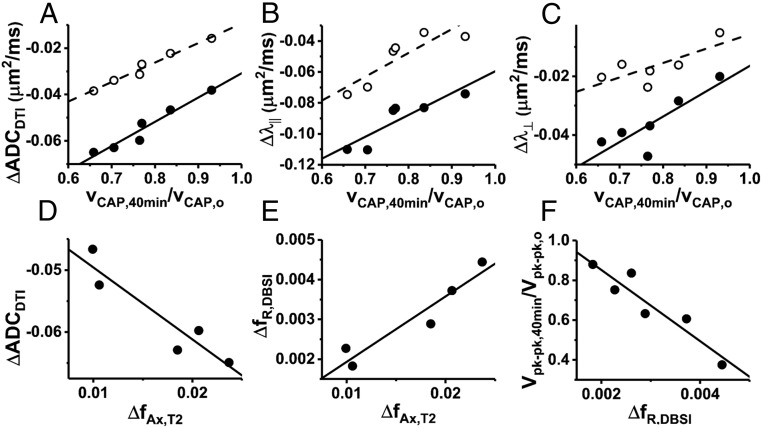
Statistically significant correlations exist between the normalized axonal CAP conduction velocity measured at the end of the 40 min × 100 Hz stimulation period (v_CAP,40min/v_CAP,0) and DTI-based diffusion fMRI response measures (Fig. 7 A–C). Data are shown for diffusion parameters ΔADC_DTI, Δλ_||, and Δλ_⊥ measured at two time points—during applied stimulation and at the poststimulus time point. Fig. 7 D and E illustrate the statistically significant correlation between dynamic T₂ spectroscopy and diffusion fMRI with 40-min 100-Hz electrical stimulation. A larger shift of water into the T₂ axonal signal component is associated with a proportional decrease in overall ADC_DTI (Fig. 8D, R² = 0.87, P = 0.02). A statistically significant correlation exists between Δf_Ax,T2 and the increase in DBSI restricted diffusion component, Δf_R (Fig. 7E). From DBSI modeling of the same diffusion data, the change in the restricted isotropic diffusion component (Δf_R) does not correlate with normalized conduction velocity, but does correlate with the normalized peak-to-peak CAP amplitude (Fig. 7F).

Fig. 7.

Correlations among different metrics of stimulus response from diffusion fMRI, electrophysiology, and dynamic T₂ spectroscopy in the 40-min × 100-Hz stimulus nerves. (A–C) The DTI-based metrics of diffusion fMRI response (ΔADC_DTI, Δλ_║, and Δλ_⊥) show statistically significant correlations with normalized CAP conduction velocity (poststimulation, filled circles/solid-line fits, R² = 0.94, P = 0.0013, R² = 0.79, P = 0.018, R² = 0.71, P = 0.035, for ΔADC_DTI, Δλ_║, and Δλ_⊥, respectively). Measured at the stimulus-on time point (open circles/dashed lines), ΔADC_DTI and Δλ_║ are statistically significantly correlated with v_{CAP,40min,norm} (R² = 0.97, P = 0.0003 and R² = 0.77, P = 0.023, respectively), but Δλ_⊥ is not. (D and E) Increasing axonal water fraction in dynamic T₂ spectra is associated with a larger decrease in ADC_DTI (R² = 0.87, P = 0.020) and an increase in the DBSI-restricted diffusion component (R² = 0.91, P = 0.013). (F) While it does not correlate with conduction velocity, an increase in the DBSI-restricted isotropic diffusion component does correlate with reduced CAP peak-to-peak amplitude (broadening out of the CAP waveform, R² = 0.88, P = 0.006).

Fig. 8.

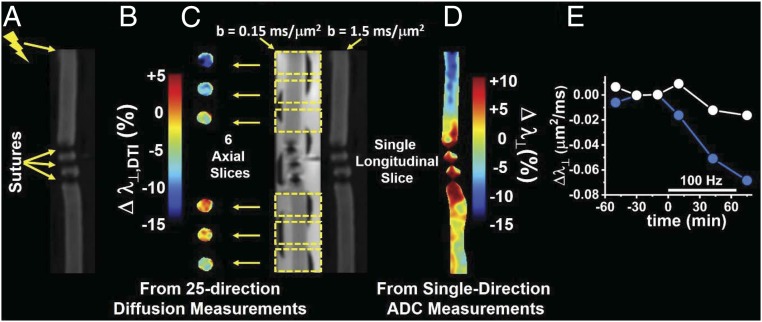
Conceptual demonstration of diffusion fMRI to locate AP conduction blockage. (A) The perfused nerve was tied off in the middle by three silk sutures, and stimulation was applied via suction electrode at the proximal end, as indicated, for a period of 60 min at 100-Hz frequency. (B) The diffusion fMRI response is depicted here as the percent change in Δλ_⊥ (from DTI analysis of the 25-direction diffusion imaging data acquired in six axial image slices) prestimulation to poststimulation. The positions of the axial slices along the nerve are shown in C. (C) Two DW longitudinal slice images along the length of the nerve with diffusion-encoding gradients applied orthogonal to the axonal fibers with b values of 0.15 and 1.5 ms/μm². The two DW images are used to generate maps of λ_⊥ from this single-diffusion-direction measurement. (D) The diffusion fMRI response Δλ_⊥ (percent change) from prestimulus and poststimulus single-direction λ_⊥ maps. (E) Time-course average Δλ_⊥ for the two slices proximal to the conduction blockage (blue) and the two most distal slices (white).

WM Diffusion fMRI for Identification of Axonal Conduction Blockage.

In Fig. 8B, the slice-by-slice differences (poststimulation vs. prestimulation) in λ⊥ are shown. Fig. 8D illustrates the resulting Δλ⊥ in a single longitudinal slice through the nerve with diffusion weighting applied in a single direction (perpendicular to the axonal fibers). Both types of images show the same trend. At the proximal end, the expected drop in λ⊥ is seen, while at the distal end, the Δλ⊥ response is muted. An interesting feature, visible most clearly in the longitudinal-slice diffusion fMRI data (Fig. 8D), is that the region of attenuated functional response extends several millimeters proximal to the first nerve ligation. Likely related to this, from the map in Fig. 8D, it is also clear that the ligation results in some pathological changes in λ⊥ extending somewhat beyond the immediate vicinity of the sutures. To compare the two halves of the nerve, the time-course average Δλ⊥ for the two most proximal and two most distal slices is shown in Fig. 8E. The two slices closest to the ligation site (one proximal and one distal) are not included in these averages.

Discussion

The DTI differences between prestimulus and poststimulus λ_⊥ can be explained by swelling of the axonal fibers and shrinkage of the ECS after the bout of sustained electrical stimulation, assuming the diffusion behavior is dominated by the diffusivity of the extracellular volume fraction (37). This presumed reduction of the ECS does not appear to be fully reversible within the time frame of the current measurements. However, the observed dynamics of λ_|| are not as obviously explained by the shrinkage of ECS. Changes of the axonal microstructure and/or differences in the free diffusivities/viscosities of intraaxonal and extracellular water could potentially cause the observed changes in λ_||. In mathematical models of diffusion, axons are often conceptualized as having a simple cylindrical geometry. In the case of PNS axons, this is an oversimplification. For instance, the cross-sectional area of axons at the nodes of Ranvier is typically on the order of one-third to one-sixth of that in the internodal region (38). Thus, activity-induced changes to the somewhat complex morphology of myelinated PNS axons may produce diffusion changes that do not necessarily lend themselves to straightforward interpretation if one has a purely cylindrical axonal geometry in mind.

On the other hand, the behavior of DBSI-derived f_R suggests that a small amount of water in the poststimulus sciatic nerve transiently finds its way into a restricted compartment. While this phenomenon is not revealed by DTI modeling of the diffusion fMRI data, it could account for some of the observed decrease in λ_|| from DTI.

It is noteworthy that Wurtz and Ellisman (35) reported the formation of transient paranodal intramyelinic vacuoles induced by repetitive in situ electrical stimulation of the frog sciatic nerve. Those investigators specifically focused on microstructural alterations of the paranodal myelin by examination of EM images of longitudinally sectioned nodes of Ranvier. The spacing between nodes of Ranvier in frog sciatic nerve is proportional to axonal diameter and may be as large as 1.5 mm (39). Thus, successfully sampling enough nodes of Ranvier via EM for statistical analysis can be exceptionally time-consuming in longitudinally sectioned specimens.

In the present work, by examining transverse-sectioned EM images of fixed frog sciatic nerves, we have achieved a more time-efficient sampling of axons; however, this sampling is not restricted to any unique axial position (nodal, paranodal, internodal, etc.). Even so, the distribution of vacuole radii in the sampling of stimulation-fixed and -fixed axons are statistically significantly different. However, since our poststimulus EM measurements were carried out at only a single time point, it cannot conclusively be proven that the transient increase in DBSI f_R is a result of submyelinic vacuole formation, but it is interesting to consider how such vacuoles could affect the CAP conduction velocity in the nerve.

The electrical disturbance of the action potential (AP) wave front, as it propagates down a given axon, serves to charge up the next downstream node of Ranvier to its threshold potential. At that point, the sodium voltage-gated channels at the node open, depolarizing the axon and sustaining the AP propagation. The physical parameters that dictate τ, the exponential time constant describing the charging at a node of Ranvier, are r_i (the longitudinal ohmic resistance to current flow in the axoplasm) and c_n (the nodal membrane capacitance), such that τ = r_i × c_n (40).

The CAP waveform is a summation of the APs arising from the entire ensemble of conducting axons within the nerve, with the larger-gauge axons conducting more rapidly than the finer-gauge axons (39). A proportional decrease in AP conduction velocity across the ensemble of axons would account for the broadening of the CAP waveform.

It is conceivable that the presence of ballooning submyelinic vacuoles, observed via EM (Fig. 3), exert enough mechanical force on the myelin sheath to subtly retract the paranodal myelin. If this were the case, it would serve to increase the nodal membrane capacitance, c_n. This would increase the nodal charging time constant, thus slowing down conduction of the AP at each node of Ranvier encountered along its path of propagation. Indeed, it has been reported that in perfused mouse sciatic nerves subjected to repetitive electrical stimulation (15 min × 200 Hz), the potassium channel-blocker, 4-aminopyridine (4-AP), is able to access K_v channels that are normally sequestered underneath the paranodal myelin (41). In unstimulated nerves, 4-AP does not have access to these normally concealed K_v channels (41).

While the presumed transient formation of submyelinic vacuoles may be related to the observed changes in nerve electrophysiology, it can be stated with certainty that repetitive electrical stimulation definitely produces microstructural alterations of the perfused nerve. This is clear from the diffusion data (both DTI and DBSI), but also from dynamic T₂ data.

The results from dynamic T₂ spectroscopy are intriguing and suggest that an increase in myelin water, which was uniformly observed for the electrically stimulated nerves, may be a feature worth investigating in other systems and in vivo. There is, additionally, a clear shrinkage of the ECS poststimulus, which is sustained throughout the observation period. Thus, dynamic T₂ spectroscopy could provide a complementary approach to noninvasively visualize structural changes associated with electrical activity in WM or PNS. Our measurements, which used nonlocalized Carr–Purcell–Meiboom–Gill (CPMG) echoes, are less demanding than in vivo imaging-mode implementation of dynamic myelin-water assessment. The correlations between the T₂ axonal water fraction and the DBSI-restricted fraction are very interesting. However, without application of exogenous T₂ relaxation agents, these correlations will not be amenable to studies in CNS, since T₂ axonal and extracellular fractions are distinctly separated only in PNS tissue.

The excellent review article by Rash outlines an extensive body of literature that describes the biophysical mechanism that could account for the microstructural changes observed in the present work (42). Namely, the K⁺ voltage-gated channels, which open up to allow egress of potassium ions from the axon during the repolarization step of AP conduction, are localized to the submyelinic axonal membrane. In the bullfrog sciatic nerve, these K_v channels are known to be distributed along the length of the internodal axonal membrane (43). Repetitive electrical activity in myelinated axons then results in an accumulation of K⁺ and its osmotically associated water in this confined space. The stimulation-induced submyelinic vacuoles observed via EM and transient poststimulus DBSI-restricted diffusion signal component suggest that this interpretation is correct in the perfused frog sciatic nerve model system.

The present diffusion fMRI results highlight some important differences between the perfused frog sciatic nerve and our earlier in vivo mouse optic nerve studies. For instance, in the optic nerve diffusion fMRI studies, there was no observable change in the axial diffusivity with repetitive axonal activation (22). And while in the mouse optic nerve the observable diffusion fMRI response in ΔADC_⊥ was rapidly reversible (22, 23), in the perfused frog sciatic nerve, Δλ_⊥ is not. It is recognized that the perfused sciatic nerve requires a rather vigorous electrical stimulation to achieve a smaller relative Δλ_⊥ than was seen in ΔADC_⊥ for the in vivo mouse optic nerve.

Some of these differences must arise from the markedly different tissue geometry in the two nerves. For instance, the ECS in the frog sciatic nerve tissue accounts for at least 50% of the total water content of the frog sciatic nerve, based upon T₂ spectroscopy measurements; hence, the axonal packing density is reduced in the frog PNS tissue compared with mouse CNS. A rule of thumb is that the ECS typically accounts for 20% of tissue volume in the normal CNS. Thus, a shift of water out of the ECS would be expected to have a larger impact on the overall diffusion characteristics in the mouse CNS. The demand for highly interconnected neurons in the CNS of higher organisms is often cited as the selective pressure that spurred the evolutionary development of dense packing and smaller gauge axons in CNS tissue. Typical mouse optic nerve axons are on the order of 1 μm in diameter and are uniformly myelinated in healthy tissue. In addition to very small unmyelinated axons, the frog PNS contains myelinated axons with a distribution of outer diameters whose upper limit is ∼16 μm (39).

There are other important differences between mouse optic nerve and frog sciatic nerve, when considering the myelin itself. The larger PNS axons tend to be blanketed by very thick myelin wrapping, sometimes >100 layers deep, whereas for the smaller axons in the CNS, fewer total layers of myelin are the rule. Additionally, the internodal spacing in mouse optic nerve is much shorter [138 μm, on average (44)] than that in frog sciatic nerve axons [wherein it ranges up to 1.5 mm (39)].

Experiments with perfused frog sciatic nerves are less technically demanding than perfused mouse optic nerves would be, due to the very robust nature of the frog nerve tissue and its larger size. Studies with perfused mouse optic nerves, including in animal models of optic neuritis and/or trauma, are a natural next step for mechanistic exploration in the mammalian CNS.

Finally, we consider the generality of the diffusion fMRI approach used here, for instance, as applied to other systems to detect WM activation or using other imaging sequences [e.g., echo-planar diffusion-weighted imaging (DW-EPI)]. In the present case, the system under study is relatively simple—a single coherent fiber orientation without crossing fibers. For samples with this type of tissue geometry, the 25-direction DW acquisition scheme has been shown to provide DBSI modeling results (fiber fractions, diffusivities, and isotropic diffusion components) in good agreement with those obtained using a more extensive 99-direction diffusion-weighting scheme when tested with nerve + gel phantoms (45). It remains to be seen whether a 25-direction diffusion scheme may be applied in samples with crossing fibers.

As became evident in the course of the present study, comparing Figs. 1 and 2 with those in the SI Appendix, Figs. S4 and S5, a higher spatial resolution yields better results, as it reduces undesirable effects of the Gibb’s ringing phenomenon, which can be amplified in derived parametric maps (36).

Regarding the imaging sequence, the DW imaging data presented here were acquired by using a multiecho spin-echo sequence. The principal advantage of this sequence, as opposed to faster DW-EPI, is that the data are clear of image distortions that often accompany the extended echo-train length in EPI sequences (46). In our case, the higher temporal resolution afforded by the DW-EPI sequence would have been preferable (allowing more extensive signal averaging and/or diffusion directions), but the DW-EPI sequence implemented on the small-animal imaging system that was available for this study performs suboptimally at the desired spatial resolution (the 64 × 64 image data are acquired at 109 μm in-plane resolution before zero-filling).

Another key difference this choice of sequence introduces is in the minimum achievable echo time. The EPI sequences have longer echo times than their spin-echo analogs. However, MRI gradient hardware capabilities also play a key role in determining the minimum echo time. When considering a shift from small-animal MRI systems to clinical MRI scanners, the smaller maximum gradient amplitude (G_max) achievable on clinical systems means that differences in echo time are further exaggerated (for the small-animal MRI system used in this study, G_max = 58 G/cm). With this hardware and higher spatial resolution, the minimum echo time was 28.8 ms. By comparison, current clinical DW-MRI data acquired with a DW-EPI using state-of-the-art hardware like that used in the Human Connectome Project has TE = 57 ms, which has G_max = 10 G/cm (47, 48). For the same targeted b value, the lower G_max on clinical systems dictates that the diffusion-weighting gradient waveforms require a longer time to play out to achieve the desired level of diffusion weighting. Thus, as evidenced by the T₂ spectroscopy data (Fig. 5A), the imaging echo time can sensitize the DW measurement to water in particular tissue compartments. Ignoring field-strength dependence of T₂ in neuronal tissue [T₂ is longer at lower B_o (49)], the 57-ms echo time would slightly tune the measurement sensitivity toward the longer-T₂ intracellular water component in PNS. The shorter T₂ of extracellular water in PNS tissue has been suggested to arise from efficient relaxation of transverse magnetization facilitated by the ubiquitous presence of collagen fibers (30). Because of the longer T₂ at clinical field strengths, the shift toward longer echo times may have a minor effect. In CNS, intracellular and extracellular water exhibit the same T₂, so any TE-dependent tuning of the diffusing water population under study should be absent. For both the clinical and small-animal diffusion MRI cases considered, the contribution of myelin water to the measurement is minimal because of its short T₂.

Our findings suggest that redistribution of tissue water plays a crucial role in the observed diffusion fMRI signal changes. The dynamic T₂ measurements detect increased myelin water content, suggesting the possible loosening of myelin sheath with repetitive electrical stimulation as well as a shrinkage of the ECS and increased axonal water fraction. These microenvironmental alterations were likely also present in the reported in vivo diffusion fMRI studies of mouse optic nerves (22, 23). Repeating the present study using perfused mouse optic nerve will definitively address the impact of myelin structural alteration on diffusion fMRI signal changes. Diffusion fMRI of myelinated axonal pathways may be an avenue worth exploring further in other experimental animal model systems and in human subjects.

Materials and Methods

All experiments were carried out using protocols approved by the Washington University School of Medicine’s Institutional Animal Care and Use Committee. Jumbo bullfrogs (Rana catesbeiana) were purchased from Rana Ranch and housed in a climate-controlled environment with a 12-/12-h light/dark cycle. The animal housing consisted of a standard clear plastic container [18″(l) × 10″(w) × 10″(h)] holding 1.5 L of water and tipped at an angle to provide a dry area within the cage. Frogs were fed pelleted chow (5LP3; Lab Diet) three times per week.

Ex Vivo Nerves.

Frogs were anesthetized in a solution of tricaine methanesulfonate (Sigma-Aldrich) at a concentration of 0.5 g/L in dechlorinated tap water with pH adjusted to 7.4. Once immobilized, frogs were decapitated and pithed. After removal of the skin, the body was pinned into a dissecting tray and a 4- to 5-cm segment of the sciatic nerve was dissected from the lower back to just proximal to its branching into peroneal and tibial nerves. During dissection, the surgical field was irrigated frequently with frog Ringer’s solution without glucose (see below) to maintain tissue moisture content. After gently debriding fat and surrounding connective tissue from the sciatic nerve, the nerve segment was tied off first at the proximal and then at the distal end with 2-0 silk suture and cut out. Twitching of the gastrocnemius muscle upon tying off the nerve at the proximal end served as a verification that the sciatic nerve had not been damaged during the dissection procedure. Once dissected, the tied-off nerve was placed in a Petri dish of oxygenated frog Ringer’s solution containing glucose at room temperature.

Frog Ringer’s Solution.

The frog Ringer’s solution recipe used was intended to match the ionic composition and osmolarity of R. catesbeiana blood as nearly as possible, although the chloride concentration was higher in our Ringer’s recipe than bullfrog blood in situ (50). Frog Ringer’s solution with glucose contained 100 mM Na⁺, 2.6 mM K⁺, 99.6 mM Cl⁻, 1 mM Mg²⁺, 1 mM Ca²⁺, 1 mM SO₄²⁻, 2.5 mM HPO₄²⁻, and 2 mM glucose, pH adjusted to 7.4. The glucose-free Ringer’s solution used for tissue irrigation during dissection was the same, except for the omission of glucose and the addition of an extra 1 mmol/L NaCl to maintain the same solution osmolarity. The frog Ringer’s solution used in perfused nerve experiments was oxygenated by heating the solution to 55 °C to displace any inert dissolved gases, and then the solution was bubbled with O₂ via a submerged gas-dispersion tube at a rate of 2 L/min during the time required for the solution temperature to drop to 30 °C (>1 h). Further thermal equilibration to room temperature occurred without bubbling of the solution. The solution, thus oxygen-saturated at 30 °C, contained ∼1.15 μmol/mL dissolved O₂ (51). In the case of perfused Rana pipiens sciatic nerves undergoing 100-Hz electrical stimulation at 20 °C, oxygen consumption by the nerve tissue has been reported to increase to 1.15 μmol O₂/h⋅g wet weight (27). The typical fresh jumbo bullfrog sciatic nerve weighs ∼15 mg/cm length. Assuming approximately similar O₂ consumption in R. catesbeiana sciatic nerve with electrical activity, at a perfusate flow rate of 3 mL/h, the oxygen supply (3.5 μmol O₂/h) would well exceed the tissue oxygen requirement of the perfused nerve (∼0.07 μmol O₂/h) with the most vigorous electrical stimulation frequency employed in this study.

Electrophysiology Flow Cell for MRI.

A perfusion flow cell was constructed from readily available materials, holding the excised nerve immobilized at the two ends with retractable suction electrodes used for electrical stimulation and recording of the CAP (SI Appendix, Fig. S1). The construction of the flow cell allowed the nerve to be drawn into the perfusion apparatus without air bubbles and the electrodes to be separated by a distance corresponding to the nerve’s native length (estimated by measuring the length of the extracted nerve tissue under the straightening-force of gravity on its own weight, ∼60 mg). Several minutes before drawing the nerve into the flow cell, fresh cuts were made at the ends of the nerve to remove the sutures. The cut nerve end would be expected to rapidly heal in Ca²⁺-containing frog Ringer’s solution (52). Once positioned into the flow cell, nerves were continuously perfused with oxygenated frog Ringer’s solution at a rate of 3.0 mL/h. The nerve was allowed 1–2 h of quiescent perfusion before the start of the MRI measurement series.

Electrical Stimulation and CAP Recording.

Electrical stimulation was delivered as 100-μs voltage pulses from a pulse/function generator (model 33210A; Agilent Technologies) into an analog stimulus isolation unit (model 2200; A-M Systems). The DC stimulus/CAP signals were carried to/from the magnet via shielded triax cables. Suction electrodes were used for nerve stimulation and CAP recording (53). In earlier experiments in this study, stimulus artifacts interfered with reliable recording of the full CAP waveform. However, in the later studies, placement of the recording amplifier grounding electrode in close proximity to the tip of the stimulating electrode was found to significantly reduce this interference (54). The CAP signal was amplified (1,000×) and filtered (high-pass cutoff, 160 Hz; low-pass cutoff, 20 kHz) via a home-built two-stage amplifier (55) before passing to a digital oscilloscope (model TBS1052B; Tektronix) for signal averaging (128 averages). The signal-averaged CAP waveform was ported to a laptop PC and saved for offline processing and analysis.

For one set of the nerves studied (the diffusion fMRI studies carried out with 40-min temporal resolution; see MRI for details), the electrical stimulation consisted of supermaximal stimulation delivered at 100-Hz frequency for a period of 40 min. In the other set of nerves (SI Appendix), imaged with 20-min temporal resolution, the nerves were stimulated first at 50 Hz × 24 min, followed by a resting period of 3 h, before undergoing a second round of electrical stimulus 100 Hz × 24 min. Three perfused nerves (SI Appendix) underwent imaging without electrical stimulation.

MRI.

MRI measurements were carried out in a 4.7-Tesla Agilent small-animal imaging system using home-built radiofrequency (RF) coils for signal transmit/receive.

Two sets of image studies.

The RF coil setup was modified during the course of these investigations. An actively decoupled transmit/receive coil pair was employed in the earlier studies (32 × 32 image matrix, 20-min temporal resolution) with a Helmholtz transmit coil and hemicylindrical surface receive coil for signal detection. For the subsequent studies, with higher spatial resolution (64 × 64 image matrix, 40-min temporal resolution), a single transmit/receive coil was used (SI Appendix, Fig. S1). Both RF coils provided comparable SNR. In the case of the higher spatial resolution imaging data, at the time point just before stimulation, the maximal SNR, with b = 0.12 ms/μm², was 104 ± 12 [mean ± SD, range: 81–134, n = 42 (seven slices from each of six nerves)]. The lowest SNR observed from the same ROIs was 7.6 ± 2.3 (range: 4.3–16.4).

As noted above, modification of the recording electrode in the later studies allowed for collection of improved electrophysiology data. Interleaved T₂ spectroscopy measurements were also introduced in the later studies. Thus, the later studies provided a richer dataset. The time-course data from the earlier studies (32 × 32 image matrix, 20-min temporal resolution) are presented in SI Appendix. For three perfusion-only nerves (no electrical stimulation), image data were acquired first with a 64 × 64 image matrix and then with a 32 × 32 image matrix (20-min temporal resolution) for the remainder of the time-course study. This provided a means to compare results obtained with the two different spatial resolutions.

Diffusion fMRI.

Diffusion fMRI data were acquired with a multiecho DW-EPI sequence (56). Acquisition parameters included TR = 1.5 s, three echoes (TE₁ = 28.8 ms, TE₂ = 8.3 ms). A maximum diffusion-weighting b value of 3 ms/μm² was employed with a 25-direction diffusion-encoding scheme and diffusion timings Δ = 18 ms, δ = 5 ms. A 1.5-mm slice thickness with a 0.5-mm gap between slices was used. The imaging field-of-view was 7 × 7 mm² with an acquisition matrix size of 32 × 32 (20 min per image) or 64 × 64 (40 min per image). The 25-direction icosahedral gradient scheme employed consisted of 25 b values, each with unique directions and amplitudes ranging, in our case, from 0.12 to 2.8 ms/μm² in increments of ∼0.1 ms/μm². The unit vectors describing the orientation of the 25 diffusion-encoding directions were uniformly distributed over a sphere subject to the constraint of icosahedral symmetry (57). This 25-direction diffusion scheme was first implemented by Kroenke et al. (58). The diffusion gradient directions are provided in SI Appendix, Table S1. For samples consisting of a single fiber orientation, the 25-direction diffusion scheme has been shown to yield DBSI results similar to those obtained by a more extensive 99-direction diffusion scheme (45).

CPMG multiecho acquisition (T₂ relaxation spectra).

In this nonlocalized spectroscopy experiment, trains of 4,096 echoes were acquired with 1-ms interecho spacing. A repetition time of 20 s was used between the start of consecutive echo trains, and data from 16 echo trains were averaged; thus, the total measurement time was 5.3 min.

MRI Data Acquisition Timeline.

The 64 × 64 data acquisition.

After setup in the magnet and verifying electrical activity of the perfused nerve, a baseline diffusion MRI scan was acquired. After this initial baseline scan, a series of interleaved diffusion MRI (40 min) and T₂ spectroscopy (5.3 min) acquisitions was initiated, with two more baseline diffusion MRI scans acquired before stimulation. The second T₂ spectroscopy dataset was acquired just before commencement of repetitive electrical stimulation (100 Hz × 40 min). One diffusion dataset was acquired during application of repetitive electrical stimulation. Upon completion of electrical stimulation, the interleaved T₂ and diffusion MRI acquisitions continued. Measurements terminated at 5 h after the start of electrical stimulation.

Conduction blockage demonstration.

As a demonstration of the concept that diffusion fMRI may be used to visualize axonal conduction blockage, we prepared a perfused frog sciatic nerve tied off in the center with three sutures (Fig. 8A). In this demo system, the ligation of the nerve served as a surrogate model for a WM lesion or nerve crush, as might be encountered in various clinical situations. Two types of diffusion MR images of the perfused nerve were acquired before and after applying electrical stimulation to the proximal end of the nerve (100 Hz × 65 min). One image set consisted of six axial slices through the nerve (three proximal to the conduction blockage and three distal to the sutures/conduction blockage; Fig. 8C) acquired with 25-direction diffusion weighting.

MRI Data Analysis.

DBSI analysis.

Raw k-space image data were multiplied by a Hamming window filter before zero-filling to a 128 × 128 matrix and denoising (59), with signal-averaging of the three acquired echoes (56). The resulting image data were then analyzed via the DBSI package (60) developed in-house and running in Matlab (Version 2015b; MathWorks). The 25-direction DW signal (k: 1–25) was modeled as contributions from a basis set of anisotropic, cylindrically symmetric diffusion tensors (i: 1 – N_Aniso) with axial and radial diffusivities (λ_||,i and λ_⊥,i, respectively) and a spectrum of isotropic diffusion with amplitude f(D) at diffusivity D, as in Eq. 1.

$$S_k={\displaystyle \sum _{i=1}^{N_{Aniso}}}{f}_i\cdot e^{-\left|\overrightarrow{b_k}\right|\cdot {\lambda }_{\perp ,i}}\cdot e^{-\left|\overrightarrow{b_k}\right|\cdot \left({\lambda }_{\parallel ,i}-{\lambda }_{\perp ,i}\right)\cdot co{s}^2{\psi }_{i,k}}+{\displaystyle \underset{a}{\overset{b}{\int }}}f\left(D\right)\cdot e^{-\left|\overrightarrow{b_k}\right|\cdot D}\cdot dD.$$ [1]

Since the frog sciatic nerve is composed of a single, coherent axonal fiber bundle (i.e., no crossing fibers), the anisotropic modeling was simplified as a single anisotropic tensor (N_Aniso = 1), referred to as the fiber component (f_fiber). The isotropic spectral components were differentiated based upon diffusivity and denoted as restricted (0 < D_R ≤ 0.3 μm²/ms), hindered, (0.3 < D_H ≤ 2.0 μm²/ms), or free (D > 2.0 μm²/ms). The DBSI diffusion model is depicted in a pictorial schematic in SI Appendix, Fig. S2. A further description of the DBSI code execution is provided in documentation provided at https://osf.io/39n4c/. By converting DICOM-formatted images to nifti format (see the DBSI Manual available at the above-referenced URL), readers may perform DBSI modeling of their own data regardless of MRI vendor.

Voxel-wise prescriptions of ROIs for analysis for a given nerve at a given imaging time point were based solely on the DBSI f_fiber parameter map. Contiguous imaging voxels within each slice that satisfied the cutoff f_fiber ≥ 0.67 were included in the nerve ROI. The nerve ROIs, prescribed in this manner and outlined by using ITK-Snap software [Version 3.6.0, University of Pennsylvania (61)] were saved, and the average diffusion parameter values in the nerve ROI for each slice were extracted from the DTI and DBSI parameter image maps by using an in-house script running in Python (Version 2.7; https://www.python.org/).

DTI analysis.

Diffusion tensor analysis of the same 25-direction DW imaging datasets was also performed. In the DTI analysis, the diffusion data were fit to a single tensor by using the linear least-squares regression approach first outlined by Basser et al. (21) and modified to not require a b = 0 ms/μm² to estimate signal intensity (the lowest diffusion-weighting employed was b = 0.12 ms/μm²).

Goodness of fit and CV analysis.

Rokem et al. (62) implemented CV as a means to evaluate model accuracy and compare performance of two different diffusion models. Choosing a 3 × 3 voxel ROI in the center of each nerve, we assessed test–retest reliability for the six nerves that underwent 100-Hz × 40-min electrical stimulation. The test–retest reproducibility (quantified in terms of an R²) was compared with the ability of the relevant model fit (DBSI or DTI) to the first measured dataset to predict the second, independent dataset (R²_CV-Model). For the purposes of CV, two prestimulus baseline time points were used (the second and third time points in Figs. 1 and 2) since the diffusion signal was not evolving in time, as it did in the poststimulus period. The goodness of fit (R²) for each of the models across time was also determined to verify that the models performed consistently by this measure as the diffusion signal evolved poststimulation.

T₂ spectral analysis.

CPMG echo data were decomposed into T₂ spectral components via nonnegative least-squares fitting (NNLS) with a first-derivative smoothing term (33). In this approach, echo-decay data were assumed to be described by an equation of the form:

$$y_i={\displaystyle \sum _{j=1}^M}{s}_j\cdot e^{-t_i/T_{2,j}};\hspace{1em}i=\mathrm{1,2},\dots ,N.$$ [2]

For the T₂ spectral analysis, n = 4,068 echoes was used (t_i: 8–4,076 ms), and the spectrum was calculated as the set of amplitudes (s_j) at M = 1,001 log-spaced T₂ grid points (T_2,j: 2–5,000 ms), minimizing the least-squares misfit subject to the first-derivative smoothing constraint. The extent of smoothing employed for each dataset (coefficient μ; ref. 33) was determined based upon the F statistic for the sum of squares of the data/model misfit compared with the misfit with no smoothing term applied (μ = 0) (63). The value of μ employed for the final accepted T₂ spectral modeling was the minimum value which resulted in P < 0.10. This statistical threshold was found to produce consistent results for estimated T₂ and component amplitudes among independent datasets and values similar to those reported in the literature for ex vivo sciatic nerves of various frog species (28, 30, 31). In PNS tissue, three T₂ decay components were observable (28–32), which were attributed to myelin water (T₂ < 30 ms), extracellular water (T₂ ∼ 50–100 ms), and intracellular water (T₂ ∼ 200 ms).

Stimulation Fixation and EM.

We excised the two sciatic nerves of a single bullfrog and assembled the nerves in separate perfusion flow cells on the benchtop. One of the nerves was stimulated for 40 min × 100 Hz (as in the in-magnet diffusion fMRI studies) and perfusion-fixed immediately at the end of the stimulation period. The other nerve rested and was perfusion-fixed at the same time as the stimulation-fixed nerve.

The fixative used for perfusion fixation contained 2% glutaraldehyde, 2 mM calcium acetate, and 20 mM sodium cacodylate. After 1 h in fixative at room temperature, the nerve-containing fixative solution was transferred to a refrigerator and stored at 4 °C for a total of 12 h. After fixation, the nerve tissue was diced into 3-mm segments and rinsed in 0.10 M cacodylate buffer at pH 7.4 with 2 mM calcium chloride three times for 10 min each time. Samples were then subjected to a secondary fixation step for 1 h in 1% osmium tetroxide/1.5% potassium ferrocyanide in cacodylate buffer. Subsequently, samples were rinsed in 0.10 M maleate buffer at pH 6.0 three times for 10 min per rinse and en bloc-stained for 1 h with 1% uranyl acetate in maleate buffer. At the completion of staining, samples were briefly washed in ultrapure water, dehydrated in a graded acetone series (50%, 70%, 90%, and 100% ×2) for 10 min each step, infiltrated with microwave assistance (Pelco BioWave Pro) into LX112 resin, and flat-embedded in a silicone mold to orient the nerve segment for cross-sectioning. Samples were cured in an oven at 60 °C for 48 h. Once the resin was cured, 70-nm thin sections were taken. TEM imaging was performed at 80 keV by using a JEOL JEM-1400 Plus microscope. From two cross-sectional specimens (one from the stimulation-fixed and one from the rested-fixed sample), EM images of individual axons were acquired at high magnification (1,500× to 15,000×, depending on the size of the axon). A total of 118 images of rested axons and 88 images of stimulation-fixed axons were acquired.

EM image segmentation.

Initially, images of 55 stimulated and 57 rested axons were segmented manually by one of the investigators to define the cross-sectional area occupied by myelin, axoplasm, and periaxonal vacuole for each axon. Over concern of rater bias in the results, images were randomized and assigned for semiautomatic segmentation by two individual raters blinded to the type of axon appearing in each image. The semiautomatic segmentation code written in-house in Matlab involved marking seed regions in myelin, axon, and regions considered to be vacuole in each image. The semiautomatic segmentation algorithm is described in SI Appendix.

Statistics.

Statistical tests were performed by using Statistica (Version 13.3; Tibco Software, Inc.). The distribution of submyelinic vacuole radii in stimulation-fixed vs. rested-fixed frog nerve axons, which follow approximately exponential distributions, were compared via the Cox–Mantel test within the Survival and Failure Time Analysis Module of Statistica. Reliability of EM segmentation [manual (nonblinded) vs. semiautomatic (blinded)] was assessed based upon the estimated total vacuole cross-sectional areas (in μm²) from each method. Total vacuole cross-sectional areas in each image were assigned to one of 11 bins (0–30 μm², scored from 0 to 10), and interrater agreement using these scores was determined via Statistica’s Attribute Agreement Analysis. For linear correlations among dynamic T₂ spectroscopy, diffusion fMRI, and electrophysiology measures of nerve response, P < 0.05 was taken as the threshold for statistical significance. Repeated-measures ANOVA with Tukey post hoc testing was used to identify the time point at which diffusion MRI parameters differed from prestimulus values in the time-course diffusion fMRI data.

Data Availability.

The executable DBSI analysis code, T₂ NNLS fitting code, and semiautomatic segmentation code are available for download (https://osf.io/39n4c/). The frog nerve data, MRI, and EM presented here are also available at this site.