Abstract
The production of particles with shape-specific properties is reliant upon the separation of micro-/nanoparticles of particular shapes from particle mixtures of similar volumes. However, compared to a large number of size-based particle separation methods, shape-based separation methods have not been adequately explored. We review various up-to-date approaches to shape-based separation of rigid micro-/nanoparticles in liquid phases including size exclusion chromatography, field flow fractionation, deterministic lateral displacement, inertial focusing, electrophoresis, magnetophoresis, self-assembly precipitation, and centrifugation. We discuss separation mechanisms by classifying them as either changes in surface interactions or extensions of size-based separation. The latter includes geometric restrictions and shape-dependent transport properties.
I. INTRODUCTION
The need for novel techniques to separate particles based on shape has recently received increased attention due to the developing applications of particularly shaped micro/nanoparticles. Shape-dependent physico-chemical properties of metal nanoparticles have recently been studied for solar energy storage (Hoggard et al., 2013) as well as biomedical applications including cell imaging and cancer treatment (Sharma et al., 2009a; 2009b), while polystyrene rods have been studied for improved efficiency in drug delivery (Barua et al., 2013 and Thompson et al., 2013). Cell sorting by shape has been an important technique for enhancing biofuel production (Velmurugan et al., 2014), and the shapes of cells have been used to determine their growth state as well as being early indicators of disease (Mitragotri and Lahann, 2009). Particles with desired shapes necessary for these applications can be synthesized in a variety of methods; however, purification is often required. For example, the most popular approach to gold nanoparticle production today is the one-pot approach first documented by Michael Faraday in 1856 (Liz-Marzán et al., 2015 and Yang et al., 2017). While this approach is widely popular due to its simplicity, products often contain a wide range of nanoparticle shapes and sizes. While the size dispersity of the product can be reduced via centrifuging, the separation of nanoparticles solely by shape is a more complex matter. Therefore, the ability to reliably separate nanoparticles ranging from nanorods to living cells based on their shapes alone will prove a critical tool in the advancement of a variety of technologies.
Despite the importance of the shape-based particle separation, its studies and development are still largely unexplored compared to those of size-based particle separations (Lenshof and Laurell, 2010; Kowalczyk et al., 2011; and Sajeesh and Sen, 2014). We review various approaches employed for shape-based separation including chromatography, microfluidic devices, electrophoresis, magnetophoresis, and centrifugation. Note here that our review focuses on micro-/nanoscale separations of rigid particles in liquid phases. Therefore, we exclude shape-separation processes of powders or particles with larger than microscale size (>10 μm), such as microsieves (Furuuchi et al., 1993), cyclones (Niazi et al., 2017), and other powder separation processes (Furuuchi and Gotoh, 1992). Approaches with differential mobility analyzers (Beranek et al., 2012), where particles are dispersed in a gas phase, are also excluded. Interesting shape-dependent particle dynamics are reported, such as the self-steering motion of rigidly connected disks in microfluidic channels (Upsal et al., 2013), Brownian motion of boomerang-shaped particles (Chakrabarty et al., 2013), and rod migration toward the center of rotating flows (Park and Butler, 2010). However, we focus on methods applied in actual separation devices.
The purpose of this review is not only to summarize various shape-based separation methods, but also to identify the principles of shape-based separations from size-based separations to shed some light on how particularly shaped samples can be obtained. We give an overview of the current shape-based separation approaches in terms of separation mechanisms (Sec. II) and review methods falling into the categories of chromatographic approaches (Sec. III), microfluidic approaches (Sec. IV), electrophoresis/magnetophoresis (Sec. V), and precipitation/centrifugation approaches (Sec. VI).
II. OVERVIEW OF SHAPE-BASED SEPARATION APPROACHES
In our opinion, one issue of the current shape-based separation methods is that there is no general approach: One successful method for a specific condition may be found by trial and error but is often not developed into a model to design other methods. Here, we propose a perspective to generalize the current methods. We classify the shape separation mechanisms into (1) changes in surface interactions and (2) shape-specific extensions of a size separation. The former applies to size exclusion chromatography (SEC), electrophoresis, and self-assembly precipitation, while the latter corresponds to the rest of the current shape separations. The separation mechanism for a size separation is typically based on either the geometric restriction of the device or a difference in size-dependent particle transport properties, which assume particles are spherical. However, if the particle is non-spherical, the properties become more complicated. For example, the diffusivity of a spherical particle can be estimated as a scalar value using the Stokes-Einstein law, while the diffusivity of a non-spherical particle has different values according to its orientation and must be estimated in a tensor form. Therefore, multiple length scales and orientations of non-spherical particles must be considered in shape-based separation.
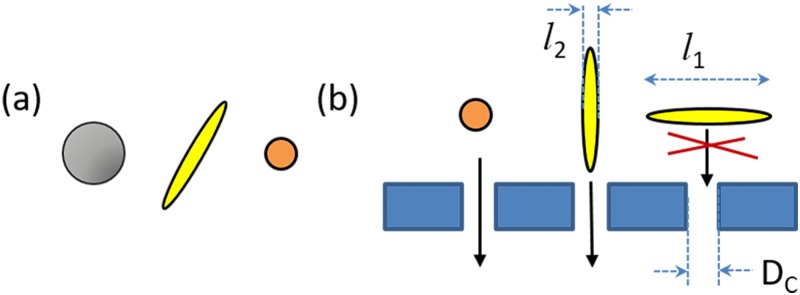
As seen in Fig. 1(a), particles with different shapes often have different sizes. The equivalent radius, req, of a particle is defined as the radius of a spherical particle with the same volume. In Fig. 1(a), the req of the axisymmetric rod-like particle is the same as that of the smaller spherical particle. If the req of particles is considerably different, the separation is practically made by size and is often confused with shape separation. However, if the particles have a similar req and therefore similar volume, as in cetyltrimethylammonium bromide (CTAB) gold nanoparticle synthesis, separation by size is no longer possible. Comparing the geometries of spherical and non-spherical particles, as in Fig. 1(b), a sphere has only one length scale, a diameter or a radius, whereas non-spherical particles have multiple length scales: ln, where n is the number of length scales of a particle. For example, axisymmetric rod-like particles have two length scales: a length of the principal axis, l1 and a thickness, l2. Consider a hypothetical separation device with a critical length scale of DC, where DC is the threshold length scale which is determined by the device geometry and operating condition. If a sphere and a rod with req < DC were placed in this device, the sphere would pass through, while the rod would only pass depending upon its geometry. If the rod has l1 > DC and l2 < DC, the rod may have req < DC but could still be oriented to be caught by the filter. Note that Fig. 1 is a simplified example of such a device. Therefore, the actual dimension involved in the separation may not be exactly l1 or l2 due to flow condition and Brownian rotation. However, this example still shows that the inherent differences between shapes are the key to both their unique properties and to their separation.
FIG. 1.
(a) The volume of the left spherical particle is larger than that of the rod-like particle, which is equivalent to that of the right spherical particle. (b) Schematic representation of a hypothetical shape separation device which separates particles by a critical length scale of DC. Whereas a spherical particle can pass through the device as long as its req < DC, a non-spherical particle has multiple lengths scales and can only pass through with the proper orientation.
Before reviewing each method, we define some common variables: L is a rods length (l1), d is a rods thickness (l2), and Ar = L/d is a rods aspect ratio.
III. CHROMATOGRAPHY
A. Size exclusion chromatography
Size exclusion chromatography (SEC) is a chromatographic technique used to determine the molecular weights of substances suspended in solution. SEC uses the pores of the preferred stationary phase as the mechanism of separation. As the mobile phase flows through a column packed with the stationary phase, the smaller, lighter molecules flow through the pores uninhibited and the larger, heavier molecules travel through the packing with resistance. The longer path of the smaller molecules allows the larger molecules to elute quicker, which causes an effective separation (Barth et al., 1994).
SEC is best known for its use in separating particles by size; however, one study performed by Wei et al. (1999) used SEC to separate particles by shape as well as by size. The separation of gold nanorods, with a mean L = 46.6 nm and mean Ar = 4.8, and gold spherical particles, with a mean diameter of 19.3 nm (the volume of the sphere is 1.09 times larger than that of the rod), was achieved by adding a mixed-surfactant system containing sodium dodecyl sulfate (SDS) and poluoxyethylene (23) dodecanol (Brij-35) in the eluent. The SDS surfactant affected how the nanoparticles adsorbed onto the column packing materials, limiting the loss of nanoparticles to the packing. It is possible that when enough SDS is introduced to the gold nanoparticles and packing material, both surfaces induce a negative charge to their respective surface. The surfaces are then electrostatically repulsed by one another and no adsorption can occur. Nanorods have a larger contact, or surface, area than spheres, and therefore would be more effectively repelled from the column packing materials with the same surface charge. Consequently, nanorods elute earlier than spherical particles. Wei et al. (1999) also showed that using just SDS as an eluent does not separate the shapes effectively. Instead, using a mixture of SDS and Brij-35 enables low adsorption onto the column packing, as well as a large separation between rods and spheres. This result suggests that SEC employed with the correct surfactants can separate differently shaped nanoparticles.
B. Field-flow fractionation
Field-flow fractionation (FFF) is a size-based particle/macromolecule separation technique in which a parabolic channel flow carrying mixed particles in the axial direction is exposed to a perpendicular, or cross-sectional, force as demonstrated in Fig. 2. According to the type of the cross-sectional force field, different acronyms are used to denote the fractionation such as FlFFF (flow field), SdFFF (sedimentation or centrifugation), EFFF (electric field), and many more. FlFFF is the most common type of fractionation and is further modified to AsFlFFF (Asymmetric FlFFF) for commercial processes (Schimpf et al., 2000 and Messauda et al., 2009).
FIG. 2.
Schematic diagram of the FFF device and the particle separation behaviors in the normal mode. Smaller spherical and rod-like particles have the same volume. Upward arrows represent the opposing transport process (particle diffusivity for the normal mode) to the cross-force field.
As demonstrated in Fig. 2, while an injected particle mixture flows in the channel, the cross-sectional particle distribution is determined by the competition between the cross-flow field, which pushes the particles toward the accumulation wall, the bottom of the channel, and the opposing transport process, resisting the cross-force field. The opposing transport process is varied by particle properties and flow condition, or “operation mode.” The most common mode is the “normal” mode where the opposing transport process is the particle diffusivity and smaller particles, having larger diffusivities, are distributed further from the accumulation wall. Because the axial flow has a parabolic velocity profile, particles with stronger opposing transport processes tend to be distributed to a higher velocity region, which results in faster elution. Therefore, understanding the various mechanisms that determine the cross-sectional particle distributions according to the operating mode is important (Schimpf et al., 2000). Theoretical models describing the shape effect of rod-like particles on the separation behaviors in FFF have been developed by a series of works by Park and Mittal in 2015, Park in 2014, and Alfi and Park in 2014, based on earlier works by Phelan and Bauer in 2009 and Beckett and Giddings in 1997. As suggested by Beckett and Giddings (1997) as well as Park and Mittal (2015), the condition for each mode is classified in terms of D⊥/U where U is the cross-flow rate and D⊥ is the rod diffusivity perpendicular to its main axis, approximated by slender-body theory (Batchelor, 1970):
| (1) |
Here, kB is the Boltzman constant, T is the absolute temperature in Kelvin, and η is the dynamic viscosity of the medium. The rod separation mechanism in each mode is summarized below.
The typical condition for a rod in normal mode is approximately 0.5 L < D⊥/U, where L is the length of the rod on its major axis. As mentioned in the previous paragraph, the difference in the particles diffusivity according to their size is the separation mechanism in this mode. However, when evaluating the diffusivity of a rod-like particle, the orientation of the rod relative to the direction of transport must be considered because the rods diffusivity is expressed in a tensor form as a function of its orientation. Additionally, the orientation of the rod is determined by both the shear of the axial flow and the Brownian rotation (Park, 2009). Therefore, the rods diffusivity should be expressed in terms of the average orientation which is a function of the Peclet number, Pe, a ratio between the shear rate and the rods rotational diffusivity (Alfi and Park, 2014). Chun et al. (2008) calculated the diffusivities of carbon nanotubes by estimating nanotubes as slender-bodies (Batchelor, 1970) aligned in the axial flow and compared the elution results of the carbon nanotubes with that of the spherical polystyrene particles with known sizes to determine the nanotube lengths. Alfi and Park (2014) calculated the rod diffusivity more accurately in terms of Pe by considering the average orientation of rods that were not perfectly aligned (Park, 2009). Based on that calculation, Park and Mittal (2015) showed that rods have lower diffusivity than spheres with the same volume and that the diffusivity values decrease with increasing Ar, which results in slower elution. However, those predictions also show that the elution order is more sensitive to size differences than differences in Ar. In other words, compared to a standard particle, the elution difference of a particle twice as large with the same Ar is comparable to the difference of a particle of standard size with an Ar of an order of magnitude larger as experimentally observed by Runyon et al. (2013).
In the steric mode, with typical conditions for a rod being D⊥/Ux < 0.5d, where d is the thickness of a rod, when the cross flow is relatively stronger, particles flow while rolling on the accumulation wall, as in Fig. 3(a). Therefore, the excluded volume effect is the opposing transport process and particles with a center-of-mass further from any wall can elute faster. As shown in Fig. 3(a), when comparing spherical particles of different sizes, larger spheres elute faster. Comparing a rod and a sphere of the same volume, the rod elutes later because the rods half thickness (0.5d) is smaller than the radius of the sphere (Phelan and Bauer, 2009).
FIG. 3.
Schematic diagram of each operating mode in FFF: All the rod-like particles have the same volume as that of the smaller spherical particles. (a) In the steric mode, d of a rod is involved in the separation mechanism. (b) For the steric-entropic mode, dashed arcs represent the unrestricted orientation distribution in bulk whereas the solid arc is the orientation distribution restricted by the wall. The ratio between the restricted orientation probability and the unrestricted bulk orientation probability controls the separation behavior. (c) In the lift-hyperlayer mode, shear-induced migration affects the separation.
The steric-entropic mode is a mechanism unique to non-spherical particles, which occurs between the steric and normal mode (0.5d < D⊥/Ux < 0.5L). Beckett and Giddings (1997) originally proposed this mode for rod-like and disk-like particles. As shown in Fig. 3(b), the orientation distribution of a particle in the near wall region, the region where a rods center-of-mass is less than 0.5L from a wall, is restricted by the excluded volume effect of the wall. As the bulk orientation distribution is restricted, the particle distribution is pushed away from the wall. As a result, rods with higher Ars and disks with larger diameters are predicted to elute faster. Gigault et al. (2013) observed that the elution of gold nanorods increased with the Ar of the rods; clay nanodisks elution was also found to confirm the proposed elution mechanism (Tadjiki and Beckett, 2018). The distance the particle distribution is pushed from the wall is calculated in terms of the steric factor, which is equivalent to the ratio between the allowed distribution restricted by the wall and the unrestricted distribution (Beckett and Giddings, 1997). Park and Mittal (2015) considered the rod orientation change due to the flow condition and the distance from a wall to improve this model. Park and Mittal (2015) also found that due to the size dependence of D⊥, the Ar-enhanced elution trend is not always possible, although the steric-entropic effect pushes more particles away from the wall. Later, Nguyen et al. (2015) observed that gold nanorods with higher Ars elute opposite to the Ar-enhanced elution trend. Monjezi et al. (submitted) extended the model by Park and Mittal (2015) to ellipsoidal rods, as the slender body model is only valid for high Ar rods, using more rigorous rod distribution calculations (Monjezi et al., 2018a; 2018b). This mechanism can qualitatively predict the experimentally observed trend that higher Ar rods elute faster regardless of size. However, for improving quantitative agreement in predictions, further development of the model considering the particle surface charge effect is suggested (Kim et al., 2012 and Kato et al., 2018).
Lastly, in the lift-hyperlayer operation mode, particles are separated by shear-induced lateral migration [see Fig. 3(c)]. Various migration mechanisms have been identified for this mode (Leighton and Acrivos, 1987; Agarwal et al., 1994; and Feng et al., 1994a; 1994b). Typically, if the axial flow rate is high enough to produce an inertial effect on the particles, larger particles experience a stronger migration effect and elute faster (Giddings, 1983). However, there is another shear-induced migration which is specific to rods in non-inertial flow conditions (Park et al., 2007 and Park and Butler, 2009). Alfi and Park (2014) predicted that rods with higher Ars migrate more and consequently elute faster in a high axial flow condition such as Pe > 100.
In summary, FFF has been experimentally applied for the shape-based separation of rod-like and disk-like particles. Theoretical models for the shape-based separation have been extensively studied, especially for rod-like particles. However, there are still limitations in quantitative agreement between model predictions and experimental data.
IV. MICROFLUIDIC DEVICES
A. Deterministic lateral displacement
Deterministic lateral displacement (DLD) has been applied for particle sorting based on shape, size (Huang et al., 2004), and deformability (Ghasemi et al., 2012). DLD is generally categorized as a passive method, i.e., the method is based on precisely designed microchannels and internal forces and not external forces (McGrath et al., 2014). However, external forces, e.g., electric (Liu, 2016) and gravitational (Jiang et al., 2015) forces, have been coupled with DLD in some studies.
A typical DLD device and its separation principle are demonstrated in Fig. 4. A DLD device is comprised of an array of micro-sized obstacles, or posts, arranged in several rows. Rows are offset from each other, so flow from previous rows always encounters obstacles in the current row. In most cases, there is a laminar flow between obstacles. Flow in the gap between obstacles can be divided into three streams. If in one row streams are named 1, 2, and 3, from left to right, in the next row they become 3, 1, and 2, respectively. After three rows, all streams are reunited into one in the same horizontal position as they began. Particles, based on their size, behave in different ways. For small particles that locate in one specific stream, the movement is the same as the streams, and after three rows, they are set in the same horizontal position. This kind of motion is called zigzag mode. Larger particles, which are unable to center in a stream, cannot return to their original horizontal positions (Huang et al., 2004). After several rows, larger particles will have migrated a considerable distance away from their original horizontal positions. This motion is called displacement mode. There is a critical diameter (DC) for separation in DLD devices. Particles with diameters larger than the DC will experience displacement mode, while particles with diameters smaller than the DC will experience zigzag mode. The migration angle of a particle is defined as the angle of its trajectory with respect to the direction of the entrance stream introduced to the DLD device. For effective separation, particles should have different migration angles so they exit from different outlets.
FIG. 4.
(a) Streams in the gap between obstacles do not mix with each other and reunite after three rows. Small particles follow the path of their stream. (b) Larger particles cannot follow streams back to their original horizontal position since their center cannot locate in first stream. Reproduced with permission from Science 304(5673), 987–990 (2004). Copyright 2004 The American Association for the Advancement of Science.
DLD has been utilized to separate particles based on their shapes including separating parasites from red blood cells (RBCs) (Holm et al., 2011), separating RBCs with different shapes (Beech et al., 2012), separating 3D printed particles with different shapes including spheres, tetrahedrons, cubes, and pyramids (Jiang et al., 2015), separating elliptical and cylindrical particles (Liu, 2016), and separating chiral particles (Bogunovic et al., 2012).
The shape separation mechanisms in DLD can be classified into two categories: Differences in the length scale involved in the separation and differences in transport properties. It is preferred that the largest length scale of a non-spherical particle is involved in the separation (Recall Fig.1(b) of Sect. II). This guarantees that the particle is in displacement mode and enables separation. Involving the largest length scale of a particle in the separation can be achieved through orientation control. In some studies, the orientation is controlled through particle confinement. Beech et al. (2012) used particle confinement to orient and sort RBCs with different shapes based on their involved length scales. In deep confined channels, non-spherical particles tend to be aligned and their smallest dimension is involved in the separation, while in shallow devices, the rotation of particles is limited and their largest length scale is involved. However, particle confinement does not always orientate rod and spiral-shaped particles as intended.
Orientation control can also be achieved through external forces. Liu (2016) separated elliptical and cylindrical particles using an electric field around the posts for orientation control. The elliptical particles have two initial orientations: long axis parallel to electric field and long axis perpendicular to the electric field, but, in either case, elliptical particles orientate with their long axis parallel to the electric field. In this condition, the electric field is more effective on circular particles than elliptical particles, so the elliptical particles act like smaller circular particles, enabling the separation.
Another approach is to use continuous rotation. Zeming et al. (2013) investigated separating RBCs using continuous rotation via I-shaped posts. In this study, the I-shaped posts destabilize flow and induce rotation in the particles on their smallest axes (Fig. 5). The authors believe that continuous rotation helps non-spherical particles emulate spherical particles based on their largest dimension and thus effects separation similar to size-based methods.
FIG. 5.
Posts induce continuous rotation for non-spherical particles. Non-spherical particles emulate spheres with diameters equal to their largest dimension. Reproduced with permission from Nat. Commun. 4, 1625 (2013). Copyright 2013 Springer Nature.
The second mechanism for shape separation in DLD is differences in transport properties. In contrast to previous approaches, this mechanism does not directly correlate separation with the size of the particles. Bogunovic et al. (2012) stated that particles with different chirality (L and Γ) have different transport properties. The separation is possible due to lift forces with opposite signs in the vorticity. However, this approach is still challenging in terms of adjusting parameters and final separation resolution. In some cases, the velocity profile of two enantiomers may be different but still indistinguishable, so the separation does not occur. Therefore, process parameters like lattice characteristics, migration angle, and laminar flow characteristics must be precisely selected so particles follow different trajectories.
Jiang et al. (2015) investigated the separation of particles of different shapes in gravity-driven deterministic lateral displacement (g-DLD). Separation in g-DLD is due to differences in particle-obstacle interactions (Devendra and Drazer, 2012). In this experiment, the fluid is stagnant, and particles are forced to move by changing the forcing angle θ: the angle between gravity and the array of posts. The critical forcing angle is the lowest angle in which the particles move and the migration angle α is greater than zero. A schematic of this experiment and a graph of the two angles are shown in Fig. 6. In this approach, cubes, spheres, and cylinders are separated from pyramids and tetrahedrons. However, the separation of cubes, spheres, and cylinders has a significantly lower resolution.
FIG. 6.
(Left) Schematic of g-DLD. At forcing angle (θ), red particles do not migrate, i.e., they are not in displacement mode, while blue particles have a migration angle of α. Thus, blue and red particles are separated at the outlet. (Right) Migration angle (α) vs forcing angle (θ) for different shapes. For small forcing angles, particles do not migrate (α = 0) and only move parallel to the columns, while forcing angles greater than the critical forcing angle (α > 0) cause particles to move across column obstacles. Reprinted with permission from Microfluid Nanofluidics 19(2), 427–434 (2015). Copyright 2015 Springer Berlin Heidelberg.
Particle behaviors and shape separation mechanisms in DLD devices can be better understood with the help of numerical modeling and simulations. Although they can also be used to predict future effective experimental designs, simulation results are either not validated through experiments or have significant deviation from experimental results. This disagreement can be due to neglected hydrodynamic interactions between particles and posts, deviation of experimental posts from the nominal shape, and imperfections of DLD device walls (Bogunovic et al., 2012).
B. Inertial focusing
Inertial focusing has been recently introduced as a method for microfluidic particle separation. This method has received a great deal of attention due to its simplicity, as it does not require an additional electric, magnetic, or thermal field. Microfluidic inertial focusing devices have already been investigated for a wide range of particle separation applications, such as enrichening biological cells (Nivedita and Papautsky, 2013 and Ozkumur et al., 2013), sorting and diagnosing DNA, and the separation of bacteria (Kim and Kim, 2016), viruses (Reece et al., 2016), and barcoded particles (Hur et al., 2011).
Interest in inertial focusing first began when randomly distributed particles were observed to focus at certain equilibrium distances from channel walls after traveling long distances in the axial direction (Segre, 1961 and Segré and Silberberg, 1962). Subsequent studies were conducted to understand this phenomenon (McLaughlin, 1993; Cherukat and McLaughlin, 1994; and Asmolov, 1999); however, it was not until recently, when lithography of microfluidic devices became feasible that inertial focusing found its place in particle sorting and separation.
Inertial focusing relies on net lift forces exerted on each individual particle. The equilibrium position of a particle in the channel is determined when the lateral forces on the particle known as lift forces are in balance. Generally, two major lift forces compete while particles are moving through a channel: the shear gradient and the wall lift forces. Shear gradient lift forces are present whenever the shear rate of the velocity field interacting with the particle surface varies with the position of the particle and force it away from the center of the velocity field. Wall lift forces are caused by fluid interactions between particles and adjacent walls. When particles are close to the channel walls, wall lift forces drive particles away from the interacting wall and toward the center of the channel (Feng et al., 1994a; 1994b). This phenomenon is illustrated in Fig. 7.
FIG. 7.
Schematic view of inertial focusing in a rectangular microchannel. (a) Two translational forces act on the spherical particle. is caused by the shear gradient and forces the particle away from the channel center. is the wall lift force and pushes the particle away from the wall. (b) Equilibrium positions of the particles are determined down the channel when the two lateral forces are in balance. (c) Fluorescent images of 20 μm diameter particles focusing at Re = 30 (100 μm wide × 27 μm high cross section). Reprinted with permission from Lab Chip 13, 1121–1132 (2013). Copyright 2013 Royal Society of Chemistry.
Microfluidic inertial focusing has been primarily studied and developed for size-based particle separation. Separation of particles based on particle shape is very challenging due to the anisotropic diffusional behavior of non-spherical particles, especially when particles have similar volumes. Studies have been conducted on separating particles based on combined size and shape effects, but only recently has inertial focusing been studied for solely shape-based separation (Di Carlo et al., 2007 and Bhagat et al., 2011).
Hur et al. (2011) studied the inertial focusing of polydimethylsiloxane particles with different sizes and shapes such as spheres, disks, and cylinders (Hur et al., 2011). The authors categorize the particles based on their motion and behavior into four major types: “focused,” “bouncing,” “translating,” and particles with no motion were categorized as “other.” “Translating” refers to particles flowing at the center of the channel with no rotational motion. This transitional behavior occurred for only a few particles at low Reynolds number: Re < 14, and not long before the fluid inertia increased downstream. Most of the cylindrical particles flowing at moderate Re: 14 < Re < 27 experienced “bouncing” motion. During this mode, particles tumbled back and forth across the channel before transitioning to the “focused” mode. The authors claim that the mechanism behind the “bouncing” mode is still unclear and needs further research. At higher flow rates with Re ∼200, the particles began to focus at two equilibrium positions along the channel. Thus, all the experiments were carried out at this flow rate. Results showed that, except for asymmetric disks, the rotational diameter was the major factor in determining the equilibrium position of the particles, rather than the particles shape.
Masaeli et al. (2012) considered sorting and separating non-spherical particles with different Ars using microfluidic inertial focusing based on particle geometry (Masaeli et al., 2012). Figure 8 shows a schematic of the device and genuine images of non-spherical particle separation in an inertial focusing microchannel. Polymeric beads were shaped into ellipsoidal rods with Ars of 3:1 and 5:1 to be tested in this experiment. The authors found that the Jeffry orbit and interaction of non-spherical particles with the wall surface is an essential part of the mechanism determining particles equilibrium focusing position. The short dimension of ellipsoidal particles is significantly lower than spherical particles with the same volume. Therefore, the ellipsoidal particles can get much closer to the channel walls. Additionally, the rotation of non-spherical particles near the walls according to the Jeffery orbit rule (Jeffery, 1922), which states that a non-spherical particle under shear flow rotates in an orbit which minimizes energy dissipation, creates an interaction in which particles are pushed away from the wall. Conditions with higher Re resulted in lower orbit time: an increase in flow caused the particles to have faster in-plane rotation. Wall-induced lift forces are greater when particles are closer to a wall and have higher Ars but decreases when particles are aligned to the direction of flow. Therefore, particles with higher Ars are focused closer to the center of the channel. In this study, high-throughput yeast cell separation was conducted with 94% purity to demonstrate the validity of this method.
FIG. 8.
Inertial focusing microfluidic device for shape-based separation of microparticles. (a) A schematic view of the device: channel height = 35 μm and width of 47 μm. (b) Particles are randomly distributed at the inlet. Two major lift forces of (wall-effect lift) and (shear-gradient lift) effect translational motion in the particles. (c) The particle equilibrium positions 4 cm downstream after being focused at the outlet ( and in balance). Equilibrium positions for particles with the same volume but different Ars, which demonstrates the existence of additional lift forces for non-spherical particles. [(d) and (e)] Actual captured frames of the inlet and outlet (scale bar = 10 μm). Reprinted with permission from Phys. Rev. X 2, 031017 (2012). Copyright 2012 American Physical Society.
Yang et al. (2012) applied inertial focusing to the separation of blood cells based on deformability (Yang et al., 2012). In the experiment, it was observed that the deformable particles were focused at a single line along the rectangular channel containing a viscoelastic solution, whereas rigid particles were distributed in different focusing positions at corners and the centerline. The device schematic view, separation mechanism, and experimental images of the particle mixtures are illustrated in Fig. 9. It is suggested that deformable particles create an additional lateral force due to their elastic behavior and disturbances in the flow, and the quantity of the lateral force is dependent on the deformability of the particle. This method of separation was demonstrated by separating less deformable, highly stiffened red blood cells (RBCs) from fresh RBCs, and polystyrene beads from fresh RBCs at a noticeable purity, showing that the separation is purely based on deformability rather than the size of the particles. The separation performance first increased up to 0.16 ml/h and then decreased with increasing flow, with performance investigated up to 0.48 ml/h.
FIG. 9.
Particle separation based on cell deformability using inertial focusing. (a) Schematic view of separation device shows how the rigid cells are separated and collected at the sides. Channel dimensions are 75 mm × 75 mm × 4 cm for the unexpanded region. The expanded region is 500 nm in width with an angle of 45°. Particle detection was carried out using bright-field and fluorescence microscopy. (b) Fluorescence image of the actual flow of deformable particles in the channel at a rate of 0.16 ml/h; fresh RBCs were marked by DiD cell-labeling dye. Reprinted with permission from Soft Matter 8, 5011–5019 (2012). Copyright 2012 Royal Society of Chemistry.
DuBose et al. (2014) conducted an experimental demonstration of shape-based separation of peanut-shaped cells from spherical cells with similar volumes using dielectrophoresis aided asymmetric double-spiral focusing channels (DuBose et al., 2014). The shape of a bioparticle can reveal numerous properties such as cell type, state, or cycle (Piagnerelli et al., 2007; Martin, 2009; Mitragotri and Lahann, 2009; and Ebert et al., 2010). Therefore, the separation of shape-dependent bioparticles to achieve high purity samples is essential in many clinical and industrial applications. The results of the experiment demonstrated the feasibility of the separation at noticeably high rates. A numerical model consistent with the findings was also derived by the authors (DuBose et al., 2014).
Similarly, Lu et al. (2015) demonstrated the separation of spherical and peanut-shaped bioparticles in viscoelastic fluids using a straight channel (Lu et al., 2015). In addition to the inertial focusing effect, a shear thinning effect was also found to be a factor in the overall separation process, as it was observed previously that shear-thinning affects the particle motion causing the particle to move away from the channel's center line (Huang and Joseph, 2000; Seo et al., 2014; and Huang et al., 1997). The study also found that there is a transition from a single focusing position to two or more positions when increasing Re. The range of Re during this transition was also found to be dependent upon the particle shape. The separation mechanism is shown in Fig. 10. The authors suggest that the separation might occur because of the rotational motion of the non-spherical particles. The authors further investigated the effect of various parameters on the efficiency of the separation process (Lu and Xuan, 2015). The separation was effective at Re near 1.0. The ratio of sheath flow to particle flow had no effect on the separation, while the elasticity and the channel aspect ratio had a significant effect on the residence time of non-spherical particles.
FIG. 10.
Schematic view of the electro-inertial particle focusing device and the mechanism of separation. Stronger combined elastic and inertial lift forces result in more cross-sectional displacement for spherical particles leading to high purity separation of non-spherical particles. Reprinted with permission from Anal. Chem. 87, 11523–11530 (2015). Copyright 2015 ACS Publications.
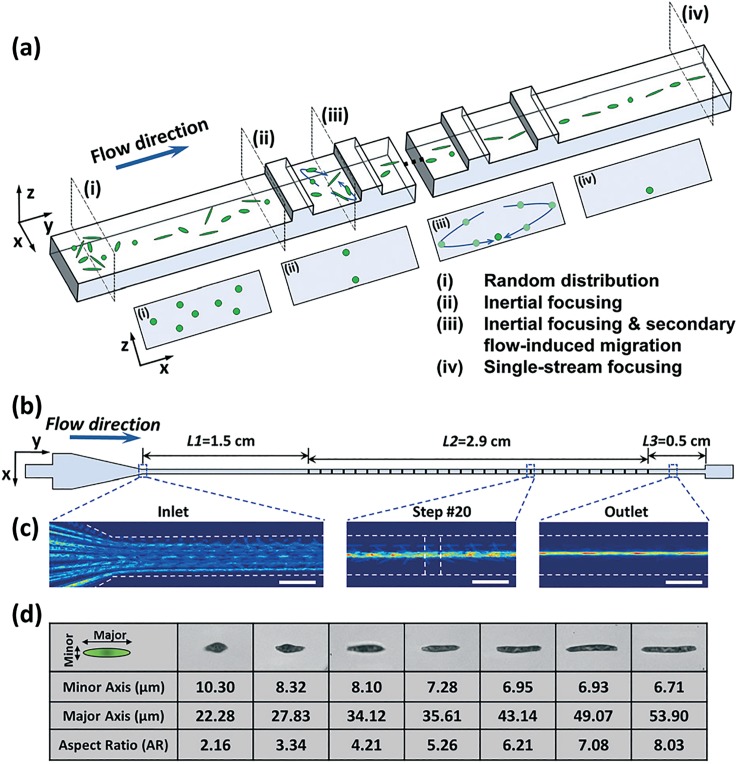
Li et al. (2016) studied the feasibility of shape-based sorting and separation of ellipsoidal Euglena gracilis cells in a straight focusing channel with periodic secondary flow induced in rectangular step structures (Li et al., 2016). Euglena gracilis bio cells have been thoroughly studied as suitable algae for biomass and biodiesel production (Takeyama et al., 1997; Yamane et al., 2001; and Chae et al., 2006), and can have different shapes and sizes due to differences in the cycle stage of the cells during culturing. The effects of Re and Ar on the focusing, rotation, and orientation of the particles was investigated. It was found that increases in increased the focusing of the particles. Also, high Ar particles showed faster rotation with increasing Re. Moreover, high Ar particles shifted from perpendicular to parallel alignment with the flow at higher Re. Figure 11 shows a 3D and top down schematic view of the device along with experimental images of focused particles and microscopic images of Euglena gracilis with different Ars.
FIG. 11.
Secondary flow induced focusing of spheroidal Euglena gracilis cells. (a) 3D view of the periodically stepped microchannel. (b) Dimension and top view of the microchannel. (c) Overlaid experimental images of focusing particles in the channel. Scale bars are 100 μm in length. (d) Microscopic images of Euglena gracilis cells variant in aspect ratio. Reprinted with permission from Lab Chip 16, 4458–4465 (2016). Copyright 2016 Royal Society of Chemistry.
Paiè et al. (2017) experimentally and computationally investigated the effect of the reservoir geometry on the separation of different sized spherical cancer cells in a trapping microfluidic device that is periodically vortex aided. The separation mechanism was driven by entrapment of the larger particles in the vortex system of reservoirs. Başağaoğlu et al. (2018) used the Lattice-Boltzmann method to perform numerical simulations to investigate the particle shape effect on the vortex-aided separation performance. Various geometries of particles, such as elliptical, star, boomerang, triangle, rectangular, circle, and curved-shaped particles, were studied. The particle trajectories and separation behavior showed strong dependence on particle shape. It was discovered that the vortices are not always successful in the selective trapping of larger particles as opposed to what was observed for spherical particles in the previous studies. The authors quantified the error in trajectories and velocities of a mixture of different-shaped particles, if their actual geometrical shapes are replaced by the circular particle geometry, as they settle in a quiescent fluid in a bounded domain or as they flow in a fluid in a microchannel. It was also found that elliptical particles have the strongest shape effect on the particle motion. By replacing the larger circular particles with larger elliptical particles, smaller particles displayed a 36% improvement in trapping, while larger particles showed a 21% decrease.
Despite the work that has been done so far, there are many questions about the application of inertial focusing in shape based separation. However, many new technologies have been developed for inertial focusing that have yet to be implemented for shape-based separation. Serpentine channels (Zhang et al., 2014a), secondary induced flow with a variety of constricted areas (Chung et al., 2013 and Zhao et al., 2017), and the use of external forces fields (Zhang et al., 2014b) may shed new light on shape-based separation via inertial focusing.
V. ELECTROPHORESIS AND MAGNETOPHORESIS
A. Electrophoresis
Electrophoresis refers to the mobility of charged particles through an electrolyte solution driven by an electric field (Strubbe et al., 2013). The introduction of gel electrophoresis, which utilizes nanopores in gels, such as agarose, as entropic barriers to increase the separation performance, marked a revolution in electrophoresis separation. Gels can be easily modified to meet the basics of separation for the desired particles, and the characteristics of the packing can vary depending on the desired application (Viovy, 2000).
Since the introduction of gel electrophoresis (Grabar, 1953), many methods, such as nanopores (Laohakunakorn et al., 2013), microfluidic arrays (Han and Craighead, 2000), and capillary electrophoresis (Harrison et al., 1993) have been developed to facilitate the separation of particles. When a large molecule, or charged particle, is placed in an electrolyte, the particle's surface will start to attract oppositely charged free ions to form a permanent or immobile zone called the Stern layer around the particle. A second layer of mobile ions surrounding the Stern layer is then shaped forming the diffuse layer. The combination of the two layers creates the electric double-layer or Debye length. The particle will then react to an existing electrical field throughout the solution. The force exerted on the particle along with the immobile layer is opposite of the force applied to the free ion layer. The mobility of the particle can be simplified into two cases where the particle Debye layer thickness is either larger or smaller than the particle radius, r. In the case of a large Debye layer, viscous and electric forces are independently in balance. Consequently, electrophoretic mobility can be expressed as total particle charge [ (C)] over drag resistance and can be simplified for a spherical particle (Huckel, 1924):
| (2) |
When the Debye layer is thin, shear is limited to a layer with the thickness of the Debye length. The mobility is then independent of the size and shape of the particle (Smoluchowski, 1903):
| (3) |
Here, is the dielectric constant for the medium (dimensionless), is permittivity of the vacuum (dimensionless), and , the zeta potential (mV), is the electrokinetic potential at the outer surface of the electric double layer (Binns, 2014). As seen in the difference between Eqs. (2) and (3), the shape effect of electrophoretic separation occurs when the Debye layer is large or when there is an interaction between particles and microstructures of gel or other devices. However, most electrophoresis applications have been developed for size-based separations, while shape-based electrophoresis separation has remained relatively unexplored both experimentally and theoretically. In this section, different methods of shape-based separation using electrophoresis are discussed.
Liu et al. (2005) investigated the performance of capillary electrophoresis separation of silver nanoparticles based on their size and shape (Liu et al., 2005). Silver nanoparticles were prepared to carry surface charges using ion sorption. As a result of the surface charges, an electric double layer prevented the particles from agglomerating. The mechanism of separation is therefore based on the surface charge of the particles rather than actually charged particles with similar features. The separation performance was first studied for the size separation of silver nanoparticles 17.0 and 49.7 nm in diameter at surfactant SDS concentrations of 0-40 mM. The results indicated that separation was feasible only in the presence of surfactant with an optimal concentration of 20 mM. When separating differently shaped particles, the Ar had an obvious effect. Nanorods with higher Ars eluted last; however, the mechanism of separation is not clear. One could infer that the particle interaction with the wall may contribute to separation and the late elution of nanorods with high Ars.
Hanauer et al. (2007) later demonstrated the separation of gold and silver nanoparticles based on shape and size using gel electrophoresis (Hanauer et al., 2007). Nanoparticles were coated with polyethylene glycol to impart surface charges. After analyzing the different locations of the gel, a separation of particles was clearly shown. Figure 12(a) shows TEM images of the particle mixture in four different locations of the gel. The original mixture was composed of 13% rods, 34% spheres, 44% triangles, and 9% was categorized as other. Figure 12(b) shows the analysis of the particle distribution for each location. It is clear that rods showed the slowest mobility and were enriched to 60% in the first location. Triangles seemed to possess the highest mobility, while spheres resided in moderate and fast locations. Figure 12(c) presented the analysis in more detail including particle sizes, such as the sphere diameter, triangle height, and the short and long dimensions of the rods. It can be concluded that longer rods have the least mobility. It is interesting to note that spherical particles showed an increase in mobility with an increase in diameter, but a trend was not found in the triangular particles. The authors mentioned that there could have been a hidden effect as a result of differences in thickness that could not be captured by TEM. Separation performance was also investigated for a mixture of spherical and rod-like particles at a ratio of 35:65. The results clearly confirm the separation of particles based on particle shape.
FIG. 12.
Gel electrophoresis separation of gold and silver nanoparticles. (a) TEM images of different locations of the gel slab. (b) Particle composition as a percentage of total counted particles with various shapes of rods, triangles, and spheres at each location. (c) The mobility of particles with different shapes and sizes (length of rods, diameter of spheres, and height of triangles). Reprinted with permission from Nano Lett., 7, 2881–2885 (2007). Copyright 2007 ACS Publications.
Xu et al. (2007) performed a similar shape/size separation of gold nanoparticles using preparative gel electrophoresis with an average pore size of 100 nm (Xu et al., 2007). A mixture of spherical gold nanoparticles with particle sizes of 5 nm, 15 nm, and 20 nm was first separated to demonstrate the capability of electrophoresis separation. Subsequently, electrophoresis separation was tested for shape separation of three different components: triangular plates, nanorods, and spherical particles. In this experiment, particles were not of the same volume. The results showed that nanospheres are the fastest, triangular nanoplates have mobility similar to spherical nanoclusters, and nanorods are the slowest, similar to the results of Hanauer et al. (2007). Unlike what has been reported in this work for the mobility of nanorods in gels, generally, as we discuss this later, the mobility of nanorods in free solutions increases as Ar increases. Although the mechanism behind the retardation of nanorods has not been investigated, we believe that nanopores may have had the greatest contribution, as longer nanorods likely experienced more encounters with barriers due to their size, while shorter nanorods and spherical particles could slip through more easily.
Hsu et al. (2012) analyzed the effect of various parameters on non-spherical polyelectrolyte particles (PEP) with the same volume and at varying Ars (Hsu et al., 2012). PEPs are macromolecules with large ionizable functional groups attached to their surfaces (Oseguera et al., 2010). The mobility of PEPs in electrolytes could be affected by additional effects such as electroosmotic retardation flow or counterion condensation. Electroosmotic retardation flow is caused by the movement of counterions inside the electric double-layer (Yeh and Hsu, 2011). The counterion condensation effect is significant where the local surface charge density of a particle exceeds a critical limit (McHale and Newton, 2011). Double-layer polarization can affect the motion of PEPs when particle double-layer thickness is large compared to the particle radius. Various factors were found to describe the rescaled mobility: the mobility relative to the mobility of a freely drained particle, of particles with different Ars. The various factors included the reciprocal Debye screening length, scaled particle charged density, electrophoretic softness of PEPs, and bulk ionic density. The mobilities of particles with higher Ars were always higher than those with lower Ars. Thus, the mobility of a spheroidal particle is higher than that of a spherical particle, and the mobility of a spherical particle is higher than that of an oblate particle. Although results of this study have not yet been applied to the analysis of the current shape dependent electrophoretic separation results, this theoretical approach is expected to be developed further for shape separation theory via electrophoresis.
B. Magnetophoresis
Magnetic fields have been broadly applied to the separation of microparticles and nanoparticles in microfluidic devices due to their non-invasive and contactless characteristics (Ahmed et al., 2018 and Hejazian et al., 2015). In magnetic separation, the fundamental principles are the magnetic force and torque acting on the particle, which are expressed as follows (Ahmed et al., 2018):
| (4) |
| (5) |
where = 4π × 10−7 N/A is the magnetic permeability of a vacuum, is the particle volume (m3), and is the gradient of the magnetic flux density B (T), m is the magnetic moment of the particle (Am2), and is the difference in the magnetic susceptibility (dimensionless) between the particle (χp) and the surrounding medium (χf). Both static and unsteady magnetic fields can be used to generate the forces and torques required for this kind of separation.
In traditional magnetic separation, non-uniform magnetic fields are used to exert magnetic forces on particles. The particle motion due to magnetic forces in a viscous medium is known as magnetophoresis. When , the particle is pulled toward the magnetic source, and this phenomenon is known as positive magnetophoresis. When , the opposite is true, and the motion is known as negative magnetophoresis. Generally, positive magnetophoresis manipulates paramagnetic and ferromagnetic particles or magnetically tagged cells in a diamagnetic fluid such as water (Adams et al., 2009; Hoshino et al., 2011; Inglis et al., 2004; 2006; Kang et al., 2012; and Mirowski et al., 2005), while negative magnetophoresis separates diamagnetic particles or cells in a magnetic fluid such as ferrofluids (Hejazian and Nguyen, 2016; Liang and Xuan, 2012; Liang et al., 2013; Vojtíšek et al., 2012; Zeng et al., 2013; Zhao et al., 2016; Zhou and Wang, 2016; and Zhu et al., 2010; 2012).
Most existing studies focus on size-based separation (Ahmed et al., 2018 and Hejazian et al., 2015). As shown in Eq. (3), particles of different sizes will experience different forces, thus allowing particle separation by size or volume. Only recently has shape-based separation been achieved in microfluidic channels in combination with magnetic fields. There are two principal methods to achieve such separation: (1) by using shape-dependent forces with non-uniform magnetic fields and (2) by using shape-dependent magnetic torques with zero magnetic force and uniform magnetic fields.
Kose et al. (2009) used a periodic, unsteady, and non-uniform magnetic field to successfully separate sickle cells from live red blood cells in a biocompatible ferrofluid. In their work, the excitation electrodes are set underneath ferrofluid microchannels as shown in Fig. 13(a). The electrodes produce time-varying magnetic forces and torques on the cells, so that cells are pushed to the top of the channel via negative magnetophoresis. When the cells reach the top wall, their rotation results in linear translation along the length of the channel. The excitation frequency, current amplitude, and the positions of the electrodes are the key factors for the average velocity of the cells. It is found that linear translation due to the magnetic torque can overcome the magnetic force resulting in continuous particle transport in the channel when the applied frequency is higher than the critical frequency. The critical frequency depends on the size, shape, and elasticity of the particles being separated. The applied frequency is used to trap particles with higher critical frequencies, while also transporting particles with lower critical frequencies. In this case, at 300 Hz, sickle cells were trapped between two electrodes, while the live red blood cells were transported through the channel.
FIG. 13.
Shape-based separations using magnetic fields: (a) Separating a mixture of sickle cell anemia from live red blood cells in ferrofluids using periodic magnetic fields. Reproduced with permission from Proc. Natl. Acad. Sci. U.S.A. 106, 21478–21483 (2009). Copyright 2009 PNAS; (b) Separating a mixture of equal-volume spherical and peanut-shaped diamagnetic particles in ferrofluids via T-shaped microfluidic channels. Reproduced with permission from Appl. Phys. Lett. 109, 102405 (2016). Copyright 2016 AIP Publishing LLC; (c) Separating a mixture of paramagnetic ellipsoidal and spherical particles under weak uniform magnetic fields. Reproduced from Lab Chip 17, 401–406 (2017a). Copyright 2016 Royal Society of Chemistry; (d) Separating a mixture of ferromagnetic ellipsoidal and spherical particles under strong uniform magnetic fields. Reproduced with permission from Phys. Rev. Lett. 119, 198002 (2017a). Copyright 2017 American Physical Society.
Zhou and Xuan (2016) successfully separated a mixture of equal-volume spherical and peanut-shaped diamagnetic particles in a ferrofluid via T-shaped microfluidic channels as shown in Fig. 13(b). In this method, a permanent magnet is positioned perpendicular to the flow direction to generate non-uniform magnetic fields. To explain the observed shape-based separation, shape-dependent magnetophoretic motion is proposed. The magnetic force and the viscous drag force are modified by the particles shape-dependent and orientation-dependent correction factors. The modified equations for the homogeneous and linearly magnetizable particles are expressed as
| (6) |
| (7) |
where Mf is the magnetization of the ferrofluid (A/m), H0 is the magnetic field at the particle center (A/m), dp is the equivalent spherical diameter of the particle (m), uf and up are the velocities of ferrofluid and particle (m/s), and fD is the drag coefficient (dimensionless) considering wall retardation effects (Happel and Brenner, 1983). Sm and Sd are particle shape-dependent correction factors (dimensionless), which are 1 for spherical particles and increases with non-sphericity (Gao et al., 2007). Om and Od are particle orientation-dependent correction factors (dimensionless), which are 1 for spherical particles and non-spherical particles moving in the direction of their major axes (Jones, 1995). By exploiting the different values of shape-dependent factors, particles of different shapes were separated. Furthermore, the effects of flow rate and the ratio of sheath ferrofluid to particle mixture flow rate were investigated. A 3D numerical simulation was implemented and gave a reasonable agreement with the experimental observations. Later, the same method was applied to separate different groups of drug-treated yeast cells that exhibited various sizes and shapes in ferrofluids (Chen et al., 2017).
The works mentioned above are all based on magnetic force. More recently, Zhou et al. (2017a) proposed a new, simple, and effective method which only uses shape-dependent magnetic torque to separate equal-volume prolate paramagnetic ellipsoidal and spherical particles under static uniform magnetic fields in a microchannel under low Re condition as shown in Fig. 13(c). Without a magnetic field, the prolate ellipsoidal particle exhibits symmetric rotational motion in the shear flow without net lateral migration and therefore do not separate. However, when a uniform magnetic field H0 is applied perpendicular to the flow (that is, where α = 0o in Fig. 13(c)), the magnetic field produces a nonzero magnetic torque:
| (8) |
where Mp and Mf are the magnetization of the particle and the fluid. The magnetic torque breaks the symmetric property of the particle rotation dynamics. The magnetic torque coupled with particle-wall hydrodynamic interactions lead to a lateral migration of particles in the microchannel as seen in Fig. 13(c). From Eq. (8), we can see that the shape-dependent lateral separation can only occur if there is a contrast of magnetic susceptibilities between the particles and the surrounding medium. Successful separation of nonmagnetic spherical and ellipsoidal particles in a ferrofluid is also reported in this paper. By further experimental and numerical investigations (Cao et al., 2018; Zhang and Wang, 2018; and Zhou et al., 2017b), it was found that the direction of the magnetic field controls the asymmetric rotation of the particles and the direction of the migration, and that the strength of the magnetic field controls the speed of migration.
Matsunaga et al. (2017a) reported the far-field hydrodynamic theory and simulations to show that permanent magnetic particles (i.e., ferromagnetic particles) can be focused and separated by size and shape in a simple shear flow and microchannel flow under a static uniform magnetic field as shown in Fig. 13(d). When a uniform magnetic field is applied in the xy plane with an arbitrary angle , the magnetic flux density . The magnetic moment of the particle , where is the orientation angles of particle. In this work, a strong uniform magnetic field was applied to hold the particles at a stable angle . From theoretical analysis, the direction of particle migration depends on the values of . When , the ellipsoidal particles move away from the wall, and when , the ellipsoidal particles move toward the wall. The strong magnetic field determines the particle orientation and the particle-wall hydrodynamic interaction controls the direction of the migration. Eventually, particles of different Ars are focused to different equilibrium positions. In a later work, full numerical simulations were reported by the same research group (Matsunaga et al., 2017b) to demonstrate various equilibrium positions of ellipsoidal ferromagnetic particles in rectangular and circular microchannels at low Re, providing a deeper understanding of the effect of channel geometry on the lateral migration.
VI. PRECIPITATION/CENTRIFUGATION
A. Precipitation by self-assembly
Self-assembly can be applied to promote shape-based particle precipitation. Gold nanoparticles produced through colloidal synthesis (Zhang et al., 2014c and Yang et al., 2017) are often impure and require some shape purification. Particles smaller than the desired size are removed from the product by centrifuging, but the remaining mixture may still contain structures of undesirable shapes. Generally, these mixtures will be populated by spherical or near spherical particles and sometimes cubes. To separate these structures, surfactant (Jana, 2003) or salt (Guo et al., 2011) is added to encourage self-assembly of the more easily precipitated nanoparticles.
During surfactant assisted self-assembly, the surfactant, often CTAB, is added, causing the shapes to precipitate via a nematic-isotropic separation with long rods precipitating before plates, and plates before spheres and near spheres, due to their higher contact area (Jana, 2003). Colloid interactions in a nematic fluid are generally much greater than interactions in an isotropic fluid which, along with boundary conditions at the interface, lead to the so called self-assembly of anisotropic nanoparticles (Sengupta, 2013). The resulting solution is then drained from the top to reveal a solution with a much higher concentration of nanoparticles of the desired shape.
In 2011, Guo et al. experimented with a method using salt to trigger self-assembly instead of a surfactant. Beginning with raw samples of gold nanorods and nanoplates, concentrations of NaCl ranging from 0.12 M to 2.5 M were added to the solutions. With results characterized by supernatant absorption spectra, NaCl concentrations as low as 0.12 M and 0.86 M resulted in noticeable decreases of absorption peaks indicative of nanoplates and nanorods, respectively; however, separation did not improve at higher salt concentrations. Increases in the salt concentration were found to decrease the separation between isotropic and anisotropic nanoparticles with only minimal separation occurring at 2.5 M NaCl. This is because much higher salt concentrations neutralize the attractive force of the surface charges imposed on the nanoparticles by introducing an electric double layer, thus restoring the natural repulsion that prevents spontaneous aggregation, or self-assembly. As with surfactant assisted self-assembly, the difference in the available contact area of different shapes is the reason anisotropic nanoparticles can be precipitated from their isotropic counterparts. Impurity levels of the resulting nanorod and nanoplate products were found to be less than 3%. This method is especially interesting for further study and commercialization as it can be conducted at both room temperature and high throughput with little cost (Guo et al., 2011).
Datskos et al. (2016) reported using a Pickering emulsion based approach to trigger self-assembly in silica nanorods. Silica nanorod samples were added to a water-pentanol system and settled after about 5 h due to the increased weight of the silica emulsion droplets. Though this method proved useful in producing dry samples of silica nanorods, spherical particles also self-assembled, and while shape separation was not the focus of the paper, it remains to be seen if this method could be tuned to separate on shape rather than self-assemble whatever particles are present (Datskos et al., 2016).
Hu et al. (2018) reported shape separation by self-assembly as dependent on the volume of CTAB, the concentration of CTAB, the temperature of the separating mixture, and aging period. For the 10 ml colloid samples, it was found that shape separation was most effective with 0.4 ml of 0.3 M CTAB and that a higher volume of CTAB was not beneficial to the separation. CTAB concentrations below 0.4 M were insufficient in separating the desired nanoparticles from the supernatant. Temperatures tested from 25 °C to 80 °C showed greater separation efficiency at higher levels. Samples with longer aging periods generally showed a greater separating effect with the most separation occurring with a 12-h aging period, but overall longer aging periods did not increase separation efficiency. A secondary separation following the same procedure was found to be necessary for greater levels of shape purity, especially when separating rods and plates (Hu et al., 2018)
Shape separation via self-assembly has been mostly dominated by surfactant-assisted methods with variations showing promise. The quality achieved through this process is dependent upon many factors that have yet to be fully characterized. The surfactant assisted method will most likely remain a compelling option for creating high quality nanoparticle solutions in the future, with competition from salt assisted methods. While many are eager to begin work with high quality nanorods, nanoplates, and even nanocubes, further research into the optimal purification of samples is still necessary. No doubt the factors discussed by Hu et al. (2018) will be further investigated, and some generalizations will be made about the process for the more frequently used metals, eventually leading to scalable models.
B. Centrifugation
Centrifugation is a process based on the differences in the sedimentation behaviors of particles. The sedimentation velocity of each particle is determined by force balances. Due to the diversity in particle shape, size, and density, the sedimentation velocities are different for every particle. If the difference in sedimentation velocity is significant, the particles can be separated through centrifugation. The sedimentation coefficient, how fast particles settle, is defined as the ratio of sedimentation terminal velocity to angular acceleration (Li et al., 2018) and has the dimension of time. The sedimentation coefficient is only dependent on the properties of the particles and the medium of centrifugation. For nanoparticles flowing with small Re, the sedimentation coefficient, s, can be derived using the force balances of centrifugal, buoyant, and drag forces:
| (9) |
Here, ρp and ρm are the densities of the particle and the medium, respectively, and f is the shape factor to account for non-spherical particle geometries. For spherical particles f = 1, and for non-spherical particles f > 1. For example, f for rod-like particles is given as (Yao et al., 2016)
| (10) |
Therefore, spheres have a higher sedimentation coefficient and velocity than non-spherical particles.
Several models have been introduced to predict sedimentation coefficients (Hubbard and Douglas, 1993; Sharma et al., 2009a; 2009b; and Xiong et al., 2011). The models estimate drag force based on centrifugation parameters (e.g., Ar, diameter, and the orientation of particles). The sedimentation coefficient and velocity are then determined based on the force balances. However, the experimental setups in many of these studies fail to precisely measure sedimentation coefficients to validate their models. Wang et al. (2016) conducted one of the few studies to measure sedimentation coefficient experimentally by studying the effects of the d and Ar of nanorods on the sedimentation coefficient. It was found that for nanorods with the same volume, the sedimentation coefficient decreased with increasing Ar. For nanorods with the same d, the sedimentation coefficient increased with increasing Ar.
Centrifugation techniques can be categorized based on the density of the medium. One approach is differential centrifugation where density is constant throughout the homogenous medium. Sharma et al. (2009a; 2009b) investigated the separation of a dilute solution of nanospheres and nanorods using differential centrifugation. Spheres and bulkier rods precipitated at the bottom, while longer, thinner rods precipitated at the side wall (Fig. 14). The difference in the drag coefficient of each particle is the driving force for the separation. Spheres and spherically isotropic particles (e.g., cubes and nanorods with small Ar) have similar drag coefficients so they cannot be separated, but nanorods with large Ars have different drag coefficients and can be located in a different band.
FIG. 14.
Differential centrifugation of gold nanoparticles is depicted with thin nanorods located on the side wall and spheres and bulkier nanorods located on the bottom wall. Reprinted with permission from Proc. Natl. Acad. Sci. U.S.A. 106, 4981–4985 (2009). Copyright 2009 National Academy of Sciences.
Several stages of centrifugation may be required to separate rods from spheres with improved purity. Boksebeld et al. (2017) used differential centrifugation to study the separation of nanorods with a low Ars (less than 6) from nanospheres. Their method utilized centrifugation in three stages. In each stage, the solution is centrifuged and the spheres are precipitated. Supernatant that is rich in rods is recovered and centrifuged again. The results show that after each stage, the monodispersity increases, but the separation does not produce high yields for lower Ars.
For enhanced separation, the density of the medium can be non-uniform: the density can be changed continuously or stepwise from top to bottom. Tyler et al. (2012) considered the separation of faceted (e.g., triangle and cube) and non-faceted particles (e.g., sphere) based on differences in sedimentation coefficients utilizing continuous density gradient centrifugation. Although the sedimentation coefficients are initially similar for all particles, the surfactants alter the coefficients for better separation. Faceted particles can absorb more surfactant compared to non-faceted particles resulting in differentially modified sedimentation coefficients (Fig. 15).
FIG. 15.
The results from the shape-based separation are shown using a continuous density gradient centrifugation by Tyler et al. (2012). The shape distributions in each fraction of separated bands are different. Reprinted with permission from J. Phys. Chem. Lett. 3, 1484–1487 (2012). Copyright 2012 American Chemical Society.
Another approach is step density gradient centrifugation where the density changes abruptly in the medium: the medium is made of several layers of liquids with different densities. This method is also called rate-zonal centrifugation. This approach is known to resolve the difficulty in recovering purified particles in both differential centrifugation and continuous density gradient centrifugation: purified particles may be remixed during recovery. In step density gradient centrifugation, each band of particles is trapped in one layer creating a sharp distribution of particles. Each layer must be viscous enough to trap one band of particles while allowing others to move to separate layers, and the interfacial forces between layers should be high enough to avoid the diffusion of layers into each other without preventing the transfer of particles between layers (Yao et al., 2016). After centrifugation, the particles are separated from each medium of its respective phase. Organic media have advantages in this step because they are easily evaporated after centrifugation.
Akbulut et al. (2012) investigated the separation of nanorods, nanospheres, and larger particles in three separate phases. The particles were trapped in each phase based on their sedimentation rate and viscous forces applied by the phases. Nanorods had the lowest sedimentation coefficient and were captured in the first phase, while nanospheres and the larger particles were trapped in the second and third phase, respectively (Fig. 16).
FIG. 16.
The results from the shape-based separation using a discontinuous density gradient centrifugation by Akbulut et al. (2012). The particles in each separated layer show different shapes. Reprinted with permission from Nano Lett. 12, 4060–4064 (2012). Copyright 2012 American Chemical Society.
Yao et al. (2016) investigated the shape separation of gold nanorods in a multilayer system with different Ars and sizes. The layers were a solution of CTAB/EG with different densities and viscosities. In their study, CTAB played a crucial role in preventing the diffusion of layers into each other while avoiding the aggregation of gold nanoparticles.
VII. CONCLUSIONS
We reviewed many successful cases of separating particles by shape through many different approaches. Despite their utility, these shape-based separation techniques and studies are limited in the following ways. First, a general approach does not exist, and some current methods are only applicable to particles with specific properties or operating conditions. As a result, there is limited versatility in design and operation. Second, there is no complete theory to quantitatively and qualitatively identify the shape effect on the separation behaviors. Current studies are generally dependent on phenomenological approaches in specific conditions and lack a systematic approach to identify the shape effects. Third, most of the up-to-date methods are the separation of rod-like particles by Ar. Separations of particles with various shapes other than rod-like particles have not been much explored. There have been attempts to develop models for the methods based on device geometry or shape-specific transport properties, such as FFF, DLD, and inertial focusing. However, the methods based on surface charge effects, such as SEC, electrophoresis, and self-assembly precipitation have room for improvement in theoretical development as well as in the separation of particles of various shapes.
ACKNOWLEDGMENTS
The authors declare that they have no conflict of interests. Supports from the University of Missouri Research Board, the Department of Mechanical and Aerospace Engineering, the Department of Chemical and Biochemical Engineering, the Intelligent Systems Center, and the Center for Biomedical Research at Missouri S&T are acknowledged.
Contributor Information
Cheng Wang, Email: .
Joontaek Park, Email: .
References
- 1.Adams, J. D., Thévoz, P., Bruus, H., and Soh, H. T., “Integrated acoustic and magnetic separation in microfluidic channels,” Appl. Phys. Lett. 95, 254103 (2009). 10.1063/1.3275577 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Agarwal, U. S., Dutta, A., and Mashelkar, R. A., “Migration of macromolecules under flow: The physical origin and engineering implications,” Chem. Eng. Sci. 49, 1693–1717 (1994). 10.1016/0009-2509(94)80057-X [DOI] [Google Scholar]
- 3.Ahmed, M., Shiddiky, M. J. A., and Nguyen, N., “Recent advances and current challenges in magnetophoresis based micro magnetofluidics,” Biomicrofluidics 12.3, 031501 (2018). 10.1063/1.5035388 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Akbulut, O., Mace, C. R., Martinez, R. V., Kumar, A. A., Nie, Z., Patton, M. R., and Whitesides, G. M., “Separation of nanoparticles in aqueous multiphase systems through centrifugation,” Nano Lett. 12(8), 4060–4064 (2012). 10.1021/nl301452x [DOI] [PubMed] [Google Scholar]
- 5.Alfi, M. and Park, J., “Theoretical analysis of the local orientation effect and the lift-hyperlayer mode of rod-like particles in field-flow fractionation,” J. Sep. Sci. 37, 876–883 (2014). 10.1002/jssc.201300902 [DOI] [PubMed] [Google Scholar]
- 6.Asmolov, E. S., “The inertial lift on a spherical particle in a plane Poiseuille flow at large channel Reynolds number,” J. Fluid Mech. 381, 63–87 (1999). 10.1017/S0022112098003474 [DOI] [Google Scholar]
- 7.Barth, H. G., Boyes, B. E., and Jackson, C., “Size exclusion chromatography,” Anal. Chem. 66(12), 595–620 (1994). 10.1021/ac00084a022 [DOI] [PubMed] [Google Scholar]
- 8.Barua, S., Yoo, J.-W., Kolhara, P., Wakankarc, A., Gokarn, Y. R., and Mitragotria, S., “Particle shape enhances specificity of antibody-displaying nanoparticles,” Proc. Natl. Acad. Sci. U.S.A. 110, 3270–3275 (2013). 10.1073/pnas.1216893110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Başağaoğlu, H., Succi, S., Wyrick, D., and Blount, J., “Particle shape influences settling and sorting behavior in microfluidic domains,” Sci. Rep. 8, 8583 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Batchelor, G. K., “Slender-body theory for particles of arbitrary cross-section in Stokes flow,” J. Fluid Mech. 44, 419–440 (1970). 10.1017/S002211207000191X [DOI] [Google Scholar]
- 10.Beckett, R. and Giddings, J. C., “Entropic contribution to the retention of nonspherical particles in field-flow fractionation,” J. Colloid Interface Sci. 186, 53–59 (1997). 10.1006/jcis.1996.4612 [DOI] [PubMed] [Google Scholar]
- 11.Beech, J. P., Holm, S. H., Adolfsson, K., and Tegenfeldt, J. O., “Sorting cells by size, shape and deformability,” Lab Chip 12(6), 1048–1051 (2012). 10.1039/c2lc21083e [DOI] [PubMed] [Google Scholar]
- 12.Beranek, J., Imre, D., and Zelenyuk, A., “Real-time shape-based particle separation and detailed in situ particle shape characterization,” Anal. Chem. 84, 1459–1465 (2012). 10.1021/ac202235z [DOI] [PubMed] [Google Scholar]
- 13.Bhagat, A. A. S., Hou, H. W., Li, L. D., Lim, C. T., and Han, J., “Pinched flow coupled shear-modulated inertial microfluidics for high-throughput rare blood cell separation,” Lab Chip 11, 1870–1878 (2011). 10.1039/c0lc00633e [DOI] [PubMed] [Google Scholar]
- 14.Binns, C., Frontiers of Nanoscience—Medical Applications of Magnetic Nanoparticles (Elsevier, 2014), Vol. 6, pp. 217–258. [Google Scholar]
- 15.Bogunovic, L., Fliedner, M., Eichhorn, R., Wegener, S., Regtmeier, J., Anselmetti, D., and Reimann, P., “Chiral particle separation by a nonchiral microlattice,” Phys. Rev. Lett. 109(10), 100603 (2012). 10.1103/PhysRevLett.109.100603 [DOI] [PubMed] [Google Scholar]
- 16.Boksebeld, M., Blanchard, N. P., Jaffal, A., Chevolot, Y., and Monnier, V., “Shape-selective purification of gold nanorods with low aspect ratio using a simple centrifugation method,” Gold Bull. 50(1), 69–76 (2017). 10.1007/s13404-017-0197-9 [DOI] [Google Scholar]
- 17.Cao, Q., Li, Z., Wang, Z., and Han, X., “Rotational motion and lateral migration of an elliptical magnetic particle in a microchannel under a uniform magnetic field,” Microfluid Nanofluidics 22, 1–9 (2018). 10.1007/s10404-017-2014-4 [DOI] [Google Scholar]
- 18.Chae, S., Hwang, E., and Shin, H.-S., “Single cell protein production of Euglena gracilis and carbon dioxide fixation in an innovative photo-bioreactor,” Bioresour. Technol. 97, 322–329 (2006). 10.1016/j.biortech.2005.02.037 [DOI] [PubMed] [Google Scholar]
- 19.Chakrabarty, A., Konya, A., Wang, F., Selinger, J. V., Sun, K., and Wei, K.-H., “Brownian motion of boomerang colloidal particles,” Phys. Rev. Lett. 111, 160603 (2013). 10.1103/PhysRevLett.111.160603 [DOI] [PubMed] [Google Scholar]
- 20.Chen, Q., Li, D., Zielinski, J., Kozubowski, L., Lin, J., Wang, M., and Xuan, X., “Yeast cell fractionation by morphology in dilute ferrofluids,” Biomicrofluidics 11(6), 064102 (2017). 10.1063/1.5006445 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cherukat, P. and McLaughlin, J. B., “The inertial lift on a rigid sphere in a linear shear flow field near a flat wall,” J. Fluid Mech. 263, 1–18 (1994). 10.1017/S0022112094004015 [DOI] [Google Scholar]
- 22.Chun, J., Fagan, J. A., Hobbie, E. K., and Bauer, B. J., “Size separation of single-wall carbon nanotubes by flow-field flow fractionation,” Anal. Chem. 80, 2514–2523 (2008). 10.1021/ac7023624 [DOI] [PubMed] [Google Scholar]
- 23.Chung, A. J., Pulido, D., Oka, J. C., Amini, H., Masaeli, M., and Di Carlo, D., “Microstructure-induced helical vortices allow single-stream and long-term inertial focusing,” Lab Chip 13, 2942–2949 (2013). 10.1039/c3lc41227j [DOI] [PubMed] [Google Scholar]
- 24.Datskos, P., Polizos, G., Bhandari, M., Cullen, D. A., and Sharma, J., “Colloidosome like structures: Self-assembly of silica microrods,” RSC Adv. 6, 26734–26737 (2016). 10.1039/C5RA25817K [DOI] [Google Scholar]
- 25.Devendra, R. and Drazer, G., “Gravity driven deterministic lateral displacement for particle separation in microfluidic devices,” Anal. Chem. 84(24), 10621–10627 (2012). 10.1021/ac302074b [DOI] [PubMed] [Google Scholar]
- 26.Di Carlo, D., Irimia, D., Tompkins, R. G., and Toner, M., “Continuous inertial focusing, ordering, and separation of particles in microchannels,” Proc. Natl. Acad. Sci. U.S.A. 104, 18892–18897 (2007). 10.1073/pnas.0704958104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.DuBose, J., Lu, X., Patel, S., Qian, S., Joo, S. W., and Xuan, X., “Microfluidic electrical sorting of particles based on shape in a spiral microchannel,” Biomicrofluidics 8, 014101 (2014). 10.1063/1.4862355 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ebert, E. C., Nagar, M., and Hagspiel, K. D., “Gastrointestinal and hepatic complications of sickle cell disease,” Clin. Gastroenterol. Hepatol. 8, 483–489 (2010). 10.1016/j.cgh.2010.02.016 [DOI] [PubMed] [Google Scholar]
- 29.Feng, J., Hu, H. H., and Joseph, D. D., “Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid Part 1. Sedimentation,” J. Fluid Mech. 261, 95–134 (1994a). 10.1017/S0022112094000285 [DOI] [Google Scholar]
- 30.Feng, J., Hu, H. H., and Joseph, D. D., “Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid Part 2. Couette and Poiseuille flows,” J. Fluid Mech. 277, 271–301 (1994b). 10.1017/S0022112094002764 [DOI] [Google Scholar]
- 31.Furuuchi, M. and Gotoh, K., “Shape separation of particles,” Powder Technol. 73, 1–9 (1992). 10.1016/0032-5910(92)87001-Q [DOI] [Google Scholar]
- 32.Furuuchi, M., Yamada, C., and Gotoh, K., “Shape separation of particulates by a rotating horizontal sieve drum,” Powder Technol. 75, 113–118 (1993). 10.1016/0032-5910(93)80071-H [DOI] [Google Scholar]
- 33.Gao, Y., Jian, Y. C., Zhang, L. F., and Huang, J. P., “Magnetophoresis of nonmagnetic particles in ferrofluids,” J. Phys. Chem. C 111, 10785–10791 (2007). 10.1021/jp0705673 [DOI] [Google Scholar]
- 34.Ghasemi, M., Holm, S. H., Beech, J. P., Bjornmalm, M., and Tegenfeldt, J. O., “Separation of deformable hydrogel micro particles in deterministic lateral displacement devices,” in Proceedings of 16th International Conference on Miniaturized Systems for Chemistry and Life Sciences, Okinawa, Japan, 28 October–1 November 2012, edited by Fujii T., Hibara A., Takeuchi S. and Fukuba T., (Chemical and Biological Microsystems Society, San Diego, 2014), pp. 1672–1674. [Google Scholar]
- 35.Giddings, J. C., “Hyperlayer field-flow fractionation,” Sep. Sci. Technol. 18, 765–773 (1983). 10.1080/01496398308068578 [DOI] [Google Scholar]
- 36.Gigault, J., Cho, T. J., MacCuspie, R. I., and Hackely, V. A., “Gold nanorod separation and characterization by asymmetric-flow field flow fractionation with UV–Vis detection,” Anal. Bioanal. Chem. 405, 1191–1202 (2013). 10.1007/s00216-012-6547-9 [DOI] [PubMed] [Google Scholar]
- 37.Grabar, P., “Methode permettant l’étude conjuguée des propriétés electrophoretiques et immunochimique d’un melange de proteines. Application au serum sanguin,” Biochim. Biophys. Acta 10, 193 (1953). 10.1016/0006-3002(53)90233-9 [DOI] [PubMed] [Google Scholar]
- 38.Guo, Z., Fan, X., Xu, L., Lu, X., Gu, C., Bian, Z., Bian, Z., Gu, N., Zhang, J., and Yang, D., “Shape separation of colloidal gold nanoparticles through salt-triggered selective precipitation,” Chem. Commun. 47, 4180–4182 (2011). 10.1039/c0cc04612d [DOI] [PubMed] [Google Scholar]
- 39.Han, J. and Craighead, H. G., “Separation of long DNA molecules in a microfabricated entropic trap array,” Science 288, 1026–1029 (2000). 10.1126/science.288.5468.1026 [DOI] [PubMed] [Google Scholar]
- 40.Hanauer, M., Pierrat, S., Zins, I., Lotz, A., and Sönnichsen, C., “Separation of nanoparticles by gel electrophoresis according to size and shape,” Nano Lett. 7, 2881–2885 (2007). 10.1021/nl071615y [DOI] [PubMed] [Google Scholar]
- 41.Happel, J. and Brenner, H., Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media (Noordhoff, 1983). [Google Scholar]
- 42.Harrison, D. J., Fluri, K., Seiler, K., Fan, Z., Effenhauser, C. S., and Manz, A., “Micromachining a miniaturized capillary electrophoresis-based chemical analysis system on a chip,” Science 261, 895–897 (1993). 10.1126/science.261.5123.895 [DOI] [PubMed] [Google Scholar]
- 43.Hejazian, M. and Nguyen, N.-T., “Magnetofluidic concentration and separation of non-magnetic particles using two magnet arrays,” Biomicrofluidics 10, 044103 (2016). 10.1063/1.4955421 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hejazian, M., Li, W., and Nguyen, N. T., “Lab on a chip for continuous-flow magnetic cell separation,” Lab Chip 15, 959–970 (2015). 10.1039/C4LC01422G [DOI] [PubMed] [Google Scholar]
- 45.Hoggard, A., Wang, L.-Y., Ma, L., and Fang, Y., “Using the plasmon linewidth to calculate the time and efficiency of electron transfer between gold nanorods and graphene,” ACS Nano 7, 11209–11217 (2013). 10.1021/nn404985h [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Holm, S. H., Beech, J. P., Barrett, M. P., and Tegenfeldt, J. O., “Separation of parasites from human blood using deterministic lateral displacement,” Lab Chip 11(7), 1326–1332 (2011). 10.1039/c0lc00560f [DOI] [PubMed] [Google Scholar]
- 47.Hoshino, K., Huang, Y.-Y., Lane, N., Huebschman, M., Uhr, J. W., Frenkel, E. P., and Zhang, X., “Microchip-based immunomagnetic detection of circulating tumor cells,” Lab Chip 11, 3449 (2011). 10.1039/c1lc20270g [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hsu, J.-P., Lin, C.-Y., Yeh, L.-H., and Lin, S.-H., “Influence of the shape of a polyelectrolyte on its electrophoretic behavior,” Soft Matter 8, 9469–9479 (2012). 10.1039/c2sm25741f [DOI] [Google Scholar]
- 49.Hu, G., Jin, W., Zhang, W., Wu, K., He, J., Zhang, Y., Chen, Q., and Zhang, W., “Surfactant-assisted shape separation from silver nanoparticles prepared by a seed-mediated method,” Colloids Surf. A 540, 136–142 (2018). 10.1016/j.colsurfa.2017.12.071 [DOI] [Google Scholar]
- 50.Huang, P. Y. and Joseph, D. D., “Effects of shear thinning on migration of neutrally buoyant particles in pressure driven flow of Newtonian and viscoelastic fluids,” J. Nonnewton. Fluid Mech. 90, 159–185 (2000). 10.1016/S0377-0257(99)00074-9 [DOI] [Google Scholar]
- 51.Huang, P. Y., Feng, J., Hu, H. H., and Joseph, D. D., “Direct simulation of the motion of solid particles in Couette and Poiseuille flows of viscoelastic fluids,” J. Fluid Mech. 343, 73–94 (1997). 10.1017/S0022112097005764 [DOI] [Google Scholar]
- 52.Huang, L. R., Cox, E. C., Austin, R. H., and Sturm, J. C., “Continuous particle separation through deterministic lateral displacement,” Science 304(5673), 987–990 (2004). 10.1126/science.1094567 [DOI] [PubMed] [Google Scholar]
- 53.Hubbard, J. B. and Douglas, J. F., “Hydrodynamic friction of arbitrarily shaped Brownian particles,” Phys. Rev. E 47(5), R2983 (1993). 10.1103/PhysRevE.47.R2983 [DOI] [PubMed] [Google Scholar]
- 54.Huckel, E., “Die kataphorese der kugel,” Phys. Z. 25, 204–210 (1924). [Google Scholar]
- 55.Hur, S. C., Choi, S.-E., Kwon, S., and Carlo, D. D., “Inertial focusing of non-spherical microparticles,” Appl. Phys. Lett. 99, 044101 (2011). 10.1063/1.3608115 [DOI] [Google Scholar]
- 56.Inglis, D. W., Riehn, R., Austin, R. H., and Sturm, J. C., “Continuous microfluidic immunomagnetic cell separation,” Appl. Phys. Lett. 85, 5093–5095 (2004). 10.1063/1.1823015 [DOI] [Google Scholar]
- 57.Inglis, D. W., Riehn, R., Sturm, J. C., and Austin, R. H., “Microfluidic high gradient magnetic cell separation,” J. Appl. Phys. 99, 08K101 (2006). 10.1063/1.2165782 [DOI] [Google Scholar]
- 58.Jana, N. R., “Nanorod shape separation using surfactant assisted self-assembly,” Chem. Commun. 15, 1950–1951 (2003). 10.1039/b303103a [DOI] [PubMed] [Google Scholar]
- 59.Jeffery, G. B., “The motion of ellipsoidal particles immersed in a viscous fluid,” Proc. R. Soc. London A 102, 161 (1922). 10.1098/rspa.1922.0078 [DOI] [Google Scholar]
- 60.Jiang, M., Budzan, K., and Drazer, G., “Fractionation by shape in deterministic lateral displacement microfluidic devices,” Microfluid Nanofluidics 19(2), 427–434 (2015). 10.1007/s10404-015-1572-6 [DOI] [Google Scholar]
- 61.Jones, T. B., Electromechanics of Particles (Cambridge University Press, 1995). [Google Scholar]
- 62.Kang, J. H., Krause, S., Tobin, H., Mammoto, A., Kanapathipillai, M., and Ingber, D. E., “A combined micromagnetic-microfluidic device for rapid capture and culture of rare circulating tumor cells,” Lab Chip 12, 2175 (2012). 10.1039/c2lc40072c [DOI] [PubMed] [Google Scholar]
- 63.Kato, H., Nakamura, A., Banno, H., and Shimizu, M., “Separation of different-sized silica nanoparticles using asymmetric flow field-flow fractionation by control of the Debye length of the particles with the addition of electrolyte molecules,” Colloids Surf. A 538, 678–685 (2018). 10.1016/j.colsurfa.2017.11.067 [DOI] [Google Scholar]
- 64.Kim, B. and Kim, J. M., “Elasto-inertial particle focusing under the viscoelastic flow of DNA solution in a square channel,” Biomicrofluidics 10, 024111 (2016). 10.1063/1.4944628 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Kim, S. T., Rah, K., and Lee, S., “Effect of surfactant on retention ratio behaviors of polystyrene latex particles in sedimentation field-flow fractionation: Effective boundary slip model approach,” Langmuir 28, 10672–10681 (2012). 10.1021/la301593b [DOI] [PubMed] [Google Scholar]
- 66.Kose, A. R., Fischer, B., Mao, L., and Koser, H., “Label-free cellular manipulation and sorting via biocompatible ferrofluids,” Proc. Natl. Acad. Sci. U.S.A. 106, 21478–21483 (2009). 10.1073/pnas.0912138106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Kowalczyk, B., Lagzi, I., and Grzybowski, B. A., “Nanoseparations: Strategies for size and/or shape-selective purification of nanoparticles,” Curr. Opin. Colloid Interface Sci. 16, 135–148 (2011). 10.1016/j.cocis.2011.01.004 [DOI] [Google Scholar]
- 68.Laohakunakorn, N., Ghosal, S., Otto, O., Misiunas, K., and Keyser, U. F., “DNA interactions in crowded nanopores,” Nano Lett. 13, 2798–2802 (2013). 10.1021/nl401050m [DOI] [PubMed] [Google Scholar]
- 69.Leighton, D. and Acrivos, A., “The Shear-induced migration of particles in concentrated suspensions,” J. Fluid Mech. 181, 415–439 (1987). 10.1017/S0022112087002155 [DOI] [Google Scholar]
- 70.Lenshof, A. and Laurell, T., “Continuous separation of cells and particles in microfluidic systems,” Chem. Soc. Rev. 39, 1203–1217 (2010). 10.1039/b915999c [DOI] [PubMed] [Google Scholar]
- 71.Li, M., Muñoz, H., Schmidt, A., Guo, B., Lei, C., Goda, K., and Di Carlo, D., “Inertial focusing of ellipsoidal Euglena gracilis cells in a stepped microchannel,” Lab Chip 16, 4458–4465 (2016). 10.1039/C6LC01118G [DOI] [PubMed] [Google Scholar]
- 72.Li, P., Kumar, A., Ma, J., Kuang, Y., Luo, L., and Sun, X., “Density gradient ultracentrifugation for colloidal nanostructures separation and investigation,” Sci. Bull. 63, 645–662 (2018). 10.1016/j.scib.2018.04.014 [DOI] [PubMed] [Google Scholar]
- 73.Liang, L. and Xuan, X., “Continuous sheath-free magnetic separation of particles in a U-shaped microchannel,” Biomicrofluidics 6, 044106 (2012). 10.1063/1.4765335 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Liang, L., Zhang, C., and Xuan, X., “Enhanced separation of magnetic and diamagnetic particles in a dilute ferrofluid,” Appl. Phys. Lett. 102, 234101 (2013). 10.1063/1.4810874 [DOI] [Google Scholar]
- 75.Liu, X., “Particle separation using electrokinetically-driven deterministic lateral displacement: A computational study,” PhD thesis (Clemson University, Clemson, SC, 2016). [Google Scholar]
- 76.Liu, F.-K., Ko, F.-H., Huang, P.-W., Wu, C.-H., and Chu, T.-C., “Studying the size/shape separation and optical properties of silver nanoparticles by capillary electrophoresis,” J. Chromatogr. A 1062, 139–145 (2005). 10.1016/j.chroma.2004.11.010 [DOI] [PubMed] [Google Scholar]
- 77.Liz-Marzán, L. M., Sánchez-Iglesias, A., Scarabelli, L., and Pérez-Juste, J., “Tips and tricks practical guide to the synthesis of gold nanorods,” J. Phys. Chem. Lett 6, 4270–4279 (2015). 10.1021/acs.jpclett.5b02123 [DOI] [PubMed] [Google Scholar]
- 78.Lu, X. and Xuan, X., “Elasto-inertial pinched flow fractionation for continuous shape-based particle separation,” Anal. Chem. 87, 11523–11530 (2015). 10.1021/acs.analchem.5b03321 [DOI] [PubMed] [Google Scholar]
- 79.Lu, X., Zhu, L., Hua, R.-M., and Xuan, X., “Continuous sheath-free separation of particles by shape in viscoelastic fluids,” Appl. Phys. Lett. 107, 264102 (2015). 10.1063/1.4939267 [DOI] [Google Scholar]
- 80.Martin, S. G., “Geometric control of the cell cycle,” Cell Cycle 8, 3643–3647 (2009). 10.4161/cc.8.22.9891 [DOI] [PubMed] [Google Scholar]
- 81.Masaeli, M., Sollier, E., Amini, H., Mao, W., Camacho, K., Doshi, N., Mitragotri, S., Alexeev, A., and Di Carlo, D., “Continuous inertial focusing and separation of particles by shape,” Phys. Rev. X 2(3), 031017 (2012). 10.1103/physrevx.2.031017 [DOI] [Google Scholar]
- 82.Matsunaga, D., Meng, F., Zoettl, A., Golestanian, R., and Yeomans, J. M., “Focusing and sorting of ellipsoidal magnetic particles in microchannels,” Phy. Rev. Lett. 119, 198002 (2017a). 10.1103/PhysRevLett.119.198002 [DOI] [PubMed] [Google Scholar]
- 83.Matsunaga, D., Zöttl, A., Meng, F., Golestanian, R., and Yeomans, J. M., “Far-field theory for trajectories of magnetic ellipsoids in rectangular and circular channels,” IMA J. Appl. Math. 83(4), 767–782 (2018). 10.1093/imamat/hxy019 [DOI] [Google Scholar]
- 84.McGrath, J., Jimenez, M., and Bridle, H., “Deterministic lateral displacement for particle separation: A review,” Lab Chip 14(21), 4139–4158 (2014). 10.1039/C4LC00939H [DOI] [PubMed] [Google Scholar]
- 85.McHale, G. and Newton, M. I., “Liquid marbles: Principles and applications,” Soft Matter 7, 5473–5481 (2011). 10.1039/c1sm05066d [DOI] [Google Scholar]
- 86.McLaughlin, J. B., “The lift on a small sphere in wall-bounded linear shear flows,” J. Fluid Mech. 246, 249–265 (1993). 10.1017/S0022112093000114 [DOI] [Google Scholar]
- 87.Messauda, F. A., Sandersona, R. D., Runyon, J. R., Ottec, T., Pasch, H., and Williams, S. K. R., “An overview on field-flow fractionation techniques and their applications in the separation and characterization of polymers,” Prog. Poly. Sci. 34, 351–368 (2009). 10.1016/j.progpolymsci.2008.11.001 [DOI] [Google Scholar]
- 88.Mirowski, E., Moreland, J., Zhang, A., Russek, S. E., and Donahue, M. J., “Manipulation and sorting of magnetic particles by a magnetic force microscope on a microfluidic magnetic trap platform,” Appl. Phys. Lett. 86, 243901 (2005). 10.1063/1.1947368 [DOI] [Google Scholar]
- 89.Mitragotri, S. and Lahann, J., “Physical approaches to biomaterial design,” Nat. Mater. 8, 15 (2009). 10.1038/nmat2344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Monjezi, S., Jones, J. D., Nelson, A. K., and Park, J., “The effect of weak confinement on the orientation of nanorods under shear flows,” Nanomaterials 8(3), 130 (2018a). 10.3390/nano8030130 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Monjezi, S., Patterson, G. K., Nelson, A. K., and Park, J., “A model for the depletion layer prediction in a dilute suspension of rigid rod-like particles under shear flows in the entire range of Peclet numbers,” Chem. Eng. Sci. 189, 394–400 (2018b). 10.1016/j.ces.2018.05.059 [DOI] [Google Scholar]
- 92.Monjezi, S., Schneier, M., Choi, J., Lee, S., and Park, J., “The shape effect on the retention behaviors of rod-like particles in field-flow fractionation: Theoretical model derivation considering the steric-entropic mode,” J. Chromtgr. A ■ (submitted). [DOI] [PubMed] [Google Scholar]
- 93.Nguyen, T. M., Liu, J., and Hackley, V. A., “Fractionation and characterization of high aspect ratio gold nanorods using asymmetric-flow field flow fractionation and single particle inductively coupled plasma mass spectrometry,” Chromatography 2, 422–435 (2015). 10.3390/chromatography2030422 [DOI] [Google Scholar]
- 94.Niazi, S., Habibian, M., and Rahimi, M., “A comparative study on the separation of different-shape particles using a mini-hydrocyclone,” Chem. Eng. Technol. 40(4), 699–708 (2017). 10.1002/ceat.201600322 [DOI] [Google Scholar]
- 95.Nivedita, N. and Papautsky, I., “Continuous separation of blood cells in spiral microfluidic devices,” Biomicrofluidics 7, 054101 (2013). 10.1063/1.4819275 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Oseguera, F. A., Pérez, E., and Goicochea, A. G. “Simulation of polyelectrolytes in solution using dissipative particle dynamics in the grand canonical ensemble: Interaction strength and salt effects,” preprint arXiv:1001.3357 (2010).
- 97.Ozkumur, E., Shah, A. M., Ciciliano, J. C., Emmink, B. L., Miyamoto, D. T., Brachtel, E., Yu, M., Chen, P. I., Morgan, B., and Trautwein, J., “Inertial focusing for tumor antigen–dependent and–independent sorting of rare circulating tumor cells,” Sci. Transl. Med. 5, 179ra147 (2013). 10.1126/scitranslmed.3005616 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Paiè, P., Che, J., and Di Carlo, D., “Effect of reservoir geometry on vortex trapping of cancer cells,” Microfluid Nanofluidics 21, 104 (2017). 10.1007/s10404-017-1942-3 [DOI] [Google Scholar]
- 100.Park, J., “Dynamics of suspensions of rod-like polymers with hydrodynamic interactions,” PhD thesis (University of Florida, Gainesville, FL, 2009). [Google Scholar]
- 101.Park, J., “Shape-based particle separation field flow fractionation: Past and current research,” Separation 34, 28–29 (2014). [Google Scholar]
- 102.Park, J. and Butler, J. E., “Inhomogeneous distribution of a rigid fibre undergoing rectilinear flow between parallel walls at high Peclet numbers,” J. Fluid Mech. 630, 267–298 (2009). 10.1017/S0022112009006545 [DOI] [Google Scholar]
- 103.Park, J. and Butler, J. E., “Analysis of the migration of rigid polymers and nanorods in a rotating viscometirc flow,” Macromolecules 43, 2535–2543 (2010). 10.1021/ma901369a [DOI] [Google Scholar]
- 104.Park, J. and Mittal, A., “An improved model for the steric entropic mode for separation of rod-like particle in field flow fractionation,” Chromatography 2, 472–487 (2015). 10.3390/chromatography2030472 [DOI] [Google Scholar]
- 105.Park, J., Bricker, J. M., and Butler, J. M., “Cross-stream migration in dilute solutions of rigid polymers undergoing rectilinear flow near a wall,” Phys. Rev. E 76(4), 040801 (2007). 10.1103/PhysRevE.76.040801 [DOI] [PubMed] [Google Scholar]
- 106.Phelan, Jr., F. R. and Bauer, B. J., “Comparison of steric effects in the modeling of spheres and rod-like particles in field-flow fractionation,” Chem. Eng. Sci 64, 1747–1758 (2009). 10.1016/j.ces.2008.10.006 [DOI] [Google Scholar]
- 107.Piagnerelli, M., Boudjeltia, K. Z., Brohée, D., Vereerstraeten, A., Piro, P., Vincent, J.-L., and Vanhaeverbeek, M., “Assessment of erythrocyte shape by flow cytometry techniques,” J. Clin. Pathol. 60, 549–554 (2007). 10.1136/jcp.2006.037523 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Reece, A., Xia, B., Jiang, Z., Noren, B., McBride, R., and Oakey, J., “Microfluidic techniques for high throughput single cell analysis,” Curr. Opin. Biotechnol. 40, 90–96 (2016). 10.1016/j.copbio.2016.02.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Runyon, J. R., Goering, A., Yong, K., and Williams, S. K. R., “Preparation of narrow dispersity gold nanorods by asymmetrical flow field-flow fractionation and investigation of surface plasmon resonance,” Anal. Chem. 85, 940–948 (2013). 10.1021/ac302571g [DOI] [PubMed] [Google Scholar]
- 111.Sajeesh, P. and Sen, A. K., “Particle separation and sorting in microfluidic devices: A review,” Microfluid Nanofluidics 17, 1–52 (2014). 10.1007/s10404-013-1291-9 [DOI] [Google Scholar]
- 112.Schimpf, M., Caldwell, K., and Giddings, J. C., Field-Flow Fractionation Handbook (Wiley-Interscience, New York, 2000). [Google Scholar]
- 113.Segre, G., “Radial particle displacements in poseuille flow of suspensions,” Nature 189, 209–210 (1961). 10.1038/189209a0 [DOI] [Google Scholar]
- 114.Segré, G. and Silberberg, A., “Behaviour of macroscopic rigid spheres in poiseuille flow part 2. Experimental results and interpretation,” J. Fluid Mech. 14, 136–157 (1962). 10.1017/S0022112062001111 [DOI] [Google Scholar]
- 123.Sengupta, A., “Liquid crystal theory,” Topographical Microfluidics 32, 7–36 (2013). 10.1007/978-3-319-00858-5_2 [DOI] [Google Scholar]
- 115.Seo, K. W., Byeon, H. J., Huh, H. K., and Lee, S. J., “Particle migration and single-line particle focusing in microscale pipe flow of viscoelastic fluids,” RSC Adv. 4, 3512–3520 (2014). 10.1039/C3RA43522A [DOI] [Google Scholar]
- 116.Sharma, V., Park, K., and Srinivasarao, M., “Colloidal dispersion of gold nanorods: Historical background, optical properties, seed-mediated synthesis, shape separation and self-assembly,” Mat. Sci. Eng. R 65, 1–38 (2009a). 10.1016/j.mser.2009.02.002 [DOI] [Google Scholar]
- 117.Sharma, V., Park, K., and Srinivasarao, M., “Shape separation of gold nanorods using centrifugation,” Proc. Natl. Acad. Sci. U.S.A. 106(13), 4981–4985 (2009b). 10.1073/pnas.0800599106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Smoluchowski, M., “Contribution à la théorie de l’endosmose électrique et de quelques phénomènes corrélatifs,” Bull. Akad. Sci. Cracovie 8, 182–200 (1903). 10.1051/jphystap:019040030091201 [DOI] [Google Scholar]
- 119.Strubbe, F., Beunis, F., Brans, T., Karvar, M., Woestenborghs, W., and Neyts, K., “Electrophoretic retardation of colloidal particles in nonpolar liquids,” Phys. Rev. X 3(2), 021001 (2013). 10.1103/physrevx.3.021001 [DOI] [Google Scholar]
- 120.Tadjiki, S. and Beckett, R., “Experimental verification of the steric-entropic mode of retention in centrifugal field-flow fractionation using illite clay plates,” J. Chromtgr. A 1538, 60–66 (2018). 10.1016/j.chroma.2018.01.041 [DOI] [PubMed] [Google Scholar]
- 121.Takeyama, H., Kanamaru, A., Yoshino, Y., Kakuta, H., Kawamura, Y., and Matsunaga, T., “Production of antioxidant vitamins, β-carotene, vitamin C, and vitamin E, by two-step culture of Euglena gracilis Z,” Biotechnol. Bioeng. 53, 185–190 (1997). [DOI] [PubMed] [Google Scholar]
- 122.Thompson, A. J., Mastria, E. M., and Eniola-Adefeso, O., “The margination propensity of ellipsoidal micro/nanoparticles to the endothelium in human blood flow,” Biomaterials 34, 5863–5871 (2013). 10.1016/j.biomaterials.2013.04.011 [DOI] [PubMed] [Google Scholar]
- 124.Tyler, T. P., Lin, P. A., Tian, Y., Gao, H. J., Gao, X. P., Sankaran, R. M., and Hersam, M. C., “Centrifugal shape sorting of faceted gold nanoparticles using an atomic plane-selective surfactant,” J. Phys. Chem. Lett. 3(11), 1484–1487 (2012). 10.1021/jz3005283 [DOI] [PubMed] [Google Scholar]
- 125.Upsal, W. E., Eral, H. B., and Doyle, P. S., “Engineering particle trajectories in microfluidic flows using particle shape,” Nature Comm. 4, 2666 (2013). 10.1038/ncomms3666 [DOI] [PubMed] [Google Scholar]
- 126.Velmurugan, N., Sung, M., Yim, S. S., Park, M. S., Yang, J. W., and Jeong, K. J., “Systematically programmed adaptive evolution reveals potential role of carbon and nitrogen pathways during lipid accumulation in Chlamydomonas reinhardtii,” Biotech. Biofuel. 7, 117–134 (2014). 10.1186/s13068-014-0117-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Viovy, J.-L., “Electrophoresis of DNA and other polyelectrolytes: Physical mechanisms,” Rev. Mod. Phys. 72, 813 (2000). 10.1103/RevModPhys.72.813 [DOI] [Google Scholar]
- 128.Vojtíšek, M., Tarn, M. D., Hirota, N., and Pamme, N., “Microfluidic devices in superconducting magnets: On-chip free-flow diamagnetophoresis of polymer particles and bubbles,” Microfluid Nanofluidics 13, 625–635 (2012). 10.1007/s10404-012-0979-6 [DOI] [Google Scholar]
- 129.Wang, R., Ji, Y., Wu, X., Liu, R., Chen, L., and Ge, G., “Experimental determination and analysis of gold nanorod settlement by differential centrifugal sedimentation,” RSC Adv. 6(49), 43496–43500 (2016). 10.1039/C6RA07829J [DOI] [Google Scholar]
- 130.Wei, G., Liu, F., and Wang, C. R., “Shape separation of nanometer gold particles by size-exclusion chromatography,” Anal. Chem. 71(11), 2085–2091 (1999). 10.1021/ac990044u [DOI] [PubMed] [Google Scholar]
- 131.Xiong, B., Cheng, J., Qiao, Y., Zhou, R., He, Y., and Yeung, E. S., “Separation of nanorods by density gradient centrifugation,” J. Chromatogr. A 1218(25), 3823–3829 (2011). 10.1016/j.chroma.2011.04.038 [DOI] [PubMed] [Google Scholar]
- 132.Xu, X., Caswell, K. K., Tucker, E., Kabisatpathy, S., Brodhacker, K. L., and Scrivens, W. A., “Size and shape separation of gold nanoparticles with preparative gel electrophoresis,” J. Chromatogr. A 1167, 35–41 (2007). 10.1016/j.chroma.2007.07.056 [DOI] [PubMed] [Google Scholar]
- 133.Yamane, Y.-i., Utsunomiya, T., Watanabe, M., and Sasaki, K., “Biomass production in mixotrophic culture of Euglena gracilis under acidic condition and its growth energetics,” Biotechnol. Lett. 23, 1223–1228 (2001). 10.1023/A:1010573218863 [DOI] [Google Scholar]
- 134.Yang, S., Lee, S. S., Ahn, S. W., Kang, K., Shim, W., Lee, G., Hyun, K., and Kim, J. M., “Deformability-selective particle entrainment and separation in a rectangular microchannel using medium viscoelasticity,” Soft Matter 8, 5011–5019 (2012). 10.1039/c2sm07469a [DOI] [Google Scholar]
- 135.Yang, T.-H., Gilroy, K. D., and Xia, Y., “Reduction rate as a quantitative knob for achieving deterministic synthesis of colloidal metal nanocrystals,” Chem. Sci. 8, 6730–6749 (2017). 10.1039/c7sc02833d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Yao, I. C., Chang, C. W., Ko, H. W., Li, H., Lu, T. C., and Chen, J. T., “Rapid separation of gold nanorods in multilayer aqueous systems via centrifugation,” RSC Adv. 6(93), 90786–90791 (2016). 10.1039/C6RA21404E [DOI] [Google Scholar]
- 137.Yeh, L.-H. and Hsu, J.-P., “Effects of double-layer polarization and counterion condensation on the electrophoresis of polyelectrolytes,” Soft Matter 7, 396–411 (2011). 10.1039/C0SM00600A [DOI] [Google Scholar]
- 138.Zeming, K. K., Ranjan, S., and Zhang, Y., “Rotational separation of non-spherical bioparticles using I-shaped pillar arrays in a microfluidic device,” Nat. Commun. 4, 1625 (2013). 10.1038/ncomms2653 [DOI] [PubMed] [Google Scholar]
- 139.Zeng, J., Deng, Y., Vedantam, P., Tzeng, T.-R., and Xuan, X., “Magnetic separation of particles and cells in ferrofluid flow through a straight microchannel using two offset magnets,” J. Magn. Magn. Mater. 346, 118–123 (2013). 10.1016/j.jmmm.2013.07.021 [DOI] [Google Scholar]
- 140.Zhang, J. and Wang, C., “Numerical study of lateral migration of elliptical magnetic microparticles in microchannels in uniform magnetic fields,” Magnetochemistry 4, 16 (2018). 10.3390/magnetochemistry4010016 [DOI] [Google Scholar]
- 141.Zhang, J., Li, W., Li, M., Alici, G., and Nguyen, N., “Particle inertial focusing and its mechanism in a serpentine microchannel,” Microfluid Nanofluidics 17, 305–316 (2014a). 10.1007/s10404-013-1306-6 [DOI] [Google Scholar]
- 142.Zhang, J., Yan, S., Alici, G., Nguyen, N., Di Carlo, D., and Li, W., “Real-time control of inertial focusing in microfluidics using dielectrophoresis (DEP),” RCS Adv. 4, 62076–62085 (2014b). 10.1039/c4ra13075h [DOI] [Google Scholar]
- 143.Zhang, W., Hu, G., Zhang, W., Qiao, X., Wu, K., Chen, Q., and Cai, Y., “Surfactant-directed synthesis of silver nanorods and characteristic spectral changes occurred by their morphology evolution,” Physica E 64, 211–217 (2014c). 10.1016/j.physe.2014.07.029 [DOI] [Google Scholar]
- 144.Zhao, W., Zhu, T., Cheng, R., Liu, Y., He, J., Qiu, H., Wang, L., Nagy, T., Querec, T. D., Unger, E. R., and Mao, L., “Label-free and continuous-flow ferrohydrodynamic separation of HeLa cells and blood cells in biocompatible ferrofluids,” Adv. Funct. Mater. 26, 3990–3998 (2016). 10.1002/adfm.201503838 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Zhao, Q., Yuan, D., Yan, S., Zhang, J., Du, H., Alici, G., and Li, W., “Flow rate-insensitive microparticle separation and filtration using a microchannel with arc-shaped groove arrays,” Microfluid Nanofluidics 21, 55 (2017). 10.1007/s10404-017-1890-y [DOI] [Google Scholar]
- 147.Zhou, R. and Wang, C., “Multiphase ferrofluid flows for micro-particle focusing and separation,” Biomicrofluidics 10, 034101 (2016). 10.1063/1.4948656 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Zhou, Y. and Xuan, X., “Diamagnetic particle separation by shape in ferrofluids,” Appl. Phys. Lett. 109, 102405 (2016). 10.1063/1.4962638 [DOI] [Google Scholar]
- 149.Zhou, R., Bai, F., and Wang, C., “Magnetic separation of microparticles by shape,” Lab Chip 17, 401–406 (2017a). 10.1039/C6LC01382A [DOI] [PubMed] [Google Scholar]
- 150.Zhou, R., Sobecki, C. A., Zhang, J., Zhang, Y., and Wang, C., “Magnetic control of lateral migration of ellipsoidal microparticles in microscale flows,” Phys. Rev. Appl. 8, 024019 (2017b). 10.1103/PhysRevApplied.8.024019 [DOI] [Google Scholar]
- 151.Zhu, T., Marrero, F., and Mao, L., “Continuous separation of non-magnetic particles inside ferrofluids,” Microfluid Nanofluidics 9, 1003–1009 (2010). 10.1007/s10404-010-0616-1 [DOI] [Google Scholar]
- 152.Zhu, T., Cheng, R., Lee, S. A., Rajaraman, E., Eiteman, M. A., Querec, T. D., Unger, E. R., and Mao, L., “Continuous-flow ferrohydrodynamic sorting of particles and cells in microfluidic devices,” Microfluid Nanofluidics 13, 645–654 (2012). 10.1007/s10404-012-1004-9 [DOI] [PMC free article] [PubMed] [Google Scholar]