Musings on mechanism: quest for a quark theory of proteins?

Abstract

The give and take between biology and physics is an important part of the history of modern science, with this partnership perhaps now more intimate than ever. In this essay, I explore the ways in which these different fields can strengthen each other through their distinct outlooks on some of the most important questions being asked about the living world. In particular, I highlight three areas where the perspective from physics might lead to deeper insights into the workings of cells. First, I consider what it means for two ostensibly unrelated problems to be the same, and how such sameness can provide unexpected insights into apparently unrelated phenomena. Second, I consider different conceptions of what constitutes a mechanistic understanding of a given phenomenon with an emphasis on nonmolecular notions of mechanism. The third idea is the importance of “toy problems” as a way of providing foundational insights into the real problems. Though my focus here is primarily on ways in which physics approaches might prove interesting in biology, I close with an example of how biology might substantially alter physics by providing a forum and the tools to uncover a fundamental understanding of nonequilibrium phenomena.—Phillips, R. Musings on mechanism: quest for a quark theory of proteins?

PHYSICS AND CELL BIOLOGY

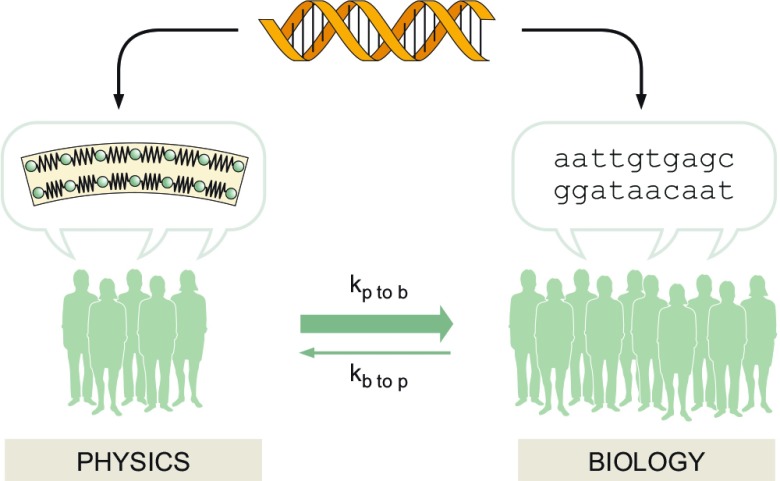
A recent editorial on these pages contained a wonderful vignette (1). At the beginning of the year, new graduate students in a program at the University of Massachusetts Medical School wondered “What do you think are the hottest fields in biology?” The answer offered by the author of that vignette: “I could have replied CRISPR, because this is my current work (and they knew it), but I surprised them instead by answering: The renewed focus on physics and cell biology.” What is it that has droves of students with physics training swarming to think about the mysteries of cellular behavior? To be sure, my experience tells me that it is much more common for a condensed matter physicist or even a string theorist to make the move to things biologic rather than to see a cell biologist declare at the age of 35 that they are going to retool and dedicate themselves to the study of topological insulators. What sets these trends making the study of the living world such an exciting forum for approaches from the physical sciences, leading to an imbalanced flux (see Fig. 1) of researchers between the two sciences, and how might the dialogue between cell biology and physics be seized on for the progress of both of them alike?

Figure 1.

Social kinetics in the life sciences. The on-rate for those with training in physics to move to biology appears to be much larger than the off-rate of those leaving biology to enter physics research.

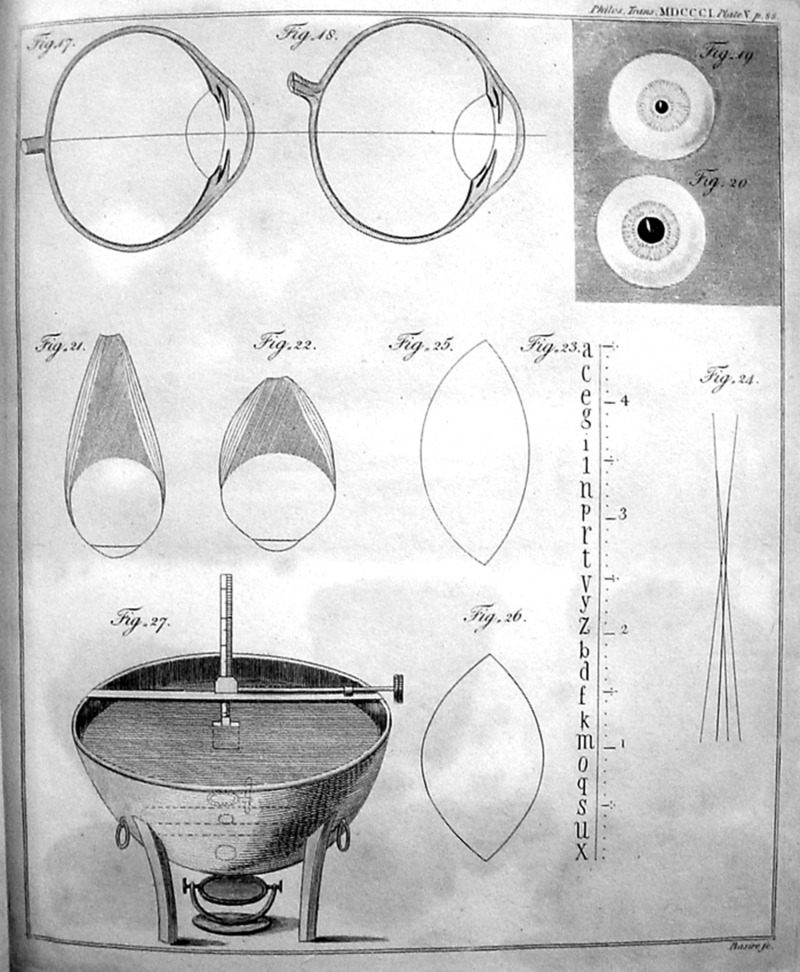
The dichotomy between biology and physics that we are used to today is actually rather new. Many of the greatest figures in both fields are known for intellectual cross training, borrowing ways of approaching problems from across the natural sciences. My background in physics draws to mind luminaries such as Robert Hooke, Thomas Young, Hermann von Helmholtz and James Clerk Maxwell, who I used to view strictly as physicists (2). But for Thomas Young, this gets the story exactly backward [for a fascinating account see Andrew Robinson’s fine book (3)]. This great polymath is known not only for his insights into interference of waves, but also for his efforts at deciphering the Rosetta stone. But, by his own account, Young was led by his work as a medical doctor and physiologist into the physics that he is so justly famous for. In his Autobiography, Young speaks about his amazing (and terrifying) experiments on his own eyes as he attempted to understand how eyes accommodate to objects at different distances [some of his original drawings from his 1801 paper (4) are shown in Fig. 2]. In these gruesome experiments, Young inserted measuring devices into the sides of his eyes to measure the size of his eyeball as he looked at objects at different distances away, attempting to test the hypothesis that accommodation is due to changes in the size of the eye itself (5, 6). In his Autobiography, Young says of his own development: “His pursuits, diversified as they were, had all originated in the first instance from the study of physic: the eye and the ear led him to the consideration of sound and light.” (Note that Young’s use of the word “physic” here refers to physiology and not physics.) Of course, there are many examples besides that of Thomas Young of k_b-to-p-type transitions (see Fig. 1) in which those interested in biological phenomena are driven to physical perspectives. The field of single-molecule biophysics, for example, is full of stellar young researchers, many of whom had their initial training in biology and made the move to more physics-based approaches.

Figure 2.

Thomas Young and his unsafe studies on the human eye! This page (plate V) from Young’s paper “On the Mechanism of the Eye” (4) shows some of Young’s thinking on the workings of the human eye. Figures 17 and 18 show sections of Young’s right eye, Figs. 19 and 20 show his left eye with different pupil dilations. Figures 21 and 22 illustrate different configurations of the muscles of the eye and their action on eye shape. (For Young’s explanations of the remaining figures, see the Bernard Becker Medical Library exhibit; http://beckerexhibits.wustl.edu/rare/win/PhilTrans1801.html).

So what exactly is the relationship between physics and biology and what should it be? Many have opined on this question and opinions range from one extreme to the other (7, 8). The great evolutionary biologist Ernst Mayr argued that biology is a different kind of science and should kick its habit of physics envy and toy mathematical models that he dismissed as beanbag genetics (9, 10). At the other end of the spectrum are the likes of Hermann von Helmholtz who, as best I can tell, never bothered with these distinctions, and instead carried on the great tradition of natural philosophy, freely ranging between topics that nowadays would occupy different departments or even schools within our universities (2). Those who arrive in biology from physics bring with them different sensibilities. They have different views of what questions are interesting, what it means to understand something and what is surprising (11). Indeed, to me one of the most important things that those with physics backgrounds bring to the study of biology is a completely different sense of what is a good biological question.

In this article, my ambition is to focus on just a few of the interesting ways in which physics and biology can play off of each other to the betterment of both. My argument has three parts. First, I will celebrate the physics tradition of saying that two things that are ostensibly quite different are in fact really the same and show how this can apply in biology too. With that argument in hand, we will turn to the issue of mechanism and the interesting ways in which this word is applied in physics that might be fruitfully employed in biology as well. Finally, I will explore the surprisingly long reach of what are sometimes known as “toy models” in physics with a call to the idea of exploiting such toy models in the study of living systems, even though they are not the real biological system.

THE SEARCH FOR SAMENESS

Young scientists and engineers of all stripes are subjected to a first indoctrination in physics during their early years in university. Shortly after beginning a foray into mechanics, these students are exposed to the seemingly sterile world of masses and springs. After drawing a free-body diagram to reckon how all the forces act on the mass, one ends up with an equation of motion that gives the position of that mass as a function of time. Little do we expect that in talking about the abstract behavior of blocks and springs, we have opened a vista onto one of the most far reaching of ideas: periodic motion around an equilibrium point. If they are lucky, these same students will later see that in fact, the mass-spring problem lays the groundwork for thinking about very different problems such as the pendulum and electrical circuits built up of resistors, capacitors and inductors. All are surprisingly described by the same equation,

where x is the displacement from equilibrium, ẋ = dx/dt is the velocity, ẍ = d²x/dt² is the acceleration, γ provides a measure of the damping, and ω is the vibrational frequency. Furthermore, depending upon the behavior of the forcing function F(t), the periodic motions can give rise to the transcendent phenomenon of resonance. This resonance idea is so far-reaching as to be astonishing; examples span from the behavior of optical resonators to the 54-minute sloshing of Lake Wakatipu in New Zealand (12). My point here is to demonstrate a fundamental principle in physics: the unity of apparently disparate phenomena.

A second example is given by the all-important wave phenomenon of interference; one of the fruits of Young’s interconnected thinking on physiology and physics. As noted in the fascinating article by Mollon (13), Thomas Young was the first to see the phenomenon of interference in all of its sameness, applying it not only to the well-known example of light, but also to auditory beats and to the seemingly obscure phenomenon of the tides in the Gulf of Tonkin, which don’t exhibit the usual twice-daily tides we are accustomed to at most beaches (14). We ourselves can see interference in the form of beautifully colored oil slicks on our driveways after a rain. Isaac Newton mapped out how the color depends upon the thickness of the film, and Thomas Young saw how to compute those colors on the basis of the simple idea of waves either reinforcing one another or canceling each other out. The critical idea of sameness is that in all of these cases, the interference phenomenon can be simply expressed as the result of several waves adding up either constructively or destructively, in a way that is relatively indifferent to whether those waves are sea waves, sound waves or light waves.

What about in biology? Can we find examples of sameness that would provide a unifying theme to disparate phenomena? One of my recent enthusiasms came from attending a several-month workshop at the Kavli Institute of Theoretical Physics (Santa Barbara, CA, USA) on the nascent and, for the moment, perhaps ill-defined field of evolutionary cell biology. The specific sameness that I find inspiring has to do with the way in which ideas from what is traditionally known as statistical physics have the same formal structure as ideas in population genetics. In statistical physics, the concept that presides over the whole field is known as the Boltzmann distribution, a concept that allows us to compute the probabilities of different microscopic states according to their energy with the probability of the form

This transcendent concept touches upon phenomena of all types, and I like to think of it as the levitation equation, since it tells us the probability that a molecule will levitate to a height h in a gravitational field or that a charged particle will settle at different positions within an electric potential. This same formula describes phenomena ranging from the pK_a of proteins and their willingness to give up charge groups to the binding curves that tell us about occupancy of molecules from receptors to hemoglobin to the conformations of semiflexible polymers, whether nucleic acids such as DNA or cytoskeletal filaments such as actin. To see the sameness between the Boltzmann formula of statistical mechanics and ideas from population genetics, consider the evolution of transcription factor binding sites (15–17). One can write a description of the time evolution of such transcription factor binding sites which in steady state yields a Boltzmann-like distribution with the selection coefficient serving the role of the energy and the population-size acting as a kind of inverse temperature (18).

My own personal favorite example of biologic sameness is offered by the phenomenon of allostery and the statistical mechanical models put forth to greet that phenomenon, namely, those of Monod-Wyman-Changeux and Koshland-Nemethy-Filmer (19–21). The striking sameness was particularly evident at a meeting at the Institut Pasteur to celebrate the 50th anniversary of the allostery concept with many of the central fields of biology on display. Neuroscience had its advocates on hand to talk about ion channels from an allostery perspective. The processes of the central dogma were represented on many fronts with researchers discussing everything from how genes are regulated by allosteric transcription factors to the structural conformations of the ribosome during translation. Human physiology was represented in the form of studies on hemoglobin. G-protein-coupled receptors took center stage as an example of how the allostery phenomenon impacts cell signaling. Other examples abounded as well including conformational changes in viral capsids, the workings of bacterial chemotaxis and molecular motors such as myosin. See Kalodimos and Edelstein, “Allosteric Interactions and Biologic Regulation (Part I)” (22) for the impressive breadth of topics described at that meeting. From my own point of view, the aspect of these talks that I found most interesting was the fact that just like the harmonic oscillator examples previously described (see Eq. 1), all of these seemingly disparate examples were described by the same fundamental equation that serves as the central equation of allostery, namely,

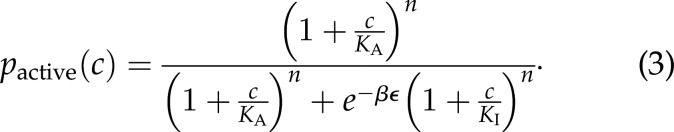Equation 3 tells us the probability of a molecule being in its active state as a function of ligand concentration c in terms of the energy difference between the inactive and active conformations ϵ and the affinity for n ligands for each state, K_A and K_I for the active and inactive states, respectively (20, 23, 24).

Despite the “endless forms most beautiful” that make biology such an exciting field, there is a different kind of beauty to be found in seeing the sameness in those endless forms. Physics provides a litany of examples of such sameness that might light the way for a similar approach to cell biology.

THE MEANING OF MECHANISM

We often hear the word “mechanism” to mean that we only have understood a given biological phenomenon when we have revealed the ways in which molecules give rise to it. But this definition of mechanism seems arbitrary by placing the entire explanatory burden on a particular length scale and is at odds with many striking examples from other corners of science. Since we know that the molecules that make up the mechanism of interest are made of atoms, why shouldn’t we insist on describing those atoms using quantum mechanics? But perhaps that doesn’t go far enough. We know in turn that those atoms have nuclei and those nuclei are themselves made of quarks. So if it is mechanistic purity that we are after, why shouldn’t we insist on a quark theory of proteins? The answer to this facetious question was already given years ago in Prof. Philip Anderson’s eloquent essay entitled “More is Different” (25, 26). There Anderson debunked the idea that knowing all the physics we want at one scale will permit us to explain phenomena at some other scale. Of course, protein structure and function is not simply applied atomic physics (or worse, nuclear or quark physics). Perhaps the physics of nonliving matter has interesting light to shed on these questions.

Continuum mechanics was originally conceived of without any knowledge of the underlying graininess of matter. And yet it provided a foundation for a mechanistic (but not microscopic) understanding of many of the world’s most familiar phenomena. Indeed, this approach was foreshadowed in Newton’s calculations showing that the behavior of the Earth as a gravitational body could be rigorously approximated by a point mass—the mass of the Earth all concentrated its center. But the approach is even more clear in later work, as scientists used the world view of Newtonian mechanics (i.e., F = ma) to describe complex situations such as the deformation of materials (such as the beam bending shown in the thought bubble of Fig. 1) or the motions of fluids. In fact, every time we utter words like density or concentration, we are engaged in precisely the kind of coarse-graining that is the essence of the great continuum theories of elasticity and hydrodynamics.

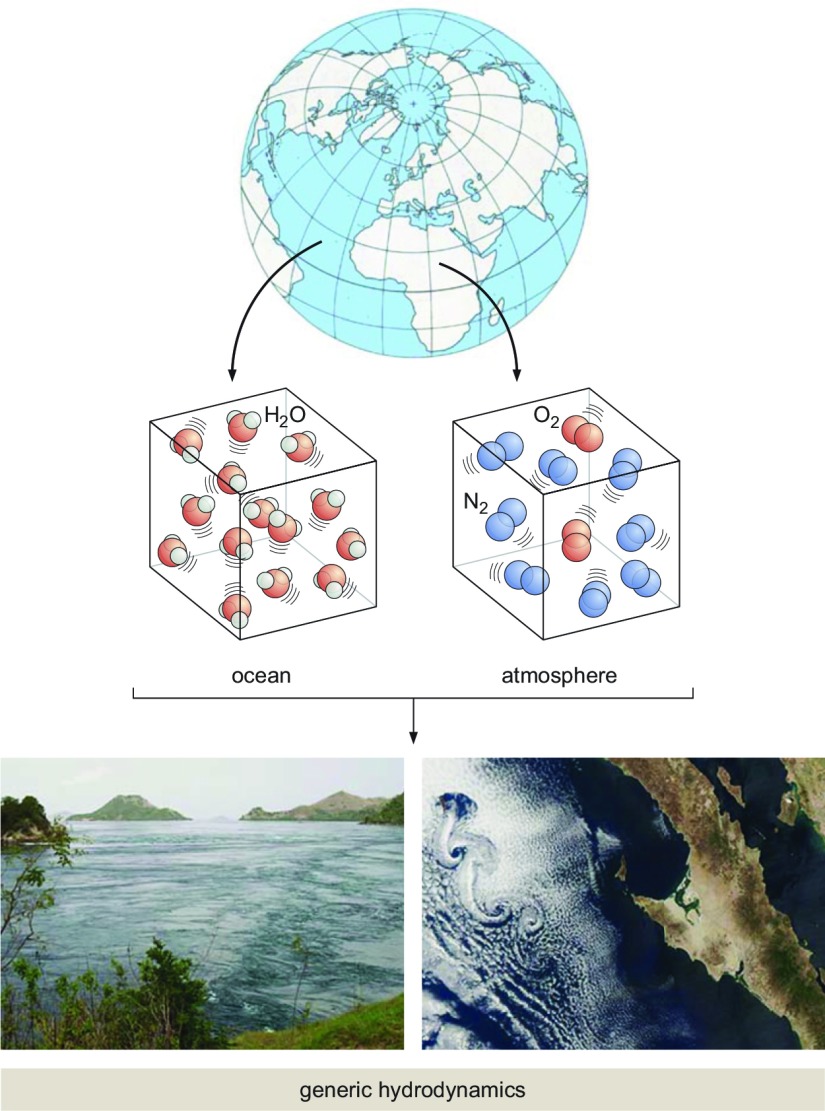
Hydrodynamics and elasticity are replete with examples of mechanisms for huge swaths of phenomenology in fluids and solids and even in more exotic forms of matter, such as liquid crystals or granular media (27). Hydrodynamics provides mechanistic explanations for observations without ever appealing to the underlying molecular reality of the fluid—be it ocean or the atmosphere (see Fig. 3)—in question. For example, the atmospheric vortices seen in the wake of the island off the coast of Baja California shown in Fig. 3 can be thought of as a direct mechanistic outcome of the laws of continuum mechanics, no molecules needed. Similarly, the beautiful cloud streets many of us have witnessed from an airplane window find their mechanistic explanation in those very same laws. Similar mechanistic explanations abound in the mechanics of solids where we can learn of the failure of epitaxially grown materials, the patterns of cracks in drying mud or even the folds in the gut (28–30).

Figure 3.

Coarse-grained microscopics gives rise to hydrodynamics. Whether we think of the ocean or the atmosphere, they are vast collections of molecules. (Note that the densities shown in the schematic are not at all to scale since atmospheric densities are way lower than those in water.) And yet, when we think of either of these situations as a continuum, the molecular details are insulated from view, resulting in the emergence of general equations of hydrodynamics, which are applicable to the formation of vortices at human scales in a narrow strait or at the scale of the entire coast of Baja in the atmosphere.

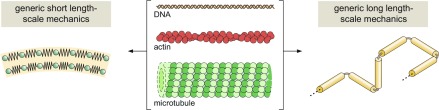
Let’s turn to biology now for some further examples. Higher-level mechanisms emerge from the behavior of polymers (and specifically, biological polymers), and these transcend the molecular particulars of the given polymer of interest as illustrated in Fig. 4. In certain short- and long- length-scale limits, all of these polymers behave in the same way. Here the sameness results from mechanisms that have nothing to do with the microscopics. The short-length scale behavior is typified by an elastic strain energy that says that the cost of bending a polymer, whether it be DNA or a microtubule, scales as the square of the curvature associated with that deformation. Meanwhile, at long length scales we can imagine the polymer as a collection of segments connected by flexible linkers leading to the random-walk model; here their overall configuration is determined by nothing more than combinatorics. The observed configurations, as measured by metrics such as the radius of gyration, result from nothing more than what configurations can happen in the most ways (i.e., the entropy is maximized). In this polymer example, mechanistic understanding from the short-length scale is that the cost to perturb systems about their equilibrium goes as the square of the geometric measure of the extent of that perturbation. The mechanism describing the long-length scale properties is in turn the notion of an entropic spring (31, 32). Together, the short- and long-length-scale properties give rise to an overarching parameter known as the persistence length that codifies these features (31, 33).

Figure 4.

Far reaching polymer mechanisms. Biological polymers come in different shapes and sizes. And yet, at small scales, the energetics of deforming them can be described by a model based on the curvature energy. At long-length scales, the response is dictated by the random-walk model. In both of these cases, the mechanistic understanding is not found by looking at molecular degrees of freedom, but rather by appealing to higher-level descriptions of the notion of springiness.

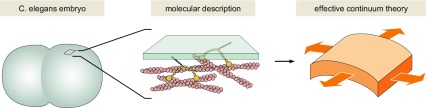
Of course, there are things that descriptions like that above are completely missing. For example, the polymers as we described them in Fig. 4 cannot account for nucleotide hydrolysis, and yet, such hydrolysis leads to many of the most wonderful aspects of cytoskeletal behavior (34). But thinking about the active processes conferred by energy consumption has led to another kind of higher-level mechanism. The driving forces that come from chemical energy can lead to other kinds of generic but rich and complex behavior that have whimsically been dubbed “molecular vitalism” (35). Through consideration of new features that emerge when chemical energy is consumed, an elevated version of the coarse-grained descriptions of hydrodynamics has emerged. The theory of active matter generalizes the continuum mechanics ideas of classic physics and teaches us how to think about the stresses (a generalization of the force concept) in systems such as the collective of molecular motors and cytoskeletal filaments found in both cells and embryos (36, 37). We illustrate this in the context of the actin cortex in Caenorhabditis elegans embryos, shown in Fig. 5.

Figure 5.

The active matter protectorate. Fluorescence microscopy studies have revealed the presence of a dynamic actin cortex in a thin layer near the surface of the embryo. The molecular basis of this active behavior in this case is collective interactions between active filaments and myosin motors. Active matter can be described by a macroscopic constitutive model in which stresses are created by virtue of these underlying molecular motions.

The active-matter concept, just like the random-walk treatment of a polymer, offers a definition of mechanism for a variety of problems that is at once powerful and yet completely devoid of any requirement that we appeal explicitly to molecules. To focus on the details of how specific molecular motors make their individual steps on the actin filaments shown in Fig. 5 misses an opportunity for a powerful concept of mechanism in much the same way that attempting to design a bridge or an airplane wing by renouncing elasticity in favor of an atomic-level description would. Thinking about the mechanics of a bridge in terms of how the iron atoms within the bridge interact with each other would miss the fundamental mechanistic level of description relevant for many problems in the mechanics of materials.

A final recent example of this same kind of higher-level mechanistic thinking—one that has become so popular it probably merits being called a fad—is the idea that the cellular interior is organized by phase transitions (38–42). Often, the mechanism that is behind the scenes when there are phase transitions is a competition between enthalpy and entropy, together defining the free energy. There are different underlying molecular implementations that tune this competition differently, but to my way of thinking, the key mechanistic insight is not which residue confers which contribution to the entropy, but rather the enthalpy-entropy balance itself.

The idea of coarse-graining is ubiquitous and far reaching in physics and is often a theoretical outcome that is sought after self-consciously. In fact, I have heard many physicists argue that one of the most lasting discoveries of the latter half of the 20th century in physics was the notion of what is technically known as the renormalization group. But the technical jargon doesn’t matter. What matters is that this collection of ideas tells us formally how to eliminate degrees of freedom, making it “one of the more profound discoveries in science, because it is a theory about theories. It has enabled physicists to become self-conscious about the way in which they construct physical theories” (43). For me, figuring out how to make theories about theories in biology is one of the great challenges of our time.

Such abstract thinking is the antithesis of the impressive but enormously complex biochemical maps that show us the hard won, detailed insights into the wiring of the biochemical pathways of the cell and leads me to think of recent efforts in which the cellular complement of proteins is treated in an extremely coarse-grained way. The idea is to think of the proteome as being constituted of several overarching protein categories. The impetus for this work came from early work on microbial physiology in which Shaechter et al. noticed that the ratio of ribosomal RNA to soluble protein had a simple linear relation with growth rate (44). Since these ribosomes are themselves roughly one third by mass made up of ribosomal proteins, what this implied is that somehow the fraction of total protein devoted to translation was a linearly increasing function of the growth rate. It is now possible to test these ideas by measuring the proteome quantitatively and to monitor how different parts of that enormous stockpile are redistributed according to growth rate (45, 46). Of course, I am not offering this story as a statement of the final word on this topic, but rather as an example of the self-conscious abstraction and simplification that might lead to deep biological insights, though at first blush seeming to ignore almost the entirety of the biochemical detail about the cell.

Though mechanism is often a code word for microscopic description, here I argue that that kind of narrow focus can actually deprive us of the right level of mechanistic understanding by missing entire classes of emergent mechanisms that are independent of microscopic particulars.

TUNING NATURE TO TEST OUR THINKING

In physics, as we have seen, you can get a surprisingly long way in understanding complex processes on the back of a simple toy model (recall the mass-spring example). Indeed, often these kinds of toy models have a surprising way of transcending their toy-model roots and becoming models of interesting real systems as well. Who would have believed that a toy model of a metal that starts out with the seemingly absurd assumption that the negatively charged electrons that make up the metal will behave as a gas of non-interacting particles inside a box and that this model could take us a long way to understanding the properties of real metals? Or that this same toy model would eventually be used to construct artificial atoms (47)?

One of my favorite examples in which toy models have been used to help us understand real systems is the case of the mechanics of one-dimensional beams. The flying buttresses of Notre Dame serve as a romantic backdrop for couples by the river Seine. But despite their impressive beauty, really, these wonderful objects are the result of enlightened empiricism; they serve the functional role of preventing the cathedral walls from collapsing. Indeed, in the words of 19th century architectural scholar Eugène-Emmanuel Viollet-le-Duc (1858), “Demander une église gothique sans arcs-boutants, c’est demander une navire sans quille ; c’est pour l’église comme pour le navire une question d’être ou de n’être pas” (To ask for a gothic cathedral without flying buttresses is the same as asking for a boat without a keel; for the church as for the boat, it is a question of to be or not to be) (48). And yet, to really understand the mechanics of the flying buttresses (and of many other structural elements that can also be thought of as slender rods including DNA and microtubules) required literally centuries of messing with the toy problem. Research at the hands of Galileo, Robert Hooke, Leonhard Euler, and many others culminated in a truly deep understanding of the toy problem of a simple, straight, homogeneous one-dimensional rod, with no reference to how these structures were used in the real setting of the cathedral. And yet, it is only by virtue of understanding this toy problem that real problems, such as the modern airplane wing, with its massive mechanical load due to the engines hanging from that wing, can be understood.

Of course, the idea of making toy problems that mimic some deeper reality we are interested in is not unique to physics. Even in a field science like ecology, this idea of creating artificial circumstances that allow us to sterilize a system to make it tractable is an accepted paradigm (49). Already in the 1960s, experiments by Robert Paine in the Pacific Northwest showed how much one might learn by artificially manipulating an ecosystem (50). In Paine’s case, by removing the large sea star Pisaster ochraceus from his study area, he was able to appreciate the role of keystone species and articulate the notion of trophic cascades. Without the top-down predation of barnacles by these sea stars, the barnacles thrived, only later to themselves be superseded by mussels. A staple of beginning ecology courses are graphs that show the number of species on these reefs as a function of time after sea star removal, which in the end, as noted in the beautiful article of Ed Yong about Paine, saw “a diverse tidal wonderland became a black monoculture of mussels” (51). Though I am sympathetic to the biologic temptation to build the cathedral now, I think there is great virtue also in openness to the value of toy models and toy experimental systems.

Cell biology has examples of its own. One of my favorites concerns the ways in which transcription factors are known to regulate many genes across the genome simultaneously (52). Before tackling that full complexity, the toy model of transcription is to examine one gene at a time and to make the simplifying assumption that different promoters are not competing for the same regulatory proteins (53–56). The role of competition across the genome can be studied by setting up a highly controlled toy system in which plasmids are used as decoys to do nothing more than pull transcription factors out of circulation. By controlling the number of plasmids and the strength of the decoy binding sites, the transcription factor titration effect can be quantitatively dissected in a way that prepares us for thinking about the real system (57, 58).

PHYSICS MEETS BIOLOGY, BIOLOGY MEETS PHYSICS

There are many ways in which fruitful interactions between physics and biology can lead to the betterment of both (7). For example, belying its name, thermodynamics has not traditionally focused on dynamics, but rather involved the study of thermostatics with an emphasis on what Herbert Callen called the “terminal privileged states” (i.e., equilibrium) of systems, rather than on the all-important issue of how complex, many-particle systems evolve over time to get to those terminal privileged states (i.e., dynamics) (59). But the breathless pace of scientific discovery in biology has revealed a long list of insights that force physicists to expand the way they think about the dynamics of that kind of matter we think of as living. Our discussion of active matter earlier in the essay gave a hint of how traditional notions of stress have had to be expanded to account for ideas such as active stresses and the swim pressure (60). But there are more challenges at the physics doorstep than simply figuring out how forces are transduced within living organisms. Many of the spatiotemporal structures we are used to in the living world are the direct result of energy flow through these systems and there remains much that we don’t understand about the energetic orchestration of such patterns.

It is hard to imagine a more compelling arena for the playing out of nonequilibrium processes than the living world, and I still hold out hope of truly revolutionary advances in our understanding of the physics of nonequilibrium systems as a result of physicists embracing the study of living matter. Though the conventional material world of everyday stuff can be thought of as different combinations of elements from the periodic table, the material genome, the language of DNA offers us a completely new category of knobs that can be manipulated to alter living materials. Indeed, these knobs might show the way in which biology can expand the physics repertoire through new conceptions of what constitutes a mechanism. Earlier in this essay, I considered ways in which the physical conception of mechanism might go beyond the traditional molecular picture driven by the amazing advances in both structural and molecular biology. But the notion of what constitutes a mechanism in the physics setting can similarly be expanded to now account for the way in which genes serve as sentinels of the molecular processes within cells giving rise to new kinds of feedback and regulation.

From the vantage point of society at large, my own take on the biology/physics interface is that I can think of no better time for those of us committed to the scientific study of the natural world to stick together. Though among ourselves biology and physics might seem worlds apart, when faced with the great challenges that lay before us, both within biology and beyond, it would behoove us to put these differences behind us and instead to recognize our deeply shared values. Andrew Dickson White, who along with Ezra Cornell, founded the great Cornell University, once penned his own views, from the perspective of the tail end of the 19th century, on the strange tensions that have always existed between those attempting to make sense of the world around them and those who view the world as beyond the ken of reason (61). So although physics and biology might conceptualize our thinking about the natural world differently, we ultimately have deeply shared values about how the tools of science can be used to find ever closer approximations to the truth.

The defining ambition of natural philosophy has been to understand the natural world. It is hard to dispute that many of the most intriguing aspects of the natural world that present themselves to our senses are those offered up by phenomena that are the exclusive domain of living organisms. In my view, those with backgrounds in all domains of the natural sciences, mathematics and engineering should share in the pleasure and privilege of studying Darwin’s “endless forms most beautiful.”