Power Estimation in Planning Randomized Two-Arm Pre-Post Intervention Trials with Repeated Longitudinal Outcomes

Abstract

Background:

Intervention effect on ongoing medical processes is estimated from clinical trials on units (i.e. persons or facilities) with fixed timing of repeated longitudinal measurements. All units start out untreated. A randomly chosen subset is switched to the intervention at the same time point. The pre-post switch change in the outcome between these units and unswitched controls is compared using Generalized Least Squares models. Power estimation for such studies is hindered by lack of available GLS based approaches and normative data.

Methods:

We derive Generalized Least Squares variance of the intervention effect. For the commonly assumed compound symmetry correlation structure, this leads to simple power formulas with important optimality properties. To maximize power given a constrained number of total time points, we investigate on the optimal pre-post allocation with the local minimization of variance.

Results:

In four examples from nursing home and HIV patients, the Toepltiz within-unit correlation of repeated measures differed from compound symmetry. We applied empirical Toeplitz based calculations for variance of the estimated intervention effect to these examples (each with up to seven longitudinal measures). Unlike what happened under compound symmetry, where power was often maximized with multiple observations being pre-intervention, for these examples, having one pre-intervention measure tended to maximize power. Attempts to approximate the Toeplitz variance structures with compound symmetry (to take advantage of the simpler formulas) resulted in overestimation of power for these examples.

Conclusions:

While compound symmetry correlation among repeated within-unit measures leads to simple power estimation formulas, this structure often did not hold. There may be strong underestimation of variance of the intervention effect estimate from incorporating short-term within-unit correlation estimates as a common compound symmetry correlation to approximate an unknown Toeplitz correlation without adequately accounting for the correlation between repeated measures declining with time.

Background

Randomized controlled trials and other experiments often evaluate repeated measures of continuous outcomes on each unit (i.e. either an individual or a facility) at systematic time points before and after an intervention begins, using two arms one which is entirely switched onto the intervention at a fixed time point and a control arm that remains in the same state [1–8]. Investigators measure longitudinal outcomes on each unit over b sequential pre-intervention time points. Then the units are randomly divided into two arms: one with intervention started at time point b+1 and one left without the intervention. The outcomes are then measured over k sequential post-intervention time points. The shortest duration clinical trial of this type is having b=0 pre-intervention and k=1 post-intervention time points; no pre-intervention measure and one post-intervention measure with randomization serving as the basis for the post-intervention comparison or the intervention arm. Increasing the number of pre-intervention measures (b) and/or post intervention measures (k) improves the precision of the estimated intervention effect and thus study power, but doing this is offset by increased study duration and costs.

In our nomenclature, “units” could be facilities such as nursing homes or persons such as HIV infected patients. For example, units could be HIV patients being treated for depression with the outcome measured at 6-month intervals with b=2 semiannual measures taken among all subjects then a randomly chosen 50% being put on an intervention with k=4 more semiannual depression measures taken among all subjects after that. The change in depression between the two pre-intervention and four post-intervention time points is compared between those who are and are not put on the intervention. This design is widely used, for example, in articles published over the past four years involving addiction, pain management, sleep, heart disease, cancer, dementia, hypothyroidism growth, medical communication, headaches, multiple sclerosis, nutrition, obesity and industrial production as outcomes and persons, animals and residence/ treatment/manufacturing facilities as units [9–15].

Power and sample size determination for planning and optimizing such longitudinal randomized trials is important [3,5–7,16]. Repeated measures within the same unit are typically positively correlated which compared to the standard setting of independence complicates power estimation as well as statistical analysis. While general linear models (GLMs) for both statistical analysis and power estimation exist [17–19], these methods require that the correlation structure of repeated measures within the same unit be estimated. This is often impossible when historical data is lacking. Going back to our example that measures depression outcomes over b=2 semiannual pre-intervention and k=4 semiannual post-intervention (or a total of 6 semiannual) it would be very likely that at the study planning stage this would be a new cohort with only limited historical data on within-unit correlation of repeated measures as use for such data for study planning would not have been anticipated 2.5 years in advance.

Our goal is to develop power estimation framework using Generalized Least Squares (GLS) estimators in planning randomized pre-post intervention longitudinal clinical trials with two intervention arms. We first consider the simplest repeated-measure correlation structure, compound symmetry (which in practice is often assumed given the absence of normative data) that leads to closed form formulas. We then study four real examples and observe that repeated-measure correlation attenuates with time leading to a more complicated repeated-measure structure known as Toeplitz (for which simple closed form formulas do not occur). The influence of pre-post intervention allocation of varying total visits on power (i.e. variance of the intervention effect estimate) for both the compound symmetry and the Toeplitz correlations of our four examples are studied. We also evaluate the ability to use a compound symmetry approximation to estimate study power for our four examples given the temptation investigators have to do this especially when limited normative data for correlation structure exists.

The paper is organized as follows: we first present a general linear model (GLM) for longitudinal data with pre-post repeated measures, then develop a generalized least squares (GLS) framework for estimation of the intervention effect and incorporated the GLS variance estimate into power estimation. Under compound symmetry, a simple GLS variance estimate formula for the intervention effect is derived and the influence of pre- (vs. post-) intervention time point allocation on this variance is evaluated. However, as compound symmetry correlation may not always hold, we empirically construct the Toeplitz correlation structures of repeated measures over seven time points from four longitudinal health care outcomes of nursing homes, hospitals and HIV infected patients. We investigated the true variances of intervention effect estimates obtained under these empirical correlation structures. The effect of pre-post allocation for varying T on these variances and closeness of variances obtained from the compound symmetry approximations that would be used by someone with limited normative data to those true variances for these settings are evaluated.

Methods (for Compound Symmetry and Toeplitz Correlation)

General linear model (GLM)

We begin with the statistical model of the intervention effect. For randomized longitudinal studies with two intervention arms, researchers encounter repeated measures of a quantitative outcome at T=b+k systematic time points with b being before and k being after the intervention is delivered to one of the arms. Let h denote the intervention arm with h=0 for control and h=1 for the new intervention. For each group, there are n_h units (n_o for the control and n₁ for the new intervention) and j={−b, −(b−1),…, −1, 1, 2,…, k} denotes the ordered times with {−b, −(b−1),…, −1} prior to and {1, 2,…, k} after the intervention onset. The goal is to assess the impact of the new intervention (versus control) on pre-post change in a longitudinal continuous outcome Y where Y_1ij is measure j from unit i in the new intervention arm and Y_oi’j’ is measure j’ from unit i’ in the control arm.

For example, consider a trial with n₀=n₁=30 hospitals in each arm. Let i denote hospitals (as “units”) where i=1,…,n_h. The “units” are measured annually for T=7 years total with b=2 years (2001 to 2002) before and k=5 (2003 to 2007) after the intervention implementation in the intervention arm (h=1). The outcome of interest, Y, could be portion of patients discharged within 30 days after surgery. Thus Y_1,3,−2 and Y_0,17,3 respectively denote the measurement taken in 2001 (2 years prior to start of the intervention) in the 3^rd hospital of the intervention arm and 2005 (3 years after the start of the intervention) in the 17^th hospital of the control arm, respectively. We assume complete data with T=b+k measures observed on each unit. Now Y_hij can be decomposed as:

$${\text{Y}}_{\text{hij}}={\alpha +\beta }_{\text{j}}{+\theta \text{Z}}_{\text{hj}}{+\epsilon }_{\text{ij}}^{*}$$ (1)

The overall means (α) for two intervention arms are equal at baseline due to randomization. The fixed time effect (β_j) is modeled to allow for temporal effect at time point j. Now ${\text{Z}}_{\text{hj}}{\text{=I}}_{\left\{\text{h=1,j>0}\right\}}$ as the intervention effect (θ) only delivers to the intervention arm (h=1) on the k post-intervention measurements. Any random unit (i^th level) effects are subsumed into the within-unit error term ${\text{ε}}_{\text{ij}}^{*}$ , where ${\epsilon }_{\text{ij}}^{*}~\text{N}(0,{\sigma }^2\text{V})$ with the correlation matrix V defined below in eqn. (2). We assume an immediate “jump effect” of size θ after the intervention begins at time j=1, that remains unchanged at subsequent time points. Note that other functions such as linear intervention effect increase $\text{j}\ast {\text{θZ}}_{\text{hj}}$ for j ≥ 1 or threshold followed by exponential decay ${\text{e}}^{-\text{j}}\ast {\text{θZ}}_{\text{hj}}$ for j ≥ 1 are possible. However, there may be settings where an immediate “jump effect” that continues forward unchanged is appropriate, such as when the intervention is a process change at a medical facility that can be implemented quickly; a drug that the body does not develop resistance or acclimation to, or an immediately successful behavioral intervention. Even if the intervention impact was not “immediate jump”, it could be close to this.

Generalized least squares (GLS) estimates

The matrix form of eqn. (1) is: $\text{Y=X}\underset{\_}{\text{β}}{\text{+ ε}}^{\text{*}}$, where ${\epsilon }_{\text{ij}}^{*}~\text{N}(0,{\sigma }^2\text{V})$. Here X represents the design matrix and Y is a vector of outcomes. For the general parameter vector $\underset{\_}{\text{β}}\text{=}(\alpha \text{,}{\text{β}}_{-(\text{b}-1)}\text{,…,}{\text{β}}_{-\text{1}}\text{,}{\text{β}}_1\text{,…,}{\text{β}}_{\text{k}},\theta )$, the corresponding design matrix X has columns (I,J_−(b−1),…, J₋₁,J₁,…, J_k, Z), with N*T rows per column. Z is a column vector of intervention indicator with Z_hj coded (0, 1) as defined above; J_−(b−1),…, J₋₁,J₁,…, J_k are columns corresponding to b+k-1 independent time coded variables as follows: for j={−(b−1), −(b-2),…, −1, 1, 2,…k), J_j={−1 at time –b (reference); 1 at time j; and 0 at all other times}. There is no column for J_−b as ${\text{β}}_{-\text{b}}=-{\displaystyle \sum _{\text{j=}-\text{(b}-\text{1)}}^{\text{k}}}{\text{β}}_{\text{j}}$ under the fixed effects constraint ${\displaystyle {\displaystyle \sum _{\text{j=}-\text{b}}^{\text{k}}}{\text{β}}_{\text{j}}=0.}$

More details on the full expansion of design matrix to a related design, the stepped wedge, can be found [20]. The covariance matrix V is made up with (n₀ + n₁) times block T diagonal matrices V₀’s with all off block diagonal matrix elements being 0. The error term measures are independent between units, and within-unit correlation structure is invariant given two visit j and j’, i.e., ${\rho }_{\text{i,jj}}{\text{,=ρ}}_{\text{i}’\text{,jj,}}\text{(i}\ne \text{I}’\text{,j}\ne \text{j’)}$. Thus,

$$\text{V}={\left(\begin{array}{ccc}{\text{V}}_{\text{0}}& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\text{V}}_{\text{0}}\end{array}\right)}_{\left({\text{n}}_{\text{0}}{\text{+n}}_{\text{1}}\right)\text{T}},$$

$$\text{where}{\text{V}}_{\text{0}}={\left(\begin{array}{cccccc}{\rho }_{\text{11}}& {\rho }_{\text{12}}& {\rho }_{\text{13}}& \cdots & {\rho }_{\text{1,T}-\text{1}}& {\rho }_{\text{1,T}}\\ {\rho }_{\text{21}}& {\rho }_{\text{22}}& {\rho }_{\text{23}}& \cdots & {\rho }_{\text{2,T}-\text{1}}& {\rho }_{\text{2,T}}\\ {\rho }_{31}& {\rho }_{32}& {\rho }_{33}& \cdots & {\rho }_{\text{3,T}-\text{1}}& {\rho }_{\text{3,T}}\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ {\rho }_{\text{T}-\text{1,1}}& {\rho }_{\text{T}-\text{1,2}}& {\rho }_{\text{T-1,3}}& \cdots & {\rho }_{\text{T}-\text{1,T}-\text{1}}& {\rho }_{\text{T}-\text{1,T}}\\ {\rho }_{\text{T,1}}& {\rho }_{\text{T,2}}& {\rho }_{\text{T,3}}& \cdots & {\rho }_{\text{T,T}-\text{1}}& {\rho }_{\text{T,T}}\end{array}\right)}_T$$ (2)

The within-unit correlation structure (ρ_ij) is often unknown in advance. Typically, correlation for any two visits would be monotonically non-increasing with |j –j’|, i.e., as the two time points are further separated, they will not become more strongly correlated [21–23].

The Generalized Least Squares (GLS) estimate for β is $\widehat{\underset{\_}{\beta }}$ in eqn. (3), which has proven properties of being the best linear unbiased estimator (BLUE) for $\widehat{\underset{\_}{\beta }}$ and uniform minimum variance (UMVU) if Y_hij is normally distributed [17].

$$\widehat{\underset{\_}{\beta }}={\left(\text{X′}{\text{V}}^{-1}\text{X}\right)}^{-1}\text{X′}{\text{V}}^{-1}\text{Y;}$$ (3)

The Generalized Least Squares variance of $\widehat{\underset{\_}{\beta }}$ is Λ in eqn. (4); a square matrix of order T+1 with the variance of $\widehat{\theta }$ the estimated intervention effect being in the last row and last column of Λ.

$$\Lambda =\left(\text{X′}{\text{V}}^{-1}\text{X}\right){-}^1{\sigma }^2.$$ (4)

General power estimation

We consider H_o : θ=0 versus H_A:θ=± θ_A where θ_A is some expected or hypothesized value for the intervention effect we wish to be able to statistically detect. Where without loss of generality, $\text{δ=}\frac{{\theta }_{Á}}{\text{σ}}$ is the effect size [24] or θ_A expressed as units of standard deviation. For practical repeated-measure designs, the normal approximation of the non-central t distribution can be applied [25]. In specific, the two distributions are almost identical when degrees of freedom (DF) γ > 30 and we have the following equations of power (1-β) in eqn. (5), in which Var $\left(\widehat{\theta }\right)$ as derived above in the GLS variance estimate in eqn. (4).

$${\theta }_{\text{A}}=\left({\text{Z}}_{1-\frac{\text{α}}{\text{2}}}+{\text{Z}}_{1-\beta }\right)\sqrt{\text{Var}\left(\widehat{\theta }\right)}$$ (5)

where αand βare Type I and Type II errors, respectively. For smaller sample sizes, it may be appropriate to approximate degrees of freedom (DF) (γ) in non-central t distribution for the mixture variance (for example, by Satterthwaite’s [26], and Kenward-Roger’s approximations [27]) and adjust eqn. (5) for this. But the full details are beyond the scope of this paper.

Repeated-measures correlation structure

As previously noted, one main difficulty in parametric analysis of longitudinal data lies in specifying covariance structure [4,23], i.e. estimating ρ_jj for j ≠ j’, as normative data from historical settings often does not exist or is limited. The simplest approximation is compound symmetry structure (V_CS) where correlations among repeated measures are assumed to be equal within the same unit; For example, V_CS is shown below with T=7.

$${\text{V}}_{\text{cs}}=\left[\begin{array}{ccccccc}1& \rho & \rho & \rho & \rho & \rho & \rho \\ \rho & 1& \rho & \rho & \rho & \rho & \rho \\ \rho & \rho & 1& \rho & \rho & \rho & \rho \\ \rho & \rho & \rho & 1& \rho & \rho & \rho \\ \rho & \rho & \rho & \rho & 1& \rho & \rho \\ \rho & \rho & \rho & \rho & \rho & 1& \rho \\ \rho & \rho & \rho & \rho & \rho & \rho & 1\end{array}\right]$$

For V_CS, correlation does not decline with time; thus ${\rho }_{\text{jj′}}\equiv {\rho }_{\text{jj}″}$ for, $\text{j}’\ne \text{j}”$ While surprisingly little empirical research has been done to confirm this structure holds given how often V_CS, is used in practice, CS has been found to be a reasonable simplification in planning longitudinal studies [5,28,29].

However, both logical reasoning and empirical data (such as that presented in the examples below) suggest that correlation declines with greater separation of time. Thus, stationary declining Toeplitz structure (V_TP) where _jj′ = ρ_|j−j′| with ${\rho }_{|\text{j}-\text{j}\text{′|=1}}\ge {\rho }_{|\text{j}-\text{j}\text{′|=2}}\ge {\text{…ρ}}_{|\text{j}-\text{j}\text{′|=T-1}}$ is reasonable or for T=7.

$${\text{V}}_{\text{cs}}=\left[\begin{array}{ccccccc}1& {\rho }_1& {\rho }_2& {\rho }_3& {\rho }_4& {\rho }_5& {\rho }_6\\ {\rho }_1& 1& {\rho }_1& {\rho }_2& {\rho }_3& {\rho }_4& {\rho }_5\\ {\rho }_2& {\rho }_1& 1& {\rho }_1& {\rho }_2& {\rho }_3& {\rho }_4\\ {\rho }_3& {\rho }_2& {\rho }_1& 1& {\rho }_1& {\rho }_2& {\rho }_3\\ {\rho }_4& {\rho }_3& {\rho }_2& {\rho }_1& 1& {\rho }_1& {\rho }_2\\ {\rho }_5& {\rho }_4& {\rho }_3& {\rho }_2& {\rho }_1& 1& {\rho }_1\\ {\rho }_6& {\rho }_5& {\rho }_4& {\rho }_3& {\rho }_2& {\rho }_1& 1\end{array}\right]$$

We note that stationarity is needed with ${\rho }_{|\text{j}-\text{j}\prime |}$ being constant over time for study planning otherwise, historical estimates of correlation cannot be applied to the future timepoints of a planned study [7,8]. However, V_TP may be hard to estimate in practice, especially in early planning stage when researchers do not have enough historical data going back T time points.

We do note that correlation may also be modeled as a deterministic function of the absolute time separation of the observations (i.e., as ρ∆t where ∆t is the difference in times which may have additive value if periodicity of evaluations varies within and between persons [3,30]. However, this is beyond the scope of this paper. Finally, once the data has been collected the restricted maximum likelihood (REML) is recommended for estimation of ρ for V_CS or $\left\{\text{ρ1,ρ2,…,}\right\}\left\{{\text{ρ1,ρ2,…,ρ}}_{\text{b+k-1}}\right\}$ for V_TP [2]. In fact, REML estimation is included as a default option in many current model-fitting software packages (e.g., Proc Mixed in SAS).

Compound symmetry correlation

Under the assumption of CS, we derive a closed form GLS formula for Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ follows. The GLS estimator of β is therefore $\widehat{\underset{\_}{\beta }}\text{=}{\left(\text{X′}{\text{V}}^{-\text{1}}\text{X}\right)}^{-\text{1}}\text{X′}{\text{V}}^{-\text{1}}\text{Y}$ and has variance $\Lambda \text{=}\left(\text{X′}{\text{V}}^{-\text{1}}{\text{σ}}^{\text{2}}\right)$ where Λ is a square matrix of order T+1. Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ is the last diagonal element of Λ. Using the inverse formula for portioned matrix as discussed [20], we calculate for the following GLS variance estimate of intervention effect. More derivations can be found in the Appendix.

$$\text{Var}\left({\widehat{\theta }}_{\text{CS}}\right)=\left(\frac{1}{{\text{n}}_0}+\frac{1}{{\text{n}}_1}\right)\frac{\left[1+\left(\text{b+k}-\text{1}\right)\rho \right]\left(1-\rho \right)}{\text{k}\left[1+\left(\text{b}-1\right)\rho \right]}{\text{σ}}^2$$ (6)

We note that after rearrangement of terms eqn. (6) is identical to the variance of intervention effect under compound symmetry presented in Section 5 from Frison and Pocock [5] who used a simpler approach of linear models on mean summary statistics that derived the same variance estimate as GLS model obtains. We are not, however, aware that this same result has been previously shown for the generally more powerful Generalized Least Squares design.

The relatively simple form of eqn. (6), simplifies investigation on optimal design in planning longitudinal study. For example, a repeated-measure design may have a constrained total number of longitudinal times T (T=b + k) because of the budget and/or time constraints. In such scenarios, finding the optimal allocation of T into b and k that maximizes power (or minimizes the sample size needed to obtain a given power) would be important. From eqn. (6), for CS structure with constrained T given ρ, the optimal b with the local minimization of variance is (as was also inferred by Frison and Pocock [5] using illustrative examples):

$${\text{b}}^{\text{*}}\text{=max}\left[\text{round}\left(\frac{\text{T+1}}{\text{2}}-\frac{\text{1}}{\text{2ρ}}\right)\text{,0}\right]$$ (7)

Note Y=round (X) rounds each element of X to the nearest integer. If an element is exactly between two integers, then Y can be either of the two integers. For example, suppose ρ=0.50 for a randomized trial, we can calculate the optimal pre-intervention measurements ${\text{b}}^{\text{*}}\text{=round}\left(\frac{\text{T+1}}{\text{2}}-\frac{\text{1}}{{\text{2}}^{\text{*}}\text{0}.\text{50}}\right)\text{=round}\left(\frac{\text{T}-\text{1}}{\text{2}}\right)$. Therefore, for odd ${\text{T,b}}^{\text{*}}\text{=round}\left(\frac{\text{T}-\text{1}}{\text{2}}\right)\text{=}\frac{\text{T}-\text{1}}{\text{2}}$; for even ${\text{T,b}}^{\text{*}}\text{=round}\left(\frac{\text{T}-\text{1}}{\text{2}}\right)\text{=}\frac{\text{T}-\text{1}}{\text{2}}\text{or}\frac{\text{T}-\text{1}}{\text{2}}$ ; Now b* is 0 for ρ=0 and approaches T/2 as ρ goes to 1.

To show how this work in practice including for comparison with our future examples involving empirical Toeplitz correlation structures, Table 1 presents examples under CS, letting T=2, 3,…, 7, and b range from 0 to T-1. We chose seven as a maximum for T which is reasonable for our examples below and for trials conducted for a maximum of 2–4 years with repeated measures at 3–6 months’ interval. In most published examples [9–15], we observed T was less than 8 as having more time points makes the study too long for practical consideration. We take ρ=0,0.25,0.50,0.75 to range from no correlation, to high correlation. Here and elsewhere we let n₀₌n₁₌30 units each in both the intervention and control arms and σ2=100 as simple common values to enable comparison across different designs and settings.

Table 1:

Illustrative variance of the intervention effect estimate Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ under compound symmetry correlation with T=2–7 and the other study design parameters standardized as follows^a

ρ=0b								ρ=0.25b
Total No Measures	Number of Measures Taken Pre-Intervention							Total No Measures	Number of Measures Taken Pre-Intervention
	b=0	b=1	b=2	b=3	b=4	b=5	b=6		b=0	b=1	b=2	b=3	b=4	b=5	b=6
T=2	3.33*	6.67						T=2	4.17*	6.25
T=3	2.22*	3.33	6.67					T=3	3.33	3.75*	6.00
T=4	1.67*	2.22	3.33	6.67				T=4	2.92	2.92*	3.50	5.83
T=5	1.33*	1.67	2.22	3.33	6.67			T=5	2.67	2.50*	2.67	3.33	5.71
T=6	1.11*	1.33	1.67	2.22	3.33	6.67		T=6	2.50	2.25	2.25*	2.50	3.21	5.63
T=7	0.95*	1.11	1.33	1.67	2.22	3.33	6.67	T=7	2.38	2.08	2.00*	2.08	2.38	3.13	5.56
ρ=0.50b								ρ=0.75b
Total No Measures	Number of Measures Taken Pre-Intervention							Total No Measures	Number of Measures Taken Pre-Intervention
	b=0	b=1	b=2	b=3	b=4	b=5	b=6		b=0	b=1	b=2	b=3	b=4	b=5	b=6
T=2	5.00*	5.00*						T=2	5.83	2.92*
T=3	4.44	3.33*	4.44					T=3	5.56	2.08*	2.38
T=4	4.17	2.78*	2.78*	4.17				T=4	5.42	1.81	1.55*	2.17
T=5	4.00	2.50	2.22*	2.50	4.00			T=5	5.33	1.67	1.27*	1.33	2.05
T=6	3.89	2.33	1.94*	1.94*	2.33	3.89		T=6	5.28	1.58	1.13	1.06*	1.22	1.98
T=7	3.81	2.22	1.78	1.67*	1.78	2.22	3.81	T=7	5.24	1.53	1.05	0.92*	0.94	1.15	1.93

^aVar $\left({\widehat{\theta }}_{\text{CS}}\right)$ with study design standardized as n₀=n₁=30, σ²=100.

^bThe common value of the compound symmetry correlation.

^*Column value of b that generates minimum variance for given the given row T.

For example, for n₀=n₁=30, σ²=100, with T=7 and b=2 visits before the intervention (and thus k=7–2=5 visits after the intervention), if CS correlation structure exists with ρ=0, the variance of the intervention effect estimate, i.e., Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ will be 1.33. However, if ρ=0.25, Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ rises to 2.00 (an increase of 50% over 1.33 when ρ=0) and if ρ=0.75, Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ drops to 1.05 (a reduction of 13.5% below 1.33 when ρ=0). These changes in Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ with ρ represent a complex interplay between amount new information brought in with new measures (which is decreasing with ρ) and amount of common effect removed by matching post intervention to pre-intervention measures (which is increasing with ρ) as given by eqn. (6). However, the ratio changes are invariant to n_o,n₁ and σ². Thus, if n₀=10, n₁=20 and σ²=40, with T=7 and b=2, Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ is still 50% higher when ρ=0.25 and 13.5% lower when ρ=0.75 compared to when ρ=0.

As T increases, Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ decreases thus power increases. However, when planning a study, this must be weighed against the extra cost and time that increasing T requires. For example, with n₀₌n₁₌30, σ²=100, ρ=0.25, starting with T=2 and b=1 pre-intervention time point, Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ is 6.25. This drops by 40% to 3.75 from increasing T to 3 (With b remaining at 1). However, further increasing T to 4 (with b still at 1) only reduces Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ another 13% (for a cumulative 53% of 6.25) down to 2.92. If the time points were 6 months apart, one would need to consider if this additional reduction of 13% was worth extending the study from 1 year to 1.5 years. Another consideration is when T is fixed, what value of b minimizes Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ in eqn. (7) and by how much. Cleary when ρ=0 there is no common within-unit effect to be removed by matching to pre-intervention measure so Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ is minimized by having maximizing k at T with b=0. As ρ increases this shifts towards larger b to remove common within-unit effect with $\text{b}\approx \frac{\text{T}}{\text{2}}$ being optimal for ρ ≥ 0.5. Although often b being one unit lower than this performs nearly as well.

Toeplitz correlation

As shown below, declining Toeplitz Correlation may occur frequently in practice which at least theoretically raises concerns about using the assumption of compound symmetry when planning studies. But there is no simple closed form for the variance of the estimated intervention effect under Toeplitz correlation V_TP, as was the case with compound symmetry in eqn. (6) rather Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ must be obtained by computer incorporating V_TP into eqn. (4). We thus explore this further in the Results Section using the empirical Toeplitz correlation structures of our four examples.

Results (for Empirically Observed Toeplitz Correlations)

Four Toeplitz correlation examples

While the formulas and properties for Compound Symmetry are easily implemented we wanted to see how well they applied to relevant data that we had in four examples with T=7 time points. The first two were collected on 365 New Jersey nursing homes being monitored every three months from the second quarter of 2011 to the fourth quarter of 2012 (seven quarters total) in the Nursing Home Compare [31] for proportions of: 1) long stay nursing home residents with weight loss (NH - WEIGHT LOSS); and 2) long-stay nursing home patients that reported fall injury (NH - FALL INJURY). Higher levels of NH - FALL INJURY and NH - WEIGHT LOSS are undesirable and targeted for improvement at a facility level. The “unit” for these examples is the facility with the repeated measures being quarterly facility values. Thus, for example, in a future study, it is conceivable that all 365 New Jersey nursing homes (NH) could be followed for b baseline time points to obtain proportions of their long stay residents with NH - WEIGHT LOSS and NH - FALL INJURY and then around 50% randomly chosen facilities be moved to a facility intervention to improve one or both outcomes with k post-intervention measures (proportions of long stay residents with each outcome) obtained from both groups for comparison of changes.

The next two examples were obtained from 1012 Bronx HIV infected women [32] who had complete data for their first seven semiannual visits at patient (PT) level: PT-CD4 counts and PT-CESD Depression scores [33]. Higher PT-CD4 and lower PT-CESD are desired and have been previously targeted for interventions. The repeated measures for these examples are from semi-annual visits of patients. It is conceivable that in a future study these patients could be followed for b baseline visits to obtain PT-CD4 counts and/or PT-CESD scores and then around 50% be put on an intervention to improve one or both outcomes with k post-intervention measures obtained from both groups for comparison of changes.

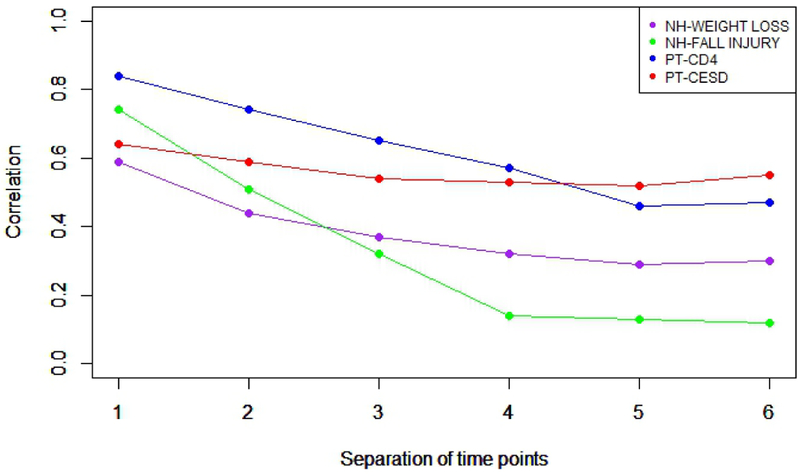
Table 2 and Figure 1 summarize the empirical Toeplitz correlation structures for the four outcomes described above estimated using the REML algorithm in the mixed procedure in SAS from our normative data. Visually, Figure 1 and Table 2 illustrate a range from starting correlations at ρ₁ of ~0.60 to ~0.85 and slight to steep generally monotonic linear declines of ~0.10 to ~0.62 going out to ρ₆.

Table 2:

Toeplitz Correlation Structures V_TP from four real examples.

Time point Separation	ρ1	ρ2	ρ3	ρ4	ρ5	ρ6
Among Quarterly Evaluations of 365 New Jersey Nursing Homes
NH-WEIGHT LOSS	0.59	0.44	0.37	0.32	0.29	0.30
NH-FALL INJURY	0.74	0.51	0.32	0.14	0.13	0.12
Among Semiannual Visits of 1012 HIV-Infected Bronx-WIHS Patients
PT- CD4	0.84	0.74	0.65	0.57	0.46	0.47
PT-CESD	0.64	0.59	0.54	0.53	0.52	0.55

Figure 1:

Visualization of Toeplitz correlation structures from four examples (T=b+k=7).

From the four examples in Figure 1, PT-CESD is qualitatively closest to compound symmetry with correlations between 0.52 and 0.64, but qualitatively the other correlation structures have rapid and/ or sustained decline in ρ starting at ρ₂ with greater separation of time points. We mow present variance estimates and optimality properties for these four examples obtained by computer using eqns. (4) and (5) incorporating VTP in Table 2 and Figure 1.

Toeplitz variance estimates

We calculated the variance of the intervention effect estimate, i.e., Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ from eqn. (4) using the identified Toeplitz correlations in Table 3 and Figure 1 over all possible b: k allocations with T=2,…, 7 for each of the four examples. As before, to permit comparability across examples, it was assumed that the variance of each outcome was σ²=100 and n₀₌ n₁₌30. This is presented in Table 3. For each example, 0= the b: k allocation for each value of T that gives the minimum variance is indicated in bold.

Table 3:

Variances of the intervention effect estimate Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ under the empirical Toeplitz correlation structures observed in our four examples with T=2–7 and the other study design parameters standardized as follows^a.

NH-WEIGHT LOSSb								NH-FALL INJURYb
Total No Measures	Number of Measures Taken Pre-Intervention							Total No Measures	Number of Measures Taken Pre-Intervention
	b=0	b=1	b=2	b=3	b=4	b=5	b=6		b=0	b=1	b=2	b=3	b=4	b=5	b=6
T=2	5.30	4.35*						T=2	5.80	3.02*
T=3	4.59	3.48*	4.26					T=3	5.03	2.90*	2.99
T=4	4.14	3.05*	3.38	4.21				T=4	4.37	2.75*	2.88	2.98
T=5	3.81	2.78*	2.95	3.34	4.20			T=5	3.75	2.63*	2.71	2.86	2.94
T=6	3.55	2.59*	2.69	2.90	3.31	4.19		T=6	3.45	2.15*	2.62	2.71	2.84	2.79
T=7	3.37	2.40*	2.48	2.62	2.86	3.28	4.15	T=7	3.17	2.06*	2.14	2.62	2.67	2.70	2.79
PT-CD4b								PT-CESDb
Total No Measures	Number of Measures Taken Pre-Intervention							Total No Measures	Number of Measures Taken Pre-Intervention
	b=0	b=1	b=2	b=3	b=4	b=5	b=6		b=0	b=1	b=2	b=3	b=4	b=5	b=6
T=2	6.13	1.96*						T=2	5.47	3.94*
T=3	5.77	1.84*	1.94					T=3	4.99	2.94*	3.57
T=4	5.45	1.80*	1.81	1.94				T=4	4.69	2.64	2.60*	3.48
T=5	5.16	1.77*	1.78	1.81	1.94			T=5	4.49	2.44	2.29*	2.49	3.41
T=6	4.83	1.77	1.75*	1.78	1.81	1.90		T=6	4.34	2.31	2.08*	2.16	2.40	3.36
T=7	4.67	1.49*	1.75	1.75	1.78	1.81	1.71	T=7	4.24	2.16	1.92*	1.92	2.04	2.31	3.26

^aVar $\left({\widehat{\theta }}_{\text{TP}}\right)$ with study design standardized as n₀=n₁=30, σ²=100.

^bThe empirical Toeplitz correlation structures for these examples are given in Table 2 and Figure 1

^*Column value of b that generates minimum variance for the given row T.

For example, with PT-CESD {T=2, b=1} and {T=5, b=2}, Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ are 3.94 and 2.29 respectively while for the same values of T and b for PT-CD4, the Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ are 1.96 and 1.78, respectively. The lower 7 for each of the four examples. As before, to permit comparability across examples, it was assumed that the variance of each outcome was variances for PT-CD4 reflect that it has higher values of ρ₁ and ρ₂. The slower declining in variance from T=2, b=1 to T=5, b=2 for PT-CD4 (which also occurs for NH - WEIGHT LOSS and NH - FALL INJURY) may reflect larger deviation from compound symmetry with ρ₁ being larger than the other correlations and thus having a more pronounced role in removing shared matched effects from adjacent pre-intervention observations.

Not surprisingly, Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ decreases for all as T increases. For T≥4, the advantages from increasing T in terms of Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ may attenuate. Also, not surprisingly, b=0 performs particularly poorly for all examples. But b=1 is the optimal choice for NH - WEIGHT LOSS, NH - FALL INJURY, and PT-CD4. For PT-CESD, which is closer to compound symmetry, b=1 is optimal for smaller T (T<4), but b=2 is optimal for larger T (T≥4). While more comprehensive analyses for other values of T and V_TP is beyond the scope of this paper, we believe that: i) V_TP presented here are likely representative of many settings ii) T ≈ 7 may be reasonable for many settings so this observation can be widely applicable.

CS variance approximation

If the actual structure of V_TP can be identified and the needed software is available, it is ideal to use it in eqn. (4) to obtain Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ for power estimation in eqn. (5). However, in practice, investigators often have limited access to: i) normative historical correlation structure data from which to obtain V_TP; ii) needed software to generate Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ from eqn. (4); iii) space in a grant proposal to explain and justly complicated parameter estimates for power estimation. Furthermore, power/sample size estimates using V_TP could have unknown robustness properties against misspecification on {ρ₁, …,ρ_T-1}. For the above reasons, investigators may opt to use a Compound Symmetry approximation even in settings where a non-CS V_TP is known or CS is not likely to hold. Indeed, in practice simpler statistical models are often fit when it is impossible or impractical to fit a more complicated model that is closer to truth. Still it is important to be aware how robust the approximation of V_TP with compound symmetry (in ways that are likely to occur) is.

For example, in many settings, the investigator may have data spanning two visits (such as data from two semiannual visits for our previous HIV+ patients, or two quarterly reports in the nursing home example) to obtain ρ₁. Or it may otherwise be possible to use other approaches to derive values for ρ₁ but not for other ρ′s. The most immediate choice (particularly if the investigator mistakenly believes the structure is V_CS) would be to use eqn. (6) with the observed or surmised ρ₁. This seems likely to lead to underestimation of the variance of the intervention effect estimate as the variance declines with ρ and for V_TP in our examples in Table 2 and Figure 1 and in general ρ₁ is the largest value.

Another option is that the investigator would try to estimate the average ρ in V_TP say as a weighted average of estimated ρ₁,ρ₂,…,ρ_T-1, i.e., ${\rho }_{\text{avg}}\text{=}\frac{\left(\text{T}-\text{1}\right){\rho }_{\text{1}}\text{+}\left(\text{T}-\text{2}\right){\rho }_{\text{2}}{\text{+…+ρ}}_{\text{T}-\text{1}}}{{\displaystyle {\sum }_{\text{i=1}}^{\text{T}-\text{1}}\text{i}}}$ and use this as the common ρ in V_TP approximation based on eqn. (6). If ρ₁,ρ₂,…,ρ_T-1 were known, then ρ_avg could be calculated directly and used as described above if the software to incorporate V_TP was unavailable. As ρ_avg will be smaller than ρ₁ if the correlation declines with temporal distance, use of ρ_avg would not have as strong a pull towards underestimation of the variance of the intervention effect as would use of ρ₁, in a V_CS approximation to V_TP.

For example, consider an investigator planning to use for NH - FALL INJURY described above as a longitudinal outcome in a randomized nursing home facility intervention with T=7. To refresh for NH - FALL INJURY in Table 2, ρ₁=0.74, ρ₂=0.51, ρ₃=0.32, ρ₄=0.14, ρ₅=0.13, ρ₆=0.12. But the investigator may not have all the normative data. If only ρ₁=0.74 were known, it might be used as a common ρ in a V_CS approximation to V_TP Alternatively, ${\rho }_{\text{avg}}\text{=}\frac{{\text{6ρ}}_{\text{1}}{\text{+5ρ}}_{\text{2}}{\text{+4ρ}}_{\text{3}}{\text{+3ρ}}_{\text{4}}{\text{+2ρ}}_{\text{5}}{\text{+ρ}}_{\text{6}}}{\text{6+5+4+3+2+1}}$ could be used in eqn. (6) under V_CS approximation to V_TP. If estimated correctly for this example, ${\rho }_{\text{avg}}\text{=}\frac{\text{6}\left(\text{0.74}\right)\text{+5}\left(\text{0.51}\right)\text{+4}\left(\text{0.32}\right)\text{+3}\left(\text{0.14}\right)\text{+2}\left(\text{0.13}\right)\text{+0.12}}{\text{21}}=0.43,$ is much less than the previously described ρ₁. The question we now address is how well use of V_CS in eqn. (6) with either (i.e., a correctly identified) ρ₁ or _avg as the common correlation performs in estimating Var $\left({\widehat{\theta }}_{\text{TP}}\right)$.

We let T range for 3 to 7 (as by default, T=2 is compound symmetry). We focus on b=1 as: i) in Table 3, b=1 typically minimizes the variance, and thus ii) b≥2 would be used only if this number of pre-intervention measures already existed in which case these could be used to identify more components of V_TP minimizing the need for a V_CS approximation. Figure 2 presents the actual Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ from V_TP and the Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ approximations using ρ₁ and ρ_avg. As before to allow for cross comparability between different estimates, we assume that σ²=100 and n₀₌n₁₌30 units in each treatment arm.

Figure 2:

Comparative variance for randomized designs over all possible b: k allocations with CS approximations.

Thus, for example, with NH - FALL INJURY for T=3 (on the x-axis in Figure 2) and b=1, Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ from V_TP shown in Table 2B is 2.90. If the investigator did not know V_TP but knew (or estimated correctly) ρ₁=0.74 and used it in eqn. (6) assuming CS, he would underestimate that variance as 2.15. However, if the investigator could obtain or correctly estimate ${\rho }_{\text{avg}}\text{=}\left(\frac{{\text{2ρ}}_{\text{1}}{\text{+ρ}}_{\text{2}}}{\text{2+1}}\text{=0.66}\right)$ and use this in eqn. (6) Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ is less underestimated, as 2.63.

For the three outcomes (PT-CD4, NH-WEIGHT LOSS, NH-FALL INJURY) where the correlations declined greatly after ρ₁ using V_CS with ₁ greatly underestimated Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ , sometimes by as much as 40% which would result in great overestimation of study power. For PT-CESD where the correlation was much closer to compound symmetry, the disparity while was much less being at most an underestimation of 13% of Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ when T=6. While not perfect, the performance of a correctly estimated ρ_avg in the V_CS approximations were much better. Often the Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ with ρ=ρ_avg was almot the same as the true Var $\left({\widehat{\theta }}_{\text{CS}}\right)$, while it sometimes underestimated Var $\left({\widehat{\theta }}_{\text{TP}}\right)$. The greatest underestimation of the variance was by 10% (for T=3 of PT-CD4).

Conclusion

The aim of this paper was to present a “usable” power and sample size estimation framework for randomized two-arm pre-post intervention trials with repeated continuous longitudinal outcomes. We developed Generalized Least Squares estimates of the intervention effect Var $\left(\widehat{\theta }\right)$ for general linear models assuming a jump effect on the outcome fully occurs immediately after the intervention is delivered.

Presented in eqn. (6) is an easily implemented formula for variance of the intervention effect estimate under the very commonly assumed compound symmetry correlation structure i.e., Var $\left({\widehat{\theta }}_{\text{CS}}\right)$. Not surprisingly, Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ decreases as the number of total visits T increases. But this must be weighed against the extra cost associated with more follow-up visits. For T that is fixed due to budget or time limitations researchers would like to determine the optimal number of pre-post intervention measures (b: k) to minimize Var $\left({\widehat{\theta }}_{\text{CS}}\right)$. From eqn. (7), the optimal b^∗ becomes larger as the correlation coefficient ρ increases for a constrained T because higher correlation increases benefits from matching on pre-intervention measurements. When ρ=0 there is no common within-unit effect, the variance is minimized by having maximizing k at T with b^∗=0. As ρ increases this shifts towards larger b∗ to remove common within-unit effect with ${\text{b}}^{\text{*}}\approx \frac{\text{T}}{\text{2}}$ being optimal for ρ≥ 0.5. But in practice smaller values also performed well with b being one unit lower than b^∗ performing nearly as well as b∗ in most cases.

Although compound symmetry is commonly used in healthcare research, the correlation structures of outcomes we evaluated from nursing homes and HIV patients behaved (sometimes very) different from CS. Therefore, further investigation on power approximation with a more general stationary declining Toeplitz correlation was needed. As simple closed form GLS variance formulas are not directly available for Toeplitz correlations, we numerically evaluated Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ using computer software in eqn. (4). While stochastically, increasing T reduced the Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ the declines were much lower especially for two of the four examples than they were with compound symmetry with T=7 giving only 24% - 32% lower Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ than T=2 for PT-CD4 and NH–FALL INJURY in studies with the same number of units. Such gains must be weighed the fact that studies with T=7 measures require 6 times as much follow up time as do those with T=2. In our four examples with fixed T, b=1 gave optimal or close to optimal results in minimizing Var $\left({\widehat{\theta }}_{\text{TP}}\right)$. Moreover, having at least one baseline pre-intervention measure is important as b=0 always produced (often substantially) larger Var $\left({\widehat{\theta }}_{\text{TP}}\right)$.

While when the correlation structure is Toeplitz, it is more accurate to estimate the variance of the intervention effect using V_TP in eqn. (4), investigators often neither have precise normative data to estimate the needed parameters ρ₁, …,ρ_T-1 nor the software/expertise to implement eqn. (4). However, in these settings, investigators often have some insight on correlations (i.e., to observe ρ₁ and/or estimate ρ_avg). In practice, as compound symmetry is often used as a default correlation structure where either observed or estimated ρ₁ or ρ_avg could be used as the common correlation in a compound symmetry approximation. Thus, we assessed how close the Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ from either of these approximations with the parameters correctly obtained was to the real Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ using closed form formula in eqn. (6) with T varied from 2 to 7 (with fixed b=1). The Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ approximations using =ρ_avg underestimated Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ by at most 10%, especially when the correlations declined dramatically over time. While the Var $\left({\widehat{\theta }}_{\text{CS}}\right)$ approximations using =ρ1 typically substantially underestimated the true Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ and thus overestimated power. Of note, we only focused on b=1 as this is typically the setting that maximizes power and where the true correlation structure could not be obtained, but results were similar for larger b (data not shown) Also there may be some other conservative approaches to overestimate Var $\left({\widehat{\theta }}_{\text{TP}}\right)$ when it cannot be calculated directly; for example by using mean summary statistics [5], or simple approximations using T=2 with b=k=1 and ρ=ρ₁.

There are some limitations in our work. For simplicity, we focused on balanced designs with equal time interval between visits and no missing data. We assumed an immediate one-time jump effect of the intervention, but in some settings, the effect may be linear cumulative or some other patterns. Also, our analysis was restricted to T ≤ 7 longitudinal measures as we observed to be the case in most previous published studies. While this need to be confirmed in future studies, we suspect, however, that the properties observed on optimal b: k allocation and compound symmetry approximation to Toeplitz correlations in our four examples, qualitatively hold when these settings are expanded. Although we assumed stationary covariance (a minimum requisite to use historical data for correlation estimation), covariance could change over time from uncontrollable mechanisms in practice. Relaxation of the above assumptions may likely lead to complicated settings that perhaps can only be addressed with simulation.

In conclusion, this paper developed a Generalized Least Squares power estimation framework based on correlation structures and investigated optimality for randomized longitudinal randomized intervention trials. Under the commonly made assumption of compound symmetry correlation, we derived a simple formula for the variance of the intervention effect estimate. However, CS may not always hold in the practice as shown in our real examples. In those examples, for T ≤ 7 total measures per unit, having b=1 pre-intervention visit typically minimized the variance of the estimated intervention effect. Furthermore, our examples suggest that if compound symmetry correlation structure is used to approximate Toeplitz correlation structure with short-term correlation assumed to hold for longer periods, there may be a strong bias towards underestimation of the variance of the intervention effect.

List of Abbreviations:

CS

Compound Symmetry

TP

Toeplitz

GLM

General Linear Model

GLS

Generalized Least Squares

NH

Nursing Home

PT

Patient