Abstract
Purpose:
Currently, the relative biological effectiveness (RBE) is assumed to be constant with a value of 1.1 in proton therapy. Although trends of RBE variations are well known, absolute values in patients are associated with considerable uncertainties. This study aims to evaluate the impact of a variable proton RBE in proton therapy liver trials using different fractionation schemes.
Methods:
Sixteen liver cancer cases were evaluated assuming two clinical schedules of 40 Gy/5 fractions and 58.05 Gy/15 fractions. The linear energy transfer (LET) and physical dose distribution in patients were simulated using Monte Carlo. The variable RBE distribution was calculated using a phenomenological model, considering the influence of the LET, fraction size and α/β value. Further, models to predict normal tissue complication probability (NTCP) and tumor control probability (TCP) were used to investigate potential RBE effects on outcome predictions.
Results:
Applying the variable RBE model to the 5 and 15 fractions schedules results in an increase in mean fraction-size equivalent dose (FED) to the normal liver of 5.0% and 9.6% respectively. For patients with a mean FED to the normal liver larger than 29.8 Gy, this results in a non-negligible increase in the predicted NTCP of the normal liver averaging 11.6%, ranging from 2.7 to 25.6%. On the other hand, decrease in TCP was less than 5% for both fractionation regimens for all patients when assuming a variable RBE instead of constant. Consequently, the difference in TCP between the two fractionation schedules did not change significantly assuming a variable RBE while the impact on the NTCP difference was highly case specific. In addition, both the NTCP and TCP decrease with increasing α/β value for both fractionation schemes, with the decreases being more pronounced when using a variable RBE compared to using RBE=1.1.
Conclusions:
Assuming a constant RBE of 1.1 most likely overestimates the therapeutic ratio in proton therapy for liver cancer, predominantly due to underestimation of the RBE-weighted dose to the normal liver. The impact of applying a variable RBE (as compared to RBE=1.1) on the NTCP difference of the two fractionation regimens is case dependent. A variable RBE results in a slight increase in TCP difference. Variations in patient radiosensitivity increase when using a variable RBE.
Keywords: proton therapy, liver cancer, relative biological effectiveness, radiobiological model, fractionation scheme
1. Introduction
Owing to the advantageous dose distribution compared to photon therapy, proton therapy has been widely applied in cancer treatments. Because the energy deposition characteristics of proton beams are different from those of photon beams, the same physical dose deposition may lead to different degrees of radiobiological effect. The relative biological effectiveness (RBE) of proton beams has been studied for decades (Raju 1995, Skarsgard 1998, Gerweck and Kozin 1999, Paganetti et al 2002, Paganetti 2014). Currently, the proton RBE is fixed with a value of 1.1 in the clinic (ICRU 2007), assuming protons are 10% more effective than photons. However, a wealth of experimental data demonstrates that the RBE depends on many factors, such as dose, linear energy transfer (LET), cell or tissue specific parameters such as α/β (Paganetti et al 2002, Paganetti 2014, Underwood and Paganetti 2016, Grassberger and Paganetti 2017). The actual RBE distribution in the patient may be heterogeneous, which might have an impact on the normal tissue complication probability (NTCP) and tumor control probability (TCP) in proton therapy. Studies on the influence of a variable RBE for prostate, brain and hypopharynx cancer cases have been published (Tilly et al 2005, Wedenberg and Tomadasu 2014, Ödén et al 2017).
Liver cancer is the second leading cause of the cancer death, with more than 700,000 death cases each year (Keane et al 2016). Radiotherapy is an important treatment option for many liver cancer patients that are not candidates for surgical resection. However, liver tumors are typically surrounded by normal liver tissue and the treatment field may cover large parts of the normal liver. Consequently, the dose delivered to the target is limited by the low dose tolerance of the normal liver, specifically to avoid radiation induced liver disease (RILD) which is the most common liver toxicity after the radiotherapy (Toramatsu et al 2013). In theory, the more conformal dose distribution in proton therapy should allow to spare most of the normal liver from high dose irradiation, which should reduce liver toxicity (Igaki et al 2018), and it is currently investigated in a randomized clinical trial (Hong et al 2016, ClinicalTrials.gov Identifier: NCT03186898).
Considering a variable RBE may lead to a different photon-equivalent dose distribution from that using RBE=1.1, and finally change the NTCP of the normal liver and TCP of the liver tumor. This study aims to understand the implications of variable RBE values based on data from an ongoing liver trial using different fractionation regimens at the Massachusetts General Hospital (MGH, ClinicalTrials.gov Identifier: NCT03186898). The focus of the study was not only on the impact of the variable RBE on the absolute NTCP and TCP values, but also on the relative effect of the variable RBE on the NTCP and TCP differences between two clinical fractionation schemes. The influence of the α/β uncertainty among the patient population was also evaluated.
2. Methods and material
2.1. Patient cases and fractionation schemes
Sixteen liver cancer cases treated with proton therapy were selected from the MGH patient database. Most of these cases (case 1~12 in table 1) were treated with 40 Gy in 5 fractions (Keane et al 2015, Hammad et al 2016), or 58.05 Gy in 15 fractions (Hong et al 2014, Hong et al 2016). The other four cases (case 13~16 in table 1) were treated with 50 Gy/5 fractions or 67.5 Gy/15 fractions. For the purpose of our analysis, each patient’s schedule was converted to 40 Gy in 5 fractions and 58.05 Gy in 15 fractions for comparison. For the conversion, the whole dose distribution was scaled., All patients considered had primary liver cancer treated with passively scattered proton therapy. The volumes of gross tumor and whole liver, and the number of fields are summarized in table 1.
Table 1.
Tumor, whole liver, and treatment characteristics for all cases.
| Case | Gross tumor volume (mL) |
Whole liver volume (mL) |
Number of fields |
Case | Gross tumor volume (mL) |
Whole liver volume (mL) |
Number of fields |
|---|---|---|---|---|---|---|---|
| Case 1 | 86.44 | 1676.78 | 2 | Case 9 | 89.7 | 1687.61 | 2 |
| Case 2 | 150.97 | 1932.99 | 4 | Case 10 | 227.9 | 1797.15 | 2 |
| Case 3 | 382.61 | 1496.59 | 2 | Case 11 | 16.45 | 2062.57 | 2 |
| Case 4 | 91.94 | 1522.65 | 4 | Case 12 | 452.36 | 2433.37 | 2 |
| Case 5 | 149.99 | 2429.46 | 2 | Case 13 | 44.34 | 2515.75 | 2 |
| Case 6 | 94.87 | 1205.96 | 2 | Case 14 | 23.1 | 1401.36 | 2 |
| Case 7 | 496.65 | 3274.57 | 2 | Case 15 | 28.55 | 1271.33 | 3 |
| Case 8 | 36.83 | 1021.76 | 2 | Case 16 | 9.21 | 1770.70 | 2 |
2.2. RBE model
In the linear-quadratic (LQ) model (Chadwick and Leenhouts 1973), the cell survival fraction, S, for the reference X-ray and the proton radiation can be described as:
| (1) |
| (2) |
where αX, βX, αp and βp are tissue specific parameters for X-ray and proton radiation, respectively. Since the RBE is defined as the ratio of the photon and proton physical dose for the same radiobiological endpoint (Paganetti 2014), the variable proton RBE can be derived for Sx=Sp as shown in equation 3.
| (3) |
In this study, a LQ model based RBE model was used in which the αp/αX and (βp/βX)1/2 were assumed to have a linear relationship with dose averaged LET (LETd) and depend on αX/βX (McNamara et al 2015).
| (4) |
| (5) |
Based on a collection of more than 70 reports of in vitro experiments (Paganetti 2014), the values of p0~3 in this model were fitted (McNamara et al 2015) to establish the RBE as a function of physical dose Dp, LETd and αX/βX for photons (referred to α/β from here).
| (6) |
In this study, the variable RBE was calculated using equation 6 where Dp represented the proton physical dose administered in a single-fraction resulting in an RBE weighted dose (‘photon equivalent dose’) for a single-fraction, dRBE. For each fractionated scheme, dRBE is applied in the same way as the physical dose per fraction in photon therapy.
2.3. Dose and LET calculations
The TOPAS Monte Carlo system (Perl et al 2012), which is a framework based on the Geant4 Monte Carlo codes (Agostinelli et al 2003), was used to calculate the three-dimensional dose and LETd distributions in this study. It has been used for dose and LET simulations in proton therapy patients previously (Grassberger et al 2011, Giantsoudi et al 2013, Sethi et al 2014). Furthermore, the treatment head in use at MGH has also been implemented in TOPAS (Paganetti et al 2004, Testa et al 2013, Polster et al 2015). An in-house code, MCAUTO (Verburg et al 2016), automatically generates the input file for patient simulations by linking the treatment planning system to TOPAS as described elsewhere (Paganetti et al 2008, Schuemann et al 2012, Schuemann et al 2014, McNamara et al 2015, Schuemann et al 2015). All simulations were performed on a high-performance research cluster with 30 parallel simulations for each patient field, each with 250000 protons starting at the entrance of the treatment head. A variance reduction method was employed in the simulations, in which particles were split when reaching two planes in the treatment head model, reducing the statistical uncertainty by a factor of 64 (Ramos-Mendez et al 2013). The output results of dose and LET distributions were processed to generate RBE and RBE weighted dose distributions utilizing CERR (Computational Environment for Radiological Research, a software platform for analyzing research results using radiation therapy treatment planning and imaging information (Deasy et al 2003)).
2.4. NTCP calculation
The NTCP of the normal liver was estimated with the Lyman–Kutcher–Burman (LKB) model (Lyman 1985, Kutcher and Burman 1989, Kutcher et al 1991), which predicts the dose-response of the normal tissue as a sigmoid relationship:
| (7) |
where
| (8) |
m is a dimensionless parameter representing the slope of the dose-response curve. TD50(v) represents the value of the dose D corresponding to the 50% probability of a complication with the fraction volume v of the tissue uniformly irradiated. It is related to the whole tissue (v=1) tolerance, which is represented by TD50(1), through a power law relationship with a parameter n representing the volume effectiveness:
| (9) |
For inhomogeneous irradiation, the v in equation 9 is replaced by Veff, as
| (10) |
where vi is the fraction volume of the sub-volume of the tissue irradiated with the dose Di. The veff can be calculated based on the dose-volume histogram (DVH), with D often set as the maximum dose in the DVH to ensure the Veff<1 (Luxton et al 2007).
The value of the parameter m, n and TD50(1) have been fitted by Dawson et al (2002) (n=0.97, m=0.12 and TD50(1)=39.8 Gy) for the normal liver, with the complication defined as the Radiation Therapy Oncology Group Grade 3 or higher RILD. This set of parameters has also been used by others when estimating the NTCP for normal liver (Dawson et al 2006, Toramatsu et al 2013, Woods et al 2016).
The parameter values are defined for a fractionation size of 1.5 Gy/fraction, taking the radiobiological effect of the dose per fraction into consideration. Thus, for the NTCP calculation, the actual RBE weighted dose in this study was normalized to the fraction-size equivalent dose (FED) of 1.5 Gy/fraction based on the LQ model (Dawson et al 2002, Kim and Tomé 2010), to correct for the difference in fractionation schemes between this work and the Dawson’s study:
| (11) |
where fS represents the reference fraction size, n and d represent the fraction number and RBE weighted dose per fraction. The normal liver is defined as the entire liver volume minus the gross tumor volume (GTV) as in Dawson et al (2002, 2005).
2.5. TCP calculation
A logistic model (Schultheiss et al 1983, Goitein et al 1985) was used to predict the TCP of the liver tumor irradiated with a dose D:
| (12) |
where TCD50 denotes the dose needed to result in a TCP of 50% and the coefficient k controls the coefficient k controls the slope of the sigmoid curve. In Lausch et al (2013), the value of TCD50 and k were fitted as 53 Gy and 4.8 for primary liver tumors for 6 months of local control, where a uniform dose distribution in the planning target volume (PTV) was assumed and the tumor dose D was converted to 2 Gy/fraction schedules with α/β=10 Gy. In the following TCP calculations, the TCP model was used together with Lausch’s fitted parameter values, and D represented the mean RBE weighted dose in the target region which was defined as PTV. The dose D was also converted to 2 Gy/fraction with equation 11 prior to the TCP calculation.
2.6. The impact of uncertainties in α/β value
As described above, not only the variable proton RBE depends on the α/β value, but also the predicted NTCP and TCP vary with α/β, since the RBE weighted dose needs to be converted to the FED with the α/β value as shown in equation 11. Tissue specific α/β values most likely vary among the patient population, and the published α/β values for the same tissue are often different (Paganetti 2017). Therefore, the impact of the α/β value uncertainty on the RBE, NTCP and TCP in liver proton therapy was further evaluated in this work.
As for the normal liver, estimated α/β values range between 2 and 3 Gy (Tai et al 2009, Dreher et al 2016, Ulrich et al 2017, Ohri et al 2018). For the liver tumor, an α/β of 10 Gy is typically suggested (Boda-Heggemann et al 2016, Fukugawa et al 2017, Unkelbach et al 2017, Su et al 2018), though some studies also report values ranging from 13 to 17 Gy (Tai et al 2008, Carabe et al 2011). In this study, an α/β of 2.5 Gy for the normal liver, and 10 Gy for the target region were used as reference in the RBE, NTCP and TCP calculation.
For NTCP considerations, α/β values of 2, 2.5 and 3 Gy were used. Though the set of parameter values of the NTCP model was fitted with α/β=2 Gy, it has also been used for α/β=2.5 Gy in some publications (Dawson et al 2006, Toramatsu et al 2013, Woods et al 2016). Accordingly, the parameter values of the LKB model were fixed when using different α/β values of the normal liver to estimate the impact of the α/β variation on the RBE and NTCP.
For the liver tumor, the uncertainty of α/β has been studied with α/β values of 7.2, 10 and 15 Gy, and the corresponding parameter values of the TCP model have also been fitted respectively by Lausch et al (2013). These α/β values were used in this work with the corresponding parameter values to study the impact of the α/β value uncertainty in TCP calculations.
3. Results
3.1. Impact of potentially variable RBE on the NTCP
The mean RBE weighted dose, mean FED normalized to 1.5 Gy/fraction, and NTCP of the normal liver for the sixteen patient cases with RBE=1.1 and variable RBE are shown in table 2. Due to the patient-specific anatomy and variation in radiation fields, the mean RBE weighted doses and mean FEDs in these patients are widely different leading to considerable differences in NTCP for both scenarios of RBE and both fractionation regimens. For example, in case 7 with 15 fractions, the mean RBE weighted dose in the normal liver using RBE=1.1 is ~24 Gy, which leads to a NTCP of more than 17%, while for case 11 it is only ~15 Gy with the NTCP approaching 0.
Table 2.
Mean RBE weighted dose, mean FED and NTCP of the normal liver (α/β=2.5 Gy).
| Case | Fraction | Prescribed dose (Gy) |
Mean RBE weighted dose | Mean FED (1.5 Gy/fraction) | NTCP | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RBE=1.1 (Gy) |
Variable RBE (Gy) |
Relative Differencea |
RBE=1.1 (Gy) |
Variable RBE (Gy) |
Relative Differencea |
RBE=1.1 | Variable RBE |
Differenceb | |||
| Case 1 | 5 | 40 | 16.51 | 17.08 | 3.5% | 38.98 | 40.78 | 4.6% | 35.7% | 50.3% | 14.6% |
| 15 | 58.05 | 23.96 | 25.53 | 6.6% | 35.12 | 38.30 | 9.1% | 12.6% | 31.2% | 18.6% | |
| Case 2 | 5 | 40 | 17.22 | 17.98 | 4.4% | 39.33 | 41.52 | 5.6% | 39.2% | 57.2% | 18.0% |
| 15 | 58.05 | 25.02 | 27.01 | 8.0% | 35.75 | 39.52 | 10.5% | 15.8% | 41.4% | 25.6% | |
| Case 3 | 5 | 40 | 14.31 | 14.94 | 4.4% | 34.46 | 36.36 | 5.5% | 9.2% | 17.5% | 8.3% |
| 15 | 58.05 | 20.76 | 22.44 | 8.1% | 30.89 | 34.20 | 10.7% | 2.0% | 8.6% | 6.6% | |
| Case 4 | 5 | 40 | 13.12 | 13.65 | 4.0% | 29.33 | 30.98 | 5.6% | 0.9% | 2.1% | 1.2% |
| 15 | 58.05 | 18.52 | 19.95 | 7.7% | 25.62 | 28.41 | 10.9% | 0.1% | 0.5% | 0.5% | |
| Case 5 | 5 | 40 | 15.51 | 15.95 | 2.8% | 32.72 | 33.99 | 3.9% | 5.2% | 8.6% | 3.4% |
| 15 | 58.05 | 22.36 | 23.53 | 5.2% | 29.93 | 32.14 | 7.4% | 1.4% | 4.1% | 2.7% | |
| Case 6 | 5 | 40 | 13.86 | 14.46 | 4.3% | 33.47 | 35.34 | 5.6% | 6.2% | 12.4% | 6.3% |
| 15 | 58.05 | 20.04 | 21.67 | 8.1% | 29.86 | 33.13 | 11.0% | 1.2% | 5.5% | 4.4% | |
| Case 7 | 5 | 40 | 16.61 | 17.04 | 2.6% | 40.81 | 42.23 | 3.5% | 49.8% | 61.4% | 11.6% |
| 15 | 58.05 | 23.98 | 25.20 | 5.1% | 36.15 | 38.72 | 7.1% | 17.1% | 33.7% | 16.6% | |
| Case 8 | 5 | 40 | 18.07 | 18.54 | 2.6% | 41.59 | 43.18 | 3.8% | 57.9% | 70.1% | 12.3% |
| 15 | 58.05 | 26.36 | 27.72 | 5.2% | 37.99 | 40.86 | 7.6% | 29.7% | 52.4% | 22.7% | |
| Case 9 | 5 | 40 | 13.16 | 13.52 | 2.7% | 28.56 | 29.70 | 4.0% | 0.6% | 1.1% | 0.5% |
| 15 | 58.05 | 18.92 | 19.93 | 5.3% | 25.85 | 27.86 | 7.8% | 0.1% | 0.4% | 0.3% | |
| Case 10 | 5 | 40 | 15.22 | 15.69 | 3.1% | 36.50 | 38.05 | 4.2% | 18.4% | 28.1% | 9.7% |
| 15 | 58.05 | 21.97 | 23.28 | 6.0% | 32.50 | 35.25 | 8.5% | 4.4% | 12.7% | 8.3% | |
| Case 11 | 5 | 40 | 10.52 | 10.85 | 3.1% | 21.91 | 22.88 | 4.4% | 4.8E-05 | 1.1E-04 | 0.0% |
| 15 | 58.05 | 15.38 | 16.27 | 5.8% | 20.57 | 22.29 | 8.4% | 1.6E-05 | 6.9E-05 | 0.0% | |
| Case 12 | 5 | 40 | 14.44 | 15.13 | 4.8% | 35.40 | 37.50 | 5.9% | 12.7% | 24.1% | 11.4% |
| 15 | 58.05 | 20.77 | 22.61 | 8.9% | 31.20 | 34.84 | 11.7% | 2.3% | 10.8% | 8.5% | |
| Case 13 | 5 | 40 | 3.82 | 4.00 | 4.7% | 8.46 | 8.98 | 6.1% | 1.1E-11 | 2.3E-11 | 0.0% |
| 15 | 58.05 | 5.51 | 5.98 | 8.5% | 7.72 | 8.60 | 11.4% | 4.2E-12 | 1.4E-11 | 0.0% | |
| Case 14 | 5 | 40 | 4.54 | 4.74 | 4.4% | 10.46 | 11.09 | 6.0% | 1.6E-10 | 3.5E-10 | 0.0% |
| 15 | 58.05 | 6.55 | 7.09 | 8.2% | 9.46 | 10.55 | 11.5% | 4.4E-11 | 1.8E-10 | 0.0% | |
| Case 15 | 5 | 40 | 9.12 | 9.47 | 3.8% | 20.39 | 21.45 | 5.2% | 1.1E-05 | 2.9E-05 | 0.0% |
| 15 | 58.05 | 13.22 | 14.16 | 7.1% | 18.58 | 20.44 | 10.0% | 2.1E-06 | 1.2E-05 | 0.0% | |
| Case 16 | 5 | 40 | 2.92 | 3.04 | 4.1% | 7.00 | 7.38 | 5.4% | 1.3E-12 | 2.2E-12 | 0.0% |
| 15 | 58.05 | 4.20 | 4.53 | 7.9% | 6.27 | 6.93 | 10.5% | 4.8E-13 | 1.2E-12 | 0.0% | |
| Mean | 5 | 40 | 3.7% | 5.0% | 6.1% | ||||||
| 15 | 58.05 | 7.0% | 9.6% | 7.2% | |||||||
(Value for variable RBE – Value for RBE=1.1)/Value for RBE=1.1.
NTCP for variable RBE – NTCP for RBE=1.1.
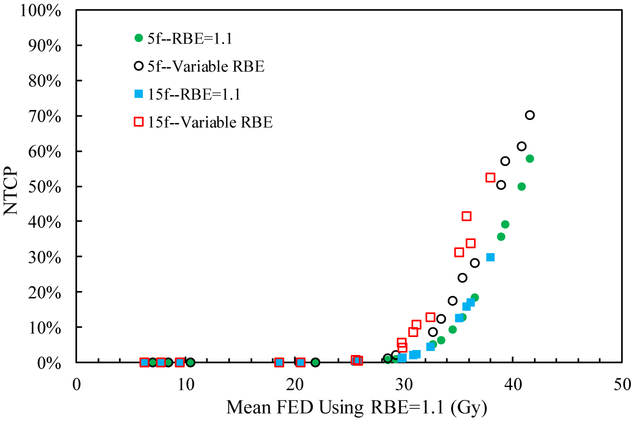
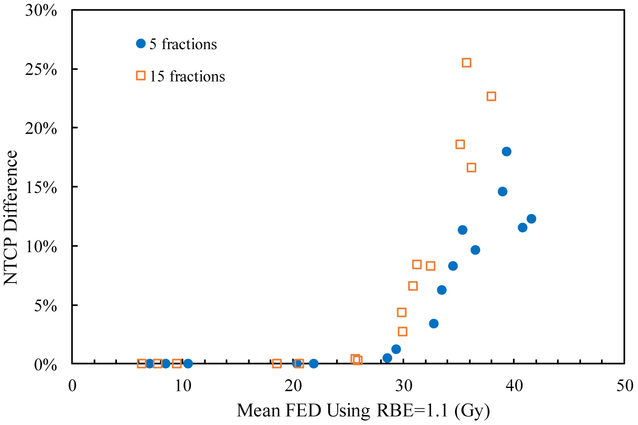
Table 2 also shows that the mean RBE weighted dose using a variable RBE is higher than that for RBE=1.1 in the normal liver for both fractionations and all cases. Thus the NTCP assuming a variable RBE is larger than that applying RBE=1.1, as shown in figure 1. The difference in NTCP between using a variable RBE and RBE=1.1 depends on the mean FED in the normal liver for all scenarios. Especially, when the mean FED using RBE=1.1 is higher than 29.8 Gy, corresponding to considerable NTCP, the difference in NTCP between RBE=1.1 and variable RBE is visible (figure 2). On the other hand, for cases with NTCP approaching 0, the impact of the variable RBE on the change of the NTCP value is negligible. For instance, for case 7 treated in 15 fractions, the NTCP with RBE=1.1 is 17.1% and considering a variable RBE increases it by 16.6%, while both the NTCPs with RBE=1.1 and variable RBE are close to 0 for case 9. Also, in case 2 with 5 fractions, the mean RBE weighted dose with variable RBE is 4.4% higher than that with RBE=1.1, and the mean FED is 5.6% higher when normalized to 1.5 Gy/fraction. Due to the large volume effect of the normal liver with the n value of the LKB model close to 1, the mean FEDs with RBE=1.1 and variable RBE are both near the TD50 of 39.8 Gy, corresponding to the steep region of the NTCP curve where only a small change of the mean FED may lead to a large difference in NTCP. And then the difference of NTCPs using RBE=1.1 and the variable RBE is 18.0%. In general, using RBE=1.1 underestimates the NTCP in the normal liver, especially when the NTCP is in the steep portion of the NTCP curve.
Figure 1.
NTCP for the sixteen cases as a function of mean FED (normalized to 1.5 Gy/fraction) using RBE=1.1 and variable RBE for the two fractionation schemes.
Figure 2.
NTCP difference between using RBE=1.1 and variable RBE for the sixteen cases for the two fractionation schemes.
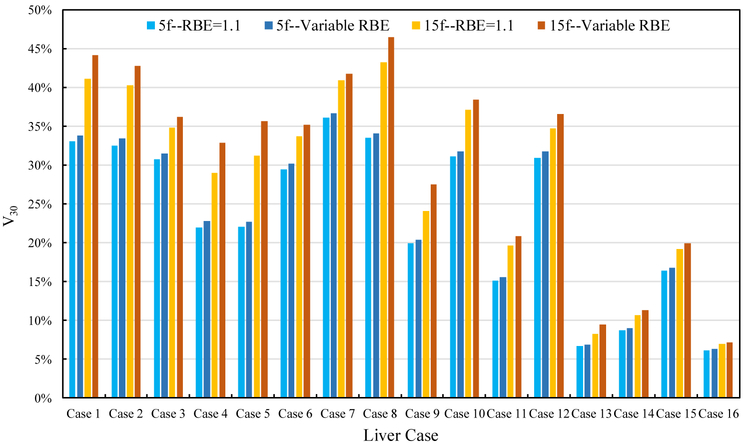
The percentage volume of the normal liver receiving >30 Gy RBE weighted dose (V30) with RBE =1.1 and variable RBE is presented in figure 3. This metric is often used to study RILD (McIntosh et al 2009, Pan et al 2010). The results show that the V30 using variable RBE is larger than that using RBE=1.1 for both fractionations and all cases, with the difference ranging from 0.1% to 4.4%.
Figure 3.
Normal liver V30 for RBE=1.1 and variable RBE for the two fractionation schemes.
The results for both fractionation schemes are presented in table 2. The relative difference of the mean RBE weighted dose using RBE=1.1 and variable RBE decreases with the fraction size in all cases, as the variable RBE is predicted to decrease with dose (McNamara et al 2015, Ödén et al 2017). Furthermore, when the RBE weighted dose distributions of the two schedules were normalized to 1.5 Gy/fraction to correct for fraction size, the mean FED for 5 fractions is larger than that for 15 fractions for RBE= 1.1, which is due to inequality of the biological effective dose (BED) in the normal liver between the two schedules. As for the variable RBE, though the mean FED also increases with fraction size, the RBE value decreases with fraction size, and finally the difference of the mean FED between two schedules is smaller than that for RBE=1.1 in all cases (see table 3). However, table 3 also shows that the impact of the variable RBE on the difference of the NTCP values between the two fractionation schemes varies with the case. As an example, when assuming a variable RBE, the NTCP difference between the two schedules decreases from 23.2% to 19.1% for case 1, while it increases from 10.4% to 13.3% for case 12.
Table 3.
Differences of the mean FEDs and NTCPs for the normal liver between the two treatment schedules for RBE =1.1 and variable RBE.
| Case | Difference in mean FED (Gy)a | Difference in NTCPa | ||
|---|---|---|---|---|
| RBE=1.1 | Variable RBE | RBE=1.1 | Variable RBE | |
| Case 1 | 3.86 | 2.48 | 23.2% | 19.1% |
| Case 2 | 3.58 | 2.00 | 23.4% | 15.8% |
| Case 3 | 3.57 | 2.16 | 7.2% | 8.9% |
| Case 4 | 3.71 | 2.57 | 0.8% | 1.6% |
| Case 5 | 2.79 | 1.85 | 3.8% | 4.5% |
| Case 6 | 3.61 | 2.21 | 5.0% | 6.9% |
| Case 7 | 4.66 | 3.51 | 32.7% | 27.7% |
| Case 8 | 3.60 | 2.32 | 28.1% | 17.7% |
| Case 9 | 2.71 | 1.84 | 0.5% | 0.7% |
| Case 10 | 4.00 | 2.80 | 14.1% | 15.4% |
| Case 11 | 1.34 | 0.59 | 0.0% | 0.0% |
| Case 12 | 4.20 | 2.66 | 10.4% | 13.3% |
| Case 13 | 0.74 | 0.38 | 0.0% | 0.0% |
| Case 14 | 1.00 | 0.54 | 0.0% | 0.0% |
| Case 15 | 1.81 | 1.01 | 0.0% | 0.0% |
| Case 16 | 0.73 | 0.45 | 0.0% | 0.0% |
| Mean | 2.87 | 1.84 | 9.3% | 8.2% |
Value for 5 fractions – Value for 15 fractions.
3.2. Impact of potentially variable RBE on the TCP
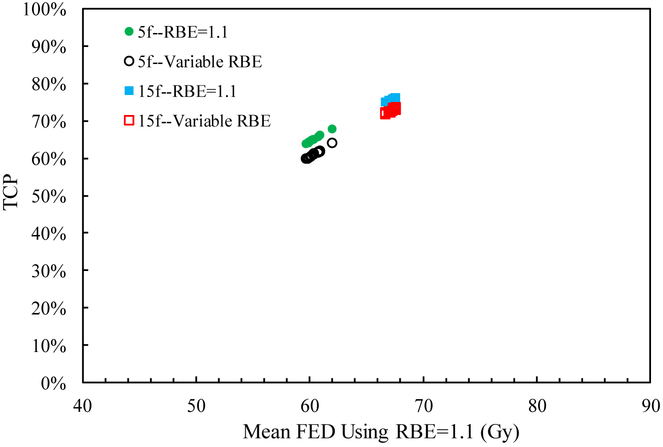
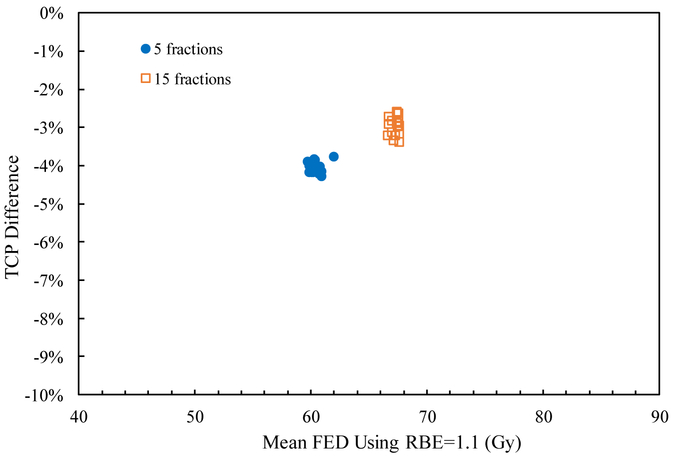
The mean RBE weighted dose, mean FED normalized to 2 Gy/fraction, and TCP for all patient cases are shown in table 4. Since the RBE weighted dose with RBE=1.1 is designed to uniformly distribute dose in the target with prescribed doses of 40 Gy and 58.05 Gy for the two schedules, the mean RBE weighted dose, mean FED and TCP values are nearly constant among the cases. The mean RBE weighted dose using a variable RBE is ~2.5% less than that using RBE=1.1 for both fractionations and all cases, which results in a smaller TCP value as shown in figure 4. This is mainly due to the high α/β value and dose level in the liver tumor, as the variable proton RBE decreases with increasing α/β value and dose level (Paganetti 2014). The differences of TCP values using RBE=1.1 and the variable RBE are also similar for all cases, about 4% for 5 fractions and 3% for 15 fractions, as shown in figure 5. Thus applying RBE=1.1 might slightly underestimate the TCP for liver tumors.
Table 4.
Mean RBE weighted dose, mean FED and TCP of the liver tumor (α/β=10 Gy).
| Case | Fraction | Prescribed dose (Gy) |
Mean RBE weighted dose | Mean FED (2 Gy/fraction) | TCP | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RBE=1.1 (Gy) |
Variable RBE (Gy) |
Relative Differencea |
RBE=1.1 (Gy) |
Variable RBE (Gy) |
Relative Differencea |
RBE=1.1 | Variable RBE |
Differenceb | |||
| Case 1 | 5 | 40 | 39.92 | 38.91 | −2.5% | 59.83 | 57.66 | −3.6% | 64.1% | 60.0% | −4.2% |
| 15 | 58.05 | 57.96 | 56.45 | −2.6% | 66.96 | 64.75 | −3.3% | 75.4% | 72.3% | −3.1% | |
| Case 2 | 5 | 40 | 40.14 | 39.16 | −2.4% | 60.30 | 58.19 | −3.5% | 65.0% | 61.0% | −4.0% |
| 15 | 58.05 | 58.33 | 56.91 | −2.4% | 67.51 | 65.42 | −3.1% | 76.2% | 73.3% | −2.9% | |
| Case 3 | 5 | 40 | 40.08 | 39.06 | −2.5% | 60.17 | 57.98 | −3.6% | 64.8% | 60.6% | −4.2% |
| 15 | 58.05 | 58.17 | 56.6 | −2.7% | 67.27 | 64.96 | −3.4% | 75.9% | 72.7% | −3.2% | |
| Case 4 | 5 | 40 | 40.91 | 39.93 | −2.4% | 61.99 | 59.85 | −3.4% | 68.0% | 64.2% | −3.8% |
| 15 | 58.05 | 57.77 | 56.46 | −2.3% | 66.68 | 64.76 | −2.9% | 75.1% | 72.3% | −2.7% | |
| Case 5 | 5 | 40 | 40.04 | 39.02 | −2.5% | 60.09 | 57.89 | −3.7% | 64.6% | 60.4% | −4.2% |
| 15 | 58.05 | 57.73 | 56.20 | −2.7% | 66.62 | 64.38 | −3.4% | 75.0% | 71.8% | −3.2% | |
| Case 6 | 5 | 40 | 40.34 | 39.34 | −2.5% | 60.74 | 58.58 | −3.6% | 65.8% | 61.8% | −4.0% |
| 15 | 58.05 | 58.40 | 56.93 | −2.5% | 67.61 | 65.45 | −3.2% | 76.3% | 73.4% | −2.9% | |
| Case 7 | 5 | 40 | 40.43 | 39.36 | −2.6% | 60.93 | 58.62 | −3.8% | 66.1% | 61.9% | −4.3% |
| 15 | 58.05 | 58.39 | 56.71 | −2.9% | 67.60 | 65.13 | −3.7% | 76.3% | 72.9% | −3.4% | |
| Case 8 | 5 | 40 | 39.95 | 38.95 | −2.5% | 59.89 | 57.74 | −3.6% | 64.3% | 60.1% | −4.1% |
| 15 | 58.05 | 58.31 | 56.83 | −2.5% | 67.48 | 65.30 | −3.2% | 76.1% | 73.1% | −3.0% | |
| Case 9 | 5 | 40 | 40.16 | 39.18 | −2.4% | 60.35 | 58.23 | −3.5% | 65.1% | 61.1% | −4.0% |
| 15 | 58.05 | 57.77 | 56.37 | −2.4% | 66.68 | 64.63 | −3.1% | 75.1% | 72.2% | −2.9% | |
| Case 10 | 5 | 40 | 40.43 | 39.39 | −2.6% | 60.93 | 58.68 | −3.7% | 66.1% | 62.0% | −4.2% |
| 15 | 58.05 | 58.38 | 56.81 | −2.7% | 67.58 | 65.27 | −3.4% | 76.3% | 73.1% | −3.2% | |
| Case 11 | 5 | 40 | 39.86 | 38.92 | −2.4% | 59.70 | 57.68 | −3.4% | 63.9% | 60.0% | −3.9% |
| 15 | 58.05 | 58.36 | 57.04 | −2.3% | 67.55 | 65.61 | −2.9% | 76.2% | 73.6% | −2.6% | |
| Case 12 | 5 | 40 | 40.33 | 39.28 | −2.6% | 60.72 | 58.45 | −3.7% | 65.8% | 61.5% | −4.2% |
| 15 | 58.05 | 58.05 | 56.43 | −2.8% | 67.10 | 64.72 | −3.5% | 75.6% | 72.3% | −3.3% | |
| Case 13 | 5 | 40 | 39.94 | 38.97 | −2.4% | 59.87 | 57.79 | −3.5% | 64.2% | 60.2% | −4.0% |
| 15 | 58.05 | 57.96 | 56.59 | −2.4% | 66.96 | 64.95 | −3.0% | 75.4% | 72.6% | −2.8% | |
| Case 14 | 5 | 40 | 40.13 | 39.19 | −2.3% | 60.28 | 58.26 | −3.4% | 65.0% | 61.2% | −3.8% |
| 15 | 58.05 | 58.24 | 56.95 | −2.2% | 67.38 | 65.48 | −2.8% | 76.0% | 73.4% | −2.6% | |
| Case 15 | 5 | 40 | 40.15 | 39.16 | −2.5% | 60.33 | 58.19 | −3.5% | 65.1% | 61.0% | −4.0% |
| 15 | 58.05 | 58.26 | 56.83 | −2.5% | 67.41 | 65.30 | −3.1% | 76.0% | 73.1% | −2.9% | |
| Case 16 | 5 | 40 | 40.16 | 39.21 | −2.4% | 60.35 | 58.30 | −3.4% | 65.1% | 61.2% | −3.9% |
| 15 | 58.05 | 58.29 | 56.98 | −2.2% | 67.45 | 65.52 | −2.9% | 76.1% | 73.5% | −2.6% | |
| Mean | 5 | 40 | −2.5% | −3.6% | −4.0% | ||||||
| 15 | 58.05 | −2.5% | −3.2% | −3.0% | |||||||
(Value for variable RBE – Value for RBE=1.1)/Value for RBE=1.1.
TCP for variable RBE – TCP for RBE=1.1.
Figure 4.
TCP for the sixteen cases as a function of mean FED (normalized to 2 Gy/fraction) using RBE=1.1 and variable RBE for the two fractionation schemes.
Figure 5.
TCP difference between using RBE=1.1 and variable RBE for the sixteen cases for the two fractionation schemes.
As for the two fractionation schemes, the mean FED using RBE=1.1 in the 15 fractions scheme is larger than that in the 5 fractions scheme in all cases. This is because the BEDs in the target region for the two schedules, 40 Gy in 5 fractions and 58.05 Gy in 15 fractions, are not exactly equivalent, i.e. 72 Gy for the 5 fractions scheme and 80.52 Gy for the 15 fractions scheme, so that the corresponding mean FEDs are also different. As a result, the TCP using RBE =1.1 in 15 fractions is about 10% larger than that for 5 fractions. Since the α/β value is relatively high in the target, the influence of fraction size on the variable RBE is small as has been shown previously (McNamara et al 2015). Consequently, the relative difference between mean RBE weighted doses using RBE=1.1 and variable RBE is small for both treatment schedules (see table 4). Table 5 shows that the difference of the TCPs between the two fractionation schedules using variable RBE is only ~1% larger than that using RBE=1.1 for all cases.
Table 5.
Differences of the mean FEDs and TCPs for the liver tumor between the two treatment schedules for RBE =1.1 and variable RBE.
| Case | Difference in mean FED (Gy)a | Difference in TCPa | ||
|---|---|---|---|---|
| RBE=1.1 | Variable RBE | RBE=1.1 | Variable RBE | |
| Case 1 | −7.14 | −7.09 | −11.3% | −12.4% |
| Case 2 | −7.21 | −7.23 | −11.1% | −12.3% |
| Case 3 | −7.10 | −6.99 | −11.1% | −12.0% |
| Case 4 | −4.70 | −4.91 | −7.1% | −8.2% |
| Case 5 | −6.54 | −6.49 | −10.4% | −11.3% |
| Case 6 | −6.88 | −6.87 | −10.5% | −11.6% |
| Case 7 | −6.66 | −6.50 | −10.1% | −11.0% |
| Case 8 | −7.59 | −7.56 | −11.9% | −13.0% |
| Case 9 | −6.34 | −6.39 | −10.0% | −11.0% |
| Case 10 | −6.65 | −6.59 | −10.1% | −11.1% |
| Case 11 | −7.86 | −7.93 | −12.3% | −13.6% |
| Case 12 | −6.38 | −6.27 | −9.9% | −10.8% |
| Case 13 | −7.09 | −7.16 | −11.2% | −12.4% |
| Case 14 | −7.10 | −7.22 | −11.0% | −12.2% |
| Case 15 | −7.08 | −7.11 | −11.0% | −12.1% |
| Case 16 | −7.10 | −7.22 | −11.0% | −12.2% |
| Mean | −6.84 | −6.85 | −10.6% | −11.7% |
Value for 5 fractions − Value for 15 fractions.
3.3. Impact of the α/β uncertainty
One of the cases (case 2, figure 6) was selected to analyze the impact of the α/β value uncertainty in the normal liver and liver tumor. The mean RBE weighted dose, NTCP of the normal liver, and TCP of the liver tumor with different α/β values are shown in tables 6 and 7.
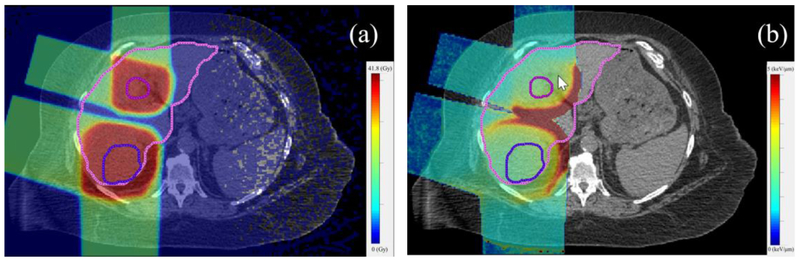
Figure 6.
Distributions of the RBE weighted dose with RBE=1.1 (a) and dose-averaged LET (only the volumes receiving more than 5% of the prescribed dose were considered) (b) in case 2. The inner contour indicates the GTV and outer contour indicates the whole liver.
Table 6.
Mean RBE weighted dose and NTCP of the normal liver in case 2 with different α/β values.
| Fraction | Prescribed dose (Gy) |
α/β (Gy) |
Mean RBE weighted dose (Gy) | NTCP | ||||
|---|---|---|---|---|---|---|---|---|
| RBE=1.1 (Gy) |
Variable RBE (Gy) |
Relative Differencea |
RBE=1.1 | Variable RBE |
Differenceb | |||
| 5 | 40 | 2 | 17.22 | 18.12 | 5.2% | 64.4% | 83.2% | 18.8% |
| 5 | 40 | 2.5 | 17.22 | 17.98 | 4.4% | 39.2% | 57.2% | 18.0% |
| 5 | 40 | 3 | 17.22 | 17.86 | 3.7% | 21.9% | 33.5% | 11.6% |
| 15 | 58.05 | 2 | 25.02 | 27.35 | 9.3% | 24.5% | 61.6% | 37.1% |
| 15 | 58.05 | 2.5 | 25.02 | 27.01 | 8.0% | 15.8% | 41.4% | 25.6% |
| 15 | 58.05 | 3 | 25.02 | 26.71 | 6.8% | 10.7% | 26.9% | 16.3% |
(Value for variable RBE – Value for RBE=1.1)/Value for RBE=1.1.
NTCP for variable RBE – NTCP for RBE=1.1.
Table 7.
Mean RBE weighted dose and TCP of the liver tumor in case 2 with different α/β values.
| Fraction | Prescribed dose (Gy) |
α/β (Gy) |
Mean RBE weighted dose | TCP | ||||
|---|---|---|---|---|---|---|---|---|
| RBE=1.1 (Gy) |
Variable RBE (Gy) |
Relative Differencea |
RBE=1.1 | Variable RBE |
Differenceb | |||
| 5 | 40 | 7.2 | 40.14 | 39.63 | −1.3% | 71.6% | 69.6% | −2.0% |
| 5 | 40 | 10 | 40.14 | 39.16 | −2.4% | 65.0% | 61.0% | −4.0% |
| 5 | 40 | 15 | 40.14 | 38.55 | −4.0% | 57.3% | 51.1% | −6.2% |
| 15 | 58.05 | 7.2 | 58.33 | 57.85 | −0.8% | 76.9% | 75.9% | −1.0% |
| 15 | 58.05 | 10 | 58.33 | 56.91 | −2.4% | 76.2% | 73.3% | −2.9% |
| 15 | 58.05 | 15 | 58.33 | 55.82 | −4.3% | 75.1% | 70.2% | −4.8% |
(Value for variable RBE – Value for RBE=1.1)/Value for RBE=1.1.
TCP for variable RBE – TCP for RBE=1.1.
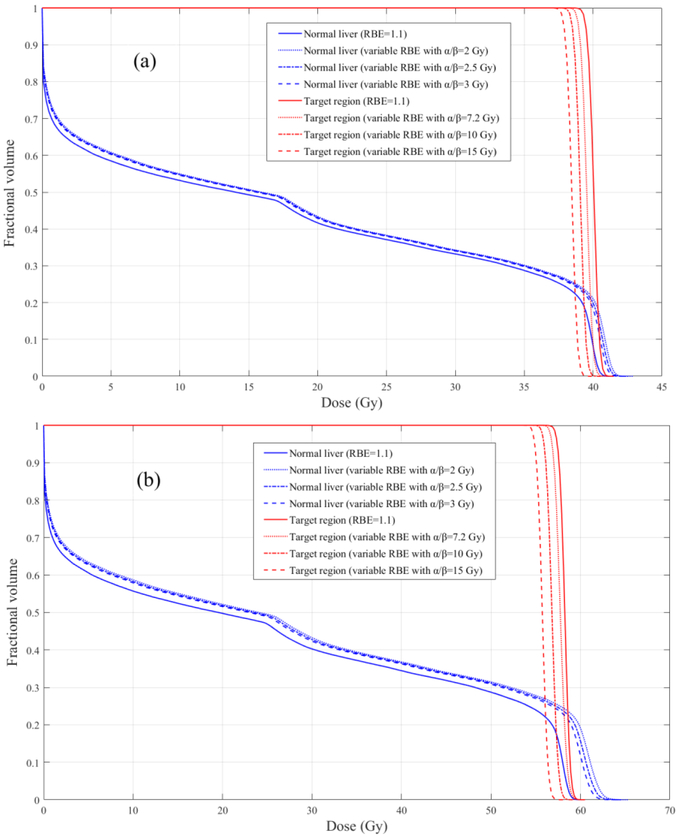
The mean RBE weighted dose in the normal liver decreases with the α/β value increasing for both schedules, which is in agreement with previous findings (McNamara et al 2015, Grassberger and Paganetti 2017). The DVHs of the normal liver with RBE=1.1 and variable RBE using different α/β values are shown in figure 7. The NTCP using RBE=1.1 and a variable RBE also decrease with α/β value. Since the variable RBE decreases with the α/β increasing, the decrease of the NTCP with variable RBE is larger than that with RBE=1.1, for both 5 and 15 fractions. As the variable RBE in the normal liver is higher than 1.1 and thus the NTCP is also higher, the difference between the NTCP values using RBE=1.1 and the variable RBE decreases with the α/β value increasing.
Figure 7.
DVHs of the RBE weighted doses in the normal liver (blue lines) and target region (red lines) with RBE=1.1 and variable RBE using different α/β values: (a) 5 fractions schedule; (b) 15 fractions schedule.
As for the target, the mean RBE weighted dose using a variable RBE decreases with the α/β value increasing for both fractionation regimens. The doses based on a variable RBE are smaller than those using RBE=1.1 as shown in figure 7. The TCP with RBE=1.1 and variable RBE also decrease with the α/β value increasing, a similar trend as for the NTCP. Since the variable RBE in the target region decreases with the α/β value, the decrease of the TCP using a variable RBE is larger than that using RBE=1.1, for both fractionation schemes. The difference between the TCP values using RBE=1.1 and the variable RBE increases with the α/β value increasing.
4. Discussion
Liver tumors are often surrounded by normal liver, and the part of the normal liver just outside the tumor border is inevitable irradiated to a high dose level and potentially high LET values (as shown in figure 6 for one of the cases). Therefore, it is important for liver treatments to evaluate the impact of a potentially variable proton RBE on the NTCP and TCP. As our results show, for different fractionations, disregarding the variable RBE may lead to an underestimation of the RBE weighted dose, V30 and NTCP for the normal liver in some cases as well as a slight overestimation of the RBE weighted dose and TCP for the tumor. However, only for patients with high mean liver dose, for which the NTCP is already higher than 0, the impact of a variable RBE on the NTCP is significant.
Though the difference of the mean FED between the two fractionation schedules is smaller when using a variable RBE, the NTCP value with the variable RBE is higher than that with RBE=1.1 for both schedules in all cases. The difference in NTCP not only depends on the difference in mean FED, but also on the corresponding slope of the NTCP curve. Therefore, as a combination of the two effects, the impact of the variable RBE on the NTCP difference between two fractionation schemes varies from patient to patient.
The TCP difference between the two schedules also depends on the difference of the mean FED in the target and the corresponding slope of the sigmoid TCP curve. Since the variable RBE is nearly constant with fraction size for the doses considered in this study, the difference of mean FEDs between the two schedules for the variable RBE is similar to that for RBE=1.1 in all cases. In addition, the TCP value with the variable RBE is less than that with RBE=1.1, and thus more sensitive to the change of the mean FED. Therefore, the TCP difference between the two schedules for the variable RBE is slightly larger than that for RBE=1.1 in all cases.
As shown in equations 6 and 11, not only the variable proton RBE, but also the NTCP and TCP models depend on the α/β value, which varies among the patient population. In this study, the result shows that a patient with a higher α/β value in the normal liver or liver tumor would be predicted to have a lower NTCP or TCP value. When the variable RBE is taken into account, which also decreases with the α/β value increasing, the decrease of the NTCP or TCP value with the α/β value is more pronounced for different fractionations. Therefore, the impact of the α/β uncertainty on the NTCP and TCP might be more significant in proton therapy than in photon therapy.
Paganetti (2017) has analyzed impact of the α/β uncertainty on the NTCP and TCP before, using a prostate and a pediatric ependymoma treatment as examples. In that study the NTCP as well as TCP decreased with decreasing α/β. The reason for this discrepancy compared to the study presented here is due to the different methods of adjusting the absolute values of α and β. While in the previous study the β value was kept constant when changing α/β, our study modified both α and β. According to equation 11, an increase in α/β results in a simultaneously increase of α and decrease of β. This resulting trend of NTCP varying with α/β has also been shown in another study (Marzi el al 2009). The actual variations of the absolute α and β values in a patient population is unclear and is beyond the scope of this research.
This study has limitations. The parameter values of the NTCP model were fitted based on patients treated with conventional photon therapy. Since the dose distribution using proton therapy in the normal liver is different from using photons, the proton specific parameter values may also be different from those for photons. Furthermore, the applied RBE model was derived from a collection of in vitro experiment results. It is unclear if such models have predictive power for tumor cells or normal tissue damage in vivo. The radiosensitivity in the normal liver and the liver tumor were assumed to be uniform with the same α/β although these would most likely be heterogeneous in patients.
5. Conclusions
The impact of a potentially variable proton RBE for liver trials was investigated. We analyzed the effects of the fraction size and α/β uncertainty based on sixteen liver cases treated with proton therapy at MGH. Disregarding a variable proton RBE may result in a significant underestimation in NTCP and a slight overestimation in TCP. Thus, the therapeutic ratio for proton therapy might be less than the expected value from assuming RBE=1.1. Furthermore, a variable RBE slightly increases the difference in TCP between fractionation schemes, while the impact on the difference in NTCP is very patient specific. Overall, interpatient variability in radiosensitivity is higher when using a variable RBE, both in the normal liver and liver tumor.
This study demonstrates the uncertainties when analyzing clinical trials that compare proton and photon therapy, but as well different fractionation regimens. In addition, it shows the potential limitations of model-based clinical trials (Langendijk et al 2018) as RBE values in proton therapy have considerable uncertainties.
Acknowledgments
This work was supported by the National Key Projects of Research and Development of China (grant number: 2016YFC0904600), and NIH NCI U19 CA-21239.
References
- Agostinelli S, Allison J, Amako KA, Apostolakis J, Araujo H, Arce P,… & Behner F (2003). GEANT4—a simulation toolkit. Nuclear instruments and methods in physics research section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 506(3), 250–303. [Google Scholar]
- Boda-Heggemann J, Attenberger U, Budjan J, Jahnke A, Jahnke L, Vogel L, … & Lohr F (2016). MRI morphologic alterations after liver SBRTMR-morphologische Veränderungen nach Leber-SBRT. Strahlentherapie und Onkologie, 192(9), 641–648. [DOI] [PubMed] [Google Scholar]
- Carabe-Femandez A, & Paganetti H (2011). Clinical consequences of relative biological effectiveness (RBE) variations in proton radiotherapy of the prostate, brain, and liver. International Journal of Radiation Oncology• Biology• Physics, 81(2), S725–S726. [DOI] [PubMed] [Google Scholar]
- Chadwick KH, & Leenhouts HP (1973). A molecular theory of cell survival. Physics in Medicine & Biology, 18(1), 78. [DOI] [PubMed] [Google Scholar]
- Dawson LA, Biersack M, Lockwood G, Eisbruch A, Lawrence TS, & Ten Haken RK (2005). Use of principal component analysis to evaluate the partial organ tolerance of normal tissues to radiation. International Journal of Radiation Oncology• Biology• Physics, 62(3), 829–837. [DOI] [PubMed] [Google Scholar]
- Dawson LA, Eccles C, & Craig T (2006). Individualized image guided iso-NTCP based liver cancer SBRT. Acta Oncologica, 45(7), 856–864. [DOI] [PubMed] [Google Scholar]
- Dawson LA, Normolle D, Balter JM, McGinn CJ, Lawrence TS, & Ten Haken RK (2002). Analysis of radiation-induced liver disease using the Lyman NTCP model. International Journal of Radiation Oncology Biology Physics, 53(4), 810–821. [DOI] [PubMed] [Google Scholar]
- Deasy JO, Blanco AI, & Clark VH (2003). CERR: a computational environment for radiotherapy research. Medical physics, 30(5), 979–985. [DOI] [PubMed] [Google Scholar]
- Dreher C, Scholz C, Pommer M, Brons S, Prokesch H, Ecker S,… & Habermehl D (2016). Optimization of Carbon Ion Treatment Plans by Integrating Tissue Specific α/β-Values for Patients with Non-Resectable Pancreatic Cancer. PloS one, 11(10), e0164473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukugawa Y, Namimoto T, Toya R, Saito T, Yuki H, Matsuyama T, … & Oya N (2017). Radiation-induced Liver Injury after 3D-conformal Radiotherapy for Hepatocellular Carcinoma: Quantitative Assessment Using Gd-EOB-DTPA-enhanced MRI. Acta Medica Okayama, 71(1), 25–29. [DOI] [PubMed] [Google Scholar]
- Gerweck LE, & Kozin SV (1999). Relative biological effectiveness of proton beams in clinical therapy. Radiotherapy and oncology, 50(2), 135–142. [DOI] [PubMed] [Google Scholar]
- Giantsoudi D, Grassberger C, Craft D, Niemierko A, Trofimov A, & Paganetti H (2013). Linear energy transfer-guided optimization in intensity modulated proton therapy: feasibility study and clinical potential. International Journal of Radiation Oncology• Biology• Physics, 87(1), 216–222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goitein M, & Schultheiss TE (1985). Strategies for treating possible tumor extension: some theoretical considerations. International Journal of Radiation Oncology* Biology* Physics, 11(8), 1519–1528. [DOI] [PubMed] [Google Scholar]
- Grassberger C, & Paganetti H (2017). Varying relative biological effectiveness in proton therapy: knowledge gaps versus clinical significance. Acta Radiologica Therapy Physics Biology, 56(6), 761–762. [DOI] [PubMed] [Google Scholar]
- Grassberger C, Trofimov A, Lomax A, & Paganetti H (2011). Variations in linear energy transfer within clinical proton therapy fields and the potential for biological treatment planning. International Journal of Radiation Oncology Biology Physics, 80(5), 1559–1566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammad AY, Schmid RK, Erickson BA, Gamblin TC, & Robbins JR (2016). The Impact of Dose on Overall Survival in Unresectable Hepatocellular Carcinoma Treated With Stereotactic Body Radiation Therapy. International Journal of Radiation Oncology• Biology• Physics, 96(2), E152. [Google Scholar]
- Hong TS, DeLaney TF, Mamon HJ, Willett CG, Yeap BY, Niemierko A,… & Arellano RS (2014). A prospective feasibility study of respiratory-gated proton beam therapy for liver tumors. Practical radiation oncology, 4(5), 316–322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hong TS, Wo JY, Yeap BY, Ben-Josef E, McDonnell EI, Blaszkowsky LS,… & Murphy JE (2016). Multi-institutional phase II study of high-dose hypofractionated proton beam therapy in patients with localized, unresectable hepatocellular carcinoma and intrahepatic cholangiocarcinoma. Journal of Clinical Oncology, 34(5), 460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ICRU. (2007). Prescribing, recording, and reporting proton-beam therapy ICRU Report No. 78 (Bethesda, MD: ICRU; ). [Google Scholar]
- Igaki H, Mizumoto M, Okumura T, Hasegawa K, Kokudo N, & Sakurai H (2018). A systematic review of publications on charged particle therapy for hepatocellular carcinoma. International journal of clinical oncology, 23(3), 423–433. [DOI] [PubMed] [Google Scholar]
- Keane FK, Tanguturi SK, Zhu AX, Dawson LA, & Hong TS (2015). Radiotherapy for liver tumors. Hepatic Oncology, 2(2), 133–146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keane FK, Wo JY, Zhu AX, & Hong TS (2016). Liver-directed radiotherapy for hepatocellular carcinoma. Liver cancer, 5(3), 198–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim Y, & Tomé WA (2010). Dose-painting IMRT optimization using biological parameters. Acta oncologica, 49(8), 1374–1384. [DOI] [PubMed] [Google Scholar]
- Kutcher GJ, & Burman C (1989). Calculation of complication probability factors for non-uniform normal tissue irradiation: The effective volume method gerald. International Journal of Radiation Oncology• Biology• Physics, 16(6), 1623–1630. [DOI] [PubMed] [Google Scholar]
- Kutcher GJ, Burman C, Brewster L, Goitein M, & Mohan R (1991). Histogram reduction method for calculating complication probabilities for three-dimensional treatment planning evaluations. International Journal of Radiation Oncology Biology Physics, 21(1), 137–146. [DOI] [PubMed] [Google Scholar]
- Langendijk JA, Boersma LJ, Rasch CR, van Vulpen M, Reitsma JB, van der Schaaf A, & Schuit E (2018). Clinical Trial Strategies to Compare Protons With Photons. In Seminars in radiation oncology, 28(2), 79–87. [DOI] [PubMed] [Google Scholar]
- Lausch A, Sinclair K, Lock M, Fisher B, Jensen N, Gaede S, … & Wong E (2013). Determination and comparison of radiotherapy dose responses for hepatocellular carcinoma and metastatic colorectal liver tumours. The British journal of radiology, 86(1027). 20130147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luxton G, Keall PJ, & King CR (2007). A new formula for normal tissue complication probability (NTCP) as a function of equivalent uniform dose (EUD). Physics in Medicine & Biology, 53(1), 23. [DOI] [PubMed] [Google Scholar]
- Lyman JT (1985). Complication probability as assessed from dose-volume histograms. Radiation Research, 104(2s), S13–S19. [PubMed] [Google Scholar]
- Marzi S, Saracino B, Petrongari MG, Arcangeli S, Gomellini S, Arcangeli G,… & Landoni V (2009). Modeling of α/β for late rectal toxicity from a randomized phase II study: conventional versus hypofractionated scheme for localized prostate cancer. Journal of Experimental & Clinical Cancer Research, 28(1), 117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntosh A, Hagspiel KD, Al-Osaimi AM, Northup P, Caldwell S, Berg C,… & Rich TA (2009). Accelerated treatment using intensity-modulated radiation therapy plus concurrent capecitabine for unresectable hepatocellular carcinoma. Cancer, 115(21), 5117–5125. [DOI] [PubMed] [Google Scholar]
- McNamara AL, Schuemann J, & Paganetti H (2015). A phenomenological relative biological effectiveness (RBE) model for proton therapy based on all published in vitro cell survival data. Physics in Medicine & Biology, 60(21), 8399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ödén J, Eriksson K, & Toma-Dasu I (2017). Inclusion of a variable RBE into proton and photon plan comparison for various fractionation schedules in prostate radiation therapy. Medical Physics, 44(3), 810–822. [DOI] [PubMed] [Google Scholar]
- Ohri N, Tomé WA, Romero AM, Mifften M, Ten Haken RK, Dawson LA,… & Jackson A (2018). Local Control following Stereotactic Body Radiation Therapy for Liver Tumors. International Journal of Radiation Oncology Biology Physics. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paganetti H (2014). Relative biological effectiveness (RBE) values for proton beam therapy. Variations as a function of biological endpoint, dose, and linear energy transfer. Physics in Medicine & Biology, 59(22), R419. [DOI] [PubMed] [Google Scholar]
- Paganetti H (2017). Relating the proton relative biological effectiveness to tumor control and normal tissue complication probabilities assuming interpatient variability in α/β. Acta Oncologica, 56(11), 1379–1386. [DOI] [PubMed] [Google Scholar]
- Paganetti H, Jiang H, Lee SY, & Kooy HM (2004). Accurate Monte Carlo simulations for nozzle design, commissioning and quality assurance for a proton radiation therapy facility. Medical physics, 31(7), 2107–2118. [DOI] [PubMed] [Google Scholar]
- Paganetti H, Jiang H, Parodi K, Slopsema R, & Engelsman M (2008). Clinical implementation of full Monte Carlo dose calculation in proton beam therapy. Physics in Medicine & Biology, 53(17), 4825–53. [DOI] [PubMed] [Google Scholar]
- Paganetti H, Niemierko A, Ancukiewicz M, Gerweck LE, Goitein M, Loeffler JS, & Suit HD (2002). Relative biological effectiveness (RBE) values for proton beam therapy. International Journal of Radiation Oncology Biology Physics, 53(2), 407–421. [DOI] [PubMed] [Google Scholar]
- Pan CC, Kavanagh BD, Dawson LA, Li XA, Das SK, Miften M, & Ten Haken RK (2010). Radiation-associated liver injury. International Journal of Radiation Oncology• Biology• Physics, 76(3), S94–S100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perl J, Shin J, Schuemann J, Faddegon B, & Paganetti H (2012). TOPAS: An innovative proton Monte Carlo platform for research and clinical applications. Medical physics, 39(11), 6818–6837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polster L, Schuemann J, Rinaldi I, Burigo L, McNamara AL, Stewart RD,… & Faddegon B (2015). Extension of TOPAS for the simulation of proton radiation effects considering molecular and cellular endpoints. Physics in Medicine & Biology, 60(13), 5053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pool AE, Mendez Romero A, Wunderink W, Heijmen BJ, Levendag PC, Verhoef C, & IJzermans JN (2010). Stereotactic body radiation therapy for colorectal liver metastases. British Journal of Surgery, 97(3), 377–382. [DOI] [PubMed] [Google Scholar]
- Raju MR (1995). Proton radiobiology, radiosurgery and radiotherapy. International journal of radiation biology, 67(3), 237–259. [DOI] [PubMed] [Google Scholar]
- Ramos-Méndez J, Perl J, Faddegon B, Schuemann J, & Paganetti H (2013). Geometrical splitting technique to improve the computational efficiency in Monte Carlo calculations for proton therapy. Medical physics, 40(4), 1718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuemann JP, Dowdell S, Grassberger C, Min C, & Paganetti H (2014). Site-Specific Range Uncertainties Due to by Dose Calculation Algorithms for Proton Therapy. International Journal of Radiation Oncology Biology Physics, 90(1), S26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuemann J, Giantsoudi D, Grassberger C, Moteabbed M, Min CH, & Paganetti H (2015). Assessing the clinical impact of approximations in analytical dose calculations for proton therapy. International Journal of Radiation Oncology Biology Physics, 92(5), 1157–1164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuemann J, Paganetti H, Shin J, Faddegon B, & Perl J (2012). Efficient voxel navigation for proton therapy dose calculation in TOPAS and Geant4. Physics in Medicine & Biology, 57(11), 3281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schultheiss TE, Orton CG, & Peck RA (1983). Models in radiotherapy: volume effects. Medical physics, 10(4), 410–415. [DOI] [PubMed] [Google Scholar]
- Sethi RV, Giantsoudi D, Raiford M, Malhi I, Niemierko A, Rapalino O,… & MacDonald SM (2014). Patterns of failure after proton therapy in medulloblastoma; linear energy transfer distributions and relative biological effectiveness associations for relapses. International Journal of Radiation Oncology• Biology• Physics, 88(3), 655–663. [DOI] [PubMed] [Google Scholar]
- Skarsgard LD (1998). Radiobiology with heavy charged particles: a historical review. Physica medica: PM: an international journal devoted to the applications of physics to medicine and biology: official journal of the Italian Association of Biomedical Physics (AIFB), 14, 1–19. [PubMed] [Google Scholar]
- Su TS, Luo R, Liang P, Cheng T, Zhou Y, & Huang Y (2018). A prospective cohort study of hepatic toxicity after stereotactic body radiation therapy for hepatocellular carcinoma. Radiotherapy and Oncology. [DOI] [PubMed] [Google Scholar]
- Tai A, Erickson B, Khater KA, & Li XA (2008). Estimate of radiobiologic parameters from clinical data for biologically based treatment planning for liver irradiation. International Journal of Radiation Oncology Biology Physics, 70(3), 900–907. [DOI] [PubMed] [Google Scholar]
- Tai A, Erickson B, & Li XA (2009). Extrapolation of normal tissue complication probability for different fractionations in liver irradiation. International Journal of Radiation Oncology• Biology• Physics, 74(1), 283–289. [DOI] [PubMed] [Google Scholar]
- Testa M, Schuemann J, Lu HM, Shin J, Faddegon B, Perl J, & Paganetti H (2013). Experimental validation of the TOPAS Monte Carlo system for passive scattering proton therapy. Medical physics, 40(12), 1719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tilly N, Johansson J, Isacsson U, Medin J, Blomquist E, & Grusell E, et al. (2005). The influence of rbe variations in a clinical proton treatment plan for a hypopharynx cancer. Physics in Medicine & Biology, 50(12), 2765–2777. [DOI] [PubMed] [Google Scholar]
- Toramatsu C, Katoh N, Shimizu S, Nihongi H, Matsuura T, Takao S, … & Onimaru R (2013). What is the appropriate size criterion for proton radiotherapy for hepatocellular carcinoma? A dosimetric comparison of spot-scanning proton therapy versus intensity-modulated radiation therapy. Radiation Oncology, 8(1). 48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulrich S, Wieser HP, Cao W, Mohan R, & Bangert M (2017). Impact of respiratory motion on variable relative biological effectiveness in 4D-dose distributions of proton therapy. Acta Oncologica, 56(11), 1420–1427. [DOI] [PubMed] [Google Scholar]
- Underwood T, & Paganetti H (2016). Variable proton relative biological effectiveness: how do we move forward?. International Journal of Radiation Oncology Biology Physics, 95(1), 56–58. [DOI] [PubMed] [Google Scholar]
- Unkelbach J, Papp D, Gaddy MR, Andratschke N, Hong T, & Guckenberger M (2017). Spatiotemporal fractionation schemes for liver stereotactic body radiotherapy. Radiotherapy and Oncology, 125(2), 357–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wedenberg M, & Tomadasu I (2014). Disregarding rbe variation in treatment plan comparison may lead to bias in favor of proton plans. Medical Physics, 41(9), 091706. [DOI] [PubMed] [Google Scholar]
- Woods K, Nguyen D, Tran A, Victoria YY, Cao M, Niu T,… & Sheng K (2016). Viability of Noncoplanar VMAT for liver SBRT compared with coplanar VMAT and beam orientation optimized 4π IMRT. Advances in radiation oncology, 1(1), 67–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verburg JM, Grassberger C, Dowdell S, Schuemann J, Seco J, & Paganetti H (2016). Automated Monte Carlo simulation of proton therapy treatment plans. Technology in cancer research & treatment, 15(6), NP35–NP46. [DOI] [PubMed] [Google Scholar]