SNP-skimming: a fast approach to map loci generating quantitative variation in natural populations

Abstract

Genome-wide association mapping (GWAS) is a method to estimate the contribution of segregating genetic loci to trait variation. A major challenge for applying GWAS to non-model species has been generating dense genome-wide markers that satisfy the key requirement that marker data is error-free. Here we present an approach to map loci within natural populations using inexpensive shallow genome sequencing. This ‘SNP skimming’ approach involves two steps: an initial genome-wide scan to identify putative targets followed by deep sequencing for confirmation of targeted loci. We apply our method to a test dataset of floral dimension variation in the plant Penstemon virgatus, a member of a genus that has experienced dynamic floral adaptation that reflects repeated transitions in primary pollinator. The ability to detect SNPs that generate phenotypic variation depends on population genetic factors such as population allele frequency, effect size, and epistasis as well as sampling effects contingent on missing data and genotype uncertainty. However, both simulations and the Penstemon data suggest that the most significant tests from the initial SNP skim are likely to be true positives – loci with subtle but significant quantitative effects on phenotype. We discuss the promise and limitations of this method and consider optimal experimental design for a given sequencing effort. Simulations demonstrate that sampling a larger number of individual at the expense of average read depth per individual maximizes the power to detect loci.

Introduction

A growing body of research infers evolutionary processes at the population level using genomic data. Many of these population genomic studies are based on shallow Illumina sequencing of barcoded individuals, notably by reduced representation sequencing methods, genome resequencing, and pool-seq (Andrews et al. 2016; Catchen et al. 2017; Schlötterer et al. 2014; Therkildsen & Palumbi 2017). These methods are inexpensive and accessible, which has enabled rapid advances in understudied systems. Evolutionary biologists can now test basic hypotheses on the process of ecological divergence and reproductive isolation by comparing genome-wide patterns of genetic polymorphism within and between populations across a landscape. For example, researchers in a variety of study systems are using data sampled across differentiated populations to identify genomic signatures of local adaptation (e.g., Bassham et al. 2017; Hoban et al. 2016; Pfeifer et al. 2018).

While the evolutionary insights gained from population genomic studies are substantial, important questions cannot be answered with genomic data alone. Adaptation in natural populations depends on trait and fitness variation segregating within populations. The extent and pattern of standing genetic variation shapes a population’s short-term response to selection. By integrating genomic data with trait or fitness data, we can begin to characterize the contributions of individual loci to additive genetic variation. This information can reveal the history of selection acting on traits within a population and whether the availability or nature of standing variation constrains a population’s response to natural selection. Moreover, we can compare the genomic basis of standing variation to that of population or species divergence to assess the contribution of standing variation to evolutionary divergence. Yet population genomic studies do not routinely incorporate phenotypic or fitness data.

To examine the genomic basis of standing genetic variation and estimate the contribution of individual loci to the total additive genetic variation, we need to sample variants according to their frequency in natural populations. A direct approach is genome-wide association mapping (GWAS). GWAS takes advantage of linkage disequilibrium (LD) between marker alleles and genetic variants with phenotypic effects (‘causal loci’), allowing one to map quantitative trait loci (QTLs) within natural populations (reviewed by Schielzeth & Husby 2014). GWAS typically require great effort and expense. LD often rapidly decays in large randomly-mating populations, and dense sampling of markers is necessary to tag genomic regions linked to causal loci. However, increasing the density of sampled sites reduces sequence depth per site for any given level of sequencing. This introduces uncertainty in genotype assignments and reduces power to detect genotype-phenotype associations. Extant GWAS methods are designed mainly for systems with extensive genomic resources. Many commonly used methods require certain genotype calls and little to no missing data (e.g., Aulchenko et al. 2007; Bradbury et al. 2007; Kang et al. 2010; Purcell et al. 2007; Rönnegård et al. 2016; Zhou & Stephens 2012; but see Parchman et al. 2012). Data meeting these criteria can be generated by SNP panels that deeply sequence large numbers of markers. SNP panels have been developed for only a few non-model species (e.g., Johnston et al. 2011; Knief et al. 2017; Santure et al. 2013; Silva et al. 2017).

One approach to increase the size and completeness of SNP datasets for GWAS is genotype imputation, where missing genotypes are assigned based on observed (“direct typed”) genotypes at adjacent markers found in the same haplotype block (Marchini & Howie 2010). Imputed genotypes are often expressed as a genotype score (estimated allelic dosage) that varies continously from 0 to 2. Several GWAS methods can handle continuous genotype scores, including EMMAX, GEMMA, and PLINK (Kang et al. 2010; Purcell et al. 2007; Zhou & Stephens 2012). However, genotype imputation usually requires a reference panel of densely-genotyped haplotypes, a fine-scale recombination map, and/or knowledge about marker order (e.g., Howie et al. 2009; Li et al. 2009). Moreover, existing imputation methods do not handle genotype uncertainty in the direct typed markers. Assuming a researcher lacks prior knowledge of haplotype blocks, one option is to assign continuous genotype scores for missing genotypes simply according to the expectation based on allele frequency (“naïve imputation”; Jarquín et al. 2014). Assigning a continuous genotype score may be preferable to integer genotypes (0, 1, or 2), but results in a point estimate that does not retain information on the underlying probability distribution for genotype.

Here we examine the utility of a two-step ‘fast track’ approach to map loci within natural populations and estimate their contribution to the additive genetic variance. Sampling a natural population in situ can be particularly informative because it captures variation in traits and fitness that is expressed under relevant environmental conditions – this variation may not easily be replicated under controlled laboratory or greenhouse conditions. The first step is a genome-wide shallow sequencing scan that finds markers associated with phenotype, using a likelihood approach to account for missing data and genotype uncertainty. Due to missing data, this initial scan will only detect a portion of the total loci associated with phenotype, and putative trait-associated SNPs will show inflated associations with phenotype. The second step interrogates these candidate SNPs by deep sequencing PCR amplicons. This step fills in missing data and removes genotype uncertainty for a given site.

As an example, we apply our method to analyze floral dimension data collected from a natural population of the plant Penstemon virgatus. In this population, segregating variation in floral traits is highly quantitative, making our dataset ideal to illustrate both the promise and challenges of mapping QTLs from shallow sequencing data. SNP-skimming does not provide an exhaustive catalog of within-population QTLs, but instead enables an initial search for loci generating within-population variation. In this study, our approach uncovered a subset of segregating sites with subtle effects on the focal trait, stamen length. Simulations of our initial genome-wide scan suggest the power to detect loci affecting phenotype is optimized by increasing the population sample size, at the expense of average read depth.

Methods

Study system and phenotypic measurements

Penstemon is a large North American genus of perennial herbs that shows a dynamic pattern of floral evolution, including repeated origins of hummingbird-adapted flowers, from the ancestral condition of hymenopteran-adapted (‘bee-adapted’) flowers (Wessinger et al. 2016; Wilson et al. 2007; Wolfe et al. 2006). Adaptation to hummingbird pollination in Penstemon involves modification of multiple floral traits, including the narrowing of the floral tube, and elongation of the stamen filaments, style, and floral tube. Since this evolutionary transition has occurred at least twelve times in Penstemon on an apparently short timescale (Wolfe et al. 2006), we hypothesize that bee-pollinated Penstemon populations harbor substantial variation in floral dimension that may be recruited for adaptation to hummingbird pollination.

We studied a large population of a bee-pollinated species, Penstemon virgatus var. asa-grayi, located in Teller Co., Colorado (38.42622 N, −105.09742 W, elevation ~ 2874 m) from June 26–28, 2016 (Fig. 1A). We sampled 291 individuals over a uniform hillside. For each individual, we measured the following three traits on two flowers per plant: (1) length of the lateral stamen filaments (‘stamen length’), (2) length of the floral tube from base to opening (‘tube length’), and (3) width of the flower at its opening (‘tube width’). We measured open flowers whose anthers had not yet dehisced in an effort to target flowers at the same developmental age. Trait measurements from replicate flowers per plant were highly correlated, therefore we averaged replicate trait measurements for analyses. We collected leaf material from each individual into silica gel and later extracted DNA from dried tissue using a modified CTAB protocol (Wessinger et al. 2016).

Fig 1.

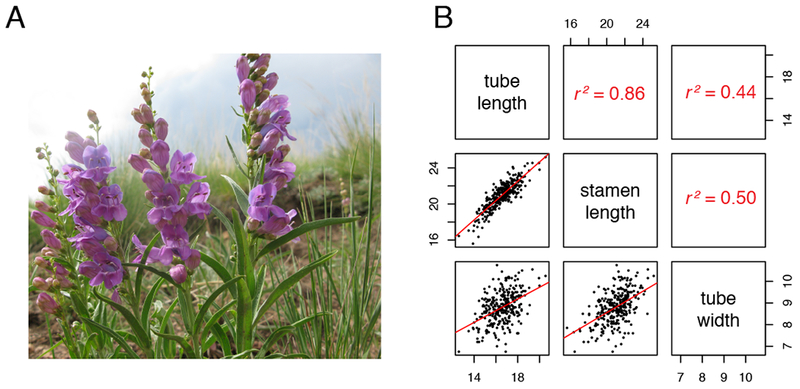
A: Representative individuals from the P. virgatus study population. B: scatterplots of pairwise floral dimension traits. Each dot is an individual plant and red lines show linear regression. Pearson’s correlations are reported above the diagonal.

MSG library preparation and sequencing

To generate a genome-wide set of polymorphic markers in the P. virgatus population sample, we used Multiplexed Shotgun Genotyping (MSG; Andolfatto et al. 2011) using the restriction enzyme MseI. This enzyme cuts frequently (recognition site: TTAA) and we expected broad coverage of the genome, but low average read depth per SNP per individual. We digested 50 ng of genomic DNA from each P. virgatus individual using MseI (New England Biolabs) and ligated one of 96 unique barcoded adapters onto each DNA sample. Up to 96 samples were pooled into each of four sublibraries that were size-selected for fragments between 250–450 bp using a Blue Pippen (Sage Science). We then amplified sublibraries for 14 PCR cycles using Phusion High-Fidelity Polymerase (New England Biolabs) and primers that incorporate unique barcoded Illumina indices. Each sublibrary was amplified in four replicate PCR reactions that were subsequently combined and purified. A single combined library with equimolar concentrations of the four sublibraries was sequenced on four Illumina HiSeq rapid run lanes (150 bp single end reads) at the University of Kansas Genome Sequencing Core.

Identification of polymorphic sites

We sorted fastq files into sample-specific read files based on adapter barcodes, allowing for one barcode mismatch, using step 1 of ipyrad (https://github.com/dereneaton/ipyrad). We then removed low quality sequence and adapter contamination using step 2 of ipyrad, which implements the cutadapt algorithm (Martin 2011). During this step, reads were trimmed to a minimum length of 75 bp if they contained adapter sequence, and reads were discarded if more than seven bases had a phred quality score less than 20. For our analyses, we took advantage of a draft reference genome assembly for P. barbatus, a close relative of P. virgatus (number of contigs = 18,827, N50 = 43,419). This assembly is not annotated and covers 92.8% of the total expected genome size of P. barbatus (696 Mbp of 750 Mbp). We expect this includes most of the gene-rich regions of the genome. We mapped filtered sequence reads from each individual to this reference assembly using BWA (Li & Durbin 2009). This generated a mapping file (.sam file) for each individual. Our MSG sequence data covered roughly 18% of the reference genome. We then used the UnifiedGenotyper algorithm in GATK (McKenna et al. 2010) to analyze the collection of 291 .sam files. GATK identifies polymorphic sites across the sample of individuals and, at each SNP for each individual, counts the number of reads matching the reference base (‘ref’ allele) and the number of reads carrying the alternative base (‘alt’ allele). Based on this information, GATK assigns likelihoods that the individual is homozygous for the ref allele, heterozygous, or homozygous for the alt allele. These likelihoods are phred-scaled for efficient representation and are normalized so that the most likely genotype is zero and values for the other two genotypes are scaled relative to the most likely genotype. The annotations for the total population at all SNPs are contained in the variant call file (.vcf) produced by GATK.

Using a custom Python script, we filtered through the .vcf file to recover SNPs matching the following criteria: (1) mapping quality score > 20, (2) genotype calls in at least 75 individuals, (3) exactly two alleles segregating in the population, and (4) frequency of the reference base in the range of 0.2–0.8 in the population sample. We expect most SNPs segregating in the population have minor allele frequency less than 0.2, but we have limited power to detect the effects of alleles that are not at intermediate frequency across sampled individuals. The filtered dataset contains 650,917 SNPs. To identify pairs of markers that are perfectly correlated across individuals in our sample, we measured LD between SNPs that were sequenced on the same 150 bp read. We used custom Python scripts that calculate LD from single-end Illumina sequence data, following the approach of Feder et al. (2012). Briefly, we filtered through the .sam files generated by BWA for reads containing our focal SNPs. When more than one site was present on a given sequencing read, we tallied the observed two locus haplotype for each pair of SNPs and calculated LD (r²). For sets of perfectly correlated SNPs with genotype calls in the same set of individuals, we randomly discarded all but one SNP. This yielded a final set of 620,473 SNPs for downstream analyses.

Estimation of allele frequencies and genotype likelihoods at low read depth

With low read depths, the observed read data for an individual at a SNP can be treated as a binomial random variable. The probability of drawing a given allele (e.g., the ref allele) depends on genotype. Ignoring sequencing error and PCR bias, this probability is 1 if the individual is homozygous for the ref allele, ½ if the individual is heterozygous, and 0 if the individual is homozygous for the alt allele. With a single read, we can distinguish between the two homozygous genotypes, but we cannot distinguish a homozygote for the ref allele from a heterozygote. With increased sequencing depth, we perform a set of k binomial experiments, where k is the number of reads sequenced in a given individual. If an individual is homozygous for the ref allele, the probability of observing the ref allele in each of k reads is 1, whereas the probability of this event in a heterozygote is (½)^k. As read depth increases, our ability to distinguish between a heterozygote and a homozygote improves because the probability of observing a single allele in a heterozygote declines.

This inability to confidently identify genotypes at low read depths is a general feature of population genomic studies. Population genomic analyses that depend on estimation of individual genotypes (e.g., GWAS) need to estimate and account for this relationship between read depth and the probability of observing a heterozygote. Assuming Hardy-Weinberg equilibrium (HWE), the probability of observing a heterozygote at read depth k is:

$$P[\text{observing het}\mid k]=2q(1-q){\tau }_k$$ (1)

where q is the sample allele frequency of the reference base and τ_k is the probability of detecting a heterozygote at read depth k. The expected value of τ_k is:

$${\tau }_k=1-2{\left(\frac{1}{2}\right)}^k$$ (2)

In other words, one minus the chance that k reads drawn from a heterozygote will either all match the ref base or all match the alt base. However, the realized probability of detecting a heterozygote may commonly be lower than this expectation and we suggest that τ_k values be estimated from the observed genomic data. For example, depending on the quality of DNA samples, amplification during library preparation might skew the balance of ref vs. alt alleles at heterozygous sites away from equality (Monnahan et al. 2015). To estimate allele frequencies and τ_k values for our dataset, we performed the following steps: (1) initial estimation of allele frequencies, (2) estimation of τ_k values given the initial allele frequency estimates, and (3) re-estimation of allele frequencies given the estimated τ_k values. We estimated q for each SNP by maximizing the likelihood of the observed genomic data and assuming independence across individuals:

$$\ln L={\Sigma }_{j=1}^n\ln \left(P\left[{\text{data}}_j\right]\right)$$ (3)

where P[data_j] is the probability of the observed data for the j'th individual. This can be written as the sum of conditional probabilities of the observed genomic data:

$$P\left[{\text{data}}_j\mid q\right]=L_{\mathit{RR}}{q}^2+L_{\mathit{RA}}2q(1-q)+L_{\mathit{AA}}{(1-q)}^2$$ (4)

where L_g is the likelihood of the observed read data if the true genotype is g, RR is a homozygote for the ref allele, RA is a heterozygote, and AA is a homozygote for the alt allele. This approach follows Monnahan et al. (2015), who derived the likelihood of genomic data across successive life stages in a selection component analysis. For this initial estimate of $\widehat{q}$, we take L_g values directly from the ‘PL’ field of the sample annotations in the .vcf file. For sites with missing data, L_RR = L_RA = L_AA = 1. These genotype likelihoods are multiplied by prior genotype probabilities that assume HWE. We maximized the likelihood of q using the optimize.brent bounded optimization implemented in SciPy (www.scipy.org).

Estimation of τ_k values

The genotype likelihoods (L_g values) from GATK provide information on the most likely genotype, according to the sequence data. A heterozygous individual is detected (L_RA is maximal) with probability τ_k. A heterozygous individual will be incorrectly detected as one of the two homozygotes (e.g., RR homozygote if L_RR is maximal) with probability (1 – τ_k)/2. We assume a heterozygote is equally likely to appear as either homozygote. Therefore, to estimate τ_k values we summed the likelihood of the observed data at a given read depth k across m SNPs and n individuals, given our maximum likelihood (ML) allele frequency estimates (${\widehat{q}}_i$):

$$\ln L={\Sigma }_{i=1}^m\ln \left(P\right[{\text{data}}_i\mid {\widehat{q}}_i,{\tau }_k\left]\right)$$ (5)

$$P[{\text{data}}_i\mid {\widehat{q}}_i,{\tau }_k]={{\widehat{q}}_i}^2+{\widehat{q}}_i(1-{\widehat{q}}_i)(1-{\tau }_k)\text{if}{L}_{\mathit{RR}}\text{is maximal}$$

$$P[{\text{data}}_i\mid {\widehat{q}}_i,{\tau }_k]=2{\widehat{q}}_i(1-{\widehat{q}}_i){\tau }_k\text{if}{L}_{\mathit{RA}}\text{is maximal}$$

$$P[{\text{data}}_i\mid {\widehat{q}}_i,{\tau }_k]={\widehat{q}}_i(1-{\widehat{q}}_i)(1-{\tau }_k)+{(1-{\widehat{q}}_i)}^2\text{if}{L}_{\mathit{AA}}\text{is maximal}$$

We optimized the likelihood of τ_k again using optimize.brent implemented in SciPy, and then re-estimated allele frequencies (q_i') using equation 5, given our ML estimates of ${\widehat{\tau }}_k$ values. In practice, these re-optimized allele frequencies were nearly identical (r²=0.999) to original allele frequency estimates.

Estimating genetic effects on phenotype

For a given trait and SNP, we sum the log-likelihood of the observed set of genomic and phenotypic data across n individuals according to eq. 3. In this case, P[data_j] is the probability of the observed genomic and phenotypic data for the j'th individual. This can be written as the sum of conditional probabilities of the observed phenotype Z in a given genotype, times the genotype probability:

$$P\left[{\text{data}}_j\right]=P[Z\mid \mathit{RR}]P\left[\mathit{RR}\right]+P[Z\mid \mathit{RA}]P\left[\mathit{RA}\right]+P[Z\mid \mathit{AA}]P\left[\mathit{AA}\right]$$ (6)

As before, we set the genotype probabilities P[RR], P[RA], and P[AA] as products of the genotype likelihoods (L_g) times the prior genotype probabilities. For the initial genome scan where read depth is low, we accounted for our estimated probability of detecting heterozygotes: in cases where the most likely genotype was homozygous (L_RR or L_AA maximal), we updated L_RA to:

$${L_{\mathit{RA}}}^{\prime }=(1-{\widehat{\tau }}_k)∕2$$ (7)

We fit a null model (H₀) where phenotype is normally distributed and its mean (μ) and variance (σ²) do not depend on genotype: P[Z|RR] = P[Z|RA] = P[Z|AA].

$$P\left[{\text{data}}_j\mid \widehat{q},\mu ,{\sigma }^2\right]=\frac{1}{\surd 2{\sigma }^2\pi }{e}^{\frac{-{(z-\mu )}^2}{2{\sigma }^2}}[L_{\mathit{RR}}{\widehat{q}}^2+L_{\mathit{RA}}2\widehat{q}(1-\widehat{q})+L_{\mathit{AA}}{(1-\widehat{q})}^2]$$ (8)

We also fit an alternative model (H₁) where mean phenotype depends on genotype according to an additive model: Z_RR ~ N(μ_RR, σ²), Z_RA ~ N(μ_RR+a, σ²), and Z_AA ~ N(μ_RR+2a, σ²). Here, μ_RR is the mean phenotype of RR individuals and a is the additive effect of the alt allele on mean phenotype.

$$P\left[{\text{data}}_j\mid \widehat{q},{\mu }_{\mathit{RR}},{\sigma }^2,a\right]=\frac{1}{\sqrt{2{\sigma }^2\pi }}{e}^{\frac{-{(z-{\mu }_{\mathit{RR}})}^2}{2{\sigma }^2}}[L_{\mathit{RR}}{\widehat{q}}^2]+\frac{1}{\surd 2{\sigma }^2\pi }{e}^{\frac{-{(z-{\mu }_{\mathit{RR}}+a)}^2}{2{\sigma }^2}}[L_{\mathit{RA}}2\widehat{q}(1-\widehat{q})]+\frac{1}{\surd 2{\sigma }^2\pi }{e}^{\frac{-{(z-{\mu }_{\mathit{RR}}+2a)}^2}{2{\sigma }^2}}[L_{\mathit{AA}}{(1-\widehat{q})}^2]$$ (9)

For each site, we compared the likelihood of H₁ to H₀ with the likelihood ratio test (LRT) statistic and tested significance using the chi-square distribution with 1 degree of freedom. We performed these calculations on the filtered .vcf file and the phenotypic data using a custom Python script that maximizes likelihoods with Broyden-Fletcher-Goldfarb-Shanno (BFGS) bounded optimization implemented in SciPy. We estimated false discovery rate (FDR) for each site with adjusted p-values (q-values; Benjamini & Hochberg 1995) using the qvalue R package (Dabney et al. 2010).

MSG on PCR amplified regions

We selected a set of six P. virgatus SNPs for deep sequencing to corroborate a potential association with stamen length in our population sample as an initial test of our approach (Table 1). To inform this selection, we leveraged information from a previous study that mapped floral trait QTL in a genetic cross between the hummingbird-adapted species P. barbatus to its close relative, the bee-adapted species P. neomexicanus (Wessinger et al. 2014). These two species are closely related to P. virgatus (Wessinger et al. 2016). In the Supporting Information S1, we describe our approach to determine whether SNPs in the current study are located near interspecific QTLs for stamen length. We chose two SNPs (SNPs 3 and 5) with high LRT values in both the P. virgatus and the interspecific F2 populations. We chose two SNPs (SNPs 1 and 2) with high LRT values in the P. virgatus population that did not show evidence of association with stamen length in the interspecific F2 population (one resides in a genomic interval that was not associated with phenotype in the interspecific dataset and the other resides in an interval that was not tagged by any interspecific markers). Finally, we chose two SNPs (SNPs 4 and 6) that had moderate LRT values in the P. virgatus population and reside in genomic intervals strongly associated with stamen length in the interspecific population.

Table 1.

Effects of SNPs targeted and deep sequenced on stamen filament length.

SNP	initial scan LRT	initial scan FDR	F2 window LRT	amplicon $\widehat{q}$	amplicon LRT	amplicon p-value	amplicon â (mm)	amplicon h2SNP
1	22.51	0.185	N/A	0.027	0.18	0.67
2	17.07	0.245	4.558	0.53	4.44	0.035	0.26	0.015
3	22.51	0.162	23.54	0.68	6.09	0.014	0.23	0.033
4	9.01	0.706	24.27	0.75	1.27	0.26
5	22.65	0.201	23.54	0.34	5.18	0.02	0.29	0.017
6	8.99	0.707	22.89

â: maximum likelihood (ML) estimate for additive effect, FDR: false discovery rate, h²_SNP: percent of total phenotypic variation explained by variation at the SNP, LRT: likelihood ratio test statistic, $\widehat{q}$: ML estimate for allele frequency of reference allele.

For deep sequencing, we used PCR amplification followed by MSG on the resulting amplicons. We used MSG for amplicon sequencing simply because it provides an efficient means to barcode individual samples for multiplexed sequencing. In our case, MSG yielded nearly full coverage (entire length of targeted amplicons) due to high frequency of the MseI cut site. However, other methods for sequencing PCR amplicons could be substituted here. We designed PCR primers to amplify a given SNP based on the local surrounding sequence. First, we extracted the set of unique reads that map to the P. barbatus scaffolds near a focal site (1 kb upstream to 1 kb downstream) from the initial .sam files generated by BWA. We then imported these sequences into Geneious (Kearse et al. 2012), assembled sequences near a given SNP to create a contiguous sequence for the local region, and designed primers that amplified the focal SNP using Primer3 (Untergasser et al. 2012). We used these primers and Bullseye polymerase mastermix (Midsci) to amplify the original DNA samples in 5 microliter reactions for 35 cycles with 56˚C annealing temperature. Amplicons of the six SNP regions for a given individual were pooled in approximate equal DNA concentrations (based on concentration estimates from eight PCR reactions for each primer set). We performed MSG on these samples using MseI as previously described, except we did not perform a size selection step. We sequenced the combined library on approximately 1/5 of a single 150 bp single end Illumina HiSeq rapid run lane.

We repeated our variant calling pipeline on the resulting .fastq files without down sampling (GATK –dt NONE flag). We filtered the .vcf file to include sites with (1) mapping quality score > 20, (2) genotype calls in at least 200 individuals, (3) exactly two alleles segregating in the population, and (4) median read depth of at least 400 reads. Inspection of the filtered .vcf file revealed that we recovered five of the six targeted SNPs. The genomic region near the remaining SNP (SNP 6) was not sequenced at high depth and therefore was excluded from downstream analyses. Incidentally, this amplicon did not amplify as strongly as the other five during PCR and perhaps experienced non-specific amplification.

For each focal SNP and closely linked sites, we calculated the likelihood of an association between genotype and phenotype as described above in eqs. 6, 8–9, taking genotype likelihoods directly from GATK. For SNPs showing an association with phenotype (p-value < 0.05), we calculated the proportion of the total phenotypic variance in the population explained by the SNP (heritability due to variation at the SNP) as:

$$h_{\left(\mathit{SNP}\right)}^2=\frac{2\widehat{q}(1-\widehat{q}){\widehat{a}}^2}{V_P}$$ (10)

where $\widehat{q}$ is the maximum likelihood estimate (MLE) for allele frequency, â is the MLE for the additive effect, and V_P is the phenotypic variance. This estimated heritability is inflated by estimation error of â (Luo et al. 2003; Monnahan & Kelly 2015).

Simulations

We performed simulations to examine the power of our pipeline to detect a locus with quantitative effects on phenotype. For each simulation, we drew the following three sets of random variables: (1) a population sample of N ‘true’ genotypes, given an allele frequency q and assuming HWE expected genotype frequencies, (2) read depth (k) for each of N individuals, assuming read depth per site per individual follows a Poisson distribution with mean and variance equal to λ, and (3) phenotypic values for each of N individuals in a sample. To simulate a site with no effect on phenotype, we drew phenotypic values for each sample in the population from a normal distribution with mean = μ and variance = V_P. To simulate a site with effects on phenotype, we drew phenotypic values from genotype-specific normal distributions with variance = V_R and genotype-specific means (RR: μ_RR, RA: μ_RA + a, AA: μ_RR + 2a). Here V_R is the residual variance that is not explained by the phenotypic effect of the simulated site:

$$V_R=V_P-2q(1-q)a^2$$ (11)

Based on the randomly drawn true genotypes and read depths, we simulated observed genotype data for each sample. If the true genotype is homozygous and k > 0, the observed genotype is the corresponding homozygote. If the true genotype is heterozygous, the observed genotype will be heterozygous with probability equal to the expected value of τ_k (eq. 2), and the probability that the observed genotype is RR or AA is (1 – τ_k)/2 for each case. Based on these observed genotypes and phenotypes, we estimated genetic effects on phenotype following the approach used for our empirical data, although here we jointly estimated q along with the other parameters and assumed τ_k follows its expected values (eq. 2). For each simulated dataset, we performed 10,000 replicate simulations.

We simulated datasets with features matching our empirical dataset to enable a direct comparison: N = 291, V_P = 2.21 mm², μ = 21 mm, and λ = 0.838. We simulated a site with allele frequency (q) = 0.34 and additive effect (a) = 0.26 mm (similar to that shown by SNP 5, see Table 1 and Results). To explore the effects of modifying our experimental design, we simulated doubling the number of individuals sampled, doubling the average read depth, and error-free genotype data for all individuals (e.g., data from a SNP array). To explore the ability of our approach to detect loci of varying effect sizes, we simulated a range of ten additive effect sizes that corresponded to SNP heritabilities ranging from 0.01 to 0.1 and calculated both the false positive rate and the power of our method to detect a true positive.

Comparison with GEMMA Bayesian Sparse Linear Mixed Model (BSLMM)

We compared SNP-skimming to the BSLMM implemented by GEMMA (Zhou et al. 2013; Zhou & Stephens 2012). GEMMA requires genotype information for all individuals, but it can take genotypes expressed as continuous genotype scores. We therefore assigned scores based on posterior genotype probabilities for all individuals at all sites before running GEMMA. We performed these analyses on our empirical dataset as well as a set of simulated datasets generated for this comparison. Details of these analyses and simulated datasets are found in Supporting Information S4.

Results

Phenotypic data

In the field-sampled P. virgatus population, tube length and stamen length were strongly positively correlated (r² = 0.86; Fig. 1B). Each of these length traits was positively correlated with tube width, although the strength of this correlation is about half as strong as the correlation between length traits (r² = 0.44–0.5; Fig 1B). Mean phenotypic values for tube length, stamen length, and tube width were 16.58 mm, 21 mm, and 8.8 mm, respectively. In the same order, the phenotypic variances were 1.41 mm², 2.22 mm², and 0.53 mm².

Genome scan for associations with floral traits

MSG on DNA extracted from 291 individuals generated a set of 620,473 filtered SNPs sequenced in at least 75 individuals (see methods). The probability of identifying a heterozygote in our initial scan depended on read depth. We found a slight bias at low read depth against heterozygotes slightly beyond the theoretical expectation, suggesting mild PCR bias from the amplification step of MSG library prep (Supporting Information S2). We imposed an FDR of 0.10 to declare genome-wide significance for genetic effects on floral traits. Only two SNPs showed an FDR < 0.10 for stamen length. No SNPs met this FDR threshold for either tube length or tube width.

Deep amplicon sequencing

We successfully amplified and deep sequenced five of the six targeted P. virgatus SNPs putatively associated with stamen length. The genomic regions containing these five SNPs were each sequenced in an average of 287 individuals with an average median read depth per individual of 1094 reads. Overall, three of the five amplified SNPs were significantly associated with stamen length (p-value < 0.05; Table 1). Two of these three SNPs were also associated with stamen length in the interspecific F2 population (Table 1). SNPs significantly associated with phenotype had subtle effects, explaining between 1.5–3.3% of the total phenotypic variance (Table 1). One SNP (SNP 3) that was associated with stamen length did not show genotype frequencies consistent with HWE. This site contains a large (300 bp) indel. This size difference apparently caused preferential amplification of the shorter allele in heterozygotes, making heterozygotes appear homozygous. Other SNPs sequenced on the ~1000 bp amplicon did show HWE expected frequencies and were also significantly associated with stamen length (Fig. 2).

Fig 2.

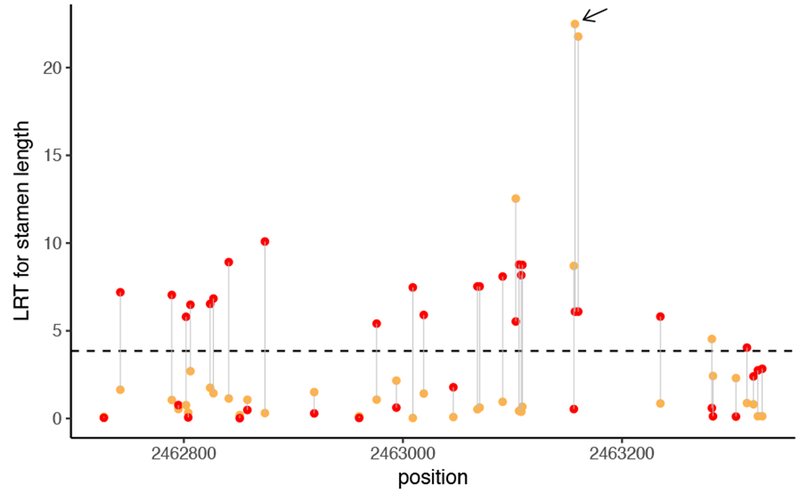
Likelihood ratio test (LRT) of SNPs across the region surrounding SNP 3 in the initial genome scan (orange) vs. deep sequencing amplicons (red). Arrow indicates SNP 3.

Two of the five amplified SNPs were not associated with stamen length after deep sequencing. One of these (SNP 1) showed a very strong association with phenotype in the initial scan, but after deep sequencing nearly all individuals were homozygous for the alt allele, even individuals previously assigned as homozygotes for the ref allele in the initial scan. The remaining SNP (SNP 4), did not show signs of spurious genotypes.

Simulations of the initial genome-wide scan

We performed simulations to examine the power of our initial scan to detect a site with quantitative effects on phenotype. Summary statistics for all simulations are provided in Supporting Information S3. We simulated four different experimental designs. For each of these, we first simulated a locus with no effect on phenotype to confirm that LRT values follow the chi-square distribution with 1 degree of freedom, which validated our use of this distribution to assign p-values. We then simulated a locus based on our empirical SNP 5 (h² = 0.017, see Table 1). Simulation of an experimental design matching our empirical study (291 individuals at ~0.838× read depth) yielded relatively few replicates (~3%) returning LRT values greater than 10, an arbitrary but reasonable value for genome-wide significance (Fig. 3A). In contrast, simulation of complete and error-free genotype data returned LRT values greater than 10 for ~18.5% of replicate simulations, indicating a greater power to detect a true association (Fig. 3A). We simulated the effects of doubling the average read depth vs. doubling the number of individuals sampled from a population. We found that doubling the number of sampled individuals improves our power to detect a true association to a greater degree (LRT > 10 for ~8.6% of simulations) compared with doubling the read depth (LRT > 10 for 6.7% of simulations) (Fig. 3A). In addition, we found a strong positive relationship between LRT value and additive effect: simulation replicates with high LRT values had substantially inflated estimated additive effects above the value modeled in the simulation (Fig. 3B).

Fig. 3.

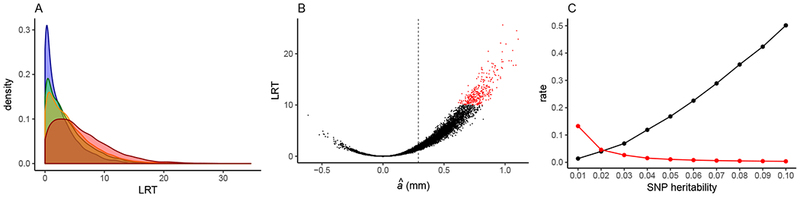
Estimated genetic effects from simulations of our genome-wide scan. Parameter values are given in text. A: Density plot showing distributions of likelihood ratio test statistic (LRT) values for 10,000 simulations of each of four modeled datasets: model of our empirical dataset (blue), doubled average read depth (green), doubled sampled individuals (orange), complete and error-free genotype data (red). B: Scatterplot showing the relationship between estimated additive effect (â) and LRT for each of 10,000 replicate simulations of our empirical dataset. Sites with LRT > 10 are in red and the simulated additive effect size (0.29 mm) is indicated with dashed line. C: Rate that a true positive is detected (black) and false positive rate (red) for SNP heritabilities ranging from 0.01–0.10.

We also simulated a range of effect sizes, assuming an experimental design matching our study, and compared the proportion of simulations that return LRT > 10 as an estimate of power. Our power to detect a true association increases with effect size (Fig. 3C). Under our design, we expect to detect a site explaining 1% of segregating variation only 1.4% of the time. This rate increases to roughly 50% for a site explaining 10% of segregating variation (Fig. 3C). The false positive rate is negatively related to effect size and is less than 5% for simulated SNP heritabilities above 1%. (Fig. 3C). We use the results of these simulations to discuss our empirical findings below.

Comparison with GEMMA BSLMM

We compared our SNP-skimming method to the BSLMM implemented in GEMMA. We briefly summarize the major results here and full details of the analyses and results are found in Supporting Information S4. We first compared these two methods’ abilities to identify associations with stamen length in our empirical dataset. Sites identified by GEMMA as having measurable effects on phenotype also showed reasonably high LRT values (LRT > 8). This overlap between the two methods is reassuring and suggests the sites identified by GEMMA also display a signal of association using our method. However, the converse is not necessarily true: many sites with high LRT values do not show signs of association with phenotype in the GEMMA analysis. For simulated datasets, both methods found that simulated causal sites displayed, on average, more evidence for an association with phenotype relative to simulated neutral sites, although our method is marginally better at detecting causal sites (details found in Supporting Information S4).

Discussion

A two-step approach can detect QTL in natural populations

Adaptation depends on features of segregating genetic polymorphisms including the size of allelic effects, pleiotropy, and epistasis. These features scale up to influence trends in adaptive evolution across larger taxonomic scales, such as parallel evolution of populations or species that show similar patterns of segregating variation (e.g., Hohenlohe et al. 2010; Jones et al. 2012). Shallow genome sequence data is now routinely generated for large numbers of barcoded individuals. Extending population genomic analyses to consider segregating phenotypic or fitness data must account for genotype uncertainty inherent in these data (Comeault et al. 2014; Monnahan et al. 2015; Parchman et al. 2012). These advances will streamline the identification of loci underpinning additive genetic variation and genetic correlations, allowing us to characterize the material basis of standing variation. SNP-skimming combines a broad but shallow initial genome scan with focused deep sequencing around targeted sites. It is a simple and inexpensive approach to localize trait-associated genomic variants.

The strength of association in the initial scan predicts significance following deep sequencing

Estimates of FDR in the initial scan may be informative predictors of whether sites remain significant following deep sequencing. Out of the four SNPs that successfully amplified and did not show spurious genotypes after deep sequencing (SNPs 2–5), the three with high initial LRT values (SNPs 2, 3, and 5) remained significant following deep sequencing (Table 1). The FDR for these sites in the initial scan ranged from 0.162–0.245. In contrast, SNP 4 had a modest LRT values and was not significant after deep sequencing. The FDR for this SNP was relatively high (0.706) and perhaps we should not be surprised that this SNP is not associated with phenotype. For these four sites, admittedly a small sample size, we see that LRT values in the initial scan reliably predict LRT values in the deep sequencing step (for sites 2-5: r² = 0.78, p = 0.022). This suggests the best strategy for success is the most obvious one: to choose sites with the highest LRT values in the initial scan for deep sequencing. In our case it was not necessary to choose sites based on a priori knowledge of the focal trait’s genetic architecture in a related organism. We expect that the success rate of our deep sequencing approach would have been greater (i.e., more of the targeted sites having significant effects on phenotype) had we simply targeted sites with greatest initial LRT values rather than choosing sites based on their overlap with interspecific QTLs. For example, we did not choose either of the two sites with FDR < 0.10 because they did not overlap with interspecific QTL.

Effects of sampling in the initial scan over- or underestimate effects on phenotype

GWAS pose an enormous multiple testing challenge and the power to detect causal loci as statistically significant depends on effect size, minor allele frequency, and epistasis (Marjoram et al. 2014). SNPs with large effect sizes and intermediate allele frequencies are more easily detected; however, the allele frequencies of segregating causal loci may be low if stabilizing selection has been historically important (Keightley & Eyre-Walker 2010). Thus, even with accurate and error-free genotype data, the loci detected in a GWAS scan may not be a comprehensive set of those that generate the observed phenotypic variance.

Missing data and genotype uncertainty further winnow the loci identified from a genome scan. For quantitative traits, the proportion of total phenotypic variation that is explained by a focal SNP may be modest, leaving substantial residual variation unexplained by SNP genotype. Due to missing data across individuals, we observe genotype for a random subset of individuals at a given site. If we were to repeatedly subsample the population, the observed association with phenotype would follow a distribution of LRT values, depending on the set of genotyped individuals. Since we often apply a stringent genome-wide threshold for significance, we only detect an association if the observed association falls in the tail of this distribution. The majority of SNPs with quantitative effects on phenotype will not display high LRT values following the initial scan and will not be detected by this SNP-skimming approach. Only those SNPs genotyped in a subset of individuals that happen to maximize an association between genotype and phenotype will have high LRT values after the initial scan. In other words, a SNP must be both associated with phenotype and lucky to be detected in the first step of our pipeline. Simulations of our initial scan confirm that a site with quantitative effects on phenotype will rarely display high LRT values, assuming the sample size and average read depth are similar to our dataset. For example, a site explaining 1.7% of the segregating variation returned LRT > 10 (a reasonable threshold for genome-wide significance) in only 3.08% of replicate simulations (Fig 3A, Supporting Information S3). As the proportion of trait heritability explained by the SNP increases, so does power to detect a causal site (Fig. 3C).

Because sites with high LRT values were genotyped in a lucky set of individuals that maximize association with phenotype, these sites will display inflated phenotypic effects following the initial scan. This phenomenon, termed the winner’s curse, is a well-described feature of GWAS studies (Göring et al. 2001). Our simulations clearly demonstrate this pattern: LRT values are strongly positively correlated with estimated additive effects (Fig. 3B). On the other hand, our initial scan underestimated the phenotypic effects of many ‘unlucky’ sites with true effects on phenotype. With complete genotype data following amplicon deep sequencing, the estimated effects of causal loci should regress towards their expected value. After amplicon sequencing, loci with true effects on phenotype should show reduced (but still significant) effects relative to their estimated effects from the initial scan, and linked sites with underestimated effects in the initial sites should become significant.

We observe this predicted pattern for the SNPs targeted for amplicon sequencing: the three sites with significant effects on stamen length (SNPs 2, 3, and 5) displayed much higher LRT values in the initial scan than they displayed following amplicon sequencing. It is more difficult to directly observe SNPs with initially underestimated effects on phenotype become significant after deep sequencing (i.e., it is impossible to target such sites based on the results of the initial scan). Yet we found that SNPs in this category were amplified and deep sequenced along with targeted sites. For example, a large number of SNPs were amplified and sequenced along with SNP 3. If a causal locus is near SNP 3, we expect that sites in very close proximity will also show an association with stamen length. Consistent with our expectations, several sites in this local vicinity had low LRT values in the initial scan but showed significant association with phenotype after deep sequencing across all individuals (Fig. 2).

Spurious results at the deep sequencing stage are easily detected

For most targeted SNPs, the deep sequencing stage of our approach obtained nearly complete and effectively hard genotype data across our population sample. In many cases, the most likely genotype for a given individual changed following deep sequencing. As expected, we saw that some individuals that were most likely homozygous in the initial scan were inferred as heterozygotes following deep sequencing. For two of the five SNPs that we successfully deep sequenced, we saw signs of PCR bias or genotyping failure. One of these (SNP 3) was sequenced on an amplicon that showed a large (~300 bp) indel polymorphism. Amplification was biased towards the shorter allele such that heterozygotes in the initial scan appeared homozygous for the shorter allele after deep sequencing. Such incidental amplification of indel polymorphisms is easily detected by running test PCRs on gel and should be avoided for best results.

The other site with signs of bias at the deep sequencing stage (SNP 1), apparently converted nearly all individuals in the sample to homozygotes for the alt allele following deep sequencing – even individuals that previously were most likely homozygous for the ref allele in the initial scan. This data appears spurious and suggests marker failure, perhaps related to PCR primer design. Although this type of event is not detectable until after amplicon sequencing, these anomalies can be identified and culled from analyses. Future studies may find that alternative methods of sequencing a targeted region are less prone to introducing error at the deep sequencing stage of this pipeline.

Simulations suggest increased sample size yields larger returns than increased sequencing depth

For a given sequencing effort, there is a tradeoff between the number of sampled individuals and the read depth per site per individual. In simulations of our genome-wide scan, we compared the effects of doubling the number of sampled individuals vs. doubling the average read depth on the power to detect loci with quantitative effects. We found that doubling the number of sampled individuals and doubling the read depth each increased the proportion of replicates with high LRT values, although the effect is more pronounced when we doubled the individuals (Fig. 3A). Here we modeled a dataset similar to our empirical dataset and found that doubling the number of sampled individuals increased the number of replicates returning an LRT > 10 nearly three-fold. Doubling the average read depth yielded a more modest two-fold increase in the number of replicates with LRT > 10. This suggests that allocation of sequencing effort using our approach should maximize the number of sampled individuals. More importantly, this result justifies our entire approach of sequencing a large multiplexed population at shallow read depth to identify causal loci.

This conclusion is consistent with work by Buerkle and Gompert (2013) showing that estimates of population allele frequency are more accurate with higher numbers of individuals, at the expense of sequencing depth. This may be an emerging theme in population genomics – increasing the number of sampled individuals provides a greater return on parameter estimation compared with increasing read depth. To explain why, consider that in our empirical dataset and our simulations, average read depth was 0.838 (almost 1). The inclusion of a single sequence read from one additional individual at a focal SNP has a large effect on the genotype likelihoods at this site: it can at least rule out one of the homozygous genotypes. The inclusion of a second read for this individual has diminishing returns on genotype likelihoods: if the individual is heterozygous, the new sequencing read has a 50% probability to identify an individual as heterozygous, but apart from this situation, the additional sequencing read does not have as large additional effects on genotype likelihoods compared with the initial sequencing read.

Interpretation of results will depend on the quality of the reference genome

SNP-skimming does require a reference genome. As demonstrated here, a very rough draft genome assembled into ~18k scaffolds can be sufficient to search for loci generating phenotypic variation. For this purpose one could use an even more fragmented assembly, although the ability to detect SNPs will of course be limited if the assembly does not cover the majority of the genome. However, researchers aiming to make broader statements on the genetic architecture of segregating variation would benefit from a reference genome assembled into chromosomes. In our case, we cannot estimate how many causal loci are represented by our collection of SNPs with high LRT values. With a more complete genome assembly, one could collapse nearby sites with high LRT values into putative causal loci to begin to characterize the number of sites underlying segregating variation and search for responsible genes.

Floral variation in the P. virgatus population

Penstemon has experienced at least 12 evolutionary transitions from bee-adapted to hummingbird-adapted flowers (Wessinger et al. 2016; Wilson et al. 2007; Wolfe et al. 2006). This remarkable display of parallelism in floral trait variation may be facilitated by alleles segregating within ancestral bee-adapted populations that permit rapid response to natural selection favoring hummingbird pollination. Despite the modest power of our QTL skimming approach, we identified three SNPs that putatively explain quantitative variation in the bee-adapted P. virgatus population sample, indicating there are likely many loci with subtle quantitative effects on floral dimension segregating within this population. The three SNPs did not necessarily overlap with genomic intervals containing interspecific QTLs, suggesting variation in stamen length has a broad genomic basis. Thus, adaptive change in stamen length is unlikely to be limited by available segregating variation. Furthermore, we expect the genomic basis of adaptive transitions to longer stamen filaments would be idiosyncratic across separate origins of hummingbird pollination. To validate potential associations between candidate sites and phenotype, we are currently propagating a second, independent sample of plants from the same P. virgatus population.

Floral tube length and stamen filament length were tightly correlated across sampled individuals in the P. virgatus population. This finding supports the hypothesis that coordinated increase in floral tube length and stamen length associated with transitions to hummingbird pollination may be aided by preexisting correlations between these traits due to tight linkage or pleiotropic loci (Wessinger et al. 2014). In our previous interspecific cross, floral tube width was not significantly correlated with tube length and stamen filament length (Wessinger et al. 2014), suggesting adaptation to hummingbird pollination in the lineage leading to P. barbatus has involved loci specific to length vs. width traits.

Floral tube width was positively correlated with the lengths of the tube and stamen filaments in the P. virgatus population, although the strength of this correlation is much weaker than the correlation between the two length traits. Sites that putatively affect stamen length also affect floral tube length for two of the three cases, but do not affect floral width (Supporting Information S5). Together, these studies suggest that, although length and width traits can be positively correlated in bee-adapted Penstemon species, transitions to hummingbird pollination utilize variation that is independent of this correlation.

Conclusions

Despite the challenges inherent to within-population QTL mapping, our two-step approach is capable of detecting loci with subtle effects on quantitative traits. Our approach merits further validation but is likely broadly useful for researchers embarking on an initial search for loci generating segregating variation within a natural population. One could elaborate our method to include additional predictors of phenotype. For example, researchers studying plastic traits in heterogeneous environments could choose to include an environmental covariate. This initial study illustrates challenges at both the shallow and deep stages that should be considered for future use of this approach. These challenges include sampling effects in the initial scan that limit our power to detect associations with phenotype and biased or spurious results from deep sequencing PCR amplicons.