Dynamic Behavior of RNA Nanoparticles Analyzed by AFM on a Mica/Air Interface

Abstract

RNA is an attractive biopolymer for engineering self-assembling materials suitable for biomedical applications. Previously, programmable hexameric RNA rings were developed for the controlled delivery of up to six different functionalities. To increase the potential for functionalization with little impact on nanoparticle topology, we introduce gaps into the double-stranded regions of the RNA rings. Molecular dynamic simulations are used to assess the dynamic behavior and the changes in the flexibility of novel designs. The changes suggested by simulations, however, cannot be clearly confirmed by the conventional techniques such as non-denaturing polyacrylamide gel electrophoresis (native-PAGE) and dynamic light scattering (DLS). Also, an in vitro analysis in primary cultures of human peripheral blood mononuclear cells does not reveal any discrepancy in the immunological recognition of new assemblies. To address these deficiencies, we introduce a computer-assisted quantification strategy. This strategy is based on an algorithmic atomic force microscopy (AFM)-resolved deformation analysis of the RNA nanoparticles studied on a mica/air interface. We validate this computational method by manual image analysis and fitting it to the simulation-predicted results. The presented nanoparticle modification strategy and subsequent AFM-based analysis are anticipated to provide a broad spectrum approach for the future development of nucleic acid-based nanotechnology.

Graphical abstract

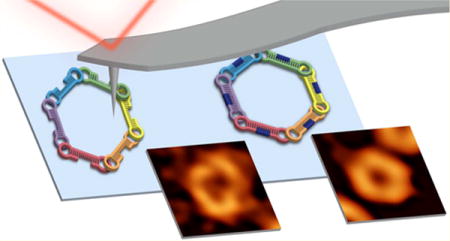
RNA is one of the underlying building blocks of life, with far-reaching roles across the biological spectrum. In the past decade, RNA has become a biopolymer of increasing focus due to its potential applications in nanomedicine.¹ Recent advancements in our understanding of RNA have shed new light on the diversity of its biological functions and have demonstrated the benefits of RNA as a potential tool for a variety of applications. Naturally occurring functional RNA structures enable the use of their precise architecture to engineer novel materials^2,3 used in RNA nanotechnology.^4,5 Through utilization of the sequence-specific long-range tertiary interactions, artificial RNAs can be programmed to self-assemble into defined 2D and 3D nanostructures^3,6–15 amenable to versatile functionalization.^11,16–30 Typically, the functionalization of RNA nano-assemblies is achieved through the extension of either the 5′- or 3′-end of each strand.²⁸ The precisely controlled composition of these nanoassemblies can then be altered by simply swapping functional monomers.²⁸ However, the number of possible functionalities normally does not exceed the number of strands entering the composition of RNA nanoassemblies since the simultaneous decoration of the 5′- and 3′-ends is complicated by possible steric clashes. We addressed this issue via spatial separation of the adjacent 5′- and 3′-ends while maintaining the original topology of the assembly. As a model system, we selected hexameric RNA rings that were previously designed and utilized in various studies.^{22,24,26–28,31–33} The assembly of the computationally designed RNA rings³⁴ is promoted by colE1-like kissing loop interactions. An experimental scheme was developed³³ to program each kissing loop, positioned at the sides of the dumbbell-shaped hairpins, to be different, thus allowing for programmable self-assembly (Figure 1). The magnesium-dependent assembly of prefolded monomers brings together the desired functionalities attached to them with the total number of functionalities (e.g., siRNAs that target different parts of the HIV-1 genome²⁶) never exceeding six at a time.

Figure 1.

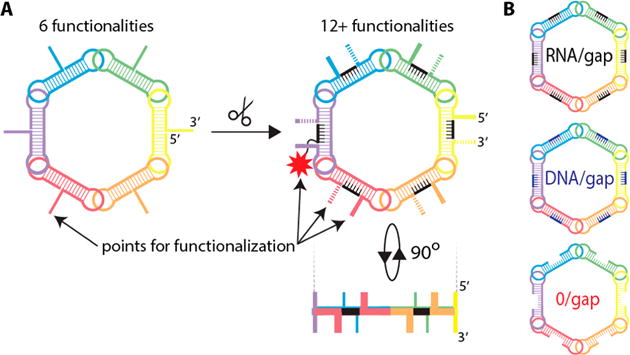
Schematic representation of RNA rings and RNA rings with six-nucleotide-long gaps. (A) Process of structure modification and the resulting possible orientations. (B) Three different constructs tested in this work. The potential attachment of a fluorophore is denoted by an asterisk.

We show that the removal of three nucleotides from both the 5′- and 3′-sides of the ring monomer leads to the formation of a six-nucleotide single-stranded RNA (ssRNA) gap that can be filled with short complementary RNA or DNA strands. Given the average ∼32.7° turn per base pair in RNA, the 5′- and 3′-ends of the modified strands point ∼196.2° away from each other and, as a result, avoid any steric hindrance of potential adducts. This simple modification increases the avenues for functionalization 3-fold by opening up the 5′- and 3′-ends of the monomer with added functionalization of a nucleic acid gap complement.

It is anticipated that the introduction of ssRNA gaps will increase the overall flexibility of RNA nanoassemblies.³³ Different computer modeling methods can assist with the design and optimization of derived nanostructure.^34,35 These methods, known as molecular dynamic (MD) simulations, utilize our understanding of RNA base pairing and predictable secondary interactions to create different structural designs and predict their dynamic 3D properties in silico.^34,35 However, accurate experimental justification of these findings is often quite challenging. Although significantly different in size and shape, RNA nanoparticles are distinguishable by some common characterization techniques such as gel electrophoresis²² and dynamic light scattering,³⁶ but the lack of resolution of the mentioned techniques makes them unsuitable for distinguishing nanoparticles with small differences in size or elasticity. Atomic force microscopy (AFM), on the other hand, has excellent potential for the visualization and probing of nanostructures. Of particular importance is the ability of AFM to acquire high-resolution topography images of nanostructures assembled from nucleic acids DNA and RNA. There is no need to label nucleic acids when probed with AFM, which is a great advantage of this method in studying the structural peculiarities of small nanoassemblies. Some studies have successfully utilized AFM for resolving structures of individual nucleic acid molecules,³⁷ nucleic acid−protein complexes,^30,38 and two- or three-dimensional structures of nucleic acids.^{22,36,39–42}

The objectives of this study were to utilize the ability of AFM to evaluate subnanometer variations in shapes of different RNA nanostructures via deformation analysis and to analyze as many observed nanostructures as possible. Our approach was to devise an automated image analysis algorithm consisting of three steps: (1) detection of individual objects, (2) differentiation of the detected objects based on computed qualifiers, and (3) computation of statistics for accepted objects. To achieve this goal, we used pattern-matching and segmentation techniques which are extensively utilized in biomedical image analysis for various types of imaging techniques (e.g., histopathology slides, quantitative immunofluorescent imaging,⁴³ and AFM analysis⁴⁴). Furthermore, we compared the sensitivity given by this approach to that of conventional techniques used for the physicochemical characterization of RNA nanoparticles (native-PAGE and DLS) and immunological assays typically applied to estimate particle recognition by the immune system. The results of this study are intended to improve a rational design of RNA nanoparticles by complementing traditional characterization with more sensitive and reliable approaches capable of detecting minute structural variations in RNA nanoparticles.

■ Materials and Methods

Molecular Dynamics Simulations

The Amber 14 software package was used to perform all of the molecular dynamics simulations, employing force field ff14SB with ff99bsc0 and chi.OL3 parameters for RNA and ez.OL1 and chi.OL4 modifications for simulations including DNA fragments.^45–48 Amber’s LEaP module was utilized to generate the topology and coordinate files.⁴⁵ The implicit solvent generalized Born (GB) model simulations^49,50 were employed with the latest corrections to the intrinsic Born radii parameters known as the GB-neck2 parameters (mbondi3, run with igb = 8 Amber MD flag).⁴⁹ The implicit solvent MD combines explicit atomic representation for solutes (RNA and DNA constructs in our case) with the solvation free energy approximated as a sum of polar and nonpolar terms. The Langevin thermostat was used with a collision frequency of 1.0 ps⁻¹. Simulations were run at 300 K, with a 2 fs time step and a Debye−Hückel (monovalent) salt screening concentration of 1.0. No cutoff was imposed on nonbonded interactions (cut = 999). The SHAKE algorithm was used to constrain all hydrogen bonds in the system. The same six-step equilibration protocol was used in all simulations that started with energy minimization. Next, heating to the target temperature of 300 K with a harmonic restraint of 15 kcal/mol/ Ų applied to the RNA/DNA was performed, followed by short MD stages with harmonic restraints gradually lowered (10.0, 1.0, 0.1, and 0.01 kcal/mol/Ų) for a total equilibration time of 2.0 ns. Unrestrained (production) MD simulations were performed for up to 250 ns, as explained below.

The previously published model of the hexameric RNA ring was used as the starting state.³³ A single dumbbell building block was modified to include the six-nucleotide gap and was subjected to comparative molecular dynamics simulations with its variants containing six-nucleotide-long RNA and DNA complements. Also, the full hexagon model with all the side dumbbells modified to simulate the six-nucleotide gap deletions was built as designed (Figure 1). In the models of the stabilized rings, these gaps were filled with complementary RNA or DNA fragments, leaving each dumbbell with only two 5′-3′ backbone breaks. Individual dumbbell models as well as the fully gapped and fully stabilized ring models were subjected to 250-ns-long MD simulations. In addition, ring models with varying numbers of stabilizing RNAs and DNAs (one, two, and three) bound to the gaps were all subjected to 100-ns-long MD simulations to simulate the impact of partial pairing on the stabilization of the rings.

Analyses of the results were performed with the aid of Amber’s cpptraj program, and the statistical tests were performed with the aid of the SigmaPlot software package. The root-mean-square deviation (RMSD) calculations were performed with cpptraj for the MD production runs (post-equilibration) with respect to the first state (conformation) of the MD and were based on a mask of all of the C4′ backbone atoms of the gapped ring (38 atoms × 6 dumbbells). The single-stranded complements were excluded from the mask to compare the results for the same number of reference points. For the evaluation of single-dumbbell dynamics, RMSD masks excluding (38 C4′ atoms) and including (44 C4′ atoms) the complementary single strands were employed, as explained in the Results and Discussion section.

Preparation and Assembly of RNA Nanoparticles

All RNA strands used in this project are listed in the Supporting Information. Complementary six-nucleotide strands and DNA oligos coding for RNA and containing T7 RNA polymerase promoter sequences were purchased from Integrated DNA Technologies and were PCR amplified using the MyTaq Mix (Bioline). PCR products were purified using the DNA Clean & Concentrator kit (Zymo Research). RNAs were produced via in vitro runoff transcription using T7 RNA polymerase (80 mM HEPES-KOH, pH 7.5; 2.5 mM spermidine; 50 mM DTT; 25 mM MgCl₂; 5 mM NTPs) and purified using denaturing 8 M urea polyacrylamide gel electrophoresis (PAGE, 15%). RNA bands were visualized with a UV lamp (short wavelength), cut, eluted in a crush-and-soak buffer (300 mM NaCl, 89 mM Tris-borate (pH 8.2), 2 mM EDTA) overnight, precipitated in 2.5 volumes of 100% ethanol, rinsed with 90% ethanol, vacuum dried, and dissolved in ultrapure water (17.8 MΩ·cm).

RNA monomer strands were mixed in an equimolar ratio along with six times the concentration of the gap complementary strand (RNA or DNA) in double-deionized water (ddiH₂O). The samples were heated to 95 °C for 2 min and snap-cooled to 4 °C for 2 min, and assembly buffer (89 mM tris-borate (pH 8.2), 2 mM MgCl₂, 50 mM KCl) was added before incubation at 30 °C for 30 min. For fluorescently labeled rings and stepwise assembly with increasing gap complements, individual monomers were mixed 1:1 with corresponding gap complementary strands, heated to 95 °C for 2 min, snap-cooled to 4 °C for 2 min, and added together in an equimolar ratio in ddiH₂O and assembly buffer as above before incubation at 30 °C for 30 min. For purification and analysis with electrophoretic mobility shift assays, 8% nondenaturing native-PAGE (37.5:1) was used in the presence of 89 mM Tris-borate (pH 8.2) and 2 mM MgCl₂. Native-PAGE gels were run for 1 h at 4 °C, 300 V. Gels for analysis (5 μL of 1 μM rings per well) were visualized with ethidium bromide total staining or with fluorescently labeled oligonucleotides using a Bio-Rad ChemiDoc MP System.

For fluorescence microscopy experiments, fluorescently labeled RNA nanoparticles were purified. For this, nanoparticle bands (25 μL of 10 μM rings per well) were visualized on native-PAGE with a UV lamp (short wavelength), cut, and eluted in assembly buffer.

For immunological studies, to avoid endotoxin contamination, all nanoparticles were prepared in LAL-grade water, following the detailed protocol.²⁸

Dynamic Light Scattering (DLS)

The sizes of RNA rings (70 μL at 0.5 μM concentration) were measured in a microcuvette (Starna Cells, Inc.) using a Zetasizer nano-ZS (Malvern Instruments). Prior to measurements, samples were centrifuged at 15 000 rpm using a bench centrifuge. All measurements were performed at room temperature according to the instrumentation protocol.

Transfection of Human Cell Lines

For cell culture experiments with RNA nanoparticles, human breast cancer MDA-MB-231 cells were grown in D-MEM medium at 37 °C in a 5% CO₂ incubator. The medium was supplemented with 10% FBS and penicillin−streptomycin. All transfection experiments were carried out using Lipofectamine 2000 (L2K) purchased from Invitrogen. Solutions of purified rings were preincubated at RT with L2K according to the manufacturer’s protocol. Prior to each transfection, the cell medium was changed to OPTI-MEM and prepared RNA rings with L2K complexes were added to the final concentration of rings to be 100 nM. The cells were incubated for 4 h followed by a change in medium (D-MEM).

Fluorescence Microscopy

To assess the intracellular integrity of RNA nanoparticles, colocalization experiments were carried out using an LSM 710 confocal microscope (Carl Zeiss) with a 63×, 1.4 NA magnification lens. MDA-MB-231 cancer cells plated in glass-bottomed dishes (Ibidi, Madison) were transfected the next day with the fluorescently labeled rings (100 nM) as indicated above. Upon the 4 h incubation at 37 °C, the cells were washed three times with PBS and incubated at room temperature for 20 min with a 4% paraformaldehyde solution to fix the samples. The samples were washed again in PBS and stored at 4 °C prior to visualization. For FAM imaging, a 488 nm line of an argon laser was used as the excitation, and the emission was collected between 493 and 557 nm. For TAMRA imaging, a DPSS 561 laser was used for excitation, and emission was collected between 566 and 680 nm.

Immunology

Blood was collected from three healthy volunteers under NCI-at-Frederick Protocol OH9-C-N046. Vacutainers containing Li-heparin were used for blood collection. The blood was processed within 2 h after collection to isolate peripheral blood mononuclear cells (PBMC) by a Ficoll Paque density gradient centrifugation technique. Standardzied protocol NCL ITA-10 (https://ncl.cancer.gov/sites/default/files/protocols/NCL_Method_ITA-10.pdf) was used. After isolation, PBMCs were resuspended in complete RPMI medium (RPMI 1640 with 10% FBS, 2 mM L-glutamine, and penicillin/streptomycin); 160 μL of the cell suspension at a concentration 1.25 × 10⁶ cells/mL was seeded per well in a 96-well plate. RNA nanoparticles at 1 μM stock solution were complexed to L2K in a 5:1 v/v ratio. After a 30 min incubation at room temperature, complexed NPs were diluted in OPTI-MEM; 40 μL of this working stock was added to PBMCs so that a final stimulation concentration of RNA nanoparticles was 10 nM. After 20 h of incubation at 37 °C, supernatants were collected and analyzed for cytokines by multiplexed ELISA (Quansys Biosciences, Logan, UT).

AFM Sample Preparation

Freshly cleaved mica was immersed in a 167 μM aqueous solution of 1-(3-aminopropyl)-silatrane (APS) for 30 min as previously described.⁵¹ The APS-modified mica pieces were rinsed in deionized water, dried in a stream of high-purity argon, and further dried under vacuum for at least 12 h. RNA samples were diluted at 4 °C in assembly buffer and immediately deposited onto APS-modified mica for 2 min from a buffered solution (assembly buffer) using the droplet method⁵² with diffusion-limited deposition of RNA nanostructures, rinsed briefly with ice-chilled deionized water, and dried with a gentle flow of argon. The concentration was optimized to avoid the overlapping of ring structures, which spans the range of ∼10−100 nM. Typically, a very good correlation between the surface coverage of RNA structures and the concentration of those structures in solution used for deposition is observed. The following concentrations were used for RNA deposition: RNA ring ∼20 nM, DNA/gap ∼100 nM, RNA/gap ∼100 nM, and 0/gap ∼100 nM.

AFM Imaging and Image Analysis

Imaging was performed with a MultiMode AFM Nanoscope IV system (Bruker Instruments, Santa Barbara, CA, USA) in tapping mode under ambient conditions. The images were recorded at a scanning rate of 1.5 Hz using an RTESPA-300 probe (Bruker Nano Inc., CA, USA) with a resonance frequency of ∼320 kHz and a spring constant of ∼40 N/m. Images were processed using the FemtoScan Online software package (Advanced Technologies Center, Moscow, Russia). Only nonoverlapping ring structures were used for analysis to avoid any influence of possible distortion due to the close proximity of other nanostructures. The cross-sectional tool was used to analyze a distance through the center of a close-up specific ring structure. Two orthogonal cross sections were taken vertically and horizontally to the image orientation. The maximum-to-maximum distance in the cross section was measured, which reports on the distance between segments of nucleic acids in the RNA ring assembly. The deformation factor (DF) was calculated as the ratio of the longer measured distance to the shorter one. The DF was then plotted as a histogram for various designs of the RNA ring nanoassemblies.

Computer-Assisted AFM Image Analysis

The detection algorithm uses a sequence of filters that give the highest response for certain shape properties of objects of interest. In this case, we looked for a circular object of a certain size, the presence of the hole in the center, and the completion of the boundary. The local maxima of the response surface were then used as seed points for the watershed segmentation algorithm which delineates each individual object.⁵³ Segmented regions are grouped into individual objects using connected component analysis, and a set of features is computed for each individual object.⁵⁴ In order to assess the shape of each object, we fit an ellipse to the segmented region and used a linear combination of the following three features as a measure of the object’s roundness⁵⁵ (Figure S1). The solidity measure is defined as the ratio between actual object area and the area of a maximum fitting circle. The eccentricity measure is defined as the ratio between the minor and major axes of an ellipse fitted to the region. Lastly, the regularity feature measures the ruggedness of the outline by measuring how much the observed perimeter differs from a perfect circle’s. The computational detection algorithm was validated with manually marked centroid locations on a subset of images and presented an F1 score of >0.85. Furthermore, we have validated the final statistics by manually segmenting several objects under all conditions and comparing the deformation factor distributions. The AFM imaging and object segmentation steps produce a noisy view of the actual shapes, and thus we compute the statistics on as large a sample set as possible.

■ Results and Discussion

Molecular Dynamics Simulations

The molecular dynamics simulations demonstrated a much higher flexibility of the gapped RNA ring (called 0/gap) compared to that of the variants stabilized with the six-nucleotide-long complementary RNA (called RNA/gap) and DNA (called DNA/gap) strands. However, despite being subject to large-scale motions that distort it greatly, the 0/gap ring maintains its overall topology in simulations. The kissing loop interactions do not open, and the shortened helices in each dumbbell (H1, four base pairs long; H2, five base pairs long) remain paired (Figure 2A,B). The range of distortions is illustrated in Figure 2B (0/gap): maximum RMSD state (36.4 Å), minimum RMSD (13.2 Å), and at the end of a 250 -ns-long run (25.0 Å). These points correspond in time to the peaks and troughs in the RMSD plot shown in Figure 2E. All ring distortions are due to twisting and bending in the single-stranded gapped regions of the dumbbell building blocks.

Figure 2.

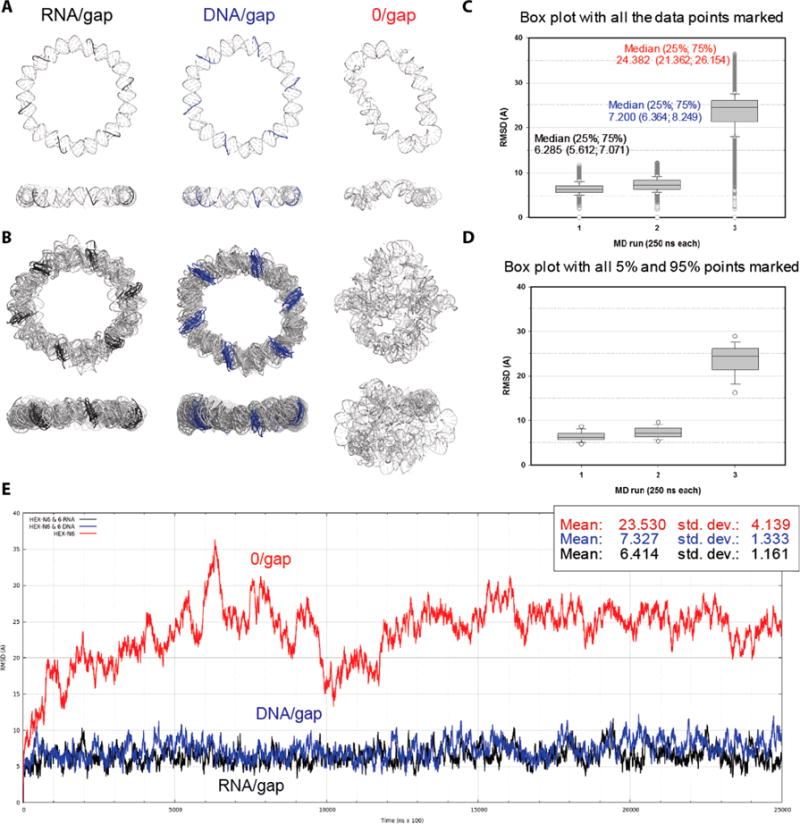
Results of molecular dynamics (MD) 250 -ns-long simulations of the gapped hexagonal ring nanostructures. (A) Minimized average structures for the entire MD simulations for (left to right) the ring with RNA complementary strands (black), the ring with DNA complements (blue), and the gapped ring without the complementary strands. (B) Overlays of the selected RMSD peak structures capturing the extents of distortions experienced in the MD simulations by the ring model variants explained in A. (C, D) Box plots of the RMSDs for the three ring models. All data points are plotted in C, while only the 5 and 95% points outside the 25−75% boxes are marked in D. The median values are shown with the 25 and 75% values (bottom and top of the boxes, respectively) listed in parentheses. All differences in the medians are statistically significant according to the Mann−Whitney rank sum test. (E) RMSD plots calculated relative to the first frame of each MD simulation for the C4′ backbone atoms shared with the gapped dumbbells (6 × 38 atoms) (i.e., excluding the single-strand data in the fully complemented ring models).

The six-nucleotide-long RNA complements stabilize the ring better than the DNA complementary sequences. The RMSD difference for the rings with a full complement of RNA and DNA stabilizing strands is small but statistically significant (Figure 2C). As the minimized average structures from the 250-ns-long MD simulations in Figure 2A show, the RNA complements maintain the hexagonal shape of the whole structure and the uniform gaps at the backbone breaks of 2.8 ± 0.2 Å. The complementary DNA strands (Figure 2B) maintain the overall shape, but the backbone gaps, especially those between the 3′ DNA ends and the dumbbell 5′ ends, are larger (4.9 ± 0.1 Å), contributing to the small difference in the RMSDs (means and medians) over the entire trajectory. The overlays of the distortion RMSD peaks in their respective MD simulations for the two ring models show a small difference in the direction of the dominant distortions. Multiple distortion peaks above 11 Å are found in the RNA−DNA hybrid ring, with two peaks at 12.1 Å RMSD. In the all-RNA ring, there is only one peak above 11 Å at 11.6 Å RMSD.

We have also explored the impact of one, two, and three, rather than all six, gap-complementary DNA and RNA strands bound to the ring on the distortion levels of the entire ring in the MD simulations. Increasing the number of stabilizing six-nucleotide-long complementary strands in the adjacent ring dumbbells gradually increases the stability (i.e., lowers the distortion levels measured by RMSD) of the whole ring, and the stabilization is more effective (statistically significant differences in RMSD) for the RNA than for the DNA complementary strands (Table ST1). Variants of the above simulations in which two and three complementary strands are evenly spaced around the ring show further damping of the ring distortions by RNA complements relative to the same number of adjacent complements. For example, two complementary RNAs attached to the opposite sides of the hexameric ring compared to two adjacent sides decrease the mean RMSD of the full ring from 16.4 to 14.9 Å, but with an increased standard deviation. This trend is less consistent for the DNA complements (Table ST1).

Individual dumbbell simulations show significant distortions for the pure gapped dumbbell, showing the potential for hairpin−gap (single-strand) interactions. RNA and DNA complementary strands bring down the individual dumbbell distortions to very low levels, with the DNA-stabilized RMSD median being slightly but statistically significantly lower (Table ST2). These results are based on the measurements of the backbone atoms common to the gapped and complemented dumbbells (38 C4′ atoms). On the other hand, the results are consistent with the full ring stabilization being better with the RNA complementary strands than with DNAs when we measure the RMSDs of all of the C4′ backbone atoms, including the RNA/DNA complement atoms (a mask of 44 C4′ atoms per dumbbell). The smaller RNA complement strand distortions and the backbone gaps reverse the relative distortion measurements for the individual dumbbells. The distortions of both stabilized gapped dumbbells are also slightly higher than those in the original dumbbell design with only one backbone break between the 5′ and 3′ nucleotides, for which comparison we chose the 44-atom mask (Table ST2). Take note that in the single-dumbbell simulations the stabilizing influence of the kissing loops on the full rings does not play a role. Thus, on the basis of all of the above measurements, it appears that the DNA complements stabilize the gapped building blocks well but introduce slightly larger geometric distortions in fully assembled hexameric rings than do their RNA complements.

Conventional Characterization of RNA Nanoparticles

All assemblies are confirmed using ethidium bromide total staining native-PAGE (Figures 3 and Figure S2). All results show unresolvable differences in electrophoretic mobility for RNA/gap, DNA/gap, 0/gap, and original RNA rings given the resolution limits of our experimental conditions. The minute difference in DLS results with the slight decrease in diameter for 0/RNA rings compared to unmodified analogs also does not explain the predicted changes in the shape and flexibility of nanoparticles. The need for further determinative qualitative and quantitative yields, absent in the native-PAGE and DLS results, dictates the use of further higher-resolution analysis techniques described later in the text.

Figure 3.

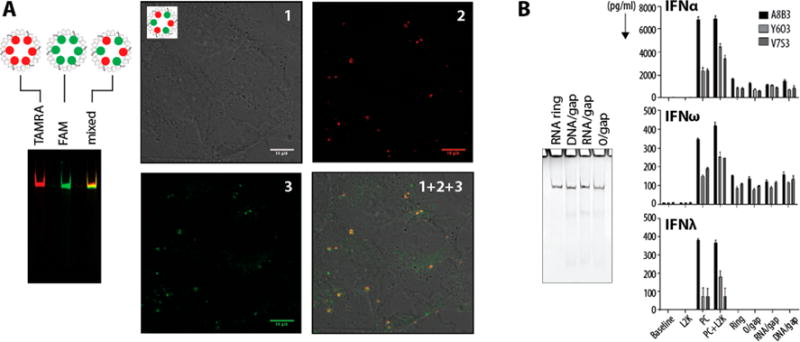
Cell culture experiments. (A) Ring assemblies with either a red 3′-TAMRA-RNA or a green 5′-FAM RNA gap complement or an alternating combination of both (denoted as mixed). The latter is used to confirm the structural integrity of rings during the intracellular colocalization in human breast cancer cells (MDA-MB-231). (B) Immunological studies were conducted in vitro using PBMC derived from three healthy donors (A8B3, Y6O3, and V7S3). ODN2216, a known potent inducer of type I IFNs, was used as the assay positive control (PC). Untreated cells were used to establish a baseline. Lipofectamine (L2K) at the same concentration as that used for the delivery of the RNA nanoparticles was used as a negative control. Both ODN2216 and L2K were also tested together to rule out any negative effects on cell viability and IFN induction when both the delivery vehicle and the IFN inducing sample are added to cells together. Nanoparticles with various modifications (ring, 0/gap, RNA/gap, and DNA/gap) were delivered using lipofectamine. Type I IFN (IFNα and IFNβ) and type III IFN (IFNλ) were analyzed in the supernatants 24 h after the addition of test samples and controls to PBMC cultures. Each bar represents a mean and a standard deviation (N = 3). No difference between nanoparticles with various modifications was identified by this test. All ring assemblies were confirmed by native-PAGE.

To demonstrate some additional possibilities for the controlled functionalization of novel constructs and to confirm the incorporation of gap-complementary strands into the rings, we introduce gap-complementary RNA strands fluorescently labeled with fluorescien (FAM) and 5-carboxytetramethylrhodamine (TAMRA) (Figure 3 and Figure S3). Labeling the gap-complementary RNAs allows for the visualization of their interactions with gapped ring monomers as well as the investigation into the formation and stepwise assembly of the hexamers stabilized by complements. The modularity of the kissing loops and the gap-complement modifications allows for different fluorophores to be selectively and simultaneously introduced into the ring assembly. The synthesis of rings with alternating fluorophore labeling, all on the same six-nucleotide-long chemical handle, is a prime example of modularity. With the functionalization of monomers A, C, and E with 5′-FAM and monomers B, D, and F with 3′-TAMRA, we are able to assemble consistent batches of alternately modified rings. The successful incorporation of both fluorophores into the ring structures is verified through the direct colocalization of the fluorescing bands (Figures 3A). This type of modification becomes cost-effective (only short oligos need to be labeled) and can be used, for example, to study the integrity of RNA nanoparticles in living cells (Figure 3A, Figure S3). Rings functionalized with two fluorophores can be traced in cells, and their structural integrity can be confirmed via confocal microscopy colocalization experiments. Additionally, using the same procedure, it would be possible to make nanoparticles with six different forms of functionalization, ranging from therapeutic payloads to fluorescent tracking linkers, covalently attached to the short RNA (or DNA) strands. Each modification would warrant further studies in functionalized gap-complementary strand additions: MD simulations and AFM analysis can be carried out on these new structures, giving us similar predictions of yield and stability, allowing for ease of future analysis and increasingly rapid development of the RNA-based nanoparticle platforms.

Immunological Studies of RNA Nanoparticles

Recognition of RNA nanoparticles by the immune cells typically culminates with the production of type I interferons (IFN). We have previously reported that IFN induction by RNA nanoparticles depends on their composition, molecular weight, and other physicochemical parameters.^22,25,28,36 Since conventional physicochemical characterization did not reveal a difference between various RNA nanostructures prepared for this study, we wanted to verify these findings by a bioassay. A type I IFN secretion assay was suitable for this purpose. According to our previous experience with RNA nanoparticles’ behavior in this assay, we did not expect to see a difference in IFN induction between different nanostructures. We also added additional analyte, type III IFN (IFNλ), to the analysis. Similar to type I IFN, this type of interferon is involved in the antiviral immune response and can also be produced by the immune cells exposed to RNA nanoparticles. We conducted experiments in vitro using primary cultures of PBMCs isolated from the whole blood of three healthy donor volunteers. A potent known IFN inducer (ODN2216) was used as the assay positive control. All tested nanoparticles resulted in the induction of type I IFNs (IFNα and IFNω) (Figure 3B). Consistent with the native-PAGE (polyacrylamide gel electrophoresis) and DLS data, there was no difference between nanoparticles with various structures in this bioassay. The induction of type III IFN was not observed (Figure 3B). Collectively, this data demonstrates that the immune cells do not distinguish the structural variability between rings and their counterparts (0/gap, RNA/gap, and DNA/gap). The bioassay data, therefore, is in agreement with conventional physicochemical characterization. The data also suggests that dynamic simulation is a more sensitive tool for identifying the structural difference between RNA nanoparticles. However, the biological significance of differences identified by the dynamic simulation is currently unknown.

Atomic Force Microscopy (AFM) and Image Analysis

The relative flexibility of the RNA ring designs was evaluated using AFM. The hexameric RNA nanostructure is assembled from six dumbbell building blocks via kissing loop interactions and appears as a ring structure on the AFM topography images. Such a ring structure is expected due to the symmetric design of the hexameric nanostructures. It is possible to trace the arrangement of individual dumbbells in some highly resolved nanostructures (Figure 4 and Figures S4 and S5). Because of strong electrostatic interactions between positively charged APS-mica and negatively charged RNA, all rings assume a flat orientation on the atomically smooth mica surface, allowing for a comparative analysis of their shapes. We hypothesized that the shape variation of the ring nanostructures on the aminopropyl-silatrane-modified mica can be used to assess the stability of the nanostructures. Any forces experienced by the RNA rings upon deposition are expected to amplify the differences in ring shape on the surface, reflecting their intrinsic stability. Therefore, comparative analysis of shape variations in AFM should correlate with the shape variations of the structures in solution. Stable rings will be mostly circular while less-stable structures adopt an elliptical shape. This was measured as the susceptibility of the rings to deformation via cross-sectional analysis of the structures. The orthogonal axes (vertical and horizontal relative to the image) drawn through the center of a ring report on the distance between nucleic acid segments within the ring. We define the ratio of the longer distance, D^L, to the shorter one, D^SH, as a deformation factor, DF = D^L/D^SH. The values of DF close to 1 correspond to a nearly circular shape of the nanostructure. A statistical distribution of DF values in different RNA structures is shown in Figure 4.

Figure 4.

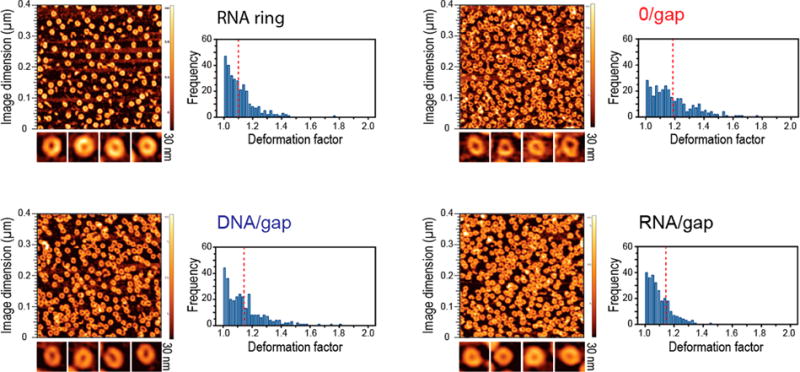
AFM of RNA rings, RNA/gap, DNA/gap, and 0/gapwith corresponding histograms of calculated deformation factors resulted from the manual analysis of AFM images. Median deformation factors are measured to be ∼1.1, ∼1.11, ∼1.14, and ∼1.18 respectively.

The original RNA rings are expected to be highly symmetric with a minimal distortion value, and thus there are minimal differences between D^L and D^SH. The histogram of DF values for RNA/gap shows that a major part of the structures are circular, with DF being 1 and slowly decaying with higher DF values. We compared the distribution of DF values for RNA/ gap and DNA/gap design with the RNA ring which now served as a positive control for our analysis. Both histograms resemble the one obtained for the original RNA ring design with a majority of the structures having median DF (DFM) values close to 1.1. Although similar, there are slight differences in the distribution of DF values for the DNA/gap design. There seems to be a longer tail in the distribution reaching farther into larger values of DF. This might indicate that the DNA complement contributes less to stability compared to the RNA complement in a similar design. The 0/gap (DFM is close to 1.2) design behavior is significantly different from the RNA/gap, the DNA/gap, and the original ring. We attribute this observation to larger fluctuations of the backbone and thus greater deformability of the ring for the gapped designs.

Next, we have extended the analysis to a larger number of RNA structures using a computer-assisted algorithm. This algorithm identifies circular objects on an AFM image and fits structures with an ellipse. DF is measured as the ratio of the major axis of the ellipse to its minor axis, with ideal roundness having a DF ratio of 1. Such an approach allows for larger sets of structures to be analyzed. Additionally, the algorithm finds both major and minor axes of an ellipse regardless of the orientation of the structure within the AFM image. We have analyzed up to 10 different images, keeping the number of nanostructures analyzed at 900 objects for each ring design randomly selected from the accepted pool of structures. Figure 5 (Figure S6) shows the distribution of the DF for each ring design. A red dashed line indicates a median DF averaged over the sampled 900 rings. We have selected objects with the roundness measure above 0.6, which allows for shape variability but precludes noncircular or ill-segmented objects from being analyzed. The median deformation is closest to 1 (DFM is ∼1.14) for the original RNA ring, indicating that the rings are mainly largely symmetric. Figure 5 shows the distributions spreading more widely into the larger DF values in the following order: RNA ring, DNA/gap (DFM is ∼1.26), RNA/ gap (DFM is ∼1.28), and 0/gap (DFM is ∼1.32). The widest spread is observed for 0/gap structures, and the smallest spread is observed for the original RNA ring. These results are in close agreement with MD simulations and the manual analysis of AFM images, suggesting that the six-nucleotide-long gap destabilizes the ring structure. The introduction of six-nucleotide-long complementary sequences makes the structures more deformation-resistant. On the basis of MD simulations, we expected similar DF values for RNA/gap and DNA/gap structures, which we also observed in AFM. Average RMSD values obtained in MD simulations are 3.2−3.7 times greater for 0/gap compared to RNA/gap or DNA/gap, respectively. Therefore, a larger difference in DF values between 0/gap and either DNA/gap or RNA/gap was expected. We associate this discrepancy with the fact that MD simulations are based on 3D behavior of the nanostructures while AFM analysis provides information about the 2D shape of the rings. Nevertheless, the shape analysis of the RNA nanostructures obtained with AFM in conjunction with the computational algorithm provides valuable information about the stability of the nanoassemblies, which agrees reasonably well with MD simulations.

Figure 5.

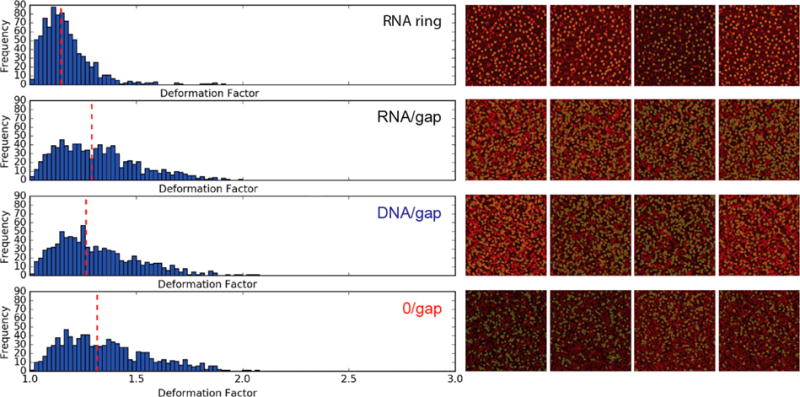
Computational algorithmic deformation analysis. Shown on the left panel are the deformation factor (DF) histograms for four types of nanostructures (top to bottom): RNA ring, RNA/gap, DNA/gap, and 0/gap rings. Median deformation factors are measured to be ∼1.14, ∼1.28, ∼1.26, and ∼1.32, respectively. We have manually defined the roundness cutoff at 0.6 in order to allow for variations in object shape but preclude very deformed shapes from being selected (Figure S6). Shown on the right is a visual representation of the AFM images with colored nanostructures selected by the algorithm and included in the deformation analysis. Figure S5 shows that the comparative trends among four types of nanostructures remain stable for different roundness cutoffs.

In conclusion, we developed an approach that allows us to distinguish the differences in dynamic behavior of RNA nanoparticles that otherwise cannot be detected by conventional experimental techniques and immune cells. Also, the experimental results and the molecular dynamics simulations support the design idea that the gapped ring can be stabilized by complementary RNA or DNA single strands. While the RNA single-stranded complements are marginally better at maintaining the dynamic stability of the rings, the DNA complements maintain the overall shape and levels of distortions in rings at comparable levels, thus leaving the nanoparticle designer the flexibility required to achieve multiple functionalities and to accomplish multiple objectives. This allows for further modularity in the design for the delivery of payloads using a pre-established existing RNA architecture in an attempt to further the development of therapeutic utility through an easily applied modification of the original strands. This, in conjunction with the computational AFM analysis, allows for the high-resolution, high-throughput analysis to rapidly and effectively quantify unforeseen effects such a small modification may have. We envision that this gap-complementary strand approach can also be possibly incorporated into other shapes to increase the modularity without interfering with the secondary structure interaction.