Probing Light Chain Mutation Effects on Thrombin via Molecular Dynamics Simulations and Machine Learning

Abstract

Thrombin is a key component for chemotherapeutic and antithrombotic therapy development. As the physiologic and pathologic roles of the light chain still remain vague, here, we continue previous efforts to understand the impacts of the disease-associated single deletion of LYS9 in the light chain. By combining supervised and unsupervised machine learning methodologies and more traditional structural analyses on data from 10 μs molecular dynamics simulations, we show that the conformational ensemble of the ΔK9 mutant is significantly perturbed. Our analyses consistently indicate that LYS9 deletion destabilizes both the catalytic cleft and regulatory functional regions and result in some conformational changes that occur in tens to hundreds of nanosecond scaled motions. We also reveal that the twoforms of thrombin each prefer a distinct binding mode of a Na+ ion. We expand our understanding of previous experimental observations and shed light on the mechanisms of the LYS9 deletion associated bleeding disorder by providing consistent but more quantitative and detailed structural analyses than early studies in literature. With a novel application of supervised learning, i.e. the decision tree learning on the hydrogen bonding features in the wild-type and ΔK9 mutant forms of thrombin, we predict that seven pairs of critical hydrogen bonding interactions are significant for establishing distinct behaviors of wild-type thrombin and its ΔK9 mutant form. Our calculations indicate the LYS9 in the light chain has both localized and long-range allosteric effects on thrombin, supporting the opinion that light chain has an important role as an allosteric effector.

Introduction

Thrombin is a multifunctional serine protease with critical coagulant and anticoagulant properties in blood coagulation cascades (Crawley, Zanardelli, Chion, & Lane, 2007; Enrico Di Cera, 2008). Meanwhile, thrombin plays important roles in tumor growth, metastasis, angiogenesis and invasion (Adams et al., 2015; Kobrinsky & Karpatkin, 2009; Nierodzik & Karpatkin, 2006; Radjabi et al., 2008). Therefore, thrombin is an attractive drug target for antithrombotic therapy (Ageno et al., 2012; Schwienhorst, 2006; Zavyalova & Kopylov, 2015) and chemotherapeutic development (Lechner, Kollars, Gleiss, Kyrle, & Weltermann, 2007; Mukherjee et al., 2009).

Activated from its precursor prothrombin, human alpha thrombin is composed of a 36-residue light and a 259-residue heavy chains (also respectively referred to as “A” and “B” chains, as shown in Figure 1). These two chains are linked to each other through a disulfide bridge between CYS1 and CYS122 (in the chymotrypsin numbering scheme) and a network of salt bridges, ionic interactions and hydrogen bonds (Bode, Turk, & Karshikov, 1992; Carter, Vanden Hoek, Pryzdial, & MacGillivray, 2010; Enrico Di Cera, 2008). In addition to the catalytic triad, several known functional sites are also located in the heavy chain of thrombin (Enrico Di Cera, 2008). Such functional sites include hydrophobic 60s and hydrophilic gamma loops, 220s loop, and anion-binding exosite I and II (Figure 1). The 220s loop is also known as “sodium binding loop” due to its specific accommodation of a Na+ ion (E Di Cera et al., 1995; E. Zhang & Tulinsky, 1997) (Figure 1), which maximizes thrombin’s catalytic function (Bush, Nelson, & Di Cera, 2006; Dang, Guinto, & Cera, 1997; R De Cristofaro, Picozzi, Morosetti, & Landolfi, 1996; Orthner & Kosow, 1980). However, unlike the catalytic heavy chain, the light chain has been less studied and considered an unnecessary activation remnant for thrombin’s function (DiBella, Maurer, & Scheraga, 1995; Hageman, Endres, & Scheraga, 1975) until the discovery of severe bleeding phenotype associated mutations in the light chain (S Akhavan et al., 2000; Sepideh Akhavan, Rocha, Zeinali, & Mannucci, 1999; Lefkowitz et al., 2000; Sun, Burkart, Holahan, & Degen, 2000).

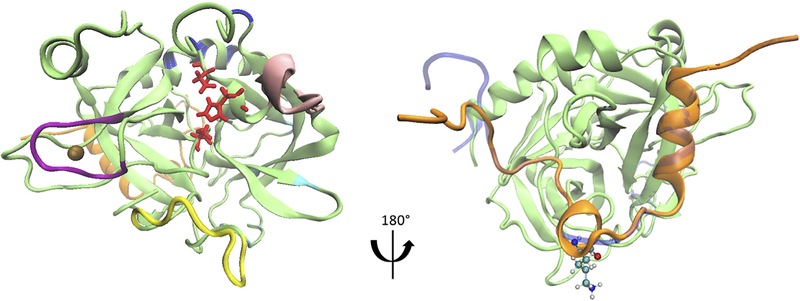
Figure 1.

Thrombin-Na+ complex structure and thrombin mutant with the ΔLYS9 deletion. (a) The thrombin structure is visualized based on PDB 4DIH and is shown in green and orange for the heavy and light chains. The 60s (in pink), 220s (in purple), and gamma (in yellow) loops and exosite I (in cyan) and II (in blue) are highlighted, as these are known regulatory regions. The side chains of the catalytic triad are displayed in red. The bound Na {+} is shown as a brown bead. (b) The side chain of LYS9 in the light chain is indicated in CPK representation. The modeled initial structure of ΔK9 mutant thrombin is shown in blue.

Moreover, the thrombin light chain has also been proposed to serve as a sensitive marker for detecting gastric cancer due to a decreased level of the circulating thrombin light chain in gastric cancer patients’ serum (though, the precise mechanism is unknown) (Ebert et al., 2005). These results suggest the light chain of thrombin should have a functional importance in its enzymatic properties and cancer development, although -- again -- the physiologic and pathologic roles of the light chain and the mechanisms behind relevant experimental observations are not yet fully understood (Carter et al., 2010; Papaconstantinou, Bah, & Di Cera, 2008).

One of two lysine residues -- LYS9 or LYS10 -- has been suggested as one of the key residue in the 36-residue light as its mutation may cause hypoprothrombinemia (S Akhavan et al., 2000). It was seen that patients with a deletion of LYS9/LYS10 presented deficient antigen levels and prothrombin activities and experienced severe bleeding (S Akhavan et al., 2000). Several in vitro experiments have shown that mutations of LYS9/LYS10 can cause dramatic perturbations of thrombin’s catalytic activities, including severely impaired interactions between thrombin and its substrates and attenuated sensitivity to sodium ions (Raimondo De Cristofaro et al., 2004, 2006; Papaconstantinou et al., 2008).

Previous computational studies using a single run of 18 ns molecular dynamics simulation have made progress into the molecular-level details, which suggests the some insertion loops as well as the catalytic triad could have subtle conformational changes due to the deletion of LYS9/LYS10 (Raimondo De Cristofaro et al., 2004, 2006). More recently, in addition tofast dynamic motions at the ps-ns timescale, thrombin’s slow time scale dynamics in surface loops, have been revealed by NMR experiments and conventional and accelerated MD calculations (Fuglestad et al., 2012), suggesting longer time scale MD simulations are required to study allosteric changes in thrombin. Given LYS9/LYS10’s significant relevance to disease and the mechanism by which a LYS9/LYS10 deleetion impairs thrombin has not been fully revealed yet, in this work, we continue the progress in understanding the role of thrombin’s light chain by combining microsecond all-atom molecular dynamics simulations of wild-type thrombin and its mutant with the deletion of the LYS9 residue with several recently developed machine learning techniques. We performed five independent 1 μs all-atom MD simulations (10 μs of simulations in total) for thrombin in the wild-type and LYS9 deletion mutant forms to probe the mutant effects regarding the conformational properties. Our calculations reveal consistent but more quantitative and detailed light chain mutation effects than previous relevant experimental and computational studies. The more extensive sampling and longer simulations in this study also suggest the deletion of LYS9 in the light chain may induce more significant perturbations on thrombin’s conformational ensembles than what was revealed previously. Through a novel application of decision tree learning on the hydrogen interaction features, we predict several key residue interactions that provide a new mechanistic insight into how the naturally occurring LYS9 deletion causes severe bleeding disorders. Furthermore, the workflow (Figure 2) that combines MD simulations and machine learning methods in this study should be not just successful in the present test case of LYS9 deletion, but also applicable in future work on other thrombin’s mutations (S Akhavan et al., 2000; Sepideh Akhavan et al., 1999; Lefkowitz et al., 2000; Papaconstantinou et al., 2008; Sun et al., 2000) and any other important disease-associated mutants of readers’ interest (such as EGFR mutations described in Zhao, Yang, Xiang, Gao, & Zeng, 2017 and other import mutations (Krishnamoorthy, Gajendrarao, Olivotto, & Yacoub, 2017; Mandal, Panda, & Das, 2017; Sutthibutpong, Rattanarojpong, & Khunrae, 2017; Thirumal Kumar et al., 2017; Tompa & Kadhirvel, 2017)).

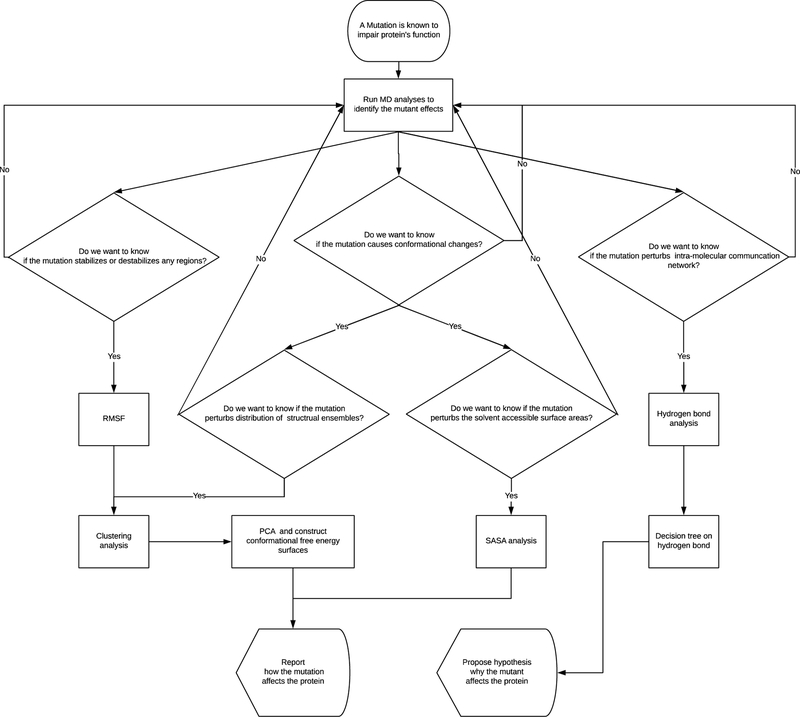
Figure 2.

A working flow chart.

Materials and Methods

Simulation systems

To gain further understanding of the light chain mutations’ structural influences at the atomic level and in the microsecond regime, we simulated human alpha thrombin in wild-type and LYS9 deletion (also referred to as ΔK9 in the following context) mutant forms.

The initial structure of the wild-type thrombin was based on the protein structure in PDB 4DIH (Russo Krauss et al., 2012). The missing residues of thrombin in this PDB (19 out of 295 residues) were modeled through Modeller (Šali & Blundell, 1993). Other missing hydrogen atoms were added via VMD’s psfgen package (Humphrey, Dalke, & Schulten, 1996), using default parameters. As no crystal structure of alpha thrombin with light chain mutations has been yet solved, here, the initial structure of the LYS9 deletion mutant was modeled via Modeller using the thrombin structure in the same PDB 4DIH as the structural template. Missing residues and hydrogen atoms for the mutant were added via the same procedures we performed for the wild-type. As a result, the initial structures of the wild-type and mutant forms have a large extent of overlaps due to the exactly same coordinates for most atoms (Figure 1). The relatively long (microsecond) time scales used in our study should ensure systems relax to their intrinsic conformational ensembles. Therefore, we expect the conformations of the wild-type and the LYS9 deletion mutant to be well-sampled by our simulations (10 runs of one microsecond simulations in total).

Simulation Configurations

Given previous identifications of slow dynamic motion of thrombin’s surface loops (Fuglestad et al., 2012) and the fact that initial structure of the mutant form is modeled based on the wild-type one, access to these longer time scale is necessary to achieve full relaxation from the wild-type structure based model and probe events that take place only on longer time scales (R. C. Godwin, Melvin, & Salsbury, 2015; R. Godwin, Gmeiner, & Salsbury, 2016; Salsbury Jr, 2010). Leveraging recent developments in GPU parallelization, we performed five one-microsecond-long all-atom MD simulations for each system, i.e. a total of 5 microseconds for wild-type thrombin and ΔK9 mutant respectively. These simulations were performed using the GPU-enabled ACEMD simulation package (Harvey & De Fabritiis, 2009) and Titan GPUs in Metrocubo workstations produced by Acellera.

To mimic the aqueous, we solvated the protein by putting an explicit TIP3P (Jorgensen, Chandrasekhar, Madura, Impey, & Klein, 1983) water box around thrombin using a 1 nm padding in VMD (Humphrey et al., 1996). Since the activation of thrombin requires Na⁺ cations, via the autoionize package in VMD, sodium chloride ions were added to neutralize the systems and the concentration of Na⁺ was set to a typical experimental value of 0.125 M (Russo Krauss et al., 2012). All ionizable residues were considered in their default protonation state at physiological pH. These procedures result in a simulation cell with more than 31,000 atoms and enable a close examination of each form of thrombin at the single molecular level. Prior to simulation, all systems underwent 1,000 cycles of conjugate gradient minimization to avoid un-physical initial configurations. All simulation runs were performed with the CHARMM27 force field that has a CMAP correction for proteins (MacKerell et al., 1998; Mackerell, Feig, & Brooks, 2004) under NPT ensemble (constant particle number, temperature and pressure). The pressure was set at 1 atm using Berendsen pressure control (Berendsen, Postma, van Gunsteren, DiNola, & Haak, 1984) with a 400 fs relaxation time. Using Langevin thermostat (Lemons, 1997) with a damping coefficient of 0.1, the temperature was maintained at 300 K. A 0.9 nm cutoff and 0.75 nm switching distance was applied for van der Waals and electrostatic forces. The smooth particle mesh Ewald method as implemented in ACEMD (Darden, York, & Pedersen, 1993; Harvey & De Fabritiis, 2009) was used to calculate the long-range electrostatics with 72 evenly spaced grid points in all three directions. The time step was set to 4 fs during the simulations due to a usage of the hydrogen mass repartitioning scheme (Feenstra, Hess, & Berendsen, 1999). Bonds involving hydrogen atoms were constrained using the SHAKE algorithm (van Gunsteren & Berendsen, 1977). Conformations sampled in the simulations were saved in the MD trajectory file in every 2,500 steps (i.e. 10 ps) for the balance of temporal resolution and cost in storage. As a result, we have an extensive sampling of 100,000 conformations across one-microsecond time scale for each simulation run.

Processing and Analysis Methods

We first aligned all frames in MD trajectories to the initial structure of wild-type thrombin through rigid body translations and rotations to minimize the root-mean-square deviation to the alpha carbons of the common residues in the wild-type and ΔK9 forms. This alignment was performed with the ‘align’ class in Python library MDAnalysis (Gowers et al., 2016; Liu, Agrafiotis, & Theobald, 2009; Michaud-Agrawal, Denning, Woolf, & Beckstein, 2011; Theobald, 2005). As we found the relaxation time (~20 ns, according to the alpha carbon atom root-mean-squared distances to the initial structure shown in Figure S1) is much smaller than the simulation time (1000 ns) for all simulation runs, we performed our analyses on the whole trajectory for each system. Although we don’t expect a global equilibrium can be reached and the full dynamics of thrombin can be captured in our simulations given the existence of μs~ms scale fluctuations revealed by experiments (Fuglestad et al., 2012), we observe that the extensive sampling in our 1 μs simulation can still result in very small block averaging errors and an approximate convergence (Figure S2). Moreover, our multiple runs of each type of simulations present similar sample distributions but not the same dynamic behaviors (Figure S1 & S3), which suggests a potential phase space sampling problem with previous computational work (Raimondo De Cristofaro et al., 2004, 2006).

Root-mean-squared fluctuations (RMSF) were computed for each alpha carbon in the wild-type and ΔK9 mutant thrombin as a first line examination of backbone mobility differences in these twoforms. The RMSF calculation was based on

$$RMSF\left(i\right)=\sqrt{\frac{\text{1}}{T}{\Sigma }_{t=\text{1}}^T{\left(r_t{}^{\alpha }-<r_t{}^{\alpha }>\right)}^{\text{2}}},$$ [1]

where r_t^α is the coordinate vector of atom α in frame t and < r_t^α > denotes the average position vector of atom α over all frames.

To explore the similarities and differences of thrombin’s conformational responses to the light chain mutation, we carried out Amorim-Hennig clustering analysis (De Amorim & Hennig, 2015; Ryan L. Melvin et al., 2016) on the concatenated trajectories of the common atoms in the wild-type and ΔK9 mutant thrombin. As a recently developed unsupervised learning technique, Amorim--Hennig (AH) clustering with a default Minkowski weight 2 (which intuitively corresponds to a Euclidean distance metric (De Amorim & Hennig, 2015)), has been shown its effectiveness and sensibilities on MD data (Ryan L. Melvin et al., 2016). In particular, without a requirement of specifying the number of clusters, this clustering method determines cluster sizes by optimizing the sihousette index -- a measure of how similar an element is to its own cluster relative to the next best cluster (Rousseeuw, 1987) -- of different grouping. As AH clustering iteratively adjusts the rescaling feature weights until convergence, it is able to identify non-spherical clusters among noise and the clustering results help differentiate local conformational changes sensitively (R.L. Melvin et al., 2016). Therefore, we applied such an automatic and non-parametric clustering method to all MD trajectories via our Python implementation available on figshare (R. Melvin & Salsbury, 2016). Depending on the size of regions of interest, we clustered the common C \alpha atoms of (1) the entire molecule and the heavy atoms (not hydrogen) of (2) the catalytic triad and (3) the regulatory region, which explicitly includes the exosite I and II, 60s, 220s, and gamma loops (details about the residue ranges see Tables S1). To save computation time, all frames of conformations in the MD trajectories were re-sampled by a striding factor of 10 in the clustering analysis.

As an important metric of inter- and intra-molecular interactions, hydrogen bonds were detected and analyzed over all conformations we sampled in the simulations of wild-type and ΔK9 mutant thrombin. Using the HydrogenBondAnalysis class in MDAnalysis (Michaud-Agrawal et al., 2011), we searched for hydrogen bonds of at least intermediate strength as defined in Steiner, 2002. Under this definition, heavy atoms of the donor and acceptor pairs atoms must be within 0.32 nm and the bond angle of heavy atom-hydrogen-heavy must be greater than 120°. If such an intermediate-strength hydrogen bond was detected between two residues, we said these two residues formed a hydrogen bond pair. Then, given a frame of conformation, we constructed a binary feature vector of all possible pairs of residues with hydrogen bonding. This reduced feature set has been recently adopted as inputs for decision tree learning and helped identify allosteric response to three type of DNA damages (Ryan L. Melvin, Thompson, Godwin, Gmeiner, & Salsbury, 2017).

As one of the most interpretable machine learning method, the decision tree algorithm returns a fitted binary classifier based on the input features (Kingsford & Salzberg, 2008). By making a couple key decisions on the input feature’s values, one can tell what class the input entity should belong to through the trained decision tree classifier. In the present study, we aim to employ this machine learning technique to identify key residue-residue hydrogen bonding motifs among all hydrogen-bonding pairs occurred in the wild-type and ΔK9 thrombin. Key decisions on the hydrogen bonding status were determined based on the comparisons on the Gini indexes from all splitting ways for each level of the decision tree. The Gini index (also called Gini impurity, denoted as I) is computed according to

$$I\left(X_m\right)={\displaystyle \sum }_k{p}_{mk}\left(1-p_{mk}\right),$$ [2]

, where p_mk is the probability of a conformation with an actual class label m (i.e. “WT” or “Mutant” here) being classified into class k in the node a training set X (Kingsford & Salzberg, 2008). If all conformations inside a node belong to the same class, the Gini index of that node is zero. A binary split on whether forming a hydrogen bond between a specific residue-residue pair can result in a more accurate classification if the Gini indexes of nodes in the splitting branch are closer to zero. A split resulting in smallest Gini indexes will be treated as top level in the decision tree and the conformations in that node will be separated into two branch of nodes accordingly. Conformations inside each node will be spited in the same way until the classification error rate reaches a user specific value. Therefore, hydrogen bond motifs that distinguish the wild-type and mutant forms can be identified from the top several levels of the decision tree.

By calling the fitctree function in the Statistics and Machine Learning Toolbox of Matlab, we performed supervised learning on residue-residue hydrogen bonding features – an N-by-M input matrix, where N is the number of conformations and M is the number of residue-residue pairs with a possible hydrogen bond -- via a construction of decision trees. By fitting decision trees on the binary hydrogen bond trajectories (i.e. the N-by-M input matrix) of interactions among non-LYS9/LYS10 residues in the wild-type and mutant thrombin, we were able classify conformations of the wild-type and ΔK9 thrombin based on the knowledge of the presence of hydrogen bonds. In other words, construction of a binary decision tree classifier based on the features of hydrogen bonding statuses provides an interpretable model to differentiate the conformational ensembles of wild-type and ΔK9 mutant forms of thrombin. Furthermore, the trained decision tree suggests a list of important hydrogen bond interactions in the intra­molecular communication network, offering testable predictions of critical interactions and suggestions for designs of further mutagenesis studies.

Since Na⁺ binding has been thought as an allosteric effector of thrombin’s enzymatic activation (Bush et al., 2006; Dang et al., 1997; R De Cristofaro et al., 1996; Orthner & Kosow, 1980; Xiao, Melvin, & Salsbury, 2017), we monitored the mean distance <d> between the sodium binding loop (220s loop) atoms and the nearest Na⁺ ion. Based on the histograms of <d> in each type of simulations and structural examinations for each peak, a frame was defined as Na⁺ bound (or say “Na⁺ on”) if the <d> associated with that frame was less than or equal to 0.93 nm and 0.95 nm respectively for wild-type and ΔK9 forms of thrombin. As seen in our previous work (Xiao et al., 2017), this mean distance captures the stable interior bindings rather than the surface ones and correlates well with the minimum distance (less than 0.4 nm) between the 220s loop atoms and the stably bound cation. Moreover, as we will see in the next section, rather than the minimum distance, the mean distance preserves some profound information about the relative position of the bound Na + to the 220s loop. Therefore, we used the mean distance <d> here to illustrate the existence of multiple interior binding modes.

For both the Na + bound and Na + unbound states, we calculated solvent accessible surface areas (SASA) of the catalytic triad and subpockets and S1–6 (residues involved see Table S1) and the whole protein. The measurement of SASA was carried out via the Shrake and Rupley algorithm (Shrake & Rupley, 1973) implemented by MDTraj. Comparisons of the distribution of these SASAs indicate direct and indirect impacts of the mutations in the light chain.

To dissect impacts of the light chain mutation on thrombin’s conformational space, principle component analysis (PCA) was performed on the concatenated trajectories of the selected common atoms in the wild-type and mutant thrombin. This technique -- commonly used for dimension reduction in machine learning -- allowed us to project high dimensional structural information onto a reduced space. Here, we constructed the conformational free energy surfaces of the regulatory region (defined in the clustering analysis) and the catalytic cleft that includes catalytic triad and S1–6 subpockets. By diagonalizing the covariance matrix for the heavy atoms in above regions of interest, we obtained dominant components capturing the majority of dynamic variance in the wild-type and mutant systems. By projecting the coordinates of corresponding heavy atoms in the aligned trajectories onto the eigenvectors with two largest eigenvalues, distinct conformations in the region of interest are expected to have distinguished projections in the reduced conformational space. Through binning the projections and converting the frequency of each bin intofree energy via

$$\Delta G=-\text{k}T\text{ln\hspace{0.17em}}\left(\frac{P}{P_0}\right),$$ [3]

where kT is the product of Boltzmann’s constant k and temperature T and P₀ is the minimum frequency among all bins, we calculate the free energy change Delta G We then constructed the conformational free energy surfaces of the interested regions. The PCA decomposition was carried out via the “pca” module in PyEmma (Scherer et al., 2015) Python package.

The conformational ensembles in the free energy wells was visualized via the Tachyon render in VMD 1.9.2 (Humphrey et al., 1996). To show potential variances of the representative structure in the selected well, as previously suggested by R. L. Melvin & Salsbury, 2016, we visualized the conformational ensembles by showing the representative structure in solid and the other conformations in the same structural ensemble as shadows. Here, the representative structure was chosen as the one that is closest to the average conformation in the most populated bin in the selected well. For the representative structures, we also displayed the side chains of the residues of interest. For the shadows, which were randomly selected 50 structures in the same bin to indicate the variance, only the backbone using the new cartoon representation was displayed for simplicity of the image.

Results

LYS9 deletion reduces the structural rigidity of main regulatory regions

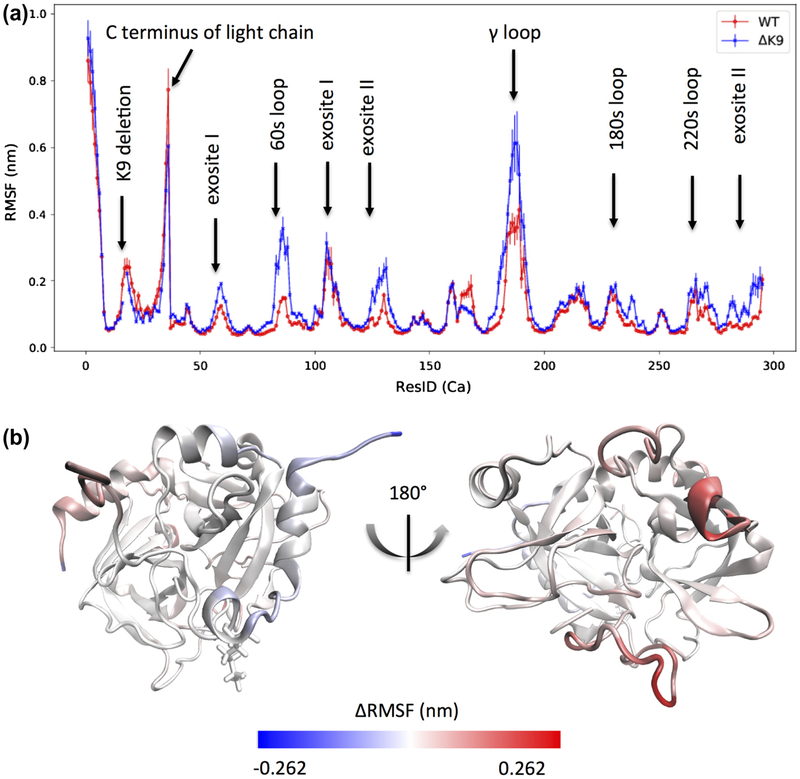
Root-mean-square fluctuations for the alpha carbons of ΔK9 (Mutant) and wild-type (WT) thrombin highlight what regions of thrombin’s backbone flexibility are affected by the deletion of LYS9 (Figure 3). The time-averaged atomic fluctuations reveal most of these regions are known functional sites of thrombin, including 60s, 180s, 220s and gamma loops, exosite I and II. In particular, these sites exhibit increased mobilities in the ΔK9 mutant thrombin (Figure 3 a & b) than the wild-type one. As indicated by the colors in Figure 3b, the rigidity of the gamma and 60s loops is significantly reduced in mutant thrombin, though this mutation (ΔK9) is distant (> 4 nm) from the gamma and 60s loops.

Figure 3.

Root-mean-square fluctuations (RMSF) for the alpha carbons of ΔK9 (Mutant) and wild-type (WT) thrombin. The blue and red colors in (a) depict the ΔK9 mutant and wild-type thrombin respectively. The residue indexes in (a) follow our sequential residue numbering scheme that all residues in the light and heavy chains are numbered from 1 to 295 and the LYS9 in the light chain thereby has a residue ID of 17. The known sites with distinct RMSF are indicated by labels. The thrombin molecule is colored based on the subtractions of RMSF (Mutant-WT) in (b) to indicate the location of the significantly affected regions.

On the hand, as shown by the left sub-figure in Figure 3b, the LYS9 deletion in the light chain appears to result in a slightly more rigid light chain. The residues near LYS9 present about 0.05 nm more fluctuations in the presence of LYS9. Similar to the C-terminus of the light chain, the backbones of the adjacent alpha helix (resid 164 to 168 in the sequential numbering scheme, i.e SER129B to ALA132) in the heavy chain are also slightly more flexible in the wild-type thrombin.

Clustering across configurations highlights deceased stability of mutant thrombin

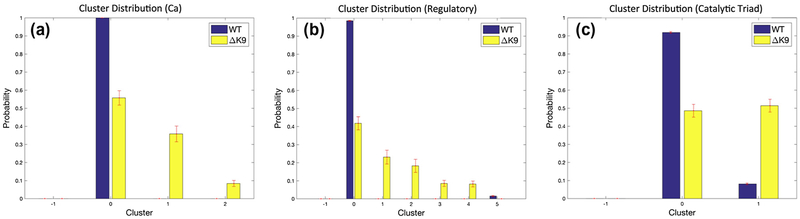
Clustering analysis of concatenated common residue trajectories for the wild-type and mutant thrombin offers quantitative estimations of the structural diversity. As shown in Figure 4, Amorim-Hennig (AH) clustering indicates the wild-type thrombin has more structurally stable ensemble and the mutant has more diverse structural ensembles. Only one primary backbone conformation is present in wild-type thrombin, while two extra conformational clusters contribute to 36% and 8% populations of the backbone conformations in the thrombin mutant (Figure 4a).

Figure 4.

Amorim-Hennig (AH) Clustering Distribution of ΔK9 (Mutant) and wild-type (WT) thrombin. Panels (a)-(c) respectively illustrate the clustering results of the Cα atoms, heavy atoms of the regulatory regions, and catalytic triad.

Except for C \alpha atoms, to take into account the side chain arrangement, we also clustered the heavy atoms of several regions of interest. Similar to the backbone clustering, the heavy atom clustering of the regulatory regions (60s, 220s and gamma loops, exosite I and II), catalytic triad demonstrates the conformational ground state is more likely to split into multiple conformationally metastable states for the thrombin mutant. In particular, the gamma loop establishes several different shapes in the mutant thrombin rather than the dominant one in the wild-type. The 60s loop also presents unique movement in the lack of LYS9 (Figure S4). While the conformational differences between the catalytic triad cluster 0 and 1 appear subtle (Figure S5), the side chains orientation of the catalytic triad in the AH detected cluster 1 becomes about 4-fold more likely to occur in the ΔK9 mutant thrombin than the wild-type.

LYS9 deletion results in perturbed hydrogen bonding network

Due to important roles of hydrogen bonding network in allosteric communication (Amor, Schaub, Yaliraki, & Barahona, 2016; Daily & Gray, 2009; Srivastava et al., 2016) and structural stability (Myers & Pace, 1996), hydrogen bonding statuses among residues were monitored and compared for both wild-type and ΔK9 mutant thrombin. While the LYS9 residue in the wild-type thrombin contributes to 15 hydrogen-bonding pairs that ΔK9 mutant thrombin can impossibly form, the mutant thrombin with a deletion of LYS9 presents 256 more unique residue-residue pairs with hydrogen bonds than the wild type. This increment in number of hydrogen-bonding pairs in the mutant thrombin is ascribable simply to the new hydrogen bonds formed in the heavy chain, since the numbers of hydrogen-bonding pairs within the light chain and between the light and heavy chains are larger in the wild-type due to an extra LYS9 (Table 1). On the other hand, as quantitatively assessed in Table 1, the wild-type thrombin has a higher mean value but slightly smaller standard deviation in the counts of the residue-residue hydrogen-bonding pairs regardless of the consideration of the LYS9 residue. These statistics imply the wild-type thrombin has a more stable conformational ensemble than the ΔK9 mutant thrombin and thrombin’s hydrogen bonding network is perturbed by the deletion of the light chain residue LYS9 in terms of the occupancy and diversity of hydrogen bonds.

Table 1.

Statistics of residue pairs with hydrogen bonds

Conf.	WT all	WT w/i A	WT w/i B	WT b/t A&B	WT all but K9	ΔK9 all	ΔK9 w/i A	ΔK9 w/i B	ΔK9 b/t A&B
Unique	2006	203	1520	283	1991	2262	191	1811	260
Mean	184.35	14.30	158.80	13.26	183.59	181.18	13.84	154.81	12.53
Std. Dev.	7.56	2.86	6.73	2.44	7.56	7.96	2.81	7.09	1.99

^*Heavy and light chains are labeled as ‘A’ and ‘B’. ‘w/i’ denotes ‘within’; ‘b/t’ denotes ‘between’.

We compared the prevalence of each hydrogen bonding pair in the wild-type and mutant thrombin systems by subtracting each hydrogen bonding pair’s occupancies in both systems. Sixteen residues pairs exhibited a considerable difference -- having a difference in occupancy of more 33% between the two systems -- in hydrogen bonding interactions (Table S2). Out of 16 pairs, 10 have a much greater occupancies in the wild-type, indicating the wild-type thrombin have a more stable structure. The hydrogen bonds between the LYS9 and ASP116, and LYS9 and PRO5 are entirely missing in the mutant thrombin due to the lack of LYS9. Moreover, the wild-type form preserves several hydrogen bonds formed within the light chain (LEU12-PHE7, LYS10-LEU6) and heavy chains (LEU40-GLY147F, TYR94-LEU60, LYS147G-GLU39, ASP221A-ASP189, LEU60-ALA56, LEU144-GLN151). While the deletion of LYS9 destabilizes these hydrogen bonding interactions, the hydrogen bonds involved the LYS9 in the wild-type form are compensated by the nearby LYS10. Instead of LYS9, in the ΔK9 mutant thrombin, LYS10 starts selectively interacting with ASP116. However, this hydrogen bond interaction between the light and heavy chain is about half likely than the hydrogen bond between LYS9 and ASP116, which is selected by the wild-type thrombin. In addition, several hydrogen bonds (SER11-LEU6, LEU12-LEU6, ARG73-GLU39, TYR94-ASP102, THR147-GLU192) are preferential by the ΔK9 mutant thrombin (Table S2), which implying the significantly changes in hydrogen bonding network are not only located beside the LYS9 residue but also distant residues around catalytic cleft.

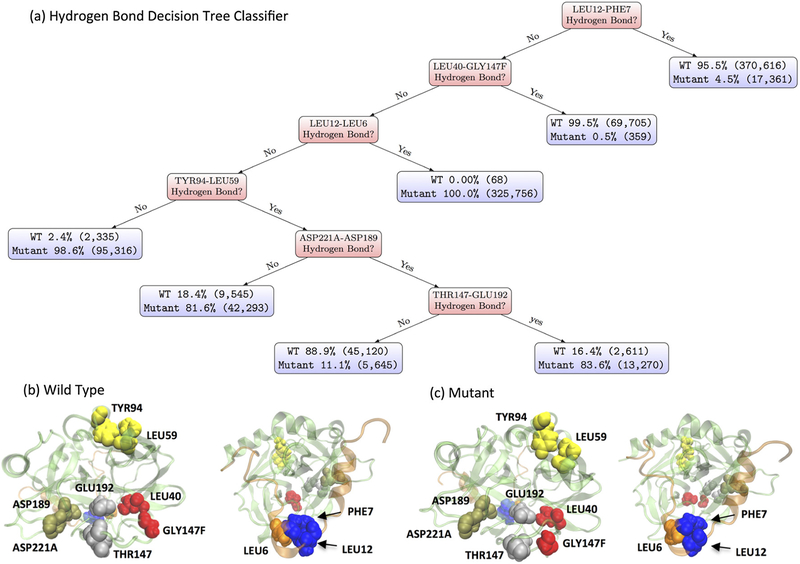
To identify underlying key hydrogen-bonding pairs of residues differentiating the wild-type and ΔK9 mutant thrombin, decision tree classifiers were constructed based on residue-residue hydrogen bonding features of the wild-type and mutant thrombin here. Via a decision tree with 169 levels of hydrogen-bonding pair decisions, we can at most classify the two types of thrombin’s conformations as accurate as 99.9985%. Pruning such full tree by 166 levels, a simple decision tree as shown in Figure 5a still yields 96.21% classification accuracy (Figure S6).

Figure 5.

Hydrogen Bond Analysis. (a) A decision tree classifier (96.21% accuracy) of ΔK9 (Mutant) and wild-type (WT) thrombin based on their residue-residue hydrogen bonding features. The percentages in the blue box denote the relative population of corresponding simulation type. The numbers within the following parentheses indicate the actual counts of structures of corresponding simulation type. Panel (b) and (c) illustrate the hydrogen bonds involved in the decision splits in (a). The wild-type and mutant thrombin structures were picked as the frames with the smallest root-mean-square distance to the average structure in each type of simulations. Each pair of residues has the same color and the order of colors (blue, red, orange, yellow, tan, silver, pink and purple) follows the decision levels.

The presences of hydrogen bonds among these six pairs of residues, which are (1) LEU12-PHE7 (2) LEU40-GLY147F (3) LEU12-LEU6 (4) TYR94-LEU59 (5) ASP221A-ASP189 (6) THR147-GLU192, establish distinct hydrogen bonding motifs of the wild-type and ΔK9 mutant thrombin. For example, the hydrogen bond motifs of (LEU12-PHE7:Yes) and (LEU12-PHE7:No, LEU40-GLY147F:Yes) cover 74.12% and 13.94% sampled conformations of wild-type thrombin, while these two motifs only occur in 3.54% of observed conformations without the K9 residue. Instead, (LEU12-PHE7:No, LEU40-GLY147F:No, LEU12-LEU6:Yes), (LEU12-PHE7:No, LEU40-GLY147F:No, LEU12-LEU6:No, TYR94-LEU59:No) and (LEU12-PHE7:No, LEU40-GLY147F :No, LEU12-LEU6:No, TYR94-LEU59:Yes, ASP221A-ASP 189:No) are mostly preferable by 92.67% sampled conformations of ΔK9 mutant thrombin. Further splits of the hydrogen bonding decision tree -- such as ASP221A-ASP189 and THR147-GLU192 -- yield a higher coverage of each type of conformations, though the purities in these leafs are less than the top level splits. The requirement of these hydrogen bonding decisions for a better coverage of the ΔK9 mutant implies a distribution shift in the conformational space due to the deletion effect. As we have seen above, the occupancies of hydrogen bonds among these six pairs of residues are 33.33% greater in one system than another (Table S2). Again, it is clear that considerable changes in hydrogen bonding network are not only localized but also long ranged allosteric (Figure 5b & c).

Weakened and perturbed Na⁺ binding in LYS9 deletion mutant thrombin

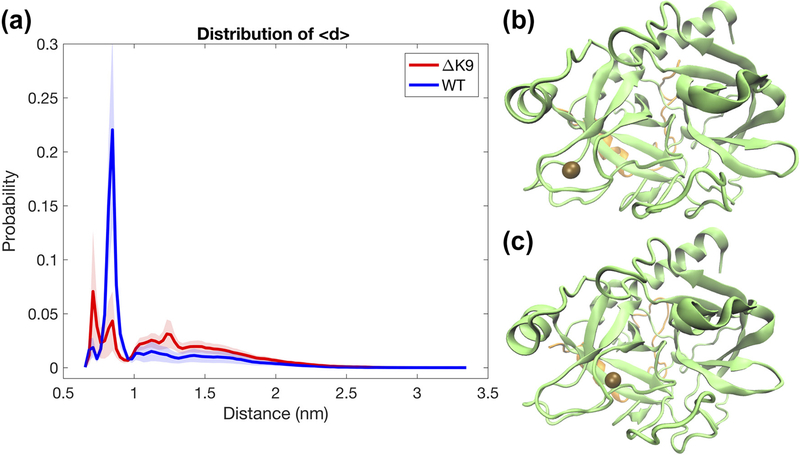
The association and dissociation of a Na⁺ ion have been observed in both wild-type and ΔK9 mutant thrombin. As assessed by the distance between the 220s loop (also known as sodium binding loop) and the nearest Na⁺ ion, the bound Na⁺ ion presents two binding modes onto the sodium binding loop in both simulations of wild-type and mutant thrombin (Figure 6). However, the first binding mode, where Na⁺ is binding outer region of the 220s loop (as shown in Figure 6b), is preferable to the ΔK9 mutant thrombin. The second binding mode (Figure 6c), where the bound Na⁺ is located at the inner the 220s loop and almost entering the S1 subpocket of thrombin, is more selected by the wild-type thrombin. The former binding mode has been seen in the crystal studies of thrombin (E Di Cera et al., 1995; E. Zhang & Tulinsky, 1997); the later one is consistent with the density distribution of Na⁺ illustrated in the previous computational work (Kurisaki, Takayanagi, & Nagaoka, 2015).

Figure 6.

Distribution of the distance between the sodium loop and the nearest Na + ion. The wild-type (WT) and ΔK9 mutant thrombin present two striking peaks representing Na + binding in the distribution plot (a). The peaks at 7 Å and 8.5 Å correspond to two binding modes of Na + as respectively illustrated in panel (b) and (c), where the bound Na + ion is shown as the brown bead.

Here, we simply defined the Na⁺ bound and unbound states of thrombin without differentiating binding mode 1 and 2. The numbers of frames of the Na⁺ bound and unbound states for wild-type and mutant thrombin are listed in Table 2. This statistics clearly indicates that the binding of Na⁺ ion becomes about half likely for the ΔK9 mutant thrombin than the wild-type, suggesting a weakened affinity of Na⁺ binding.

Table 2.

Statistics of frames with Na+-binding/unbinding.

	Bound (frames/percentage)	Unbound (frames/percentage)
Wild-type	306,521 / 61.30%	193,479 / 38.70%
ΔK9	141,974 / 28.39%	358,026 / 71.61%

LYS9 deletion perturbs solvent accessible surface areas

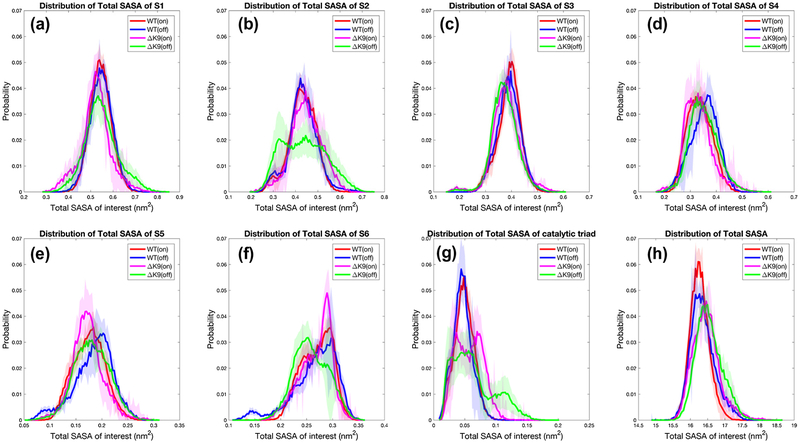
As a reflection of conformations and meaningful quantity for interacting substrates, solvent accessible surface areas (SASA) of catalytic subpockets S1–6, catalytic triad and the whole protein were computed for wild-type and ΔK9 mutant thrombin in Na + bound and Na + unbound states. As shown in Figure 7, the wild-type and mutant thrombins exhibit significantly distinct distributions of SASAs of the catalytic cleft and event the whole protein.

Figure 7.

Distributions of solvent accessible surface area (SASA). Regarding conformations with a bound/unbound Na {+} ion (denoted as on/off), the SASA distribution of the catalytic sub-pocket S1–6 residues are plotted respectively for wild-type (WT) and ΔK9 mutant thrombin in panels (a)-(f). The SASA distribution of the catalytic triad and the SASA of the whole protein are also plotted in (g) and (h).

The ΔK9 mutant thrombin in general presents a wider distribution of SASAs than the wild-type (Figure 7), suggesting more dynamic structural ensembles. In particular, when there is no Na + attaching to the interior of sodium binding loop, the mutant thrombin exhibits highly perturbed SASA distributions of S2, S6 and catalytic triad. The binding of a Na + ion make the mutant thrombin turn more wild-type-like in terms of the distribution of the catalytic subpockets’ SASAs.

The catalytic triad’s SASA of the mutant thrombin is altered dramatically, regardless of the status of Na + binding. As seen in Figure 7g, the multiple distinct peaks than the single one of the wild-type indicate the catalytic triad residues and their vicinity area establish less stable conformations than they have in the wild-type thrombin. The catalytic triad is more exposed when K9 is not present in the light chain. Similarly, although the wild-type thrombin has one residue than the ΔK9 mutant one, the deletion of the K9 in fact leads to a more solvent exposed surface area for the whole protein molecule.

LYS9 deletion disrupts thrombin’s conformational free energy profiles

Conformational free energy profiles of the wild-type and ΔK9 mutant thrombin were estimated via principal component analysis, which is a very sensitive approach to reflect dominant structural differences in the wild-type and mutant thrombin. Na + bound/unbound states were also considered as what we did in the SASA analysis, aiming to reveal the independent and combined influences of the LYS9 deletion and the known allosteric effector of Na + ions.

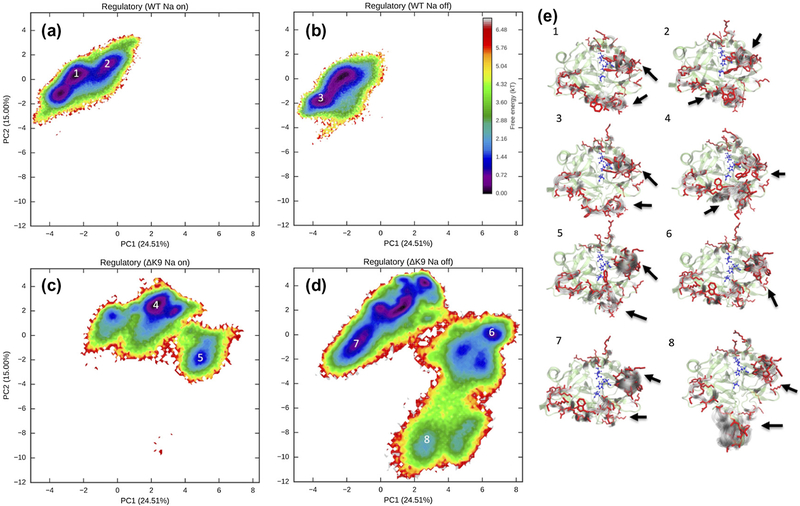
As shown in Figure 8, the conformational free energy surface of the regulatory regions, including the 60s, 220s and gamma loops and exosite I and II, is dramatically perturbed by the deletion of LYS9. The primary conformational free energy well of above regulatory sites shifts to a large region that is inaccessible for wild-type thrombin. While the wild-type thrombin primarily establishes one narrow well, the mutant thrombin presents multiple spread wells. Furthermore, the binding of Na⁺ mainly alters populations of the wild-type thrombin among several conformations with subtle structural differences in the regulatory regions (Figure 8e). However, unlike wild-type thrombin, the Na⁺ binding stabilizes some conformations of the regulatory regions that are only presented by the mutant thrombin rather than the wild-type. These conformations have a greater blockage of the catalytic cleft by the gamma loop but a more exposed catalytic triad due to the extension of the 60s loop (Figure 8e).

Figure 8.

Conformational free energy surfaces of the regulatory regions. Regarding conformations with a Na+ binding/unbinding, four free energy surfaces are plotted for wild-type (WT) and ΔK9 mutant thrombin respectively in panels (a), (b), (c), and (d) to compare the mutant and ion effects. Structural ensembles corresponding to the labeled wells on the free energy surfaces are visualized in panel (e). The representative structures of the whole protein are displaced via the NewCartoon representation in transparent green. The representative structure of the side chains in the regulatory regions are indicated by the Licorice representation in red. Gray shadows in NewCartoon representation display the variances in the regulatory regions. The side chains of the catalytic triad residues are shown in blue. Significant conformational differences in the regulatory regions are highlighted by the arrows.

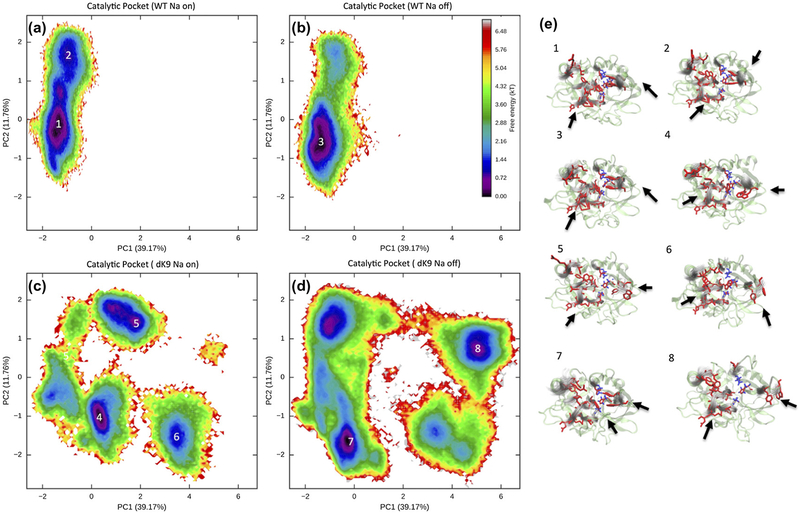
The conformational free energy surfaces of the catalytic cleft, including the catalytic triad and substrate pockets S1–6, also reveal that the LYS9 deletion causes a striking disruption of the shape of the catalytic site. While the wild-type thrombin illustrates a major stable conformational free energy well in Figure 9a & b, the mutant thrombin displays multiple separate wells in the free energy surfaces (Figure 9c & d). The catalytic clef of the ΔK9 mutant thrombin is thus not as stable as the one in the wild-type thrombin. The mutant’s 60s loop is able toflip up and the end of the 220s loop exhibits more variances in its orientations (Figure 9e). Again, the binding of Na⁺ to the mutant thrombin stabilizes the conformations that are not seen in the wild-type thrombin.

Figure 9.

Conformational free energy surfaces of the catalytic pocket. Regarding conformations with a Na+ binding/unbinding, four free energy surfaces are plotted for wild-type (WT) and ΔK9 mutant thrombin respectively in panels (a), (b), (c), and (d) to compare the mutant and ion effects. Structural ensembles corresponding to the labeled wells on the free energy surfaces are visualized in panel (e). The visualization strategy here is the same as in Figure 7. As indicated by the arrows, PC1 captures much of the variance in 60s loop, and PC2 mainly captures different shapes in the S1 sub-pocket.

Discussion

Our quantitatively comparisons of the wild-type and ΔK9 mutant thrombin above consistently indicate significant impacts of the light chain residue LYS9 on thrombin in molecular level and structural ensemble aspect. By quantifying the distributions of possible conformational states in the wild-type and mutant forms, we reveal that thrombin’s structural stability decreases in terms of more diverse population of the conformational states in the absence of the LYS9 (Figure 4). Note that previous urea-induced denaturation and disulfide scrambbling experiments also suggest that the overall structural stability of the wild-type thrombin should be higher than the ΔK9 form (Raimondo De Cristofaro et al., 2006). Our Amorim-Hennig clustering analysis presents experimentally consistent results, suggesting the effectiveness of this recently developed non-parametric clustering algorithm in MD analysis.

Through a total of 10 microseconds of all-atom molecular dynamics simulations, we see that the reduced stability in the ΔK9 mutant thrombin was ascribed to the increased mobilities of thrombin’s regulatory regions including the 60s, 180s, 220s and gamma loops, and exosite I and II (Figure 3). The conformational free energy surfaces of these regulatory regions confirm that the increased mobility results in conformational changes and metastable states. While previous single run of 18ns MD simulation reveals the deletion of LYS9 may lead to subtle conformational changes in the thrombin’s catalytic triad and the 60s loop (Raimondo De Cristofaro et al., 2004), our multiple runs of longer simulations show that the ΔK9 form should have a much more perturbed catalytic pocket and 60s loop. Figure 9 illustrates several different distortions of the catalytic cleft in the mutant thrombin. Basically, the 60s loop is destabilized by the light chain deletion of LYS9. When a Na+ ion is not bound to the 220s loop, 60s loop can flip up and lead to a fully exposed S2 subpocket (Figure 9e). In the mutant thrombin, the movement of residues in S3 subpocket also can result in a self-inhibited conformation that has previously been seen in the crystal structure of thrombin mutant D102N (Gandhi, Chen, Mathews, & Di Cera, 2008).

As indicated in Figure 7, all subpockets are distorted by the LYS9 deletion. As a long range allosteric effect, different preferential orientations of the side chains in the mutant thrombin also lead to population shifts in the conformational free energy surfaces of the catalytic cleft comparing to the wild-type thrombin (Figure 9). Moreover, the hydrophilic gamma loop, which restricts the access of substrate to the catalytic cleft, is destabilized in the ΔK9 form and establishes a variety of poses in the slow time scale (tens to hundreds of nanoseconds) motions (Figure 8). Therefore, our multiple runs of microsecond simulations and comprehensive analyses reveal additional and more significant conformational changes that have not been previously uncovered. This is probably due to the limitation of the crystallization as well as the limited time scale and sampling in previous studies.

The hydrogen bond detection provide further insights of the structure and intra-molecular interactions, considering the fact that thrombin is an allosteric enzyme and that the light chain interacts with the heavy chain via a network of hydrogen bonding interaction and salt bridges. Our statistics of the hydrogen bonds indicate an overall weakened hydrogen bonding network in the absence of LYS9, consisting with the consequence of destabilization we have discussed before. Our calculation suggests the salt bridge between LYS9 and ASP116 is a critical interaction between the light chain and heavy chain. Although LYS10 tends to compensate the lost of this interaction, the likelihood of forming this salt bridge in the ΔK9 mutant is about a half of the wild-thrombin.

In order to understand how the light chain deletion conducts an allosteric signal to the distant region of the protein, it is necessary to identify hidden patterns that can distinguish the conformational ensembles of the wild-type and mutant forms. As hydrogen bonds play an important role in allosteric communication (Amor, Schaub, Yaliraki, & Barahona, 2016; Daily & Gray, 2009; Srivastava et al., 2016), we searched the simplest hydrogen bonding motifs via decision tree learning. Via this machine learning methodology, in additional to the hydrogen bond between LYS9 and ASP116, we predict six pairs of such interactions -- (1) LEU12-PHE7, (2) LEU40-GLY147F, (3) LEU12-LEU6, (4) TYR94-LEU59, (5) ASP221A-ASP189, and (6) THR147-GLU192 -- play a profound role in thrombin’s intra-molecular signaling and structural stability. Different hydrogen bonding statuses of these pairs are likely responsible for propagating the signal from the light chain and causing allosteric effects. We suggest future experimental and computational mutation studies should first consider these residues for further understanding of thrombin’s allostery.

Na⁺ ions, known as an allosteric modulator of thrombin, has been revealed ~2-fold frequent to bind to the thrombin in wild-type form than the ΔK9 one in our simulations. Such results are consistent with the observation that ΔK9 thrombin has a half gain in the intrinsic fluorescence intensity of upon sodium concentration than wild-type form does (Raimondo De Cristofaro et al., 2006). Furthermore, although Na⁺ ions are able to recognize the sodium-binding loop, it is the first time to see that the bound Na⁺ ion presents a different preference of binding in the wild-type and mutant forms. In the ΔK9 mutant thrombin, a Na⁺ tends to stay in the outer site of the 220s loop that has been seen in the crystal structure (E Di Cera et al., 1995; E. Zhang & Tulinsky, 1997). For the wild-type thrombin, the interior of the 220s loop is more favorable for the bound Na⁺. The statistics also suggest the deeper binding is more thermodynamically stable than the one solved by the crystallography studies before. This find provides a mechanistic insight into the reduced affinity of Na⁺ to thrombin considering the fact that the more stable deep binding is not preferred by the Δ K9 mutant form. This result triggers us interest to investigate the association/dissociation pathways of Na + and functional differences of these two binding modes in the future study.

From the SASA analysis and free energy surface construction, we can see the binding of Na + ion stabilizes the structural ensembles of thrombin. Subpockets S2, S3 and S6 appear more wild-type like after Na + binding according to the SASA distribution (Figure 7). On the other hand, according to figure 8 & Figure 9, the regulatory regions and the whole catalytic cleft tends to be stabilized into some unique conformations that are inaccessible for the wild-type form. Therefore, the LYS9 deletion appears to cause a primary influence on the entire protein, while the binding of a Na⁺ ion offers a secondary perturbation.

Conclusions

Thrombin has been considered as an allosteric enzyme (see the review by Enrico Di Cera, 2008). In this study, we see significant conformational differences in the wild-type and ΔK9 forms of thrombin. The deletion of the LYS9 perturbs the interaction network within the light, heavy chains as well as between them. Such perturbations cause significant and profound conformational changes in the catalytic and regulatory sites. Our calculations presented here are consistent with previous experimental and computational work. Our results support the opinion that the light chain is the allosteric effector instead of the activation remnant discussed by Carter et al., 2010. Moreover, it expands our understanding of how the disease-associated LYS9 deletion impairs thrombin’s biophysical properties from the following aspects.

Firstly, our study shows that there are more significant conformational changes occurring in the longer time scale (tens to hundreds of nanoseconds) in the ΔK9 thrombin. For instance, the 60s loop can completely flip up and result in a fully exposed S2 subpocket in the absence of LYS9. The gamma loop also establishes more diverse poses in the ΔK9 thrombin, which may further affect substrates’ recognition to the catalytic pocket. We provide a more detailed dynamic perspective of ΔK9 thrombin.

Secondly, we identify a list of residues with critical hydrogen bonds. These residues, i.e. LYS9, ASP116, LEU12, PHE7, LEU40, GLY147F, LEU6, TYR94, LEU59, ASP221A, ASP189, THR147 and GLU192, are likely playing an important role in the intramolecular interaction network of thrombin. We hypothesize that the hydrogen bonds among these residues are responsible for transmitting the allosteric signals from the light chain to the entire protein. We suggest these residues should be first looked at in the future mutagenesis study in order to understand thrombin’s allosteric pathway and response to mutations.

Thirdly, we reveal a second Na+ binding mode in thrombin for the first time. We show that the wild-type and ΔK9 thrombins present different preferences between the two Na + binding modes. These observations further suggest a mechanistic explanation of the reduced sensitivity to the Na+ binding for the ΔK9 thrombins. Meanwhile, we clarify that the binding of a Na+ ion should play a secondary role in regulating thrombin’s conformational ensembles comparing with the LYS9 deletion.

Moreover, this work combines microsecond molecular dynamics simulations and machine learning techniques to probe the LYS9/LYS10 deletion’s influences on thrombin and the corresponding mechanisms. The decision tree learning uncovers hydrogen bond motifs that distinguish the wild-type thrombin from its ΔK9 mutant. These critical hydrogen bonds are likely key components that transmit the allosteric signals to the either protein from the single deletion in the light chain. Although only one light chain mutation has been discussed here, it is necessary to study this important mutation first as a test case for understanding other disease-related mutations in the light chain. Given the new insights into how and why the LYS9 deletion perturbs thrombin, we will work on other thrombin mutations in the future. The methodology presented in this work should be also applicable for other systems if one interests in understanding the molecular response to any type of perturbations such as mutations and ligand binding.

Supplementary Material

Supplementary material

Table S1. Residue indexes of regions of interest.

Table S2. Residue-residue hydrogen bonds with significant occupancy differences in wild-type and ΔK9 mutant thrombin.

Figure S1. Time series plots of common alpha carbons’ root-mean-squared distance to the initial structure of thrombin.

Figure S2. Blocked standard error of RMSD. The solid line represent the average BSE across 5 runs of each type simulation.

Figure S3. Time series of the common alpha conbons’ dominant principal components. Time series plots of the first two principal components of the common alpha carbons in the wild-type and ΔK9 mutant forms.

Figure S4. Representative structures with √2σ variances for clusters of the regulatory region.

Figure S5. Representative structures with √2σ variances for clusters of the catalytic triad.

Figure S6. Pruning errors for the decision tree.

Abbreviations and symbols

ΔK9

LSY9 deletion form

MD

Molecular dynamics

RMSF

root-mean-square fluctuations

Na+

sodium

PCA

principal component analysis

NPT

isothermal-isobaric ensemble

PME

particle mesh Ewald