Skip to main content
PMC home page
AoB Plants logoLink to AoB Plants
. 2018 Oct 11;10(5):ply066. doi: 10.1093/aobpla/ply066

Deacclimation kinetics as a quantitative phenotype for delineating the dormancy transition and thermal efficiency for budbreak in Vitis species

Alisson P Kovaleski 1,✉, Bruce I Reisch 1, Jason P Londo 1,2,✉
PMCID: PMC6207836  PMID: 31572566

Abstract

Bud dormancy and cold hardiness are critical adaptations for surviving winter cold stress for temperate perennial plant species. In grapevine, acquisition of cold hardiness requires dormancy induction in the early winter and careful maintenance of dormancy state throughout winter. With sufficient exposure to low, non-freezing temperatures (chilling requirement), grapevine buds transition between early (endodormant) and late winter (ecodormant) states. The objective of this study was to uncover the relationship between fulfilment of the chilling requirement and the effects of various temperatures on loss of cold hardiness (deacclimation). The relationship between chilling requirement and temperature as it affects the rate of deacclimation (kdeacc) was examined for dormant cuttings of Vitis vinifera, V. aestivalis, V. amurensis and V. riparia. The effect of temperature on kdeacc was exponential at low and logarithmic at high temperatures. Deacclimation rates also increased in magnitude as chilling accumulated demonstrating a change in deacclimation potential (Ψdeacc), following a logarithmic response. The combination of Ψdeacc and kdeacc indicates genotype-specific thermal efficiency for deacclimation and growth in Vitis that may be overlooked by simple growing degree-day computations. The Ψdeacc and kdeacc parameters are genotype-specific and will greatly increase the refinement of models predicting effects of climate change on phenology. Deacclimation rates represent a quantitative determinant of dormancy transition and budbreak in grapevine and will assist researchers in selecting germplasm for differences in chilling requirement and thermal efficiency.

Keywords: Bud, budbreak, cold hardiness, deacclimation, dormancy, grapevines, phenology, rates, supercooling, Vitis

Perennial plants use bud dormancy as a strategy to survive stressful environments, such as cold temperatures during winter. This strategy is dependent on the ability of the dormant bud to track the length of winter, avoiding early spring budbreak. In this study, we demonstrate that as winter progresses, the sensitivity of grapevine buds to temperature increases. This demonstrates a link between dormancy state and loss of winter hardiness. The kinetics of the process also describe early bud phenology. With this understanding, we can now model the response of buds to current and future climate conditions.

Introduction

Due to their general stationary habit, plants have evolved many different coping mechanisms to survive stressful conditions in their environment, such as drought and temperature. With regard to winter in temperate climates, annual plants typically survive as dehydrated seeds while perennial plants develop dormancy and cold hardiness. Dormancy is the temporary cessation of visible growth in meristem containing structures, such as buds, and is divided in three types: para-, endo- and ecodormancy (Lang et al. 1987). Paradormancy is the suspension due to physiological factors within the plant but outside of the dormant structure, such as the suppression of lateral growth by the apical meristem (i.e. apical dominance). Paradormant buds transition into endodormancy as daylength and temperatures decrease, a state suspension of growth due to unknown endogenous factors within the dormant structure, preventing growth during times when environmental conditions fluctuate between conducive and inhibitory (Horvath et al. 2003). During endodormancy, it is generally understood that exposure to low, non-freezing temperatures is necessary (chilling requirement) to transition to the third dormancy type, ecodormancy (Campoy et al. 2011). Tissues maintain a dormant state during ecodormancy due to unsuitable environmental conditions (Lang et al. 1987).

Concomitantly with the onset of dormancy, plants from areas where temperatures drop below freezing develop cold hardiness through different mechanisms. Some plants, or plant tissues, tolerate intracellular ice formation, in which cells are extremely dehydrated by the formation of extracellular ice, and the remaining water is bound (Burke et al. 1976) likely solidifying in a glass-like state. Other plants present a freezing resistance mechanism where water supercools in the intracellular spaces (Burke et al. 1976). Supercooling is a process through which water can remain in liquid state below its equilibrium freezing point, down to a maximum of ~ −40 °C (Bigg 1953). These species are typical of mid-latitude temperate climates, where temperatures do not drop below −40 °C during the winter. In buds that present supercooling ability, such as those of grapevines (Vitis spp.), cold hardiness may be measured through differential thermal analysis. This method uses thermoelectric modules that record voltage changes associated with the release of heat due to phase change of water into ice (Mills et al. 2006). Two peaks can be identified in grapevine buds using differential thermal analysis: a high temperature exotherm, typically around −5 °C; and a low temperature exotherm (LTE), which varies depending on the environmental conditions experienced by the bud. The high temperature exotherm represents the freezing of extracellular water (Andrews et al. 1984), which is normal to the process of resisting cold. The LTE, however, is the freezing of intracellular water, and it happens when the supercooling point has been exceeded (Mills et al. 2006). The LTE represents the lethal temperature for a given bud, and is correlated with manual assessments of bud death (Wolf and Cook 1994). Mean LTE has since been adopted as a consistent and routine measurement of bud cold hardiness in grapevine (Mills et al. 2006; Ferguson et al. 2011).

Cold hardiness follows a general U-shaped pattern during the winter, with three different stages: acclimation, maintenance and deacclimation. This pattern is thought to be primarily driven by air temperature (Ferguson et al. 2011, 2014; Londo and Kovaleski 2017), although other climatic aspects may also be important, such as relative humidity and daily thermal amplitude (Antivilo et al. 2017). Acclimation appears to occur primarily during endodormancy, while deacclimation is enhanced during ecodormancy (Ferguson et al. 2011, 2014; Londo and Kovaleski 2017). The transition between endo- and ecodormancy may occur towards the end of the acclimation stage depending on the climate and genotype, or during the maintenance stage of cold hardiness. This transition is typically evaluated by collecting dormant buds from the field and placing them in growth permissive conditions, followed by monitoring the time needed to reach budbreak (Weinbaum et al. 1989; Lloyd and Firth 1990; Cook and Jacobs 2000; Fan et al. 2010; Zhang and Taylor 2011). The chilling requirement has been considered to be met when 50 % budbreak occurs within a time threshold [e.g. 3 weeks for peaches (Prunus persica; Lloyd and Firth 1990); 4 weeks for grapevines (Londo and Johnson 2014)]. This method represents a subjective threshold for the transition from endo- to ecodormancy. As a result, determining the molecular and metabolic cues and the consequences of this transition, such as budbreak, are very difficult to determine and poorly understood (Penfield 2008).

As the dynamics of acclimation and deacclimation change with dormancy state (Ferguson et al. 2011, 2014), and dormancy state is determined by accumulation of chilling hours, a future climate may create issues for both cold hardiness and budbreak phenology. Average global temperatures are increasing (Walsh et al. 2014), although episodes of acute cold weather in the northern hemisphere are likely to increase as well through more frequent arctic oscillations (Kolstad et al. 2010). In addition to direct effects to cold hardiness, increasing temperatures will enhance chill accumulation in higher latitudes, while lower latitudes will experience a decrease (Luedeling et al. 2011). Changes in chill accumulation may modify the dynamics of dormancy transitions both in deciduous tree crops and other woody perennials, causing excessive responsiveness to warm spells or erratic budbreak and growth. This will ultimately require a shift towards higher latitudes and elevations of tree crops and assisted migration of forest species as they lag behind their optimal climate niche (Gray and Hamann 2013). Specific studies linking environmental factors to understand plant phenology in order to evaluate impacts of climate change are needed (Cleland et al. 2007; Chmielewski et al. 2018), especially during spring phenology (Vitasse et al. 2014). Therefore, it is important to understand how both temperature and dormancy status affect the loss of cold hardiness. The objective of this study was to understand the relationship between chill accumulation, the dormancy transition and temperature effects on the loss of cold hardiness and budbreak in wild and cultivated grapevines.

Methods

Buds of four different species were collected at up to nine levels of chill accumulation during the dormant seasons of 2014/15, 2015/16 and 2016/17 (seeSupporting Information—Table S1 for details on collections). Vitis vinifera ‘Cabernet Franc’, ‘Cabernet Sauvignon’, ‘Riesling’ and ‘Sauvignon blanc’ were collected from local vineyards (42.705N, 76.973W; and 42.845N, 77.004W), while V. aestivalis (two clones: PI483138, PI483143), V. amurensis (three clones: PI588632, PI588635, PI588641) and V. riparia (four clones: PI588275, PI588562, PI588653, PI588711) were collected from the USDA Plant Genetic Resources Unit in Geneva, NY. Buds from nodes 3 to 20 from the base of V. vinifera canes were used, while for the other species, buds beyond position 20 were used due to constraints regarding the number of available clones, as in Londo and Kovaleski (2017).

Hourly weather data from the closest Network for Environment and Weather Applications station (NEWA; http://www.newa.cornell.edu/) were used to compute chill accumulation using the ‘North Carolina’ model (Shaltout and Unrath 1983). The start date for each season was chosen based on when chill started to consistently accumulate instead of being negated, as determined by the North Carolina model. These dates were 11 September 2014, 19 September 2015 and 24 September 2016.

Upon collection, canes were cut into single- or two-node cuttings, randomized to prevent bias associated with node selection and placed submerging the basipetal cut surface in cups of water. The cups were placed into growth chambers at 2, 4, 7, 8, 10, 11, 22 or 30 °C. Not every genotype or temperature was used at all collection points. This information is available in Supporting Information—Table S1. Differential thermal analysis was used to estimate the cold hardiness of individual buds as represented by their LTE [see Mills et al. (2006) for details], the standard measure for grapevine. Briefly, buds are excised from the cane and placed on thermoelectric modules in plates. The plates are placed in a programmable freezer and subjected to a cooling rate of −4 °C h−1. Changes in voltage due to heat release in the freezing of water are measured by the thermoelectric module and recorded using a Keithley data logger (Tektronix, Beaverton, OR, USA) attached to a computer. Between 4 and 8 buds were sampled at any time point per treatment to determine mean LTE, and the intervals between measurement days varied between chill accumulation level and temperature treatment, with details provided in Supporting Information—Table S1. Because lower rates of deacclimation were expected in buds placed at lower temperatures and lower chill accumulations, lower temperature treatments were typically assessed with wider separation between time points compared with high temperature treatments [seeSupporting Information—Table S1].

An experiment was also designed to compare temperature effects on budbreak of buds collected from grapevines that were considered to be fully chilled (1440 chill accumulation; Londo and Johnson 2014). Buds held at constant temperatures (2, 4, 7, 11, 22 °C) had their budbreak recorded following the modified E-L scale (Coombe and Iland 2005) for all V. vinifera and V. riparia. Five buds were randomly selected and E-L number recorded in the same sampling interval as for LTE [seeSupporting Information—Table S1] until buds were past stage 3 or bud material was exhausted.

Data analysis

Based on sample size across temperatures and across sampled years, data sets for V. vinifera were analysed separately for each cultivar, while data for accessions of V. aestivalis, V. amurensis and V. riparia were combined at the species level. Analyses were separated into the effect of chill accumulation and the effect of temperature on rate of deacclimation. The data sets used for each analysis are specified in Supporting Information—Table S1. All data analysis was performed using R (ver. 3.3.0; R Development Core Team 2008).

Effect of chill accumulation.

Individual rates were calculated using linear regression for each temperature and chill accumulation as factors (slopes in Supporting Information—Table S1). These rates were used to assess the effect of chill accumulation, hereafter referred to as deacclimation potential (Ψdeacc), on the rate of deacclimation (kdeacc). Although every temperature treatment within a chill accumulation had the same data for Day 0 (field collection), temperatures were allowed to have different intercepts in order to reduce the effect of Day 0 on kdeacc. From this regression model, data points that had a studentized residual ≥2.5 were considered outliers and removed from the data set, and the model was re-fit. The kdeacc at each chill accumulation were then transformed to percentage for 4, 7, 10, 11 and 22 °C, standardizing to their kdeacc at highest chill accumulation (either 1440—7 and 11 °C—or 1580 chill units—4, 10 and 22 °C). The Ψdeacc was estimated as a logistic regression. Initial estimation used the drc library, but final estimation used the nls() function with the port algorithm, following the equation: Ψdeacc(%)= 1001+ e[b × (lnChill −c)], where b and c are the estimated parameters, and Chill is the chill accumulation at the time of sample collection. The parameter c is the inflection point of the logistic and b is the slope associated with the logistic regression.

Effect of temperature.

Instead of using rates from the above linear models, the complete data sets were used with the effect of temperature as a continuous variable. The values for the different chill accumulation points were normalized to that of full chill by dividing by the Ψdeacc at any given chill accumulation. The relationship between deacclimation rate and temperature did not appear to be strictly linear [seeSupporting Information—Fig. S1A]. The rates were plotted as an Arrhenius plot (log-transformed rates, inverse temperature) to visualize the potential for two different response curves split by temperature. Two separate responses were clearly noted [seeSupporting Information—Fig. S1B] and the data were divided into two sets to study the effect of temperature. Linear, exponential and logarithmic curves were examined to determine the best fit of the regression. Exponential responses were calculated as kdeacc= m × e(n × T), where m and n are the parameters estimated, and T is the temperature in °C. Logarithmic responses were calculated as kdeacc=q ×ln(T−r), where q and r are the parameters estimated, and T is the temperature in °C. For both exponential and logarithmic responses, parameters were estimated using nls(), with the port algorithm.

Fitness of effects of chill and temperature.

The fits of all non-linear curves (effect of chill accumulation, low and high temperatures) were tested using Effron’s pseudo-R2 with the Rsq function in the soilphysics library. The final model for loss of cold hardiness is then ΔLTE(T, Chill)= kdeacc × Ψdeacc × t, where the change in LTE (ΔLTE) is a function of the temperature (T) it was exposed to, how much chill accumulation (Chill) had passed before exposed to deacclimation temperatures and the time (t) of exposure. A linear model was used to evaluate the accuracy of the predictions using the complete data set, where instead of temperature, kdeacc={m × e(n × T),  T<12 °Cq ×ln(T−r),  T≥12 °C was used, and instead of accumulated chill, the Ψdeacc was used. The β associated with the estimated kdeacc and Ψdeacc was expected to be 1 in this model (ΔLTE = β × kdeacc × Ψdeacc × time), considering estimations were appropriate.

Budbreak.

In order to evaluate whether the same temperature effects governing deacclimation and loss of cold hardiness (measured as LTE) also controlled differences in the temporal rate of budbreak, a linear model was used. For this, forward selection was conducted with a reduced model containing an intercept only, and a full model containing all possible interactions of growing degree-days [GDD = kdeacc × t (day)], temperature, species and genotype as explanatory variables for bud growth stage. The forward selection was corrected based on the Bayesian information criterion (BIC).

Results

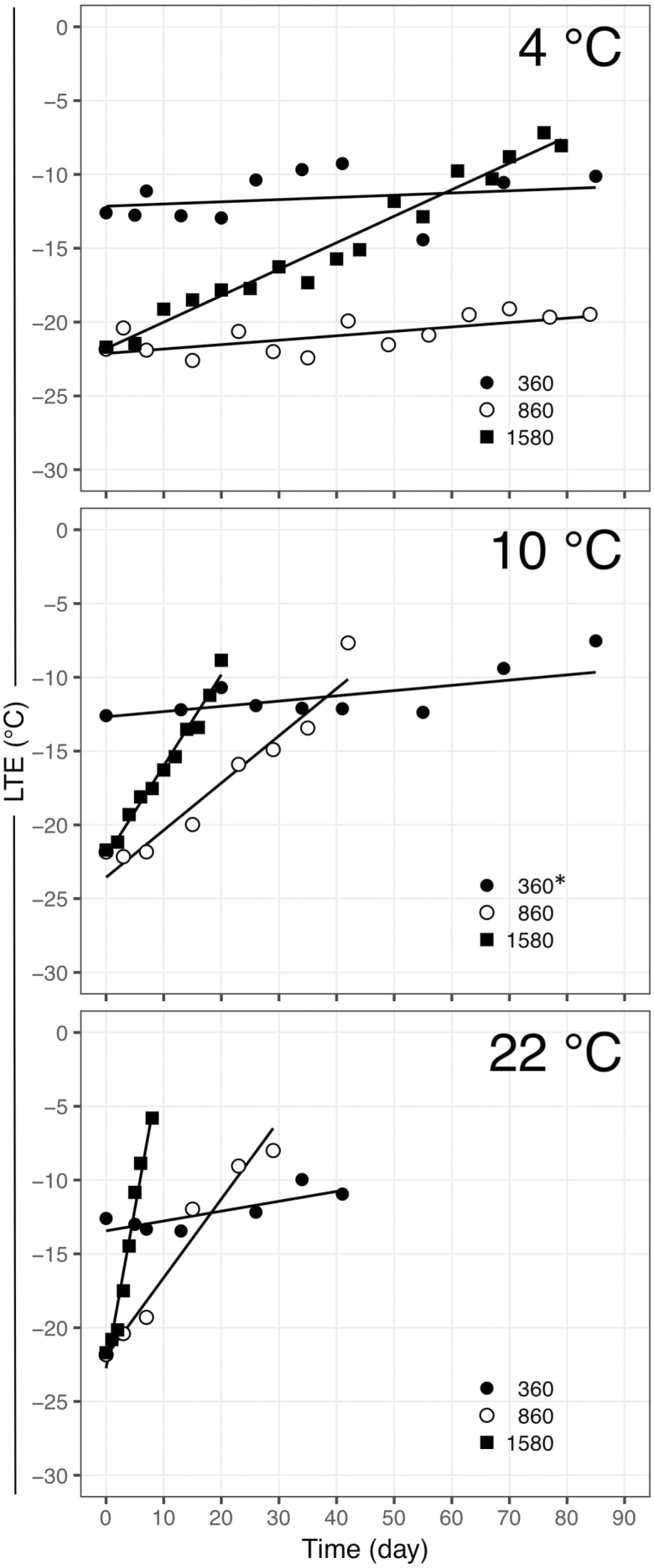
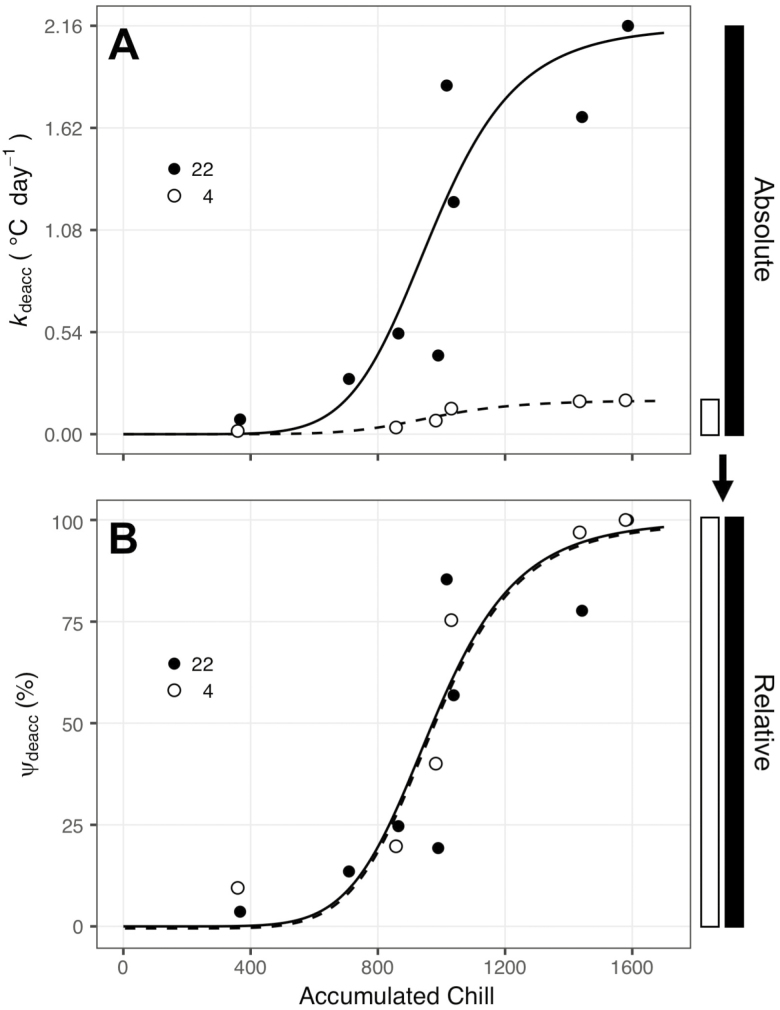
After removing outliers using multiple linear regression, data sets kept ≥90 % of the observations for all genotypes, with the exception of V. amurensis, which had 19.5 % of observations removed [seeSupporting Information—Table S2]. Deacclimation rates are linear within each of the temperatures tested regardless of the level of chilling accumulation of the buds. However, the slope of this linear relationship increased as chilling accumulation increased, resulting in increasingly faster deacclimation at all temperatures (Fig. 1). In absolute values, deacclimation rates were always higher at high temperatures compared with low temperatures, regardless of chill accumulation (Fig. 2A). When the rates of deacclimation at these different chilling accumulations were normalized to the maximum rate at each temperature, we observed a logistic relationship (Fig. 2B). We termed this relationship the deacclimation potential (Ψdeacc), which is simply the level to which a genotype will deacclimate, at any temperature, depending on chill accumulation. Pseudo-R2 values for logistic fits of Ψdeacc were greater than 0.87 for all genotypes except for ‘Cabernet Sauvignon’ and V. amurensis (0.65 and 0.79, respectively; seeSupporting Information—Table S2). The parameter c is the natural logarithm of the inflection point, and there was little difference in this parameter for the genotypes tested (e.g. extremes were 6.77 and 6.88, for ‘Sauvignon blanc’ and ‘Riesling’, respectively, which is equivalent to 872–972 chill units).

Figure 1.

Figure 1.

Open in a new tab

Deacclimation of Vitis vinifera ‘Riesling’ buds at three temperatures (4, 10 and 22 °C) collected from the field at three different chill accumulations (360, 860 and 1580). *Buds at 360 chill accumulation were deacclimated at 11 °C.

Figure 2.

Figure 2.

Open in a new tab

Deacclimation potential (Ψdeacc) of Vitis vinifera ‘Riesling’ buds collected at different chill accumulations in two temperatures (4 and 22 °C). (A) Absolute deacclimation rates (kdeacc) for 4 and 22 °C. (B) Relative deacclimation rates (kdeacc) for 4 and 22 °C normalized to deacclimation rate at 1580 chill units (100 %) within each temperature. The relationship between deacclimation potential and accumulated chill was described as the deacclimation potential (Ψdeacc) by the equation: Ψdeacc(%)= 1001+ e[−7.23 × (lnChill −6.88)], with a pseudo-R2 = 0.87.

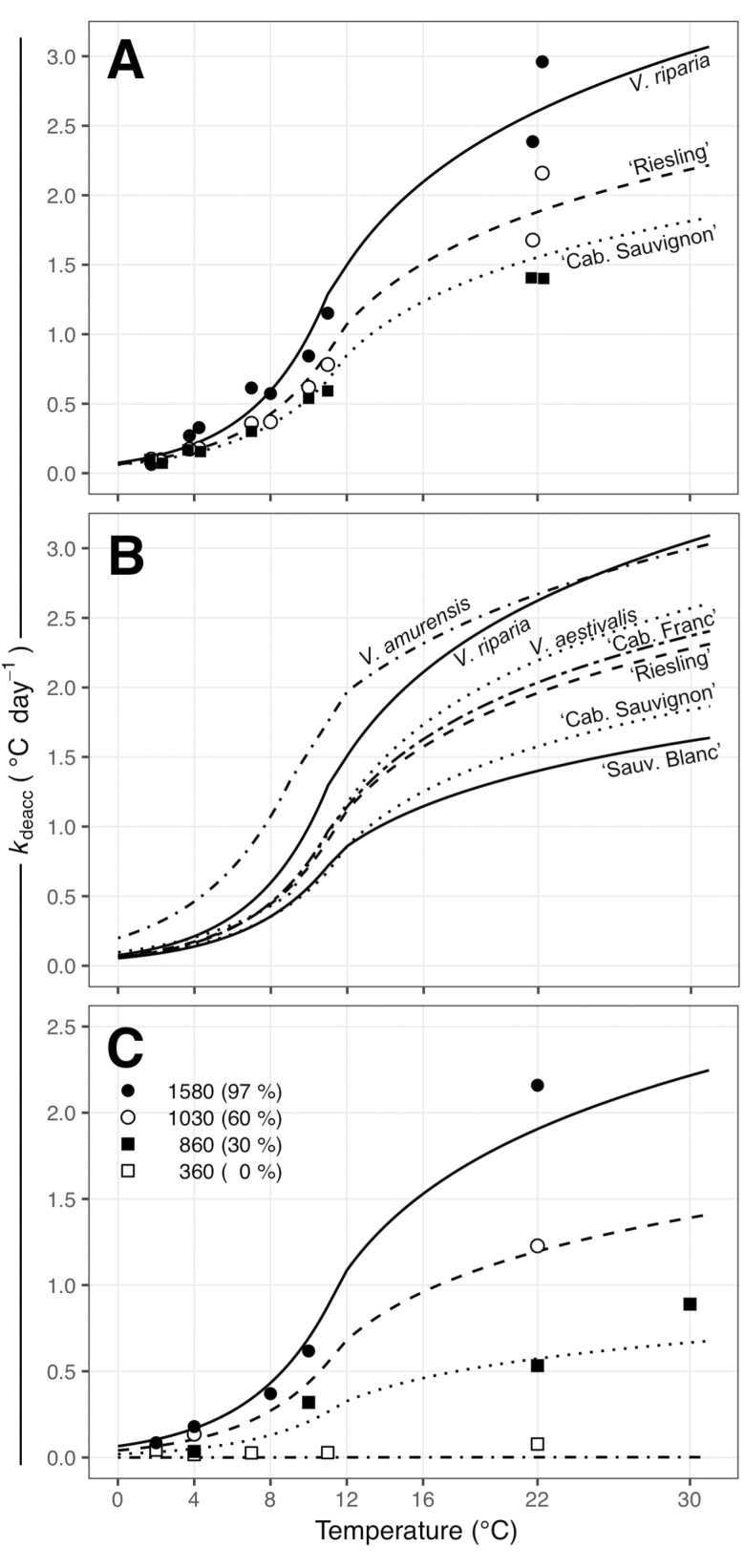
While deacclimation at any one temperature is linear and slope is dependent on chilling accumulation, comparing deacclimation rates across a range of temperatures reveals that the relationship between deacclimation rates and temperature is more complex and suggests genotype level specificity in temperature response. To establish the relationship between temperature and deacclimation rate (kdeacc), kdeacc at different chill accumulations were normalized based on calculated Ψdeacc to remove the effect of chill (kdeacc[T = i, chill =j]/Ψdeacc[chill=j]; seeSupporting Information—Fig. S1A). This normalization was performed to look at the effect of temperature regardless of how chilling accumulation is affecting rates. Initial linear regressions under-predicted low temperature deacclimation rates and indicated an erroneous gain rather than loss of cold hardiness at 2 °C (data not shown). The Arrhenius plot [seeSupporting Information—Fig. S1B] demonstrated a clear discontinuity occurs between low and high temperatures. Additionally, an exponential response was a better fit for low temperatures, while a logarithmic fit was better for high temperatures, in comparison to linear fits [seeSupporting Information—Table S3]. Genotypes within V. vinifera (i.e. cultivars), which were analysed separately, had higher R2 values compared with the other species, which had multiple genotypes combined. A deceleration of the increase of kdeacc as temperature increased was observed, which justifies the different behaviours used to model responses (exponential and logarithmic for low and high temperatures, respectively). The estimation of temperature effects for low and high temperature intersect between 10 and 11 °C due to uncertainty in the exact temperature where there is a change in behaviours. This is primarily due to the lack of data points between 11 and 22 °C. All the V. vinifera cultivars had similar deacclimation rates at low temperatures, but ‘Riesling’ and ‘Cabernet Franc’ had higher deacclimation rates at high temperatures than ‘Cabernet Sauvignon’ and ‘Sauvignon blanc’ (Fig. 3A and B). Vitis riparia and V. aestivalis had similar rates to those of V. vinifera at low temperatures, but V. riparia had estimated rates similar to V. amurensis in higher temperatures (Fig. 3B). Vitis aestivalis was similar to the faster V. vinifera (‘Cabernet Franc’ and ‘Riesling’). Vitis amurensis showed the highest deacclimation rates at both low and high temperatures. The combined effect of temperature and Ψdeacc is illustrated in Fig. 3C for ‘Riesling’, demonstrating that the shape of kdeacc in response to temperature is the same, but ‘compressed’ at lower chill accumulations due to a lower deacclimation potential.

Figure 3.

Figure 3.

Open in a new tab

Deacclimation rates of Vitis buds as a function of temperature. (A) Deacclimation rates at >90 % deacclimation potential for three different Vitis genotypes: V. riparia (closed circle—full line), V. vinifera ‘Riesling’ (open circles—dashed line) and V. vinifera ‘Cabernet Sauvignon’ (closed squares—dotted line). (B) Predicted curves for deacclimation rates of seven Vitis genotypes. (C) Deacclimation rates of V. vinifera ‘Riesling’ at different chill accumulations as a function of temperature [predicted deacclimation potential (Ψdeacc) shown in parenthesis]: 1580 (closed circle—full line), 1030 (open circle—dashed line), 860 (closed square—dotted line), 360 (open square—dashdotted line).

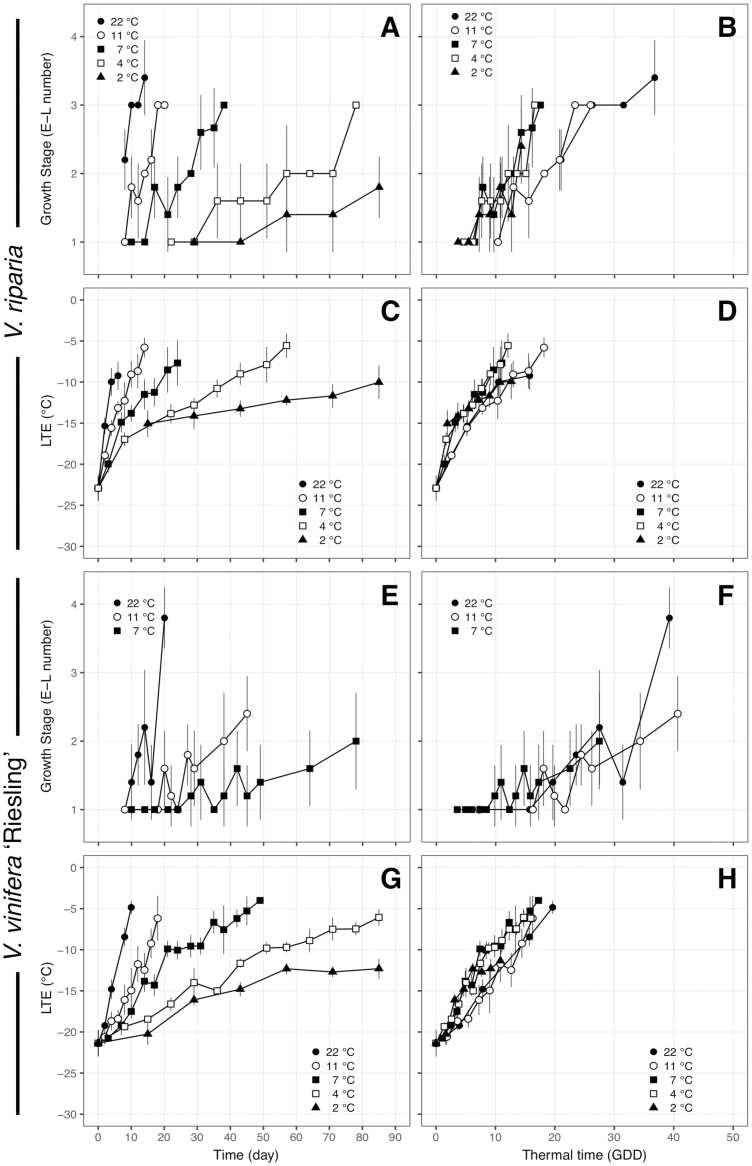
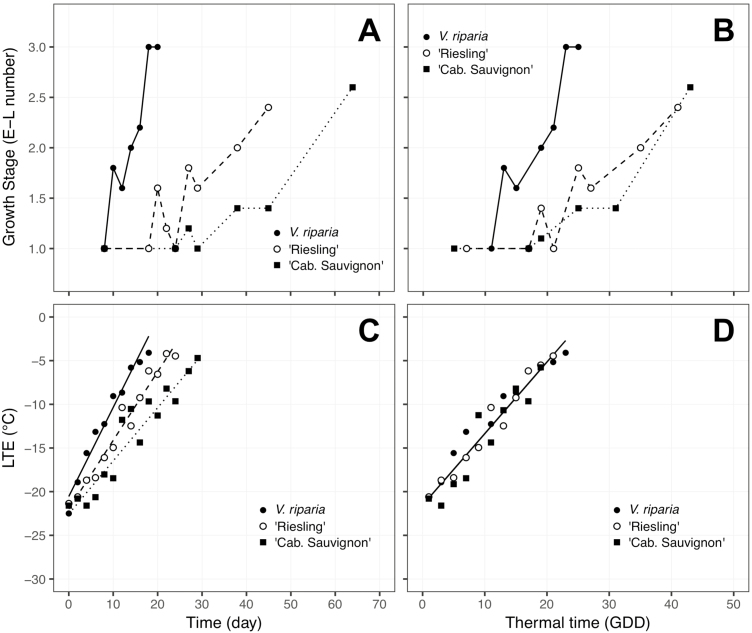
The model which resulted from the forward selection using BIC for budbreak stage was a multiple linear regression using an intercept and GDD × species interaction (Budbreak stage (species) = a +b × GDD), with P < 0.001 and adjusted-R2 = 0.66, effectively demonstrating that early bud phenology follows the same temperature response as deacclimation, but there are still differences at a species level. The effect of kdeacc, i.e. the effect of temperature, on budbreak can be seen in Fig. 4. When budbreak phenology stage (Fig. 4A and E) or deacclimation (Fig. 4C and G) is plotted for V. riparia and V. vinifera ‘Riesling’ with respect to time, a clear separation was observed between temperatures. When this time is normalized by computing a relative thermal time (GDDs) accounting for differences in kdeacc between genotypes, budbreak and deacclimation for all temperatures are ‘stacked’ (Fig. 4B, D, F and H). Within the same temperature, budbreak occurs at different times for different genotypes (Fig. 5A), but is grouped within species when using GDDs (Fig. 5B).

Figure 4.

Figure 4.

Open in a new tab

Deacclimation and bud phenology of Vitis riparia and V. vinifera ‘Riesling’ in relation to time (A, C, E, G) and thermal time in GDD (B, D, F, H). Bud phenology as the ‘E-L number’ (Coombe and Iland 2005) is shown for five temperatures in V. riparia and three temperatures in ‘Riesling’, as no bud development was recorded within 90 days at 2 and 4 °C for ‘Riesling’. Growing degree-days were calculated based on kdeacc for each genotype [seeSupporting Information—Table S2] at any given temperature multiplied by time in days. Bars indicate standard deviation.

Figure 5.

Figure 5.

Open in a new tab

Deacclimation and bud phenology of Vitis riparia (closed circle—full line), V. vinifera ‘Riesling’ (open circle—dashed line) and V. vinifera ‘Cabernet Sauvignon’ (closed square—dotted line) at 11 °C in relation to time (A, C) and thermal time in GDD (B, D).

Discussion

Chilling accumulation, dormancy state, cold hardiness and budbreak are complex traits driven by the interaction of physiology and climate. Due to this interaction, a comprehensive understanding of the role of temperature in these processes is needed to correctly assess the responses of plants to a future climate, specifically concerning winter and early spring phenology. This study was conducted to gain a better understanding of how deacclimation processes (loss of cold hardiness) and resulting budbreak are impacted by the interaction between dormancy and temperature as well as test a method for predicting dormancy transition and chilling requirement in grapevine.

Midwinter warming events are of major concern for temperate crop species as well as native and naturalized forests. In trees within their natural ranges, little to no damage occurs during the autumn because their adaptive freeze resistance readily withstands the minimum temperatures they usually encounter (Vitasse et al. 2014). However, damage can be substantial following atypical warm events in late winter and false springs when plants have transitioned endodormancy and the potential for deacclimation increases exponentially (Vitasse et al. 2014). For example, a late spring freeze in 2007 in North America caused widespread damage in midwestern forests and across agricultural croplands, delaying and reducing canopy establishment by 16–34 days (Gu et al. 2008). Bokhorst et al. (2009) reported significant damage in sub-Artic dwarf shrub vegetation when midwinter temperatures rose above freezing for 2 weeks (maximum ~7 °C) followed by the return of freezing temperatures. An important question remains; what are the threshold temperatures for these increased risks? The effect of low, above freezing temperatures may be overlooked for their potential to affect deacclimation and contribute to early spring frost damage.

The response of plant phenology to temperature is typically modelled as a linear relationship. For example, Ferguson et al. (2011, 2014) used a linear response of the rates of deacclimation in relation to temperature for 21 V. vinifera and two V. labruscana cultivars. Different rates and base temperatures were used for endo- and ecodormant buds to predict changes in cold hardiness and budbreak. In their assessment, all of the V. vinifera cultivars present in our study had a base temperature ≥4 °C during ecodormancy. However, we observed deacclimation at and below this threshold (2 °C), which is reflected in the better fit of the exponential relationship suggested in this study [seeSupporting Information—Table S2]. Deacclimation rates at low temperatures were also much higher for the wild grapevine species V. amurensis and V. riparia (Fig. 3B), two species frequently used in grapevine breeding programmes with the goal of increasing the cold hardiness of hybrid cultivars. Our results demonstrate that the threshold temperature for deacclimation risk begins as low as 2 °C in grapevines, and depending on genotype and chill accumulation may be quite high. This suggests that breeders could be inadvertently choosing germplasm that also contributes to increased risk during midwinter warm events and late spring frost damage in new varieties.

Variation at the cultivar or accession level has been observed within species for cold hardiness (Arora et al. 2004; Ferguson et al. 2011, 2014; Salazar-Gutiérrez et al. 2014,2016; Szalay et al. 2017), although deacclimation rates may or may not differ (Arora et al. 2004; Ferguson et al. 2011, 2014; Szalay et al. 2017). It has been suggested that there is no correlation among species between the maximum cold hardiness or climate of origin and the rate of deacclimation (Arora et al. 2004; Kalberer et al. 2006). Vitasse et al. (2014), however, suggest that the rate of deacclimation is more related to temperature fluctuations in the area where species evolved, diminishing the potential for deacclimation in locations where frequent temperature fluctuations occur in the winter. In our case, V. riparia and V. amurensis, two species from colder climates as compared with V. vinifera, had higher kdeacc at all (V. amurensis) or at moderate to high temperatures (V. riparia) (Fig. 4B). Vitis aestivalis, however, did not appear to differ from the V. vinifera cultivars, in agreement with the assessment by Kalberer et al. (2006). Kalberer et al. (2006) also suggested that field and controlled studies can result in different responses to temperature. In our study, however, we observed higher rates of deacclimation in V. amurensis and V. riparia compared with V. aestivalis, which is comparable and follows the same behaviour as the ‘responsiveness’ described by Londo and Kovaleski (2017) using field observations.

Several other studies have examined aspects of deacclimation in grapevine during the winter. For example, Cragin et al. (2017) examined short-term deacclimation (4 days) during ecodormancy in V. vinifera ‘Chardonnay’ and ‘Cabernet Sauvignon’ and suggested that the initial cold hardiness level impacts deacclimation rate. Our results do not support this finding as the deacclimation rates for all genotypes at 860 and 1580 chilling hours were very different while their initial LTE were not (illustrated for ‘Riesling’ in Fig. 1). Chilling accumulation was not reported by Cragin et al. (2017), but the deacclimation rates reported for ‘Cabernet Sauvignon’ ranged from 0.6 to 1.9 °C day−1 depending on year and sample point and are in general agreement with our results for this cultivar. A study by Rubio et al. (2016) examined the effect of temperature on the gain and loss of cold hardiness in V. vinifera ‘Thompson Seedless’. They report deacclimation of cuttings with low chill accumulation after 3 weeks of exposure to 14 °C, but an assessment of the patterns we observe in this study is not possible due to a single field collection time point and single temperature exposure. Other work on deacclimation in azalea (Rhododendron spp.; Kalberer et al. 2007) and Vaccinium spp. (Arora et al. 2004) reported species level differences in deacclimation but not at multiple sampling points or at different chill accumulations, precluding the ability to make many direct comparisons to the current study. The results reported here do indicate that there are species, and in fact, genotype level differences in deacclimation rate and response to chilling as described by deacclimation potential. Our results suggest there may be more variation for deacclimation behaviour in other perennial woody species that could be assessed. Due to the high number of sampling points and genotypes, the results presented in this study represent the most comprehensive measurement of deacclimation as it is affected by chilling in a perennial species. These results unravel one layer of the complexity of dormancy, chilling and deacclimation and should now enable the development of precise prediction models for midwinter cold hardiness, spring frost and freeze risk, and phenotypes for selection of germplasm.

Our results demonstrate that the nature of the endo- to ecodormancy transition can be assessed by a quantitative increase in rates of deacclimation as evaluated by deacclimation potential, Ψdeacc (Fig. 2). Describing chilling hour requirement and approximating the endo- to ecodormancy transition using forcing assays is a standard experiment conducted in a number of species (Weinbaum et al. 1989; Lloyd and Firth 1990; Cook and Jacobs 2000; Fan et al. 2010; Zhang and Taylor 2011), including wild and cultivated grapevines (Londo and Johnson 2014). Those important studies have been the foundation of germplasm selection for years and continue to be an early indication of suitability within different climates. However, our method represents a major step forward in determining the dormancy transition without relying on the arbitrary assumptions currently used in forcing assays to determine ‘chilling fulfilment’; such as having 50 % budbreak occur within 28 days (Londo and Johnson 2014). Budbreak becomes apparent only after the freeze mechanisms associated with cold hardiness are lost (Figs 4 and 5; Ferguson et al. 2014; Salazar-Gutiérrez et al. 2014), although earlier stages of growth within the dormant bud (e.g. increase in turgor) are likely associated with the loss of hardiness. Thus, the amount of time needed to reach 50 % budbreak in forcing assays is a combination of (i) the time needed to fully deacclimate, and (ii) time required for deacclimated buds to reach a visible change in phenological stage. This two-part chronology of budbreak likely occurs in all perennial species. Our study leverages the ability to assess loss of hardiness through decreasing supercooling ability of grapevine buds as a way to quantitatively assess rates of deacclimation and their changes due to chilling.

Studies in other plant species indicate evidence for a role of deacclimation potential in determining budbreak phenology. In their review, Cannell and Smith (1983) show results from different forest species in which the time to budbreak is reduced in an exponential manner. This is similar to our assessment of Ψdeacc, where the upper portion of the logistic is like the exponential decrease in time to budbreak. The logistic behaviour of Ψdeacc in relation to chill accumulation explains the continuous increase risk of damage of midwinter warm spells followed by the return of low temperatures the later they occur until 100 % Ψdeacc is achieved (Fig. 2). It is likely that, similar to the behaviour described in our study, forest species also have increased deacclimation rates with higher chill accumulation, seen as a decrease in the time to budbreak. Additionally, it is important to note that while canopies may be able to recover from midwinter bud kill events, damage to the reproductive buds in the case of fruit and nut crops will reduce yields in the season following damage.

Bud phenology timing appears to follow the same temperature response as deacclimation within grapevines (Figs 4 and 5). Therefore, it is possible that loss of cold hardiness may represent early stages of growth within the bud, such as increase in turgor of cells, and that the differences in bud development in regard to GDDs (Fig. 5B) between species are due to different bud morphology. To date there have been no studies comparing early morphological development in buds of different Vitis species. Andreini et al. (2009) showed a difference in thermal time requirements between different V. vinifera genotypes grouped in late, intermediate and early budbreak categories, and Londo and Johnson (2014) observed differences in time to budbreak for ‘Riesling’ and ‘Cabernet Sauvignon’ when evaluated at the same chill accumulations. In this study, ‘Riesling’ also had earlier budbreak compared with ‘Cabernet Sauvignon’ (Fig. 5A), and it is clear that GDDs calculated using a single base temperature would result in different thermal time requirements to reach budbreak. Our results demonstrate that the shape of the relationship between chilling accumulation and deacclimation rate was similar for all genotypes, but also revealed a difference in thermal efficiency (Fig. 3B). Simply put, when exposed to a given temperature, genotypes have a different capability to use that temperature for deacclimation (e.g. V. riparia > V. vinifera ‘Riesling’ > V. vinifera ‘Cabernet Sauvignon’) (Fig. 3A). Adjusting for the difference in thermal efficiency (e.g. kdeaccRiesling> kdeaccCab.Sauvignon at any given temperature; Fig. 3A), both V. vinifera genotypes have the same GDD requirements for budbreak (Fig. 5B). Therefore, forcing assays using budbreak phenology as the method of determining chilling fulfilment would falsely infer that inherently slow deacclimators (low thermal efficiency), such as ‘Cabernet Sauvignon’, require higher chill accumulation to transition from endo- to ecodormancy. Our results suggest that the chilling requirement may be much more similar between genotypes than previously implied, but thermal efficiency determines the variation observed in budbreak data. Thus, evaluations that reveal a ‘high-chill requirement’ phenotype based on budbreak data may be a combination of both higher chill requirement and a generally lower temperature efficiency (low kdeacc and low growth rates inherent to the genotype). Despite adjusting GDDs for thermal efficiency at a genotype level, phenological development in V. riparia remained faster relative to V. vinifera in this study (Fig. 5). This indicates that some species level differences in growth and development remain unresolved between species in grapevine.

Conclusions

Mechanistic descriptions of cold hardiness and dormancy are required for our understanding of how climate change may affect phenology in the future. Previous studies have shown that budbreak occurs after loss of cold hardiness, and it is general knowledge that buds that have broken have little to no cold hardiness. What we show in this study is that the kinetics of the two processes are the same. Our results demonstrate that phenological variation between genotypes may not be determined only by chilling requirement. Instead, this temporal variation appears to be driven by differences in deacclimation rate between genotypes at all levels of chilling fulfilment. We demonstrate here the basis for the historical observation of ‘less GDD requirement for higher chill accumulation’: the response to the same temperature changes as chill accumulates, demonstrated by the deacclimation potential (Ψdeacc). Our data also demonstrate that assessments of deacclimation rates using the binary categorization of ‘endo-’ and ‘ecodormant’ material is an oversimplification, as there is a continuum of response in deacclimation rates as chill is accumulated. Finally, we demonstrate an objective, quantitative method for determining the chilling requirement and dormancy transition in grapevine and perhaps other perennial species that utilize supercooling for cold hardiness [e.g. peach, cherry (Prunus spp.), azalea, larch (Larix kaempferi)]. This method provides a measure of thermal efficiency that appears to be species- and genotype-specific and may prove useful for modelling how perennial species will be impacted by future shifts of winter and spring temperatures.

Sources of Funding

This work was partially supported by the National Institute of Food and Agriculture, U.S. Department of Agriculture, through the Northeast Sustainable Agriculture Research and Education programme under subaward number GNE16-130; by U.S. Department of Agriculture appropriated funds for project number 1910-21220-006-00D; and by CAPES, Coordenação de Aperfeiçoamento de Pessoal de Nível Superior, Brazil.

Contributions by the Authors

A.P.K., B.I.R. and J.P.L. designed this research. A.P.K. performed the experiments and analysed the data. A.P.K. and J.P.L. wrote the manuscript. B.I.R. reviewed drafts of the manuscript.

Conflict of Interest

None declared.

Supporting Information

The following additional information is available in the online version of this article—

Table S1. Information associated with each deacclimation experiment for each genotype used. Linear models were fit per genotype using chill accumulation and temperature as factors.

Table S2. Parameter estimates and model fits for deacclimation potential, low and high temperature deacclimation rates, and linear relationship between low temperature exotherm (LTE) and the deacclimation rate × deacclimation potential for seven Vitis genotypes.

Table S3. Comparison of model fits using linear and non-linear approaches for low and high temperature deacclimation rates for seven Vitis genotypes.

Figure S1. Effect of temperature on deacclimation rates of Vitis vinifera ‘Riesling’. (A) Scaled deacclimation rates (based on deacclimation potential) at three different chill accumulations in response to temperature; (B) Arrhenius plot of scaled deacclimation rates. Tick marks in both panels are equivalent and mirrored (e.g. 0 °C = 3.66 × 1000 K−1).

Supplementary Information
Click here for additional data file. (246KB, docx)

Data

The complete data sets and codes used for analysis are available at http://dx.doi.org/10.17632/nnk3strzcg.1.

Acknowledgements

The authors would like to acknowledge and thank the following people for contributing to the field collection and processing of dormant bud tissues used in this study: K. Deys, B. Srmack, J. Keeton, B. Martens and M. Baseggio. The authors also thank Dr T. Martinson, Cornell University, for use of freezer facilities, and Anthony Road Wine Co. and Ravines Wine Cellars for access to V. vinifera samples.

Literature Cited

  1. Andreini L, Viti R, Scalabrelli G.. 2009. Study on the morphological evolution of budbreak in Vitis vinifera L. Vitis 4:153–158. [Google Scholar]
  2. Andrews PK, Sandidge CR III, Toyama TK.. 1984. Deep supercooling of dormant and deacclimating Vitis buds. American Journal of Enology and Viticulture 35:175–177. [Google Scholar]
  3. Antivilo FG, Paz RC, Keller M, Borgo R, Tognetti J, Juñent FR.. 2017. Macro- and microclimate conditions may alter grapevine deacclimation: variation in thermal amplitude in two contrasting wine regions from North and South America. International Journal of Biometeorology 61:2033–2045. [DOI] [PubMed] [Google Scholar]
  4. Arora R, Rowland LJ, Ogden EL, Dhanaraj AL, Marian CO, Ehlenfeldt MK, Vinyard B.. 2004. Dehardening kinetics, bud development, and dehydrin metabolism in blueberry cultivars during deacclimation at constant, warm temperatures. Journal of the American Society for Horticultural Sciences 129:667–674. [Google Scholar]
  5. Bigg EK. 1953. The supercooling of water. Proceedings of the Physical Society Section B 66:688–694. [Google Scholar]
  6. Bokhorst SF, Bjerke JW, Tømmervik H, Callaghan TV, Phoenix GK.. 2009. Winter warming events damage sub-Arctic vegetation: consistent evidence from an experimental manipulation and a natural event. Journal of Ecology 97:1408–1415. [Google Scholar]
  7. Burke MJ, Gusta LV, Quamme HA, Weiser CJ, Li PH.. 1976. Freezing and injury in plants. Annual Review of Plant Physiology 27:507–528. [Google Scholar]
  8. Campoy JA, Ruiz D, Egea J.. 2011. Dormancy in temperate fruit trees in a global warming context: a review. Scientia Horticulturae 130:357–372. [Google Scholar]
  9. Cannell MGR, Smith RI.. 1983. Thermal time, chill days and prediction of budburst in Picea sitchensis. Journal of Applied Ecology 20:951–963. [Google Scholar]
  10. Chmielewski FM, Götz KP, Weber KC, Moryson S.. 2018. Climate change and spring frost damages for sweet cherries in Germany. International Journal of Biometeorology 62:217–228. [DOI] [PubMed] [Google Scholar]
  11. Cleland EE, Chuine I, Menzel A, Mooney HA, Schwartz MD.. 2007. Shifting plant phenology in response to global change. Trends in Ecology & Evolution 22:357–365. [DOI] [PubMed] [Google Scholar]
  12. Cook C, Jacobs G.. 2000. Progression of apple (Malus × domestica Borkh.) bud dormancy in two mild winter climates. The Journal of Horticultural Science and Biotechnology 75:233–236. [Google Scholar]
  13. Coombe BG, Iland P.. 2005. Grapevine phenology. In: Dry PR, Coombe BG, eds. Viticulture, vol 1: resources. Ashford, Australia: Winetitles, 210–248. [Google Scholar]
  14. Cragin J, Serpe M, Keller M, Shellie K.. 2017. Dormancy and cold hardiness transitions in winegrape cultivars Chardonnay and Cabernet Sauvignon. American Journal of Enology and Viticulture 68:195–202. [Google Scholar]
  15. Fan S, Bielenberg DG, Zhebentyayeva TN, Reighard GL, Okie WR, Holland D, Abbott AG.. 2010. Mapping quantitative trait loci associated with chilling requirement, heat requirement and bloom date in peach (Prunus persica). The New Phytologist 185:917–930. [DOI] [PubMed] [Google Scholar]
  16. Ferguson JC, Moyer MM, Mills LJ, Hoogenboom G, Keller M.. 2014. Modeling dormant bud cold hardiness and budbreak in twenty-three Vitis genotypes reveals variation by region of origin. American Journal of Enology and Viticulture 65:59–71. [Google Scholar]
  17. Ferguson JC, Tarara JM, Mills LJ, Grove GG, Keller M.. 2011. Dynamic thermal time model of cold hardiness for dormant grapevine buds. Annals of Botany 107:389–396. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gray LK, Hamann A.. 2013. Tracking suitable habitat for tree populations under climate change in western North America. Climatic Change 117:289–303. [Google Scholar]
  19. Gu L, Hanson PJ, Post WM, Kaiser DP, Yang B, Nemani R, Pallardy SG, Meyers T. 2008. The 2007 Eastern US spring freeze: increased cold damage in a warming world?BioScience 58: 253–262. [Google Scholar]
  20. Horvath DP, Anderson JV, Chao WS, Foley ME.. 2003. Knowing when to grow: signals regulating bud dormancy. Trends in Plant Science 8:534–540. [DOI] [PubMed] [Google Scholar]
  21. Kalberer SR, Leyva-Estrada N, Krebs SL, Arora R.. 2007. Frost dehardening and rehardening of floral buds of deciduous azaleas are influenced by genotypic biogeography. Environmental and Experimental Botany 59:264–275. [Google Scholar]
  22. Kalberer SR, Wisniewski M, Arora R.. 2006. Deacclimation and reacclimation of cold-hardy plants: current understanding and emerging concepts. Plant Science 171:3–16. [Google Scholar]
  23. Kolstad EW, Breiteig T, Scaife AA.. 2010. The association between stratospheric weak polar vortex events and cold air outbreaks in the Northern Hemisphere. Quarterly Journal of the Royal Meteorological Society 136:886–893. [Google Scholar]
  24. Lang GA, Early JD, Martin GC, Darnell RL.. 1987. Endo-, para-, and ecodormancy: physiological terminology and classification for dormancy research. HortScience 22:371–377. [Google Scholar]
  25. Lloyd J, Firth D.. 1990. Effect of defoliation time on depth of dormancy and bloom time for low-chill peaches. HortScience 25:1575–1578. [Google Scholar]
  26. Londo JP, Johnson LM.. 2014. Variation in the chilling requirement and budburst rate of wild Vitis species. Environmental and Experimental Botany 106:138–147. [Google Scholar]
  27. Londo JP, Kovaleski AP.. 2017. Characterization of wild North American grapevine cold hardiness using differential thermal analysis. American Journal of Enology and Viticulture 68:203–212. [Google Scholar]
  28. Luedeling E, Girvetz EH, Semenov MA, Brown PH.. 2011. Climate change affects winter chill for temperate fruit and nut trees. PLoS One. doi: 10.1371/journal.pone.0020155. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Mills LJ, Ferguson JC, Keller M.. 2006. Cold-hardiness evaluation of grapevine buds and cane tissues. American Journal of Enology and Viticulture 57:194–200. [Google Scholar]
  30. Penfield S. 2008. Temperature perception and signal transduction in plants. The New Phytologist 179:615–628. [DOI] [PubMed] [Google Scholar]
  31. R Development Core Team 2008. R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; http://www.R-project.org. (27 August 2018). [Google Scholar]
  32. Rubio S, Dantas D, Bressan-Smith R, Pérez FJ.. 2016. Relationship between endodormancy and cold hardiness in grapevine buds. Journal of Plant Growth Regulation 35:266–275. [Google Scholar]
  33. Salazar-Gutiérrez MR, Chaves B, Anothai J, Whiting M, Hoogenboom G.. 2014. Variation in cold hardiness of sweet cherry flower buds through different phenological stages. Scientia Horticulturae 172:161–167. [Google Scholar]
  34. Salazar-Gutiérrez MR, Chaves B, Hoogenboom G.. 2016. Freezing tolerance of apple flower buds. Scientia Horticulturae 198:344–351. [Google Scholar]
  35. Shaltout AD, Unrath CR.. 1983. Rest completion prediction model for ‘Starkrimson Delicious’ apples. Journal of the American Society for Horticultural Sciences 108:957–961. [Google Scholar]
  36. Szalay L, Molnár A, Kovács S.. 2017. Frost hardiness of flower buds of three plum (Prunus domestica L.) cultivars. Scientia Horticulturae 214:228–232. [Google Scholar]
  37. Vitasse Y, Lenz A, Körner C.. 2014. The interaction between freezing tolerance and phenology in temperate deciduous trees. Frontiers in Plant Science. doi: 10.3389/fpls.2014.00541. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Walsh J, Wuebbles D, Hayhoe K, Kossin J, Kunken K, Stephens G, Thorne P, Vose R, Wehner M, Willis J, Anderson D, Doney S, Feely R, Hennon P, Kharin V, Knutson T, Landerer F, Lenton T, Kennedy J, Somerville R. 2014. Chapter 2: our changing climate. In: Melillo JM, Richmond T, Yohe GW, eds. Climate change impacts in the United States: the Third National Climate Assessment. Washington, DC: U.S. Global Change Research Program, 19–67. doi: 10.7930/J0KW5CXT. [DOI] [Google Scholar]
  39. Weinbaum SA, Polito VS, Muraoka TT.. 1989. Assessment of rest completion and its relationship to appearance of tetrads in anthers of ‘Nonpareil’ almond. Scientia Horticulturae 38:69–76. [Google Scholar]
  40. Wolf TK, Cook MK.. 1994. Cold hardiness of dormant buds of grape cultivars: comparison of thermal analysis and field survival. HortScience 29:1453–1455. [Google Scholar]
  41. Zhang J, Taylor C.. 2011. The dynamic model provides the best description of the chill process on ‘Sirora’ pistachio trees in Australia. HortScience 46:420–425. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (246KB, docx)

Articles from AoB Plants are provided here courtesy of Oxford University Press

RESOURCES