Tuning nuclear depolarization under MAS by electron T_1e

Abstract

The Cross-Effect (CE) Dynamic Nuclear Polarization (DNP) mechanism under Magic Angle Spinning (MAS) induces depletion or “depolarization” of the NMR signal, in the absence of microwave irradiation. In this study, the role of T_1e on nuclear depolarization under MAS was tested experimentally by systematically varying the local and global electron spin concentration using mono-, bi- and tri-radicals. These spin systems show different depolarization effects that systematically tracked with their different T_1e rates, consistent with theoretical predictions. In order to test whether the effect of T_1e is directly or indirectly convoluted with other spin parameters, the tri-radical system was doped with different concentrations of GdCl₃, only tuning the T_1e rates, while keeping other parameters unchanged. Gratifyingly, the changes in the depolarization factor tracked the changes in the T_1e rates. The experimental results are corroborated by quantum mechanics based numerical simulations which recapitulated the critical role of T_1e. Simulations showed that the relative orientation of the two g-tensors and e-e dipolar interaction tensors of the CE fulfilling spin pair also plays a major role in determining the extent of depolarization, besides the enhancement. This is expected as orientations influence the efficiency of the various level anti-crossings or the “rotor events” under MAS. However, experimental evaluation of the empirical spectral diffusion parameter at static condition showed that the local vs. global e-e dipolar interaction network is not a significant variable in the commonly used nitroxide radical system studied here, leaving T_1e rates as the major modulator of depolarization.

Graphical Abstract

T_1e modulates nuclear depolarizarion in Cross-Effect Dynamic Nuclear Polarizarion under Magic-Angle Spinning

1. Introduction

Dynamic Nuclear Polarization (DNP) combined with Magic Angle Spinning (MAS) Nuclear Magnetic Resonance (NMR) has been shown to be a powerful tool for elucidating molecular structure information of a variety of biological compounds^1–3 and material surfaces.^4–7 The signal enhancement from MAS-DNP has led to drastic time savings, easily reducing experimental time from days to hours and enabling NMR experiments that were not feasible before, such as heteronuclear correlation measurements with low natural abundance nuclei.^8,9 DNP is a method of transferring the magnetization or polarization from unpaired electron spins from a polarizing agent, typically a free radical, to nuclear spins that are dipolar coupled to the unpaired electron spins of the radical. Because of the potential of DNP to fundamentally transform the capabilities of solid-state MAS NMR, much work has gone into rationally designing radical-based DNP agents to obtain maximum signal enhancements or other favorable properties at high magnetic fields and faster spinning frequency.^10–17

The key performance metrics for DNP include a high NMR signal enhancement factor, a short DNP build-up time constant, and a minimal reduction of the thermally polarized NMR signal by the paramagnetic bleaching effect, and the more recently discovered depolarization mechanism operational under MAS. Depolarization under MAS occurs independent of microwave (μw) irradiation, as will be discussed in the theory section. The focus of this study is to understand the role of electron spin dynamics in tuning depolarization, which is quantified as the ratio of NMR signal under spinning and static condition, in the absence of μw irradiation, i.e., є_depo=〈S_spin〉/〈S_static〉. Much of the current development has focused on synthesizing and testing tethered nitroxide bi-radicals such as TOTAPOL,¹⁰ AMUPOL¹⁸ and TEKPOL,¹⁵ while there are also studies of tri-radicals such as DOTOPA¹⁹ and mixed multi-radicals.^20,21 However, the design principle for multi-radicals that yield the strongest DNP performance, in particular under MAS conditions, is still debated and relies on empirical testing, as the performance-driving factors are not entirely understood. The complexity comes from the strong dependence of the DNP performance on many interconnected internal parameters, such as temperature, relaxation rates, radical concentration, glass forming quality of the solvent, and external parameters such as the main magnetic field, the MAS frequency and the μw field strength. Apart from this, the relative orientation of the g-tensors, and the electron-electron (e-e) coupling tensors are also dominant factors modulating the DNP performance. Despite the recognition that there are a multitude of interrelated factors, a general presumption is that designing DNP polarizing agents with long electron spin lattice relaxation times, T_1e, is a desirable design principle for achieving high DNP performance through better electron spin saturation.¹⁵ However, long T_1e also enhances the depolarization mechanism, adversely affecting the DNP performance. The question we ask is whether the effect of T_1e a dominant factor in tuning the depolarization effect among different DNP polarizing agents under available experimental conditions for DNP. We address this question with experimental and theoretical data.

On the experimental side, we performed MAS DNP experiments at ~7 Tesla and 25 K to measure the DNP enhancement and depolarization factors, as well as the electron T_1e relaxation rate. We compared these properties between a mono-, di- and tri-nitroxide radical, while also deliberately shortening the T_1e through the addition of a paramagnetic relaxation agent, GdCl₃, without affecting other relevant factors of the spin system (e-e and e-n interaction tensors) for DNP. We also measured the electron spin saturation and spectral diffusion parameters (under static conditions) of various mono-, bi-, and tri- nitroxide radicals to evaluate the strength and property of the e-e dipolar interaction network. Finally, we correlated experimental T_1e data with the extent of nuclear spin depolarization under MAS.

The experimental observations are corroborated with quantum mechanical numerical simulations of a coupled e-e-¹H three spin system using the SpinEvolution package²² that recently introduced the pseudo secular e-n hyperfine interactions to enable DNP simulations under MAS. Through simulations, we estimated the influence of T_1e on nuclear depolarization. There is a significant body of theoretical work on calculating DNP enhancements and depolarization effects under MAS that inspired this study.^23–27 However, this is the first report to calculate MAS DNP parameters using SpinEvolution which is an exceptionally effective program, yielding the calculation of 3-spins with 100 orientations within two minutes. Comparison and validation on select calculations using SpinEvolution are provided in the supplementary information (SI). Also, the calculation is based on fully quantum mechanical descriptions, without the Landau-Zener (LZ) assumption for the e-e-¹H transitions.

2. Cross effect theory under MAS

Presumably, the most effective DNP mechanism under MAS is the cross effect (CE).²⁸ This will be the mechanism of concern in this paper for delineating the effect of electron spin dynamics on nuclear depolarization under MAS-DNP conditions. To do so, we first briefly discuss the basic theory behind CE. Pedagogically, the CE mechanism can be defined as the following: two dipolar or exchange coupled electron spins with a frequency difference that is approximately equal to a hyperfine coupled nuclear Larmor frequency undergo an energy conserving flip-flop process that can cause the simultaneous flips of the two electron spins and the nuclear spin, i.e. when ω_e1-ω_e2=ω_n, where ω_e1, ω_e2 and ω_n are the Larmor frequencies of the two electrons and the nucleus, respectively. Such flip-flop in the spin states leads to transfer of polarization amongst the spins. The amount of polarization transfer to the nuclear spin from the electron spin is proportional to the difference in the two electron spin polarizations relative to the nuclear spin polarization. Therefore, driving the spin system towards a larger electron spin polarization difference is essential for achieving significant DNP transfer. Ideally, selective μw irradiation on one of the two coupled electron spins should be used to create a large polarization difference between the two electron spins that fulfill the CE condition. Practically, this is achieved through the saturation of a portion of the EPR spectrum of the nitroxide radical- the polarization difference between electrons is subsequently transferred to the coupled nuclear spins.

All of the above holds true for static samples, but the CE under MAS becomes considerably more complex. Nuances about the CE mechanism under MAS have been contributed by the groups of Tycko and Vega.^23-25 In static samples, the energies of the spins are fixed in time, and therefore the same pairs of electron spins always fulfil the CE condition, while under MAS the matching conditions change in time. This is because the large g-anisotropy of the nitroxide radical causes the resonance frequency of the electron spin to oscillate over the course of the MAS rotor period, causing multiple different energy level-crossings and anti-crossings of dipolar coupled electron spins throughout the rotor period, as first detailed by Thurber et. al.²⁵ Some of these resonances fulfill the CE conditions with respect to the nuclei, leading to polarization exchange between the electron spins and the nuclei. These energy oscillations owing to MAS increase the combinations of spin pairs fulfilling the CE conditions. Important to note - while the number of crossings per unit time is directly proportional to the spin rate and depends on the orientations of the spin interaction tensors, the effectiveness of the anti- or avoided-crossing depends on the magnitude of the e-e and the e-n couplings (i.e. the strength of the perturbations, or the off-diagonal terms) and crossing rate (i.e. the rate of change in energy or the rate of change of the diagonal terms), as illustrated in the LZ expression,^25,29 which gives the probability of an adiabatic transition for two state systems. As shown in the equation below, the adiabatic transition probability is inversely proportional to the rate of change of energies of a two-state system (A), and directly proportional to the strength of perturbation (E) that mixes the two states.

$$\text{Probability}(\text{adiabatic or anti-crossing})=1-\text{exp}(-\pi {\mathrm{E}}^2∕\mathrm{A}).$$ (1)

Thurber and Tycko²⁶ were the first to uncover that the same rotor-synchronous level-crossings under MAS that lead to the enhancement, can also lead to a reduction in nuclear polarization. Without μw irradiation, e-e coupling at resonance conditions (ω_e1= ω_e2) causes an exchange or equalization of the polarization across the EPR line. The operational CE Hamiltonian, however, can lead to the transfer of magnetization from the nucleus to the electron spins, and therefore leading to a reduction in the nuclear spin signal.

Traditionally, DNP signal enhancements were calculated by the NMR signal area with μw irradiation divided by the NMR signal without μw irradiation, i.e. є_on/off= 〈S_{mw_on}〉/〈S_{mw_off}〉. However, as the nuclear depolarization effect (є_depo) artificially lowers the unenhanced (μw off) Boltzmann NMR signal, i.e. the denominator in calculating the enhancement factor, this effect can lead to an inflation in the DNP enhancement factor that does not represent the absolute NMR signal gain by DNP, as discussed in several recent studies.^26,27,30 The intensity of the NMR signal with μw irradiation turned off is further attenuated by paramagnetic effects (PE), but typically to a lesser extent than by depolarization by CE under MAS, especially at ultra low temperature.

There are multiple controllable factors affecting the extent of depolarization, such as the MAS frequency, the external magnetic field strength, the spin relaxation rates- electron T_1e and nuclear T_1n, and the radical concentration, apart from other intrinsic spin parameters of the radical. The dependence of spinning frequency on depolarization has been reported on in the literature.^26-27 Typically, faster spinning leads to greater depolarization up to a threshold spin rate when depolarization reaches a plateau value, typically between 2-5 kHz with commonly used nitroxide biradical.

The makeup of the electron spin network is another critical factor in modulating depolarization. The e-e coupling facilitates spin diffusion towards equalization of the polarization. Full quantum mechanical description of electron spectral diffusion is beyond the scope of present theoretical framework. However, using the LZ model the effect of inter- and intra-molecular electron coupling has been studied in biradicals, showing that intermolecular e-e couplings can further diminish the nuclear Boltzmann polarization compared to the case when inter-e-e couplings are ignored.^26,27,31

Last, but not least, relaxation rates are critical modulators of depolarization, especially the T₁ relaxation rates as they govern the rate with which the system attains its equilibrium state when perturbed by spinning and μw. The nuclear spin relaxation rate constant, T_1n, directly affects the nuclear depolarization. Longer T_1n leads to larger depolarization and also larger enhancement. Here, it is important to point out that the T_1n of nuclei is shortened by faster MAS, presumably due to CE interactions as shown by Thurber et. al.²⁶ and also reported by Mentink-Vigier et. al.²⁷ The effect of the spin-lattice relaxation time of the electron spin, T_1e, on depolarization has also been discussed in the literature - the focus of this study. The polarization distribution across the EPR line, and therefore the polarization difference between the electron spins that fulfil the CE requirement is modified by MAS depending on the magnitude of the spin rate relative to 1/T_1e, as numerically simulated at 9.4 T by Thurber and Tycko.²⁶ As predicted by their theoretical model, for shorter T_1e, the polarization difference depends linearly on the effective EPR resonance frequency following the Boltzmann distribution, but longer T_1e causes significant deviation from the thermal polarization condition. While MAS causes the polarization difference in electrons to generally decrease, spin-lattice relaxation restores their polarization towards the Boltzmann equilibrium if 1/T_1e is high relative to the spin rate. This finding is consequential for the tuning of DNP conditions. Many contemporary bi-radicals are designed to increase the efficacy of the CE mechanism through an increase in T_1e to enhance its saturability by μw irradiation, while simulations have shown that increasing the T_1e can also increase depolarization.^15,18 Thus presumably, there is an intermediate “Goldilock” T_1e value that balances these two competing effects. However, direct measurements of T_1e in conjunction with nuclear depolarization under MAS are not reported in the literature, and as such it is unclear whether T_1e is a dominant modulator of nuclear depolarization, amongst the cornucopia of factors that also modulate nuclear depolarization. Our study is narrowly focused on answering whether long T_1e dominantly modulates nuclear depolarization, and as such overrides other factors that modulate nuclear depolarization. We accompany our experimental observations with a fully quantum mechanical simulation of the MAS DNP effect.

3. Methods

3.1. DNP NMR under MAS at 25 K and 7 T

NMR/DNP measurements were performed with a Revolution NMR LLC MAS probe operational at 25 K, and outfitted with a Thomas Keating Ltd. corrugated waveguide inside a 7 T Bruker wide bore magnet. The design of the low temperature (LT) MAS probe is a replication of the Thurber and Tycko design as published recently and relies on nitrogen and helium gas for spinning and cooling the sample, respectively.^32,33

A Virginia Diode Inc. μw source with a frequency range from 193-201 GHz with nominal output power of 140 mW was employed in a quasi-optical (QO) DNP bridge as shown in Fig. 1. Two parabolic focusing mirrors focus/converge the μw beam into the corrugated waveguide that extends from the top of a MAS probe. Room temperature nitrogen gas is used for the bearing and drive of the probe, and cold helium gas is used to cool the sample space, using a stator similar to that described by Thurber et. al.^32,33 A solution of each radical species was made by dissolving the radicals in 60:30:10 v/v% D₈-glycerol:D₂O:H₂O at a 20 mM global electron spin concentration.

Figure 1.

(a) Quasi-optical Bridge with (1) isolator and two focusing parabolic mirrors, (2) microwave waveguide extending from top of (3) 4 mm Revolution NMR LLC. probe. (b) Bottom of probe head, (4) radio frequency transmission line, (5) Thomas Keating Ltd. Corrugated waveguide with miter bend, (6) stator, and (7) cooling helium gas inlet.

A zirconia rotor with an outer diameter of 4 mm, an inner diameter of 2.36 mm, a length of 46 mm, and a total sample volume of 0.044 ml was employed. The sample was centred in the rotor using two teflon spacers at its either ends. The sample was packed by first loosely packing 60 mg of KBr, then pipetting 20 mg of the radical solution into the rotor and gentle mixing. Here, KBr was added in order to monitor the sample temperature in situ through the measurement of ⁷⁹Br T_1n as shown by Thurber et. al.³⁴ The resulting NMR signal was recorded with a Bruker 300 MHz spectrometer. The packed rotor was placed in the MAS stator and liquid helium was used to cool the sample space until an average LT of 25 K was reached (1 litre/hour), while room temperature nitrogen gas (10 litre/hour) was used for the bearing and drive pressure. For sanity check, the sample temperature was recorded by measuring the T_1n of ⁷⁹Br before and after the enhancement measurement, and confirmed that an average sample temperature at 25 K ± 2 K was maintained.

3.2. Pulsed EPR under static conditions at 25 K and 7 T

All EPR measurements were performed using the Han lab’s home-built dual static DNP/EPR spectrometer operating at 193-201 GHz, as described above and published elsewhere.^35,36 This spectrometer employs the same Virginia Diode Inc. μw source as used in the MAS-DNP measurements. A QO scheme focuses the Gaussian μw beam to a corrugated waveguide positioned in the center of a home built static EPR probe inside a Bruker 7 T wide bore magnet, as described in an earlier publication.³⁵ This EPR spectrometer employs a phase sensitive induction mode detection scheme, where the ~200 GHz EPR signal is mixed down to 3 GHz, then mixed with a 3 GHz reference signal. The DC in-phase and out-of-phase signal components are then processed using the SpecMan4EPR software. Details of the dual EPR/DNP spectrometer quasi-optic, probe, and detection design are detailed by Siaw et. al.³⁵ The electron spin-lattice relaxation time (T_1e) of the nitroxide radical solutions were measured using a saturation recovery solid echo detection pulse sequence. For ELDOR measurement, the pump frequency is stepped across the entire EPR spectrum while the probe frequency is held constant. Two VDI solid-state microwave sources were employed for ELDOR experiments--one for pump (saturation) frequency and the other for probe (detection) frequency.³⁷ Two sources are necessary because the process of changing between two microwave frequencies is longer than the delay used between the excitation and detection pulses for ELDOR measurements. Additionally, the use of two sources allows for background free ELDOR acquisitions due to hysteresis that can occur between the pump and probe frequencies. We note that both T_1e and ELDOR experiments were performed under static conditions, but at otherwise comparable temperature and magnetic field.

3.3. Numerical Simulations

The numerical simulation shown in this manuscript were performed using the SpinEvolution package, which is a widely used software for NMR simulation, especially for solid state powder sample.²² Recently, the package’s capability has been extended to perform DNP simulation through the incorporation of the e-n pseudo secular hyperfine coupling term in the internal Hamiltonian, providing a platform for fast and efficient DNP simulations.^22,38 This program relies on numerically solving the time-dependent von Neumann equation of motion by dividing the calculation of time evolution into multiple time-independent steps of small time intervals. This is the same approach as used in other simulation packages (e.g. SPINACH³⁹ and SIMPSON⁴⁰), as well as the simulation programs used for MAS DNP written by Thurber et. al.²⁵ and Mentink-Vigier et. al.²⁴ However, Thurber and Mentink-Vigier incorporated the spin relaxation effect differently. In the Thurber approach, the propagator is calculated at each time step in the Hilbert space, and then the relaxation effect applied on the evolved density matrix at each step. Mentink-Vigier’s calculation is performed in the Liouville space, while incorporating relaxation effects together with all other spin interactions during time-evolution. The rotor-synchronized time evolution propagator is calculated, which is then used for stroboscopic rotor-synchronized time-evolution. The SpinEvolution package offers the flexibility to use either of the two approaches by selecting the appropriate “-lv” option.²² In this paper, we have used the approach used by Mentink-Vigier as it leads to faster calculation for small spin systems given the rotor-synchronization detection. However, for a larger spin system, calculations in the Liouville space calculation will get exponentially slower due the the large matrix dimensions. In such cases, calculation in the reduced Liouville space³¹ or Hilbert space (Thurber’s approach) would become more economical.

The simulation shown here are performed on a 3-spin system, including 2 electron spins and 1 nuclear spin. The inter-spin dipolar coupling between the electrons, e₁-e₂, electrons and nucleus, e₁-n and e₂-n, are taken to be 19 MHz (~14 Å), 2.5 MHz (~3.2 Å) and 0.08 MHz (~10 Å), respectively. The principal axis components of the g-tensors of the electrons are taken to be: g_x=2.0094, g_y=2.006, g_z=2.0017, inspired by nitroxide radicals. Unless otherwise mentioned, the g-tensor of the second electron spin is related to the first electron spin by a set of Euler angles, (70°,82°,0°) and the relative e₁-e₂ dipolar tensor orientation given by the angles (124°,94°,0°). These are pseudo-random orientations for TOTAPOL molecule. The exact orientations of these tensors are unknow due to flexibility of these molecule. The principal axis orientation of the dominant e₁-n coupling is chosen to be the same as the g-tensor of e₁. The relaxation rates, T_1n and T_2e are set as 4 s and 10 μs, respectively, inspired by experimental data.

4. Results and Discussion

4.1. Experimental: Effect of T_1e on depolarization

All MAS DNP experiments were carried out at 7 Tesla, at LT of 25 K and relying on a QO-DNP setup powered by a solid-state source yielding a peak μw power of 140 mW, as described in the Methods section. The ¹H DNP enhancement є_on/off of each radical solution was determined by calculating the ratio of ¹H NMR signal with and without μw irradiation. Figure 2a shows the є_on/off value as the spinning rate is increased from 0 to 5 kHz. The various mono-, bi-, and tri-radicals follow a similar enhancement factor trend with respect to the MAS frequency: there is an initial increase in enhancement from static to ~1 kHz for each radical, with AMUPOL yielding the largest є_on/off of all radicals at 1 kHz spinning rate with an є_on/off= 38. As the spinning rate is increased further, there is a significant decline in є_on/off values for all radicals measured. At 3 kHz, the є_on/off of AMUPOL falls below the є_on/off of DOTOPA-ethanol, so that at 5 kHz spinning rate DOTOPA-ethanol yielded the largest enhancement (є_on/off = 17), followed by AMUPOL (є_on/off = 11), TOTAPOL and 4AT, both yielding an є_on/off ~ 5. The є_on/off values are greatest with DOTOPA-ethanol under MAS DNP at 25 K and 7 T. Next, we look into the effect of depolarization and paramagnetic bleaching effects that can lower the baseline NMR signal in the absence of μw irradiation and under MAS.

Figure 2.

(a) Enhancement (є_on/off) vs. spin rate at ~7 T, the enhancement was calculated from μw_on / μw_off signal of 4AT (red), TOTAPOL (purple), AMUPOL (pink), and DOTOPA-ethanol (blue). (b) The NMR signal (є_depo) vs. spin rate without microwave irradiations, normalized to the NMR signal at 0 kHz. (c) The absolute ¹H NMR signal enhancement (є_absolute) vs. spin rate for each radical frozen solution after correcting for paramagnetic bleaching and depolarization effect. Temperature was set to 25 K. ¹H signal was directly detected using 10 s build up time.

Figure 2b shows the ¹H NMR signal reduction due to depolarization for each radical-solvent system as the spinning rate is increased. Here, the NMR signal was normalized with respect to the ¹H NMR signal at 0 kHz spinning rate for each radical, individually. Both bi-radicals, TOTAPOL and AMUPOL, and the tri-radical, DOTOPA-ethanol, yielded greater depolarization with increasing spinning rate, whereas 4AT and the sample without the polarizing agent yield fairly constant ¹H NMR signal levels with spinning rate.

This reduction in the ¹H NMR signal below the level from thermal polarization with increasing spinning rate is a characteristic of the depolarization effect. The depolarization constant was quantified as the ratio of NMR signal under 5 kHz spinning and static condition, in the absence of μw irradiation, i.e., є_depo= 〈S_spin〉/〈S_static〉. Notably, AMUPOL leads to maximum nuclear signal depolarization, with є_depo=0.4, leading to an overestimation (or the depolarization-factor, 1/є_depo) by ~2.5 in the DNP enhancement using є_on/off.

In order to calculate the absolute sensitivity gain from DNP (є_absolute) one must take into account the paramagnetic bleaching effect, where proximity to a free electron spin causes the nuclear T₂ to shorten and broaden the NMR signal beyond detectability.^27,30,41 The paramagnetic bleaching factor (є_bleach) is defined as the static (0 kHz) ¹H NMR signal intensity without radical in the solvent divided by the ¹H NMR signal measured under equivalent conditions with the addition of nitroxide radical. The absolute signal enhancement (є_absolute) at 25 K is the є_on/off multiplied by the depolarization, є_depo and divided by the paramagnetic bleaching factor, є_bleach.

$${∊}_{\text{absolute}}={∊}_{\text{on}∕\text{off}}.{∊}_{\text{depo}}∕{∊}_{\text{bleach}}$$ (2)

The calculated є_absolute for each radical is shown in Fig. 2c. Here, we see that DOTOPA-ethanol shows marginally larger enhancement compared to the rest of the radicals measured at 1 kHz. But as the spinning rate is increased to 5 kHz, all radicals yielded a rather comparable absolute enhancement factor. Mentink-Vigier et. al. performed MAS DNP measurements with a commercial Bruker DNP system at 94 K and 9.4 T, and reported the є_absolute of AMUPOL to be 1.5 times that of TOTAPOL, and contrast it to the є_on/off value for AMUPOL that is 3.3 times that of TOTAPOL.²⁷ In our QO DNP system at 25 K at 7 T, we observe that accounting for depolarization and paramagnetic bleaching yields comparable є_absolute for AMUPOL and TOTAPOL, though AMUPOL still slightly outperforms TOTAPOL. We hypothesize that this is due to the power limitation of our 140 mW QO DNP system, where the DNP enhancement has not reached its maximum value to more strongly compensate for the depolarization effect. However, the μw power limitation does not prevent us from fully examining the role of T_1e on depolarization as no μw is needed for this.

Next, we report on T_1e and the depolarization factor measured at comparable temperature and external magnetic field of the DNP measurements. Using a home-built pulsed EPR instrument^35,36 at 7 T we measured the T_1e of various DNP polarizing agents in the samples as prepared for DNP, using an echo detected saturation recovery pulse sequence shown in the inset of Fig. 3(a) and at a μw frequency of 193.887 GHz. The resulting saturation recovery decay curve is fit to a bi-exponential,

$$M_t=\mathit{1}-a.\mathit{exp}[-t∕T_{\mathit{le}}]-b.\mathit{exp}[-t∕T_{\mathit{SD}}]$$ (3)

where T_SD is the time constant describing the faster spectral diffusion, whose effect becomes visible in the saturation recovery curve as the μw pulses only excite a portion of the nitroxide EPR line, so that spectral diffusion from spins at different EPR frequencies contribute to the signal recovery.³³ The slower time constant is the relevant T_1e value. Figure 3(b) shows the measured depolarization factor plotted against the experimentally measured T_1e for each frozen radical solution. The plot shows an unmistaken correlation between longer T_1e and a greater ¹H є_depo under MAS at 5 kHz. This demonstrates that one of the key factors leading to significant depolarization observed with AMUPOL under various conditions is its long T_1e. In fact, long T_1e was among the design principle for AMUPOL, as well as another family of radicals, such as bTUrea and bTbK that should enhance the saturation efficiency with μw power, leading to higher CE, but also to higher depolarization.

Figure 3.

(a) Pulse schematic of saturation recovery experiment for T_1e measurement. T_1e fit of DOTOPA-ethanol saturation recovery curve. (b) Depolarization factor, 1/є_depo, measured (using direct ¹H detection at 5 kHz spinning) vs. T_1e of all radicals measured at 25 K.

Apart from different T_1e values, the various radicals studied here also have different spin interaction parameters, such as the relative g-tensor orientation, as well as the e-e dipolar tensor. Thus, to further disentangle the effect of T_1e from the other spin dynamics factors, we design an experiment to exclusively alter T_1e by adding Gd³⁺ ions at low concentrations of <1 mM where only T_1e, but not T_1n is measurably shortened, as experimentally demonstrated in previous studies by Walker et. al. and Johannesson et. al.^48-49 Specifically, GdCl₃ was added to the DOTOPA-ethanol solution at two different concentrations of 0.1 mM and 1 mM. We found that the T_1e of the DOTOPA-ethanol is reduced from 4 ms to 2 ms with 0.1 mM Gd³⁺, as well as the depolarization-factor, 1/є_depo significantly reduced by 32%. Upon addition of the higher GdCl₃ concentration of 1 mM to the DOTOPA-ethanol solution, the T_1e is reduced from 4 ms to 0.1 ms, and the depolarization-factor, 1/є_depo reduced by 98 %, and hence essentially no nuclear depolarization was observed. This result clearly demonstrates that given the same CE-inducing e-e dipolar interaction network of a given radical system, the extent of depolarization can still be significantly tuned, simply by altering its T_1e.

4.2. Experimental: Multi electron-spin effect: Electron Spectral Diffusion Rate on Depolarization

One parameter that has been omitted thus far in our discussion is electron spectral diffusion (eSD), which describes how a network of dipolar coupled electron spins redistributes polarization across the EPR line. The Vega and Goldfarb groups developed a method of measuring and simulating the phenomenological rate constant of eSD (Λ^eSD) in static DNP.^42,43 However, the of eSD rate under MAS conditions has not been characterized, neither theoretically nor experimentally. This is due to a large anisotropy of the electron spins, which causes time dependent mixing of electron spin polarization across the EPR line. Experimentally, this measurement requires the capability to perform pulse EPR detection under MAS - no such instrument exists to date. Nevertheless, we can measure Λ^eSD (static) through electron-electron double resonance (ELDOR) experiment for different radical systems in static systems, and report on the local and global electron spin network of the different radical system. This will help deconvolute the effect of Λ^eSD and T_1e on depolarization under MAS conditions.

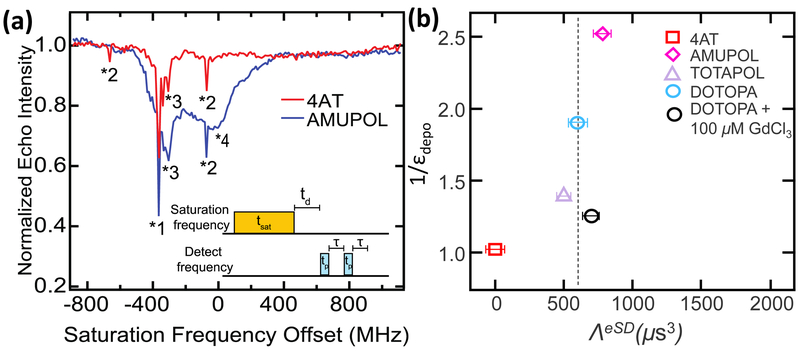
To begin, we briefly explain the measurement and fit of experimental ELDOR spectra, which has been fit with the ELDOR-model⁴² of Vega et. al. to extract the phenomenological eSD parameter, Λ^eSD. ELDOR is a pump-probe experiment. A saturation pulse (pump) is applied at a frequency of F_Saturation, which is swept across the EPR line, while the electron detection pulses (probe) are applied using another synthesizer with frequency, F_detect. The ELDOR pulse sequence and resulting spectra for F_detect=193.52 GHz are shown in Fig. 4a for AMUPOL and 4AT. The ELDOR spectra of all other detection frequencies, and of the other radicals are shown in the SI. The large peak at −390 MHz offset (marked with *1, in Fig. 4a) is where F_Saturation = F_detect. The peaks at −360 MHz and −340 MHz (marked with *3) are representative of the electron hyperfine coupling to ¹⁴N and ²H, respectively. The sharp peaks at −90 MHz and −690 MHz offset are due to strong electron hyperfine coupling to ¹H (marked with *2). The electron depolarization for positions marked with *2 and *3 are direct observations of the solid-effect transitions (F_Saturation or ω_μw=ω_e±ω_0n) for the various nuclei in the system. The broad peak at the center of the EPR line (*4) is due to spectral diffusion between the spins irradiated at F_Saturation and the detected spins at F_detect. This effect is most pronounced around the EPR center peak where the largest electron spin population lies. The lack of any observable spectral diffusion for the mono radical implies that the presence of intramolecular e-e coupling is critical for spectral diffusion at 20 mM spin concentration.

Figure 4.

(a) ELDOR spectrum of 4-amino TEMPO (4AT) and AMUPOL at a detection frequency of 193.52 GHz (or −390 MHz, offset), and at 25 K. Peak labels are as follows: (*1) where the detection frequency equals the saturation frequency, (*2) Hyperfine coupling to the ¹H spin in system, (i.e. ¹H solid effect), (*3) hyperfine coupling to ²H and ¹⁴N, and (*4) broad peak at center of the EPR line due to spectral diffusion between irradiated and detected electron spins. (b) Correlation of Depolarization factor, 1/є_depo, measured (at 5 KHz) vs. Λ^eSD of all radicals measured at static condition in an ELDOR experiment depicted in figure 4 (a).

In the ELDOR model, the simulated nitroxide EPR line that is inhomogeneously broadened due to the anisotropy in the g-tensor is divided into spin-packets of electrons, “bins”, with the same average frequency (v_j), average polarization (P_e), and equal bin frequency width (Δ_bin). Each bin contains a number of electron spins, f_j, given by the normalized EPR lineshape. The polarization of the bins are calculated by solving a set of coupled rate equations for all P_e(v_j). The rate constants in these coupled rate equations are dependent on the microwave irradiation frequency, v_j, and amplitude, P_e(v_j), T_1e, T_2e, and the polarization exchange rate between the bins, $w_{j,j^{\prime }}^{\mathit{eSD}}$, as defined by the eSD exchange constant (Λ^eSD) given in the following equation:

$$w_{j,j^{\prime }}^{\mathit{eSD}}=\frac{{\Lambda }^{\mathit{eSD}}}{{({\nu }_j-{\nu }_{j^{\prime }})}^2}$$ (4)

where (v_j – v_j′) is the frequency difference between two bins. The simulated ELDOR profiles are constructed from the experimentally determined values of f_j, T_1e, and the total electron spin concentration. To simulate the ELDOR profile, first the nitroxide EPR lineshape was simulated using the EasySpin simulation package for matlab.⁴⁴ The simulated EPR line was then divided into frequency bins, and the spectral diffusion rate $w_{j,j^{\prime }}^{\mathit{eSD}}$ simulated between the different bins using equation (4).

Figure 4b shows a plot mapping the correlation of the Λ^eSD value versus the depolarization factor for all radicals measured. Surprisingly, the Λ^eSD values for the two bi- and the tri-radical species are the nearly the same at 25 K, while the mono-radical 4AT showed no spectral diffusion. This finding is interesting for reason: it shows that Λ^eSD (static) does not have an effect on the differing depolarization factor measured for each frozen radical solution at the same global electron spin concentration of 20 mM and at 25 K, leaving T_1e rates as the major modulator of depolarization.

5. Numerical Simulation: Effect of T_1e on depolarization

Thus far we have demonstrated experimentally that T_1e is a major modulator of nuclear depolarization. In this section, we corroborate our experimental finding with numerical simulation of a model spin system described in Methods. First, the effects of spinning on NMR signal with and without μw irradiation was calculated, as shown in Fig. 5a and b. Figure 5a maps the ¹H є_on/off for spinning rate (v_r) between 250 Hz to 10 kHz, with T_1e set to 3 ms and μw power v₁ (μw) to 0.1 MHz respectively. As expected, the є_on/off initially increases with the spinning frequency and then decreases sharply. Figure 5b shows the calculated nuclear depolarization є_depo for the same spinning range for v_r. As expected, є_depo decreases with increasing spinning rate, and consequently the absolute enhancement, є_absolute, (Fig. 5c) diminishes more rapidly at higher spinning frequency in comparison to є_on/off. For comparison, the є_on/off (gray) and є_absolute (blue) are overlaid in Fig. 4c. In a nutshell, the reason for an initial increase in enhancement from static to spinning followed by a decrease at faster spinning is due to the counteracting effect on є_absolute from CE probability and level crossing rates, both enhanced under MAS.

Figure 5.

Numerically simulated ¹H enhancement and depolarization for e-e-¹H spin system at ~7 T (¹H frequency = 294.026 MHz ) as a function of spin rate for T_1e fixed to 3 ms. є_on/off, є_depo, and є_absolute are plotted in blue in (a), (b), and (c), respectively. In (c), є_on/off is overlaid in gray. All the spin parameters are given in method section. μw power was set to 0.1 MHz.

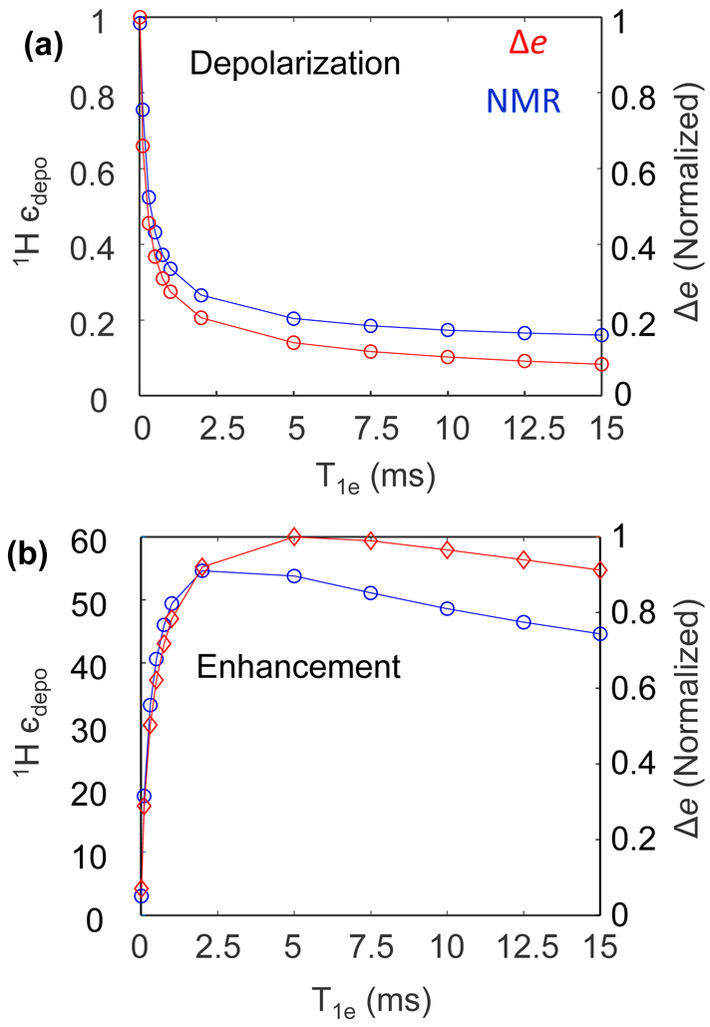
Next, we showed the dependence of depolarization and enhancement for a fixed spinning frequency (5 kHz) and varying T_1e (Fig. 6). The simulated depolarization (є_depo) of the ¹H NMR signal monotonically decreases with increasing T_1e before reaching a plateau value at T_1e= ~8ms (Fig. 6a). This is consistent with experimental observation that saw increased depolarization with increased T_1e between below 2 to 6 ms (see Fig. 3). On the right-hand y axis, the normalized difference in the two electron spin polarizations, Δe, is plotted with respect to the same x-axis. Remarkably, Δe tracks the same trend as the nuclear depolarization. Lower Δe leads to greater nuclear depolarization, and vice versa. This is because the polarization exchange between the CE-fulfilling electron spins and nucleus at the CE rotor event is proportional to the polarization difference between the two electrons and nucleus.²³ The μw-driven absolute DNP signal enhancement (є_absolute) is also T_1e dependent, and in general increases with longer T_1e as reflected in Fig. 6b. Interestingly, we observed that there is an optimum value for T_1e to reach the maximum DNP enhancement. We also monitored Δe under μw irradiation. Again, Δe tracks the same trend as є_absolute. The value for the optimum T_1e depends on μw irradiation parameters and spin rate. However, it is evident that a too long T_1e is not optimal due to depolarization, and consequently for maximizing the absolute DNP enhancement.

Figure 6.

Numerically simulated (a) depolarization and (b) enhancement for e-e-¹H spin system at 7 T as a function of T_1e at 5 kHz spinning (Blue). 0.1 MHz MW power was used for (b). Corresponding electron polarizations difference is also plotted in red. All the spin parameters are the same as in Fig. 5.

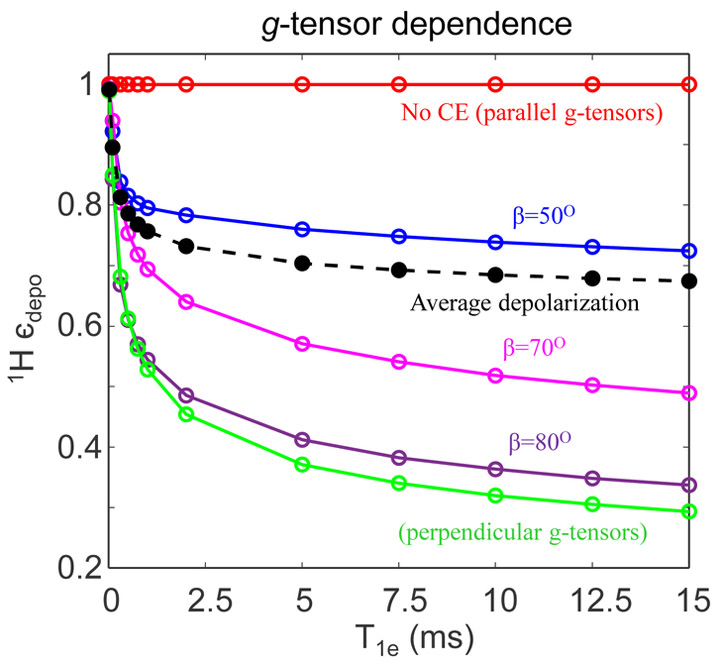
We next dissected the dependence of depolarization on T_1e and relative g-tensors orientation. The simulations shown so far represent exemplary results for a somewhat randomly chosen e-e-¹H system in terms of g-tensor orientation and the dipolar coupling tensors for coupled, CE fulfilling, electron spins. It is, however, understood that the relative orientations of the g-tensors of the coupled electron spins are important as they determine the resonance conditions leading to both CE and the e-e polarization exchange, as well as the probability and efficiency of the rotor-synchronous level crossing events. It should be noted that the question we ask is different from that of Mentik-Vigner et. al.²⁷ who studied the effect of powder orientation of a radical (fixed e-e-¹H spin system) in the external magnetic field, i.e. for different crystal/molecule orientation with respect to external magnetic field in the lab frame, on depolarization. In contrast, the focus of our calculation is to change the radical system itself by varying the relative g-tensors orientation and calculate the average depolarization effect for the powder sample.

In Fig. 7, ¹H є_depo is plotted against T_1e for varying β that is associated with the g-tensors in the Euler angles set {α,β,γ}, while keeping all the other spin parameters same as in the simulations presented in Figures 5 and 6. Molecule to rotor powder averaging is performed for each of these orientations using a repulsion scheme.⁴⁵ We observe that for certain orientations, there is maximum depolarization, especially for the near perpendicular orientation between the two electron spin g-tensors (Figure 7, green). Only when the two g-tensors are parallel to each other, no depolarization NMR signal is observed (Figure 7, red). This finding was expected, as such orientations will result in the Zeeman energies of the two electron spins to be equal, so that the CE condition that requires their frequency difference to correspond to that of the nuclear Larmor frequency cannot be fulfilled at any rotor position. When averaging over all the selected orientations, we observe smaller nuclear depolarization, with average ¹H є_depo equalling ~ 0.7 compared to ~ 0.3 for perpendicular orientations for this spin system.

Figure 7:

Numerically simulated depolarization for e-e-¹H spin system at 7 T as a function of T_1e at 5 kHz spinning for different relative g-tensor orientations. All the spin parameters are the same as earlier. Only the orientation of electron-2 in the spin system is changed by varying β in the euler angle set {0,β,0}.

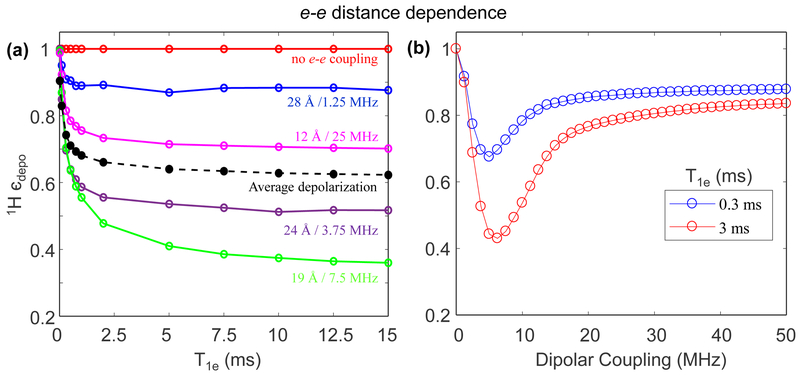
Next, we considered the effect of the e-e dipolar coupling tensor on nuclear spin depolarization. In the simulations presented thus far, we have fixed the e-e dipolar tensor to the orientation {124°, 94°, 0°} and strength of ~19 MHz (14 Å). To keep it simple, we only change the coupling strength, but keep the dipolar tensor orientations with respect to the g-tensors unchanged. The simulated results shows, in Fig. 8a, that there is an intermediate range for the e-e dipolar coupling strength that leads to maximum depolarization. Zero e-e coupling shows no depolarization, simply because CE Hamiltonian strength is zero. As the e-e coupling strength increases the CE Hamiltonian strength also increases, resulting in greater depolarization. The e-e coupling strength also determines the magnitude of polarization exchange between the two electrons when they reach degenerate conditions ( i.e. at dipolar rotor event). Therefore, we need to take into account both the CE rotor event as well as the dipolar rotor events. In a similar context, Mentink-Vigier et. al. have statistically predicted that if the dipolar rotor events are diabatic (non-adiabatic) in nature (because of small e-e coupling) then it leads only to a partial polarization exchange between the two electrons.²⁷ Such dipolar rotor event will have an effect to reduce the polarization difference between two electron, and this can eventually result in larger nuclear depolarization. However, very strong e-e dipolar coupling leads to adiabatic crossing that maintains the polarization difference between the electrons spins, resulting in smaller nuclear depolarization at CE rotor event. Nonetheless, the depolarization effect cannot be fully nullified by increasing the e-e dipolar strength beyond a limit. This is evident in the simulation shown in Fig. 8b that maps ¹H є_depo as a function of e-e dipolar strength, at T_1e = 0.3 ms and 3 ms , with all other parameters held the same as in Fig. 8a. Clearly, ¹H є_depo as a function of e-e dipolar coupling strength has the feature of an “anharmonic potential well” - for a certain e-e coupling value where є_depo reaches a minimum (i.e. maximum nuclear depolarization), but at large e-e dipolar coupling є_depo reaches a plateau whose value is determined by relaxation rates and relative g-tensor orientations.

Figure 8.

(a) Numerically simulated depolarization for e-e-¹H spin system at 7 T as a function of T_1e at 5 kHz spinning for different e-e distance/dipolar coupling in the spin system described earlier. All the spin parameters are the same as described earlier. (b) Numerically simulated depolarization as a function of dipolar coupling for T_1e set to 0.3 ms (blue) and 3 ms (red) at 5 kHz spinning using the same spin system.

The presence of J-coupling (or exchange coupling) increases the net effect of the e-e coupling strength at the rotor crossings, independent of orientations. Strong J-coupling therefore reduces the orientation dependence of the e-e dipolar coupling. Furthermore, the relative orientation of the g-tensors with respect to the dipole couplings tensor is also critical for CE. This is because the strength of the Hamiltonian at the resonance condition is not the only factor modulating nuclear depolarization, but also the time sequence of various rotor events. An in-depth analysis is needed to understand the most favourable spin-interaction orientations for DNP that optimizes both the Hamiltonian and the sequence for the various crossings to maximize the CE, while minimizing nuclear depolarization. This analysis is beyond the scope of the present manuscript.

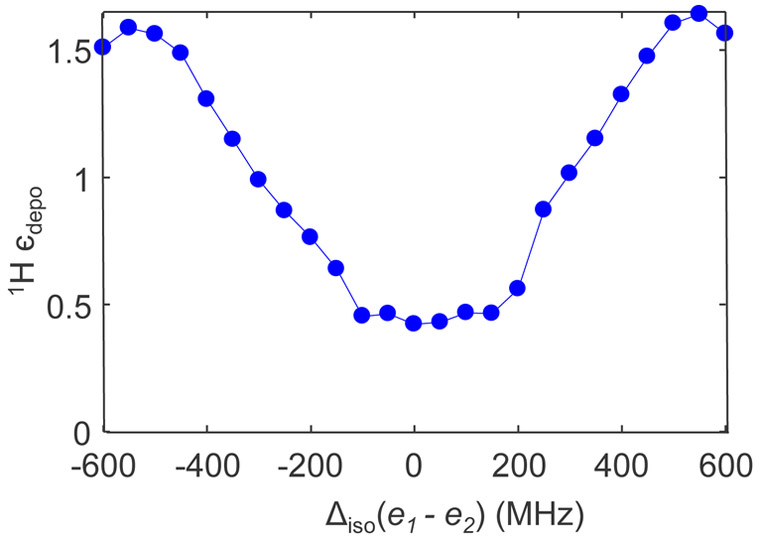
Finally, we take advantage of the in-silico DNP analysis to predict depolarization of a biradical where the two electron spins have different isotropic chemical shifts. Temp-Trityl, a new family of radical, belongs to this category of radicals that have shown to minimize depolarization and maximize DNP enhancement at high magnetic field (¹H > 800 MHz).^46,47 Inspired by this, we considered the case of e-e-¹H with one of electrons having g-anisotropy of trityl {g_x,g_y,g_z =2.0034, 2.0031, 2.0027} and the other having g-anisotropy of nitroxide {g_x,g_y,g_z =2.0094, 2.006, 2.0017}. Figure 9 shows the dependence of ¹H є_depo on the isotropic chemical shift difference (△_iso) of these two electrons. Greater nuclear depolarization, or smaller ¹H є_depo is seen as the absolute △_iso decreases towards 0. Large △_iso minimizes the probability of dipolar rotor event that tend to reduce the polarization difference between the two CE fulfilling electron spins, and result in smaller nuclear depolarization (larger ¹H є_depo). When △_iso is ~ 300 MHz, which corresponds to the average △_iso between trityl and tempo, the nuclear depolarization is significantly reduced resulting in ¹H є_depo =0.95. This shows the great potential of narrow-broad combo-radicals as a solution to reduce ¹H depolarization, as discussed recently in literature.⁴⁷ Also, it is very interesting to note that for certain conditions, є_depo can be larger than one. Theoretically both enhancement as well as depolarization of nuclear spin is possible owing to the same CE under MAS, depending on the electron polarization gradient.

Figure 9.

Numerically simulated depolarization for e-e-¹H spin system at 7 T as a function of difference in the isotropic chemical shift of a narrow radical (like trityl) and broad radical (like 4AT) at 5 kHz spinning using the coupling interaction tensors same as in Fig. 5.

Taken together, these simulations demonstrated that T_1e, the spin rate, the two electrons spin g-tensor orientation, and the e-e dipolar coupling all influence nuclear depolarization due to CE under MAS. Using these results, we analyzed the experimental results shown in Figures 2 and 3. It was observed that AMUPOL leads to maximum depolarization. Relatively long T_1e of AMUPOL, owing to its rigidity, is likely the primary cause of the large depolarization seen with AMUPOL. In addition, close to perpendicular orientation of the nitroxides in AMUPOL also contributes to its depolarization. TOTAPOL has similar dipolar coupling strengths as AMUPOL, while it populates a wide range of relative g-tensor orientations. We can rationalize the smaller depolarization effect seen with TOTAPOL with the shorter T_1e of TOTAPOL compared to AMUPOL. In case of 4AT, which is a mono-radical, the averaging over both g-tensors and dipolar couplings between the two random orientations satisfying CE may reduce the nuclear depolarization, but this is difficult to evaluate without considering a greater e-e ensemble representing 4AT in solution. It should be noted that the reduction in nuclear depolarization owing to non-optimally oriented g-tensors and small dipolar coupling also attenuates the CE enhancement.

What is clear is that the experimental results with a diverse set of commonly used radicals for DNP of 4AT, TOTAPOL, AMUPOL and DOTOPA-ethanol, and with the addition of GdCl₃, showed a clear correlation between T_1e and є_depo. This means that the differences in the other factors, such as e-e dipolar coupling strengths and relative g-tensor orientation, are less dominant factors in these systems. This is further corroborated by our finding that the empirical spectral diffusion parameter, Λ^eSD, under static condition is indistinguishable between these different radical systems studied here. While the physical interpretation of Λ^eSD is subject of ongoing studies by Vega and coworkers,^42,43 these results show that the average e-e dipolar coupling network is comparable between the different bi- and tri-radical systems, ensured by keeping the total electron spin concentration constant (here at 20 mM). For achieving high absolute DNP enhancements, focusing on modulating T_1e is hence a promising approach to optimize є_absolute, once radical systems with promising CE DNP performance have been identified. We demonstrated such an example: the effect of depolarization in DOTOPA-ethanol can be nullified simply by reducing it’s T_1e upon doping with adequate concentrations of GdCl₃ dopants.

6. Conclusion and Outlook

In this study we carried out MAS DNP experiments at 25 K and 7 Tesla, and showed that nuclear depolarization can cause an inflated є_on/off by up to 60 % with commonly used bi- and tri- nitroxide radicals at 20 mM global electron spin concentration. The mono-radical at 20 mM spin concentration showed no significant depolarization. The nuclear depolarization effect is owing to an equalization of the electron spin polarization across the EPR line facilitated by MAS, where the extent of this depolarization is strongly influenced by the T_1e of the nitroxide radicals. Consequently, the deliberate shortening of T_1e by the addition of a paramagnetic relaxing agent such at Gd³⁺ to the nitroxide spin system reduced the nuclear depolarization effect. The experimental studies were accompanied with fully quantum mechanical numerical simulations of depolarization effects, enabled by the SPIN-EVOLUTION package. These simulations showed that T_1e is indeed a major modulator of nuclear depolarization, but that other factors, such as the two electron spin relative g-tensor orientation and the e-e dipolar coupling, also influence nuclear depolarization under MAS, consistent with findings in the literature.^26,27 Intriguingly, the experimental results showed that setting the global electron spin concentration to 20 mM for commonly used nitroxide radicals was sufficient to keep all factors sufficiently comparable, so that T_1e was the dominant modulator. This was corroborated with two-frequency ELDOR experiments carried out under static conditions that extracted phenomenological spectral diffusion rate constants that were found to be within error for the bi-, and tri- nitroxide radical systems under the here used experimental conditions. The extent to which spectral diffusion plays a role in equalizing the electron spin polarization in the CE process and its effect on nuclear depolarization have not been discussed in the literature, and should be subject of future studies. When entirely different radical systems are considered for MAS DNP, e.g. narrow-broad mixed radicals, radicals with different g-anisotropy and tensor orientation, or strongly coupled radicals, the predominance of T_1e in modulating nuclear depolarization may not hold. In fact, if a radical could be designed whose CE fulfilling electron spin pairs do not exchange electron spin polarization (non-overlapping), depolarization effects should be minimal under MAS.