Advances in ultrasound elasticity imaging

Abstract

The most troublesome of ultrasonic B-mode imaging is the difficulty of accurately diagnosing cancers, benign tumors, and cysts because they appear similar to each other in B-mode images. The human soft tissue has different physical characteristics of ultrasound depending on whether it is normal or not. In particular, cancers in soft tissue tend to be harder than the surrounding tissue. Thus, ultrasound elasticity imaging can be advantageously used to detect cancers. To measure elasticity, a mechanical force is applied to a region of interest, and the degree of deformation measured is rendered as an image. Depending on the method of applying stress and measuring strain, different elasticity imaging modalities have been reported, including strain imaging, sonoelastography, vibro-acoustography, transient elastography, acoustic radiation force impulse imaging, supersonic imaging, and strain-rate imaging. In this paper, we introduce various elasticity imaging methods and explore their technical principles and characteristics.

Introduction

Ultrasound imaging shows the anatomical structures of the human body by imaging the amplitude of received echoes from the boundaries where the acoustic impedances differ. Since, however, the acoustic impedances between cancerous and normal tissues are almost identical, cancers in soft tissue are not clearly delineated from the surrounding tissue, and thus cannot be clearly differentiated [1]. There have been ongoing research efforts to measure intrinsic ultrasonic properties of the soft tissue and cancer. Methods of measuring tissue parameters and presenting their values as image are known as tissue parameter imaging techniques [2–8]. Among such parameters, there are the speed of sound, attenuation coefficient, scatterer density, nonlinear parameter, and elasticity. The values of these parameters in lesion tissue are different from those in normal tissue to within ± 10% [2]. In the case of using reflection mode as in ultrasonic imaging, an accurate measurement of these parameters is not easy. However, elasticity can be measured relatively easily compared to other parameters, and hence the elasticity imaging mode has been rapidly commercialized [9].

Elasticity imaging measures the stiffness of cancerous tissue relative to that of the surrounding tissue and represents the spatial distribution of the stiffness as an image. Being a traditional method of identifying lesion stiffness, the palpation technique has been widely used to examine the state of cancerous tissue close to the surface of the human body as in the case of diagnosing breast cancer. However, since the performance of the palpation technique depends on the skill, experience, and expertise of the examiner, methods of using ultrasound have been sought after for more quantitative diagnosis. The measurement of stiffness can be relatively easily accomplished using the reflection mode of a diagnostic ultrasound scanner. Strain imaging is implemented by applying a force to tissue close to the skin and measuring the displacement [7]. However, since the strain imaging is disadvantageous in that the resulting elasticity distribution is qualitative, the quantitative shear modulus imaging is achieved by measuring the shear wave speed quantitatively. Since the shear wave can be generated by a high-intensity ultrasound, it neither requires special skills on the part of the doctor nor causes any inconvenience to the patient, aiding in tumor diagnosis. This paper explains the physics of ultrasound related to elasticity as well as the principles, advantages, and disadvantages of various known elasticity imaging methods.

Physics of elasticity

When tissue is subject to external force, the amount of deformation in tissue depends on its elasticity. The Young’s modulus is defined as [10]

$$E=\frac{\mathit{\sigma }}{\mathit{\epsilon }}=\frac{F}{\left(\frac{\mathrm{\Delta }L}{L}\right)}$$ 1

where σ is the applied stress, ɛ is the strain, and F is the force applied per unit area. Since the direction of force and displacement is identical, the Young’s modulus is also called compressional modulus. The shear modulus represents the amount of displacement in a configuration where one surface is fixed and the other is free to move. The shear modulus is defined as follows [10]:

$$\mathit{\mu }=\frac{F}{\left(\frac{\mathrm{\Delta }x}{L}\right)}$$ 2

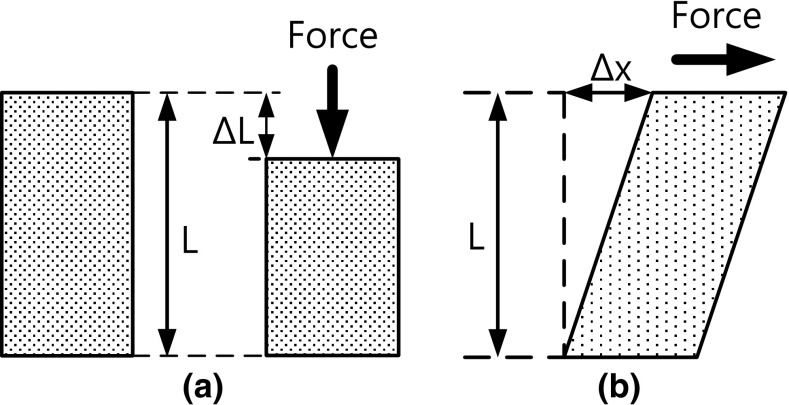
In the case of the Young’s modulus, the medium either compresses or dilates, while in the case of the shear modulus, the medium only changes its shape without change in its volume. Fig. 1 shows the concept of the Young’s modulus and the shear modulus.

Fig. 1.

a Young’s modulus, b shear modulus

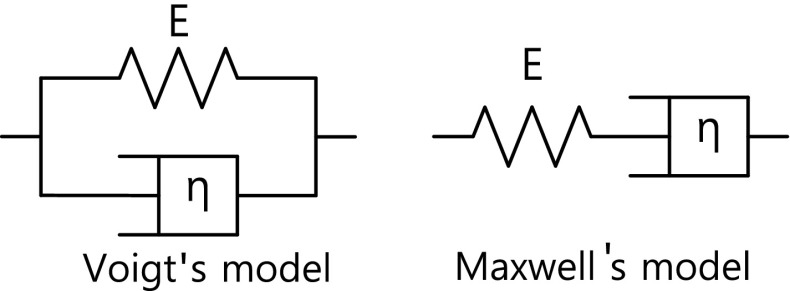
In practice, the human body exhibits the property of viscoelasticity as well as elasticity. Fig. 2 is a model of the human elasticity in which E and η represent the elasticity of the spring member (solid) and the viscosity of the dashpot member (fluid), respectively. One is the Voigt’s model, and the other is the Maxwell’s model [11]. Since the cells of the human body are filled with liquid, the tissue exhibits the characteristic of porosity. When the tissue is subjected to an external force, it exhibits a viscoelastic property due to liquid flow and causes a time delay in the movement of soft tissue. As a result, the temporal behavior of strain in the case of a human body is not simply described by (1).

Fig. 2.

A model of the viscoelastic property of the human body where E is the elasticity, and η is the viscosity

The soft tissue of the human body is incompressible because it does not compress under an external force applied. Thus, the tissue alters its shape only without change in its volume. The Poisson’s ratio ν represents the negative ratio of the transverse to axial strain, and is close to 0.5 for the case of the tissue of the human body. The speed of an ultrasound wave that propagates through the human body is affected by the value of elasticity. While propagating, a longitudinal wave compresses and expands the medium, in which it propagates, in the direction of its propagation. The speed c _l of a longitudinal wave, whose vibration direction is the same as the propagation direction, is expressed as [12]

$$c_l=\sqrt{\frac{E(1-\mathit{\nu })}{\mathit{\rho }(1+\mathit{\nu })(1-2\mathit{\nu })}}$$ 3

and has a value ranging from 1400 m/s to 1600 m/s. The speed c _s of a shear wave, whose vibration direction is perpendicular to the propagation direction, is expressed as

$$c_s=\sqrt{\frac{\mathit{\mu }}{2\mathit{\rho }(1+\mathit{\nu })}}\approx \sqrt{\frac{\mathit{\mu }}{3\mathit{\rho }}}$$ 4

and ranges from a few to several tens of m/s in the human soft tissue.

Table 1 shows the categorization of elasticity imaging methods that are known in the literature according to how the stress is applied and how the elasticity is measured.

Table 1.

Classification of elasticity imaging methods according to operating frequency and source of stress

Operating frequency	Stress source	Imaging parameter	Imaging method
Less than 5 Hz	Manual palpation	Strain	Strain imaging
Sine wave less than 500 Hz	Mechanical vibration	Shear modulus	Sonoelastography
	Acoustical oscillating radiation force	Nonlinearity (resonance frequency)	Vibro-acoustography
Impulse	Mechanical impulse	Shear modulus	Transient elastography
	Acoustical radiation force impulse	Maximum displacement	ARFI imaging
		Shear modulus	Supersonic imaging

Up to now, among strain imaging methods, acoustic radiation force impulse (ARFI) imaging, supersonic imaging methods have been commercialized. In what follows, we will explain the technical principle of each imaging method.

Strain imaging

For the first time, Ophir et al. imaged the elasticity of biological tissues in 1991 [7]. They measured the amount of deformation, i.e., the strain of a medium subjected to external compression. For objects consisting of tissues with different stiffness values, the soft tissue tends to deform more than the hard tissue. Differentiating the displacements at spatial positions, one can obtain the relative rate of displacement change.

In practice, for the case of applying an external force to the human body, the distribution of the stress inside the body is difficult to estimate in reflection mode. Therefore, only the strain is measured and imaged. Strain imaging can be used to diagnose cancer or tumor at locations proximal to the human skin, such as the breast, prostate, and thyroid. The Ophir team reported the clinical test results of the strain imaging technique until the late 1990s to verify its efficacy [13–15].

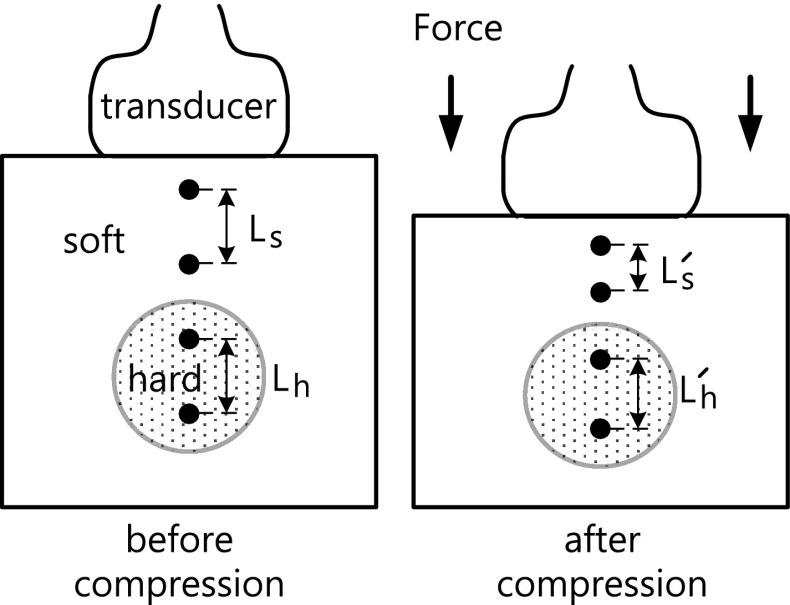
The most important signal processing steps in strain imaging are the estimation of displacement and displacement gradient. When applying compression to the breast or prostate, the ultrasonographer places the ultrasonic probe to the skin, pushes it slowly, and then releases. The action is repeated until a satisfactory strain image is obtained. The acquisition of ultrasonic echo data proceeds as follows. Echo data are acquired from a medium of interest before and after applying compression to it. When subjected to the applied compression, the scatterers in the medium undergo different displacements depending on their elasticity. By estimating the displacement at all imaging points before and after applying compression and computing the change in displacements relative to adjacent imaging points, one can obtain a strain image. Fig. 3 shows the process of acquiring ultrasonic data and estimating strain. Measuring the distance between some point of interest before compression and that point after compression yields strain S _soft for the soft region and strain $S_{hard}$ for the hard region, as follows:

$$S_{soft}=\frac{L_s-L_s^{\prime }}{L_s},S_{hard}=\frac{L_h-L_h^{\prime }}{L_h}$$ 5

where $S_{soft}>S_{hard}$.

Fig. 3.

Strain estimation model in strain imaging

Displacements are estimated from RF data using crosscorrelation, autocorrelation, or speckle pattern tracking [16–18]. To be able to observe strain images in real time, a fast method of estimating displacements is necessary. The first practical fast displacement estimation methods are the phase zero root seeking [17] and the combined autocorrelation [18]. The former shifts one signal against the other so that the phase difference between the two signals becomes zero, where the amount of shift corresponds to the displacement. The latter directly converts the phase difference between the two signals to an estimate of the displacement to reduce the computation time. Both strain imaging methods operated on complex baseband signals so the amount of data to be processed was reduced. In addition, using digital signal processors, they produced strain images in real time. Pesavento et al. [17] and Shiina et al. [18] reported clinical results of breast and prostate cancers obtained in real time. In the late 2000s and early 2010s, the advances in semiconductor technology and the availability of graphics processing units for fast computation solved the processing time bottleneck [19–21].

The waveforms of the echoes before and after applying compression are different, so displacement estimation methods based on correlation incur estimation errors. There were many research efforts geared toward reducing the estimation errors [22–27]. Among them, some noteworthy methods are the signal stretching technique that expands the post-compression echo signal by a factor corresponding to the amount of the compression to reduce the displacement estimation errors due to signal decorrelation, the linear regression technique that combats against the deleterious effect of noise in displacement differentiation, and the central frequency compensation technique.

The spatial resolution of strain imaging depends on the data window length and is less than several mm [28]. The lower limit on the achievable spatial resolution when imaging the human body is considered to be 2 mm. The human tissue has a Poisson’s ratio of approximately 0.5 and is incompressible. A medium of interest subjected to stress expands in directions other than the direction of the applied strain. Upon the application of a large amount of stress, the distribution of scatterers in a medium where the ultrasound wave propagates changes, thus increasing the decorrelation between the pre- and post-compression echo signals and resulting in large errors in displacement estimation. Strain imaging yields quality images when the applied strain is less than several percent [29]. Furthermore, the ultrasonic probe should be placed on the skin and pushed slowly in the scan line direction. The skill of the ultrasonographer manipulating the ultrasonic probe considerably affects the strain image quality.

Sonoelstography

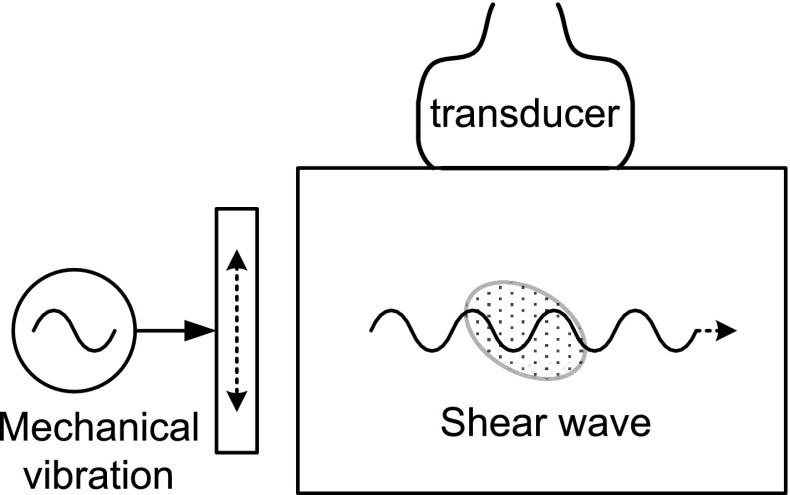
When the human body is subjected to a mechanical sinusoidal harmonic vibration, a shear wave having a complex pattern is generated, which in turn causes the soft tissue to vibrate. The amplitude of the vibration is smaller in the hard tissue than that in the soft tissue. As a result, the movement in the hard tissue is slower than that in the soft tissue. Fig. 4 shows a data acquisition scheme of sonoelastography. A shear wave is generated by mechanically vibrating the tissue in a direction parallel to its surface, i.e., in the axial direction as shown in the figure. Sonoelastography refers to a technique for imaging the vibration speed using the Doppler principle, and was reported by the Parker group [30, 31]. The vibration pattern changes significantly depending on the vibration source frequency and the medium characteristic. At the time of their publications, it was difficult to image a fast vibrating medium using clinical ultrasound scanners, so they improved the diagnostic utility by observing the vibration patterns for various frequencies. Compared to an inverse method that directly estimates the stiffness distribution, this method is disadvantageous because indirectly observing the vibration pattern makes it difficult to obtain a high-resolution distribution of stiffness. They alleviated the disadvantage by observing the vibration of a medium when a low-frequency shear wave propagated in it.

Fig. 4.

Data acquisition scheme of sonoelastography

When two vibrators were used that had distinct vibration frequencies, a low-frequency shear wave was generated by the beat phenomenon, and propagated slowly in the medium. The shear wave that propagated slowly was referred to as a crawling wave. Since the medium moved at a low speed, the vibration was easy to image using the Doppler imaging modality [32, 33].

Considering the fact that the complex vibration patterns in the human body are not amenable to quantitative analysis, it is envisioned that the commercialization of sonoelastography may be difficult.

Vibro-acoustography

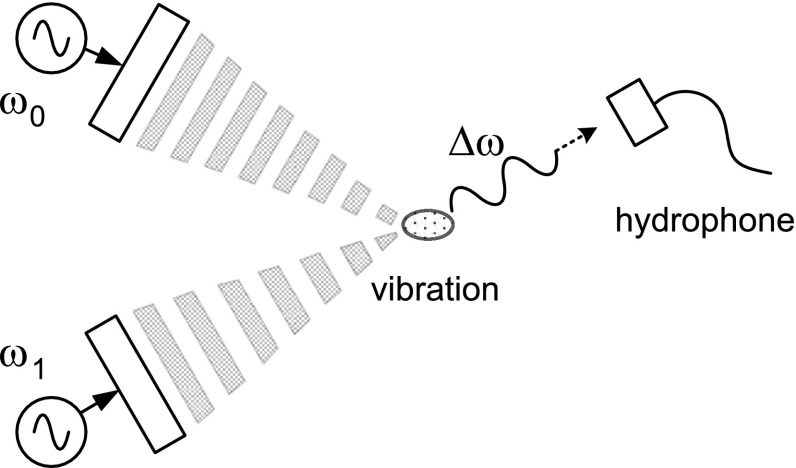
In a region where two sinusoidal waves superpose, a beat phenomenon occurs due to nonlinearity. Thus, in a region where the fields of two continuous ultrasonic waves whose frequency difference is small superpose, a beat signal having the difference frequency is generated, and the medium vibrates at the beat signal frequency. Since the beat signal has a different vibration amplitude depending on the elasticity of medium, observing the vibration characteristics with frequency leads us to determine the elasticity [34–37]. Since the beat signal is of low frequency that is less than several hundred kHz, it can be measured using a hydrophone. The spatial resolution can be obtained by controlling the area of the region where ultrasound signals superpose, and ultrasound waves need to be successively focused at every imaging point to produce an image. Fig. 5 shows a data acquisition scheme of vibro-acoustography. Increasing the frequency of the beat signal produces high-resolution elasticity images.

Fig. 5.

Data acquisition scheme of vibro-acoustography

A clinical study showed that the method could image the calcified artery of the human breast at a higher resolution than X-ray mammography [37]. Vibro-acoustography features high-resolution images, but has a drawback that the data acquisition time is very long. They modified the method such that a point of a blood vessel was vibrated by an ultrasound wave, and the propagation of vibration along the vessel was observed to detect any vessel anomaly. The modified method was termed shearwave dispersion ultrasound vibrometry (SDUV) [38].

Transient elastography

Tissue elasticity can be determined from the propagation characteristic of a shear wave generated by applying a mechanical shock to soft tissue within a short time interval. The transient elastography introduced by the Fink group uses a mechanical impulse [39]. If a mechanical shock is applied to the human tissue using a mechanical vibrator, a longitudinal wave propagates along the shock direction, and a shear wave is generated in the lateral (i.e., transverse) direction. The shear modulus can be determined by measuring the speed of the shear wave that propagates slowly in the human tissue. The tissue motion caused by the propagating shear wave was observed using a high frame rate imaging technique [40]. It was clinically shown that the elasticity of the breast cancer could be quantitatively measured. However, the transient elastography is cumbersome to use because it requires a mechanical driver. No ensuing further research results have been reported.

Acoustic radiation force

When applying a stress to the human body using an ultrasonic probe, the quality of elasticity image depends on the skill of the ultrasonographer, and the use of a mechanical mechanism increases the complexity of the data acquisition system. In the case of using a mechanical harmonic vibration, noise due to mechanical vibration gives the patient discomfort. A high-intensity ultrasonic wave generates a radiation force. Methods have been investigated to control the magnitude and position of the stress generated by an acoustic radiation force at a selected focal point due to a high-intensity ultrasonic wave. Those methods are advantageous in that there is no need for the ultrasonographer to move the ultrasonic probe and that there is no need for any additional mechanical apparatus.

While propagating into the human body, a longitudinal wave vibrates in the same direction as the propagation direction, and applies a force to the tissue. This force is referred to as an acoustic radiation force impulse, and has the following relationship [41]:

$$F=\frac{W_{absorbed}}{c}=\frac{2\mathit{\alpha }I}{c}$$ 6

where F is the acoustical radiation force (kg s⁻² cm⁻²), α is the attenuation coefficient of the tissue (m⁻¹), W _absorbed is the power absorbed by the medium at a given spatial location (W m⁻³), c is the speed of ultrasound in the tissue (m/s), and I is the temporal average intensity at a spatial location (W m⁻²).

Fig. 6 shows the principle of exciting an ARFI pulse using an ultrasonic wave and the generation of a shear wave. The pushed tissue returns to its original state, generating a mechanical vibration. Then a generated shear wave propagates in both directions perpendicular to the transmit direction of the ultrasonic wave.

Fig. 6.

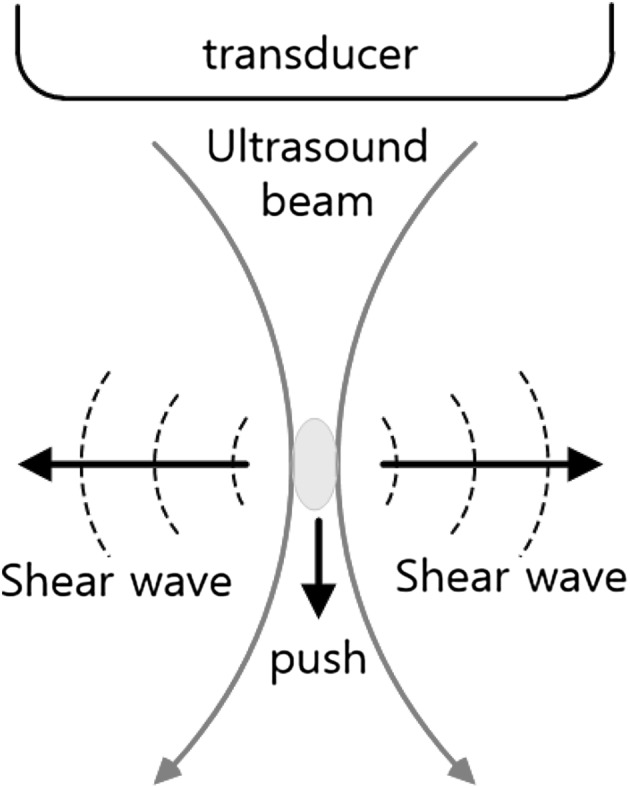
Pushing in ARFI and generation of shear wave

Commercially implemented elasticity imaging methods based on the acoustic radiation force can be divided into acoustic radiation force impulse (ARFI) imaging [41] that measures the displacement of the pushed tissue and shear wave elasticity imaging (SWEI) [42] that measures the propagation speed of the shear wave generated by the acoustic radiation force.

High frame rate imaging

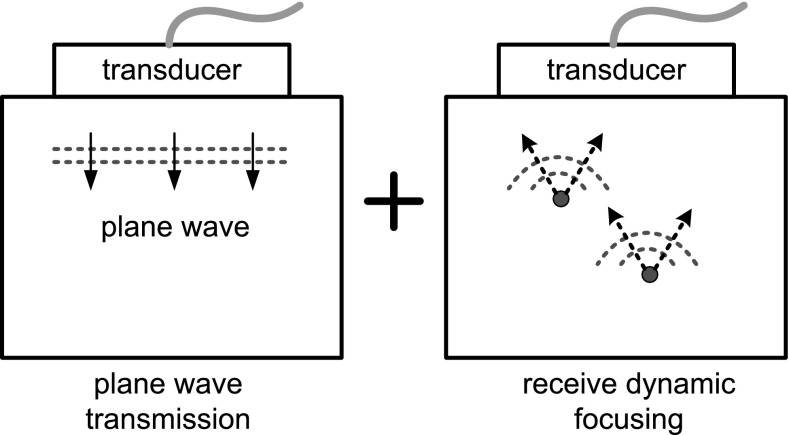
In conventional ultrasonic imaging that acquires one scan line at a time, it takes approximately several tens of ms to produce one frame of image. Accordingly, tens of image frames are displayed per second. However, to observe the motion of tissue, we need to acquire several thousand frames per second. To this end, instead of employing the transmit focusing, a pulsed plane wave is transmitted, and the echo data are acquired at all receive elements as shown in Fig. 7. Since the pulsed plane wave passes through all imaging area, the entire image can be produced by only a single transmission. Without using transmit focusing, this method can achieve a frame rate of as high as up to 10,000 frames per second (fps) depending on the imaging depth [40]. This method is used to observe tissue movement in ARFI and shear wave propagation in supersonic imaging, and recently to image Doppler vector velocity at a high frame rate [43]. In plane wave transmission, the image resolution can be improved without decreasing the frame rate by synthetically focusing the ultrasound fields transmitted in different directions [44].

Fig. 7.

High frame rate imaging scheme combining plane wave transmission and receive dynamic focusing

Acoustic radiation force impulse imaging

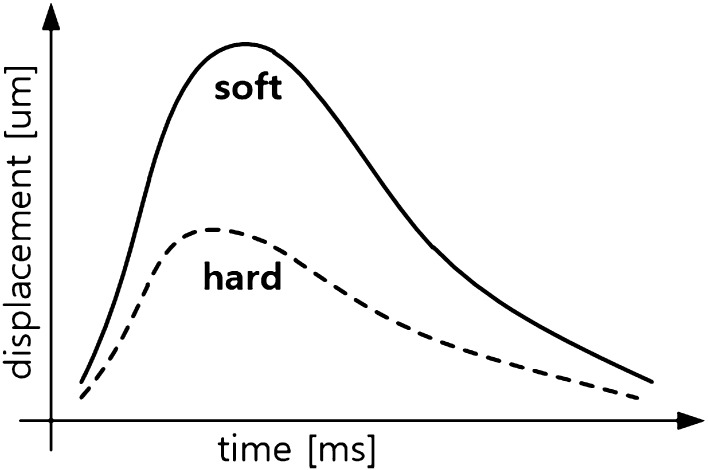
When applying a high-intensity focused ultrasound wave to a small region, the tissue is pushed by the acoustic radiation force. The maximum displacement of the tissue due to pushing represents its elasticity, and the time it takes the pushed tissue to return to its original state represents the viscosity of the tissue. Fig. 8 shows the different displacements of the soft and hard tissues, with respect to time, depending on their elasticity. The displacement of the hard tissue peaks earlier than that of the soft tissue. In contrast, the maximum displacement is larger in the soft tissue than in the hard tissue. This principle was employed in what was termed ARFI imaging [45–49] where a region of interest was irradiated by a high-intensity focused ultrasonic impulse, and its movement is monitored using a high frame rate imaging technique.

Fig. 8.

Comparison of displacements with time, induced by ARFI, for soft and hard tissues

The maximum displacement of the tissue, which is proportional to the elasticity, can be used to differentiate cancers, In the ARFI technique, the region where a pushing force is generated is confined to the focal point of a transmit ultrasound pressure field. Hence, the data acquisition time to obtain an elasticity image of a large area is several seconds. Siemens has marketed an ARFI imaging product with a trademark of Virtual Touch, but to overcome the qualitative nature of ARFI image, the shear wave speed at a single point is measured, and the tissue elasticity is displayed as a numerical value along with ARFI image [50].

Park et al. measured the shear modulus quantitatively from the displacement versus time curve of an ultrasound tissue phantom when pushed by an ARFI excitation [51]. The group also introduced a qualitative method of measuring the stiffness of an entire imaging area using a single plane wave transmission [52]. Foucher et al. diagnosed the cirrhosis by applying a mechanical impulse to the skin surface and observing the shear wave propagating inside the liver [53].

Supersonic imaging

Methods of generating an acoustic radiation force and measuring the speed of shear wave include shear wave elasticity imaging (SWEI) [42] and supersonic imaging technique [54–56]. The axial vibration of a longitudinal wave generated by ARFI at the focal point of a transmit ultrasound field generates a shear wave that vibrates in the lateral direction. The shear wave propagates very slowly at a speed of 1 to 10 m/s, but the longitudinal wave propagates at 1540 m/s on average. Thus, by observing the tissue motion using a high frame rate imaging technique, the shear wave speed can be measured. The speed of the shear wave is dependent on the shear modulus of the tissue, as can be seen in (4). Since the elastic Lamé coefficient is greater than μ by a factor of 10⁶ and the Poisson’s ratio is close to 0.5 in a soft medium, μ can be approximated by

$$\mathit{\mu }\approx 3\mathit{\rho }{c}_s^2$$ 7

By measuring the propagation speed of the shear wave in the medium, one can determine the Young’s modulus quantitatively. Since the shear modulus varies over a wide range depending on the type of medium, measuring the shear modulus rather than the Young’s modulus helps to discern lesions more clearly. The supersonic imaging technique produces a plane shear wave using the ARFI technique and measures its propagation speed inside the medium to determine the shear modulus over the entire imaging region simultaneously.

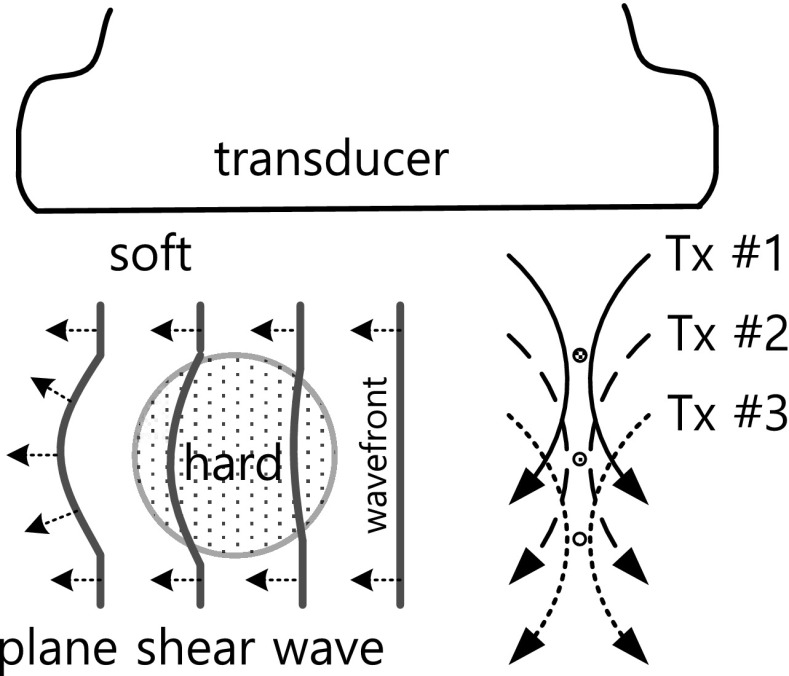
Fig. 9 shows the generation and propagation of the plane shear wave in a lesion under the supersonic imaging technique. The generation of the plane shear wave utilizes the principle that at a focal point a shear wave is generated in the lateral direction. If we rapidly shift the focal point in the axial direction and successively repeat the transmission, the wavefronts of the generated shear waves superpose, producing the plane shear wave. The wavefront of the plane shear wave propagates at a different speed in a medium with a different shear modulus. The shear modulus is determined by determining the propagation speed of the plane shear wave. Bae et al. [57] improved the accuracy of computing the shear wave speed by considering the propagation direction of the shear wave in a two-dimensional plane.

Fig. 9.

Generation and propagation of plane shear wave in the hard lesion under supersonic imaging technique

Strain rate imaging

The 2-D color flow mapping method is widely used in the diagnosis of heart disease, but it is an indirect diagnostic method since lesions of the heart wall are discerned using the distribution of blood flow velocity. The tissue Doppler method is used to observe the motion of the heart wall directly. Although the tissue Doppler method is capable of imaging the moving velocity of the heart wall, the accurate identification of a lesion that moves at the same velocity as a normal heart tissue that encloses the lesion is a challenging task.

Observing the change over time in the motion of the heart wall enables one to detect lesions. For this purpose, the strain rate is introduced, and is defined as the temporal derivative of strain [58, 59] as follows:

$$\dot{\mathit{\epsilon }}=\frac{d\mathit{\epsilon }}{dt}$$ 8

By observing the temporal change in the displacement of the heart wall, we can determine the velocity, strain, and strain rate. Among them, the strain rate aids in observing the dynamic motion of the heart wall easily. The temporal motion of the heart tissue is computed off line by processing B-mode images acquired at a rate of several hundred fps.

Conclusion

Since the B-mode imaging modality has difficulty in accurately diagnosing soft tissues, such as cancers, benign tumors, and cysts, researchers have attempted to find other ultrasonic methods of imaging tissue parameters. Among them, the elasticity imaging modality has been successfully commercialized. Although strain imaging is relatively straightforward to implement, and has been implemented by almost every ultrasound scanner manufacturer, it has the disadvantage that the resulting image is qualitative. Both ARFI imaging and supersonic imaging, which provide quantitative elasticity estimates, are effective in the detection of cancers, and help to reduce discomfort to the patient because the need for invasive biopsy is obviated.

Compliance with ethical standards

Conflict of interest

All authors declare that they have no conflict of interest.