Statistical non-parametric mapping in sensor space

Abstract

Establishing the significance of observed effects is a preliminary requirement for any meaningful interpretation of clinical and experimental Electroencephalography or Magnetoencephalography (MEG) data. We propose a method to evaluate significance on the level of sensors whilst retaining full temporal or spectral resolution. Input data are multiple realizations of sensor data. In this context, multiple realizations may be the individual epochs obtained in an evoked-response experiment, or group study data, possibly averaged within subject and event type, or spontaneous events such as spikes of different types. In this contribution, we apply Statistical non-Parametric Mapping (SnPM) to MEG sensor data. SnPM is a non-parametric permutation or randomization test that is assumption-free regarding distributional properties of the underlying data. The method, referred to as Maps SnPM, is demonstrated using MEG data from an auditory mismatch negativity paradigm with one frequent and two rare stimuli and validated by comparison with Topographic Analysis of Variance (TANOVA). The result is a time- or frequency-resolved breakdown of sensors that show consistent activity within and/or differ significantly between event or spike types. TANOVA and Maps SnPM were applied to the individual epochs obtained in an evoked-response experiment. The TANOVA analysis established data plausibility and identified latencies-of-interest for further analysis. Maps SnPM, in addition to the above, identified sensors of significantly different activity between stimulus types.

Introduction

Establishing the significance of observed effects is a requirement for meaningful interpretation of clinical or experimental data. Recordings of spontaneous brain activity can yield clinically relevant fragments of activity such as inter-ictal epileptic spikes. In an Event-Related Potential (ERP) or Event-Related Field (ERF) experiment, an Electroencephalography (EEG) or Magnetoencephalography (MEG) device records the brain activity in response to or preceding a sensory, cognitive, or motor event. In a group study, several subjects are exposed to the same experimental paradigm and their brain activities are recorded. All of these scenarios have in common that multiple realizations of the same brain activities are available. In order to increase the signal-to-noise-ratio, recorded activities of the same type are typically averaged, but averaging is only justified if there is consistency within the data that enter the average. This is where the need for a consistency test emerges. If different types of brain activity have been recorded, such as different spike types or brain activity related to different stimulus types, the main research interest is usually to establish and characterize the differences between them. A difference test helps in this regard.

Traditional statistical measures in sensor space such as the t test make disputable assumptions regarding repeatability and independence [1, 2]. Therefore, a new non-parametric family of methods has recently attracted attention as it became computationally feasible for the analysis of ERP group studies [3]. Although–misleadingly–referred to as Topographic Analysis of Variance (TANOVA) [4], no analysis of variance is being conducted, but rather a non-parametric permutation or randomization test. TANOVA is usually applied to per-subject averaged data in the context of group studies and yields similarities within and differences between groups of subjects. It calculates significance on the level of samples and for complete topographic maps, not on the level of sensors.

To establish significance on the level of sensors or source locations, another family of non-parametric methods lends itself: originating in the functional neuroimaging field, Statistical non-Parametric Mapping (SnPM) by non-parametric permutation or randomization tests uses a maximum statistic to control the Family-Wise Error Rate (FWER) [5]. On the source location level, Current Density Reconstruction (CDR) SnPM has been applied to source analysis results obtained from averaged data in the context of group studies and used to assess differences between groups of subjects [6, 7]. On the sensor level, a maximum statistic over all samples has already been described [8, 9].

Comparability of multiple realizations of data, especially between subjects in a group study, is not always a given: For MEG recordings, there is typically no guarantee that the relative location of the head in the MEG helmet is the same between recordings. As a consequence, approaches comparing data on a channel-by-channel basis can be flawed. To a lesser degree, the same arguments holds for EEG studies, where subjects’ heads may have different sizes and, especially if electrode caps are used, the locations of electrodes relative to the head geometry will differ between subjects. Moving away from sensor data and calculating and comparing the distribution of source activity inside the brain may help, however, a variety of sometimes subtle issues arise. Most of these relate to the transition from individual head and brain anatomy to the template space in which results are going to be compared. But even then, due to the highly individual functional organization of the cortex, functionally equivalent brain responses may vary between subjects because of different locations or orientations of the cortical areas involved. Such dilemmas can obviously be avoided by performing consistency and difference tests on a per-subject level. In order to establish significance, multiple observations need to be available. Hence, tests that work on the level of individual subjects or patients require multiple realizations of brain activity as input data. This will typically be the individual epochs recorded in an ERP/ERF experiment, or multiple spikes.

Non-parametric statistical tests such as TANOVA and SnPM employ permutation or randomization techniques in order to create multiple realizations of input data. The number of randomizations is typically in the order of thousands. As a consequence, the resulting computational complexity may seem to be prohibitive to the application of such tests to individual epochs, whose number is usually in the hundreds, as opposed to the number of subjects in a group study, which is often below thirty.

We have developed a computational framework that allows the efficient application of TANOVA and SnPM not only to averaged group study data, but to all individual samples and epochs for single-subject data, and even to the individual epochs of all subjects participating in a group study. In the context of this framework, we have previously demonstrated the application of TANOVA to MEG [10] and EEG [11] sensor data and of CDR SnPM to source images [11] obtained from single-subject EEG data, using a temporal multiple comparison correction [11] for sample-by-sample evaluations. In this paper, we use SnPM for the analysis of MEG sensor data topography maps (referred to as Maps SnPM) and compare with TANOVA. The outcome of Maps SnPM is a time- or frequency-resolved breakdown of channels (sensors) that exhibit consistency within event type and channels that differ significantly between event types. Unlike described in previous publications, the statistical analysis is conducted sample-by-sample as opposed to using a maximum statistic over all samples [8, 9], thus following an approach already presented for group data [2], but using a multiple comparison correction that is based on the spectral properties of the data. For Maps SnPM, in addition to the test for significant differences between conditions, a within-condition consistency test is proposed which can be used to justify testing for differences on a sample-by-sample basis.

An auditory ERF MEG experiment eliciting Mismatch Negativity (MMN) is used to demonstrate the methods. The experiment employs two types of deviant stimuli which differ in how easy they can be discriminated from the standard stimulus. Using two types of deviants makes it possible to compare statistical analyses of otherwise equivalent data that are expected to differ in MMN and other oddball-dependent brain responses. Single-subject MEG data was used because with MEG recordings, between-subject comparisons of data on the sensor level are afflicted with more of the issues described above than is the case for EEG.

Methods

Mismatch negativity experiment

Acquisition and use of human subject data described in this submission has been approved by the Human Subject Research Ethics Committee/Institutional Review Board of Academia Sinica, Taiwan. Written consent forms were obtained from all participants.

For the MMN experiment, meaningful Mandarin syllables that all share the vowel/i/but differ in tonal contours were presented to native Mandarin speakers. The three syllables used as auditory stimuli were yi1 (“cloth”), yi2 (“aunt”), and yi3 (“chair”). Phonologically, yi1 can be categorized as a high–level tone, yi2 as a high-rising tone, and yi3 as a low-dipping tone. This same set of stimuli was already used in [12], where a comprehensive description of the experiment can be found. In this context, it is relevant to know that syllables yi2 and yi3 are harder to discriminate than yi1 and yi3 [13].

MEG recording

The subject, a healthy adult native Mandarin speaker without history of neurological or psychological disorders, lay in a magnetically shielded room and attended to a silent movie while passively listening to the stimuli. Stimuli were delivered binaurally using sound tubing. Yi3 was used as the standard stimulus, while yi1 and yi2 served as deviants. These three stimulus types will subsequently be referred to as standard, dev1, and dev2. An initial 20 trials of standards were followed by a pseudo-randomized presentation of 800 standard stimuli and 100 of each deviant, with at least two successive standards between deviants. The stimulus duration was 250 ms, with an inter-stimulus interval (ISI) of 500 ms. MEG data were recorded using a 157-channel axial gradiometer whole-head MEG system (Yokogawa Electric Corporation, Tokyo, Japan) with a sampling frequency of 1 kHz.

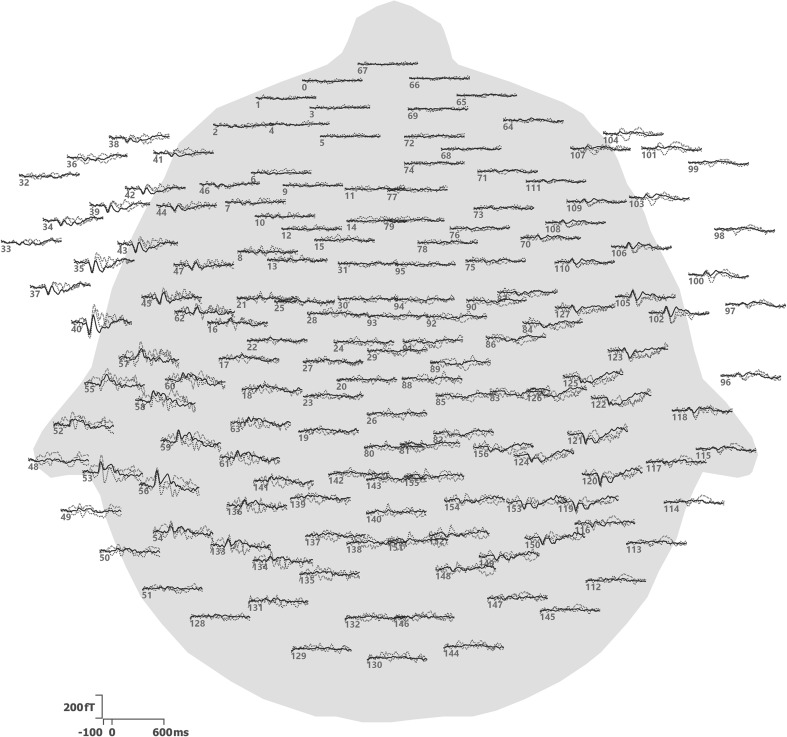
Data were baseline-corrected, filtered from 1 to 40 Hz and epoched from 100 ms before to 600 ms after stimulus onset. The initial 20 standard stimuli were excluded, as well as any epochs with signals exceeding ±1.5 pT, since signals of this magnitude are likely due to artifacts. The remaining epochs were down-sampled to 200 Hz. Averages for all three stimulus types were computed (Fig. 1). Signal processing was performed in the CURRY 8 software (Compumedics, Charlotte, NC, USA).

Fig. 1.

Averages for the three stimulus types, plotted at the locations of the sensors. Sensors are identified by their numbers. Waveforms cover latencies from −100 to 600 ms. Dashed red lines are used for dev1, dotted blue lines for dev2, and solid black lines for standard. The sensor array is viewed from above using a spherical projection, with the nose pointing upwards

Topographic analysis of variance

In the context of a TANOVA, two different non-parametric randomization tests were performed for all epochs: a consistency test per event type, and a test for differences between event types. Both tests have already been described [4] and are summarized here for reference only.

The consistency test evaluates field topography (map) similarity across epochs. The test is performed independently for each event type and each sample. Here, the Null Hypothesis is that epochs of the same event type are unrelated, i.e. that random maps have been measured. If the Null Hypothesis holds, randomly perturbing channels within each epoch’s maps should not deteriorate the average map across all epochs (the terms channel and sensor are used interchangeably).

For each sample s and E _c epochs of event type c, the test is performed as follows: First, the observed mean global field power (MGFP) P _s,c,0 of the average over all epochs e of the individual vectors of sensor data (maps) d _s,c,e is computed as

$$P_{s,c,0}=\text{mgfp}\left(\frac{1}{E_c}\sum _{e=1}^{E_c}{\mathbf{d}}_{s,c,e}\right)\text{with}\text{mgfp}\left(\mathbf{d}\right)=\sqrt{\frac{1}{M}\sum _{i=1}^M{\left(d_i-\frac{1}{M}\sum _{j=1}^M{d}_j\right)}^2}$$ 1

where M is the number of channels. Then, for a total of R repetitions, the channels within each map are randomly shuffled or perturbed. Typically, perturbation is used if the total number of perturbations is computationally feasible, while randomization is used in all other scenarios, including most real-world applications. For each repetition r, this yields new randomized maps d _s,c,e,r, and a new global field power P _s,c,r can be computed according to

$$P_{s,c,r}=\text{mgfp}\left(\frac{1}{E_c}\sum _{e=1}^{E_c}{\mathbf{d}}_{s,c,e,r}\right)$$ 2

The probability p _s,c of the Null Hypothesis is the fraction of values P _s,c,r that are larger than or equal to P _s,c,0. Small values of p, traditionally p < 0.05, indicate rejection of the Null Hypothesis, or consistency between epochs of the same event type. The number of possible permutations is M! [5] and must be larger than the number of randomizations. This is typically the case for 8 and more channels.

The test for differences between event types is again performed independently for each sample. Here, the Null Hypothesis is that there is no difference between event types, i.e. that the same maps occur regardless of event type. If the Null Hypothesis holds, randomly perturbing maps across event types should not alter the average maps per event type.

When just two event types are compared, the MGFP of the difference of the averaged maps per event type can serve as the measure. For each sample, the test is performed as follows: In a first step, the observed global field power P _s,0 of the difference of the averages over all epochs of event types c = 1 and c = 2 is computed as

$$P_{s,0}=\text{mgfp}\left(\frac{1}{E_1}\sum _{e=1}^{E_1}{\mathbf{d}}_{s,1,e}-\frac{1}{E_2}\sum _{e=1}^{E_2}{\mathbf{d}}_{s,2,e}\right)$$ 3

For R repetitions, maps are then randomly shuffled across event types. For each repetition r, randomized maps d _s,c,e,r are obtained and the global field power P _s,r can be computed according to

$$P_{s,r}=\text{mgfp}\left(\frac{1}{E_1}\sum _{e=1}^{E_1}{\mathbf{d}}_{s,1,e,r}-\frac{1}{E_2}\sum _{e=1}^{E_2}{\mathbf{d}}_{s,2,e,r}\right)$$ 4

Again, the probability p _s of the Null Hypothesis is the fraction of values P _s,r that are larger than or equal to P _s,0. Small values of p indicate significant map differences between event types. Because a map-based, global measure of map similarity has been used, no correction for multiple testing across channels is necessary. The number of possible permutations, which again must be larger than the number of randomizations, is (E ₁ + E ₂)!/(E ₁!E ₂!) [5], which is typically the case for 8 and more epochs per type.

To validate the results of the Maps SnPM test described below, a TANOVA channel impact map can be computed. The channel impact map allows visualizing the impact of each individual channel onto the difference between event types and can be used to pick the channel that best illustrates the observed difference. It is calculated based on the singular value decomposition (SVD) [14] of all average maps per subject and event type used to determine the observed global field power P _s,0, which in the single-subject, two event-type scenario can be written as

$$\left[\frac{1}{E_1}\sum _{e=1}^{E_1}{\mathbf{d}}_{s,1,e},\frac{1}{E_2}\sum _{e=1}^{E_2}{\mathbf{d}}_{s,2,e}\right]=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^T$$ 5

Here, U is an M × M orthogonal matrix, Σ is an M × 2 non-negative diagonal matrix containing the singular values in descending order, V ^T is the transpose of the 2 × 2 orthogonal matrix V, and U ^T U = V ^T V = I. The first column of U corresponds to the first singular value in Σ. The individual values in this column are therefore a first-order measure of how strongly each channel is responsible for the variability between average maps per event type. For each sample s, the channel impact map c _s can therefore be expressed as the vector of absolute values of the first column of U, normalized to its largest entry:

$${\mathbf{c}}_s=\frac{1}{ma{x}_i\left|U_{i,1}\right|}\left[\begin{array}{c}\left|U_{1,1}\right|\\ ⋮\\ \left|U_{M,1}\right|\end{array}\right]$$ 6

As both the consistency test and the difference test are performed sample by sample, false positives are to be expected. A test for the significance of consecutive rejections of the Null Hypothesis can establish, whether such periods of significance are significant themselves and has been described in [4].

Optionally, data may be collapsed across samples-of-interest to increase the Signal-to-Noise Ratio (SNR). Averaged maps may be normalized before computing the difference, in order to ignore absolute effect sizes. An extension to more than two and to different categories of event types using a measure called global dissimilarity has been described in [1]. TANOVA computation times scale linearly with the number of samples, number of randomizations, and number of channels. If the EEG/MEG input data are transformed into the frequency domain using e.g. a Fast Fourier Transform (FFT), TANOVA analysis will work sample-by-sample in the frequency domain. For increased computational performance, calculations can be parallelized on the level of samples and/or randomizations.

TANOVA analysis was performed using the CURRY 8 software. For this paper, an experiment-wide significance level $\overline{\mathit{\alpha }}$ of 0.05 was used. Map normalization was used for the difference tests, such that for each sample, the MGFP per map was equal to 1. The complete time range from −100 to 600 ms was analyzed.

Statistical non-Parametric Mapping

The input data for SnPM can be CDR source images, but also beamformer results or voltage topographies [9]. In this case, MEG field topography maps are analyzed and the term Maps SnPM is used to designate the method. All data points of these MEG field topography maps have been recorded by technically identical sensors within a small range of distances from the subject’s head. As a consequence, using MEG field topography maps as input data for SnPM yields uniform spatial sensitivity of the statistical test [8]. In order to stick to established terminology, the terms image and voxel will be used, which in this case denote field topography map and sensor/channel data, respectively. As for TANOVA, a consistency test per event type and a test for differences between event types can be performed.

The consistency test evaluates image/field topography map similarity across epochs. It is performed independently for each event type and each sample. Here, the Null Hypothesis is that epochs of the same event type are unrelated, i.e. that images are random. If the Null Hypothesis holds, randomly perturbing voxels/channels within each epoch’s image should not deteriorate the average image across all epochs.

For each sample s and event type c, the test is performed as follows: First, for each voxel n, a t-value is obtained using a one-sample t test. This t value t _s,c,n,0 scores the hypothesis that the mean voxel intensity across all E _c images is zero:

$$t_{s,c,n,0}=\frac{\overline{i_{s,c,\ast ,n}}}{\mathit{\sigma }\left(i_{s,c,\ast ,n}\right)/\sqrt{E_c}}$$ 7

Here, i _s,c,e,n is the n-th voxel of image I _s,c,e and the asterisk * denotes the dimension (epochs, in this case) over which the average and standard deviation (SD) σ have been calculated. Then, for a total of R repetitions, the voxels within each image are randomly shuffled. For each repetition r, this yields new randomized images I _s,c,e,r, and new t-values t _s,c,n,r can be computed according to

$$t_{s,c,n,r}=\frac{\overline{i_{s,c,\ast ,r,n}}}{\mathit{\sigma }\left(i_{s,c,\ast ,r,n}\right)/\sqrt{E_c}}$$ 8

The SD σ used for computing the t-values in Eqs. 7 and 8 is special in that it is additionally spatially smoothed. The reason for smoothing is that likely errors in estimating the SD or variance from voxel to voxel would otherwise lead to noisy t-statistic images, although in a typical recording setup the variance should be spatially smooth [5]. Smoothing may be implemented as taking the average across all voxels, or alternatively by using a smoothing kernel. This smoothing kernel must take into account, that the sensor map images I are not defined on a regular lattice as is usually the case for pixel images, but according to the MEG sensor layout. A different smoothing kernel should therefore be used per sensor, which might employ a (distance-weighted) average of the nearest sensors.

After randomization, a significance threshold t _s,c is computed as the (1 − p)100th percentile across repetitions, based on the largest absolute t-values across all voxels per repetition. This maximum t-statistic controls the FWER and is a means of multiple comparison correction across voxels [15]. For all voxels with |t _s,c,n,0| < t _s,c the Null Hypothesis is confirmed, while for all other voxels consistency across epochs has been established. To visualize the locations-of-consistency as a channel topography map, a t-statistic image can be generated based on |t _s,c,n,0| where values of t below the significance threshold are set to zero.

The test for differences between event types is again performed independently for each sample. Here, the Null Hypothesis is that there is no difference between event types, i.e. that the same images occur regardless of event type. If the Null Hypothesis holds, randomly perturbing images across event types should not alter the average images per event type.

For each sample s, the test is performed as follows: First, an F test is performed using a one-way Analysis of Variance (ANOVA) for each voxel n where the event types c are regarded as the factors [16]. The F-value F _s,n,0 thus obtained measures the hypothesis that the voxel means of all E _c images per event type are equal. For R repetitions, images are then randomly shuffled across event types. For each repetition r, randomized images I _s,c,e,r are obtained and F-values F _s,n,r can be computed per voxel. Next, a significance threshold F _s is computed as the (1 − p)100th percentile across repetitions, based on the largest F-values across all voxels per repetition (maximum F-statistic). For all voxels with F _s,n,0 < F _s the Null Hypothesis is confirmed, while for all other voxels it has been established that they are significantly different. To visualize the locations of significance, an F-statistic image can be generated based on F _s,n,0 where values of F below the significance threshold are set to zero. Because a global measure of image difference has been used, no further correction for multiple testing across voxels is necessary. While the F test per se is known to be non-robust against deviations from normality, in the context of SnPM it is only the ordering of, not the absolute F values that determine significance.

Again, a test for the significance of consecutive rejections of the Null Hypothesis can be performed [2]. Optionally, data may be collapsed across samples-of-interest to increase the SNR. Images may be normalized before entering the calculations. Normalization allows comparing relative as opposed to absolute field magnitudes. An extension to different categories of event types is possible using ANOVA for multiple factors [16]. Maps SnPM computation times scale linearly with the number of samples, number of randomizations, and number of channels. As for TANOVA, Maps SnPM can also be used on FFT-transformed data and will then work in the frequency domain. Parallelization is possible on the level of samples and/or randomizations. Maps SnPM analysis was performed using the CURRY 8 software. Again, an experiment-wide significance level $\overline{\mathit{\alpha }}$ of 0.05 was used. Map normalization and σ-averaging were applied. The complete time range from −100 to 600 ms was analyzed.

Multiple comparison correction

Neither TANOVA nor SnPM per se require a multiple comparison correction across sensors, because both process measures based on complete topography maps, not individual sensors: for TANOVA, this measure is the difference MGFP, while for SnPM it is a maximum statistic. However, both types of statistical analysis are performed for each sample independently. Analyzing neighboring samples leads to multiple comparisons if they do not represent independent measures, which is the case if the spectral content of the data is impaired by low-pass filtering or otherwise limited. Therefore, a temporal multiple comparison correction has to account for the oversampling introduced by low-pass filtering.

Of course, even in a low-pass-filtered dataset, every sample is different, making it not quite straightforward to determine the number of non-independent comparisons n to correct for. The approach taken here has been introduced in [11] and is based on the consideration that, according to the Nyquist-Shannon sampling theorem [17], after filtering using a cutoff frequency of f _c, data may later be resampled at 2 f _c without losing information. If the original sampling frequency is f _s, the number of ways to perform this resampling is f _s/2f _c, which equals the number of samples that could be used as the first sample. As a consequence, the number of comparisons n to consider when analyzing low-pass filtered data sample by sample is

$$n=\frac{f_s}{2f_c}$$ 9

The corresponding multiple comparison-corrected significance level α using the Šidák correction [18] is

$$\mathit{\alpha }=1-{\left(1-\overline{\mathit{\alpha }}\right)}^{1/n}=1-{\left(1-\overline{\mathit{\alpha }}\right)}^{2f_c/f_s}$$ 10

with $\overline{\mathit{\alpha }}$ the experiment-wide significance level.

For this paper, using low-pass filtered data with f _c = 40 Hz and $\overline{\mathit{\alpha }}$ = 0.05, a corrected significance threshold of α = 0.0203 was used and values of p < 0.0203 were regarded as significant. Here, the cutoff frequency of 40 Hz was defined as the frequency at which the transmission curve of the FFT-based low-pass filter dipped below 50%. As suggested by Manly [19], the corresponding required number of repetitions was chosen to be R = 50/α = 2462.

Results

After excluding epochs with signals exceeding ±1.5 pT, 982 epochs of 141 samples each remained: 99 of type dev1, 99 of type dev2, and 784 of type standard. These epochs were subjected to TANOVA and Maps SnPM analysis. Table 1 shows the numbers and ranges of significant samples obtained.

Table 1.

Numbers and ranges of significant samples obtained for consistency and difference tests

	TANOVA		Maps SnPM
	No. of samples	Latency ranges (ms)a	No. of samples	Latency ranges (ms)a
dev1 Consistency	82	40–50, 80–130, 145–205, 275–400, 515–600	77	35–50, 80–135, 145–205, 220–225, 290–340, 365–400, 515–535, 555–600
dev2 Consistency	79	25–40, 80–130, 145–310, 220–225, 335–350, 385–395, 455–470, 525–550, 560–600	65	85–130, 150–185, 200–265, 335–355, 390–405, 455–470, 555–600
standard Consistency	122	10–65, 80–600	121	0–25, 45–65, 75–600
dev1/standard Difference	32	185–255, 300–340, 380–405, 510–515	39	180–250, 300–340, 370–430
dev2/standard Difference	11	175–190, 455–475	17	170–200, 450–470, 485–495

^aPre-stimulus latencies not included

TANOVA consistency (Fig. 2) was established for dev1 at 82, dev2 at 79, and standard at 122 samples. TANOVA differences (Fig. 3) between dev1 and standard were significant for 32 samples and differences between dev2 and standard were significant for 11 samples, not including the 225 ms latency. Channel impact maps for the 225 ms latency indicated involvement of the posterior lateral channels. The 225 ms latency was used as an example to illustrate channel impact and channel significance maps, as it in some cases borders on or lies within latencies of non-significance.

Fig. 2.

TANOVA consistency test results for stimulus types dev1 (first row), dev2 (second row), and standard (third row). White areas indicate consistency, with p < 0.0203, while gray areas indicate that significance could not be established. Waveforms are MGFPs of the average per stimulus type and shown for guidance only. To the left of each row, field topography maps are shown for the 225 ms latency. The contour line distance is 10 fT and negative contour lines are dashed and rendered in blue, while positive contour lines are solid and red. The zero-line is solid and black. The sensor array is viewed from above using a spherical projection, with the nose pointing upwards

Fig. 3.

TANOVA difference test results for stimulus types dev1 vs. standard (first row) and dev2 vs. standard (second row). White areas indicate significant topography map differences, with p < α, while gray areas indicate that significance could not be established. Waveforms are p values, displayed using a logarithmic scale. The horizontal dotted line marks the corrected significance threshold of α = 0.0203. The numbers in the upper right of each row are the p values for the 225 ms latency. To the left of each row, channel impact maps are shown, where darker colors indicate a higher impact. The sensor array is viewed from above using a spherical projection, with the nose pointing upwards

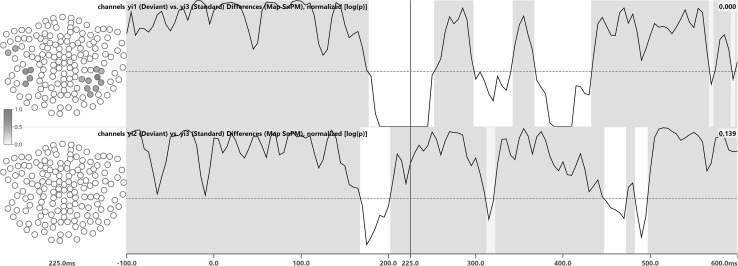
Maps SnPM consistency (Fig. 4) was established for 77, 65, and 121 samples, respectively. For the 225 ms latency, consistency was established for 3 left lateral channels (dev1), 4 bilateral channels (dev2), and 53 bilateral channels (standard). Maps SnPM differences (Fig. 5) between dev1 and standard were significant for 39 samples and differences between dev2 and standard were significant for 17 samples, not including the 225 ms latency. For the 225 ms latency, 15 channels, all of them located in the posterior lateral region, were determined to be significantly different between dev1 and standard.

Fig. 4.

Maps SnPM consistency test results for stimulus types dev1 (first row), dev2 (second row), and standard (third row). White areas indicate significant consistency on the channel level in at least one channel, with p < α, while gray areas indicate that significance could not be established for any channel. Waveforms are p values, displayed using a logarithmic scale. The horizontal dotted line marks the corrected significance threshold of α = 0.0203. The numbers in the upper right of each row are the p values for the 225 ms latency. To the left of each row, channel significance maps are shown, where darker colors indicate higher t values and thus significance, while all other channels that are not significant are rendered in white. For comparability, channel significance maps are normalized to their largest entry. The sensor array is viewed from above using a spherical projection, with the nose pointing upwards

Fig. 5.

Maps SnPM difference test results for stimulus types dev1 vs. standard (first row) and dev2 vs. standard (second row). White areas indicate significant channel data differences in at least one channel, with p < α, while gray areas indicate that significance could not be established for any channel. Waveforms are p values, displayed using a logarithmic scale. The horizontal dotted line marks the corrected significance threshold of α = 0.0203. The numbers in the upper right of each row are the p values for the 225 ms latency. To the left of each row, channel significance maps are shown, where darker colors indicate higher F values and thus significance, while all other channels that are not significant are rendered in white. For comparability, channel significance maps are normalized to their largest entry. The sensor array is viewed from above using a spherical projection, with the nose pointing upwards

The combined computation times of consistency and difference tests on a 2.3 GHz Core i7 CPU with 2462 randomizations each for 157 channels and 982 epochs, performed for all 141 samples per epoch at 200 Hz, were 218 s for TANOVA and 254 s for Maps SnPM.

Discussion

Consistency tests

Consistency test results are calculated for each stimulus type independently and test the consistency between individual epochs of the same stimulus type. If the subject does not pay attention to the stimuli or is otherwise unable to perceive or process the presented stimuli, the consistency test will fail. The consistency test will also fail if the number of epochs is too small or the SNR per epoch is too low.

The waveforms overlaid onto the TANOVA consistency test results in Fig. 2 are the MGFP of the averaged data per stimulus type. The MGFP summarizes the amount of variance in the data and therefore scales with the overall SNR. As a consequence, it shows dominant peaks that may occur in different groups of channels, while a small MGFP indicates low activity across all channels. Consistency is typically established for latencies where the SNR of the average is high, which explains why there is a correspondence between the amplitude of the MGFP and the latencies-of-consistency detected by TANOVA and Maps SnPM. For TANOVA, this correspondence can be observed in Fig. 2.

Both TANOVA (Fig. 2) and Maps SnPM (Fig. 4) revealed fewer samples-of-consistency for the deviant stimuli dev1 and dev2 than for the standards. This is due to the fact that for the deviants, by definition, fewer epochs were recorded than for the standards. Fewer epochs lead to noisier averages and therefore lower consistency. In some cases, consistency was detected before stimulus onset, which can be explained by the relatively low ISI of 500 ms only, potentially leading to spillover of activity from the previous stimulus [20].

Difference tests

In the difference tests (Figs. 3, 5), fewer latencies-of-significance were identified for the dev2/standard comparison than for dev1/standard. This is due to the fact that Mandarin syllables yi2 (dev2) and yi3 (standard) sound more similar than yi1 (dev1) and yi3 (standard). Both dev1 as well as dev2 and standard were found to be different around 200 ms (N200/MMN). The fact that significant latencies occurred earlier for dev2/standard than for dev1/standard should not be taken as proof of an earlier occurrence of the magnetic MMN itself: latencies with significant differences, be it overall (TANOVA) or on the sensor level (Maps SnPM) just indicate that differences in map topographies or sensor data actually do exist and are not due to chance.

Both TANOVA and Maps SnPM detected differences between dev1 and standard after 300 ms. These differences might indicate the MEG equivalent of a P300 brain response, which has previously been observed in passive listening conditions [21]. Likewise, the dev1/standard differences found around 400 ms could be suggestive of a magnetic N400, which has also been reported to sometimes occur during passive listening [22]. The MMN paradigm used in this experiment is certainly not a typical experiment for P300 and N400 components to be elicited. Therefore, other origins for the 300 and 400 ms differences should not be ruled out.

Channel impact maps and sensor significance maps

Comparing the sensor significance maps for the Maps SnPM consistency tests for the 225 ms latency (Fig. 4) with the corresponding averaged maps (Fig. 2) shows, that channels with larger amplitudes and correspondingly higher SNR are more likely to be determined as significant in the consistency test than low-amplitude channels.

The Maps SnPM difference tests (Fig. 5) identified 15 left and right lateral posterior channels as significant for dev1 at 225 ms. The TANOVA difference channel impact maps (Fig. 3) confirm that these are the channels contributing most strongly to the topography differences at that latency [12]. For dev2 at 225 ms, no channels bearing significant differences were identified. The corresponding gray backdrop also indicates that significant differences could not be established for any channel at that latency. TANOVA difference channel impact maps are auto-scaled, which means that the number of channels exceeding a given threshold does not disclose anything about the number of actually significant channels. To calculate channel significances, Maps SnPM needs to be used. Channel significance maps are calculated per sample.

Comparison of TANOVA and Maps SnPM

While in the consistency tests TANOVA found 7.6% more significant samples than Maps SnPM, in the difference tests the ratio was reversed and TANOVA yielded a 23% smaller number of significant samples than Maps SnPM (see Table 1). On the whole, TANOVA identified a 2.2% larger number of significant samples. Based on the existing data, it cannot be concluded that either method shows a higher overall sensitivity. TANOVA works on the level of topographic maps and does not calculate significance on the sensor level. The proposed new method Maps SnPM, however, comes with the added benefit of identifying the exact sensors for which significance has been established. This added benefit provides a strong incentive to use Maps SnPM for the statistical analysis of sensor data.

Conclusions

TANOVA and Maps SnPM were applied to the individual epochs obtained in an evoked-response experiment. The TANOVA analysis demonstrated data plausibility and identified latencies-of-interest for further analysis, such as source reconstruction. Maps SnPM, in addition to the above, identified sensors of significantly different activity between stimulus types. The maximum statistic used in SnPM summarizes the individual channel statistics into a single measure, thus addressing the spatial multiple comparison problem. The extension to the individual epochs of subjects in a group study is straightforward. The application to EEG data is possible as an alternative to using the method on MEG data.

Compliance with ethical standards

Conflict of interest

The CURRY software used in this submission is a commercial product of Compumedics USA, Charlotte, NC, USA. The authors of this paper are employees of Compumedics Europe GmbH, Hamburg, Germany. Both Compumedics Europe GmbH and Compumedics USA are subsidiaries of Compumedics Ltd., Melbourne, Australia.