Electrodeless conductivity tensor imaging (CTI) using MRI: basic theory and animal experiments

Abstract

The electrical conductivity is a passive material property primarily determined by concentrations of charge carriers and their mobility. The macroscopic conductivity of a biological tissue at low frequency may exhibit anisotropy related with its structural directionality. When expressed as a tensor and properly quantified, the conductivity tensor can provide diagnostic information of numerous diseases. Imaging conductivity distributions inside the human body requires probing it by externally injecting conduction currents or inducing eddy currents. At low frequency, the Faraday induction is negligible and it has been necessary in most practical cases to inject currents through surface electrodes. Here we report a novel method to reconstruct conductivity tensor images using an MRI scanner without current injection. This electrodeless method of conductivity tensor imaging (CTI) utilizes B1 mapping to recover a high-frequency isotropic conductivity image which is influenced by contents in both extracellular and intracellular spaces. Multi-b diffusion weighted imaging is then utilized to extract the effects of the extracellular space and incorporate its directional structural property. Implementing the novel CTI method in a clinical MRI scanner, we reconstructed in vivo conductivity tensor images of canine brains. Depending on the details of the implementation, it may produce conductivity contrast images for conductivity weighted imaging (CWI). Clinical applications of CTI and CWI may include imaging of tumor, ischemia, inflammation, cirrhosis, and other diseases. CTI can provide patient-specific models for source imaging, transcranial dc stimulation, deep brain stimulation, and electroporation.

Introduction

Mobile ions and charged molecules in a biological tissue conduct electrical current when an electric field is applied endogenously or exogenously. Following Ohm’s law, the current density is proportional to the electric field with the electrical conductivity as the proportionality constant. The electrical conductivity of an electrolyte at a macroscopic scale is determined by the sum of the products of concentrations and mobility of the charge carriers [1]. Since the conductivity is a passive material property, its measurement requires a probing method to produce current passing through the medium. One may then measure the induced voltage or magnetic field to estimate the conductivity value [2].

A biological tissue has a complicated structure of cells, extracellular matrix, and extracellular fluid. Cells have thin insulating membranes, intracellular fluid, and organelles. Dominant charge carriers in extracellular and intracellular fluids are ions such as sodium, potassium, chloride, and calcium. The concentration of a charge carrier is a scalar quantity independent of the frequency of a probing current. Mobility of a charge carrier is determined by the inherent properties of the particle itself such as its size and shape as well as the environmental properties such as temperature, hydration, and viscosity of the fluid. In addition, the structural properties such as size, shape, density, and layout of cells, extracellular matrix materials, and intracellular organelles also affect mobility. Among these, the structural properties may give rise to anisotropic mobility.

Anisotropy is observed in tissues such as muscle and white matter. It is prominent at low frequency since thin insulating cell membranes block low-frequency current and make the entire cells appear as insulators. Anisotropy mostly disappears at high frequency above 1 MHz since high-frequency current effectively passes through cell membranes to make the cellular structure disappear in effect. The conductivity is, therefore, a scalar quantity at high frequency and can be expressed as a tensor at low frequency.

Electrical impedance tomography (EIT) reconstructs conductivity images by injecting ac currents and measuring boundary voltages using multiple surface electrodes [3, 4]. It produces low-resolution functional images of time-changes of a conductivity distribution with clinical applications such as lung ventilation and perfusion imaging [5]. Magnetic resonance electrical impedance tomography (MREIT) visualizes internal conductivity distributions by injecting dc currents and measuring induced magnetic flux densities using an MRI scanner [6–8]. High-resolution conductivity imaging in MREIT demands current injections of a few milliamperes for satisfactory image quality and this may cause adverse effects of nerve and muscle stimulations depending on a chosen imaging area.

Noting that diffusion weighted MRI provides information about water mobility in a biological tissue, diffusion tensor imaging (DTI) has been utilized for conductivity tensor imaging assuming that the conductivity tensor is a scalar multiple of the water diffusion tensor [9, 10]. To convert the water diffusion tensor to conductivity tensor, either a fixed scale factor was used [11] or current-injection methods were adopted to determine the position-dependent scale factor in diffusion tensor MREIT (DT-MREIT) [8, 12]. On the other hand, magnetic resonance electrical properties tomography (MREPT) provides conductivity and permittivity images at the Larmor frequency of an MRI scanner (about 128 MHz at 3 T) [13–15]. It is based on a B1 mapping technique to measure the effects of eddy currents induced by RF pulses. At the Larmor frequency, however, useful low-frequency conductivity contrast information disappears. Since most physiological events occur at low frequencies of below 1 kHz, we are interested in non-invasive in vivo imaging methods to quantitatively visualize low-frequency conductivity tensor distributions.

In this paper, a new electrodeless low-frequency conductivity tensor imaging (CTI) method is proposed based on the following two observations.

• Information about the concentration of a charge carrier is embedded in the high-frequency conductivity and the concentration is independent of frequency.

• Mobility of a charge carrier is proportional to that of a water molecule when they exist in the same microscopic environment.

Without requiring current injection, the proposed CTI method can be easily implemented in a clinical MRI scanner. Theoretical derivation of CTI will be followed by the details of its implementation based on B1 mapping and multi-b diffusion weighted imaging methods. Results of animal imaging experiments will be presented and discussed. Limitations of the proposed method related with a few required assumptions will be remarked in terms of the theoretical and also practical aspects. In this paper, we will focus on constructing a new framework for CTI and future studies will be suggested for more rigorous validations of the proposed CTI method. All variables in this paper are functions of a position vector r = (x, y, z) with a few exceptions which will be clearly distinguished from the context.

Methods

Derivation of CTI formula

Tables 1 and 2 summarize the charge carriers and the symbols of the physical quantities, respectively, considered in this section. This section is based on a few assumptions which will be discussed later in this paper. First, we assume that high-frequency probing currents pass through thin insulating cell membranes. Then, the high-frequency conductivity σ_H of a macroscopic voxel can be expressed as

$$\begin{array}{cc}\hfill {\sigma }_H& =\chi {\sigma }_e+\left(1-\chi \right){\sigma }_i\hfill \\ \hfill & =\chi \sum _{j=1}^{M}q{A}_v{z}^{\left(j\right)}{\gamma }_e^{\left(j\right)}{c}_e^{\left(j\right)}{m}_e^{\left(j\right)}+\left(1-\chi \right)\sum _{j=1}^{N}q{A}_v{z}^{\left(j\right)}{\gamma }_i^{\left(j\right)}{c}_i^{\left(j\right)}{m}_i^{\left(j\right)}.\hfill \\ \hfill \end{array}$$ 1

Choosing the first charge carrier (j = 1) as a reference, mobility of the jth charge carrier is

$$m_{\text{e}}^{\left(j\right)}=k^{\left(j\right)}{m}_e^{\left(1\right)}\text{and}{m}_{\text{i}}^{\left(j\right)}=k^{\left(j\right)}{m}_i^{\left(1\right)}$$ 2

where k^(j) is a constant for each j with k⁽¹⁾ = 1. The mobility-weighted effective concentrations ${\overline{c}}_e$ and ${\overline{c}}_i$ can be defined as

$${\overline{c}}_e=\sum _{j=1}^{M}q{A}_v{z}^{\left(j\right)}{\gamma }_e^{\left(j\right)}{c}_e^{\left(j\right)}{k}^{\left(j\right)}\text{and}{\overline{c}}_i=\sum _{j=1}^{N}q{A}_v{z}^{\left(j\right)}{\gamma }_i^{\left(j\right)}{c}_i^{\left(j\right)}{k}^{\left(j\right)}.$$ 3

The high-frequency conductivity is then expressed as

$${\sigma }_H=\chi {\overline{c}}_e{m}_e^{\left(1\right)}+\left(1-\chi \right){\overline{c}}_i{m}_i^{\left(1\right)}.$$ 4

From the Einstein relation, we have

$$m_{\text{e}}^{\left(1\right)}=\left(\frac{q}{k_{B}T}\right)d_e^{\left(1\right)}\text{and}{m}_i^{\left(1\right)}=\left(\frac{q}{k_{B}T}\right)d_i^{\left(1\right)}$$ 5

where k_B is the Boltzman constant and T is the absolute temperature. The diffusion coefficients $d_e^{\left(1\right)}$ and $d_i^{\left(1\right)}$ are determined by Stoke’s radius of the particle and the medium viscosity. Considering that the reference charge carrier and water molecule exist in the same microscopic environment, we set

$$m_{\text{e}}^{\left(1\right)}=K{d}_e^w\text{and}{m}_i^{\left(1\right)}=K{d}_i^w$$ 6

for some constant K. We further assume that

$${\overline{c}}_i=\beta {\overline{c}}_e$$ 7

for some constant β. From (4) to (7), ${\overline{c}}_e$ is expressed as

$${\overline{c}}_e=\frac{1}{K}\frac{{\sigma }_H}{\chi d_e^w+\left(1-\chi \right)d_i^w\beta }$$ 8

which is independent of the choice of the reference charge carrier.

Table 1.

Charge carriers in a biological tissue. P is the last charge carrier to be considered with its net charge of ± qz^(j)C

Index (j)	1	2	3	4	…	M or N
Charge carrier	Na+	K+	Cl−	Ca2+	…	$P^{\pm z^{\left(j\right)}}$

Table 2.

Symbols of physical quantities included in the derivation of the CTI formula in Eq. (10)

Quantity	Symbol	Unit
Absolute value of the charge of the electron	q	1.6 × 10−19 C
Avogadro’s number	A v	6.02 × 1023 1/mol
Extracellular and intracellular conductivities	σe and σi	S/m
Extracellular and intracellular activity coefficients of the jth charge carrier	${\gamma }_e^{\left(j\right)}\text{and}{\gamma }_i^{\left(j\right)}$	$0<{\gamma }_e^{\left(j\right)},{\gamma }_i^{\left(j\right)}<1$
Extracellular and intracellular concentrations of the jth charge carrier	$c_e^{\left(j\right)}\text{and}{c}_i^{\left(j\right)}$	mol/m3
Extracellular and intracellular mobility of the jth charge carrier	$m_e^{\left(j\right)}\text{and}{m}_i^{\left(j\right)}$	m2/Vs
Extracellular and intracellular water diffusion coefficients	$d_e^w\text{and}{d}_i^w$	m2/s
Extracellular and intracellular mobility tensors of the jth charge carrier	${\mathbf{M}}_e^{\left(j\right)}\text{and}{\mathbf{M}}_i^{\left(j\right)}$	m2/Vs
Extracellular and intracellular water diffusion tensors	${\mathbf{D}}_e^w\text{and}{\mathbf{D}}_i^w$	m2/s
Volume fraction of extracellular space	χ	0 < χ < 1
High-frequency and low-frequency conductivities	σH and σL	S/m
Conductivity tensor	C	S/m

Since low-frequency conduction currents flow only in the extracellular space (Fig. 1a), we set $m_i^{\left(1\right)}=0$ in Eq. (4) at low frequency to get the low-frequency conductivity σ_L of a presumed isotropic macroscopic voxel as

$${\sigma }_L=\chi {\overline{c}}_e{m}_e^{\left(1\right)}=K\chi {\overline{c}}_e{d}_e^w=\frac{\chi {\sigma }_H}{\chi d_e^w+\left(1-\chi \right)d_i^w\beta }{d}_e^w=\eta d_e^w$$ 9

where η is a position-dependent scale factor. For an anisotropic macroscopic voxel, $m_e^{\left(1\right)}$ in (9) is replaced by ${\mathbf{M}}_e^{\left(1\right)}$ (Fig. 1b) to get the low-frequency conductivity tensor C as

$$\mathbf{C}=\chi {\overline{c}}_e{\mathbf{M}}_e^{\left(1\right)}=K\chi {\overline{c}}_e{\mathbf{D}}_e^w=\frac{\chi {\sigma }_H}{\chi d_e^w+\left(1-\chi \right)d_i^w\beta }{\mathbf{D}}_e^w=\eta {\mathbf{D}}_e^w$$ 10

where we assume ${\mathbf{M}}_e^{\left(1\right)}=K{\mathbf{D}}_e^w$. The formulae in Eq. (9) and (10) provide a new framework for electrodeless low-frequency conductivity imaging using MRI. As mentioned early in this section, these formulae are based on a few assumptions, of which validations will be discussed later in this paper as future studies.

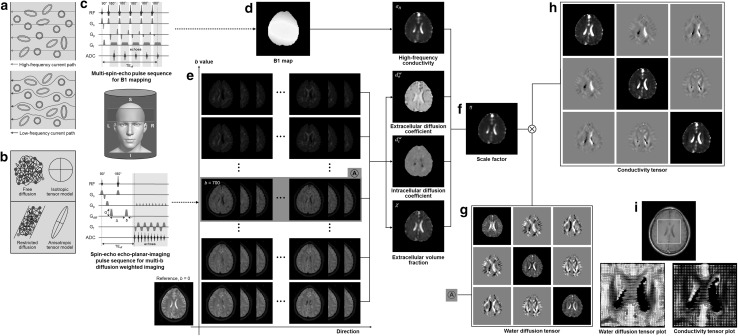
Fig. 1.

a High-frequency current passes through cells and low-frequency current flows through only the extracellular space. b We may express mobility of a charge carrier in free motion as a scalar or isotropic tensor variable and in restricted or hindered motions as an anisotropic tensor variable. The electrical conductivity is, therefore, expressed as a scalar quantity at high frequency and a tensor quantity at low frequency. c Conductivity tensor images are reconstructed from two separate scans of B1 mapping and multi-b diffusion weighted imaging. d The high-frequency conductivity image is reconstructed from the B1 map. e–g The variables associated with mobility and volume fraction are extracted from the multi-b data sets. h, i These are combined to produce the conductivity tensor image

Implementation of CTI

Figure 1 depicts the image reconstruction process of the proposed CTI method. Motions of charge carriers contributing to low-frequency conduction currents are restricted in the extracellular space and hindered by cells and extracellular matrix materials. This results in σ_L that is smaller than σ_H (Fig. 1a). Structural directionality of a tissue gives rise to an anisotropic conductivity that can be expressed as a tensor C (Fig. 1b). The electrodeless CTI method requires two separate MRI scans. One is the multi-b diffusion weighted imaging method to estimate $d_e^w$, $d_i^w$, χ, and ${\mathbf{D}}_e^w$. The other is the B1 mapping method to estimate σ_H (Fig. 1c).

Estimation of $d_e^w$, $d_i^w$, and χ

Diffusion weighted imaging measures the effects of Brownian motions of water molecules in a voxel to provide quantitative information about the tissue microstructure and its functions [16, 17]. A pair of diffusion encoding gradients are applied to measure the average water diffusion with a chosen b value defined as

$$b={\gamma }^2{\delta }^2{G}^2\left(\mathrm{\Delta }-\frac{\delta }{3}\right)$$ 11

where γ is the gyromagnetic ratio of hydrogen, δ is the width of the gradient pulse, G is the gradient strength, and ∆ is the diffusion time [18]. Denoting the jth direction of the gradient as a unit vector g_j, the acquired diffusion weighted MR image value S_b,j of a voxel is expressed as

$$S_{b,j}=S_0{e}^{-b{D}_{b,j}}=S_0{e}^{-b{\mathbf{g}}_j^T{\mathbf{D}}_b{\mathbf{g}}_j}$$ 12

where S₀ is the MR image value without diffusion gradient, D_b,j is the diffusion coefficient for the chosen b value along the g_j direction, and D_b is the symmetric 3 × 3 diffusion tensor at the b value.

The diffusion weighted images from all gradient directions for each b value are averaged to get the image S_b as

$$S_b=\frac{1}{N_D}\sum _{j=1}^{N_D}{S}_0{e}^{-b{\mathbf{g}}_j^T{\mathbf{D}}_b{\mathbf{g}}_j}$$ 13

where N_D is the number of gradient directions. Using the Taylor series expansion, we can see that the image S_b still exhibits the exponential decay property at each voxel:

$$S_b\approx S_0\left(1-\frac{b}{N_D}\sum _{j=1}^{N_D}{\mathbf{g}}_j^T{\mathbf{D}}_b{\mathbf{g}}_j\right)\approx S_0{e}^{-\frac{b}{N_D}\sum _{j=1}^{N_D}{\mathbf{g}}_j^T{\mathbf{D}}_b{\mathbf{g}}_j}=S_0{e}^{-b{\overline{D}}_b}$$ 14

where ${\overline{D}}_b$ is the average diffusion coefficient of the voxel over all the gradient directions at the chosen b value.

Since the macroscopic voxel includes both extracellular and intracellular spaces, the plot of S_b at each voxel as a function of b can be fitted to a decay curve of multiple exponentials. To estimate $d_e^w$, $d_i^w$, and χ in Eqs. (9) and (10), we adopt a three compartment model [19]. We assume that the intracellular space is one compartment consisting of both intracellular water and solid components. It should be noted that the effective diffusivity of water molecules in the intracellular compartment is smaller than that of free water diffusion [20, 21]. The extracellular space is subdivided into two compartments: the extracellular water (ECW) compartment of free water molecules and the extracellular matrix (ECM) compartment of a mixture of water molecules and solid components. The data in Eq. (14) is then fitted to the following equation for each voxel:

$$S_b=S_0·\left(v_{\mathit{ecm}}{e}^{-b{d}_{\mathit{ecm}}^w}+v_{\mathit{ecw}}{e}^{-b{d}_{\mathit{ecw}}^w}+v_i{e}^{-b{d}_i^w}+v_o\right)$$ 15

where v_ecm, v_ecw, and v_i are the volumes of the extracellular matrix, extracellular water, and intracellular compartments, respectively, with v_o denoting an offset value. Note that $d_{\mathit{ecm}}^w$ and $d_{\mathit{ecw}}^w$ are the water diffusion coefficients of the extracellular matrix and extracellular water compartments, respectively. For the extracellular isotropic free water compartment, we set $d_{\mathit{ecw}}^w$ = 3 × 10⁻³ mm²/s [22, 23]. The extracellular volume fraction χ is estimated at each voxel as

$$\chi =\frac{v_{\mathit{ecm}}+v_{\mathit{ecw}}}{v_{\mathit{ecm}}+v_{\mathit{ecw}}+v_i}.$$ 16

The extracellular diffusion coefficient $d_e^w$ is estimated as

$$d_e^w=\frac{v_{\mathit{ecm}}}{v_{\mathit{ecm}}+v_{\mathit{ecw}}}{d}_{\mathit{ecm}}^w+\frac{v_{\mathit{ecw}}}{v_{\mathit{ecm}}+v_{\mathit{ecw}}}{d}_{\mathit{ecw}}^w.$$ 17

Estimation of ${\mathbf{D}}_e^w$

From (12), we get

$$\frac{1}{b}ln\left(\frac{S_{b,j}}{S_0}\right)=-{\mathbf{g}}_j^T{\mathbf{D}}_b{\mathbf{g}}_j.$$ 18

Since there are six unknowns in the 3 × 3 symmetric diffusion tensor D_b, we may use at least six gradient directions to determine D_b for each b-value. This conventional water diffusion tensor D_b, however, includes the effects of both extracellular and intracellular spaces. To estimate ${\mathbf{D}}_e^w$ in Eq. (10), we must extract the effects of the extracellular space only. Though we may use a model similar to Eq. (15) for this goal, we found that the problem to extract ${\mathbf{D}}_e^w$ from a three compartment model is ill-posed. We, therefore, adopted the following model including 13 unknowns [24, 25]:

$$\frac{S_{b,j}}{S_0}=\left(1-\xi \right)e^{-b{\mathbf{g}}_{\text{j}}^T{\mathbf{D}}_F^w{\mathbf{g}}_j}+\xi e^{-b{\mathbf{g}}_{\text{j}}^T{\mathbf{D}}_S^w{\mathbf{g}}_j}$$ 19

where ${\mathbf{D}}_F^w$ and ${\mathbf{D}}_S^w$ are the fast and slow diffusion tensors, respectively, and ξ is a weight factor.

Before separating ${\mathbf{D}}_F^w$ and ${\mathbf{D}}_S^w$ in Eq. (19), we first estimate ξ using the averaged signal in Eq. (14). Noting that the signal from the fast component is negligible at a high b-value, the weight ξ is calculated from Eq. (14) at two high b-values of b₁ and b₂ as

$$\xi =\frac{1}{S_0}\left(S_{b_1}+b_1\frac{S_{b_1}-S_{b_2}}{b_2-b_1}\right)$$ 20

where we set b₁ = 4500 and b₂ = 5000 s/mm² in our calculation.

For a high b-value, Eq. (19) is simplified to

$$S_{b,j}\approx \xi S_0{e}^{-b{\mathbf{g}}_{\text{j}}^T{\mathbf{D}}_S^w{\mathbf{g}}_j}.$$ 21

The slow diffusion tensor ${\mathbf{D}}_S^w$ with six unknowns is extracted by fitting the measured data at b = 4500 s/mm², for example, with at least six gradient directions to Eq. (21) using the weighted least square method [26]. The fast diffusion tensor ${\mathbf{D}}_F^w$ with six unknowns is then obtained from the measured data at b = 700 s/mm² [11] with at least six gradient directions from

$$S_{b,j}-S_0\xi e^{-b{\mathbf{g}}_j^T{\mathbf{D}}_S^w{\mathbf{g}}_j}\approx \left(1-\xi \right)S_0{e}^{-b{\mathbf{g}}_j^T{\mathbf{D}}_F^w{\mathbf{g}}_j}.$$ 22

Assuming that water diffusion in the extracellular space is less restricted and hindered compared to that in the intracellular space, we set the extracellular diffusion tensor as ${\mathbf{D}}_e^w\approx {\mathbf{D}}_F^w$ [27].

Estimation of β

From (7), β can be expressed as

$$\beta =\frac{{\overline{c}}_i}{{\overline{c}}_e}=\frac{{\sum }_{j=1}^N{z}^{\left(j\right)}{\gamma }_i^{\left(j\right)}{c}_i^{\left(j\right)}{k}^{\left(j\right)}}{{\sum }_{j=1}^M{z}^{\left(j\right)}{\gamma }_e^{\left(j\right)}{c}_e^{\left(j\right)}{k}^{\left(j\right)}}$$ 23

where k^(j) is the mobility ratio between the jth charge carrier and the reference charge carrier (j = 1). According to the Stokes–Einstein relation, mobility m of a charge carrier depends on the medium viscosity ς and hydration diameter d_h, that is, m = 1/3πςd_h. Therefore, k^(j) can be expressed as

$$k^{\left(j\right)}=\frac{m_{\text{e}}^{\left(j\right)}}{m_e^{\left(1\right)}}=\frac{m_{\text{i}}^{\left(j\right)}}{m_i^{\left(1\right)}}=\frac{d_h^{\left(1\right)}}{d_h^{\left(j\right)}}.$$ 24

Substituting Eq. (24) into Eq. (23) and assuming that γ^{( j)}_i ≈ γ^{( j)}_e, β is expressed as

$$\beta =\frac{{\sum }_{j=1}^N{z}^{\left(j\right)}\frac{c_i^{\left(j\right)}}{d_h^{\left(j\right)}}}{{\sum }_{j=1}^M{z}^{\left(j\right)}\frac{c_e^{\left(j\right)}}{d_h^{\left(j\right)}}}.$$ 25

In our calculation, four major ions of Na⁺, Cl⁻, K⁺, and Ca²⁺ are considered. We set the values of c_e for Na⁺, Cl⁻, K⁺, and Ca²⁺ as 154, 129, 3.10, and 1.30 mmol/liter, respectively [28]. The values of c_i were 19.67, 3.30, 89.93, and 1 × 10⁻³ mmol/liter for Na⁺, Cl⁻, K⁺, and Ca²⁺, respectively [28]. The hydration diameter values were $d_h^{{\text{Na}}^{+}}=716$, $d_h^{{\text{Cl}}^{-}}=664$, $d_h^{{\text{K}}^{+}}=661$, and $d_h^{{\text{Ca}}^{2+}}=824\text{pm}$ [29]. The value of β was then calculated as 0.41. Since there is no method to estimate β at every voxel to the best of our knowledge, we used this value for all voxels.

Estimation of σ_H

Using the time-harmonic vector representation at the Larmor frequency, the relation between the B1 field denoted as B₁ and the electrical tissue properties of conductivity σ_H and permittivity ε_H is expressed as [30]

$${\mathrm{\nabla }}^2{\mathbf{B}}_1=i\omega {\mu }_0\left({\sigma }_H+i\omega {ϵ}_H\right){\mathbf{B}}_1-\mathrm{\nabla }\left({\sigma }_H+i\omega {ϵ}_H\right)\times \frac{\mathrm{\nabla }\times {\mathbf{B}}_1}{{\sigma }_H+i\omega {ϵ}_H}$$ 26

where μ₀ is the magnetic permeability of the free space. An MRI scanner with a single transmit coil and multiple receive coils is used in this paper to estimate σ_H from the measured B1 map.

We introduce the phasor notation to denote the transversal B1 field of the MRI scanner as $B_1=\left|B_1\right|e^{i{\varphi }_1}$. The positive rotating component of the transmit B1 field is denoted as $B_1^{+}=\left|B_1^{+}\right|e^{i{\varphi }_1^{+}}$. Similarly, the negative rotating component of the receive B1 field from the lth receive coil is denoted as $B_{1,l}^{-}=\left|B_{1,j}^{-}\right|e^{i{\varphi }_{1,l}^{-}}$. Using a multi-echo pulse sequence to eliminate any B0 phase contributions, the complex MR image value $S_l^k$ of a voxel from the lth receive coil and kth echo can be expressed as

$$\begin{array}{cc}\hfill S_l^k& =V_1{M}_0^k{B}_{1,l}^{-}sin(V_2\mathrm{\alpha }\left|B_1^{+}\right|)e^{i{\varphi }_1^{+,k}}\hfill \\ \hfill & =V_1{M}_0^k\left|B_{1,l}^{-}\right|sin(V_2\mathrm{\alpha }\left|B_1^{+}\right|)e^{i({\varphi }_1^{+,k}+{\varphi }_{1,l}^{-,k})}\hfill \\ \hfill \end{array}$$ 27

where V₁ and V₂ are the system dependent constants and $M_0^k$ is a quantity determined by the proton density, tissue relaxation parameters, and nominal flip angle α of the RF excitation [31]. Note that ${\varphi }_1^{+,k}+{\varphi }_{1,l}^{-,k}$ is the transceiver phase at the lth coil. Though the transmit filed $B_1^{+}$ can be measured using the double angle method [32], the receive filed $B_{1,l}^{-}$ is not measurable. The complex MR images in Eq. (27) from all receive coils are combined as

$$\begin{array}{cc}\hfill {\tilde{S}}^k& =\sum _{l=1}^{N_C}{S}_l^k=V_1{M}_0^{k}sin(V_2\alpha \left|B_1^{+}\right|)\left(\sum _{l=1}^{N_C}{B}_{1,l}^{-}\right)e^{i{\varphi }_1^{+,k}}\hfill \\ \hfill & =V_1{M}_0^{k}sin(V_2\alpha \left|B_1^{+}\right|){\tilde{B}}_1^{-}{e}^{i{\varphi }_1^{+,k}}\hfill \\ \hfill & =V_1{M}_0^{k}sin(V_2\alpha \left|B_1^{+}\right|)\left|{\tilde{B}}_1^{-}\right|e^{i({\varphi }_1^{+,k}+{\tilde{\varphi }}_1^{-,k})}.\hfill \\ \hfill \end{array}$$ 28

Since the noise in the measured transceiver phase data can be amplified during the following image reconstruction process, it is desirable to denoise ${\varphi }_1^{+,k}+{\tilde{\varphi }}_1^{-,k}$ in Eq. (28). This can be done by averaging all transceiver phases from all echo signals since they should be identical in theory. Considering that the amount of noise in the phase image is inversely proportional to $\left|{\tilde{S}}^k\right|$, the phase averaging over all echoes was implemented as a weighted average using the weight of

$$w_k=\frac{{\left|{\tilde{S}}^k\right|}^2}{{\sum }_{k=1}^{N_E}{\left|{\tilde{S}}^k\right|}^2}$$ 29

for the kth echo where N_E is the number of echoes [33]. The channel combined average transceiver phase ϕ_tr is

$${\varphi }_{\mathit{tr}}=\sum _{k=1}^{N_E}{w}_k({\varphi }_1^{+,k}+{\tilde{\varphi }}_1^{-,k}).$$ 30

Presumably assuming that the conductivity and permittivity are piecewise constant, Eq. (26) is simplified to

$${\mathrm{\nabla }}^2{\mathbf{B}}_1=i\omega {\mu }_0\left({\sigma }_H+i\omega {ϵ}_H\right){\mathbf{B}}_1.$$ 31

Using the phasor notation, σ_H can be expressed as

$${\sigma }_H\approx \frac{1}{{\mu }_0\omega }\text{Im}\left\{\frac{{\mathrm{\nabla }}^2{B}_1}{B_1}\right\}=\frac{1}{{\mu }_0\omega }\left(2\frac{\mathrm{\nabla }\left|B_1\right|}{\left|B_1\right|}·\mathrm{\nabla }{\varphi }_1+{\mathrm{\nabla }}^2{\varphi }_1\right).$$ 32

We further assume that the B1 field is varying slowly with its negligible gradient of $\mathrm{\nabla }\left|B_1\right|\approx 0$ for both $B_1^{+}$ and ${\tilde{B}}_1^{-}$ [14, 34, 35]. Noting that Eq. (32) holds for both $B_1^{+}$ and ${\tilde{B}}_1^{-}$ [13, 14], the high-frequency conductivity estimate is given as

$${\sigma }_H=\frac{1}{2{\mu }_0\omega }{\mathrm{\nabla }}^2{\varphi }_{\mathit{tr}}.$$ 33

Since the piecewise constant assumption does not hold in practice, the reconstructed image of σ_H using Eq. (33) includes artifacts at the boundaries of conductivity contrast [15, 36, 37].

Assuming that ${\sigma }_H\gg \omega {ϵ}_H$ and $\mathrm{\nabla }\left|B_1\right|\approx 0$ for both $B_1^{+}$ and ${\tilde{B}}_1^{-}$, Gurler and Ider [38] transformed Eq. (26) into

$$-c{\mathrm{\nabla }}^2\left(\frac{1}{{\sigma }_H}\right)+\mathrm{\nabla }{\varphi }_{\mathit{tr}}·\mathrm{\nabla }\left(\frac{1}{{\sigma }_H}\right)+{\mathrm{\nabla }}^2{\varphi }_{\mathit{tr}}\left(\frac{1}{{\sigma }_H}\right)=2{\mu }_0\omega$$ 34

where c is a constant to suppress spurious oscillations in the reconstructed image of σ_H at the cost of blurring the image. Image reconstruction of σ_H is achieved by numerically solving Eq. (34) for σ_H with ϕ_tr as data. To avoid excessive blurring, c should be kept as small as possible [38]: c = 0.025 for canine data in our calculation. Note that this method does not require the piecewise constant assumption needed to derive the formula in Eq. (33).

Imaging experiments

Animal experiments

Two laboratory beagles (3 and 7 years old, weighing 6 and 8 kg) without a history of known disease were scanned. They had no signs of metabolic and neurological problems. To prevent dribbling, we injected 0.1 mg/kg of atrophine sulfate. Ten minutes later, we anesthetized the dog with intramuscular injection of 0.2 ml/kg Zolazepam (Zoletil 50, Virbac, France). The dog was located inside the bore of a 3 T MRI scanner with an eight-channel RF coil (Achieva TX, Philips Medical Systems, the Netherlands). We intubated the dog using an endotracheal tube and began general anesthesia using a veterinary anesthesia system (VME, MATRX, USA). We used 2% isoflurane mixed with oxygen at 800 ml/min flow rate. Ventilation was machine-controlled by using a ventilator (M-2002, Hallowell EMC, USA) at 15 bpm respiration rate and 200 ml tidal volume. After finishing in vivo imaging, the dog was sacrificed by an intravenous injection of 2 mmol/kg KCl (KCl-40 inj, Daihan Pharmacy, Korea) for postmortem scans. All experimental protocols were approved by the institutional animal care and use committee of Kyung Hee University (KHUASP-14-25). All methods were carried out in accordance with the relevant guidelines and regulations.

Multi-b diffusion weighted imaging experiments

Multi-b diffusion weighted imaging data sets were obtained using the single-shot spin-echo echo-planar-imaging pulse sequence (Fig. 1c) [39]. We applied the diffusion weighting gradients in 15 directions with b values of 50, 150, 300, 500, 700, 1000, 1400, 1800, 2200, 2600, 3000, 3600, 4000, 4500, and 5000 s/mm². Imaging parameters were as follows: repetition time (TR) = 2000 ms, echo time (TE) = 70 ms, slice thickness 4 mm, flip angle 90°, number of excitations 2, number of slices 5, and acquisition matrix 64 × 64. The matrix size of 64 × 64 was extended to 128 × 128 for subsequent data processing steps. To reduce spurious noise effects, we applied a 7 × 7 local spatial averaging window using the diffusion-relaxation-dependent non-local filtering [40].

MREPT imaging experiments

The multi-spin-echo pulse sequence with multiple refocusing pulses was adopted (Fig. 1c). Before data acquisition, we applied a volume shimming method with the volume defined to cover the brain region. Imaging parameters were as follows: TR = 1500 ms, data acquisition time (TS) = 3.584 ms, TE = 15 ms, number of echoes 6, number of averaging 4, slice thickness 4 mm, number of slices 5, acquisition matrix 128 × 128, and field-of-view 150 × 150 mm² for the animal experiments.

Results

We reconstructed σ_H images from the acquired transceiver phases of the B1 maps using both Eqs. (33) and (34) (Fig. 1d). In this paper, we included the σ_H images using Eq. (34) only since they were superior to those using Eq. (33) in terms of the image quality as discussed later. The image variables of $d_e^w$, $d_i^w$, χ, and ${\mathbf{D}}_e^w$ were extracted from the multi-b data sets (Fig. 1e–g). From these, we reconstructed the images of the conductivity tensor C by computing η using Eq. (10) (Fig. 1h, i).

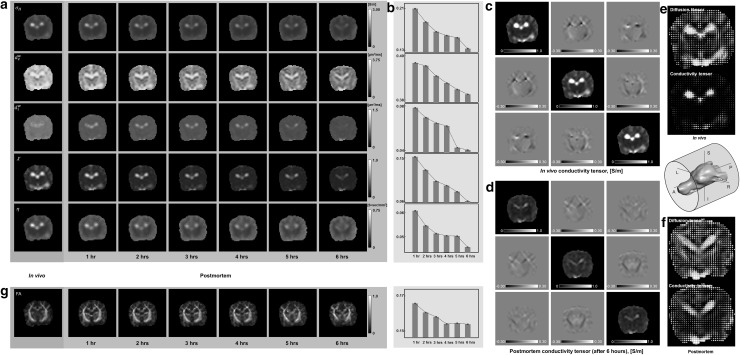
Figure 2 shows the in vivo and postmortem images of the canine brain until 6 hours after euthanizing the animal. The images of all intermediate variables including σ_H, $d_e^w$, $d_i^w$, χ, and η clearly show that distinct structural features gradually diminished after death (Fig. 2a). Their standard deviations over the entire brain area decreased monotonically after death (Fig. 2b). This means that the brain tissues were gradually destroyed after death to produce the postmortem images of less contrast. The reconstructed in vivo and postmortem conductivity tensor images showed similar phenomena (Fig. 2c, d). This indicates that the conductivity values measured from extracted tissue samples in Gabriel et al. [41], for example, could be different from those of in vivo tissues.

Fig. 2.

Images of a canine brain until 6 hours after euthanizing the animal. Structural features in the intermediate image variables in a gradually diminished after death. Computed image standard deviations in b indicate that brain tissues were destroyed after death to produce smaller image contrast. In vivo and postmortem images of C in (c) and (d), respectively, as well as fractional anisotropy (FA) maps in g also show diminished contrast and anisotropy after death. Conductivity and water diffusion tensors in e and f are compared in their tensor plots before and after death, respectively. Tensors with their maximal eigenvalues in the x, y, and z directions are marked by red, green, and blue colors, respectively. (Color figure online)

Discussion

There exist two major practical limitations in the phase-based MREPT adopted in this paper. One is related with the assumption of the piecewise constant conductivity in Eq. (33) and the other is the assumption of the uniform B1 field in both Eqs. (33) and (34). The piecewise constant conductivity assumption does not hold in practice and produced artifacts in the reconstructed σ_H images using Eq. (33) at the boundaries of conductivity contrast [37]. To reduce the artifacts, the Laplacian of the transceiver phase was evaluated using a second-order weighted polynomial function [15, 36]. A Gaussian radial basis function was used to determine the weighting factor from the MR magnitude image in a local window. Due to the Gaussian smoothing operation, the reconstructed conductivity values of σ_H using Eq. (33) were underestimated. For this reason, we used the σ_H images from Eq. (34) instead of those using using (33) for subsequent CTI image reconstructions. In Eq. (34), however, we also assumed that $\mathrm{\nabla }\left|B_1^{+}\right|=0\text{and}\mathrm{\nabla }\left|B_1^{-}\right|=0$, which do not hold in practice. Though this could have produced some errors, the phase-based MREPT using Eq. (34) produced reasonably accurate images of σ_H [38]. Considering recent progresses in MREPT, we expect better accuracy of σ_H images in future studies [42]. One possibility is to use an MRI scanner with multiple transmit coils as well as multiple receive coils to improve the image quality as demonstrated in [43].

We used the multi-b diffusion weighted imaging method to transform the high-frequency conductivity into the low-frequency conductivity tensor. The problem to estimate position-dependent values of $d_e^w$, $d_i^w$, and χ using the three-compartment model is, however, vulnerable to noise in the measured multi-b diffusion weighted image data set. We could alleviate this by including the extracellular water compartment with the fixed water diffusion coefficient of $d_{\mathit{ecw}}^w$ = 3 × 10⁻³ mm²/s [22, 23] in the model. When we used a general three-compartment model without reducing the number of unknowns, the image of χ was quite noisy and underestimated its pixel values especially in the CSF region where χ should be close to 1. The erroneously smaller values of χ in the CSF region deteriorated the quality of the reconstructed conductivity tensor image in the same region. In addition to the modified three-compartment model used in this paper, incorporation of microstructural information into the parameter estimation process may improve the accuracy of the reconstructed values of χ as well as $d_e^w$ and $d_i^w$ [22].

In this paper, we set ${\mathbf{D}}_e^w\approx {\mathbf{D}}_F^w$ and this means that the extracellular water diffusion corresponds to the fast water diffusion component, which is controversial [24]. Future studies should include developing other methods to reliably estimate ${\mathbf{D}}_e^w$ with better accuracy.

For diffusion weighted imaging, we used the spin echo echo-planar imaging technique [39] also known as the single-shot spin echo echo-planar imaging technique. It substantially reduces the scan time and motion artifacts [44]. However, this fast imaging sequence is prone to the magnetic susceptibility and may cause geometrical distortions [45] especially in local regions adjacent to the air in the head. The fast echo-planar imaging sequence suffers from additional distortions caused by the eddy currents from rapid switching of the gradient pulses [45]. Since the proposed CTI method is based on two MRI scans of multi-b diffusion weighted imaging and B1 mapping, these distortions may cause pixel misalignments between those two scans. Though we adopted the post-processing methods by Leemans et al. [46] to minimize the geometrical distortions, more rigorous analyses about the effects of the geometrical distortions are desirable in future studies.

Since we could not find any method to experimentally determine β at every voxel, we estimated its value for all voxels using Eq. (25) with available literature values of intracellular and extracellular concentrations and hydration diameters of four predominant ions. In future studies, it will be worthwhile to pursue a method to experimentally estimate β for each voxel to separately quantify ${\overline{c}}_e$ and ${\overline{c}}_i$.

The major assumption of the proposed CTI method is the proportionality between the conductivity tensor and water diffusion tensor. Though there exist numerous other publications based on this assumption and we speculate that the assumption is valid under the conditions described in this paper, there is no experimental validation study yet mainly due to the lack of any experimental technique. In our future studies, we plan to validate this key assumption by using giant vesicles. Depending on how many of $d_e^w$, $d_i^w$, χ, β, and ${\mathbf{D}}_e^w$ are experimentally determined with enough accuracy or assumed to be constant, we may interpret the reconstructed image of C as a conductivity tensor or conductivity weighted image, that is, CTI or CWI.

Conclusion

The developed CTI method can provide conductivity tensor or conductivity weighted images using a clinical MRI scanner without added hardware. Since the image contrast is based on ensemble averages of microscopic motions of charge carriers in a structured tissue, macroscopic CTI image parameters may lead to new methods to extract quantitative information about the tissue microstructure and its functions. It would be meaningful to quantitatively examine the images of σ_H, $\frac{d_e^w}{\chi d_e^w+\left(1-\chi \right)d_i^w\beta }$, $\frac{{\mathbf{D}}_e^w}{\chi d_e^w+\left(1-\chi \right)d_i^w\beta }$, and ${\overline{c}}_e$ together with the image of C.

We suggest clinical studies considering the following observations [47–50].

• Changes in concentrations of charge carriers are reflected in ${\overline{c}}_e$ from which pathological changes of tumor, cirrhosis, inflammation, and bleeding can be examined.

• Structural changes are reflected in $\frac{d_e^w}{\chi d_e^w+\left(1-\chi \right)d_i^w\beta }$ or $\frac{{\mathbf{D}}_e^w}{\chi d_e^w+\left(1-\chi \right)d_i^w\beta }$, which can be related with demyelination and ion channel openings, for examples, as well as pathological changes.

• Changes in cell size and density are reflected in χ and σ_L, which can provide information about cell swelling, for example.

• Conductivity tensor images can be used in patient-specific models for electromagnetic source imaging and electrical stimulation techniques such as tDCS, DBS, and electroporation.

Non-clinical applications in material and food sciences, biology, and chemistry are also expected after validating the key assumptions needed to derive the CTI formulae.

Conflict of interest

The authors have no conflict of interest to declare.

Ethical approval

All animal procedures were approved by the institutional animal care and use committee of Kyung Hee University (KHUASP-14-25). All methods were carried out in accordance with the relevant guidelines and regulations.