Abstract
Parkinson’s disease (PD) is a widespread degenerative syndrome that affects the nervous system. Its early appearing symptoms include tremor, rigidity, and vocal impairment (dysphonia). Consequently, speech indicators are important in the identification of PD based on dysphonic signs. In this regard, computer-aided-diagnosis systems based on machine learning can be useful in assisting clinicians in identifying PD patients. In this work, we evaluate the performance of machine learning based techniques for PD diagnosis based on dysphonia symptoms. Several machine learning techniques were considered and trained with a set of twenty-two voice disorder measurements to classify healthy and PD patients. These machine learning methods included linear discriminant analysis (LDA), k nearest-neighbors (k-NN), naïve Bayes (NB), regression trees (RT), radial basis function neural networks (RBFNN), support vector machine (SVM), and Mahalanobis distance classifier. We evaluated the performance of these methods by means of a tenfold cross validation protocol. Experimental results show that the SVM classifier achieved higher average performance than all other classifiers in terms of overall accuracy, G-mean, and area under the curve of the receiver operating characteristic plot. The SVM classifier achieved higher performance measures than the majority of the other classifiers also in terms of sensitivity, specificity, and F-measure statistics. The LDA, k-NN and RT achieved the highest average precision. The RBFNN method yielded the highest F-measure.; however, it performed poorly in terms of other performance metrics. Finally, t tests were performed to evaluate statistical significance of the results, confirming that the SVM outperformed most of the other classifiers on the majority of performance measures. SVM is a promising method for identifying PD patients based on classification of dysphonia measurements.
Keywords: Parkinson’s disease, Dysphonia measurements, Machine learning, Classification
Introduction
Parkinson’s disease (PD) is a progressive, neurodegenerative movement disorder that causes general loss of motor abilities in elderly patients. As a result of gradual loss of nigrostriatal dopaminergic neurons [1], PD symptoms include resting tremor, gait rigidity, postural instability, and voice impairment [2] in roughly 90% of the patients [3]. These symptoms can potentially be detected by computer-aided-diagnosis systems based on advanced machine learning techniques. Machine learning techniques including linear discriminant analysis (LDA) [4], AdaBoost algorithm [5], k nearest-neighbors (k-NN) algorithm and Bayes classifier [6], regression trees (RT) [7], support vector machines (SVM) [8–14], decision trees (DT), naive Bayes (NB), and multilayer perceptron (MLP) [12] are widely employed in the design of medical decision support systems. Indeed, machine learning techniques have been commonly used in the design of computer-aided-diagnosis (CAD) systems with applications in classification of brain magnetic resonance images [15–17], mammograms [18, 19], electroencephalography of seizures [20, 21], retinal pathologies [22, 23], electrocorticogram signals [24], heartbeat signals [25], and arrhythmias [26]. Several machine learning techniques have been employed for supporting the diagnosis of Parkinson’s disease (PD) including SVM [1], artificial neural networks (ANN) [27, 28], LDA [29], and fuzzy k-NN [30]. PD symptoms that are especially well suited for detection by machine learning include diminished vocal volume, monopitch, disturbance of voice quality, and irregular rapid rate of speech, which are associated with hypokinetic dysarthria [31].
The purpose of our current study is to evaluate the performance of several machine learning techniques in correctly classifying healthy (control) and PD patients based on dysphonia measurements. We consider seven machine learning classifiers, namely LDA [32], k-NN algorithm [33, 34], NB [35], RT [36], radial basis function neural network (RBFNN) [35, 37], SVM [38], and the well-known classical Mahalanobis distance classifier (MDC).
Four previous studies have compared different machine learning techniques for PD classification using the dysphonia dataset we use here [39–42]. In [39], four machine learning techniques were used, including a multi-layer feed-forward neural network, a combination of neural network and principal components analysis [39], regression analysis, and a decision tree. The input dataset was arbitrarily separated into training (65%) and testing (35%) sets. The findings indicated that the multi-layer feed-forward neural network achieved the best accuracy, evaluated by the receiver operating curve and the cumulative lift function. In [40], four machine learning techniques including SVM, least square SVM, a multilayer perceptron neural network, and general regression neural network method were employed, for monitoring Parkinson’s disease progression. Tenfold cross validation was performed to assess the accuracy of the predictive systems. The results indicated that the least square SVM achieved the best performance among the models applied in that study, as evaluated by mean absolute error (MAE), mean square error (MSE), and correlation coefficients. The authors in [41] used quadratic discriminant analysis and achieved 91.8% ± 2.0 overall correct classification rate, 95.4% ± 3.2 true positive classification performance, and 91.5% ± 2.3 true negative performance. Finally, the authors in [42] used a linear prediction approach based on regression analysis and regression trees. They found that regression trees outperform standard linear regression model in terms of the mean absolute error (MAE) statistic.
Recall that neural network and decision trees were employed in [39], regression techniques based on support vector machine and neural network in [40], discriminant analysis in [41], and linear regression analysis and regression trees in [42]. Therefore, our current work enriches earlier studies [39–42] used for the tracking of Parkinson’s disease progression by comparing the performance of statistical machine learning techniques (LDA, k-NN, NB, SVM, MDC) to artificial intelligence methods (RBFNN, RT). Indeed, we compare the performance of k-NN, NB, RBFNN, and MDC, which were not evaluated by [39–42], to the performance of LDA SVM, and RT. In addition, the authors in [39] did not consider a cross validation protocol to obtain statistically robust results. Applying cross-validation is important, since it makes it possible to avoid overfitting, and to perform statistical inference and thus to draw solid conclusions. In addition, our work is balanced between statistical and non-statistical techniques. Finally, to evaluate the performance of each machine learning and artificial intelligence classifier, we used a large set of standard performance metrics commonly used in the design of computer-aided-diagnosis systems. The metrics we used include classification accuracy, sensitivity (recall), specificity, precision, F-measure, G-mean, and area under curve (AUC).
The paper is organized as follows. Section 2 introduces the machine learning and artificial intelligence classifiers and performance measures. Section 3 presents the data, classification results and comparisons. These results and comparisons are discussed in Sect. 4. Finally, our work is concluded in Sect. 5.
Methods
The machine learning classifiers used in our study include LDA, k-NN, NB, RT, RBFNN, SVM, and MDC. These classifiers are all very popular in the literature as they are simple to implement and require tuning of only a limited number of parameters. They are briefly described below, along with the performance measures we used: classification accuracy, sensitivity (recall), specificity, precision, F-measure, G-mean, and area under curve (AUC).
Machine learning classifiers
LDA [32] has become a standard baseline method in classification, due to its simplicity and interpretability. Based on Fisher’s discrimination criterion, it generates a linear projection matrix used to improve classification accuracy. In particular, it employs linear decision boundaries to maximize the proportion of between-class and within-class variability. These linear decision boundaries are obtained by applying eigenvalue decomposition to the scatter matrices and assuming that the scatter matrix is nonsingular. More precisely, LDA generates a discriminant function that separates samples into two or more groups by minimizing the expected misclassification cost and maximizing the ratio of between groups (S b) and within groups (S w) variances. LDA assumes that all predictors are normally distributed and that the covariance matrices are identical. The within group (S w) and between groups (S b) variances are given by:
| 1 |
| 2 |
where x i, L i, and μ i are respectively dysphonia pattern, the number and the mean of the labeled set in the ith class; and, μ is the mean of all classes and T is the transpose operator. Then, the maximization of the ratio between S b and S w is obtained by finding W* that satisfies:
| 3 |
where W is eigenvector of .
The k-NN algorithm [33, 34] is a nonparametric supervised classifier in which retrieving nearest neighbors is based on the concept of similarity. It clusters a set of data points into groups and classifies new data based on a measure of similarity (such as the Euclidean distance). Its main advantage is that it does not assume the form of a fitted model. In particular, it is entirely based on data-driven learning. Technically, given a value k and a feature vector to classify I, it locates the k nearest neighbors of I in the sample set and uses the categories of neighbors to determine the class of I. This structure imposes a lower computational burden. Therefore, the k-NN algorithm is fast. In general, it yields accurate results. The common algorithm of k-NN is as follows:
Compute the Euclidean distances between a new object o and all the objects in the set used for learning;
Choose the k objects from the learning set that are closest to o;
Classify o to the group associated with the largest number the k objects.
After locating the k nearest neighbors, the class of the new object is identified by using a voting algorithm such as majority voting or weighted-sum voting [34]. In our current study, we implemented the simple majority voting algorithm.
In summary, the formal k-NN classifier algorithm is as follows [43]:
| 4 |
where t is the training data, o is the object to be classified, P is the assigned class of the new object, k is the number of closest neighbors to be considered, and d e is the Euclidean distance given by:
| 5 |
where L is length of each of data vector. In this work, the parameter k is set to one.
The NB classifier [35] takes a probabilistic approach for calculating the class membership probabilities based on the conditional independence assumption. The NB is simple to use, since it requires no more than one iteration during the learning process to generate probabilities. In principle, NB seeks to model the classes assigned to the training data by a probability density function. Then, objects are associated with the most probable class. The NB classifier attributes a new set of features to the most probable target class (c) according to:
| 6 |
By assuming the uniformity of and using the chain rule, the most probable target class (c) can be expressed as follows:
| 7 |
where Prob(c) is estimated by the frequency of c in the training data, and Prob(f i|c) is estimated by a Gaussian distribution function.
The RT, commonly known as Classification and Regression Trees (CART) [36], is a nonparametric method for estimating a regression function. The RT determines a set of if–then rules and minimizes the misclassification cost by considering both misclassification rate and variance. The major advantages of RT follow. First, it does not require assumptions regarding the distribution of predictors. Second, it can grip highly skewed numerical data and categorical inputs by using ordinal or non-ordinal tree construction [36]. In principle, RTs are designed to solve binary tasks, employ the Gini index to rank tests, and prune trees by a cost-complexity model. The classification tree performed by RT is represented graphically using nodes and branches, where each node indicates a decision about one of the attributes, and gives rise to two branches. As a final point, there is a terminal leaf node where homogeneity is obtained and the decision about the assigned class is taken. The tree is built by recursively partitioning the learning dataset into two subsets by binary split until the terminal nodes are achieved. When a new case is presented to the tree, it undergoes the tests in the nodes where each test has exclusive and exhaustive outputs. As recommended by the authors in [36], the Gini index is employed to diminish impurities in tree construction. The Gini index G(t) of impurity of a node t is given by [36]:
| 8 |
where i and j are classes of the output, and p(t) refers to the relative frequency of the first class. For instance, the goodness of the split of a data set D into subsets D 1 and D 2 is defined by:
| 9 |
where n, n 1 and n 2 are the sizes of D, D 1 and D 2, respectively.
The ANN [35, 37] are nonlinear mathematical models used to mimic human cognition, where information is being processed via biological neurons. They use supervised mean-squared error learning implemented with a gradient descent method to perform a nonlinear mapping of the data. ANN are capable of identifying patterns and are robust to noise. In addition, ANN are not based on suppositions regarding the data. Instead, they are data driven, therefore the larger the dataset the better the performance of the network. In this study, a radial basis function neural network (RBFNN) [35, 37] was employed. The RBFNN is a supervised-learning feed-forward network with fixed and simple architecture. For instance, the architecture of the RBFNN consists of three layers: an input layer, only one hidden layer, and the output layer. The neurons of the hidden layer hold radial basis activation functions where information obtained from the input layer is processed. Then, the information processed by the radial basis functions of the hidden layer is given to the output layer. Indeed, the RBFNN is simple, fast and flexible as it uses radial basis functions to fit data. In particular, the RBFNN acts locally to approximate the function under study thanks to its radial basis functions. The network output for an input pattern x is given by:
| 10 |
where j = 1,2,…n, y i(x) is the RBFNN jth output, I is the number of units in the hidden layer, w ij is the weight used to connect the ith hidden unit and jth output node, and ϕ is the radial basis function (RBF) expressed as follows:
| 11 |
where c and σ > 0 denote the center and width of the RBF, respectively. In our work, the values of the parameters c and σ of the RBF are optimized by using k-means clustering approach [44]. The optimized values for c and σ were 119.11 and 4.09, respectively. In addition, the initial weights were randomly set to small values in the range [0,1]. The number of neurons in the input layer is equal to the number of features in the initial dataset, and the number of neurons in the hidden layer is also set to the number of features in the input layer. Finally, there is one neuron in the output layer that reports the predicted output (0 or 1). We employed the gradient descent algorithm to train the RBFNN so as to minimize the least means squares of output layer.
The SVM [38] employs a hyper-plane based on structural risk minimization principles in order to distinguish classes. This is obtained by maximizing the space between classes and the hyper-plane. More importantly, the SVM’s capacity to generalize results is superior relative to other methods, and it is capable of evading local minima [38]. The linear SVM is given by:
| 12 |
where x is data, y is class label, w is the weight vector orthogonal to the decision hyper-plane, b is offset of the hyper-plane, T is transpose operator. The solution to the linear SVM is found by maximizing the margin used to separate classes. This is equivalent to solving the following minimization problem:
| 13 |
Subject to,
| 14 |
where ξ (ξi ≥ 0, i = 1,2, …, n) is a slack variable used to indicate the allowed degree of misclassification error, and C > 0 is a penalty parameter which is simply the upper bound on the error, and n is number of instances. The nonlinear SVM classifier employs a kernel function K to separate nonlinear data. It is expressed as follows:
| 15 |
where α is the Lagrange multiplier, K is a kernel function, and b is a constant. In our work, we adopted the radial basis function, widely used as a nonlinear Kernel in the SVM framework and is given by:
| 16 |
where δ > 0 is a scale parameter defined as 1/σ 2 and σ is the width of the radial basis function. We set the value of the slack variable ξ to 0.001. We optimized the cross-validated SVM classifier’s penalty parameter C and scale parameter δ by using Bayesian optimization [45]. The obtained values of the optimized parameters C and δ were 959.94 and 18.69, respectively.
Lastly, the MDC is suitable for data clustering and classification since it is multivariate, scale-invariant and takes into account the correlations between variables under study. Its main advantage is simplicity and suitability to detect outliers in data. Technically, the Mahalanobis distance d(x,y) between n-dimensional points x and y, with respect to a given n-by-n covariance matrix S, is given by:
| 17 |
Performance measures and cross-validation protocol
Finally, classification accuracy, sensitivity (also termed ‘recall’), specificity, precision, F-measure, G-mean, and area under curve (AUC) are all employed to assess the effectiveness of each machine learning classifier in distinguishing between healthy subjects and PD patients. They are expressed as follows:
| 18 |
| 19 |
| 20 |
| 21 |
| 22 |
| 23 |
where TP, TN, FP and FN denote true positives (i.e. PD), true negatives (i.e. healthy control), false positives, and false negatives, respectively. Furthermore, TPrate = TP/p and TNrate = TN/n, where p is number of positive samples (PD patients) and n is number of negative samples (healthy subjects). Finally, the area under curve (AUC) is given by:
| 24 |
where FPrate is false positive rate and t is a varying parameter in [0,1].
For robustness of the experimental results, k-fold cross validation protocol is employed in this work. In particular, we adopted the tenfold cross-validation scheme in which the original sample is randomly partitioned into 10 subsamples of equal size. A single subsample is retained as the validation data for testing the model, and the remaining nine subsamples are used as training data. Next, the cross-validation process is repeated ten times with each of the ten subsamples employed exactly once for the validation. At each repetition, each of classification performance measures is computed. Subsequently, its associated average and standard deviation over ten repetitions are calculated.
Experimental results
Dataset
We used the dataset used also by [39–42] to conduct comparative performance analysis of different classifiers in distinguishing between healthy (control) and PD patients based on dysphonia measurements. The dataset contains 22 features (dysphonia measurements) computed from voice records of 147 PD patients and 48 healthy control (HC) subjects. Thus, the total number of subjects is 195. The 22 voice features are presented in Table 1 as in [39–42].
Table 1.
| Dysphonia patterns | Description |
|---|---|
| Fo (Hz) | Average vocal fundamental frequency |
| Fhi (Hz) | Maximum vocal fundamental frequency |
| Flo (Hz) | Minimum vocal fundamental frequency |
| Jitter (%) | Jitter in percentage |
| Jitter (Abs) | Absolute value |
| RAP | Relative amplitude perturbation |
| PPQ | Period perturbation quotient |
| DDP | Difference of differences between cycles, divided by average period |
| Shimmer | Local shimmer |
| Shimmer (dB) | Shimmer in decibels |
| Shimmer:APQ3 | Three point amplitude perturbation quotient |
| Shimmer:APQ5 | Five point amplitude perturbation quotient |
| MDVP:APQ | Amplitude perturbation quotient |
| Shimmer:DDA | Average absolute difference between consecutive differences between amplitudes of consecutive periods |
| NHR | Noise-to-harmonics ratio |
| HNR | Harmonics-to-noise ratio |
| RPDE | Recurrence period density entropy |
| DFA | Detrended fluctuation analysis |
| Spread1 | Nonlinear measure of fundamental frequency |
| Spread2 | Nonlinear measure of fundamental frequency |
| D2 | Correlation dimension |
| PPE | Pitch period entropy |
Results
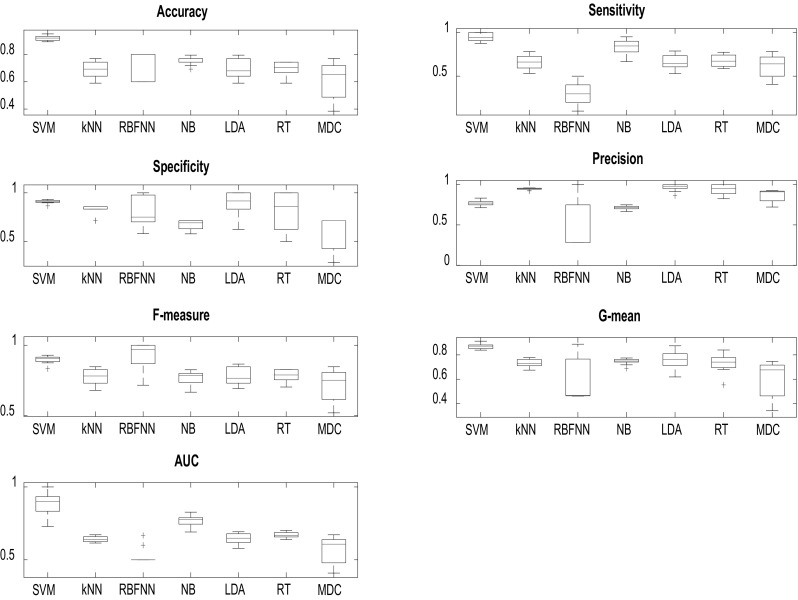
Recall that all classifiers are trained with all twenty-two dysphonia measurements, following a tenfold cross-validation protocol in order to draw statistically robust results. We employed the Matlab© software to perform all classification tasks. The average and standard deviation of each of the performance measures across the ten iterations are provided in Table 2. The boxplots of the distribution of each performance measure across classifiers are presented in Fig. 1. One can observe that for each performance measure the distribution across classifiers is unique. In addition, one can also observe that RBFNN exhibits large variability in terms of precision and G-mean. Furthermore, it is interesting to observe that SVM exhibits small variability in terms of accuracy, sensitivity, specificity, precision, F-measure, and G-mean.
Table 2.
Summary of evaluation results
| Performance measures | |||||||
|---|---|---|---|---|---|---|---|
| Accuracy | Sensitivity | Specificity | Precision | F-measure | G-mean | AUC | |
| SVM | 0.92 ± 0.02 | 0.95 ± 0.05 | 0.91 ± 0.02 | 0.77 ± 0.03 | 0.90 ± 0.03 | 0.87 ± 0.02 | 0.89 ± 0.08 |
| k-NN | 0.69 ± 0.06 | 0.67 ± 0.08 | 0.81 ± 0.06 | 0.95 ± 0.01 | 0.78 ± 0.05 | 0.73 ± 0.03 | 0.64 ± 0.02 |
| RBFNN | 0.67 ± 0.09 | 0.29 ± 0.12 | 0.80 ± 0.16 | 0.49 ± 0.33 | 0.92 ± 0.10 | 0.59 ± 0.19 | 0.53 ± 0.06 |
| NB | 0.75 ± 0.02 | 0.84 ± 0.09 | 0.66 ± 0.05 | 0.71 ± 0.02 | 0.77 ± 0.04 | 0.74 ± 0.02 | 0.77 ± 0.04 |
| LDA | 0.70 ± 0.07 | 0.67 ± 0.09 | 0.88 ± 0.12 | 0.96 ± 0.04 | 0.79 ± 0.06 | 0.77 ± 0.07 | 0.65 ± 0.03 |
| RT | 0.70 ± 0.04 | 0.68 ± 0.07 | 0.79 ± 0.18 | 0.93 ± 0.05 | 0.79 ± 0.04 | 0.73 ± 0.07 | 0.67 ± 0.01 |
| MDC | 0.63 ± 0.13 | 0.63 ± 0.13 | 0.61 ± 0.15 | 0.87 ± 0.07 | 0.63 ± 0.13 | 0.73 ± 0.11 | 0.62 ± 0.14 |
The range of all performance measures is between 0 and 1. For each classifier, the experiments were performed following a tenfold cross-validation protocol. The table shows the average and standard deviation across the ten cross-validations for each performance measure obtained separately from each of the classifiers
Fig. 1.
Boxplots of distributions of performance measures for all classifiers. Each performance was measured following a ten-fold cross-validation protocol. Note that the red horizontal lines represent the median values. (Color figure online)
According to Fig. 1 and Table 2, the SVM achieved the highest average accuracy (0.92 ± 0.02, mean ± standard deviation), sensitivity (0.95 ± 0.05), specificity (0.91 ± 0.02), G-mean (0.87 ± 0.02), and AUC (0.89 ± 0.08). However, the average F-measure obtained by SVM (0.90 ± 0.03) was lower than that obtained by RBFNN (0.92 ± 0.10; RBFNN achieved the highest average F-measure statistic). In addition, the average precision reached by SVM (0.77 ± 0.03) was lower than that achieved by LDA (0.96 ± 0.04; LDA achieved the highest average precision measure). Overall, the SVM achieved higher average evaluation measures than all classifiers considered in this study, except for the F-measure and precision statistics. In addition, NB reached higher average accuracy, sensitivity and AUC (0.75 ± 0.02, 0.84 ± 0.09, 0.77 ± 0.04, respectively) than k-NN, RBFNN, LDA, RT, and MDC. The average F-measure (0.79 ± 0.06) and G-mean (0.77 ± 0.07) achieved by LDA were higher than those obtained by k-NN, NB and MDC. LDA achieved higher average G-mean and AUC than RBFNN did. Finally, one can observe that the RBFNN classifier achieved the lowest average AUC (0.53 ± 0.06).
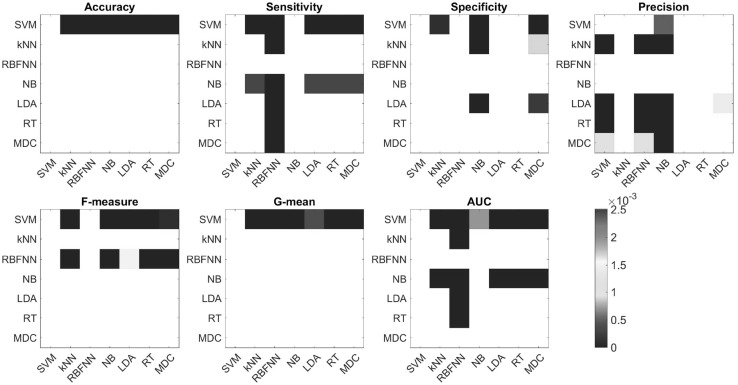
Finally, we applied two-tailed t tests to determine, for each performance measure, whether the means of the measure obtained by two different classifiers were different at a 5% significance level. To correct for multiple comparisons, we applied the conservative Bonferroni correction, which set a corrected threshold of 0.0025. Table 3 presents the p values from these tests. The performance of the SVM classifier in terms of accuracy, G-mean, and AUC performance measures is statistically different from those of all other classifiers. Additionally, the performance of the SVM classifier in terms of sensitivity, precision, and F-measure statistics is statistically different from those of the other classifiers with a few exceptions: NB in terms of sensitivity; RBFNN, LDA, and RT in terms of specificity; and RBFNN in terms of precision and F-measure. Based on the results presented in Table 3, we can conclude that approximately half (71/147) of the compared pairs of distributions of performance measures obtained from different classifiers are different. This finding can also be observed in Fig. 2, where heat maps of p values presented in Table 3 are shown for better visualization of the results. These formal statistical results confirm the preliminary conclusions drawn from boxplots displayed in Fig. 1. Importantly, performance measures associated with SVM are in most cases statistically different from those of the other classifiers. In summary, our experimental results show that SVM performs significantly better than LDA, k-NN, NB, RT, RBFNN, and MDC.
Table 3.
Summary of t tests p values for testing whether the performance of 2 methods is different
| SVM | k-NN | RBFNN | NB | LDA | RT | MDC | |
|---|---|---|---|---|---|---|---|
| Accuracy | |||||||
| SVM | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| k-NN | 0.0000 | 0.6881 | 0.0094 | 0.7604 | 0.7753 | 0.1589 | |
| RBFNN | 0.0000 | 0.6881 | 0.0158 | 0.5661 | 0.4709 | 0.2795 | |
| NB | 0.0000 | 0.0094 | 0.0158 | 0.0521 | 0.0051 | 0.0062 | |
| LDA | 0.0000 | 0.7604 | 0.5661 | 0.0521 | 0.9335 | 0.1241 | |
| RT | 0.0000 | 0.7753 | 0.4709 | 0.0051 | 0.9335 | 0.1070 | |
| MDC | 0.0000 | 0.1589 | 0.2795 | 0.0062 | 0.1241 | 0.1070 | |
| Sensitivity | |||||||
| SVM | 0.0000 | 0.0000 | 0.0026 | 0.0000 | 0.0000 | 0.0000 | |
| k-NN | 0.0000 | 0.0000 | 0.0003 | 0.9511 | 0.6772 | 0.4333 | |
| RBFNN | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| NB | 0.0026 | 0.0003 | 0.0000 | 0.0003 | 0.0003 | 0.0003 | |
| LDA | 0.0000 | 0.9511 | 0.0000 | 0.0003 | 0.7323 | 0.4099 | |
| RT | 0.0000 | 0.6772 | 0.0000 | 0.0003 | 0.7323 | 0.2561 | |
| MDC | 0.0000 | 0.4333 | 0.0000 | 0.0003 | 0.4099 | 0.2561 | |
| Specificity | |||||||
| SVM | 0.0001 | 0.0258 | 0.0000 | 0.6219 | 0.0960 | 0.0000 | |
| k-NN | 0.0001 | 0.6158 | 0.0000 | 0.1030 | 0.7539 | 0.0009 | |
| RBFNN | 0.0258 | 0.6158 | 0.0263 | 0.1539 | 0.8461 | 0.0126 | |
| NB | 0.0000 | 0.0000 | 0.0263 | 0.0000 | 0.0352 | 0.3167 | |
| LDA | 0.6219 | 0.1030 | 0.1539 | 0.0000 | 0.1852 | 0.0002 | |
| RT | 0.0960 | 0.7539 | 0.8461 | 0.0352 | 0.1852 | 0.0210 | |
| MDC | 0.0000 | 0.0009 | 0.0126 | 0.3167 | 0.0002 | 0.0210 | |
| Precision | |||||||
| SVM | 0.0000 | 0.0083 | 0.0005 | 0.0000 | 0.0000 | 0.0012 | |
| k-NN | 0.0000 | 0.0000 | 0.0000 | 0.1751 | 0.5064 | 0.0034 | |
| RBFNN | 0.0083 | 0.0000 | 0.0274 | 0.0000 | 0.0000 | 0.0011 | |
| NB | 0.0005 | 0.0000 | 0.0274 | 0.0000 | 0.0000 | 0.0000 | |
| LDA | 0.0000 | 0.1751 | 0.0000 | 0.0000 | 0.1619 | 0.0016 | |
| RT | 0.0000 | 0.5064 | 0.0000 | 0.0000 | 0.1619 | 0.0396 | |
| MDC | 0.0012 | 0.0034 | 0.0011 | 0.0000 | 0.0016 | 0.0396 | |
| F-measure | |||||||
| SVM | 0.0000 | 0.4685 | 0.0000 | 0.0000 | 0.0000 | 0.0001 | |
| k-NN | 0.0000 | 0.0000 | 0.6035 | 0.7624 | 0.8011 | 0.2026 | |
| RBFNN | 0.4685 | 0.0000 | 0.0000 | 0.0015 | 0.0000 | 0.0000 | |
| NB | 0.0000 | 0.6035 | 0.0000 | 0.4211 | 0.3813 | 0.3128 | |
| LDA | 0.0000 | 0.7624 | 0.0015 | 0.4211 | 0.9186 | 0.1520 | |
| RT | 0.0000 | 0.8011 | 0.0000 | 0.3813 | 0.9186 | 0.1400 | |
| MDC | 0.0001 | 0.2026 | 0.0000 | 0.3128 | 0.1520 | 0.1400 | |
| G-mean | |||||||
| SVM | 0.0000 | 0.0000 | 0.0000 | 0.0004 | 0.0000 | 0.0000 | |
| k-NN | 0.0000 | 0.0212 | 0.3839 | 0.1812 | 0.8562 | 0.0184 | |
| RBFNN | 0.0000 | 0.0212 | 0.0121 | 0.0105 | 0.0294 | 0.7453 | |
| NB | 0.0000 | 0.3839 | 0.0121 | 0.3462 | 0.5230 | 0.0101 | |
| LDA | 0.0004 | 0.1812 | 0.0105 | 0.3462 | 0.2431 | 0.0066 | |
| RT | 0.0000 | 0.8562 | 0.0294 | 0.5230 | 0.2431 | 0.0367 | |
| MDC | 0.0000 | 0.0184 | 0.7453 | 0.0101 | 0.0066 | 0.0367 | |
| AUC | |||||||
| SVM | 0.0000 | 0.0000 | 0.0007 | 0.0000 | 0.0000 | 0.0000 | |
| k-NN | 0.0000 | 0.0000 | 0.0000 | 0.5594 | 0.0058 | 0.0338 | |
| RBFNN | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.2181 | |
| NB | 0.0007 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| LDA | 0.0000 | 0.5594 | 0.0000 | 0.0000 | 0.1252 | 0.0243 | |
| RT | 0.0000 | 0.0058 | 0.0000 | 0.0000 | 0.1252 | 0.0038 | |
| MDC | 0.0000 | 0.0338 | 0.2181 | 0.0000 | 0.0243 | 0.0038 | |
For each performance measure. We applied two-tail t test to test whether the means of the measure obtained from two different classifiers were different. The resulting p values are reported in the table. For statistical significance we consider a p value of 0.05, corrected for multiple comparisons using the Bonferroni correction to 0.0025. Bold font indicates significant difference at this 0.0025 α level
Fig. 2.
Heat-maps of p values associated with the t test values presented in Table 3, thresholded according to the Bonferroni corrected threshold (0.0025; see also Table 3). Colored entries indicate that the method presented in the row performed better than the method presented in the column, in a statistically significant manner. Note that although the statistical test we performed to test the null hypothesis that performances of a pair of methods are not different, here we combine the p values of these tests together with the average performances presented in Table 2, to present which measure performed better than the other. White entries present comparisons which we did not make (along the diagonal), or comparisons that yielded no statistically significant difference (Color figure online)
Discussion
Our results show that the SVM is the best machine learning classifier for classifying PD patients and control subjects, since it obtained the highest score in all performance measures except for precision and F-measure. Still, it achieved the second best F-measure. Recall that the authors in [40] compared regression models in tracking of PD development based on MAE, MSE and coefficient of correlation. They found that least square support vector machines outperformed both multilayer perceptron neural network and general regression neural network in distinguishing between healthy and PD patients. Therefore, both our study and the study in [40] show evidence of the suitability of the SVM in modeling vocal features for PD detection and monitoring. Note that the RBFNN and SVM associated key parameters were optimized in our study. In addition, note that the sample size is sufficiently large (195 patients) and that we used tenfold cross validation which is a reliable technique widely used for avoiding overfitting.
The results obtained in [39] indicate that the feed-forward neural network outperformed the DMNeural, regression and decision trees by achieving an overall classification score of 92.9% based on a fixed partition of data with 65% for training and 35% for testing. It is difficult to compare our results, based on tenfold cross-validation, with those obtained in [39] where no cross validation protocol was performed. In our study, the performance of RBFNN, the neural network classifier, was compared to that of an SVM classifier based on ten-fold cross validation protocol for statistical robustness of the results. The experimental findings showed strong evidence of the effectiveness of the SVM against the RBFNN.
We investigated the effectiveness of seven machine learning techniques. This is in contrast to the four models studied in [39]. According to the results we present in Tables 2 and 3, the SVM performs significantly better than the other classifiers we examined. This is an important result in the design of CAD systems for clinical applications as clinicians are most concerned with effective detection of patients with PD and thus need to make use of the most suitable classifier available. It is interesting to indicate that highest AUC, which is a performance metric that is based on a combination of sensitivity and specificity, was obtained by the SVM classifier.
Our findings identify the SVM as more attractive than the other machine learning classifiers considered in this work for use in differentiating individuals with PD from HC. The SVM’s superiority as a machine learning classifier can be explained by several features. Firstly, it is based on structural risk minimization principles and forms the hyper-plane so that negative and positive instances are separated. This is accomplished by maximizing the space between classes and the hyper-plane by using a nonlinear kernel. In addition, the optimization result of the SVM classifier is global. In other words, it is immune to being trapped in local minima. Lastly, it has superior generalization capability [38] thanks to its salient advantages cited previously. These attractive features contribute to the SVM’s success in mapping dysphonia measurements.
As a final note, although RBFNN are known to be effective in modeling nonlinear data for classification purposes, they underperformed relative to all other machine learning classifiers employed in this work. This may be explained by the fact that the dataset size is small (195 patients and subjects combined) relative to what RBFNN requires. Indeed, RBFNN are data-driven and data-consuming machines that require large data sets for performing well. Therefore, a larger data set is required to achieve better mapping and learning with RBFNN, unlike all other classifiers for which 195 subjects and patients form a reasonably large sample. Especially, the SVM is robust even when the data size is small and holds good generalization capability [38]. It bears mentioning, however, that despite a relatively unsuccessful performance, RBFNN achieved the highest F-measure, which is desirable when a data set is unbalanced. Thus, perhaps there are other experimental conditions in which RBFNN would shine.
Conclusion
This study applies a variety of machine learning techniques to the task of distinguishing healthy subjects and PD patients based on dysphonia measurements. We compared the performances of linear discriminant analysis (LDA), k nearest-neighbors (k-NN), naïve Bayes (NB), regression trees (RT), radial basis function neural networks (RBFNN), support vector machine (SVM), and Mahalanobis distance classifier (MDC). The support vector machine classifier shows superior performance compared to the other classifiers. For our analysis, we optimized the parameters of the RBFNN and the SVM. To further improve the performance of the SVM and other machine learning classifiers, future work can consider feature selection.
Acknowledgements
We thank Rachel Szwimer and Hui Harriet Yan for scientific English editing.
Conflict of interest
Salim Lahmiri, Debra Ann Dawson and Amir Shmuel declare that they have no conflict of interest in relation to the work in this article.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Contributor Information
Salim Lahmiri, Email: salim.lahmiri@mail.mcgill.ca.
Amir Shmuel, Email: amir.shmuel@mcgill.ca.
References
- 1.Rojas A, Górriz JM, Ramírez J, Illán IA, Martínez-Murcia FJ, Ortiz A, Gómez Río M, Moreno-Caballero M. Application of empirical mode decomposition (EMD) on DaTSCAN SPECT images to explore Parkinson disease. Expert Syst Appl. 2013;40:2756–2766. doi: 10.1016/j.eswa.2012.11.017. [DOI] [Google Scholar]
- 2.Lee S-H, Lim JS. Parkinson’s disease classification using gait characteristics and wavelet-based feature extraction. Expert Syst Appl. 2012;39:7338–7344. doi: 10.1016/j.eswa.2012.01.084. [DOI] [Google Scholar]
- 3.Little MA, McSharry PE, Hunter EJ, Ramig LO. Suitability of dysphonia measurements for telemonitoring of Parkinson’s disease. IEEE Trans Biomed Eng. 2009;56:1015–1022. doi: 10.1109/TBME.2008.2005954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Shabani H, Mikaili M, Noori SMR. Assessment of recurrence quantification analysis (RQA) of EEG for development of a novel drowsiness detection system. Biomed Eng Lett. 2016;6:196–204. doi: 10.1007/s13534-016-0223-5. [DOI] [Google Scholar]
- 5.Kumari VSR, Rajesh Kumar P. Fuzzy unordered rule induction for evaluating cardiac arrhythmia. Biomed Eng Lett. 2013;3:74–79. doi: 10.1007/s13534-013-0096-9. [DOI] [Google Scholar]
- 6.Bountris P, Topaka E, Pouliakis A, Haritou M, Karakitsos P, Koutsouris D. Development of a clinical decision support system using genetic algorithms and Bayesian classification for improving the personalised management of women attending a colposcopy room. Healthc Technol Lett. 2016;3:143–149. doi: 10.1049/htl.2015.0051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Vaijeyanthi V, Vishnuprasad K, Santhosh Kumar C, Ramachandran KI, Gopinath R, Kumar AA, Yadav PK. Towards enhancing the performance of multi-parameter patient monitors. Healthc Technol Lett. 2014;1:19–20. doi: 10.1049/htl.2013.0041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Das MK, Ari S. Patient-specific ECG beat classification technique. Healthc Technol Lett. 2014;1:98–103. doi: 10.1049/htl.2014.0072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lahmiri S, Boukadoum M. New approach for automatic classification of Alzheimer’s disease, mild cognitive impairment and healthy brain magnetic resonance images. Healthc Technol Lett. 2014;1:32–36. doi: 10.1049/htl.2013.0022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Charisis VS, Hadjileontiadis LJ. Use of adaptive hybrid filtering process in Crohn’s disease lesion detection from real capsule endoscopy videos. Healthc Technol Lett. 2016;3:27–33. doi: 10.1049/htl.2015.0055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tripathy RK, Sharma LN, Dandapat S. A new way of quantifying diagnostic information from multilead electrocardiogram for cardiac disease classification. Healthc Technol Lett. 2014;1:98–103. doi: 10.1049/htl.2014.0080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kambhampati SS, Singh V, Manikandan MS, Ramkumar B. Unified framework for triaxial accelerometer-based fall event detection and classification using cumulants and hierarchical decision tree classifier. Healthc Technol Lett. 2015;2:101–107. doi: 10.1049/htl.2015.0018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sayeed Ud Doulah ABM, Fattah SA, Zhu W-P, Ahmad MO. DCT domain feature extraction scheme based on motor unit action potential of EMG signal for neuromuscular disease classification. Healthc Technol Lett. 2014;1:26–31. doi: 10.1049/htl.2013.0036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gandomkar Z, Bahrami F. Method to classify elderly subjects as fallers and non-fallers based on gait energy image. Healthc Technol Lett. 2014;1:110–114. doi: 10.1049/htl.2014.0065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sahu O, Anand V, Kanhangad V, Pachori RB. Classification of magnetic resonance brain images using bi-dimensional empirical mode decomposition and autoregressive model. Biomed Eng Lett. 2015;5:311–320. doi: 10.1007/s13534-015-0208-9. [DOI] [Google Scholar]
- 16.Lahmiri S. Glioma detection based on multi-fractal features of segmented brain MRI by particle swarm optimization techniques. Biomed Signal Process Control. 2017;31:148–155. doi: 10.1016/j.bspc.2016.07.008. [DOI] [Google Scholar]
- 17.Lahmiri S. Image characterization by fractal descriptors in variational mode decomposition domain: application to brain magnetic resonance. Phys A. 2016;456:235–243. doi: 10.1016/j.physa.2016.03.046. [DOI] [Google Scholar]
- 18.Choi JY. A generalized multiple classifier system for improving computer-aided classification of breast masses in mammography. Biomed Eng Lett. 2015;5:251–262. doi: 10.1007/s13534-015-0191-1. [DOI] [Google Scholar]
- 19.Mert A, Kılıç N, Akan A. An improved hybrid feature reduction for increased breast cancer diagnostic performance. Biomed Eng Lett. 2014;4:285–291. doi: 10.1007/s13534-014-0148-9. [DOI] [Google Scholar]
- 20.Bajaj V, Pachori RB. Epileptic seizure detection based on the instantaneous area of analytic intrinsic mode functions of EEG signals. Biomed Eng Lett. 2013;3:17–21. doi: 10.1007/s13534-013-0084-0. [DOI] [Google Scholar]
- 21.Mohammadi MR, Khaleghi A, Nasrabadi AM, Rafieivand S, Begol M, Zarafshan H. EEG classification of ADHD and normal children using non-linear features and neural network. Biomed Eng Lett. 2016;6:66–73. doi: 10.1007/s13534-016-0218-2. [DOI] [Google Scholar]
- 22.Lahmiri S. High frequency based features for low and high retina hemorrhage classification. IET Healthc Technol Lett. 2017 doi: 10.1049/htl.2016.0067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lahmiri S, Gargour C, Gabrea M. Automated pathologies detection in retina digital images based on the complex continuous wavelet transform phase angles. IET Healthc Technol Lett. 2014;1:104–108. doi: 10.1049/htl.2014.0068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Xu F, Zhou W, Zhen Y, Yuan Q. Classification of motor imagery tasks for electrocorticogram based brain–computer interface. Biomed Eng Lett. 2014;4:149–157. doi: 10.1007/s13534-014-0128-0. [DOI] [Google Scholar]
- 25.Zhang Z, Luo X. Heartbeat classification using decision level fusion. Biomed Eng Lett. 2014;4:388–395. doi: 10.1007/s13534-014-0158-7. [DOI] [Google Scholar]
- 26.Raj S, Maurya K, Ray KC. A knowledge-based real time embedded platform for arrhythmia beat classification. Biomed Eng Lett. 2015;5:271–280. doi: 10.1007/s13534-015-0196-9. [DOI] [Google Scholar]
- 27.Åström F, Koker R. A parallel neural network approach to prediction of Parkinson’s disease. Expert Syst Appl. 2011;38:12470–12474. doi: 10.1016/j.eswa.2011.04.028. [DOI] [Google Scholar]
- 28.Babu GS, Suresh S, Mahanand BS. A novel PBL-McRBFN-RFE approach for identification of critical brain regions responsible for Parkinson’s disease. Expert Syst Appl. 2014;41:478–488. doi: 10.1016/j.eswa.2013.07.073. [DOI] [Google Scholar]
- 29.Cho C-W, Chao W-H, Lin S-H, Chen Y-Y. A vision-based analysis system for gait recognition in patients with Parkinson’s disease. Expert Syst Appl. 2009;36:7033–7039. doi: 10.1016/j.eswa.2008.08.076. [DOI] [Google Scholar]
- 30.Zuo W-L, Wang Z-Y, Liu T, Chen H-L. Effective detection of Parkinson’s disease using an adaptive fuzzy k-nearest neighbor approach. Biomed Signal Process Control. 2013;8:364–373. doi: 10.1016/j.bspc.2013.02.006. [DOI] [Google Scholar]
- 31.Skodda S, Rinsche H, Schlegel U. Progression of dysprosody in Parkinson’s disease over time—a longitudinal study. Mov Disord. 2009;24:716–722. doi: 10.1002/mds.22430. [DOI] [PubMed] [Google Scholar]
- 32.McLachlan GJ. Discriminant analysis and statistical pattern recognition. Hoboken: Wiley; 2004. [Google Scholar]
- 33.Cover T, Hart P. Nearest neighbor pattern classification. IEEE Trans Inf Theory. 1967;13:21–27. doi: 10.1109/TIT.1967.1053964. [DOI] [Google Scholar]
- 34.He QP, Wang J. Fault detection using the K-nearest neighbor rule for semiconductor manufacturing processes. IEEE Trans Semicond Manuf. 2007;20:345–354. doi: 10.1109/TSM.2007.907607. [DOI] [Google Scholar]
- 35.Russell S, Norvig P. Artificial intelligence: a modern approach. Upper Saddle River: Prentice Hall; 2003. [Google Scholar]
- 36.Breiman L, Friedman JH, Olshen RA, Stone CJ. Classification and regression trees. Belmont: Wadsworth; 1984. [Google Scholar]
- 37.Poggio T, Girosi F. Networks for approximation and learning. Proc IEEE. 1990;78:1481–1497. doi: 10.1109/5.58326. [DOI] [Google Scholar]
- 38.Vapnik VN. The nature of statistical learning theory. New York: Springer; 1995. [Google Scholar]
- 39.Das R. A comparison of multiple classification methods for diagnosis of Parkinson disease. Expert Syst Appl. 2010;37:1568–1572. doi: 10.1016/j.eswa.2009.06.040. [DOI] [Google Scholar]
- 40.Eskidere Ö, Ertas F, Hanilçi C. A comparison of regression methods for remote tracking of Parkinson’s disease progression. Expert Syst Appl. 2012;39:5523–5528. doi: 10.1016/j.eswa.2011.11.067. [DOI] [Google Scholar]
- 41.Little MA, McSharry PE, Roberts SJ, Costello DAE, Moroz IM. Exploiting nonlinear recurrence and fractal scaling properties for voice disorder detection. Biomed Eng Online. 2007;6:23. doi: 10.1186/1475-925X-6-23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Tsanas A, Little MA, McSharry PE, Ramig LO. Accurate telemonitoring of Parkinson’s disease progression by non-invasive speech tests. IEEE Trans Biomed Eng. 2010;57:884–893. doi: 10.1109/TBME.2009.2036000. [DOI] [PubMed] [Google Scholar]
- 43.Ergena B, Baykarab M, Polat C. An investigation on magnetic imaging findings of the inner ear: a relationship between the internal auditory canal, its nerves and benign paroxysmal positional vertigo. Biomed Signal Process Control. 2014;9:14–18. doi: 10.1016/j.bspc.2013.09.007. [DOI] [Google Scholar]
- 44.Flake GW. Square unit augmented, radially extended, multilayer perceptrons. In: Montavon G, Orr GB, Müller K-R, editors. Neural networks: tricks of the trade. Lecture Notes in Computer Science, vol. 7700. Berlin: Springer; 2012. pp. 143–161. [Google Scholar]
- 45.Hastie T, Tibshirani R, Friedman J. The elements of statistical learning, data mining, inference, and prediction. 2. New York: Springer; 2009. [Google Scholar]