Dynamics of blood flow: modeling of Fåhraeus and Fåhraeus–Lindqvist effects using a shear-induced red blood cell migration model

Abstract

Blood flow in micro capillaries of diameter approximately 15–500 μm is accompanied with a lower tube hematocrit level and lower apparent viscosity as the diameter decreases. These effects are termed the Fåhraeus and Fåhraeus–Lindqvist effects, respectively. Both effects are linked to axial accumulation of red blood cells. In the present investigation, we extend previous works using a shear-induced model for the migration of red blood cells and adopt a model for blood viscosity that accounts for the suspending medium viscosity and local hematocrit level. For fully developed hematocrit profiles (i.e., independent of axial location), the diffusion fluxes due to particle collision frequency and viscosity gradients are of equal magnitude and opposite directions. The ratio of the diffusion coefficients for the two fluxes affects both the Fåhraeus and Fåhraeus–Lindqvist effects and is found related to the capillary diameter and discharge hematocrit using a well-known data-fit correlation for apparent blood viscosity. The velocity and hematocrit profiles were determined numerically as functions of radial coordinate, tube diameter, and discharge hematocrit. The velocity profile determined numerically is consistent with the derived analytical expression and the results are in good agreement with published numerical results and experimental data for hematocrit ratio and hematocrit and velocity profiles.

Introduction

The reduction in the tube hematocrit (H_T) in comparison with the discharge hematocrit (H_D), in the approximate capillary diameter range 15–500 μm [1], is known as the Fåhraeus effect [2] and is attributed to high concentration of red blood cells (RBCs) in the core region of the area of flow. The drop in the apparent viscosity, observed by Martini [3] and Fåhraeus and Lindqvist [4], is called the Fåhraeus–Lindqvist effect. Most of the blood flow resistance in the vascular system occurs in micro vessels with diameters in the range of 10–300 μm [5]. The approximate range of blood vessel diameters is from 3 μm to 3 cm [6]. For a capillary diameter (D) below 7 μm and as low as 2.7 μm, both the apparent viscosity and H_T increase sharply. The mechanisms for changes of the apparent viscosity with D are discussed in [7].

A recent review of blood viscosity models as a function of local hematocrit and/or shear rate can be found in Hund et al. [8]. The models include, among others, the Krieger–Dougherty model, the Quemada model, and a modified Krieger–Dougherty model by Hund et al.

Haynes [9] proposed a marginal zone theory in which RBCs concentrate in the core region, while the outer zone is a RBC-free layer. Haynes assumed the outer zone thickness to be uniform and independent of capillary diameter (D). Haynes’ approach using a two-zone concept was extended in [1, 10–12]. Fournier [1] used a published relation for viscosity as a function of hematocrit and assumed the viscosity to be uniform in the core region. Using published data for apparent viscosity yielded results showing an increase in the relative outer zone thickness with decreasing capillary diameter [1]. Sharan and Popel [10] considered the suspending medium viscosity to be different from the plasma viscosity and used Pries et al.’s data-fit correlations for both the hematocrit ratio H_T/H_D and the relative apparent viscosity of blood [6]. Chebbi [11] extended the marginal zone theory of Haynes [9] and the developments by Fournier [1] and Sharan and Popel [10] by considering viscous dissipation and microvascular network problems involving bifurcations while using the correlation of Pries et al. for H_T/H_D [6]. Sriram et al. [12] used the Quemada model to obtain the viscosity of the core region layer. A numerical solution was obtained using the data-fitted equations in Pries et al. [6] for calibration to obtain the cell-free layer thickness as a function of H_D [12].

In a different development, Leighton and Acrivos [13] proposed mechanisms for particle diffusion in non-uniform shear flow involving a flux in the direction of decreasing frequency of interactions between particles, along with another flux in the direction of lower viscosity. Phillips et al. [14] extended the work of Leighton and Acrivos [13], amended the forms of the fluxes, and included them in a conservation equation for the particle concentration. Using the Krieger–Dougherty model for blood viscosity [15], Phillips et al. [14] obtained an analytical expression for the variation of the particle concentration as a function of radial position in capillary flow, in agreement with the computational works of Weert [16] and Mansour et al. [17]. Using the particle migration model of Phillips et al. [14] (also used in [16]) along with the Quemada model for blood viscosity [18], Mansour et al. [17] found the flux coefficients to depend on H_T and dimensionless radial position. The effect of red blood cells’ elasticity [19] on RBC migration is addressed in [20–22], with the model of Mavrantzas and Beris [23, 24], proposed for polymer solutions, adopted for blood flow dynamics by including Fickian cell migration in addition to elastic-stress induced migration instead of shear-induced migration as in the Leighton and Acrivos model [13].

Governing equations

The hematocrit and velocity profiles satisfy the conservation of mass and momentum equations.

Hematocrit level profile

The hematocrit level H is defined as the RBC volume fraction. At steady state, the fully developed hematocrit profile in capillary flow is only a function of the radial coordinate r. The tube and discharge hematocrit levels H_T and H_D are cross-sectional averages defined as [25]:

$$H_T=\frac{\underset{A}{\int }H\mathit{dA}}{A}$$ 1

$$H_D=\frac{\underset{A}{\int }H{v}_z\mathit{dA}}{\underset{A}{\int }{v}_z\mathit{dA}}$$ 2

For H and v functions of r only, the equations take the following form:

$$H_T=\frac{\underset{0}{\overset{R}{\int }}2\mathit{\text{πrHdr}}}{\pi R^2}$$ 3

$$H_D=\frac{\underset{0}{\overset{R}{\int }}2\mathit{\text{πrHv}}{}_{z}dr}{\pi R^2{v}_{\mathit{av}}}$$ 4

where R is the capillary tube inner radius.

The RBC conservation equation includes the accumulation term in addition to the advection and the diffusion terms.

$$\frac{\partial H}{\partial t}+\overrightarrow{v}\cdot \nabla H=-\nabla \cdot \overrightarrow{J}$$ 5

At steady state, the above equation reduces in the fully developed region to:

$$0=-\frac{1}{r}\frac{\partial \left({\mathit{rJ}}_r\right)}{\partial r}$$ 6

where J_r is the total hematocrit flux in the radial direction. The Phillips et al. model [14] (extending the work of Leighton and Acrivos [13]) is adopted for the diffusional terms resulting from gradients in the hematocrit level, shear rate, and viscosity with

$$J_r=J_c+J_{\mu }$$ 7

where

$$J_c=-K_c{a}^2\left(H^2\frac{\mathit{d\sigma }}{\mathit{dr}}+\mathit{H\sigma }\frac{\mathit{dH}}{\mathit{dr}}\right)$$ 8

$$J_{\mu }=-K_{\mu }\sigma H^2\frac{a^2}{\mu }\frac{\mathit{d\mu }}{\mathit{dr}}$$ 9

in which a is the red blood cells radius and σ denotes the shear rate:

$$\sigma =-\frac{{\mathit{dv}}_z}{\mathit{dr}}$$ 10

Velocity profile

The two boundary conditions are the no-slip condition at the wall:

$$\mathrm{B}.\mathrm{C}.1\mathrm{at}r=R,v_z=0$$ 11

and the symmetry condition at the centerline:

$$\mathrm{B}.\mathrm{C}.2\mathrm{at}r=0,\frac{{\mathit{dv}}_z}{\mathit{dr}}=0\left(\text{or}\frac{{\mathit{dv}}_z}{\mathit{dr}}\text{finite}\right)$$ 12

Using the notations in Bird et al. [26], the momentum balance in the z-direction reduces to:

$$\frac{1}{r}\frac{d}{\mathit{dr}}\left(\mathit{r\tau }\right)=-\frac{\mathit{dP}}{\mathit{dz}}$$ 13

where dP/dz is the pressure gradient and the shear stress τ is given as a function of the shear rate σ by:

$$\tau =\mathit{\mu \sigma }$$ 14

Both terms in Eq. (13) are constant as one term of the equation depends on r and the other term depends on z.

Integrating with respect to r while using:

$$\mathrm{\tau }\text{finite}\mathrm{at}\mathrm{r}=0$$ 15

gives

$$\tau =\mathit{\mu \sigma }=-\frac{\mathit{dP}}{\mathit{dz}}\frac{r}{2}$$ 16

In dimensionless form, we have

$$\frac{d{\overline{v}}_z}{d\overline{r}}=-\frac{\overline{r}}{2\overline{\mu }}$$ 17

where

$${\overline{v}}_z=\frac{v_z}{\mathrm{\Omega }{v}_{\mathit{av}}};\overline{r}=\frac{r}{R};\overline{\mu }=\frac{\mu }{{\mu }_p};\mathrm{\Omega }=-\frac{\mathit{dP}}{\mathit{dz}}\frac{R^2}{v_{\mathit{av}}{\mu }_p}$$ 18

Expressing v_av as

$$v_{\mathit{av}}=\frac{\underset{0}{\overset{R}{\int }}2\pi {\mathit{rv}}_z\mathit{dr}}{\pi R^2}$$ 19

in terms of the defined dimensionless variables yields

$$\mathrm{\Omega }=\frac{1}{2\underset{0}{\overset{1}{\int }}{\overline{v}}_z\overline{r}d\overline{r}}$$ 20

The Poiseuille equation defines the apparent viscosity as

$${\mu }_{\mathit{app}}=\frac{1}{8}\left(-\frac{\mathit{dP}}{\mathit{dz}}\right)\frac{R^2}{v_{\mathit{av}}}$$ 21

This gives a simple relationship between Ω and μ_app:

$$\mathrm{\Omega }=8\frac{{\mu }_{\mathit{app}}}{{\mu }_p}$$ 22

Integrating the RBC conservation equation, Eq. (6), yields

$$J_c+J_{\mu }=\frac{C}{r}$$ 23

where C is an integration constant.

J_c and J_μ can be expressed in dimensionless form using Eqs. (8) and (9):

$${\overline{J}}_c=-K_c{\left(\frac{a}{R}\right)}^2\left[H^2\frac{d\overline{\sigma }}{d\overline{r}}+H\overline{\sigma }\frac{\mathit{dH}}{d\overline{r}}\right];{\overline{J}}_c=\frac{J_c}{\mathrm{\Omega }{v}_{\mathit{av}}};\overline{\sigma }=\frac{\sigma }{\mathrm{\Omega }{v}_{\mathit{av}}/R}$$ 24

$${\overline{J}}_{\mu }=-K_{\mu }\overline{\sigma }{H}^2{\left(\frac{a}{R}\right)}^2\frac{1}{\overline{\mu }}\frac{d\overline{\mu }}{d\overline{r}};{\overline{J}}_{\mu }=\frac{J_{\mu }}{\mathrm{\Omega }{v}_{\mathit{av}}}$$ 25

In addition, the fluxes are finite at the centerline:

$$J_c\mathrm{\text{and}}{J}_{\mu }\text{are}\text{finite}\text{at}r=0$$ 26

Using Eqs. (23) and (26) shows that the integration constant C is zero. Substituting ${\overline{J}}_c$ and ${\overline{J}}_{\mu }$from Eqs. (24) and (25), respectively into ${\overline{J}}_c+{\overline{J}}_{\mu }=0$ yields after simplification:

$$H\frac{d\overline{\sigma }}{d\overline{r}}+\overline{\sigma }\frac{\mathit{dH}}{d\overline{r}}=-\zeta \overline{\sigma }\frac{H}{\overline{\mu }}\frac{d\overline{\mu }}{d\overline{r}}$$ 27

where ζ is defined as K_μ/K_c.

Using the chain rule, along with $\overline{\sigma }=\overline{r}/\left(2\overline{\mu }\right)$, Eq. (17), yields in dimensionless form:

$$\overline{r}\frac{\mathit{dH}}{d\overline{r}}\left[1+\frac{\zeta -1}{\overline{\mu }}H\frac{d\overline{\mu }}{\mathit{dH}}\right]=-H$$ 28

Expressing Eq. (28) in dimensional form gives

$$r\frac{\mathit{dH}}{\mathit{dr}}\left[1+\frac{\zeta -1}{\mu }H\frac{\mathit{d\mu }}{\mathit{dH}}\right]=-H$$ 29

Hematocrit and velocity profiles

To solve for the hematocrit and velocity profiles, a viscosity model is required. In the present work, the Krieger–Dougherty eq. [15] is adopted:

$$\mu ={\mu }_p{\left(1-\frac{H}{H_m}\right)}^{-n}$$ 30

where n = 1.82 and H_m is the maximum hematocrit level.

The hematocrit and velocity changes are governed by Eqs. (17) and (28), subject to the two boundary conditions:

$$H=H_w\mathrm{at}\overline{r}=1$$ 31

$${\overline{v}}_z=0\mathrm{at}\overline{r}=1$$ 32

where H_w is the hematocrit level at the capillary wall.

Substituting for viscosity from the Krieger–Dougherty equation into the differential equations provides:

$$\overline{r}\frac{\mathit{dH}}{d\overline{r}}\left[1+\frac{\left(\zeta -1\right)n}{H_m}H{\left(1-\frac{H}{H_m}\right)}^{-1}\right]=-H$$ 33

$$\frac{d{\overline{v}}_z}{d\overline{r}}=-\frac{\overline{r}}{2}{\left(1-\frac{H}{H_m}\right)}^n$$ 34

Integrating Eq. (33) provides r as a function of H, in agreement with Eq. (30) in Ref. [14] where the value of n = 1.82.

$$\overline{r}=\frac{H_w}{H}{\left[\frac{H_m-H}{H_m-H_w}\right]}^{\left(\zeta -1\right)n}$$ 35

Substituting for $\overline{r}$and integrating Eq. (34) yields the following expression for the dimensionless velocity profile:

$${\overline{v}}_z=\frac{H_w^2}{2H_m^n{\left(H_m-H_w\right)}^{2q}}\underset{H_w}{\overset{H}{\int }}\frac{{\left(H_m-H\right)}^s}{H^3}\left[H_m+\left(q-1\right)H\right]\mathit{dH};s=\left(2\zeta -1\right)n-1;q=\left(\zeta -1\right)n$$ 36

Using the dimensionless profiles, H_T and H_D can be calculated from:

$$H_T=2\underset{0}{\overset{1}{\int }}\overline{r}\mathit{Hd}\overline{r}$$ 37

$$H_D=2\mathrm{\Omega }\underset{0}{\overset{1}{\int }}\overline{r}H{\overline{v}}_{z}d\overline{r}$$ 38

Analytical Solution for the Velocity Profile

The following Taylor series expansion is used:

$${\left(H_m-H\right)}^s=H_m^s\left[1+\sum _{k=1}^{\infty }{b}_k{H}^k\right]$$ 39

where

$$b_k={\left(\frac{-1}{H_m}\right)}^k\frac{s\left(s-1\right)\left(s-2\right)\dots \left(s-k+1\right)}{k!}$$ 40

Substituting into Eq. (36) and integrating yields

${\overline{v}}_z=\frac{H_w^2{H}_m^{s-n}}{2{\left(H_m-H_w\right)}^{2q}}\left[H_{m}A+\left(q-1\right)B\right]$

where

$$A=\frac{1}{2}\left(H_w^{-2}-H^{-2}\right)+b_1\left(H_w^{-1}-H^{-1}\right)+b_{2}ln\left(\frac{H}{H_w}\right)+\sum _{k=3}^{\infty }\frac{b_k}{k-2}\left(H^{k-2}-H_w^{k-2}\right);B=-\frac{1}{H}+\frac{1}{H_w}+b_{1}ln\left(\frac{H}{H_w}\right)+\sum _{k=2}^{\infty }\frac{b_k}{k-1}\left(H^{k-1}-H_w^{k-1}\right)$$ 41

Solution procedure

The data-fit relations obtained by Pries et al. [6] (based on many in vitro experimental values for the apparent viscosity) are used. The expression found for the relative viscosity is given by [6]:

$$\overline{\mu }=\frac{\mu }{{\mu }_p}=1+\left({\overline{\mu }}_{0.45}-1\right)\frac{{\left(1-H_D\right)}^C-1}{{\left(1-0.45\right)}^C-1}$$ 42

where:

$${\overline{\mu }}_{0.45}=220e^{-1.3D}+3.2-2.44e^{-0.06D^{0.645}};C=\left(0.8+e^{-0.075D}\right)\left(-1+\frac{1}{1+{10}^{-11}{D}^{12}}\right)+\frac{1}{1+{10}^{-11}{D}^{12}}$$ 43

Substituting the former equation into Eq. (42) yields a relationship that takes the following form:

$$\overline{\mu }=\frac{\mu }{{\mu }_p}=F\left(H_D,D\right)$$ 44

where F is a lengthy expression that can be readily determined from Eqs. (42) and (43).

For given values of the discharge hematocrit H_D and the apparent viscosity$\overline{\mu }$, it is possible to find the capillary diameter D numerically by trial and error using the Regula–Falsi method.

Krieger–Dougherty model parameters

The model parameters for blood flow modeling are summarized in Hund et al. [8]. The value of n is close to 2 for blood, while it is theoretically 1.66 in the case of suspended solid spheres [8]. The value used in [14, 16, 17] is 1.82.

The maximum hematocrit fraction H_m is thought to be in the range 0.98–1 [8]. The value considered for H_m in [14] is 0.68 for solid spheres.

In the present model, we used n = 1.82. Changing n to 2 did not produce any significant changes in the results. The value of H_m = 0.67 was selected for the purpose of comparison with the published numerical results in [16, 17]. On the other hand, the value of H_m = 0.98 (in the range recommended in Hund et al. [8]) was selected for comparison with the numerical results of Sriram et al. [12] and the experimental data [28–31] reported in [12].

Numerical procedure for ζ selected

The value of H_w is required in order to integrate Eqs. (33) and (34), while using the boundary conditions, Eqs. (31) and (32).

(i) For given values of the discharge hematocrit H_D and D, trial and error using the secant method can be used to satisfy:

$$H_D=\frac{\underset{0}{\overset{1}{\int }}\overline{r}H{\overline{v}}_{z}d\overline{r}}{\underset{0}{\overset{1}{\int }}{\overline{v}}_z\overline{r}d\overline{r}}$$ 45

(ii) If H_T is provided, H_w is determined by trial and error to satisfy Eq. (37).

In both the cases (i) and (ii), the reduced apparent viscosity can be found as:

$$\frac{{\mu }_{\mathit{app}}}{{\mu }_p}=\frac{1}{16\underset{0}{\overset{1}{\int }}{\overline{v}}_z\overline{r}d\overline{r}}$$ 46

Once H_w is found, the hematocrit ratio H_T/H_D can be found from the numerical integration results.

Numerical procedure for the determination of ζ as a function of D and H_D

For a fixed value of ζ, H_w, H_T, H_D, H_T/H_D and μ_app/μ_p are determined as discussed in Section 5.1. The proper value of D is determined so as to satisfy both Eqs. (45) and (46):

$$F\left(H_D,D\right)=\frac{1}{16\underset{0}{\overset{1}{\int }}{\overline{v}}_z\overline{r}d\overline{r}}$$ 47

Using different values of ζ for a given value of H_D provides the relation between ζ and capillary diameter D.

Results

Comparison with the results of Weert [16] and Mansour et al. [17]

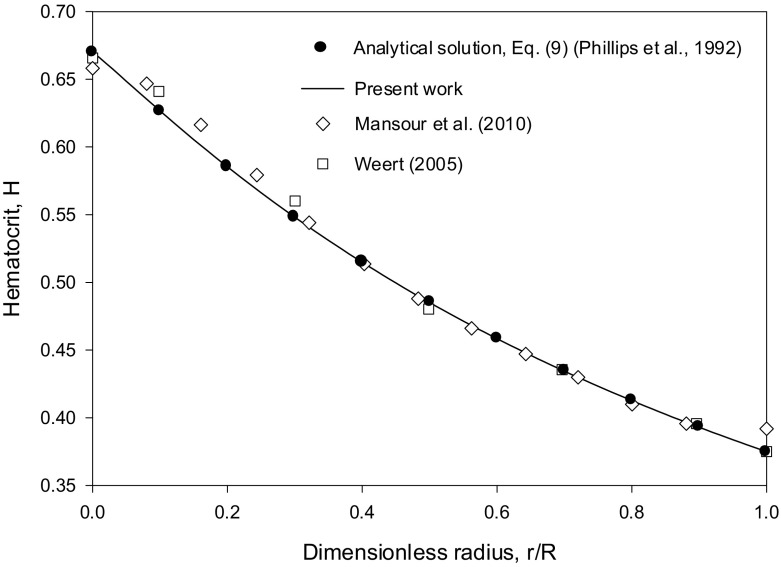
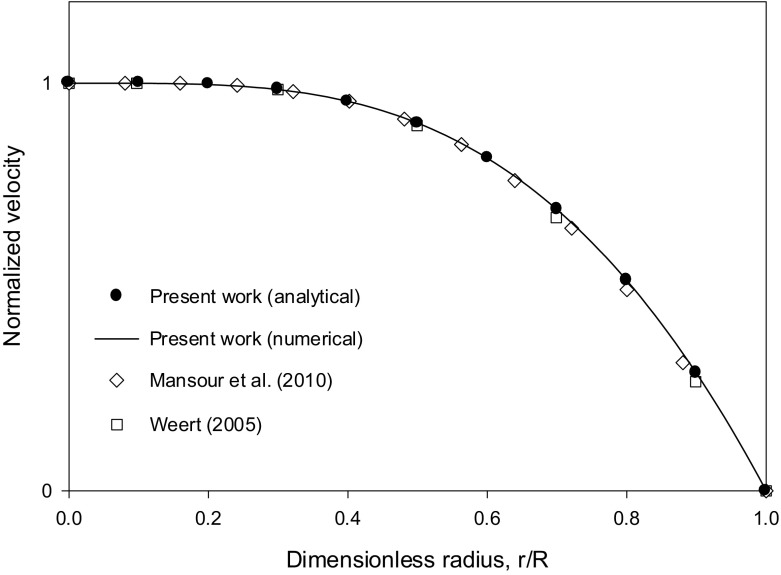
Both numerical results were obtained in the case of blood flow with H_T = 0.45 using the ratio ζ = K_μ/K_c = 0.62/0.41 = 1.512, along with the Krieger–Dougherty viscosity model for blood with n = 1.82. The values of H_m used in [16, 17] are close as seen in Fig. 1 (about 0.66–0.67). The value H_m = 0.67 was selected in the present work. The simulations in [17] were run using ANSYS Fluent CFD software. Weert [16] used a Galerkin finite element simulation code. The profiles obtained for the hematocrit and the normalized velocity to the centerline value are shown in Figs. 1 and 2, respectively. The present numerical results obtained by the Runge–Kutta integration of Eqs. (33) and (34), are in excellent agreement with the analytical solution (Eq. (30) in [14] for the hematocrit profile equivalent to the generalized Eq. (35) in the present work with n = 1.82) and the derived analytical expression, Eq. (41) for the velocity profile. Both profiles are in good agreement with the numerical solutions in [16, 17] as seen from Figs. 1 and 2. The derived analytical expression, Eq. (41), is an infinite series. Keeping only the first terms in the infinite series expansion (up to k = 10 in Eq. (41)) was found sufficient (Figs. 1 and 2).

Fig. 1.

Comparison of the Runge–Kutta numerical integration results for the hematocrit profile (using Eqs. (33) and (34)), the analytical solution, Eq. (30) in [14] (generalized Eq. (35) in the present work with n = 1.82) and the numerical solutions in [16, 17] for the case H_T = 0.45, using K_μ = 0.62, K_c = 0.41 (ζ = 1.512) and H_m = 0.67

Fig. 2.

Comparison of the Runge–Kutta numerical integration results for the normalized velocity profile (using Eqs. (33) and (34)), the analytical solution, Eq. (41) and the numerical solutions in [16, 17] for the case H_T = 0.45, using K_μ = 0.62, K_c = 0.41 (ζ = 1.512) and H_m = 0.67

Comparison with Sriram et al.’s numerical results [12] and reported experimental data [27–31]

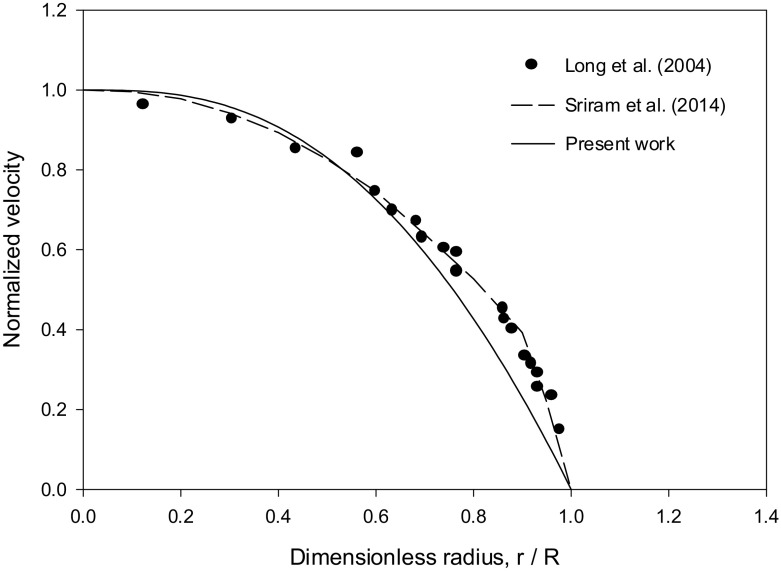
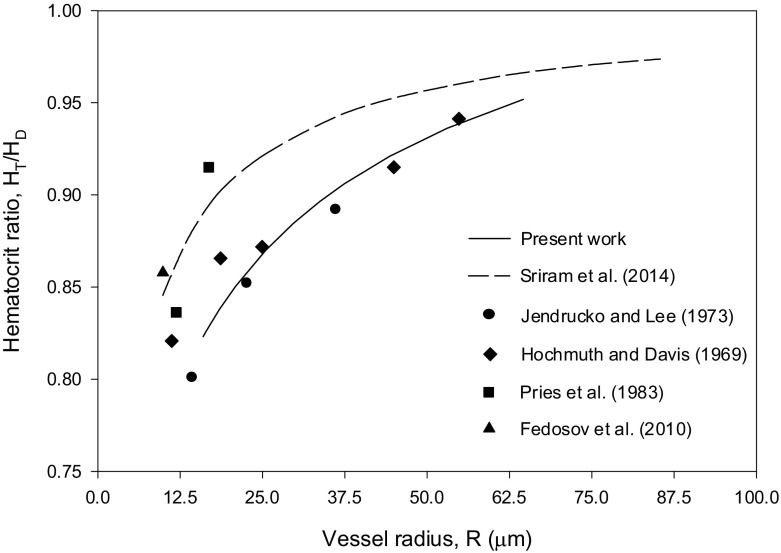
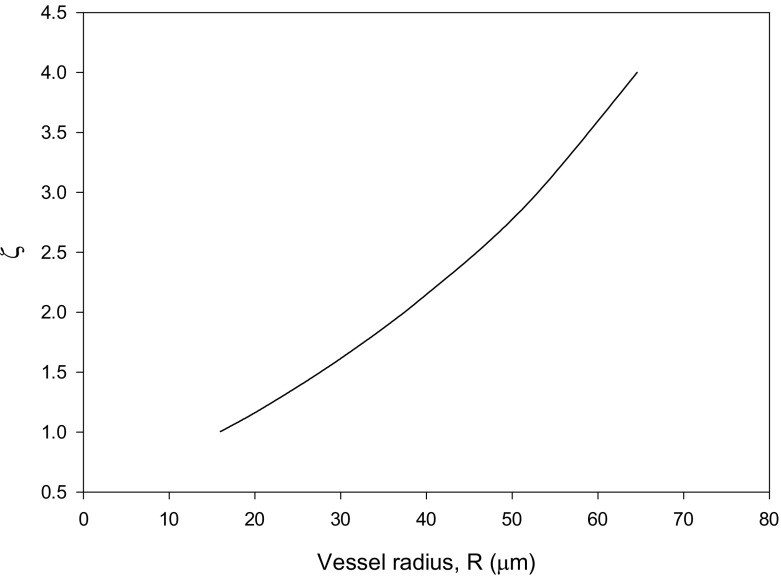
Sriram et al. [12] compared their results for the velocity profile with the experimental data of Long et al. [27] for H_D = 0.335, pressure gradient = 3732 dyn/cm³ and R = 27.1 μm. The Krieger–Dougherty parameters used in the present work are n = 1.82 and H_m = 0.98. The velocity and hematocrit ratio profiles, shown in Figs. 3 (H_D = 0.335) and 4 (H_D = 0.405), are in favorable agreement with the experimental data in [28–31]. The values obtained for ζ show higher values at larger values of R as can be seen from Fig. 5.

Fig. 3.

Comparison of the normalized velocity profile results with the experimental data in [27] and the numerical results in [12] for the case H_D = 0.335, pressure gradient = 3732 dyn/cm³ and R = 27.1 μm

Fig. 4.

Comparison of the hematocrit ratio results with the numerical results in [12] and the reported experimental data [27–31] for the case HD = 0.405

Fig. 5.

Results for ζ = K_μ/K_c versus vessel radius R for the case H_D = 0.405

Conclusions

The shear-induced model for the migration of red blood cells of Phillips et al. [14], extending the model of Leighton and Acrivos [13], was used along with the Krieger–Dougherty model for blood viscosity [15] to solve for fully developed velocity and hematocrit profiles. The diffusion coefficients ratio for the viscosity gradient and particle collision frequency fluxes can be determined as a function of capillary diameter and discharge hematocrit using the data-fit correlation for apparent blood viscosity of Pries et al. [6]. The analytical expressions for the velocity and hematocrit profiles are consistent with the numerically determined values. In addition, the numerical results are in favorable agreement with published numerical results and experimental data for hematocrit and velocity profiles and hematocrit ratio. The present simulations do not detect the change in the slope of the velocity profile near the wall as seen from experimental data. This is apparently due to the fact that the model of Phillips et al. [14] does not capture the free RBC zone when using the Krieger–Dougherty model for blood viscosity. This point could be addressed in further investigations.

Compliance with ethical standards

Conflict of interest

The author declares that he has no conflicts of interest.