Abstract
Since epileptic seizure is unpredictable and paroxysmal, an automatic system for seizure detecting could be of great significance and assistance to patients and medical staff. In this paper, a novel method is proposed for multichannel patient-specific seizure detection applying the earth mover’s distance (EMD) in scalp EEG. Firstly, the wavelet decomposition is executed to the original EEGs with five scales, the scale 3, 4 and 5 are selected and transformed into histograms and afterwards the distances between histograms in pairs are computed applying the earth mover’s distance as effective features. Then, the EMD features are sent to the classifier based on the Bayesian linear discriminant analysis (BLDA) for classification, and an efficient postprocessing procedure is applied to improve the detection system precision, finally. To evaluate the performance of the proposed method, the CHB-MIT scalp EEG database with 958 h EEG recordings from 23 epileptic patients is used and a relatively satisfactory detection rate is achieved with the average sensitivity of 95.65% and false detection rate of 0.68/h. The good performance of this algorithm indicates the potential application for seizure monitoring in clinical practice.
Keywords: Epilepsy, Seizure detection, Scalp EEG, The earth mover’s distance, BLDA classification
Introduction
Epilepsy is a transient breakdown of the brain neuronal activity, which clinically produces an involuntary behavior or consciousness disturbances, such as a whole-body convulsion, a sensory hallucination, or a lapse of sensation [1–3].There are approximately 1% of people in the world suffers from this disease, as well as 1 out every 3 patients continues to undergo frequent seizures despite multiple drug therapy, which influences people’s normal daily life seriously [4, 5]. Electroencephalography (EEG) plays an important part in the diagnosis and treatment of epilepsy according to recording and monitoring electrical activity of the brain with the electrodes placed along the scalp, even invasive electrodes [6]. However, it is a tedious, expensive and time-consuming task with a large number of EEG recordings inspected by neurologists visually to detect seizures. Therefore, an automatic system capable of detecting seizure onset quickly could ease the burden of medical staff and help the treatment of patients.
The situation is seizure onset detection remains a complicating challenge because EEG’s variability among individuals with epilepsy. The location of seizure activities and the spectral content of the rhythmic activity are various for different patient. Moreover, there are quite a bit of overlap associated with non-seizure and seizure in EEG recordings. For the scalp EEG, the detecting task is more difficult, because the activity of neurons in deep brain almost can’t reflect on the scalp EEG and some disruptive factors exist in EEG recordings, such as muscle contractions and eye flutter [7].
Research in automatic seizure detection has developed in the past few decades. One of the earliest seizure detection algorithm was proposed by Gotman in 1982 [8]. The approach searched a number of EEG channels with a frequency band between 3 and 20 Hz, and EEGs were broken down into half-waves, extracted the amplitude and duration features for seizure detection. Later, Khan and Gotman developed a method based on the discrete wavelet transform (DWT) [9], which used the DWT divide EEG signals into five bands and computed the EEG features for the chosen scales. The early patient-specific seizure onset detector was developed by Qu [10]. The algorithm employed the nearest-neighbor classifier for classification which was trained on EEG feature vectors form a single patient respectively. Meier proposed a seizure detection algorithm that was not patient-specific but was seizure-specific [11]. For the past few years, many kinds of signal processing technologies were applied for EEG analysis and seizure detection, such as Hilbert–Huang transform (HHT) [12], Stockwell transform [13], nonlinear analysis [14], sparse representation [15] and so on. Meanwhile, various linear and nonlinear features were proposed to differentiate the non-seizure and seizure EEG recordings, such as coefficient of variation [16], line length [17], approximate entropy [18], and higher order spectra [19] etc.
The earth mover’s distance (EMD) is a cross-bin distance function that compares Histogram-based local descriptors, where the distribution comparison is modeled as a transportation problem. It is proposed by Rubner et al. [20] to compare distributions for image retrieval tasks. Since that time, the EMD has aroused much interest of researchers and institutions and shown the good property of feature behave. Grauman [21] used it for shape matching and Indyk and Thaper [22] presented a fast approximation EMD algorithm. Tan and Ngo [23] applied EMD’s partial matching ability for common pattern discovery. Unlike the above previous efforts, only forcing on image and pattern matching, we applied the EMD to distinguish the different periods of epileptic EEG signals for seizure detection.
There is a large amount of pattern classification and machine learning algorithms for classification, such as Fisher Linear Discriminant analysis (FLDA), Boosting, Neural Network (NN) and Support Vector Machine (SVM). Compared with these above classifiers, the Bayesian linear discriminant analysis (BLDA) has particular advantages with avoiding over-fitting to high dimensional and adjusting parameter automatically, which could be seen as an expansion of FLDA. It has shown good performance in the area of brain-computer interface [24, 25]. Therefore the current work applies BLDA as the classifier to classify the features.
In this paper, a novel method is presented based on the earth mover’s distance and BLDA for seizure detection and the experiment results illustrate the effectiveness of the proposed method. The text is organized as follows: a brief introduction of the scalp EEG dataset is shown in Sect. 2. Then in Sect. 3, the method is described in details, which includes EMD feature extraction, BLDA classification and postprocessing. The performance of this experiment is showed in Sect. 4 and followed by a discussion in Sect. 5 as well as a conclusion in Sect. 6.
Scalp EEG dataset
In this paper, the scalp EEG dataset used to evaluate our system comes from the Children’s Hospital Boston, which includes the continuous scalp EEG recordings from pediatric patients with intractable seizures suffering medication withdrawal for epilepsy surgery evaluation [26]. Unlike previous works focusing on adult EEG, we work on pediatric scalp EEG, which exhibits greater variability in the activity of seizure. The EEG recordings were collected from 23 subjects and grouped into 24 cases. Each case come from one patient except that the case 21 was obtained 1.5 years after case 01 with the same female patients. All EEG recordings were sampled at 256 Hz, mostly using a bipolar electrode montage of 23 channels (18 or 20 in a few cases).
The total recordings included 958.2 h continuous scalp EEG and 187 seizures with the duration of 0.5–20 min. The beginning and ending time of each seizure onset were judged by epilepsy experts previously. For every patient, there were 18–145 h EEG recordings including periods of wake and sleep, and at least three seizures. The details of the used EEG database are illustrated in Table 1. Because case 24 was added to this dataset in December 2010, the etiology of this patient is unknown.
Table 1.
Details of the CHB-MIT scalp EEG database used in this work
| Case | Seizure origin | EEG length (h) | Number of used seizures | Mean seizure duration (s) |
|---|---|---|---|---|
| 1 | Temporal | 40.5 | 7 | 63.14 |
| 2 | Frontal | 35.3 | 3 | 57.33 |
| 3 | Temporal | 38 | 7 | 57.43 |
| 4 | Temporal, occipital | 144.6 | 4 | 94.5 |
| 5 | Frontal | 39 | 5 | 111.6 |
| 6 | Temporal | 62.2 | 7 | 14.86 |
| 7 | Temporal | 67 | 3 | 108.33 |
| 8 | Temporal | 20 | 5 | 183.8 |
| 9 | Frontal | 66.6 | 4 | 70.25 |
| 10 | Temporal | 50 | 7 | 63.86 |
| 11 | Frontal | 34.8 | 3 | 268.67 |
| 12 | Frontal | 22.7 | 39 | 37.13 |
| 13 | Temporal, Occipital | 30 | 8 | 47.88 |
| 14 | Temporal | 26 | 8 | 21.13 |
| 15 | Frontal, Temporal | 41 | 20 | 99.6 |
| 16 | Temporal | 18 | 7 | 8.57 |
| 17 | Temporal | 20 | 3 | 97.67 |
| 18 | Temporal, Occipital | 36.3 | 6 | 52.83 |
| 19 | Frontal | 29.9 | 3 | 78.67 |
| 20 | Temporal | 26.6 | 8 | 36.88 |
| 21a | Temporal | 30.8 | 4 | 49.75 |
| 22 | Temporal, Occipital | 31 | 3 | 68 |
| 23 | Frontal | 26.6 | 7 | 60.57 |
| 24 | – | 21.3 | 16 | 31.94 |
| Total | – | 958.2 | 187 | – |
aCase 21 was obtained 1.5 years after case 1 for the same patient
In this study, the continuous scalp EEG recordings are divided into segments without overlap to analysis. Each epoch lasts for 4 s with 1024 points due to sampling rate of 256 Hz. With the purpose of training the classifier, the training dataset was composed which includes several seizures chosen randomly from the seizure parts and the same number of non-seizure parts for each patient. Multiple training seizures are necessary in consideration of the impact of the diversity of seizures for detection performance. In total, 1.98 h of seizure and non-seizure data with 42 seizure events of all patients were used as the training dataset. To test the performance of the algorithm, all of the rest of EEG recordings composed the testing dataset for each individual. The testing dataset contains nearly 956 h EEG recordings and 145 seizures totally, which is long enough to evaluate this method effectively.
Methods
System overview
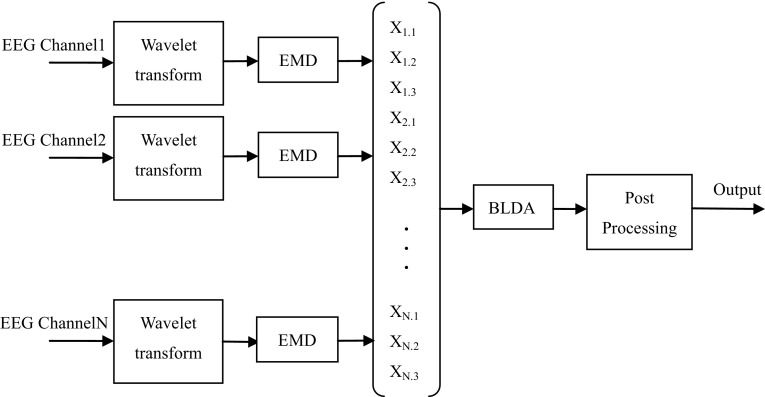
The architecture of the proposed system is illustrated in Fig. 1, which contains four stages of this method, i.e. wavelet transform, EMD feature extraction, BLDA classification and post-processing. In the following parts, all stages of this system are made a detailed description and explanation.
Fig. 1.
The framework of seizure detection system, where the EMD extraction, classification based on BLDA and postprocessing are shown schematically
Signal processing and feature extraction
In our study, the long-term EEG recordings were divided into segments and then the DWT was used to each segment. Wavelets could be seen as a set of functions to represent highly transient phenomena such as spikes in the EEG, and the DWT is helpful for suppressing the high frequency noises in EEG recordings and providing the flexibility in analyzing EEG signals. Since the Daubechies-4 wavelet is more suitable to match the characteristics of the EEG [9], we used this wavelet conducting wavelet decomposition to the original EEG segments with five scales. As our data were sampled at 256 Hz, the five frequency bands were 64–128 Hz, 32–64 Hz, 16–32 Hz, 8–16 Hz, and 4–8 Hz corresponding to decomposition scales 1–5. Even the seizure rhythmic activities have a broader frequency range, the most activities are included in the frequency range of 3–30 Hz. Moreover, the 0–4 Hz band is ignored because this frequency band often occurs in non-ictal sleep EEG. Besides, seizure activities in the 2–3 Hz range are usually not restricted to that range in the process of seizure onset [27]. Hence, scale 3, 4 and 5 were selected to extract features since the seizure activities are mostly represented by the three scales.
Extracting effective features from the original EEG data is a critical step and determines the result is good or not to a great extent. In this algorithm, the earth mover’s distance (EMD) is extracted as the EEG feature to measure the dissimilarity between two signatures for classification. A signature of size ,, is a concise representations of distribution, where is the location of the jth element and is its weight. According to [28], the histogram can be viewed as a special type of signature in which the median of each bin corresponds to the position , and the histogram values are equal to the weight in S.
The EMD could be regarded as a transportation problem which calculates the minimum cost to transform one distribution into other. Given two signatures and , the signature P is defined as the suppliers and N is defined as the consumers. The problem is to find a least-expensive flow from the suppliers to the consumers to minimize the cost
| 1 |
with the following constraints:
| 2 |
Here, is the ground distance between element pi and . This can be viewed as a special linear programming problem, which is solved applying the transportation simplex (TS) algorithm [20]. Finally, we obtain the optimal flow F, and the EMD is defined as the following formula:
| 3 |
Due to the last constraint of Eq. (2), the total weight of the smaller signature is used as the normalization factor. This factor need be taken into consideration to avoid biasing smaller signature when the two signatures have different total weight.
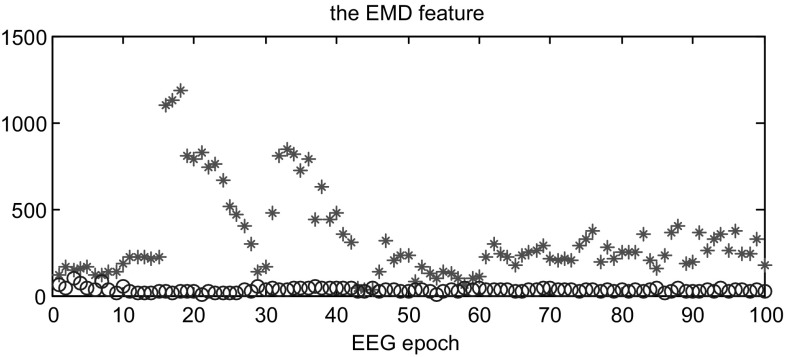
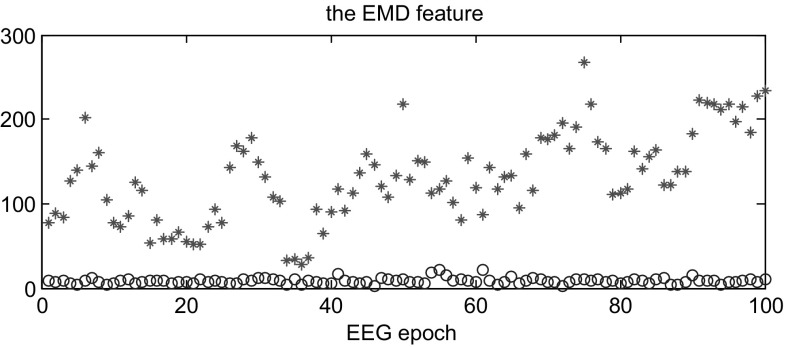
As mentioned before, the EEG signals are separately segmented into 4-second epochs and the three scales were selected after wavelet transform from each channel. Hence, we computed the histogram of each sub-band and put the three histograms together to create one histogram as a signature for each EEG epoch. Then, one signature of non-seizure epoch was chosen randomly as the reference substance and computed the earth mover’s distance with other signatures as the EEG features fed to BLDA classifier. The selection of the reference is random between the periods of at least 2 h before seizure onset and 2 h after seizure end, which could avoid adverse effects of the beginning and ending of seizure onsets as well as evade the bias of preselection. In addition, the seizure data is more varied and changeable, which is not suitable as the stable reference to measure the difference of two categories. Figures 2 and 3 illustrates the values of earth mover’s distance from the training and testing data. Here we randomly choose part of the training data and testing data of case 1 consisting of seizure and non-seizure segments. As shown in both Figs. 2 and 3, most of the EMD for non-seizure epoch is much lower than seizure epoch and the overlap between them is small, which is very favorable for classification.
Fig. 2.
The feature of the non-seizure and seizure EEG epochs from the training dataset. ‘circle’: the non-seizure EEG epochs; ‘asterisk’: the seizure EEG epochs
Fig. 3.
The feature of the non-seizure and seizure EEG epochs from the testing dataset. ‘circle’: the non-seizure EEG epochs; ‘asterisk’: the seizure EEG epochs
BLDA classifier
In this paper, the Bayesian linear discriminant analysis is employed for classification, which can be viewed as an extension of Fisher’s discriminant analysis (FLDA). Compared with the FLDA [29], it applies regularization during the training process to prevent overfitting to high dimensional and noisy datasets. Furthermore, all the model parameters are estimated automatically in the classification process, which reduce time consuming in the training and classification procedure.
The BLDA also means performing regression in a Bayesian framework [24]. Assuming the weight vector used in Bayesian regression satisfies Gaussian distribution, the likelihood function for the weights is:
| 4 |
here X is the matrix made up of training feature vectors, y denotes a vector of the regression targets, denotes the inverse variance of the noise, N is the number of samples in the training dataset, and D denotes the pair{X; y}.
For the weight vector , its prior distribution is expressed as:
| 5 |
here D denotes the number of features and is a D + 1 dimensional, diagonal matrix,
| 6 |
According to the Bayes rule, the posterior distribution is also Gaussian and can be computed as:
| 7 |
Then, the mean m of the posterior satisfies the following equations:
| 8 |
Thus we get the linear discriminant equation . Here, denotes a new input vector for classification. Hence the linear discriminant result depend on the parameters and . According to an iterative algorithm proposed by MacKay [30], the two parameters are optimized to minimize the regression error to obtain the optimal classification discriminant surface.
Postprocessing
In the last stage of system, the postprocessing technique was applied for the outputs of the BLDA classifier to obtain the proper classification results. As can be seen in Fig. 4, the postprocessing process includes a smoothing of the BLDA outputs, applying a threshold, and using a collar operation.
Fig. 4.
The detailed structure of post-processing, including smoothing, threshold judgment and collar technique
To removing the burrs of the BLDA outputs, a forward moving linear average filter is applied, which is a convolution with a rectangular pulse of unit area [31]. Although this filter is simple but effective for reducing random noise, as well as keeping the sharpest part. It is defined:
| 9 |
where is the input signal, is the filtered signal, N is the smoothing length. Hence, some chattering characteristics lasting a short time can be modified using this smoothing process. In this work, the smoothing length is different for each patient and is determinated through getting the best classification result of training data in the training stage. Then, the length was fixed in the testing stage for this patient.
Then, the smoothed outputs were compared to a threshold, which is adjusted for each patient by using the same criterion as the determination of smoothing length. The binary decisions were obtained: 1—non-seizure; 0—seizure. If the output is greater than the value of threshold, the epoch is labeled as non-seizure; otherwise it is marked as seizure. The value of threshold is patient specific in this paper. However, seizure onset is changing gradually and the forward smoothing procedure make the beginning of seizures varying obscure. Hence, a collar operation was applied in the last step to compensate for the missing of pre-seizure. Each detected binary decision was extended from forward side by x epochs. Besides, a seizure was defined as a paroxysmal burst lasting at least 6 s which is clearly different from the background [32], so at least two consecutive epochs marked 0 were declared as a seizure event. It is helpful for avoiding some false detections for brief, normal but seizure-like activities.
Experimental results
All the experiments were processed in MATLAB7.0 environment running in an AMD Sampson processor. Firstly, the EEG recordings from each channel were segmented into 4-s epochs separately and we executed wavelet decomposition to EEGs with five scales and chose scale 3, 4 and 5 extracting the EMD features using the method we mentioned in Sect. 3.2. The set of features extracted from all channels make up feature vectors to capture the spatial information between the multiple channels. The training data and testing date were selected randomly from all EEG recordings for each individual. Afterwards, the feature vectors were put into the BLDA classifier we described in Sect. 3.3 for classification. We describe the performance according to four statistical measures: sensitivity, specificity, recognition accuracy and the false detection rate, which are defined as following.
| 10 |
| 11 |
| 12 |
The true positive (TP) means the number of seizure epochs correctly identified by both our system and the EEG specialists, and the non-seizure epochs correctly identified both by our method and the experts is defined as true negative (TN). False positive (FP) denotes the number of seizures identified only by our system but not experts. Furthermore, to assess our algorithm’s feasibility, the false detection rate is calculate in this work. A series of consecutive FPs which are not overlapped with the labeled seizures is defined as a false detection and the false detection rate means the number of false detections per hour.
The overall performance of our proposed system is exhibited in Table 2. To evaluate our method more accuracy, a large amount of non-seizure EEG data are used to be tested in our experiment, which last more than one hundred hours for one individual. From Table 2, we can see all results for each patient according to the four statistical measures. It can be viewed that the best results with the sensitivity of 100%, the specificity of 99.84%, the recognition accuracy of 99.84%, and the false detections rate of 0.03/h were achieved for different patients, respectively. In addition, the means of sensitivity, specificity for all the 24 patients were greater than 95.0%, and the mean of false detections rate was less than 0.7/h.
Table 2.
The results to evaluate the performance of our detection method for each patient
| Case | Sensitivity (%) | Specificity (%) | Recognition accuracy (%) | False detections/h | detected seizures/tested seizures |
|---|---|---|---|---|---|
| 1 | 100 | 99.42 | 99.42 | 0.1 | 6/6 |
| 2 | 100 | 98.89 | 98.90 | 0.43 | 2/2 |
| 3 | 97.65 | 99.12 | 99.12 | 0.35 | 6/6 |
| 4 | 94.34 | 94.57 | 94.57 | 0.56 | 2/2 |
| 5 | 100 | 99.21 | 99.21 | 0.13 | 4/4 |
| 6 | 76.92 | 92.68 | 92.67 | 0.93 | 3/3 |
| 7 | 100 | 98.61 | 98.63 | 0.12 | 2/2 |
| 8 | 92.77 | 98.06 | 98.01 | 0.47 | 4/4 |
| 9 | 100 | 99.76 | 99.76 | 0.05 | 3/3 |
| 10 | 100 | 99.84 | 99.84 | 0.04 | 6/6 |
| 11 | 100 | 99.65 | 99.65 | 0.12 | 2/2 |
| 12 | 77.22 | 80.54 | 80.47 | 2.57 | 27/34 |
| 13 | 70.51 | 97.85 | 97.77 | 0.52 | 5/6 |
| 14 | 89.66 | 96.79 | 96.78 | 0.99 | 5/5 |
| 15 | 98.55 | 97.53 | 97.54 | 0.41 | 18/18 |
| 16 | 100 | 60.69 | 60.72 | 4.76 | 3/3 |
| 17 | 98.07 | 98.63 | 98.63 | 0.31 | 2/2 |
| 18 | 100 | 96.17 | 96.18 | 0.61 | 5/5 |
| 19 | 100 | 99.56 | 99.56 | 0.1 | 2/2 |
| 20 | 100 | 95.00 | 95.01 | 1.56 | 6/6 |
| 21 | 100 | 99.23 | 99.23 | 0.2 | 2/2 |
| 22 | 100 | 99.73 | 99.73 | 0.03 | 2/2 |
| 23 | 100 | 99.40 | 99.40 | 0.2 | 6/6 |
| 24 | 100 | 96.99 | 97.01 | 0.73 | 14/14 |
| Mean | 95.65 | 95.75 | 95.74 | 0.68 | 137/145 |
Furthermore, fifteen patients (patients 1, 2, 5, 7, 9,10,11,16, 18, 19, 20, 21, 22, 23 and 24), nearly two-thirds of all the patients, achieved the sensitivity of 100%. The specificities of twenty-two patients are greater than 92% and among them, there are ten patients having the specificity higher 99%. Specially, for patient 16, the specificity is low because the duration of seizure onset is very short and owing to detecting seizure, a lot of non-seizures are identified as seizures mistakenly. Moreover, 145 seizure events were used as testing data totally and 137 seizures were detected successfully as shown in the last column of Table 2.
Discussion
Our goal is to develop an automatic seizure detector with perfect performance for clinical application with higher sensitivity and lower false detection rate. But the two targets have the oppositional physical meanings which are contradictory to each other. The high sensitivity may cause the false detection rate to rise, likewise the lower false detection rate may cause detection of seizures missed and give up some sensitivity. Therefore, a suitable and valid feature is important and meaningful for the productivity of seizure detection system.
So far, the earth mover’s distance has been widely used in many applications as a valid feature, making a good performance. In our study, the EMD has showed powerful separability to non-seizure and seizure EEG data. Although the seizure characteristics is varied and changeable, the dissimilarity between two periods of EEG always exists, which is represented using the EMD feature and the distance between the different periods is larger than the distance of the same periods. Figure 5 illustrates the obvious changes of our feature and the part between the two vertical lines is one seizure identified by experts for patient 15. The satisfying results in Table 2 indicated that the feature has great discriminatory power for classification. In addition, it can obviously be viewed that there is a gradual change between non-seizure and seizure EEG epochs. Hence, the smoothing filter and collar tool are helpful to locate seizure more precisely.
Fig. 5.
The EMD feature extracted from an hour EEG recordings which contain one seizure event from patient 15
Furthermore, the wavelet transform and postprocessing procedures could improve the system performance availably. The DWT decomposed the EEG recordings into different scales and the distribution of EEG epoch was created with the specific frequency domain, which could guarantee the calculation of the EMD and eliminate the high frequency noises in EEG recordings. Therefore, the EEG signal of each channel was decomposed into three special subbands and EMD features were extracted at every subband respectively. For one patient, if the number of channels is N, the feature dimensionality of the extracted features is 3 × N. Thus, the feature of each dimension contains both the spatial information and frequency domain information, which is useful for classification. Moreover, after the BLDA classifier, a smoothing filter and a collar operation were carried for the outputs of BLDA instead of comparing with a threshold immediately. These operations greatly reduced the possible missed-detection and misjudgment, as well as increased the accuracy of seizure location.
There are several classic EEG databases applied for the research of seizure detection, such as the Bonn EEG dataset [33–35], the Freiburg Hospital dataset [36] and the scalp EEG dataset used in this work. The scalp EEG database in this work is relatively large and has been applied for seizure detection with different levels of success. Compared with other detection systems for epilepsy patients, the classification accuracy obtained in the current study based such a large dataset is relatively high. Nasehi and Pourghassem [37] developed a seizure onset detection algorithm with the dynamic cascade feed-forward neural networks (DCFNN), which tested on 844 h of the same EEG recordings and the results showed that it could distinguish 98% from 163 seizures as well as specificity of 91%. The specificity was lower than our method with specificity of 95.75%, even though only three seizures were missed in his study. Khan et al. [38] designed a seizure detector based on discrete wavelet transform which was evaluated on 5 subjects with 65 seizures from the same scalp EEG database. Relative values of energy and a normalized coefficient of variation (NCOV) were computed on the wavelet coefficients as features thereby classified using simple LDA classifier. In comparison to their system, the sensitivity of our algorithm is better with the larger dataset of 23 patients. Moreover, contrasting with the two classifiers, simple LDA classifier and BLDA classifier, the BLDA algorithm is superior to LDA in terms of classification, especially when the database is large.
Orosco et al. [39] proposed a patient non-specific seizure detection method based on stationary wavelet transform and a new set of energy and spectral features were extracted. The proposed method was tested in the same dataset of 18 epileptic patients and reached the mean sensitivity of 87.5% and false positive rate of 0.9/h. Recently, Samiee et al. [40] applied the sparse rational decomposition and the local gabor binary patterns (LGBP) for the off-line supervised detection of epileptic seizures and achieved the overall sensitivity of 70.4% and the overall specificity of 99.1% on the identical dataset with 163 h. In addition, Tsiouris et al. [41] designed an unsupervised methodology for the detection of epileptic seizures, which exploits the available medical knowledge using a simple rule-based seizure detection logic, and reached on average up to 89% of seizure detection sensitivity for this long-term EEG recordings. The comparison of the performance between our method and other methods for the same dataset are summarized in Table 3.
Table 3.
Related works and the comparison of the performance for the identical EEG dataset
| Authors | Number of patients | Total of EEG data (h) | detected seizures/tested seizures | Sensitivity (%) | Specificity (%) | False detection rate (/h) |
|---|---|---|---|---|---|---|
| Nasehi and Pourghassem [37] | 23 | 844 | 160/163 | – | 91 | – |
| Khan et al. [38] | 5 | – | 61/65 | – | 100 | – |
| Orosco et al. [39] | 18 | 152.8 | – | 87.5 | 99.9 | 0.9 |
| Samiee et al. [40] | 23 | 163 | – | 70.4 | 99.1 | 0.35 |
| Tsiouris et al. [41] | 23 | 980 | – | 89 | 95 | 8.1 |
| This work | 23 | 958.2 | 137/145 | 95.65 | 95.75 | 0.68 |
Furthermore, future research is still in process to devise an automatic seizure detector for clinical application despite existing novel method. In our study, the parameters of the method, such as threshold of classifier, are adjustable for different individual. How to install these parameters automatically to reduce workload will be considered in the further research. In addition, more valid features will be combined with the earth mover’s distance to enhance our algorithm in future study.
Conclusion
In this study, we presented a novel method of multi-channel seizure detection based on the earth mover’s distance and BLDA for scalp EEG recordings. The earth mover’s distance, as a fresh and effective feature, is extracted to distinguish non-seizure and seizure EEG recordings, and the BLDA classifier is applied in this work to obtain the classification results quickly and efficiently. The algorithm has been validated on a large pediatric scalp EEG database and the experimental results show that this proposed method makes a good performance with high sensitivity and acceptable false detection rate. In future work, we will concentrate on integrating more available features and classifiers to improve the performance and robustness of the seizure detector.
Funding
This study was funded by National Natural Science Foundation of China (No. 61701279) and Shandong Provincial Natural Science Foundation (No. ZR2017PF006), and jointly supported by the National Natural Science Foundation of China (Nos. 61572284, 61502272, 61702299 and 61501283), and China Postdoctoral Science Foundation (No. 2015M582129).
Conflict of interest
All authors declared that they have no conflicts of interest to this work.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
References
- 1.Hunyadi B, Signoretto M, Van Paesschen W, Suykens JA, Van Huffel S, De Vos M. Incorporating structural information from the multichannel EEG improves patient-specific seizure detection. Clin Neurophysiol. 2012;123(12):2352–2361. doi: 10.1016/j.clinph.2012.05.018. [DOI] [PubMed] [Google Scholar]
- 2.Sharma P, Khan YU, Farooq O, Tripathi M, Adeli H. A wavelet-statistical features approach for nonconvulsive seizure detection. Clin EEG Neurosci. 2014;45(4):274–284. doi: 10.1177/1550059414535465. [DOI] [PubMed] [Google Scholar]
- 3.Fu K, Qu J, Chai Y, Zou T. Hilbert marginal spectrum analysis for automatic seizure detection in EEG signals. Biomed Signal Process Control. 2015;18:179–185. doi: 10.1016/j.bspc.2015.01.002. [DOI] [Google Scholar]
- 4.Shoeb A, Edwards H, Connolly J, Bourgeois B, Treves ST, Guttag J. Patient-specific seizure onset detection. Epilepsy Behav. 2004;5(4):483–498. doi: 10.1016/j.yebeh.2004.05.005. [DOI] [PubMed] [Google Scholar]
- 5.Jr CWH, Sarkar A. Mutual information in natural position order of electroencephalogram is significantly increased at seizure onset. Med Biol Eng Comput. 2011;49(2):133–141. doi: 10.1007/s11517-010-0684-0. [DOI] [PubMed] [Google Scholar]
- 6.Faust O, Acharya UR, Adeli H. Adeli. A Wavelet-based EEG processing for computer-aided seizure detection and epilepsy diagnosis. Seizure. 2015;26:56–64. doi: 10.1016/j.seizure.2015.01.012. [DOI] [PubMed] [Google Scholar]
- 7.Qu H, Gotman J. A patient-specific algorithm for the detection of seizure onset in long-term EEG monitoring: possible use as a warning device. IEEE Trans Biomed Eng. 1997;44:115–122. doi: 10.1109/10.552241. [DOI] [PubMed] [Google Scholar]
- 8.Gotman J. Automatic recognition of epileptic seizures in the EEG. Electroencephalogr Clin Neurophysiol. 1982;54(5):530–540. doi: 10.1016/0013-4694(82)90038-4. [DOI] [PubMed] [Google Scholar]
- 9.Khan YU, Gotman J. Wavelet based automatic seizure detection in intracerebral electroencephalogram. Clin Neurophysiol. 2003;114(5):898–908. doi: 10.1016/S1388-2457(03)00035-X. [DOI] [PubMed] [Google Scholar]
- 10.Qu H, Gotman J. A seizure warning system for long-term epilepsy monitoring. Neurology. 1995;45:2250–2254. doi: 10.1212/WNL.45.12.2250. [DOI] [PubMed] [Google Scholar]
- 11.Meier R, Dittrich H, Schulze-Bonhage A, Aertsen A. Detecting epileptic seizures in long-term human EEG: a new approach to automatic online and real-time detection and classification of polymorphic seizure patterns. J Clin Neurophysiol. 2008;25:119–131. doi: 10.1097/WNP.0b013e3181775993. [DOI] [PubMed] [Google Scholar]
- 12.Zhu JD, Lin CF, Chang SH, Wang JH, Peng TI, Chien YY. Analysis of spike waves in epilepsy using Hilbert–Huang transform. J Med Syst. 2015;39(1):170. doi: 10.1007/s10916-014-0170-6. [DOI] [PubMed] [Google Scholar]
- 13.Kalbkhani H, Shayesteh MG. Stockwell transform for epileptic seizure detection from EEG signals. Biomed Signal Process Control. 2017;38:108–118. doi: 10.1016/j.bspc.2017.05.008. [DOI] [Google Scholar]
- 14.Hsu KC, Yu SN. Detection of seizures in EEG using subband nonlinear parameters and genetic algorithm. Comput Biol Med. 2010;40(10):823–830. doi: 10.1016/j.compbiomed.2010.08.005. [DOI] [PubMed] [Google Scholar]
- 15.Yuan Q, Zhou W, Yuan S, Li X, Wang J, Jia G. Epileptic EEG classification based on kernel sparse representation. Int J Neural Syst. 2014;24(04):1450015. doi: 10.1142/S0129065714500154. [DOI] [PubMed] [Google Scholar]
- 16.Liu Y, Zhou W, Yuan Q, Chen S. Automatic seizure detection using wavelet transform and SVM in long-term intracranial EEG. IEEE Trans Neural Syst Rehabil Eng. 2012;20(6):749–755. doi: 10.1109/TNSRE.2012.2206054. [DOI] [PubMed] [Google Scholar]
- 17.Logesparan L, Casson AJ, Rodriguez-Villegas E. Optimal features for online seizure detection. Med Biol Eng Comput. 2012;50(7):659–669. doi: 10.1007/s11517-012-0904-x. [DOI] [PubMed] [Google Scholar]
- 18.Guo L, Rivero D, Pazos A. Epileptic seizure detection using multiwavelet transform based approximate entropy and artificial neural networks. J Neurosci Methods. 2010;193(1):156–163. doi: 10.1016/j.jneumeth.2010.08.030. [DOI] [PubMed] [Google Scholar]
- 19.Chua KC, Chandran V, Acharya UR, Lim CM. Application of higher order spectra to identify epileptic EEG. J Med Syst. 2011;35(6):1563–1571. doi: 10.1007/s10916-010-9433-z. [DOI] [PubMed] [Google Scholar]
- 20.Rubner Y, Tomasi C, Guibas LJ. The earth mover’s distance as a metric for image retrieval. Int J Comput Vis. 2000;40(2):99–121. doi: 10.1023/A:1026543900054. [DOI] [Google Scholar]
- 21.Grauman K, Darrell T. Fast contour matching using approximate earth mover’s distance. IEEE Conf Comput Vis Pattern Recognit. 2004;1:220–227. [Google Scholar]
- 22.Indyk P, Thaper N. Fast color image retrieval via embeddings. In: International workshop on statistical & computational theories of vision 2003.
- 23.Tan H, Ngo CW. Common pattern discovery using earth movers distance and local flow maximization. IEEE Int Conf Comput Vis. 2005;2:1222–1229. [Google Scholar]
- 24.Hoffmann U, Vesin JM, Ebrahimi T, Diserens K. An efficient P300-based brain–computer interface for disabled subjects. J Neurosci Methods. 2008;167(1):115–125. doi: 10.1016/j.jneumeth.2007.03.005. [DOI] [PubMed] [Google Scholar]
- 25.Lei X, Yang P, Yao D. An empirical Bayesian framework for brain computer interfaces. IEEE Trans Neural Syst Rehabil Eng. 2009;17:521–529. doi: 10.1109/TNSRE.2009.2027705. [DOI] [PubMed] [Google Scholar]
- 26.Shoeb AH, Guttag JV. Application of machine learning to epileptic seizure detection. In: International conference on machine learning 2010. pp. 975–982.
- 27.Saab ME, Gotman J. A system to detect the onset of epileptic seizures in scalp EEG. Clin Neurophysiol. 2005;116:427–442. doi: 10.1016/j.clinph.2004.08.004. [DOI] [PubMed] [Google Scholar]
- 28.Ling H, Okada K. An efficient earth mover’s distance algorithm for robust histogram comparison. IEEE Trans Pattern Anal Mach Intell. 2006;29(5):840–853. doi: 10.1109/TPAMI.2007.1058. [DOI] [PubMed] [Google Scholar]
- 29.Fathima T, Khan YU, Bedeeuzzaman M, Farooq O. Discriminant analysis for epileptic seizure detection. In: international conference on devices and communications 2011. pp. 1–5.
- 30.MacKay DJC. Bayesian interpolation. Neural Comput. 1992;4(3):415–447. doi: 10.1162/neco.1992.4.3.415. [DOI] [Google Scholar]
- 31.Temko A, Thomas E, Marnane W, Lightbody G, Boylan G. EEG-based neonatal seizure detection with Support Vector Machines. Clin Neurophysiol. 2011;122:464–473. doi: 10.1016/j.clinph.2010.06.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Grewal S, Gotman J. An automatic warning system for epileptic seizures recorded on intracerebral EEGs. Clin Neurophysiol. 2005;116(10):2460–2472. doi: 10.1016/j.clinph.2005.05.020. [DOI] [PubMed] [Google Scholar]
- 33.Wang L, Xue W, Li Y, Luo M, Huang J, Cui W, Huang C. Automatic epileptic seizure detection in EEG signals using multi-domain feature extraction and nonlinear analysis. Entropy. 2017;19(6):222. doi: 10.3390/e19060222. [DOI] [Google Scholar]
- 34.Li Y, Wang X, Luo L, Li K, Yang X, Guo Q. Epileptic seizure classification of EEGs using time–frequency analysis based multiscale radial basis functions. IEEE J Biomed Health Inform. 2018;22(2):386–397. doi: 10.1109/JBHI.2017.2654479. [DOI] [PubMed] [Google Scholar]
- 35.Li Y, Cui W, Luo M, Li K, Wang L. Epileptic seizure detection based on time-frequency images of EEG signals using Gaussian mixture model and gray level co-occurrence matrix features. Int J Neural Syst. 2018;28(7):1850003. doi: 10.1142/S012906571850003X. [DOI] [PubMed] [Google Scholar]
- 36.Majumdar KK, Vardhan P. Automatic seizure detection in ECoG by differential operator and windowed variance. IEEE Trans Neural Syst Rehabil Eng. 2011;19(4):356–365. doi: 10.1109/TNSRE.2011.2157525. [DOI] [PubMed] [Google Scholar]
- 37.Nasehi S, Pourghassem H. Epileptic seizure onset detection algorithm using dynamic cascade feed-forward neural networks. In: IEEE international conference on intelligent computation and bio-medical instrumentation 2011. pp. 193–195.
- 38.Khan YU, Rafiuddin N, Farooq OAutomated seizure detection in scalp EEG using multiple wavelet scales. In: IEEE international conference on signal processing, computing and control (ISPCC) 2012. pp. 1–5.
- 39.Orosco L, Correa AG, Diez P, Laciar E. Patient non-specific algorithm for seizures detection in scalp EEG. Comput Biol Med. 2016;71(C):128–134. doi: 10.1016/j.compbiomed.2016.02.016. [DOI] [PubMed] [Google Scholar]
- 40.Samiee K, Kovács P, Gabbouj M. Epileptic seizure detection in long-term EEG records using sparse rational decomposition and local Gabor binary patterns feature extraction. Knowl Based Syst. 2017;118:228–240. doi: 10.1016/j.knosys.2016.11.023. [DOI] [Google Scholar]
- 41.Tsiouris ΚΜ, Markoula S, Konitsiotis S, Koutsouris DD, Fotiadis DI. A robust unsupervised epileptic seizure detection methodology to accelerate large EEG database evaluation. Biomed Signal Process Control. 2018;40:275–285. doi: 10.1016/j.bspc.2017.09.029. [DOI] [Google Scholar]