Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Sep 13;34(40):12083–12092. doi: 10.1021/acs.langmuir.8b01272

FRET Reveals the Formation and Exchange Dynamics of Protein-Containing Complex Coacervate Core Micelles

Antsje Nolles †,‡, Ellard Hooiveld †, Adrie H Westphal †,§, Willem J H van Berkel †, J Mieke Kleijn ‡, Jan Willem Borst †,§,*
PMCID: PMC6209312  PMID: 30212214

Abstract

graphic file with name la-2018-012727_0010.jpg

The encapsulation of proteins into complex coacervate core micelles (C3Ms) is of potential interest for a wide range of applications. To address the stability and dynamic properties of these polyelectrolyte complexes, combinations of cyan, yellow, and blue fluorescent proteins were encapsulated with cationic-neutral diblock copolymer poly(2-methyl-vinyl-pyridinium)128-b-poly(ethylene-oxide)477. Förster resonance energy transfer (FRET) allowed us to determine the kinetics of C3M formation and of protein exchange between C3Ms. Both processes follow first-order kinetics with relaxation times of ±100 s at low ionic strength (I = 2.5 mM). Stability studies revealed that 50% of FRET was lost at I = 20 mM, pointing to the disintegration of the C3Ms. On the basis of experimental and theoretical considerations, we propose that C3Ms relax to their final state by association and dissociation of near-neutral soluble protein–polymer complexes. To obtain protein-containing C3Ms suitable for applications, it is necessary to improve the rigidity and salt stability of these complexes.

Introduction

The encapsulation of proteins is important in many applications, such as the controlled delivery of functional ingredients in foods, medical formulations, industrial enzymatic processes, and protein storage. In all cases, adequate encapsulation is required while keeping the bioactivity or functionality intact. Micelles composed of polyelectrolyte complexes, so-called complex coacervate core micelles (C3Ms), are promising structures for protein protection, stabilization, and controlled delivery.1−6 C3Ms are simple to prepare by mixing protein solutions with oppositely charged diblock copolymer solutions in stoichiometric charge ratios.7,8 Micellar structures are then spontaneously formed and are small enough to remain in solution. The inner core of C3Ms has a high loading capacity; hundreds of protein molecules can be incorporated into one micelle.1 The micellar core provides a relatively water-rich environment, thereby shielding protein molecules from the bulk solution while protein structure and functionality are preserved and any immune response is reduced. Because the formation of C3Ms is driven by electrostatic interactions, contributed by Coulombic attraction and entropic counterion release,9−11 the pH and ionic strength strongly influence the formation, dynamics, and stability of these structures.

While the structure and morphology of C3Ms have been the subject of many studies, the stability and dynamic aspects of micelles and the exchange of molecules between individual C3Ms have been scarcely investigated. In 1998, Cohen Stuart and co-workers were the first to study the rate of formation of C3Ms, composed of poly((dimethylamino)ethyl-methacrylate)-co-poly(glyceryl-methacrylate) (PDMAEMA-co-PGMA) and poly(acrylic-acid)158 (PAA158), using dynamic light scattering.7 They found that micelle formation took place on time scales of 0.01 to 100 s depending on the ionic strength. Before equilibrium was reached, a relatively high transient turbidity was found, which they attributed to macroscopic phase separation (the formation of transient large aggregates) on short time scales (<1 ms), after which the dense phase rearranges into C3Ms. A corresponding molecular model was tested using self-consistent field theory.12 Similar results were found by Hofs et al.13 for C3Ms consisting of poly([4-(2-aminoethylthio)butylene]hydrochloride)49-b-poly(ethylene-oxide)212 (PAETB49-b-PEO212) and poly(acrylic-acid) (PAA) of various lengths. For the formation of C3Ms from poly((methacryloyloxyethyl)trimethylammonium chloride)530 (PMOTAC530) and poly(ethylene oxide)113-b-poly(methacrylic acid)122 or 294 (PEO113-b-PMAA122 or 294) at an ionic strength of 10 mM, Holappa et al.14 found two processes occurring on different time scales: a process with a kinetic coefficient of 0.0126 s–1, which was attributed to the “insertion and expulsion” of single chains, and a slow process with a kinetic coefficient of 7.77 × 10–5 s–1, which was attributed to the “merging and splitting” of C3Ms. The final equilibrium state of C3Ms was reached only after about 16 h. The authors discussed their findings in terms of a model that was introduced by Dormidontova15 describing the micellization of polymeric surfactants (hydrophilic–hydrophobic block copolymers). Zhang et al.16 also referred to this model for the formation of their C3Ms in deionized water composed of poly(ethylene-oxide)113-b-poly(sodium-4-styrene-sulfonate)47 (PEO113-b-PSSNa47) and poly(ethylene-oxide)113-b-poly(quaternized-2-(dimethylamino)ethyl-methacrylate)48 (PEO113-b-PQDMA48). They observed a fast relaxation process (within 2.6 ms), which they related to initial quasi-equilibrium complex formation. A slower process (within 0.4 s) was attributed to structural rearrangements leading to final equilibrium complexes and was supposed to proceed through a micelle fusion–fission mechanism. Very long relaxation times were reported by Lindhoud et al.4 for two different protein-containing three-component C3Ms, i.e., PAA42-b-PAAm417/PDMAEMA150/lysozyme (poly(acrylic-acid)42-b-poly(acyl-amide)417 and poly(N,N-dimethylaminoethyl-methacrylate)150, respectively) and P2MVP41-b-PEO205/PAA139/α-lactalbumin (poly(2-methyl-vinyl-pyridinium-iodide)41-b-poly(ethylene-oxide)205 and poly(acrylic-acid)139, respectively), at low ionic strength. For lysozyme-containing C3Ms, a relaxation time of 2 days was found, while C3Ms containing α-lactalbumin did not reach equilibrium in their experiment of 2 weeks. Differences in relaxation behavior were explained from the diversity in molecular properties, in particular, the nature of used polyelectrolytes: weak or strong. The authors pointed to the possible advantage of quenched systems in which over longer periods no rearrangements in micelles occur so that proteins are really trapped and cannot leave them.

Most of the studies mentioned above concern the dynamics of C3Ms formed by the coacervation of two polyelectrolyte chains. Only the systems of Lindhoud et al. involved protein-containing C3Ms, which is also the focus of this article.17 Understanding the dynamics and stability of protein-containing C3Ms under different conditions is crucial for designing functional protein-containing micellar structures. In the present study, Förster resonance energy transfer (FRET) between mTurquoise2 (a cyan fluorescent protein) and SYFP2 (strongly enhanced yellow fluorescent protein 2) was used to study the kinetics of formation of C3Ms, the dynamics of protein exchange between these structures, and their salt stability. An important difference with the protein-containing structures described by Lindhoud et al. is that no homopolymer with the same charge sign as the protein is incorporated in C3Ms.17 As a result, many more protein molecules can be accommodated in one micelle (several hundred instead of about 10), while the micellar structures are much more dynamic.

Previously, we have compared the degree of encapsulation of a range of Aequorea victoria (AV)- and Anthozoa-derived fluorescent proteins (FPs) and the effect on their spectral properties.17 The encapsulation of these FPs was established with the use of cationic-neutral diblock copolymer poly(2-methyl-vinyl-pyridinium)128-b-poly(ethylene-oxide)477 (P2MVP128-b-PEO477), which is also used in the present study. Furthermore, for most of the FPs, including the three AV-derived FPs used in the present study, encapsulation was performed at pH 9, at which they have a negative charge of 9–11. On the basis of similar preferred micellar compositions (PMCs (∼0.7)), C3M sizes (∼34.5 nm), and encapsulation efficiencies (∼100%), we concluded that all AV-derived FPs are encapsulated in the same way and with the same affinity. The results further showed that mTurquoise2 and SYFP2 are the best candidates for FRET studies regarding the dynamics of C3Ms. For both mTurquoise2 and SYFP2, encapsulation in C3Ms resulted in only minor changes in fluorescence properties. Next to that, mTurquoise2 has a high quantum yield (ΦmTurquoise2 = 0.93) and SYFP2 has a high extinction coefficient (εSYFP2,515nm = 101 000 M–1 cm–1).18,19 Therefore, we have selected these two FPs for the present study, while SBFP2 (strongly enhanced blue fluorescent protein 2) was used as an invisible protein substitute to lower the fluorescence signal of interest while keeping the total protein concentration constant.17

On the basis of the results of the presented kinetic FRET experiments in this study, we propose a model to describe the formation and relaxation of protein-containing C3Ms. To roughly quantify the Gibbs energy of C3M formation using this model, we take the number of proteins encapsulated in one micelle as 450 and the critical micelle concentration (CMC) at the PMC as 100 nM protein, as previously found for enhanced green fluorescent protein (EGFP),1 which is an AV-derived FP as well. The obtained insights also allow us to develop strategies for generating a tunable stability of micelles for different applications.

Experimental Section

Materials

Poly(2-vinylpyridine)128-b-poly(ethylene-oxide)477 (P2VP128-b-PEO477, Polymer Source Inc., Canada, Mw/Mn = 1.10, Mn = 34.5 kg/mol) was quaternized following a procedure described elsewhere.1 For P2MVP128-b-PEO477 (Mn = 50.8 kg/mol), a final degree of quaternization of approximately 87% was obtained, implying that the polymer bears approximately 112 positive charges. A stock solution of P2MVP128-b-PEO477 (50 μM) was prepared by dissolving the polymer in 10 mM borate buffer (pH 9.0), and the solution was stored at −20 °C. All solutions were filtered through 0.20 μm poly(ether sulfone) membrane syringe filters (Advanced Microdevices Pvt. Ltd., Ambala Cantt, India). All other chemicals were from commercial sources and of the purest grade available.

Protein Production

The genes of mTurquoise2 and SYFP2-His were cloned into bacterial expression vector pTYB12 (New England Biolabs Inc., Ipswich, MA, USA) to generate FP fusions with a chitin-binding domain and an intein.20−22 The cDNA of SBFP2 in a pRSETb vector was kindly provided by Dr. Joachim Goedhart, University of Amsterdam.23 For protein production, E. coli BL21 cells were used. Details on protein production and purification are described elsewhere.2 After on-column cleavage, mTurquoise2 and SYFP2-His were acquired without the chitin-binding domain. SBFP2 and SYFP2 still contained the His tag after purification. Purified protein stock solutions of mTurquoise2 (21.7 μM), SYFP2 (29.5 μM), and SBFP2 (35.5 μM) were stored in 10 mM borate buffer (pH 9.0) at 4 °C.

Protein concentrations were determined with a Pierce BCA protein assay (Pierce Biotechnology, Rockford, IL, USA) using a bovine serum albumin standard as a reference. The purity of all fluorescent proteins was checked by SDS-PAGE.

Absorption and Steady-State Fluorescence Spectroscopy

Absorption spectra of 1 μM SBFP2, mTurquoise2, or SYFP2 in 10 mM borate buffer (pH 9.0) were recorded on a Hewlett-Packard 8453 diode array spectrophotometer at 20 °C. Spectrophotometer settings were controlled using the UV–visible ChemStation software package (Hewlett-Packard, Palo Alto, CA, USA).

Steady-state fluorescence spectra were recorded on a Cary Eclipse spectrofluorimeter (Varian Inc., Middelburg, The Netherlands). Excitation and emission slits were set to yield bandwidths of 5 nm. Samples were measured in 1 mL quartz cuvettes with a path length of 1 cm. Fluorescence emission spectra of 1 μM mTurquoise2 and SYFP2 in 10 mM borate buffer (pH 9.0) were separately measured at excitation wavelengths of 440 and 490 nm, respectively. FRET was determined by using fluorescence intensities from donor (475 nm) and acceptor channels (527 nm, Figure 1). For the FRET experiments, fluorescence emission spectra were obtained using an excitation wavelength of 440 nm, and emission was recorded between 450 and 600 nm. All measurements and incubations prior to the measurements were performed at 20 °C.

Figure 1.

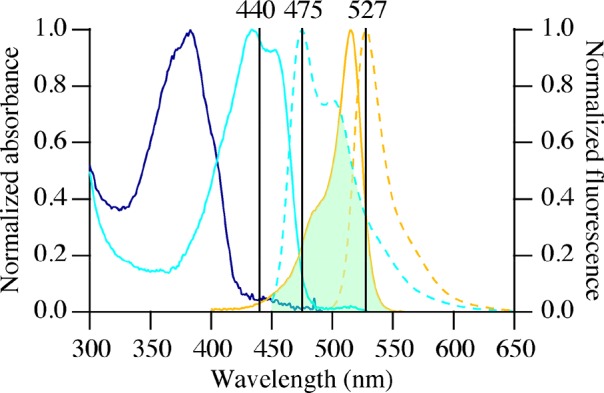
Figure 1

Open in a new tab

Normalized absorption spectra of SBFP2 (blue line), mTurquoise2 (cyan solid line), and SYFP2 (orange solid line) and fluorescence emission spectra of mTurquoise2 (cyan dashed line) and SYFP2 (orange dashed line). The listed wavelengths at the top of the graph indicate the following from left to right: excitation wavelength of mTurquoise2 (donor excitation), emission wavelength of mTurquoise2 (donor channel), and emission wavelength of SYFP2 (acceptor channel). The green area indicates the spectral overlap between mTurquoise2 and SYFP2.

C3M Preparations

In general, the encapsulation of FPs with polymers into C3Ms was achieved by first diluting fluorescent protein stock solutions in 10 mM borate buffer (pH 9.0) to a final protein concentration of 1 μM and a FRET pair composition of 1:1 (mTurquoise2/SYFP2), followed by the addition of polymer to a final concentration of 0.18 μM. C3Ms were prepared at a F+ ratio of 0.70, which is the PMC at pH 9.0 of proteins with diblock copolymer P2MVP128-b-PEO477.17 The PMC is expressed as F+ = [n+]/([n+] + [n–]), with [n+] = c+N+ referring to the total concentration of positively charged groups on the polymer and [n–] = c–N– being the total concentration of negatively charged groups on the protein molecules.

The net charges of FPs as a function of pH were calculated using the PROPKA 3.1 software package .24,25 At pH 9.0, the charges (N–) of SBFP2, mTurqouise2, and SYFP2 are −8.96, −11.30, and −9.75, respectively, which are used to calculate [n–].

Equilibrium States of C3Ms with Differing FRET Pair Amounts

Protein solutions with different amounts of the FRET pair were obtained by varying the FRET pair/SBFP2 ratio between 0.1 and 1.0. C3Ms were formed by mixing the protein solution with an aliquot of a stock solution of P2MVP128-b-PEO477. The resulting solutions were left to equilibrate for 3 h prior to recording the fluorescence emission spectra.

Formation of C3Ms

A protein solution of a 50% FRET pair was prepared (25% mTurquoise2, 25% SYFP2, and 50% SBFP2) to follow the formation of C3Ms at the PMC. An equilibrated protein solution and an aliquot of a stock solution of P2MVP128-b-PEO477 were mixed rapidly in a quartz cuvette and placed in a fluorescence spectrophotometer sample compartment. Fluorescence emission spectra were recorded with a time interval of 30 s. The obtained data set was fitted using IGOR Pro 6.11 (Wavemetrics, Inc., Lake Oswego, OR, USA).

Protein Exchange between C3Ms

Two separate C3M solutions were prepared, one with mTurquoise2-C3Ms and one with SYFP2-C3Ms but both with varying amounts of SBFP2, so that after mixing the final FRET pair/SBFP2 ratios varied between 0.20 and 0.50. The C3M solutions were left to equilibrate for 3 h prior to the measurement. To follow the protein exchange between C3Ms, equilibrated solutions of mTurquoise2-C3Ms and SYFP2-C3Ms with the same SBFP2 amounts were mixed rapidly in a quartz cuvette and placed in the fluorescence spectrophotometer sample compartment. Fluorescence emission spectra were recorded with a time interval of 30 s. The obtained data were fitted using global analysis with IGOR Pro 6.11.

Salt Titration of C3Ms

To test the salt stability of protein-containing C3Ms, first a solution of C3Ms containing a 50% FRET pair was prepared at the PMC. Next, by the addition of small aliquots of a 500 mM NaCl solution, the NaCl concentration was gradually changed from 0 (initial) to 37.0 (final) mM, corresponding to an ionic strength change from 2.5 to 39.5 mM. To determine the dilution effect of the addition of NaCl, a control experiment was performed by adding corresponding volumes of 10 mM borate buffer (pH 9.0) to preformed 50% FRET pair C3Ms. Fluorescence emission spectra were recorded at the start of the experiment and after every addition of NaCl or buffer.

Dynamic Light Scattering

Dynamic light scattering (DLS) measurements were performed on an ALV instrument equipped with a 22 mW Uniphase model 1145P HeNe laser operating at 632.8 nm and an ALV/Dual High QE ADP detector unit with a fiber splitting device for two detectors connected to an external ALV7004 multiple tau digital correlator (ALV-Laser Vertriebsgesellschaft m-b.H., Langen, Germany). The detection angle, θ, was set at 90°, and all measurements were performed at 20 °C.

For the determination of the salt stability of C3Ms, 500 μL solutions of 50% FRET pair C3Ms were prepared at the PMC. NaCl concentrations ranging from 0 (initial) to 37.0 mM (final) were obtained upon addition from a stock solution, corresponding to an ionic strength change from 2.5 to 39.5 mM.

DLS autocorrelation curves were generated from 10 individual intensity traces and averaged. The CONTIN method26,27 was used to analyze the distribution of the radii of the C3Ms. The data were analyzed with the AfterALV data analysis software program (AfterALV 1.0d, Dullware, The Netherlands).

FRET Data Analysis

FRET is a spectroscopic phenomenon that is applied in different research disciplines to study (bio)molecular interactions.28,29 This phenomenon involves nonradiative energy transfer from a fluorescent donor to an acceptor and can take place only if the following three prerequisites are met: (1) there is an overlap between donor fluorescence emission and acceptor excitation spectra, (2) the distance between both fluorophores is in the range of 1–10 nm, and (3) there is an appropriate orientation of the dipole moments of both fluorophores. These three conditions determine the propensity of energy transfer, which is reported as FRET efficiency. Most fluorescent proteins emit in the visible spectrum and have overlapping spectra and therefore are widely used for FRET experiments.30,31 The most effective combination for FRET is the pair formed by cyan (CFP) and yellow (YFP) fluorescent proteins.

C3Ms containing mTurquoise2 and SYFP2 display FRET, which is demonstrated in Figure 2 (red solid line), showing that the fluorescence emission of SYFP2 takes place upon excitation of mTurquoise2 (excitation at 440 nm, Figure 1). Furthermore, steady-state fluorescence data in Figure 2 shows that in FRET experiments the cross-talk of mTurquoise2, i.e., the fluorescence emission of the donor at 527 nm, and direct excitation of SYFP2 at 440 nm occur. Both contributions were taken into account for the calculation of the overall FRET. The ratio of the SYFP2 to mTurquoise2 fluorescence intensities (RFRET) is expressed as

graphic file with name la-2018-012727_m001.jpg 1

with fDexAem being the measured fluorescence intensity in the acceptor channel upon donor excitation, which is corrected for spectral cross-talk and direct excitation of the acceptor, and fDex being the measured fluorescence intensity in the donor channel after donor excitation, which is corrected for detection efficiencies of the dyes following a procedure described elsewhere.32 Both corrected parameters are also used to calculate the transfer efficiency, E:

graphic file with name la-2018-012727_m002.jpg 2

The Förster radius is calculated using

graphic file with name la-2018-012727_m003.jpg 3

and

graphic file with name la-2018-012727_m004.jpg 4

where ΦD is the donor quantum yield in the absence of an acceptor (ΦmTurquoise2 = 0.93), n is the refractive index of the intervening solution (n = 1.41),2 which was calculated from the change in fluorescence lifetimes of EGFP and mEGFP molecules inside the core of the micelles compared to that of the proteins free in solution, and κ2 is the orientation factor describing the relative orientation of the transition dipoles of donor and acceptor (κ2 = 0.475).33,34 The overlap integral, J, is a function of the wavelength, λ, and is calculated using fD(λ) and εA(λ) as the wavelength-dependent emission spectrum of the donor and the wavelength-dependent molecular extinction coefficient of the acceptor (εSYFP2,515nm = 101 000 M–1 cm–1), respectively.

Figure 2.

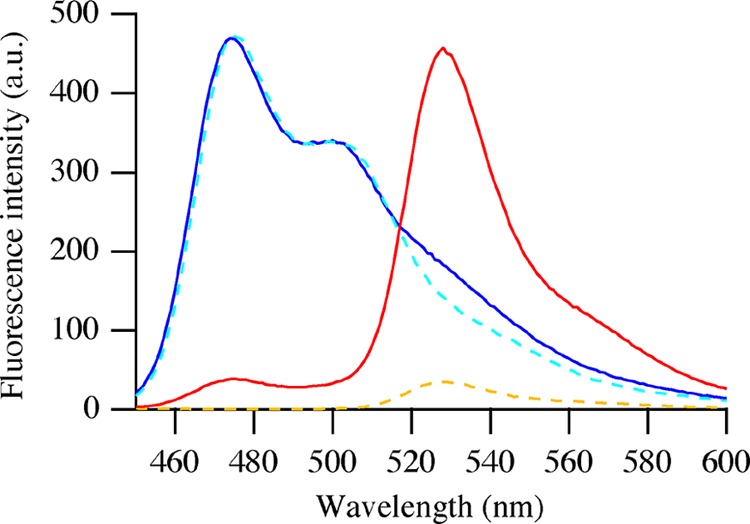
Figure 2

Open in a new tab

Steady-state fluorescence emission spectra of mixed C3Ms containing mTurquoise2 and SYFP2 (red solid line), of mixed mTurquoise2 and SYFP2 free in solution (blue solid line), of mTurquoise2 in C3Ms (cyan dashed line), and of SYFP2 in C3Ms (orange dashed line). Proteins are at equimolar concentrations with a total concentration of 1 μM, and excitation was at 440 nm.

For the calculation of the Förster radius, R0, between mTurquoise2 and SYFP2 in the micelles, we used some results from our previous work.17 The emission spectrum of encapsulated mTurquoise2 and the excitation spectrum of encapsulated SYFP2 were used in eq 4. In eq 3, a refractive index of 1.41 for the micellar core was used, which was determined from the decrease in fluorescence lifetimes upon encapsulation of EGFP and mEGFP.2 Furthermore, a κ2 value of 0.475 was used because the fluorescent proteins are restricted in their movement inside the C3Ms.33,34 On the basis of these values, a Förster radius of 53.4 Å was calculated for mTurquoise2 and SYFP2 inside the C3Ms. Herewith, the second prerequisite of FRET is met. Furthermore, a Förster radius of 53.4 Å is larger than the dimensions of an FP, which are 24 Å in diameter and 42 Å in height.35,36

Gibbs Energy of Association of C3Ms as a Function of Ionic Strength

The protein-containing C3Ms display salt-dependent association/dissociation behavior, which follows an apparent two-state equilibrium process (Supporting Information). Therefore, the equilibrium can be described as

graphic file with name la-2018-012727_m005.jpg 5

with its corresponding equilibrium constant

graphic file with name la-2018-012727_m006.jpg 6

The shift in the equilibrium toward the dissociation of the C3Ms upon increasing the ionic strength is due to the screening of the electrostatic interactions between the negatively charged proteins and the positively charged diblock copolymers. At sufficiently high salt concentrations, FRET will not take place because the micelles have fallen apart and the distance between the FPs is large, resulting in high donor and low acceptor fluorescence intensities. At low salt concentration, the C3Ms are stable and thus the FPs are in close proximity, which leads to a high FRET efficiency.

The increase in the donor fluorescence intensity and the corresponding decrease in the acceptor fluorescence intensity display sigmoidal behavior as a function of ionic strength. Figure S4 shows the ionic strength dependence of these fluorescence intensities, normalized between their minimum and maximum values. We calculated Kassociation at each ionic strength from the normalized fluorescence intensities of the donor and acceptor and its increase and decrease, respectively, compared to the start of the salt titration (0 mM NaCl). These normalized fluorescence intensities are proportional to the concentration of C3Ms and the concentration of dissociated C3Ms, respectively.

The Gibbs energy of association (ΔGassociation0) of C3Ms was calculated at each salt concentration by applying eq 7

graphic file with name la-2018-012727_m007.jpg 7

with gas constant R and absolute temperature T. A plot of ΔGassociation0 against ionic strength, I, yields a straight line according to

graphic file with name la-2018-012727_m008.jpg 8

where ΔGassociation,water0 is the Gibbs energy of C3M formation at zero ionic strength and m is the slope of the line.

Results

FRET Efficiency in C3Ms with Varying FRET Pair Concentrations

Figure 2 shows the fluorescence emission spectra of equimolar amounts of mTurquoise2 and SYFP2 free in solution as well as encapsulated in C3Ms upon excitation at 440 nm. Encapsulating mTurquoise2 and SYFP2 together in C3Ms yields a strong reduction of the donor fluorescence intensity and the sensitized emission of SYFP2. In these experiments, the concentrations of fluorescent proteins are the same, and from the reduction of fluorescence intensity of mTurquoise2, a FRET efficiency of about 90% was estimated.

To determine the FRET efficiency at different FRET pair concentrations in C3Ms, SBFP2 was used to change the FRET pair amount in a C3M by replacing both mTurquoise2 and SYFP2 while keeping the final protein concentration constant. Because SBFP2 has a charge distribution that is similar to those of mTurquoise2 and SYFP2 and a similar value for its PMC (0.70) and it does not absorb light at 440 nm (Figure 1), it has been used as an “invisible” protein substitute.17Figure 3A shows fluorescence emission spectra for C3M solutions with different FRET pair amounts consisting of 1 μM total protein and 0.18 μM polymer. Clearly, a FRET pair amount of 10% already shows energy transfer in C3Ms between mTurquoise2 and SYFP2. At increasing FRET pair amounts, the donor fluorescence intensity further decreases and the acceptor fluorescence intensity increases. Related ratio RFRET (eq 1) increases in an almost linear fashion for increasing FRET pair amounts (Figure S1). The corresponding FRET efficiency (eq 2) follows an asymptotic curve, reaching a maximum of ∼0.90 for a FRET pair amount of 100% (Figure 3B). The correlation of RFRET with the FRET pair content in C3Ms (Figure S1) confirms that all three proteins have similar interactions with the diblock copolymer. When the interactions of the FPs with the copolymer are significantly different, this could lead to an unbalanced uptake of the FRET pair proteins, which would be reflected in a nonlinear increase in FRET with increasing FRET pair amounts.

Figure 3.

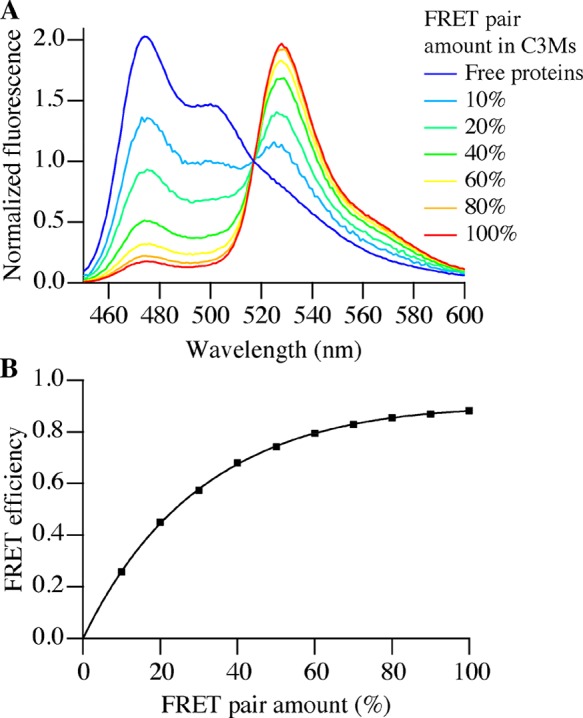
Figure 3

Open in a new tab

Normalized fluorescence intensities of the mTurquoise2 and SYFP2 FRET pair in C3Ms at different FRET pair amounts (10 to 100%: FRET pair/SBFP2 ratio) upon donor excitation (440 nm). The total protein concentration was kept at 1 μM using SBFP2 to replace both mTurquoise2 and SYFP2 to keep the FRET pair composition constant at 1:1 (mTurquoise2/SYFP2) and change the FRET pair amount in the C3Ms. The concentration of P2MVP128-b-PEO477 was 0.18 μM. (A) Fluorescence emission spectra at different FRET pair amounts (normalized at 517 nm). (B) FRET efficiency as a function of the FRET pair amount. The solid line is a guide to the eye.

Kinetics of Micellization

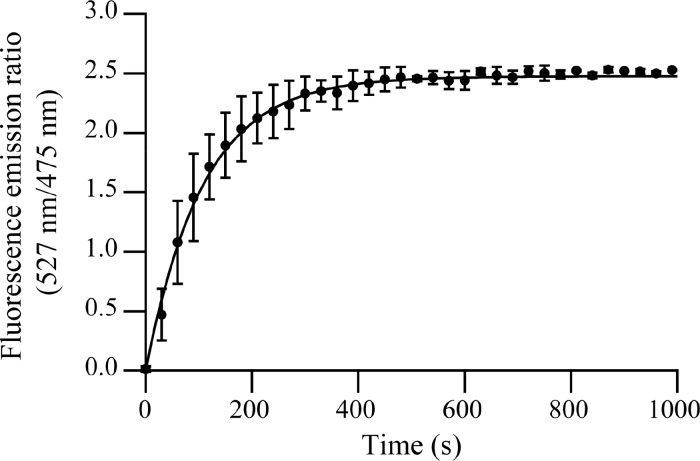
To measure the kinetics of C3M formation, we monitored changes in FRET by measuring the fluorescence intensities of mTurquoise2 and SYFP2 as a function of time. Figure 4 shows the time dependency of the ratio of SYFP2 to mTurquoise2 fluorescence intensities after mixing a solution of proteins (at a FRET pair amount of 50%) with a polymer solution. The concentrations after mixing were 0.25 μM mTurquoise2, 0.25 μM SYFP2, 0.50 μM SBFP2, and 0.18 μM P2MVP128-b-PEO477. After mixing, the amount of FRET increases, indicating the formation of C3Ms. After about 600 s, a plateau is reached with a similar ratio of the SYFP2 to mTurquoise2 fluorescence intensity as found for equilibrated C3Ms (24 h) with the same FRET pair amount (RFRET,eq ≈ 2.5, Figure S1A). The time course of the concentration of mTurquoise2 not involved in FRET during C3M formation was fitted for different reaction order models (Supporting Information and Figure S2). Only the plot of the natural logarithm of the concentration of mTurquoise2 molecules that are not involved in FRET against time (ln[mTurquoise2] vs t) shows linear behavior (Figure S2B), indicating first-order kinetics. Consequently, the time-dependent change of RFRET was fitted to

graphic file with name la-2018-012727_m009.jpg 9

where RFRET,eq is the ratio of SYFP2 to mTurquoise2 fluorescence intensity at equilibrium and k is the kinetic coefficient. The parameters obtained from the fit are a kinetic coefficient (first-order rate constant), k, of (9 × 10–3) ± (1 × 10–3) s–1 and a final RFRET,eq of 2.47 ± 0.02 (number of experiments (nexp) = 2). Thus, the relaxation time of formation of C3Ms (τ = 1/k) is about 100 s.

Figure 4.

Figure 4

Open in a new tab

Fluorescence emission ratio of SYFP2 to mTurquoise2 (527 nm/475 nm, RFRET) as a function of time following the mixing of solutions of polymer and proteins (final concentrations: 0.25 μM mTurquoise2, 0.25 μM SYFP2, 0.50 μM SBFP2, and 0.18 μM P2MVP128-b-PEO477). The solid line is the curve obtained using eq 9, with RFRET,eq = 2.47 and k = 9 × 10–3 s–1. Error bars represent the spread of the data (nexp = 2).

Protein Exchange between Preformed C3Ms

To determine the dynamics of protein exchange between C3Ms, we monitored changes in FRET after mixing C3Ms containing SYFP2 with C3Ms containing mTurquoise2 at different final FRET pair amounts (between 50 and 20%, Figure 5). For example, for a final FRET pair amount of 20% the micelles initially contain 0.20 μM SYFP2, 0.80 μM SBFP2, and 0.18 μM P2MVP128-b-PEO477 (for C3Ms containing SYFP2) and 0.20 μM mTurquoise2, 0.80 μM SBFP2, and 0.18 μM P2MVP128-b-PEO477 (for C3Ms containing mTurquoise2). Accordingly, the C3Ms with the other final FRET pair amounts are mixed.

Figure 5.

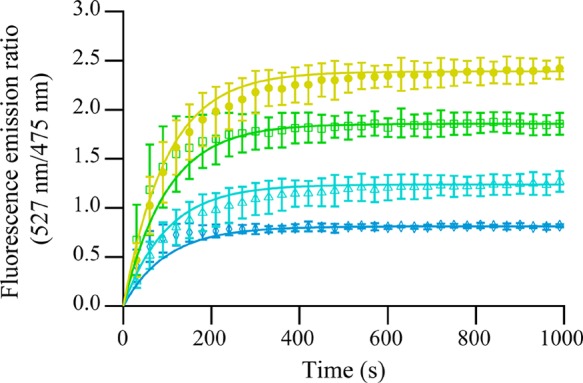
Figure 5

Open in a new tab

Fluorescence emission ratio of SYFP2 to mTurquoise2 (527 nm/475 nm) as a function of time following the exchange of proteins between SYFP2-C3Ms and mTurquoise2-C3Ms at different final FRET pair amounts: 50% (yellow solid dots), 40% (green open squares), 30% (cyan open triangles), and 20% (blue open diamonds). The total concentrations of proteins and polymer are 1 and 0.18 μM, respectively. The solid lines are the curves obtained using eq 9, with k = 1.0 × 10–2 s–1 and RFRET,eq = 2.39 for 50%, RFRET,eq = 1.86 for 40%, RFRET,eq = 1.24 for 30%, and RFRET,eq = 0.81 for 20%. Error bars represent the standard deviation (nexp = 4).

Immediately upon mixing of the micelle solutions, the FRET amount increases, indicating the exchange of FPs between C3Ms. Within about 200 s, a plateau is reached with ratios similar to those of the corresponding equilibrated C3Ms (0.8–2.3, Figure S1A). The change in RFRET with time was globally fitted according to first-order reaction kinetics (eq 9, Figure S3). The obtained kinetic coefficient, k, is (1.0 × 10–2) ± (0.1 × 10–2) s–1 and the final ratios, RFRET,eq, are listed in Table 1. Apparently, the relaxation time for the exchange of FPs between C3Ms to reach their equilibrium compositions is comparable to the relaxation time of formation, i.e., about 100 s.

Table 1. Final Fluorescence Emission Ratios of SYFP2 to mTurquoise2 (RFRET,eq) after C3M Protein Exchange with a Kinetic Coefficient of (1.0 × 10–2) ± (0.1 × 10–2) s–1a.

FRET pair amount (%) RFRET,eq
20 0.81 ± 0.01
30 1.24 ± 0.01
40 1.86 ± 0.02
50 2.39 ± 0.02
Open in a new tab
a

Standard deviations are based on multiple measurements (nexp = 4).

Salt Stability of C3Ms

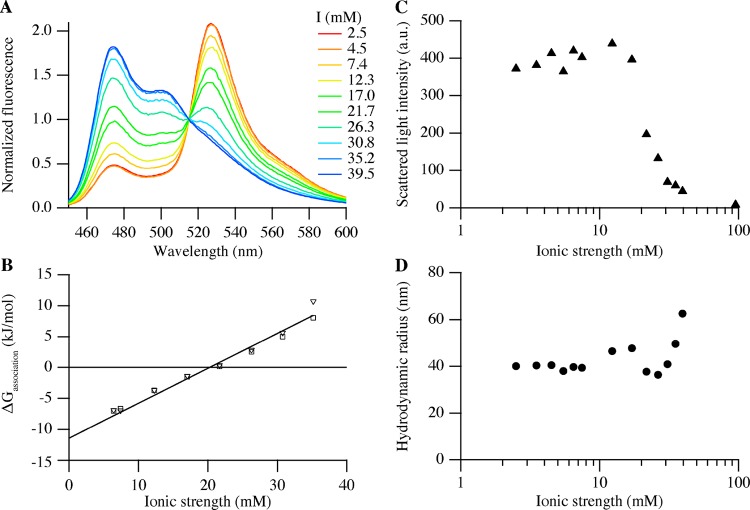
It is well known that ionic strength is a parameter that strongly affects the complexation of oppositely charged polyelectrolytes. We therefore investigated the influence of salt (NaCl) concentration on the stability of 50% FRET pair C3Ms. Figure 6A shows the dependency of the normalized fluorescence spectra of C3Ms on ionic strength (I), considering both buffer and added salt. It can be seen that the donor fluorescence intensity increases and the acceptor fluorescence intensity decreases with increasing ionic strength (Figure S4). The salt ions screen the electrostatic interaction between proteins and polymers, and as a result, a 50% decrease in FRET was observed at an ionic strength of 20 mM (Figure S4). DLS experiments showed a decrease in scattering intensity above an ionic strength of 15 mM (Figure 6C), confirming a decline in the number of C3Ms.

Figure 6.

Figure 6

Open in a new tab

Salt stability of 50% FRET pair C3Ms consisting of 0.25 μM mTurquoise2, 0.25 μM SYFP2, 0.50 μM SBFP2, and 0.18 μM P2MVP128-b-PEO477. (A) Steady-state fluorescence emission spectra (normalized to the intensity at 517 nm) at different ionic strengths (nexp = 3). (B) Gibbs energy of association of C3Ms as a function of ionic strength calculated from the donor (squares) and acceptor (inverted triangles) separately. (C and D) DLS results of the salt stability of C3Ms: (C) the scattered light intensity and (D) the hydrodynamic radius, both as a function of ionic strength shown on a log scale (nexp = 1).

The stability, defined as the change in the Gibbs energy of association (ΔGassociation0) of C3Ms, was calculated over a range of ionic strengths using eq 8, and the results are shown in Figure 6B. Extrapolation of these data to 2.5 mM ionic strength (0 mM NaCl, 10 mM borate buffer, pH 9) leads to an apparent stability of C3Ms of −10.0 kJ/mol or −4.1kBT (with kB being the Boltzmann constant). We will come back to the meaning of this change in Gibbs energy in the Discussion section.

Discussion

On the basis of our kinetic results, we propose a model for the formation and relaxation of FP-containing C3Ms, in line with commonly accepted two-state models for the formation of simple surfactant micelles.37−39 This model implies that immediately after the mixing of protein and diblock copolymer solutions electrically neutral protein–polymer complexes are formed. Such a process is comparable to the fast formation of large intermediate aggregates as found for PAA-containing C3Ms.7,9 Because for our systems we never observed a light-scattering intermediate, we assume the initial formation of small soluble protein–polymer complexes (SCs). Above a certain concentration, these SCs start to aggregate, forming complex coacervate microphases that grow spontaneously. While for simple, oppositely charged polyelectrolytes this growth proceeds until two macroscopic phases are formed, here growth is limited by the hydrophilic neutral chains of the diblock copolymer, which remain in the polymer-poor phase. Because growth occurs in three dimensions, the volume of the microphases increases more strongly than their surface area, hence the available area per neutral chain decreases, driving the chains together. Repulsion between these chains stops the growth of the complex coacervate cores, yielding defined sizes of the micelles.8,37

The formation of C3Ms should have two minima in the Gibbs energy, i.e., one at low aggregation number and one at the optimum aggregation size (Figure 7). These minima correspond to the two states in the model: SCs and C3Ms. The maximum between these two states is the nucleation barrier for the aggregation of SCs (or the dissociation of C3Ms) and is caused by two opposite contributions: the negative “volume” contribution due to attraction between oppositely charged polyelectrolyte chains and protein molecules and a positive “surface” contribution due to the surface tension between the complex coacervate phase and the solution. Because this surface tension is quite low,40 the surface contribution is small compared to the contribution due to the aggregation of SCs, leading to a relatively low nucleation barrier.

Figure 7.

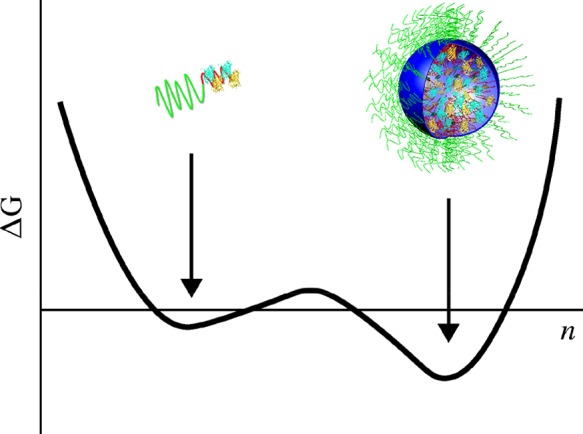
Figure 7

Open in a new tab

Schematic representation of the Gibbs energy of C3M formation as a function of aggregation number n. The curve shows two minima: one at low aggregation number corresponding to SCs and one at the optimum aggregation size for C3Ms.

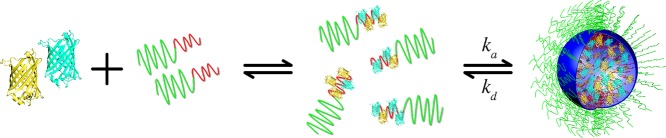
Linking this theory to our experimental results yields a proposed model for the formation of C3Ms, which is summarized in Figure 8. Upon mixing of protein and diblock copolymer solutions, first a rapid formation of SCs occurs; the second step is a slower process in which C3Ms relax to their final equilibrium state due to the association and dissociation of SCs to and from the micelles.

Figure 8.

Figure 8

Open in a new tab

Schematic representation of C3M formation. Upon mixing of protein and diblock copolymer solutions, a rapid formation of SCs occurs. These SCs are assumed to be near-neutral protein–polymer complexes. Subsequently, the formation of C3Ms is a slower process in which SCs continuously associate to and dissociate from C3Ms, with the corresponding rate constants ka and kd, respectively.

It is reasonable to assume that the formation of SCs is diffusion-controlled. This implies that this process would be on the micro- to millisecond time scale,16 which is much too fast to be monitored by our FRET measurements. This would mean that not the formation of SCs but the increase in the volume of core material (complex coacervate microphases) is reflected by the fluorescence emission ratio of SYFP2 to mTurquoise2 as a function of time after mixing protein and polymer solutions.

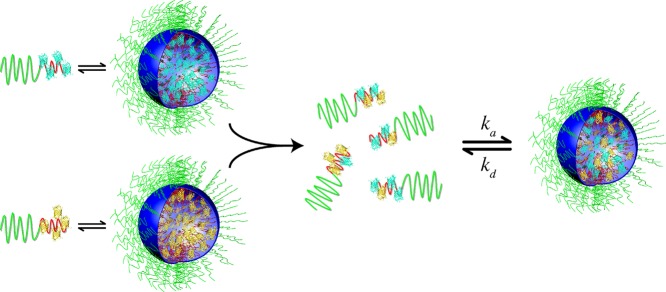
In the C3M mixing experiments, changes in FRET reflect the gradual exchange of core material. Actually, this process is not that different from the relaxation process observed in the formation of C3Ms and is depicted in Figure 9: after the mixing of the two types of equilibrated C3Ms, further association and dissociation of SCs occur, allowing C3Ms to relax to their final equilibrium composition. This explains why we observed similar kinetic coefficients and relaxation times of about 100 s for the formation of C3Ms and for the exchange of proteins between them. An alternative mechanism for the exchange of proteins and the relaxation of micelles by “fusion and fission” is less likely14−16 because the neutral hydrophilic PEO units form a dense stabilizing corona preventing the merging of C3Ms.

Figure 9.

Figure 9

Open in a new tab

Schematic representation of protein exchange between C3Ms. Upon mixing of equilibrated C3Ms with their corresponding SCs, the SCs become mixed. These mixed SCs associate and dissociate with the C3Ms with rate constants of ka and kd, respectively, resulting in a population of mixed C3Ms.

The rate at which SCs associate with (growing) C3Ms, ra, is proportional to the concentrations of SCs and C3Ms

graphic file with name la-2018-012727_m010.jpg 10

in which ka is the association rate constant (Figures 8 and 9) and [SC] and [C3M] denote molar concentrations of SCs and C3Ms, respectively. Our FRET measurements of C3M formation and the exchange between C3Ms convincingly revealed first-order kinetics; therefore, either [SC] or [C3M] should be constant on the time scale of the experiment. For that reason, eq 9 would represent pseudo-first-order kinetics. We can rule out that [SC] would be constant because the increase in FRET is due to the conversion of SCs into complex coacervate microphases (Figures 8 and 9), resulting in a decrease in [SC] during the measurements. Consequently, [C3M] should be constant to explain the order of the reaction. This is possible only if during the FRET measurements the nucleation of new micelles does not happen anymore and only micelle growth takes place.

The dissociation rate, rd, of SCs from C3Ms is proportional to the concentration of C3Ms and the average number of SCs, n, that the C3Ms contain

graphic file with name la-2018-012727_m011.jpg 11

in which kd is the dissociation rate constant (Figure 8). Thus, the net change in the concentration of SCs in time can be expressed as

graphic file with name la-2018-012727_m012.jpg 12

At equilibrium, −d[SC]/dt is zero, n is constant, and eq 12 reduces to

graphic file with name la-2018-012727_m013.jpg 13

This implies that in the final state and provided that the concentrations of protein and polymer are high enough to form micelles, the concentration of SCs is independent of the total concentration of protein and polymer. The concentration of SCs at equilibrium approximately corresponds to the critical micelle concentration (CMC), which we have expressed previously in terms of the free protein concentration.1 For large aggregation numbers, n, the CMC is related to the Gibbs energy of micellization:41

graphic file with name la-2018-012727_m014.jpg 14

For simplicity, we assume that soluble complexes correspond to one polymer chain (with the number of charged groups being about +112) with on average 10 to 11 protein molecules (with a net charge of about −10), resulting in more or less electrically neutral moieties. Previously, the CMC for encapsulated EGFP was found at 100 nM protein at a PMC of 0.65.1 As explained in the Introduction, the CMCs for the FPs used in the present study are very similar. Expressing the CMC via the diblock copolymer concentration, a value of 18 nM is found. By substituting this value into eq 14, we estimate the Gibbs energy of micellization to be −44 kJ/mol or −18kBT at an ionic strength of 2.5 mM. This is the free-energy gain when an SC associates with a C3M.

The decrease in FRET during the salt titration reflects an increase in the average distance between mTurquoise2 and SYFP2. This is probably due to the disintegration of the micellar cores because salt ions screen the attractive electrostatic interaction between the protein molecules and the charged block of the polymer, thereby lowering the entropic contribution of counterion release to the stability. We assume that electrostatic interactions play a role, particularly in the formation of SCs, because the formation of C3Ms results from the assembly of these near-neutral entities. Therefore, the addition of salt would especially affect the stability of SCs. The Gibbs energy of association obtained from the salt titration reflects this stability. At an ionic strength of 2.5 mM, ΔGassociation is −10.0 kJ/mol or −4.1kBT (Figure 6B). Together with the Gibbs energy of the insertion of an SC into the micelle, ΔGmicellization (eq 14), a rough estimate of the overall Gibbs energy of formation of a C3M, is

graphic file with name la-2018-012727_m015.jpg 15

with n being the aggregation number of SCs in a C3M. From the number of charges on the polymer (112) and the protein (9 to 11), we assume that on average 10 to 11 protein molecules are associated with 1 polymer chain. About 450 proteins are encapsulated in 1 C3M;1 therefore, on the basis of charge, about 40 diblock copolymers together with the proteins make up 1 C3M. Taking the aggregation number equal to the number of diblock copolymers per C3M, i.e., n ≈ 40, eq 15 yields a value for ΔGC3M of about −2160 kJ/mol or −880kBT/micelle (at 2.5 mM ionic strength).

Although the overall stability of C3Ms thus seems to be quite high, their structure is highly dynamic and SCs with proteins are easily dissociated from and reassociated with C3Ms, resulting in a rapid exchange of proteins between the micelle core and bulk solution. This has a huge impact on the practical applicability of C3Ms as protein carriers: the protein molecules reside part of the time outside the C3Ms and thus are unprotected. In addition, half of the micelles dissociate at an ionic strength of 20 mM, which makes these systems inapplicable under physiological conditions.

To improve the stability and reduce the dynamics of C3Ms, several options exist. For example, one could choose to add an additional homopolymer to obtain three-component C3Ms; as shown by Lindhoud et al.,4 such C3Ms can have very long relaxation times. The cause of this phenomenon is not clear, however, and a disadvantage is that much less protein molecules per micelle can be accommodated. Alternatively, one could modify the protein, as has been done by Obermeyer et al.,42 who increased the net charge of several proteins by converting positively charged lysine residues to negatively charged residues. These negatively charged proteins were encapsulated with strong polycations, resulting in the improved stability of the micelles to increased ionic strength as the net charge on the protein increased. In view of our findings, a very effective option for trapping proteins would be to cross-link the charged blocks of the diblock copolymers in the C3M cores by using amide bonds.43,44 By doing so, it is not possible for proteins to leave micelles in the form of almost neutral SCs, and the energy barrier to escape on their own will be much higher. An additional advantage of this approach is that the proteins do not need to be modified.

Conclusions

In this article, the formation of protein-containing C3Ms, the protein exchange between them, and their salt stability have been studied using FRET. Energy transfer was followed between mTurquoise2 and SYFP2, which come in close proximity to each other in C3Ms upon mixing with diblock copolymer P2MVP128-b-PEO477. At an ionic strength of about 20 mM, FRET in such a micellar solution reduces to 50% of its initial value as a result of the weakening of the electrostatic interactions between polymers and proteins. Both the formation of C3Ms and the protein exchange between C3Ms follow first-order kinetics with a relaxation time of about 100 s, implying that the structures are dynamic. The similarity between both processes can be explained by a two-state model in which the equilibration of C3Ms to their final size and composition involves the association and dissociation of small near-neutral protein–polymer complexes (SCs). On the basis of the salt stability results, the proposed model, and the assumption that an SC comprises 1 diblock copolymer molecule and about 10 protein molecules, we estimate the overall Gibbs energy of C3M formation to be −880kBT/micelle.

Acknowledgments

Financial support from the Graduate School VLAG (Wageningen, The Netherlands) is gratefully acknowledged. We thank Dr. Joachim Goedhart (University of Amsterdam) for providing us with the pRSETb vector containing SBFP2 and Prof. Frans Leermakers (Wageningen University and Research) for fruitful discussions.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.8b01272.

  • Fluorescence emission ratio of SYFP2 to mTurquoise2 in C3Ms, C3M formation and protein exchange kinetics, and normalized donor and acceptor fluorescence intensities as a function of ionic strength (PDF)

Author Contributions

A.N. purified SBFP2, mTurquoise2, and SFYP2, analyzed data, and wrote the manuscript. E.H. and J.W.B. performed the experiments. A.H.W. assisted with data interpretation. A.N., E.H., J.M.K., W.J.H.v.B., and J.W.B. designed the experiments. A.H.W., J.M.K., W.J.H.v.B., and J.W.B. contributed to the writing of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

la8b01272_si_001.pdf (559.6KB, pdf)

References

  1. Nolles A.; Westphal A. H.; de Hoop J. A.; Fokkink R. G.; Kleijn J. M.; van Berkel W. J. H.; Borst J. W. Encapsulation of GFP in complex coacervate core micelles. Biomacromolecules 2015, 16 (5), 1542–1549. 10.1021/acs.biomac.5b00092. [DOI] [PubMed] [Google Scholar]
  2. Nolles A.; van Dongen N. J. E.; Westphal A. H.; Visser A. J. W. G.; Kleijn J. M.; van Berkel W. J. H.; Borst J. W. Encapsulation into complex coacervate core micelles promotes EGFP dimerization. Phys. Chem. Chem. Phys. 2017, 19 (18), 11380–11389. 10.1039/C7CP00755H. [DOI] [PubMed] [Google Scholar]
  3. Lindhoud S.; de Vries R.; Norde W.; Cohen Stuart M. A. Structure and stability of complex coacervate core micelles with lysozyme. Biomacromolecules 2007, 8 (7), 2219–2227. 10.1021/bm0700688. [DOI] [PubMed] [Google Scholar]
  4. Lindhoud S.; Norde W.; Cohen Stuart M. A. Reversibility and relaxation behavior of polyelectrolyte complex micelle formation. J. Phys. Chem. B 2009, 113 (16), 5431–5439. 10.1021/jp809489f. [DOI] [PubMed] [Google Scholar]
  5. Harada A.; Kataoka K. Pronounced activity of enzymes through the incorporation into the core of polyion complex micelles made from charged block copolymers. J. Controlled Release 2001, 72 (1–3), 85–91. 10.1016/S0168-3659(01)00264-4. [DOI] [PubMed] [Google Scholar]
  6. Yuan X. F.; Yamasaki Y.; Harada A.; Kataoka K. Characterization of stable lysozyme-entrapped polyion complex (PIC) micelles with crosslinked core by glutaraldehyde. Polymer 2005, 46 (18), 7749–7758. 10.1016/j.polymer.2005.02.121. [DOI] [Google Scholar]
  7. Cohen Stuart M. A.; Besseling N. A. M.; Fokkink R. G. Formation of micelles with complex coacervate cores. Langmuir 1998, 14 (24), 6846–6849. 10.1021/la980778m. [DOI] [Google Scholar]
  8. Voets I. K.; de Keizer A.; Cohen Stuart M. A. Complex coacervate core micelles. Adv. Colloid Interface Sci. 2009, 147–148, 300–318. 10.1016/j.cis.2008.09.012. [DOI] [PubMed] [Google Scholar]
  9. Hofs B.; Voets I. K.; de Keizer A.; Cohen Stuart M. A. Comparison of complex coacervate core micelles from two diblock copolymers or a single diblock copolymer with a polyelectrolyte. Phys. Chem. Chem. Phys. 2006, 8 (36), 4242–4251. 10.1039/b605695d. [DOI] [PubMed] [Google Scholar]
  10. de Vries R.; Cohen Stuart M. A. Theory and simulations of macroion complexation. Curr. Opin. Colloid Interface Sci. 2006, 11 (5), 295–301. 10.1016/j.cocis.2006.09.004. [DOI] [Google Scholar]
  11. Kriz J.; Dybal J.; Dautzenberg H. Cooperative interactions of unlike macromolecules: 3. NMR and theoretical study of the electrostatic coupling of sodium polyphosphates with diallyl(dimethyl)ammonium chloride-acrylamide copolymers. J. Phys. Chem. A 2001, 105 (31), 7486–7493. 10.1021/jp010185b. [DOI] [Google Scholar]
  12. Besseling N. A. M.; Cohen Stuart M. A. Self-consistent field theory for the nucleation of micelles. J. Chem. Phys. 1999, 110 (11), 5432–5436. 10.1063/1.478438. [DOI] [Google Scholar]
  13. Hofs B.; de Keizer A.; Cohen Stuart M. A. On the stability of (highly aggregated) polyelectrolyte complexes containing a charged-block-neutral diblock copolymer. J. Phys. Chem. B 2007, 111 (20), 5621–5627. 10.1021/jp0714318. [DOI] [PubMed] [Google Scholar]
  14. Holappa S.; Kantonen L.; Andersson T.; Winnik F.; Tenhu H. Overcharging of polyelectrolyte complexes by the guest polyelectrolyte studied by fluorescence spectroscopy. Langmuir 2005, 21 (24), 11431–11438. 10.1021/la051866r. [DOI] [PubMed] [Google Scholar]
  15. Dormidontova E. E. Micellization kinetics in block copolymer solutions: Scaling model. Macromolecules 1999, 32 (22), 7630–7644. 10.1021/ma9809029. [DOI] [Google Scholar]
  16. Zhang J.; Chen S.; Zhu Z.; Liu S. Stopped-flow kinetic studies of the formation and disintegration of polyion complex micelles in aqueous solution. Phys. Chem. Chem. Phys. 2014, 16 (1), 117–127. 10.1039/C3CP53608D. [DOI] [PubMed] [Google Scholar]
  17. Nolles A.; Westphal A. H.; Kleijn J. M.; van Berkel W. J. H.; Borst J. W. Colorful packages: Encapsulation of fluorescent proteins in complex coacervate core micelles. Int. J. Mol. Sci. 2017, 18 (7), 1557. 10.3390/ijms18071557. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Goedhart J.; von Stetten D.; Noirclerc-Savoye M.; Lelimousin M.; Joosen L.; Hink M. A.; van Weeren L.; Gadella T. W. J.; Royant A. Structure-guided evolution of cyan fluorescent proteins towards a quantum yield of 93%. Nat. Commun. 2012, 3, 751. 10.1038/ncomms1738. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Kremers G. J.; Goedhart J.; van Munster E. B.; Gadella T. W. J. Cyan and yellow super fluorescent proteins with improved brightness, protein folding, and FRET Förster radius. Biochemistry 2006, 45 (21), 6570–6580. 10.1021/bi0516273. [DOI] [PubMed] [Google Scholar]
  20. Chong S.; Mersha F. B.; Comb D. G.; Scott M. E.; Landry D.; Vence L. M.; Perler F. B.; Benner J.; Kucera R. B.; Hirvonen C. A.; Pelletier J. J.; Paulus H.; Xu M. Q. Single-column purification of free recombinant proteins using a self-cleavable affinity tag derived from a protein splicing element. Gene 1997, 192 (2), 271–281. 10.1016/S0378-1119(97)00105-4. [DOI] [PubMed] [Google Scholar]
  21. Evans T. C. Jr.; Xu M. Q. Intein-mediated protein ligation: harnessing nature’s escape artists. Biopolymers 1999, 51 (5), 333–342. . [DOI] [PubMed] [Google Scholar]
  22. Xu M. Q.; Paulus H.; Chong S. Fusions to self-splicing inteins for protein purification. Methods Enzymol. 2000, 326, 376–418. 10.1016/S0076-6879(00)26066-7. [DOI] [PubMed] [Google Scholar]
  23. Kremers G. J.; Goedhart J.; van den Heuvel D. J.; Gerritsen H. C.; Gadella T. W. J. Improved green and blue fluorescent proteins for expression in bacteria and mammalian cells. Biochemistry 2007, 46 (12), 3775–3783. 10.1021/bi0622874. [DOI] [PubMed] [Google Scholar]
  24. Rostkowski M.; Olsson M. H.; Sondergaard C. R.; Jensen J. H. Graphical analysis of pH-dependent properties of proteins predicted using PROPKA. BMC Struct. Biol. 2011, 11, 6. 10.1186/1472-6807-11-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Olsson M. H. M.; Sondergaard C. R.; Rostkowski M.; Jensen J. H. PROPKA3: Consistent Treatment of Internal and Surface Residues in Empirical pK(a) Predictions. J. Chem. Theory Comput. 2011, 7 (2), 525–537. 10.1021/ct100578z. [DOI] [PubMed] [Google Scholar]
  26. Provencher S. W. Contin - a general-purpose constrained regularization program for inverting noisy linear algebraic and integral-equations. Comput. Phys. Commun. 1982, 27 (3), 229–242. 10.1016/0010-4655(82)90174-6. [DOI] [Google Scholar]
  27. Provencher S. W. A constrained regularization method for inverting data represented by linear algebraic or integral equations. Comput. Phys. Commun. 1982, 27 (3), 213–227. 10.1016/0010-4655(82)90173-4. [DOI] [Google Scholar]
  28. Förster T. Zwischenmolekulare energiewanderung und fluoreszenz. Ann. Phys. 1948, 437, 55–75. 10.1002/andp.19484370105. [DOI] [Google Scholar]
  29. Stryer L. Fluorescence energy transfer as a spectroscopic ruler. Annu. Rev. Biochem. 1978, 47, 819–846. 10.1146/annurev.bi.47.070178.004131. [DOI] [PubMed] [Google Scholar]
  30. Zhang J.; Campbell R. E.; Ting A. Y.; Tsien R. Y. Creating new fluorescent probes for cell biology. Nat. Rev. Mol. Cell Biol. 2002, 3 (12), 906–918. 10.1038/nrm976. [DOI] [PubMed] [Google Scholar]
  31. Piston D. W.; Kremers G. J. Fluorescent protein FRET: the good, the bad and the ugly. Trends Biochem. Sci. 2007, 32 (9), 407–414. 10.1016/j.tibs.2007.08.003. [DOI] [PubMed] [Google Scholar]
  32. Hohlbein J.; Craggs T. D.; Cordes T. Alternating-laser excitation: single-molecule FRET and beyond. Chem. Soc. Rev. 2014, 43 (4), 1156–1171. 10.1039/C3CS60233H. [DOI] [PubMed] [Google Scholar]
  33. Steinberg I. Z. Nonradiative energy transfer in systems in which rotatory brownian motion is frozen. J. Chem. Phys. 1968, 48 (6), 2411–2413. 10.1063/1.1669461. [DOI] [Google Scholar]
  34. Eisinger J.; Dale R. E. Interpretation of intramolecular energy transfer experiments. J. Mol. Biol. 1974, 84 (4), 643–647. 10.1016/0022-2836(74)90122-3. [DOI] [PubMed] [Google Scholar]
  35. Ormö M.; Cubitt A. B.; Kallio K.; Gross L. A.; Tsien R. Y.; Remington S. J. Crystal structure of the Aequorea victoria green fluorescent protein. Science 1996, 273 (5280), 1392–1395. 10.1126/science.273.5280.1392. [DOI] [PubMed] [Google Scholar]
  36. Yang F.; Moss L. G.; Phillips G. N. J. The molecular structure of green fluorescent protein. Nat. Biotechnol. 1996, 14 (10), 1246–1251. 10.1038/nbt1096-1246. [DOI] [PubMed] [Google Scholar]
  37. Sams P. J.; Wyn-Jones E.; Rassing J. A new model describing the kinetics of micelle formation from chemical relaxation studies. Chem. Phys. Lett. 1972, 13 (3), 233–236. 10.1016/0009-2614(72)85049-8. [DOI] [Google Scholar]
  38. Laughlin R. G.The Aqueous Phase Behavior of Surfactants; Academic Press: London, 1994. [Google Scholar]
  39. Leermakers F. A. M.; Eriksson J. C.; Lyklema J.. Association Colloids and Their Equilibrium Modelling. In Fundamentals of Interface and Colloid Science: Soft Colloids; Lyklema J., Ed.; Academic Press: Amsterdam, 2005; Vol. 5. [Google Scholar]
  40. Spruijt E.; Sprakel J.; Cohen Stuart M. A.; van der Gucht J. Interfacial tension between a complex coacervate phase and its coexisting aqueous phase. Soft Matter 2010, 6 (1), 172–178. 10.1039/B911541B. [DOI] [Google Scholar]
  41. Phillips J. N. The energetics of micelle formation. Trans. Faraday Soc. 1955, 51 (4), 561–569. 10.1039/tf9555100561. [DOI] [Google Scholar]
  42. Obermeyer A. C.; Mills C. E.; Dong X. H.; Flores R. J.; Olsen B. D. Complex coacervation of supercharged proteins with polyelectrolytes. Soft Matter 2016, 12 (15), 3570–3581. 10.1039/C6SM00002A. [DOI] [PubMed] [Google Scholar]
  43. Bourouina N.; Cohen Stuart M. A.; Kleijn J. M. Complex coacervate core micelles as diffusional nanoprobes. Soft Matter 2014, 10 (2), 320–331. 10.1039/C3SM52245H. [DOI] [PubMed] [Google Scholar]
  44. Kim J. O.; Ramasamy T.; Yong C. S.; Nukolova N. V.; Bronich T. K.; Kabanov A. V. Cross-linked polymeric micelles based on block ionomer complexes. Mendeleev Commun. 2013, 23 (4), 179–186. 10.1016/j.mencom.2013.07.001. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

la8b01272_si_001.pdf (559.6KB, pdf)

Articles from Langmuir are provided here courtesy of American Chemical Society

RESOURCES