Abstract.
Accurate measurements of microelastic properties of soft tissues in-vivo using optical coherence elastography can be affected by motion artifacts caused by cardiac and respiratory cycles. This problem can be overcome using a multielement ultrasound transducer probe where each ultrasound transducer is capable of generating acoustic radiation force (ARF) and, therefore, creating shear waves in tissue. These shear waves, produced during the phase of cardiac and respiratory cycles when tissues are effectively stationary, are detected at the same observation point using phase-sensitive optical coherence tomography (psOCT). Given the known distance between the ultrasound transducers, the speed of shear wave propagation can be calculated by measuring the difference between arrival times of shear waves. The combined multitransducer ARF/psOCT probe has been designed and tested in phantoms and ex-vivo studies using fresh rabbit heart. The measured values of shear moduli are in good agreement with those reported in literature. Our results suggest that the developed multitransducer ARF/psOCT probe can be useful for many in-vivo applications, including quantifying the microelasticity of cardiac muscle.
Keywords: optical coherence tomography and elastography, multielement ultrasound transducer probe, acoustic radiation force, shear wave elasticity imaging, cardiac muscle
1. Introduction
Shear wave elasticity imaging (SWEI) has been widely used for mapping elastic properties of soft tissues1 and remains a very active research area. It is well known that the viscoelastic properties of soft tissues can be indicative of overall tissue health, and their changes might indicate development of certain diseases and lesions.2,3 Recent progress has enabled high-quality quantitative SWEI of deep tissues.4 Overall, SWEI is based on the excitation of one or several shear waves in tissues with consequent measurements of their propagation speed. Assuming the density of the soft tissue, the shear elastic modulus of tissue traversed by the shear wave can be reconstructed.5 This approach is employed in numerous applications in biomedical engineering and medicine, where assessment of biomechanical parameters of soft tissues at microlevel with high spatial resolution is required.6–8
There are several excitation and imaging approaches capable of shear modulus assessment of soft tissues, for example, mechanical extensiometry,9 magnetic resonance elastography (MRE),10 and ultrasound elastography.3 However, some of these approaches, such as mechanical extensiometry, are destructive and, therefore, applicable for ex-vivo tissue assessment only. MRE is a nondestructive imaging technique but it mostly operates on large-scale parts of tissues and could not be used to assess tissue elasticity on a micrometer level and with high resolution. Although a micro-MRE imaging technique has been reported recently, the approach requires tissue preparation and could not be used in-vivo.11 Even ultrasound elastography may not be suitable for this application because very small displacements caused by shear wave propagation are expected in relatively stiff tissues, such as heart muscle.
Recently, optical coherence elastography (OCE) was proposed for nondestructive, high-resolution SWEI of soft tissues at the micrometer scale.12–15 This approach is based on generating a shear wave in a sample with consequent measurement of the shear wave propagation speed using phase-sensitive optical coherence tomography (psOCT) where the axial component of particle velocity is measured accurately using phase changes of the spectral interferograms. This makes it possible to detect tissue displacement well below 1 mm—detection of displacements has been reported using phase-sensitive measurements.16 Shear waves in tissues can be created using various methods, such as a laser pulse,17 mechanical actuator,18 air-pulse system,19 ultrasound,20 and the Lorentz force.21 The speed of shear wave propagation can be calculated as a ratio of a distance between the excitation and observation points (i.e., travel distance) to the time of shear wave propogation.22 Alternatively, shear wave velocity measurements can be performed by changing the distance between the point of excitation and the point of observation.19 For example, using an air-pulse system to create a shear wave and psOCT system to measure displacement of phantom surface at different distances away from the point of excitation, noncontact assessment of Young’s modulus was in good agreement with the results of standard uniaxial testing.23
Overall, feasibility of OCE to assess microelasticity of soft tissues has been successfully demonstrated suggesting that OCE may become a powerful and informative tool for preclinical and clinical applications. However, in-vivo measurements of biomechanical properties of internal tissues or measurements in areas where access is limited require a special probe. Such probe should be as miniature as possible, ideally comparable with endo- or intravascular devices, such as OCT catheters24 or devices used in laparoscopic surgery. In addition, to avoid motion artifacts, this probe should allow for fast and preferably noncontact measurement in tissues of moving organs, such as heart or tissues subjected to motion due to the respiratory cycle. To overcome possible motion artifacts, all measurements of shear wave propagation must be acquired within a short segment of the cardiac cycle and respiratory cycle when the tissues are effectively stationary. Generally, cardiac rates are several times greater rather than respiratory rates. Therefore, in small animals, all measurements should be completed within a short () data acquisition window at the end of expiration in a ventilation cycle and triggered by peak in QRS complex within the cardiac cycle.25
While OCT detection of shear waves can be performed using miniature probes,26 limited access to internal tissues effectively narrows the choice of shear wave excitation methods. An ultrasound transducer can be used to generate an acoustic radiation force (ARF) and create shear waves in tissues.27,28 Therefore, an array of transducers can be integrated with a small OCT probe such that the shear wave observation point (OCT beam) and shear wave excitation points (ultrasound beams) are located along a straight line. Multiple shear waves can be created at different points in tissue simultaneously or one right after another using different ultrasound transducers while psOCT can be used to detect the shear waves. If shear waves are created simultaneously by an array of ultrasound transducers, the measurement can be performed quickly thus avoiding motion artifacts leading to errors in shear modulus reconstruction. Indeed, assuming a very soft tissue with relatively low speed of shear wave of , propagation of shear waves over 5-mm distance can be measured within a 10-ms window.
The multitransducer ultrasound ARF/psOCT probe would be useful for many in-vivo applications, for example, to assess the microelasticity of cardiac muscle that is damaged by myocardial infarction (MI).29 Indeed, tissues damaged by MI exhibit elevated stiffness compared to that of benign cardiac muscles,23,30,31 and development of new therapeutic methods of heart self-renewal requires in-vivo monitoring of new cardiomyocyte delivery and proliferation in cardiac muscles.32
The goal of the paper is to investigate the feasibility of miniature ultrasound transducers to create shear wave displacements measurable by psOCT, and then to design a multielement ultrasound transducer probe and prototype a combined ARF/psOCT probe capable of assessing microelasticity properties of cardiac tissues.
2. Materials and Methods
2.1. Design and Operation of Ultrasound Transducers
To test the capability of small ultrasound transducers to create shear waves that are detectable by a psOCT system, a miniature ultrasound transducer was designed and manufactured. The diagram and microphotograph of the transducer are shown in Fig. 1(a). This transducer is comprised of a lead zirconate titanate (PZT) crystal with two thin vacuum sputtered nickel electrodes (T120-A4E-602, Piezo Systems, Inc.). The thickness of the rectangular crystal was 0.020 in. (). The backing was made out of electrically conductive epoxy (E-Solder 3022, VonRoll Insulation, Inc.). Metal housing made out of brass tube (#8126, Precision Metals, Inc.) with outer and inner diameter of 2.38 and 1.7 mm, respectively, was used both as the transducer holder and as the shield for the 32-gauge center conductor located inside the housing.
Fig. 1.
(a) Diagram and microphotograph of the miniature ultrasound transducer. The scale bar is 2 mm. (b) Alignment of the ultrasound transducer and an OCT intravascular catheter. Thick red and thin blue arrows indicate the ultrasound and OCT beams, respectively. The scale bar is 2 mm.
At the tip, the upper half of the metal housing was removed over a length of . The remaining lower half of the housing was slightly flattened such that its internal width in this area was 2.7 mm, where the rectangular PZT crystal with backing was glued using the conductive epoxy as shown in Fig. 1(a). The center wire was electrically and mechanically fixed to the top crystal electrode using the same epoxy. The housing and center wire were connected to an amplifier via coaxial cable. The center frequency of the transducer, measured using a vector network analyzer (E5061B, Keysight Technologies, Inc.) was 4.8 MHz.
2.2. Phase-Sensitive Optical Coherence Tomography Probe and System
A commercial intravascular OCT imaging catheter (Dragonfly™ OPTIS™, Abbott, Inc.) without sheath was used as an OCT imaging probe. The OCT probe was connected to a custom-built phase-stabilized OCT system. The overall system’s design is similar to that described elsewhere;33 however, there were a few important differences. Instead of optical signal from a fiber Bragg grating, every digitized OCT trace was started from an electrical trigger provided by the swept source (Axsun Technologies, Inc.). The trace repetition frequency was 50 kHz, center wavelength and bandwidth were 1312 and 115 nm, respectively, and average trace power was about 40 mW. The system employed a 10-mm Mach-Zehnder interferometer for k-clock generation. The k-clock signal was acquired as a reference simultaneously with the interference signal via a dual-channel 1500-MSa/s analog-to-digital convertor (5771, National Instruments, Inc.) pipelining data directly to a field-programmable gate array (FPGA) (Kintex-7, Xilinx, Inc.). Remapping was performed by the FPGA using the k-clock as a double data rate clock (both edges were utilized). The real-valued trace was zero padded to make it analytic, and an inverse discrete Fourier transform yielded a complex-valued trace. With the sweep range 1255 to 1369 nm, the 2600-point traces spanned 10 mm in air. The envelope of each trace then becomes one of the A-lines in an OCT frame. The frame was then phase unwrapped to correct for phase aliasing and differentiated with respect to trace number (which corresponds to time), integrated, and scaled appropriately to yield an M-mode psOCT image of displacement as function of depth and time. The refractive index of water-based tissues and phantoms was assumed to be 1.32 for the whole spectral range of the swept source.
Each M-mode OCT image was collected synchronously with an ultrasound burst transmission to initiate the shear wave. OCT image collection started a few milliseconds prior to the US burst to show the displacement of a sample before, during, and after the shear wave propagation. Typical psOCT images were composed of 1000 traces placed one after another. Given trace repetition frequency of 50 kHz, displacement data were collected over a 20-ms window.
2.3. Transducer Validation
The ability of the psOCT method to measure tissue displacements at micrometer-scale level is well known.12 However, the capability of the small ultrasound transducer to create shear waves with a magnitude detectable by psOCT needed to be investigated. The small size custom-build ultrasound transducer was tested initially using a phantom designed to mimic both the shear elasticity and acoustic properties of soft tissues.34–36 The phantom was made from 8 wt. % porcine gelatin (G2500-1KG, Sigma®, Sigma-Aldrich, Inc.) and 1 wt. % silica particles (717185-1KG, Aldrich®, Sigma-Aldrich, Inc.) with average size of . To increase the optical contrast for psOCT measurements, a thin layer of graphite powder (635 Flake, Asbuty Online, Inc.) was deposited on the imaged surface of the phantom.
The phantom was placed in a water tank with both the ultrasound transducer and the OCT probe positioned on top of the phantom. Both ultrasound transducer and OCT probe were immersed into water. The distance from the ultrasound transducer to the phantom was . As shown in Fig. 1(b), the OCT probe was aligned with the ultrasound transducer such that ultrasound beam and optical beam were parallel. The distance between the ultrasound and OCT beams was .
The ultrasound transducer was operated using a function generator (AFG3022C, Tektronix, Inc.) and power amplifier (A150, E&I, Inc.). The function generator provided a burst of sinusoidal signals at 4.8-MHz frequency while M-mode psOCT image was collected. The burst duration and energy delivered to the transducer were 0.11 ms (500 cycles at 4.8 MHz) and 1.7 mJ, respectively.
2.4. Integrated ARF/psOCT Probe
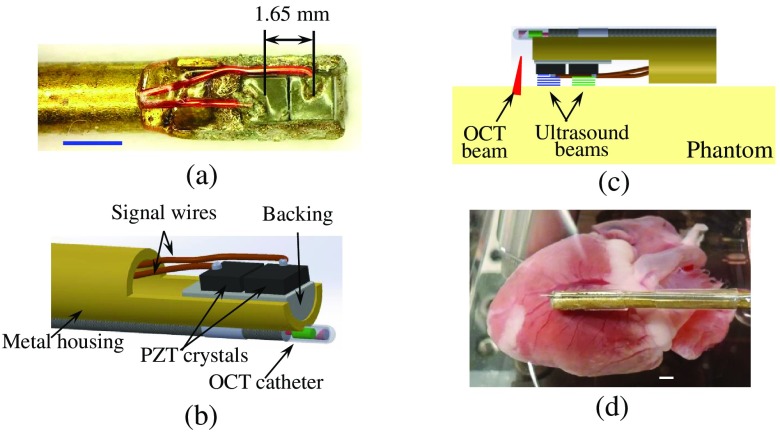
We have designed and built a multielement ultrasound transducer probe as shown in Fig. 2(a). Two ultrasound transducers were glued at the tip of the metal housing such that surfaces of the crystals were parallel. The distance between centers of the transducers was 1.65 mm. Each transducer was connected to an amplifier using a 32-gauge signal wire. The fully assembled ultrasound probe was coated by a thin layer of silicone to provide electrical isolation.
Fig. 2.
(a) Microphotograph of the multitransducer ultrasound array with transducer size of square. The scale bar is 2 mm. (b) A diagram of the assembled multitransducer ARF/psOCT probe. (c) A diagram of phantom experiments. (d) Photograph of the ARF/psOCT probe positioned above the rabbit heart. Scale bar is 2 mm.
The diagram of the assembled ARF/psOCT probe is shown in Fig. 2(b). The same OCT imaging probe was integrated with the two-element ultrasound transducer probe into a single device. The tip of OCT probe was positioned as close to the ultrasound transducers as possible. Furthermore, the ultrasound transducers and the point where OCT beam entered the tissue were aligned along a straight line.
2.5. Phantom and Ex-Vivo Validation of Multitransducer ARF/psOCT Probe
The multitransducer ARF/psOCT probe was initially validated in phantom studies. A set of four phantoms with the same geometrical, optical, and ultrasound properties, but different elastic properties, was made. For optical and ultrasound scattering, the same concentrations of silica particles (1 wt. %) and graphite particles (0.5 wt. %) were added to gelatin solutions. Shear moduli of the phantoms were varied using 10, 12.5, 15, and 25 wt. % gelatin concentrations. The size of all phantoms was . In the experiments, both the phantoms and the ARF/psOCT probe were immersed in water such that the distance between ultrasound transducers and the phantom was as shown in Fig. 2(c). Two shear waves were created by the different ultrasound transducers of the array consequently using an electrical burst of 0.46-mJ energy and duration, and two M-mode psOCT images were collected. The delay between the first A-line of each psOCT image and the ultrasound burst was 5 ms. For the same location and under the same conditions, shear waves were induced in each phantom five times by each ultrasound transducer and detected by the psOCT system to demonstrate the repeatability of measurements.
For ex-vivo validation of the multitransducer ARF/psOCT probe, the fresh heart of an atherosclerotic Watanabe rabbit kept on a high cholesterol diet for more than 3 years was used in the experiments. The heart was obtained from a rabbit euthanized at the end of an experimental study covered by IACUC protocol A16101 at Georgia Institute of Technology. Prior to experiments, the fresh heart was kept in saline. During the experiments, the heart was placed in a water tank and the ARF/psOCT probe was positioned such that the distance between ultrasound transducer and heart surface was as shown in Fig. 2(d). ARF was generated by each ultrasound transducer separately using a 1.7-mJ electrical burst of 0.11-ms duration. The measurements were repeated five times.
The speed of each shear wave was calculated based on the distance of 1.65 mm between the centers of the ultrasound transducers and delay between times of arrival of the shear waves induced by different ultrasound transducers of the ARF/psOCT probe. Shear modulus of the phantom was estimated using the following equation:
| (1) |
where stands for shear modulus, is tissue density, and is the calculated shear wave speed.
3. Results and Discussion
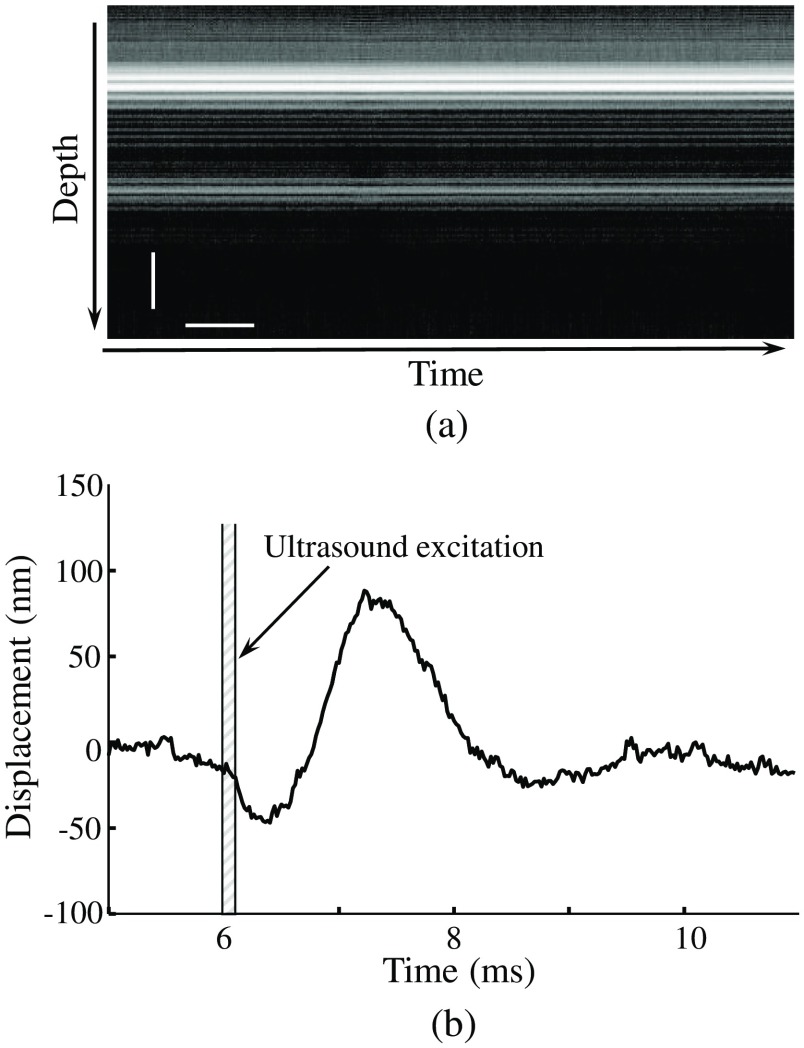
A typical psOCT M-mode image of phantom is shown in Fig. 3(a). The shear wave displacement profile reconstructed from the M-mode image is shown in Fig. 3(b). Ultrasound excitation to generate shear wave is depicted by a shaded area confined by two vertical solid lines. Clearly, a ultrasound transducer can create a shear wave with the peak-to-peak displacement magnitude of 150 nm, which can be reliably detected by psOCT imaging.
Fig. 3.
(a) Typical M-mode psOCT image of a phantom. The vertical and horizontal scale bars are and 2 ms, respectively. (b) Shear wave detected in phantom. The magnitude of the displacement is smaller than the pixel size of .
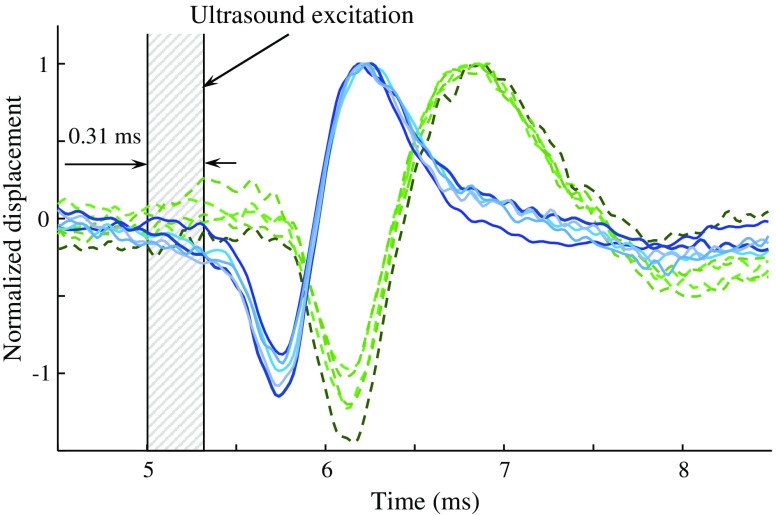
Figure 4 demonstrates the results of the ARF/psOCT measurements in the 10 wt. % gelatin phantom. Solid blue-colored lines depict the shear waves induced by the ultrasound transducer [see Fig. 2(c)] positioned closer to the point of observation (i.e., OCT beam). Dashed green-colored lines correspond to the shear waves created by the ultrasound transducer located further away from OCT beam. The normalized shear displacements demonstrate the repeatability of the results. Ultrasound excitation is depicted by shaded area between two vertical lines.
Fig. 4.
Shear waves induced in 10 wt. % gelatin phantom by ultrasound transducers closer (solid blue-colored lines) and further (dashed green-colored lines) from the OCT observation spot.
The times of shear wave arrival created by the different transducers were and , respectively () resulting in time delay. The speed of the shear wave was calculated to be . Assuming the density of all phantoms to be , the shear modulus of the 10% gelatin phantom was estimated to be using Eq. (1). In the phantoms with gelatin concentration of 12.5%, 15%, and 25%, the measured speeds of shear waves were calculated to be , , and , respectively. Corresponding shear moduli of these phantoms were calculated to be , , and , respectively. These results demonstrate a monotonic increase of shear moduli with gelatin concentration. Our measurements qualitatively agree with the literature data,37 while the differences can be possibly attributed to addition and greater concentration of optical and/or ultrasound scatterers.
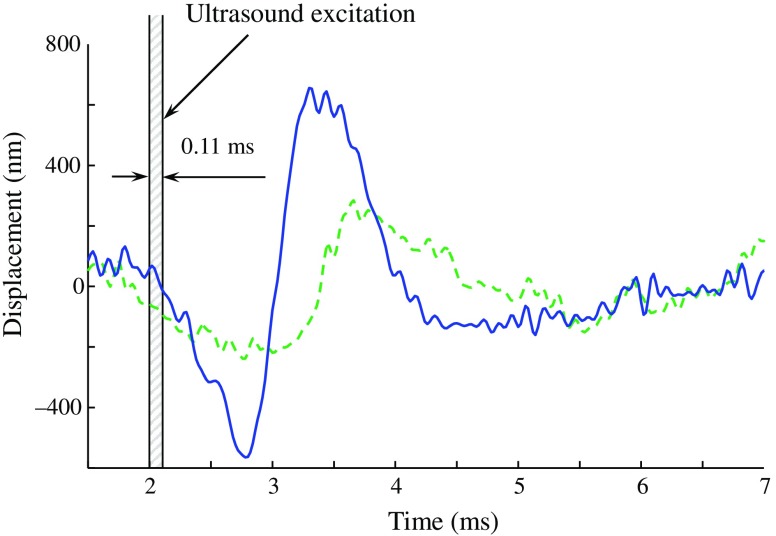
The developed multitransducer ARF/psOCT probe was tested in ex-vivo studies. Representative shear waves for each ultrasound transducer are shown in Fig. 5. The duration of the ARF excitation is shown using shaded area between two vertical black lines. The solid blue line and the dashed green line in Fig. 5 correspond to the shear waves generated by the ultrasound transducer that is located closer to and further from the optical beam, respectively.
Fig. 5.
Representative shear waves produced in rabbit heart muscle by different ultrasound transducers of the ARF/psOCT probe located closer to its tip (solid blue line) and further from the tip (dashed green line).
Times of arrival of the shear waves created by ultrasound transducers located closer to and further from point of observation were measured to be and , respectively. Given the 1.65-mm distance between the transducers, the shear wave speed was estimated to be . Assuming the density of cardiac muscle to be , the cardiac muscle shear modulus was calculated to be using Eq. (1).38 Our results are in good agreement with the measurement in the murine heart.23 At the same time, lower values of shear elastic modulus of human heart tissues are also reported.39 This discrepancy could be explained by differences between rabbit and human tissues and the fact that we have used a heart from an atherosclerotic rabbit genetically prone to cardiac disease.
The calculations of shear moduli using Eq. (1) assume that shear waves propagate in an infinite medium. Obviously, this assumption is too strong for both phantoms and heart muscle thus speeds of shear waves and, therefore, shear moduli are slightly underestimated.40 In the future, the ultrasound transducer can also be used to measure directly the thickness of the heart muscle, which would allow for correction of the measured speeds of shear waves and, therefore, shear moduli.
Comparison of experimental results shown in Figs. 3(b) and 5 demonstrates that the magnitude of shear waves in the stiffer heart is greater than that in the softer phantom. One possible explanation is that the interaction between ultrasound waves and gelatin phantom with silica particles was less efficient compared to that with cardiac muscle. Also, the quality of ultrasound transducers in the ARF/psOCT probe was higher compared to the transducer used in the initial tests. In any case, reconstruction of shear modulus relies on temporal characteristics of shear waves rather than on their magnitude, and the only requirement is that shear displacements must be detectable in tissues by psOCT.
Combination of an ultrasound transducer and a miniature OCT probe has been shown previously for two-modality intravascular imaging.41 However, the ARF/psOCT probe reported here has been designed quite differently. First of all, in intravascular ultrasound imaging catheters, both the center frequency and bandwidth of an ultrasound transducer need to be high for better spatial resolution. On the contrary, ARF excitation is more efficient at lower frequencies and narrow bandwidths, which require thicker PZT crystals. The thicker crystal increases the size of the probe, and, therefore, there is a trade-off between the thicknesses of the crystal and the size of the ARF/psOCT probe. Second, the multitransducer ARF/psOCT probe was designed for quantitative measurements of shear elasticity within a wide range of shear moduli. Indeed, the experimental results presented in Figs. 4 and 5 demonstrate that the shear modulus of both soft () and hard () tissues can be measured in . The multitransducer ARF/psOCT probe enables measurements to be performed very quickly so that tissues are effectively stationary. Third, intravascular OCT imaging catheters are designed such that both imaging depth and spatial resolution are maximized. In contrast, the OCT detector in ARF/psOCT probe must be optimized for detection of very small motions while the lateral resolution is less important.
Unlike air pulse or laser-based excitation of a shear waves, ARF excitation requires an acoustic coupling between the ultrasound transducer and soft tissues. Such coupling can be created by a drop of physiological 0.9% saline that is delivered to the transducers inside a protection sheath, similar to catheters for intravascular imaging. Note that the water filled 0.2- to 0.3-mm gap between the ultrasound transducer and heart muscle will not affect the measurements because the typical shear wave displacements are much smaller than the size of the gap.
The current prototype of the multitransducer ARF/psOCT probe needs further miniaturization. First, the size of ultrasound transducers should be further decreased with simultaneous improvement of ARF generation efficiency. This could be achieved using lower frequency PZT crystals and different backing materials. Second, instead of commercial OCT catheters, a custom OCT detector needs to be designed. Third, the rigid part of the current prototype needs to be redesigned such that the tip of the probe can be remotely manipulated using, for instance, a robotic guidewire to operate the probe remotely.42
While the two-transducer ARF/psOCT prototype was successfully tested ex-vivo, in-vivo evaluation using an animal model is still required. Future work also includes development and manufacturing a cost-effective two-channel power amplifier and its synchronization with electrocardiography equipment to confirm that shear modulus of heart muscle can be reliably measured in-vivo.
In a clinical environment, the proposed multitransducer ARF/psOCT probe could be potentially adapted in endoscopic or invasive procedures, such as intracardiac ultrasound imaging. Shear elasticity of human heart tissues is comparable with that of rabbit hearts or less.39,43 Given lower human cardiac and respiratory rates,44 the shear elasticity of heart tissue and atherosclerotic vessel tissue45 could be assessed using an endoscope-like or catheter-like ARF/psOCT probe.
4. Conclusion
A design of a multitransducer ARF/psOCT probe to assess biomechanical properties has been introduced and successfully tested both in phantom studies and ex-vivo. Shear waves were created, and propagation speeds were measured both in phantoms and in rabbit heart. It was found that the ARF/psOCT probe and method are suitable for assessment of tissues with shear moduli varying in a wide range that covers almost all soft tissues. Shear wave propagating with speed ranging from 2.8 to , which correspond to shear moduli in the range of 8.6 to 41 kPa, can be reliably measured. The ARF/psOCT probe was used to assess elasticity of a rabbit heart muscle. Our measurements of shear wave speed and shear modulus for the rabbit heart muscle agree well with the experimental results reported by other groups for murine and human heart muscle tissue. Overall, the combined multitransducer ARF/psOCT probe can be used for assessment of microelasticity properties of cardiac tissues.
Acknowledgments
This work was supported in part by the National Institutes of Health under Grant No. R01HL130804.
Biographies
Andrei B. Karpiouk is a senior research scientist of the Electrical and Computer Engineering Department at Georgia Institute of Technology. He received his MS and PhD degrees in laser physics from the Moscow Engineering Physics Institute in 1994 and 2002, respectively. His research interests are in combined medical imaging and sensing, microengineering and prototyping, biomedical engineering, research of laser-tissue interaction processes, and measurements of biomechanical properties of soft tissues. He has published about 70 papers, proceedings and abstracts.
Donald J. VanderLaan is a senior research engineer of electrical and computer engineering at the Georgia Institute of Technology. He is involved in development and prototyping of novel combined imaging systems. His research interests include new designing of imaging algorithms, building of custom electronic circuits, assembling opto-electronic parts and optical components and integrating different imaging technologies. He is also actively pursuing his own project to obtain a PhD in electrical and computer science.
Kirill V. Larin is a professor of biomedical engineering at the University of Houston. He received his MS degree in laser physics and mathematics from the Saratov State University in 1995 and PhD in biomedical engineering from the University of Texas Medical Branch, Galveston, in 2002. He has published more than 130 papers in the field of biomedical optics and biophotonics. He is inducted as Fellow of SPIE in 2015 and OSA in 2016.
Stanislav Y. Emelianov is a professor of electrical and computer engineering, biomedical engineering, and radiology at the Georgia Institute of Technology and Emory University School of Medicine. Furthermore, he is director of the Ultrasound Imaging and Therapeutics Research Laboratory. Throughout his career, he has been devoted to the development of advanced imaging methods capable of detecting and diagnosing cancer and other pathologies, assisting treatment planning, and enhancing image-guided therapy and monitoring of the treatment outcome.
Disclosures
Dr. A. B. Karpiouk, Mr. D. J. VanderLaan, and Dr. S. Y. Emelianov are the cofounders of DecisIV Interventions, LLC—a company pursuing intravascular photoacoustic imaging. DecisIV Interventions does not support this work. Dr. K.V. Larin does not have any conflicts of interest.
References
- 1.Sarvazyan A. P., et al. , “Shear wave elasticity imaging: a new ultrasounic technology of medical diagnostics,” Ultrasound Med. Biol. 24, 1419–1435 (1998). 10.1016/S0301-5629(98)00110-0 [DOI] [PubMed] [Google Scholar]
- 2.Aglyamov S. R., Skovoroda A. R., “Mechanical properties of soft biological tissues,” Biophysics 45, 1103–1111 (2000). [PubMed] [Google Scholar]
- 3.Sarvazyan A., et al. , “An overview of elastography—an emerging branch for medical imaging,” Curr. Med. Imaging Rev. 7, 255–282 (2011). 10.2174/157340511798038684 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gao L., et al. , “Imaging of the elastic properties of tissue—a review,” Ultrasound Med. Biol. 22, 959–977 (1996). 10.1016/S0301-5629(96)00120-2 [DOI] [PubMed] [Google Scholar]
- 5.Hachemi M. E., Calle S., Remenieras J. P., “Transient displacement induced in shear wave elastography: comparison between analytical results and ultrasound measurements,” Ultrasonics 44, e221–e225 (2006). 10.1016/j.ultras.2006.06.022 [DOI] [PubMed] [Google Scholar]
- 6.Bastard C., et al. , “Transient micro-elastography: a novel non-invasive approach to measure liver stiffness in mice,” World J. Gastroenterol. 17, 958–975 (2011). 10.3748/wjg.v17.i8.968 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kennedy K. M., et al. , “Quantitative micro-elastography: imaging of tissue elasticity using compression optical coherence elastography,” Sci. Rep. 5, 1–12 (2015). 10.1038/srep15538 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Qian X., et al. , “Multi-functional ultrasonic microelastography imaging system,” Nat. Sci. Rep. 7, 1–11 (2017). 10.1038/s41598-016-0028-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hoeltzel D. A., et al. , “Strip extensiometry for comparison of the mechanical response of bovine, rabbit, and human corneas,” Trans. ASME 114, 202–215 (1992). [DOI] [PubMed] [Google Scholar]
- 10.Muthupillai R., et al. , “Magnetic resonance elastography by direct visualization of propagating acoustic strain waves,” Science 269, 1854–1857 (1995). 10.1126/science.7569924 [DOI] [PubMed] [Google Scholar]
- 11.Othman S. F., et al. , “Microscopic magnetic resonance elastography (μMRE),” Magn. Reson. Med. 54, 605–615 (2005). 10.1002/mrm.20584 [DOI] [PubMed] [Google Scholar]
- 12.Larin K. V., Sampson D. D., “Optical coherence elastography—OCT at work in tissue biomechanics [Invited],” Biomed. Opt. Express 8, 1172–1202 (2017). 10.1364/BOE.8.001172 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Schmitt J. M., “OCT elastography: imaging microscopic deformation and strain of tissue,” Opt. Express 3, 199–211 (1998). 10.1364/OE.3.000199 [DOI] [PubMed] [Google Scholar]
- 14.Wang S., Larin K. V., “Shear wave imaging optical coherence tomography (SWI-OCT) for ocular tissue biomechanics,” Opt. Lett. 39, 41–44 (2014). 10.1364/OL.39.000041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang S., Larin K. V., “Optical coherence elastography for tissue characterization: a review,” J. Biophotonics 8, 279–302 (2015). 10.1002/jbio.v8.4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lan G., et al. , “Common-path phase-sensitive optical coherence tomography provides enhanced phase stability and detection sensitivity for dynamic elastography,” Biomed. Opt. Express 8, 5253–5266 (2017). 10.1364/BOE.8.005253 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Grasland-Mongrain P., et al. , “Generation of shear waves by laser in soft media in the ablative and thermoelastic regimes,” Appl. Phys. Lett. 109, 2219011–2219015 (2016). 10.1063/1.4968538 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhu J., et al. , “Longitudinal shear wave imaging for elasticity mapping using optical coherence elastography,” Appl. Phys. Lett. 110, 201101–201106 (2017). 10.1063/1.4983292 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wang S., et al. , “A focused air-pulse system for optical-coherence-tomography-based measurements of tissue elasticity,” Laser Phys. Lett. 10, 076605 (2013). 10.1088/1612-2011/10/7/075605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ambroziński L., et al. , “Acoustic micro-tapping for noncontact 4D imaging of tissue elasticity,” Sci. Rep. 6, 1–11 (2016). 10.1038/s41598-016-0001-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wu C., et al. , “Lorentz force optical coherence elastography,” J. Biomed. Opt. 21, 090502 (2016). 10.1117/1.JBO.21.9.090502 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Nguyen T.-M., et al. , “Shear wave elastography using amplitude-modulated acoustic radiation force and phase-sensitive optical coherence tomography,” J. Biomed. Opt. 20, 016001 (2015). 10.1117/1.JBO.20.1.016001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wang S., et al. , “Noncontact quantitative biomechanical characterization of cardiac muscle using shear wave imaging optical coherence tomography,” Biomed. Opt. Express 5, 1980–1992 (2014). 10.1364/BOE.5.001980 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Atif M., et al. , “Catheters for optical coherence tomography,” Laser Phys. Lett. 8, 629–646 (2011). 10.1002/lapl.v8.5 [DOI] [Google Scholar]
- 25.Johnson K., “Introduction to rodent cardiac imaging,” Inst. Lab. Anim. Res. 49, 27–34 (2008). 10.1093/ilar.49.1.27 [DOI] [PubMed] [Google Scholar]
- 26.Gora M. J., et al. , “Endoscopic optical coherence tomography: technologies and clinical applications [Invited],” Biomed. Opt. Express 8, 2405–2444 (2017). 10.1364/BOE.8.002405 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chen S., Fatemi M., Greenleaf J. F., “Quantifying elasticity and viscosity from measurement of shear wave speed dispersion,” J. Acoust. Soc. Am. 115, 2781–2785 (2004). 10.1121/1.1739480 [DOI] [PubMed] [Google Scholar]
- 28.Erpelding T. N., Hollman K. W., O’Donnell M., “Mapping age-related elasticity changes in porcine lenses using bubble-based acoustic radiation force,” Exp. Eye Res. 84, 332–341 (2007). 10.1016/j.exer.2006.10.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lonborg J., et al. , “Impact of acute hyperglycemia on myocardial infarct size, area at risk, and salvage in patients with STEMI and the association with exenatide treatment: results from a randomized study,” Diabetes 63, 2474–2485 (2014). 10.2337/db13-1849 [DOI] [PubMed] [Google Scholar]
- 30.Engler A. J., et al. , “Embryonic cardiomyocytes beat best on a matrix with heart-like elasticity: scar-like rigidity inhibits beating,” J. Cell. Sci. 121, 3794–3802 (2008). 10.1242/jcs.029678 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wang S., et al. , “Biomechanical assessment of myocardial infarction using optical coherence elastography,” Biomed. Opt. Express 9, 728–742 (2018). 10.1364/BOE.9.000728 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kochegarov A., Lemanski L. F., “New trends in heart regeneration: a review,” J. Stem Cells Regener. Med. 12, P61–P68 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Manapuram R. K., Manne V. G. R., Larin K. V., “Phase-sensitive swept source optical coherence tomography for imaging and quantifying of microbubbles in clear and scattering media,” J. Appl. Phys. 105, 102040 (2009). 10.1063/1.3116614 [DOI] [Google Scholar]
- 34.Karpiouk A. B., et al. , “Assessment of shear modulus of tissue using ultrasound radiation force acting on a spherical acoustic inhomogeneity,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56, 2380–2387 (2009). 10.1109/TUFFC.2009.1326 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Karpiouk A. B., Wang B., Emelianov S. Y., “Development of a catheter for combined intravascular ultrasound and photoacoustic imaging,” Rev. Sci. Instrum. 81, 014901 (2010). 10.1063/1.3274197 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.VanderLaan D., et al. , “Real-time intravascular ultrasound and photoacoustic imaging,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 64, 141–149 (2017). 10.1109/TUFFC.2016.2640952 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zhang X., Qiang B., Greenleaf J. F., “Comparison of the surface wave method and the indentation method for measuring the elasticity of gelatin phantoms of different concentrations,” Ultrasonics 51, 157–164 (2011). 10.1016/j.ultras.2010.07.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ward S. R., Lieber R. L., “Density and hydration of fresh and fixed human skeletal muscle,” J. Biomech. 38, 2317–2320 (2005). 10.1016/j.jbiomech.2004.10.001 [DOI] [PubMed] [Google Scholar]
- 39.Kanai H., “Propagation of spontaneously actuated pulsive vibration in human heart wall and in vivo viscoelasticity estimation,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 52, 1931–1942 (2005). 10.1109/TUFFC.2005.1561662 [DOI] [PubMed] [Google Scholar]
- 40.Mo J., et al. , “Bias of shear wave elasticity measurements in thin layer samples and a simple correction strategy,” SpringlerPlus 5, 1341 (2016). 10.1186/s40064-016-2937-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Yin J., et al. , “Novel combined miniature optical coherence tomography ultrasound probe for in vivo intravascular imaging,” J. Biomed. Opt. 16, 060505 (2011). 10.1117/1.3589097 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kim Y., et al. , “Toward the development of a flexible mesoscale MRI-compatible neurosurgical continuum robot,” IEEE Trans. Rob. 33, 1386–1397 (2017). 10.1109/TRO.2017.2719035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Rump J., et al. , “Fractional encoding of harmonic motions in MR elastography,” Magn. Reson. Med. 57, 388–395 (2007). 10.1002/mrm.21152 [DOI] [PubMed] [Google Scholar]
- 44.Burns E., “QT interval life in the fastlane,” https://lifeinthefastlane.com/ecglibrary/basics/qt_interval (2017).
- 45.Baldewsing R. A., et al. , “Young’s modulus reconstruction of vulnerable atherosclerotic plaque components using deformable curves,” Ultrasound Med. Biol. 32, 201–210 (2006). 10.1016/j.ultrasmedbio.2005.11.016 [DOI] [PubMed] [Google Scholar]