Assessing Individual and Disseminated Effects in Network-Randomized Studies

Abstract

Implementation trials often involve clustering via risk networks, where only some participants directly receive the intervention. The individual effect is that among directly treated persons beyond being in an intervention network; the disseminated effect is that among persons engaged with those directly treated. In this article, we employ a causal inference framework and discuss assumptions and estimators for individual and disseminated effects and apply them to the HIV Prevention Trials Network 037 Study. HIV Prevention Trials Network 037 was a phase III, network-level, randomized controlled human immunodeficiency virus (HIV) prevention trial conducted in the United States and Thailand from 2002 to 2006 that recruited injection drug users, who were assigned to either an intervention group or a control group, and their risk network members, who received no direct intervention. Combining individual and disseminated effects, we observed a 35% composite rate reduction in the adjusted model (risk ratio = 0.65, 95% confidence interval: 0.47, 0.90). Methodology is now available for estimating the full set of these effects, enhancing knowledge gained from network-randomized trials. Although the overall effect gains validity from network randomization, we show that it will generally be less than the composite effect. Additionally, if only index participants benefit from the intervention, as the network size increases, the overall effect tends toward the null—an unfortunate and misleading conclusion.

The field of implementation science studies how best to translate and scale up research evidence into practice. These studies often involve a natural clustering by social network, facility, or community. In such network-randomized trials, only some members of networks randomized to the intervention arm directly receive the intervention. Individual and disseminated effects can be targets of inference. The disseminated or indirect effect is the impact of the intervention on the network members who were not directly exposed in the intervention networks. The individual or direct effect is the impact of the intervention on those who directly received the intervention, the index participants in intervention networks, beyond being an intervention network member. The composite effect is the effect of the intervention on index participants compared with network control members—that is, the maximal attainable benefit of the intervention. For example, a health-care professional may educate an index participant, also known as the ego, who then in turn may educate or otherwise influence members of his or her risk network, also known as the alter-egos, to modify their risky practices. In this setting, there is interest in the effect of the intervention on persons who were directly educated as well as those sharing risk networks with the index participant.

The terms individual and disseminated are used in this paper to avoid confusion with these terms used in the mediation literature, where direct effects and indirect effects are terms used to describe parameters addressing different scientific questions (1). We present a summary of the vernacular from relevant literature on the present topic and provide our recommended terms in Table 1. Compared with previous terminology, our terms are more agnostic to the relative magnitudes and desirability of dissemination.

Table 1.

Terminology for Estimation of Individual and Disseminated Effects in Network-Randomized Studies

Recommended Term	Alternative Term(s)	Definition	Parameter of Interest	Network-Randomized Design Estimator
				Aggregatea	Stratifiedb
Individual	Direct	Effect on persons directly receiving an intervention beyond being in an intervention network	$E{\left[Y_{kij}\left(1,1\right)\right]}^{\mathrm{c}}-E{\left[Y_{kij}\left(0,1\right)\right]}^{\mathrm{d}}$	${\hat{\mathrm{\gamma }}}_3$	${\hat{\mathrm{\alpha }}}_1-{\hat{\mathrm{\beta }}}_1$
Disseminated	Indirect, social diffusion, diffusion of innovation, contamination, spillover	Effect on persons who received an intervention indirectly through the index participant	$E[Y_{kij}(0,1)]-E{[Y_{kij}(0,0)]}^{\mathrm{e}}$	${\hat{\mathrm{\gamma }}}_2$	${\hat{\mathrm{\beta }}}_1$
Composite	Total	Combined individual and disseminated effects; effect among index members in intervention networks contrasted with effect among network members in control networks	$E[Y_{kij}(1,1)]-E[Y_{kij}(0,0)]$	${\hat{\mathrm{\gamma }}}_2+{\hat{\mathrm{\gamma }}}_3$	${\hat{\mathrm{\alpha }}}_1$
Overallf	Crude	Effect among members of intervention networks contrasted with effect among members of control networks	$E{\left[Y_{kij}(\cdot ,1)\right]}^{\mathrm{g}}-E{\left[Y_{kij}(\cdot ,0)\right]}^{\mathrm{h}}$	${\hat{\mathrm{\beta }}}_1^{⁎}$

Abbreviation: GEE, generalized estimating equation.

^a For a network-randomized design, rate difference parameters of the individual, disseminated, and composite effects, respectively, can be estimated from an aggregate GEE model with an identity link and binomial variance: $E\left[Y_{kij}|R_{ki},X_k,{\mathit{Z}}_{ki}\right]={\mathrm{\gamma }}_0+{\mathrm{\gamma }}_1{R}_{ki}+{\mathrm{\gamma }}_2{X}_k+{\mathrm{\gamma }}_3{X}_k{R}_{ki}+{\mathrm{\gamma }}_4{\mathit{Z}}_{ki}.$

^b For a network-randomized design, rate difference parameters of the individual, disseminated, and composite effects, respectively, can be estimated from a stratified GEE model with an identity link and binomial variance: $E\left[Y_{kij}|R_{ki},X_k,{\mathit{Z}}_{ki}\right]=I\left(R_{ki}=0\right)\times ({\mathrm{\beta }}_0+{\mathrm{\beta }}_1{X}_k+{\mathrm{\beta }}_2{\mathit{Z}}_{ki})+I\left(R_{ki}=1\right)\times ({\mathrm{\alpha }}_0+{\mathrm{\alpha }}_1{X}_k+{\mathrm{\alpha }}_2{\mathit{Z}}_{ki}).$

^c$Y_{kij}\left(1,1\right)$ is the potential outcome for participant $i$ at visit $j$ in network $k$, if, possibly contrary to fact, this participant was an index member in a network randomized to the intervention group. $E\left[X\right]$ is the expectation of the random variable $X$.

^d$Y_{kij}\left(0,1\right)$ is the potential outcome for participant $i$ at visit $j$ in network $k$, if, possibly contrary to fact, this participant was a network member in a network randomized to the intervention group.

^e$Y_{kij}\left(0,0\right)$ is the potential outcome for participant $i$ at visit $j$ in network $k$, if, possibly contrary to fact, this participant was a network member in a network randomized to the control group.

^f For a network-randomized design, the parameter of the overall effect is estimated from a GEE model with an identity link and binomial variance: $E[Y_{kij}|X_k]={\mathrm{\beta }}_0^{\ast }+{\mathrm{\beta }}_1^{\ast }{X}_k.$

^g$Y_{kij}\left(\cdot ,1\right)$ is the potential outcome for participant $i$ at visit $j$ in network $k$, if, possibly contrary to fact, this participant was in a network randomized to the intervention group.

^h$Y_{kij}\left(\cdot ,0\right)$ is the potential outcome for participant $i$ at visit $j$ in network $k$, if, possibly contrary to fact, this participant was in a network randomized to the control group.

In causal inference methodology, a fundamental assumption of much work is the stable unit treatment value assumption or SUTVA (2), which includes an assumption of no dissemination, or interference, between individuals. No dissemination requires that the potential outcomes for one individual are unaffected by the intervention assignment of other individuals. In this paper, the primary research interest is precisely in relaxing the no-dissemination assumption of the stable unit treatment value assumption and quantifying disseminated effects.

Earlier work on methods for assessing dissemination assumed 2-stage randomization, where networks were first randomized to an intervention allocation strategy and then, within a network, individuals were randomized according to their network’s allocation strategy (3, 4). Estimators of individual and disseminated effects were motivated by vaccine studies, where herd immunity is a good example of a disseminated effect (5, 6). Permutation-based variance estimators were developed for these doubly randomized designs (4). When a study is not doubly randomized, these estimators of individual and disseminated effects are no longer valid because of the potential for bias due to confounding at the network level, the individual level, or both. Tchetgen Tchetgen and VanderWeele (7) proposed inverse-probability–weighted estimators of individual and disseminated effects for studies in which randomization is not required at the individual or group level. This approach was applied to an individually randomized study of cholera vaccine, where individuals were clustered by groups of households (8). This approach was then applied to a study design with more than 1 index member and unequal treatment probabilities in the second stage (9).

In this paper, using multivariable outcome models rather than inverse-probability–weighted models, we develop alternative estimators of individual, disseminated, and composite causal effects for a setting with randomization only at the network level and 1 index participant per network, a study design frequently utilized in drug abuse and addiction research (10–12), and provide methods for asymptotic inference. We discuss the causal inference framework and assumptions for this setting. We prove some general results of interest in this setting that demonstrate the utility of the methods proposed. We apply these methods to a network-randomized human immunodeficiency virus (HIV) prevention trial in the HIV Prevention Trials Network (HPTN) (13–15) to obtain estimates of the individual, disseminated, composite, and overall intervention effects. Lastly, we discuss some limitations of this approach and identify future methodological directions for causal inference in network-randomized studies.

METHODS

Assumptions and notation

The sufficient conditions for valid estimation of causal effects have been previously described (16). We assume no dissemination between networks. Because the networks are randomized to the intervention group, on average, exchangeability at the network level holds. Networks randomized to the intervention group will be, on average, comparable to networks randomized to the control group. There is an additional exchangeability assumption that allows for valid estimation of all the parameters of interest in this setting. Within each network, conditional on a set of measured covariates, the potential outcomes of the voluntary index participants and nonindex network members are, on average, the same as those that would be expected if any other network member volunteered to be the index participant, regardless of whether the network was randomized to the intervention group or not. We call this conditional index exchangeability.

Let $K$ be the total number of networks, $k=1,\dots ,K$, with $i=1,\dots ,n_k$ participants in network k, where each participant i has $j=1,\dots ,m_{ki}$ visits and $\sum _{k=1}^K{n}_k=N$ is the total sample size of the study. Let ${\mathit{Z}}_{ki}$ be a vector of measured baseline covariates for participant $i$ in network k. Define $Y_{kij}$ as the outcome for the ith participant in the kth network at the jth visit. Let $X_k$ be the network-level intervention in network k assigned at the start of the trial and define an indicator $R_{ki}$ for the individual-level index status, where $R_{ki}=1$ if participant i in network k is an index participant, and $R_{ki}=0$otherwise. For example, investigators assign HIV risk networks to either train their index member to be a peer educator and provide all members with HIV counseling and testing or provide all members with HIV counseling and testing only. In network k, we have an $n_k$ vector of observed index status indicators ${\mathit{R}}_k=\left(R_{k1},R_{k2},\dots ,R_{k{n}_k}\right)$, constrained in this paper to $\sum _{i=1}^{n_k}{R}_{ki}=1$ and $n_k$ vectors of baseline covariates ${\mathit{Z}}_k=\left(Z_{k1},Z_{k2},\dots ,Z_{k{n}_k}\right)$. Each participant has potential outcomes ${\mathit{Y}}_{kij}(\mathit{r},x)$, which correspond to the $2\times n_k$ vector of potential outcomes for individual i in network k at time j under the index status indicator vector ${\mathit{R}}_k=\mathit{r}$ and intervention assignment $X_k=x$. Because an individual’s potential outcomes depend on the network-level intervention, dissemination is possible in this setting. A contrast between any 2 of these potential outcomes is a measure of a causal effect. For example, a representation of the individual causal effect in an intervention network where the second participant was the index member compared with one where the last participant was the index member is

$$E\left\{{\mathit{Y}}_{kij}\left[\left(0,1,\dots 0\right),1\right]\right\}-E\left\{{\mathit{Y}}_{kij}\left[\left(0,0,\dots 1\right),1\right]\right\}.$$

Because the number of index members in network k is fixed to 1 by design, there are $J_k=\left(\begin{array}{c}{n}_k\\ 1\end{array}\right)=n_k$ possible configurations of index participants in each network k. In general, each network member has $2\times n_k$ potential outcomes, with $n_k$ corresponding to intervention status and $n_k$ corresponding to control status. With these many potential outcomes within networks, it is difficult to choose the causal effects of interest. Conditional on baseline covariates, we assume that there is exchangeability between the $2\times n_k$ possible configurations when there is 1 index participant in network k; that is, $Y_{kij}\left(\mathit{r},x\right)\perp {\mathit{R}}_k|{\mathit{Z}}_k$. Baseline covariates are sufficient to control for confounding of the effect of self-selected index status on the outcome. Because there is only 1 index participant per network, we can validly denote the potential outcomes by $R_{ki}=r$ and $X_k=x$. Under these circumstances, the number of potential outcomes for each participant, $Y_{kij}\left(r,x\right),$ is reduced to 4—that is, 2 for each of the 2 possible network-level intervention assignments, $Y_{kij}(1,1),Y_{kij}(1,0),Y_{kij}(0,1),\mathrm{and}{Y}_{kij}(0,0)$. For example, let $Y_{kij}(1,1)$ be the potential outcome for participant i at visit j in network k, if, possibly contrary to fact, this participant was an index member in a network randomized to the intervention.

Causal framework and estimands

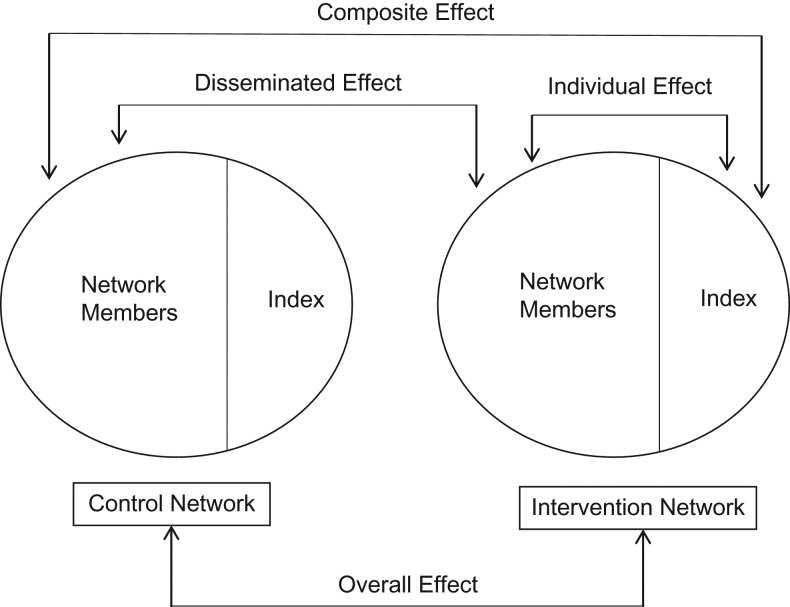
The individual effect is defined as the effect of the intervention among index members in intervention networks beyond being in an intervention network (Figure 1)—that is, ${\mathrm{risk}/\mathrm{rate\; difference}}^I\left({\mathrm{RD}}^I\right)=E\left[Y_{kij}\left(1,1\right)\right]-E\left[Y_{kij}\left(0,1\right)\right]$. The disseminated effect is defined as the intervention effect among the nonindex network members—that is, ${\mathrm{RD}}^D=E\left[Y_{kij}\left(0,1\right)\right]-E\left[Y_{kij}(0,0)\right]$. Composite and overall effects combine the individual and disseminated effects in 2 different ways. The composite effect is the sum of the disseminated and

Figure 1.

Subsets of data used for each estimator (individual, disseminated, composite, and overall) of individual and disseminated effects in network-randomized studies. Based on a format provided Halloran and Struchiner (5).

individual effects—that is,

$$\begin{array}{ll}{\mathrm{RD}}^{\mathrm{Comp}}\hfill & =E\left[Y_{kij}\left(1,1\right)\right]-E\left[Y_{kij}\left(0,1\right)\right]\hfill \\ \hfill & +\left\{E\left[Y_{kij}\left(0,1\right)\right]-E\left[Y_{kij}\left(0,0\right)\right]\right\}\hfill \\ \hfill & =E\left[Y_{kij}\left(1,1\right)\right]-E\left[Y_{kij}\left(0,0\right)\right].\hfill \end{array}$$

The composite effect is the maximum possible effect of the intervention—that is, the effect of being an index member in an intervention network compared with being a network member in a control network.

The overall effect is the average effect among all intervention network members compared with all control network members. In Web Appendix 1 (available at https://academic.oup.com/aje), we derive the parametric relationship between the individual and disseminated effects and the overall effect, and we show that when network sizes vary,

$$\begin{array}{ll}{\mathrm{RD}}^{\mathrm{Overall}}\hfill & =E\left[Y_{kij}(\cdot ,1)\right]-E\left[Y_{kij}\left(\cdot ,0\right)\right]\hfill \\ \hfill & ={\mathrm{RD}}^D+{\mathrm{RD}}^I\times E_R[R_{ki}]={\mathrm{RD}}^D+{\mathrm{RD}}^I\times \frac{K}{N},\hfill \end{array}$$

which will always be smaller than ${\mathrm{RD}}^{\mathrm{Comp}}={\mathrm{RD}}^D+{\mathrm{RD}}^I$ as long as ${\mathrm{RD}}^I$ and ${\mathrm{RD}}^D$ have the same sign, as would typically be the case. When network sizes are constant with $n_k=n$ for all $k$, ${\mathrm{RD}}^{\mathrm{Overall}}={\mathrm{RD}}^D+{\mathrm{RD}}^I\times \frac{1}{n}$. When the sign differs, the overall effect will be smaller than the composite only in certain cases. For example, if the average network size is 3, ${\mathrm{RD}}^I=1$, and ${\mathrm{RD}}^D=-3$, then ${\mathrm{RD}}^{\mathrm{Comp}}=-2$, which is smaller than ${\mathrm{RD}}^{\mathrm{Overall}}=-2.67$. It is typically not expected for individual and disseminated effects to be in opposite directions, but it is technically possible. Because the overall effect depends on spurious features of the study design, including the size of the networks and the number of index members, it will not be generalizable from one study to the next or to any scaled-up population, unless these features remain constant.

When there is no disseminated effect, the overall effect will always be less than or equal to the composite effect. We also show that the overall effect will equal the composite effect only when the individual effect is null, a rather unlikely occurrence in our motivational setting. In Web Appendix 1, we additionally show properties for the relationship between the overall risk ratio and the composite risk ratio.

In Web Appendix 2, we illustrate these relationships through some numerical studies motivated by HPTN 037. If the individual and disseminated effects are in the same direction, the magnitude of the overall effect decreases as the network size increases. In the extreme, when there is no disseminated effect, the overall effect will approach the null as the network size increases, while the composite effect remains constant.

Estimation and inference for individual and disseminated effects

In network-randomized trials, the overall effect estimate has an immediate causal interpretation. In contrast, index status is not randomized. The index participants are recruited and then the remaining network members are recruited by the index participant. Hence, the individual, disseminated, and composite effects only have a causal interpretation when the estimator is fully adjusted for confounding.

Generalized estimating equations (GEEs) (17) with a log link and working binomial variance can be used to estimate relative risks or rates, and an identity link and working binomial variance can be used to estimate risk or rate differences and their confidence intervals adjusted for confounding (18, 19). These models also adjust the estimated parameter variances for correlation within networks and, if the data are longitudinal, across visits within a participant. For log and identity links as employed in this paper, the conditional and marginal model parameters of interest are equivalent, because the conditional mean is additive for the fixed and random effects; thus, the estimated effects can be interpreted as participant-level estimates and/or population-level estimates (20).

One way to estimate these parameters is by using an aggregate model. Assuming that the effects of the covariates ${\mathit{Z}}_{ki}$ are not modified by index status $R_{ki}$ and that the linear model with the identity link fits the data, let

$$E\left[Y_{kij}|R_{ki},X_k,{\mathit{Z}}_{ki}\right]={\mathrm{\gamma }}_0+{\mathrm{\gamma }}_1{R}_{ki}+{\mathrm{\gamma }}_2{X}_k+{\mathrm{\gamma }}_3{X}_k{R}_{ki}+{\mathrm{\gamma }}_4{\mathit{Z}}_{ki}.$$

It follows that the effect of being an index member in a control network is

$$\begin{array}{c}E\left[Y_{kij}|R_{ki}=1,X_k=0,{\mathit{Z}}_{ki}\right]\hfill \\ -E\left[Y_{kij}|R_{ki}=0,X_k=0,{\mathit{Z}}_{ki}\right]={\mathrm{\gamma }}_1.\hfill \end{array}$$

In a network-randomized trial, there could be residual confounding even after adjusting for covariates ${\mathit{Z}}_{ki}$, so subtracting these terms accounts for possible unmeasured confounding due to self-selection of index status when estimating individual and composite effects (21, 22). Thus, the individual RD can be estimated by

$$\begin{array}{ll}{\widehat{\mathrm{RD}}}_a^I\hfill & =\hat{E}\left[Y_{kij}|R_{ki}=1,X_k=1,{\mathit{Z}}_{ki}\right]\hfill \\ \hfill & -\hat{E}\left[Y_{kij}|R_{ki}=0,X_k=1,{\mathit{Z}}_{ki}\right]\hfill \\ \hfill & -\{\hat{E}\left[Y_{kij}|R_{ki}=1,X_k=0,{\mathit{Z}}_{ki}\right]\hfill \\ \hfill & -\hat{E}\left[Y_{kij}|R_{ki}=0,X_k=0,{\mathit{Z}}_{ki}\right]\}\hfill \\ \hfill & ={\hat{\mathrm{\gamma }}}_0+{\hat{\mathrm{\gamma }}}_1+{\hat{\mathrm{\gamma }}}_2+{\hat{\mathrm{\gamma }}}_3+{\hat{\mathrm{\gamma }}}_4{\mathit{Z}}_{ki}\hfill \\ \hfill & -\left({\hat{\mathrm{\gamma }}}_0+{\hat{\mathrm{\gamma }}}_2+{\hat{\mathrm{\gamma }}}_4{\mathit{Z}}_{ki}\right)-{\hat{\mathrm{\gamma }}}_1={\hat{\mathrm{\gamma }}}_3.\hfill \end{array}$$

When estimating the disseminated effect, only information from nonindex network members is included; therefore, residual confounding of $R_{ki}$ is not a concern. Adjustment for observed baseline covariates ${\mathit{Z}}_{ki}$ is needed because randomization in the full study sample does not necessarily guarantee exchangeability of $X_k$ within subgroups of participants. The disseminated RD can be estimated by

$$\begin{array}{ll}{\widehat{\mathrm{RD}}}_a^D\hfill & =\hat{E}\left[Y_{kij}|R_{ki}=0,X_k=1,{\mathit{Z}}_{ki}\right]\hfill \\ \hfill & -\hat{E}\left[Y_{kij}|R_{ki}=0,X_k=0,{\mathit{Z}}_{ki}\right]\hfill \\ \hfill & ={\hat{\mathrm{\gamma }}}_0+{\hat{\mathrm{\gamma }}}_2+{\hat{\mathrm{\gamma }}}_4{\mathit{Z}}_{ki}-({\hat{\mathrm{\gamma }}}_0+{\hat{\mathrm{\gamma }}}_4{\mathit{Z}}_{ki})={\hat{\mathrm{\gamma }}}_2.\hfill \end{array}$$

Similarly, the composite RD can be estimated by

$$\begin{array}{ll}{\widehat{\mathrm{RD}}}_a^{\mathrm{Comp}}\hfill & =\hat{E}\left[Y_{kij}|R_{ki}=1,X_k=1,{\mathit{Z}}_{ki}\right]\hfill \\ \hfill & -\hat{E}\left[Y_{kij}\right|R_{ki}=0,X_k=0,{\mathit{Z}}_{ki}]\hfill \\ \hfill & -\{\hat{E}\left[Y_{kij}|R_{ki}=1,X_k=0,{\mathit{Z}}_{ki}\right]\hfill \\ \hfill & -\hat{E}\left[Y_{kij}|R_{ki}=0,X_k=0,{\mathit{Z}}_{ki}\right]\}\hfill \\ \hfill & ={\hat{\mathrm{\gamma }}}_0+{\hat{\mathrm{\gamma }}}_1+{\hat{\mathrm{\gamma }}}_2+{\hat{\mathrm{\gamma }}}_3+{\hat{\mathrm{\gamma }}}_4{\mathit{Z}}_{ki}\hfill \\ \hfill & -\left({\hat{\mathrm{\gamma }}}_0+{\hat{\mathrm{\gamma }}}_4{\mathit{Z}}_{ki}\right)-{\hat{\mathrm{\gamma }}}_1={\hat{\mathrm{\gamma }}}_2+{\hat{\mathrm{\gamma }}}_3.\hfill \end{array}$$

Alternatively, if the effects of covariates ${\mathit{Z}}_{ki}$ differ by index status $R_{ki}$, a stratified model could be used (Web Appendix 3). The estimators of the risk or rate ratio of the 3 effects of interest are defined analogously and can be estimated using a GEE with a log link and a working binomial variance. SAS code provided in Web Appendix 4 demonstrates how to obtain these estimates and their corresponding variances. Analyses were performed using SAS, version 9.4 (SAS Institute, Inc., Cary, North Carolina).

Illustrative example

The HPTN 037 Study (23) was a phase III randomized controlled HIV-preventive intervention trial among people who inject drugs in the United States and Thailand (13). Following a network-randomized design, the index participants were eligible if they reported having injected drugs at least 12 times in the past 3 months, while the network members had to have injected drugs or had sex with the index member within the past 3 months. This study assessed the efficacy of a network-oriented peer education intervention in promoting HIV risk reduction behaviors among people who injected drugs. Participants were followed for up to 30 months with biannual visits (2002–2006), with a median follow-up time of 18 months (quartile 1 = 6 months; quartile 3 = 24 months), to obtain information on HIV incidence and risk behaviors. The study was underpowered for the primary outcome, HIV incidence, so this analysis focused on the occurrence of reported HIV risk behaviors. The study was carried out at 2 sites: Chiang Mai, Thailand, and Philadelphia, Pennsylvania. At the time of the study, there was a “war on drugs” in Thailand, which may have reduced trust among people who injected drugs, possibly making the intervention less effective. Therefore, following the recommendation of the study investigators (Carl Latkin, Johns Hopkins Bloomberg School of Public Health, personal communication, 2016), this analysis only included participants at the Philadelphia site. Index participants whose network was randomized to the intervention arm received an educational intervention at baseline and education boosters at 6 and 12 months. Participants in both the intervention and control arms received HIV counseling and testing at each study visit. In the primary analysis of this trial, Latkin et al. (13) reported the overall effect estimated by a 2-level GEE that accounted for correlations between participants within a network and between visits within participants.

Shared cotton, an indicator variable for sharing needle/syringe “works,” was selected as an outcome because it nicely exemplified our methods. A more comprehensive clinical outcome measure, any injection-related risk behavior, included the following: sharing injection equipment (needles, “cookers,” cotton, and rinse water), front- and back-loading (i.e., injecting drugs from one syringe to another), injecting drugs with people one did not know well or in a “shooting gallery,” and not properly disinfecting injection equipment. Following the original analysis of this study, these outcomes were assessed among participants who reported having injected drugs in the last 6 months at baseline. Statistical tests comparing the prevalences of risk behaviors at baseline between network and index members were performed using a GEE model that accounted for within-network correlation.

First, the cumulative incidence of ever reporting the outcome by 30 months of follow-up was analyzed using GEEs to account for correlations within networks, using the robust sandwich estimator with a working exchangeable correlation matrix (24, 25). Next, the longitudinal data were used to assess the effects of the intervention on the intervisit incidence rates of sharing “works” and of any injection-related risk behavior using a multilevel GEE model. For estimation of the individual and disseminated effects, these models were adjusted for baseline covariates that were known or suspected risk factors for the outcome. For a few outcomes, the models did not converge and log Poisson models, which provide consistent but not fully efficient estimates of the relative risk, were used (26, 27). All statistical tests performed were 2-sided.

RESULTS

At the Philadelphia site of the HPTN 037 trial, there were 696 participants, and 560 participants had at least 1 follow-up visit, with a total of 1,598 person-visits. At this site, 336 participants (48%) were in intervention networks (Table 2). At baseline, participants in intervention networks had a comparable prevalence of reported injection drug risk behavior in the past month (84%) as those in control networks (86%); however, index participants reported more risk behaviors at baseline (89%) than network members did (84%; P = 0.07).

Table 2.

Baseline Characteristics (%) of Participants in the HIV Prevention Trials Network 037 Study (n = 696), by Treatment Group, Philadelphia, Pennsylvania, 2002–2006

Characteristic	Network Randomizationa
	Intervention Network (n = 336)	Control Network (n = 360)
Individual participant’s role
Index participant	33	33
Network member	67	67
Network sizeb	3 (1.27)	3 (1.04)
Male sex	68	69
Age, yearsb	41 (10)	40 (10)
Participation in a drug treatment programc	22	32
Housingc
Spending the night on the street or in a car, park, or abandoned building	25	24
Spending any time in jail	19	15
Sexual risk behaviord
More than 1 sex partner	42	40
Unprotected sex in the past week	50	50
Unprotected sex with nonprimary partner	16	19
Injection drug use behaviore
Injection drug use
Past 6 months	93	94
Past month	99	97
Heroin	94	96
Heroin with cocaine	42	35
Heroin with amphetamine	1	1
Cocaine	37	37
Amphetamine	2	2
No. of days on which drugs were injected in past month
0–5	9	9
6–14	8	9
15–29	24	16
Every day	59	65
Injection risk behaviors in past monthf
Shared rinse water	44	51
Shared cooker	57	62
Shared cotton	41	46
Used a front- or back-loaded syringe	21	23
Injected with an unclean syringe	13	15
Passed a syringe to someone else	48	53
Used a syringe after someone else	37	39
Injected with someone one did not know well	19	22
Injected in a shooting gallery	61	56
Did not clean syringe after use	14	13

Abbreviation: HIV, human immunodeficiency virus.

^a There were 112 intervention networks and 120 control networks. Values for polytomous variables may not sum to 100% because of rounding.

^b Values are expressed as mean (standard deviation).

^c In the past 6 months.

^d In the past month.

^e Injection drug use behaviors are reported only for participants reporting injection drug use in the past 6 months.

^f Injection risk behaviors are reported only for participants reporting injection drug use in the past month.

Table 3 presents the cumulative incidence of the risk behavior sharing “works” and any report of injection-related risk behavior. Table 4 presents the results for the effect of the intervention on the risk of each outcome by 30 months after baseline. For both outcomes, there was no evidence that the stratified model fitted better than the aggregate model on either scale based on an informal comparison of the log likelihoods. Tables 5 and 6 display the results of 6-month intervisit incidence rate differences and ratios for sharing “works” and any report of injection-related risk behavior from the longitudinal data. Based on an informal comparison of the log likelihoods, the stratified model was a better fit than the aggregate model on the ratio scale for both outcomes and on the difference scale for the any-report outcome only.

Table 3.

Cumulative Incidence of Ever Reporting Drug-Injection–Related Risk Behavior by 30 Months After Baseline Among Participants in the HIV Prevention Trials Network 037 Study (n = 651), Philadelphia, Pennsylvania, 2002–2006

Network Randomization	Index Participants			Network Participants
	Total No. of Persons	Reported No. of Persons	30-Month Cumulative Incidence, %	Total No. of Persons	Reported No. of Persons	30-Month Cumulative Incidence, %
Any shared works
Treatment group	112	10	9	202	28	14
Control group	120	24	20	217	42	19
Combined controla	337	66	20
Any risk behavior
Treatment group	112	48	43	202	75	37
Control group	120	58	48	217	97	45
Combined controla	337	155	46

Abbreviation: HIV, human immunodeficiency virus.

^a Both index members and network participants in control networks.

Table 4.

Effects of the Intervention on the Risk of Ever Reporting Drug-Injection–Related Risk Behavior by 30 Months After Baseline Among Participants in the HIV Prevention Trials Network 037 Study (n = 651), Philadelphia, Pennsylvania, 2002–2006

Effect	Stratified Models								Aggregate Models
	Unadjusted		Adjusteda		Unadjusted		Adjusteda		Unadjusted		Adjusteda		Unadjusted		Adjusteda
	RDb	95% CI	RDb	95% CI	RR	95% CI	RR	95% CI	RDb	95% CI	RDb	95% CI	RR	95% CI	RR	95% CI
Any shared “works”
Individual	−5	−16, 7	−7	−20, 5	0.65	0.28, 1.51	0.47	0.18, 1.21	−5	−16, 6	−8	−19, 3	0.65	0.28, 1.47	0.52	0.23, 1.15
Disseminated	−6	−14, 1	−5	−13, 2	0.69	0.42, 1.13	0.75	0.45, 1.25	−6	−14, 1	−5	−13, 3	0.69	0.42, 1.14	0.76	0.46, 1.25
Composite	−11	−20, −2	−13	−22, −3	0.45	0.22, 0.89	0.35	0.16, 0.78	−11	−20, −2	−13	−22, −4	0.45	0.22, 0.89	0.39	0.20, 0.78
Overall	−8	−14, −2	−8	−14, −2	0.60	0.39, 0.92	0.61	0.39, 0.94	−8	−14, −2	−8	−14, −2	0.60	0.39, 0.92	0.61	0.39, 0.94
Any risk behaviorc
Individual	2	−14, 18	0	−18, 17	1.07	0.73, 1.56	0.99	0.68, 1.45	2	−13, 18	0	−16, 15	1.07	0.76, 1.53	0.97	0.68, 1.39
Disseminated	−8	−18, 2	−5	−16, 5	0.83	0.64, 1.07	0.88	0.69, 1.13	−8	−18, 2	−7	−17, 4	0.83	0.64, 1.06	0.85	0.66, 1.10
Composite	−5	−18, 7	−6	−20, 8	0.89	0.67, 1.18	0.88	0.66, 1.16	−5	−18, 7	−7	−20, 6	0.89	0.67, 1.18	0.83	0.62, 1.10
Overall	−7	−15, 1	−7	−16, 2	0.85	0.69, 1.04	0.85	0.69, 1.04	−7	−15, 1	−7	−16, 2	0.85	0.69, 1.04	0.85	0.69, 1.04

Abbreviations: CI, confidence interval; HIV, human immunodeficiency virus; RD, risk difference; RR, risk ratio.

^a Adjusted for sex (male vs. female), age (years), marital status (single vs. not single), education (high school or more vs. not completing high school), and employment (unemployed vs. employed) and for time-varying covariates set to their baseline values: “crack” cocaine use (yes vs. no), powdered cocaine use (yes vs. no), benzodiazepine use (yes vs. no), heroin use (yes vs. no), participation in a drug treatment program in the past 6 months (yes vs. no), spent the night on the street in the past 6 months (yes vs. no), spent time in jail in the past 6 months (yes vs. no), frequency of excessive alcohol use (getting drunk vs. not), injected heroin in the past month (yes vs. no), injected both heroin and cocaine in the past month (yes vs. no), injected cocaine in the past month (yes vs. no), and number of days of injecting drugs in the past month (≤5 days, 6–14 days, or 15–29 days vs. every day).

^b Per 100 persons.

^c For the outcome “any risk behavior,” on the ratio scale the model excluded the “number of days injected” variable because of model convergence issues. Models for the overall effect also excluded having injected cocaine. The stratified model for individual, disseminated, and composite effects also excluded having spent time in jail, heroin use, and having injected cocaine.

Table 5.

Six-Month Intervisit Incidence Rate Ratios and Rate Differences for the Effect of the Randomized Intervention on the Rate of Sharing “Works” During Follow-up Among Participants With at Least 1 Follow-up Visit, HIV Prevention Trials Network 037 Study, Philadelphia, Pennsylvania, 2002–2006

Intervention	Unadjusted				Baseline-Adjusteda,b
	RR	95% CI	RDc	95% CI	RR	95% CI	RDc	95% CI
Stratified Models
Individuald	0.58	0.23, 1.48	−0.05	−0.14, 0.04	0.41	0.16, 1.06	−0.08	−0.18, 0.01
Disseminatede	0.66	0.38, 1.12	−0.04	−0.09, 0.02	0.59	0.36, 0.97	−0.04	−0.09, 0.02
Compositef	0.38	0.18, 0.81	−0.09	−0.16, −0.02	0.24	0.11, 0.55	−0.12	−0.19, −0.05
Overallg	0.56	0.35, 0.89	−0.05	−0.10, −0.01	0.52	0.32, 0.83	−0.06	−0.11, −0.01
Aggregate Models
Individual	0.56	0.25, 1.26	−0.06	−0.13, 0.02	0.55	0.25, 1.19	−0.08	−0.15, 0.00
Disseminated	0.69	0.04, 1.17	−0.03	−0.09, 0.02	0.64	0.38, 1.08	−0.03	−0.09, 0.02
Composite	0.39	0.18, 0.81	−0.09	−0.16, −0.02	0.35	0.17, 0.73	−0.11	−0.18, −0.04
Overall	0.56	0.35, 0.89	−0.05	−0.10, −0.01	0.52	0.32, 0.83	−0.06	−0.11, −0.01

Abbreviations: CI, confidence interval; HIV, human immunodeficiency virus; RD, rate difference; RR, rate ratio.

^a Adjusted for sex (male vs. female), age (years), marital status (single vs. not single), education (high school or more vs. not completing high school), and employment (unemployed vs. employed) and for time-varying covariates set to their baseline values: “crack” cocaine use (yes vs. no), powdered cocaine use (yes vs. no), benzodiazepine use (yes vs. no), heroin use (yes vs. no), participation in a drug treatment program in the past 6 months (yes vs. no), spent the night on the street in the past 6 months (yes vs. no), spent time in jail in the past 6 months (yes vs. no), frequency of excessive alcohol use (getting drunk vs. not), injected heroin in the past month (yes vs. no), injected both heroin and cocaine in the past month (yes vs. no), injected cocaine in the past month (yes vs. no), and number of days of injecting drugs in the past month (≤5 days, 6–14 days, or 15–29 days vs. every day).

^b One participant was missing information on spending the night on the street (in the past 6 months) and spending time in jail (in the past 6 months) at baseline.

^c Per 100 person-visits.

^d There were 58 events, 782 person-visits, and 270 people included.

^e There were 158 events, 1,319 person-visits, and 463 people included.

^f There were 132 events, 1,095 person-visits, and 387 people included.

^g There were 174 events, 1,598 person-visits, and 560 people included.

Table 6.

Six-Month Intervisit Incidence Rate Ratios and Rate Differences for the Effect of the Randomized Intervention on the Rate of Any Drug-Injection–Related Risk Behavior During Follow-up Among Participants With at Least 1 Follow-up Visit, HIV Prevention Trials Network 037 Study, Philadelphia, Pennsylvania, 2002–2006

Intervention	Unadjusted				Baseline-Adjusteda,b
	RR	95% CI	RDc	95% CI	RR	95% CI	RDc	95% CI
Stratified Models
Individuald	0.97	0.64, 1.48	−0.02	−0.15, 0.12	0.92	0.60, 1.40	−0.06	−0.19, 0.07
Disseminatede	0.73	0.55, 0.97	−0.09	−0.17, 0.00	0.71	0.54, 0.93	−0.08	−0.16, −0.01
Compositef	0.71	0.52, 0.97	−0.10	−0.21, 0.00	0.65	0.47, 0.90	−0.14	−0.24, −0.03
Overallg	0.72	0.57, 0.90	−0.09	−0.16, −0.02	0.69	0.56, 0.86	−0.09	−0.16, −0.03
Aggregate Models
Individual	0.96	0.67, 1.39	−0.02	−0.14, 0.10	0.91	0.62, 1.33	−0.05	−0.17, 0.07
Disseminated	0.75	0.57, 0.98	−0.08	−0.16, 0.00	0.72	0.55, 0.94	−0.08	−0.16, 0.01
Composite	0.72	0.53, 0.98	−0.10	−0.21, 0.01	0.65	0.47, 0.90	−0.13	−0.23, −0.02
Overall	0.72	0.57, 0.90	−0.09	−0.16, −0.02	0.69	0.56, 0.86	−0.09	−0.16, −0.03

Abbreviations: CI, confidence interval; HIV, human immunodeficiency virus; RD, rate difference; RR, rate ratio.

^a Adjusted for sex (male vs. female), age (years), marital status (single vs. not single), education (high school or more vs. not completing high school), and employment (unemployed vs. employed) and for time-varying covariates set to their baseline values: “crack” cocaine use (yes vs. no), powdered cocaine use (yes vs. no), benzodiazepine use (yes vs. no), heroin use (yes vs. no), participation in a drug treatment program in the past 6 months (yes vs. no), spent the night on the street in the past 6 months (yes vs. no), spent time in jail in the past 6 months (yes vs. no), frequency of excessive alcohol use (getting drunk vs. not), injected heroin in the past month (yes vs. no), injected both heroin and cocaine in the past month (yes vs. no), injected cocaine in the past month (yes vs. no), and number of days of injecting drugs in the past month (≤5 days, 6–14 days, or 15–29 days vs. every day).

^b One participant was missing information on spending the night on the street (in the past 6 months) and spending time in jail (in the past 6 months) at baseline.

^c Per 100 person-visits.

^d There were 204 events, 782 person-visits, and 270 people included.

^e There were 433 events, 1,319 person-visits, and 463 people included.

^f There were 381 events, 1,095 person-visits, and 387 people included.

^g There were 509 events, 1,598 person-visits, and 560 people included.

There was a significant 40% overall reduction on the ratio scale (95% confidence interval (CI): 8, 61) for the risk of ever sharing “works” by 30 months after baseline (Table 4). In contrast, there was a substantially larger, significant 61% reduction on the ratio scale in the adjusted composite risk of ever sharing “works” due to the intervention (95% CI: 22, 80). The individual effect was nearly twice as large as the disseminated effect (risk ratios were 0.52 and 0.76, respectively).

In the longitudinal data, the overall intervention effect was significantly protective, with a 44% rate reduction on the ratio scale (95% CI: 11, 65) for sharing “works” (Table 5). Based on the adjusted stratified models, a significant protective effect was observed among network members, with a 41% rate reduction on the ratio scale (95% CI: 3, 64) and a somewhat greater 59% individual rate reduction (95% CI: 6, 84). A significant 76% composite adjusted rate reduction on the ratio scale was observed (95% CI: 45, 89).

For the risk of ever making any report of injection risk behavior by 30 months, there was a nearly null individual effect, while the disseminated effect showed some suggestion of protection (Table 4). In the adjusted aggregate models, there was a non–statistically significant 17% reduction on the ratio scale in the composite risk of any report due to the intervention (95% CI: 10, 38) and a comparable overall risk reduction (Table 4). The longitudinal analysis of the “any injection-related risk behavior” outcome demonstrated a statistically significant protective overall effect, with a 28% rate reduction on the ratio scale (95% CI: 10, 43) (Table 6). Based on the adjusted stratified models, the intervention provided a 29% rate reduction on the ratio scale among network members (95% CI: 7, 46), but the individual effect did not achieve statistical significance (rate ratio = 0.92, 95% CI: 0.60, 1.40). A significant 35% adjusted composite rate reduction on the ratio scale for any behavior was observed (95% CI: 10, 53). As a sensitivity analysis, we used a compound symmetrical correlation matrix within a network between subjects and a first-order autoregressive correlation matrix within-subject over time; the results were comparable to those reported in Tables 5 and 6.

DISCUSSION

In this paper, we developed estimators for individual and disseminated effects in network-randomized trials. Because networks were randomized to the intervention, the overall effect estimate has a causal interpretation. However, the overall effect is influenced by ancillary factors, such as the size of the networks, and will typically underestimate the composite effect (see Web Appendices 1 and 2). When there is no unmeasured confounding and the model is correctly specified, individual and disseminated effect estimates also have causal interpretations and provide a more in-depth understanding of the intervention’s impact.

In the HPTN 037 trial, the overall effect of the intervention was statistically significant, with an estimated 28% reduction in risk of any injection-related risk behavior; however, although there was evidence for a significant 29% disseminated risk reduction, the individual effect did not achieve statistical significance for that same outcome. The original investigators reported only the overall effects (13), which we found were slightly to moderately attenuated compared with the composite effects, which reveal the full power of the intervention. Somewhat surprisingly, the disseminated effect was stronger than the individual effect for the report of any injection-related risk behavior, suggesting that this intervention has substantial resonance within the network beyond the effect of directly receiving the intervention. Without consideration of dissemination, efforts to understand the full array of mechanisms by which the intervention achieved its goal would likely be overlooked.

The assumption of no unmeasured covariates associated with the treatment and outcome (or with the index status and outcome) cannot be empirically verified. For example, in HPTN 037, an individual’s unmeasured communication skills may affect whether or not he or she comes forward to be an index, and this may lead to unmeasured differences between index and nonindex members. Future work could involve extensions to address unmeasured confounding when evaluating disseminated effects. In addition, the methods for incidence rate measures assume that there is no bias due to dependent loss to follow-up, and in the longitudinal analysis, the missing visit process is ignorable (i.e., missing a visit is independent of the outcome conditional on intervention status and observed baseline covariates). If this assumption is questionable, censoring weights could be employed in the analysis (28, 29). These methods assume no dissemination between networks, although it is possible in some settings that some network members will be in the risk networks of more than 1 index member. In HPTN 037, indexes may interact with participants outside of their observed risk network because they may frequent the same neighborhoods and venues. These methods could thus be extended to accommodate dissemination between networks as well as within networks. In the HPTN 037 trial, effect modification was observed for sex and participation in a drug treatment program. Future work could entail estimation of these within-stratum effects and an application of such methods as g-estimation to ascertain population-level effects (30).

These methods could also be extended to correct for bias due to misclassification or measurement error in the self-reported outcome or covariates (31). We assume that the reported effect estimates are not subject to social desirability effects, which could vary by intervention arm over time, and dissemination may reinforce this. Furthermore, the indexes may have underreported risk connections or study investigators may have missed some networks entirely. More accurate ways to elicit and recruit network member nominations and contact information could be developed, and methods to infer unobserved or misclassified risk and social connections could be improved.

A network-based program can be implemented at a reduced cost, because only a subset of participants needs to receive the intervention. The example highlights the need for methods to adequately power trials to assess individual and disseminated effects. Future work could include evaluating the disseminated effects of treatment as prevention and similar interventions in HIV trials, including extensions for networks with more than 1 index participant (32–36). Extension of these methods to estimate both individual and disseminated effects of the components of multifaceted interventions is needed for future complex HIV implementation science research, particularly that engaging drug-user or sexual risk networks.

Abbreviations

CI

confidence interval

GEE

generalized estimating equation

HIV

human immunodeficiency virus

HPTN

HIV Prevention Trials Network

RD

risk/rate difference