Anisotropic Composite Material Phantom to Improve Skeletal Muscle Characterization Using Magnetic Resonance Elastography

Abstract

The presence and progression of neuromuscular pathology, including spasticity, Duchenne’s muscular dystrophy and hyperthyroidism, has been correlated with changes in the intrinsic mechanical properties of skeletal muscle tissue. Tools for noninvasively measuring and monitoring these properties, such as Magnetic Resonance Elastography (MRE), could benefit basic research into understanding neuromuscular pathologies, as well as translational research to develop therapies, by providing a means of assessing and tracking their efficacy. Dynamic elastography methods for noninvasive measurement of tissue mechanical properties have been under development for nearly three decades. Much of the technological development to date, for both Ultrasound (US)-based and Magnetic Resonance Imaging (MRI)-based strategies, has been grounded in assumptions of local homogeneity and isotropy. Striated skeletal and cardiac muscle, as well as brain white matter and soft tissue in some other organ regions, exhibit a fibrous microstructure which entails heterogeneity and anisotropic response; as one seeks to improve the accuracy and resolution in mechanical property assessment, heterogeneity and anisotropy need to be accounted for in order to optimize both the dynamic elastography experimental protocol and the interpretation of the measurements. Advances in elastography methodology at every step have been aided by the use of tissue-mimicking phantoms. The aim of the present study was to develop and characterize a heterogeneous composite phantom design with uniform controllable anisotropic properties meant to be comparable to the frequency-dependent anisotropic properties of skeletal muscle. MRE experiments and computational finite element (FE) studies were conducted on a novel 3D-printed composite phantom design. The displacement maps obtained from simulation and experiment show the same elliptical shaped wavefronts elongated in the plane where the structure presents higher shear modulus. The model exhibits a degree of anisotropy in line with literature data from skeletal muscle tissue MRE experiments. FE simulations of the MRE experiments provide insight into proper interpretation of experimental measurements, and help to quantify the importance of heterogeneity in the anisotropic material at different scales.

Graphical abstract

1. Introduction

1.1. Background and Motivation

Changes in mechanical properties of skeletal muscle tissue are associated with many diseases including spasticity, Duchenne’s muscular dystrophy (Qin et al., 2014), hyperthyroidism (Bensamoun et al., 2007), atrophy (Ringleb et al., 2007), paraplegia (Basford et al., 2002), patellofemoral syndrome (Botanlioglu et al., 2013), and myositis (McCullough et al., 2011; Lieber and Friden, 2000; Sack et al., 2013). Electrical conduction in muscles is related to the degree of structural anisotropy (Garmirian et al., 2009); indeed, changes in muscle anisotropy may be a marker for the progression of neuromuscular disorders (Chin et al., 2008). Hence, a technique capable of noninvasively and quantitatively assessing muscular tissue viscoelasticity and anisotropy as it relates to the structural and functional properties of muscles, would potentially improve diagnosis and monitoring of the progression of diseases and their response to therapy.

Magnetic Resonance Elastography (MRE) is capable of noninvasively quantifying mechanical properties of muscular tissues in vivo (Bensamoun et al., 2007; Basford et al., 2002; Ringleb et al., 2007; Jenkyn et al., 2003). MRE is a dynamic elasticity imaging technique to generate quantitative maps depicting viscoelastic properties of biological tissues through the excitation and subsequent analysis of mechanical wave motion. MRE contrast is akin to the physician practice of palpation; yet, MRE is quantitative and potentially offers advantages in precision, operator-independence, and access to tissues not reachable by touch. Initial MRE studies focused on tissues or specimens that were assumed isotropic and locally homogeneous (Muthupillai et al., 1995). These simple models were used to characterize numerous organs and anatomical regions including brain (Atay et al., 2008; Clayton et al., 2013; Green et al., 2008; Johnson et al., 2013; Murphy et al., 2013; Sack et al., 2008), breast (Sinkus et al., 2005) and liver (Asbach et al., 2008; Klatt et al., 2010; Mariappan et al., 2009). In an MRE experiment, tissue mechanical properties are estimated from imaged displacement data using inversion algorithms: different approaches have been used including those based on the estimation of the wavelength at a location in the image, such as the Local Frequency Estimation (LFE) method, and those based on an inversion of the governing differential equations the Helmholtz Inversion Method and the Algebraic Inversion of the Differential Equation (AIDE) each with a multitude of variations based on assumptions, typically local homogeneity and isotropy (Manduca et al., 1996; Doyley, 2012; Papazoglou et al., 2008). Also, optimization algorithms based on the minimization of an error function have been used (Chatelin et al., 2016). For improved accuracy, directionally-dependent viscoelastic response (anisotropy) should be taken into account, which is significant in many biological tissues and at specific length scales (Lieber and Friden, 2000; Feng et al., 2013; Sack et al., 2008; Romano et al., 2012; Feng et al., 2017; Wuerfel et al., 2010; Schmidt et al., 2018; Green et al., 2008). In particular, muscle tissue typically exhibits a microstructure that is intrinsically heterogeneous, with hierarchical arrangements of constituents like fibers and fiber bundles surrounded by an intricate collagen network (Lieber and Friden, 2000). These characteristics make homogeneity and isotropy non-suitable assumptions. While various approaches have been proposed in the literature on the measurement of the anisotropy in brain tissue (Feng et al., 2013; Feng et al., 2017; Romano et al., 2012; Green et al., 2008; Wuerfel et al., 2010; Schmidt et al., 2018) and in skeletal muscle tissue (Gennisson et al., 2003; Garmirian et al., 2009; Papazoglou et al., 2006; Green et al., 2013; Wang et al., 2013; Guo et al., 2016; Qin et al., 2014; Aristizabal et al., 2014), there is not yet an accepted standard for the identification of the mechanical properties of anisotropic and viscoelastic tissues through MRE (Ryu and Jeong, 2017).

Inversion algorithms for anisotropic cases have been investigated including their suitability for incompressible or nearly incompressible transverse isotropic (NITI) materials (Romano et al., 2012; Rouze et al., 2013; Tweten et al., 2015; Tweten et al., 2017; Qin et al., 2013; Royer et al., 2011; Schmidt et al., 2016; Clayton et al., 2013). But, due to the scattering phenomena introduced by inhomogeneities and the elongation of the wavefronts occurring in MRE experiments, the estimation of the material parameters for the anisotropic and heterogeneous media through a completely analytical inversion algorithm still needs to be developed.

The design of phantom materials exhibiting controlled anisotropic and rate-dependent responses is a useful tool to develop and evaluate new approaches for inversion in MRE (Chakouch et al., 2015). Phantoms have not only been used as a means of validation and standardization of MRE, but also to improve the performance and reliability of MRE inversion algorithms (Cao et al., 2017). Most studies with phantoms have focused on mimicking isotropic elastic material as in (Muthupillai et al., 1995). Anisotropic phantoms with different shear moduli in the planes parallel and perpendicular to the fiber direction have been built by Green et al., 2008 and Oudry et al., 2009. They implemented a cross-validation between Ultrasound-based Transient Elastography (UTE) and MRE for copolymer-in-oil phantoms formed from a mixture of styrene-ethylene/butylene-styrene (SEBS) copolymer and mineral oil. Viscoelastic and transverse isotropic phantoms have been fabricated using cryogel PVA in Wan et al., 2014, Chu and Rutt, 1997 and Millon et al., 2006, where the oriented mechanical properties in cryo-hydrogels were induced by applying controlled strain to the PVA sample stretching the physical crosslinks of the polymeric chains during low temperature thermal cycles. In Chatelin et al., 2014 and Chatelin et al., 2016, physically crosslinked anisotropic PVA hydrogels, capable of replicating fibrous biological tissues, were created. Further examples of anisotropic phantoms are found in Namani et al., 2009, where magnetically aligned fibrin gels were built manually positioning the principal axis of the samples either parallel or perpendicular to the direction of the shear excitation, in Sakai et al., 2008, where a diffusion phantom was designed with micro water channels created on solid Silicon gels through chemical etching, in Qin et al., 2013, where agreement is found between MRE and direct measurements of the shear anisotropy combining MRE and Diffusion Tensor Imaging (DTI) on a composite materials phantom made of Spandex fibers in PVA matrix, and in Schmidt et al., 2016, where measurements of the fast and slow shear wave speeds in aligned fibrin gel phantoms were made.

1.2. Objectives

The aim of the present work is to develop and characterize a composite phantom for MRE experiments that has uniform controllable anisotropic properties meant to be comparable to the frequency-dependent anisotropic properties of skeletal muscle. The materials combination and structure is different from prior designs found in the literature (Qin et al., 2013; Chatelin et al., 2014; Chatelin et al., 2016; Namani et al., 2009; Sakai et al., 2008; Millon et al., 2006; Wan et al., 2014; Chu and Rutt, 1997). The novel anisotropic phantom was used in MRE experiments exploiting geometrically focused radially converging shear wave excitation as found in computational simulations in Clayton 2013 and in experimental studies by (Yasar et al., 2013). Finite element models were used to simulate the MRE experiments. To this purpose, homogenization analyses were performed to determine macroscopic material parameters and to save computational costs. Studies using such a phantom could clarify the influence of anisotropy, heterogeneity and viscoelasticity on shear wave motion, and help to optimize MRE protocols – experimental (pulse sequence and physical setup) and computational (measured signal analysis and inverse modeling) – to estimate mechanical properties in anisotropic tissues, such as skeletal muscle.

2. Materials and methods

2.1. Phantom manufacturing

Three different phantoms have been fabricated for the MRE experiments: a 3D printed anisotropic composite made of 15% w/v crosslinked gelatin solution for the fibers and of 5% w/v gelatin solution for the matrix, and two homogeneous and isotropic phantoms for the constituent materials of the anisotropic phantoms (5% w/v and 15% w/v crosslinked). The ideal geometry for a composite material mimicking the muscle tissue may be that of unidirectional fibers. However, this material arrangement is impracticable in terms of actual implementation through the 3D printing process employed in this study; so, an additional layer of fibers in a different direction is necessary to give support to the whole structure. (Alternate additive manufacturing strategies may be able to overcome this limitation in the future.) The solution strategy (Figure 1) was to print a grid structure with two identical families of fibers aligned along two orthogonal directions and to embed it in a gelatin matrix. The fiber network is obtained through the printing of gelatin with higher percentage of crosslinker embedded in a softer matrix made of the same gelatin, with spacing between fibers of 0.8 mm in the horizontal direction and 1.8 mm in the vertical direction. The fiber volume fraction value for the composite phantoms is about 10%; the nozzle diameter of the fibers is 200 μm.

Figure 1.

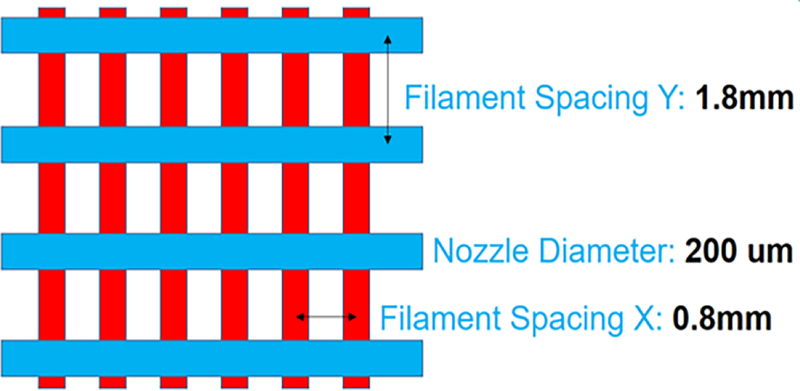
Geometrical features of the 3D printed gelatin phantom.

Gelatin powder is weighed and transferred to a 50 mL conical tube. In order to prevent clustering of undissolved gelatin powder, the tube is shaken and tilted to side so that the gelatin is scattered along the walls of the tube. An appropriate amount of sterile phosphate-buffered saline (PBS) is added. The powder is then gently added to a water bath and, when all the powder has been added to the solution, it is vortexed. At the end of the vortex procedure the solution is let sit for 10 minutes until all bubbles rise. At this point the printing cartridge can be loaded with gelatin. Gelatin must be added to the cartridge, immediately after retrieval from the water bath, with a pipette along the side to prevent air bubbles. An agar plug is added and pushed down until air escapes. Then the cartridge is capped and incubated in the bioplotter head (3D-Bioplotter, EnvisionTEC) at 30°C. At this point the gelatin is ready to be extruded from the cartridge tip. The printing stage must be properly cleaned with ethanol to avoid impurities in the printed product, and it has to be cooled down to 10°C immediately before the printing. The printing process needs to be performed quickly in order to avoid dehydration. The printed scaffold can now be cross-linked. EDC (1-ethyl-3-(3-dimethylaminopropyl) carbodiimide hydrochloride) is used as the cross-linker. It is set out at room temperature for 15–30 minutes. A 15 mM EDC/6 mM NHS (N-hydroxysuccinimide) is prepared in a sterile beaker dissolving it into deionized water or PBS at room temperature. The solution is added to the phantom container to have cross-linking, preferably on ice. After 1 hour, the cross-linker solution is removed and added back to the beaker. Then, deionized water or 70% ethanol is added to scaffolds and the phantom is incubated overnight. After 15 hours the phantom is washed in deionized water and placed in a petri dish with the lid off. PBS is added dropwise to prevent air bubbles and fill the rest of the dish to the cover. As a final stage, the phantom is stored in refrigerator in PBS. The fibrous structure is then embedded in 5% w/v gelatin. Gelatin is inserted through a long and thin needle and, eventually, air bubbles formed have to be aspirated to avoid distortions in the MRI images. The final step is punching the phantom with a cylindrical puncher. The 3D printed structure was punched along one of the two fibers direction so that only one family of fibers is actually visible in a transversal (axial) slice of the test tube for MRE (Figure 2).

Figure 2.

Starting from the left: Schematic of the punching direction, Anisotropic embedded phantom, Composite phantom inside the test tube.

2.2. MRE experiments

MRE experiments were performed in a 56-mm vertical bore MR scanner (Bruker 11.74 Tesla, Billerica, MA) with the same setup and actuator as in (Yasar et al., 2013). The samples positioned inside a borosilicate glass NMR test tube of 8 mm inner diameter were mechanically excited with mono-frequency vibrations in the range from 600 to 3000 Hz using a preloaded piezo actuator with a 15 μm travel range (1000/50 N, Physik Instrumente, MA, USA). Note, this is a unique setup for phantom or in vitro studies taking advantage of geometric focusing within the cylindrical container to extend the frequency range of analysis. Translation to in vivo or clinical studies would necessitate an alternative actuator arrangement such as in (Latta et al., 2011) and (Feng et al., 2018).

In order to have an interpretable shear wave propagation pattern for reconstruction algorithms that rely on presence of at least a half wavelength, the lower bound of the frequency range was selected on the basis of the ratio between the tube diameter and the wavelength. Low frequencies correspond to longer wavelengths; thus, since the internal diameter of the test tube is only 8 mm, at lower frequencies, less than one wavelength is visible, making it difficult to estimate the material properties. The upper bound of the frequency range was selected so to minimize mechanical attenuation which can result in reduced phase-to-noise ratio of the MR signal. The MRE images obtained at frequencies above 3000 Hz showed low phase-to-noise ratio. The excitation given by the actuator on the test tube is parallel to the tube axis and this motion generates shear waves that radially propagate in a converging focusing fashion from the external boundary of the sample to the central axis of the test tube, as long as there is sufficient adhesion of the gelatin on the tube walls after the curing process (see Figure 3). The tube acts as a rigid body oscillating along the axial direction. In order to minimize compression waves in the axial direction of the tube, both its ends are left open.

Figure 3.

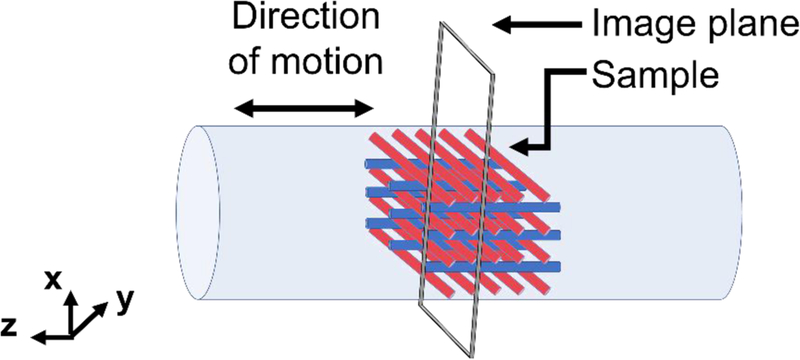
Schematic of the experimental setup.

A gradient echo SLIM MRE pulse sequence (Klatt et al., 2013) was used for studies in the MRI scanner. The imaging parameters were the following: image acquisition matrix=128×128, FOV=10×10 mm, slice number=1, slice thickness=1 mm, and MEG strength = 1200 mT/m with eight time offsets. In this work the wave propagation in the plane perpendicular to the z direction (excitation direction) was the major component of interest; so, the motion was encoded by concentrating the gradient power in the slice direction and setting to zero the gradient amplitudes along the other two directions using a SLIM sequence (Klatt et al., 2013).

2.3. Experimental data treatment

2.3.1. Description of the inversion methods for the homogeneous samples

The material parameters used in the numerical simulations were obtained through an identification process performed on MRE experiments carried out on homogeneous material samples of the single constituents. For a viscoelastic, isotropic and homogeneous medium and assuming an infinite height cylinder of radius α the displacement is given by the following formula in radial coordinates:

$$u_z\left(r,t,k\right)=u_{za}\frac{J_0\left(kr\right)}{J_0\left(ka\right)}{e}^{j\omega t}$$ (1)

with $k=\omega \hspace{0.17em}\hspace{0.17em}\sqrt{\frac{\rho }{{\mu }_{\text{R+}}j{\mu }_I}}$ being the shear wave number, a being the internal radius of the test tube, ⍵ the angular frequency of the mechanical excitation and J₀(z) being the Bessel function of the first kind 0^th order, with ,$j\hspace{0.17em}=\sqrt{-1,}$ ρ the density and µ_I and µ_R the imaginary (loss) and real (storage) part of the complex shear modulus, respectively (Yasar et al., 2013). For isotropic homogeneous phantoms, radial displacement profiles sectioned every 20° were used to post-process the MRE experimental data as obtained from encoding of the complex wave images in the slice direction. MRE_DeVIANT software was used for this purpose and the complex shear modulus of the sample as function of frequency was estimated (Yasar et al., 2013). Line profiles were matched with the analytical closed form solution of the cylindrical coordinate wave equation reported in equation (1). This approach allows one to calculate imaginary and real parts of the complex shear modulus at every frequency through a customized Matlab code and the “Global Optimization” toolbox that is used to perform a nonlinear curve fitting routine for geometrical focusing shear (GFS) waves using 100 trials. Every profile is fit individually and then an average of both real and imaginary parts of the shear modulus for the profiles at each frequency is taken. The algorithm uses the following function presented in (Yasar et al., 2013):

$$\widehat{f}\left(r,\mu ,\theta ,s,\delta \right)=s\ast u_z\left(r+\delta ,t,k_{\beta }\left(\mu \right)\right)\ast e^{-j\theta }+\beta$$ (2)

It takes into account some uncertainties such as: s, the amplitude scale; θ, the phase of the wave propagation to correct measurements made not at zero starting phase; δ, the symmetry shift, offset of the spatial position of the center of the experimental line profile. This accounts for the fact that the center of the wave pattern can be shifted by any non-axisymmetry; and β, zero offset, bias represented by a complex value that compensates for reflected compression waves. The built-in nonlinear curve fit function “lsqcurvefit” is used, which exploits the “Levenberg-Marquardt” search algorithm that minimizes the following objective function defined as the sum of the square of the absolute difference between the estimated cylindrical wave equation closed form solution and the experimental data:

$$Err\left(\mu ,\theta ,\beta ,s,\delta \right)=\frac{{\Sigma }_{n=-N{\left|f\left(r_n\right)-\widehat{f}(r_n,\text{μ},\theta ,\beta ,s,\delta \right|}^2}^N}{2N+1}$$ (3)

Here $r_n=\frac{n}{N}a$ with a being the internal radius of the cylinder. Thus, considering the linear profile, 2N+1 is the total number of data points across a diameter and n indicates each data point. This algorithm allows for the estimation of complex and unbounded parameters. Because of the low SNR due to attenuation at high frequency and because of the high number of parameters, local minima may occur. In order to obtain the solution for the absolute minimum, multiple random starting points have been selected.

2.4. Finite element modeling of the experiments

An MRE experiment on a test tube made of a composite phantom has been simulated through a FE model in the frequency domain by using the commercial code Abaqus/CAE (v6.14) (Dassault Systemes Simulia Corp., Providence, RI, USA). The fiber network of the composite sample has been simulated as an equivalent homogeneous orthotropic material with a frequency-dependent viscoelastic tensor and definition of storage and loss moduli. For the sake of computational cost savings, the following assumptions have been made: i) the test tube has been assumed to be long and the free ends are not affecting the displacements in the central section of the tube; ii) the axially-polarized displacements are the only component playing a relevant role in the shear wave propagation. With these assumptions, only a thin slice in the central part of the tube has been modeled and one quarter of the whole cross section is considered (Figure 4) by utilizing symmetry along two perpendicular planes in the wave propagation modes. Furthermore, in order to simulate a virtually infinitely long tube, periodic boundary conditions have been set on the top and bottom sections of the slice:

$$u_z^{top}=u_z^{bottom}$$ (4)

Figure 4.

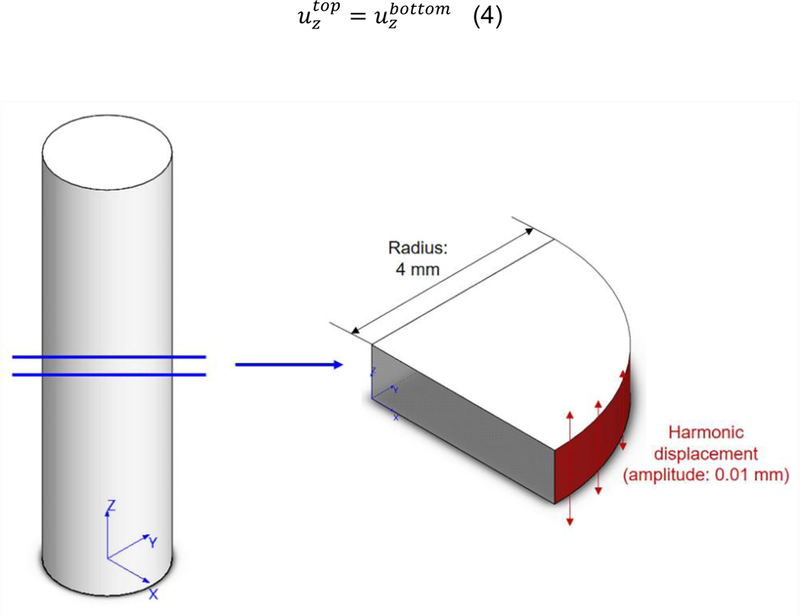
Geometrical simplification adopted to run simulations of the MRE experiments: simulations are performed on a slice of unitary height belonging to the central part of the cylindrical MRE phantom.

The radius of this cylinder is 4 mm to meet the geometrical requirements of a real MRE sample and the thickness of the modelled slice is 1 mm. On the symmetry planes, the displacement components perpendicular to the planes have been set to zero; the harmonic loading is applied on the external surface of the slice, along the axial direction. The amplitude of the harmonic loading was set to 0.01 mm. A steady state dynamic simulation was performed in the frequency domain by exploring the same frequency range as that used in the MRE experiments. The material properties for the homogenized orthotropic material were provided to the finite element model through a FORTRAN subroutine (UMAT) in which the frequency-dependent storage and loss elastic orthotropic tensors are coded. In order to determine the components of the elastic tensors of the homogenized material model on the basis of the material properties of the single constituents, homogenization analyses were performed (Mei and Vernescu, 2010). For this purpose, a representative volume element (RVE), whose repetition in the three space directions generates the whole structure, was defined. This cell contains a piece of fiber of one layer and four quarters of fibers belonging to the above and underlying layers, respectively (Figures 5, 6 and 7).

Figure 5.

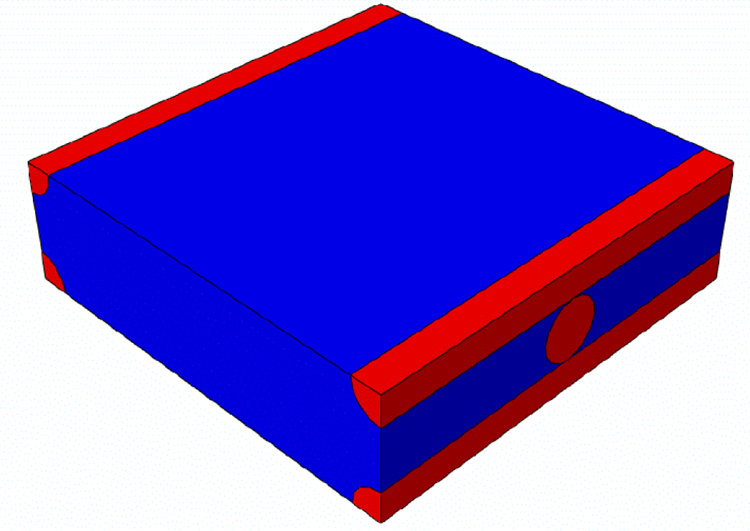
Representative volume element (RVE) of the composite material on which homogenization is performed. Fibers in the two orthogonal directions are colored in red, while the gelatin matrix is in blue.

Figure 6.

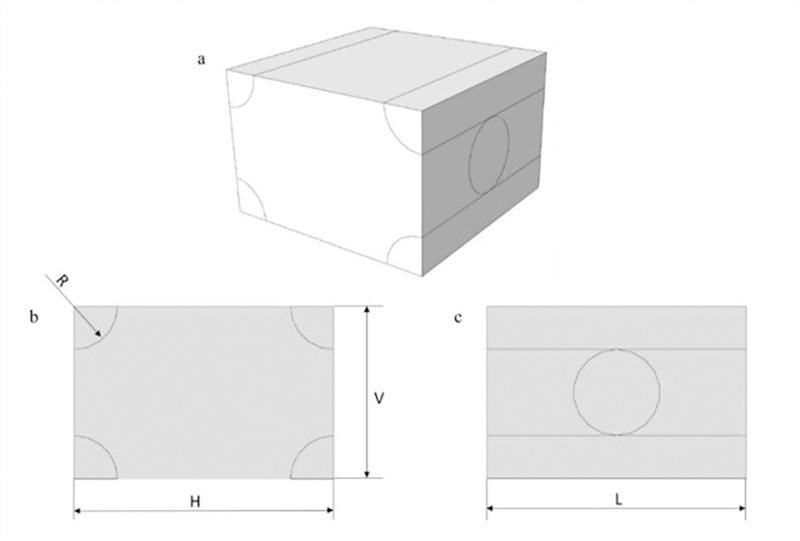
RVE geometrical parameters.

Figure 7.

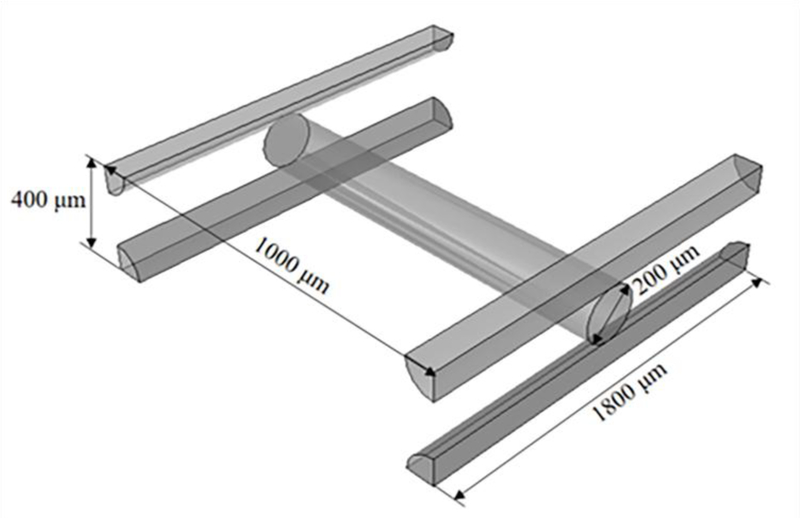
Geometrical parameters of the 3D printed structure, with a spacing of 0.8 mm in the horizontal direction and a spacing of 1.8 mm in the vertical one.

The FE grid defined on the domain of the RVE is reported in Figure 8.

Figure 8.

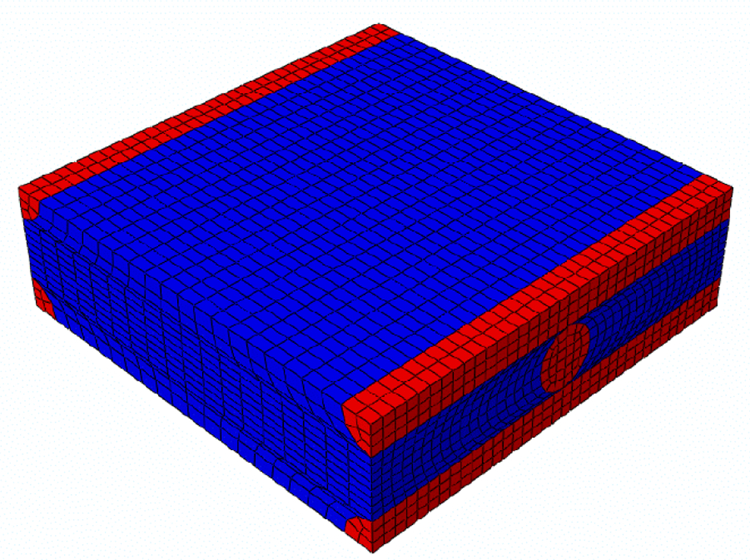
RVE mesh (Total number of nodes: 12041, Total number of elements: 10368, 10368 linear hexaedral elements of type C3D8).

The material properties assigned to the RVE are those extracted from the MRE experiments performed on the 5% w/v homogeneous and isotropic gelatin for the matrix and on the 15% w/v crosslinked homogeneous and isotropic gelatin for the fibers. A special toolbox of Abaqus, Homtools (Lejeunes and Bourgeois, 2011), was used to apply periodicity conditions to the RVE to simulate an infinite repetition of the RVE constituting the whole composite material.

The aim of homogenization is to derive the global mechanical properties of the composite orthotropic material from the mechanical properties of the single components. To do this, a series of static displacement simulations on the RVE were performed to determine the various columns of the orthotropic storage elastic tensor, which takes the following form:

$$C=\left[\begin{array}{l}\frac{1-v_{yz}{v}_{zy}}{E_y{E}_z\Delta }\hspace{0.17em}\hspace{0.17em}\frac{v_{yx}+v_{zx}{v}_{yz}}{E_y{E}_z\Delta }\hspace{0.17em}\frac{v_{zx}+v_{yx}{v}_{zy}}{E_y{E}_z\Delta }\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\\ \frac{v_{xy}+v_{xz}{v}_{zy}}{E_z{E}_x\Delta }\hspace{0.17em}\hspace{0.17em}\frac{1-v_{zx}{v}_{xz}}{E_z{E}_x\Delta }\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{v_{zy}+v_{zx}{v}_{xy}}{E_z{E}_x\Delta }\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\\ \frac{v_{xz}+v_{xy}{v}_{yz}}{E_z{E}_x\Delta }\hspace{0.17em}\hspace{0.17em}\frac{v_{yz}+v_{xz}{v}_{yx}}{E_z{E}_x\Delta }\hspace{0.17em}\hspace{0.17em}\frac{1-v_{xy}{v}_{yx}}{E_z{E}_x\Delta }\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{G}_{xy}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{}0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{G}_{xy}\hspace{0.17em}\hspace{0.17em}0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{G}_{xy}\end{array}\right]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \text{ with}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\Delta =\frac{1-v_{xy}{v}_{yx}-v_{yz}{v}_{zy}-v_{xz}{v}_{xz}-2v_{xy}{v}_{yz}{v}_{zx}}{E_x{E}_y{E}_z}\hspace{0.17em}\hspace{0.17em}$$ (5)

Here E_i is the elastic Young’s modulus along the i^th direction and υ_ij is the Poisson’s ratio in the i-j coordinate plane. The loss (imaginary part) tensor takes the same form as equation (5) but with imaginary components of the elastic moduli. The homogenized parameters were obtained by making 6 FE simulations on the RVE. For each of the above analyses, displacement boundary conditions representing the six unitary macroscopic strains were applied. The components of the elastic tensors were obtained through spatial average of the local stress distribution in the RVE. This procedure was repeated twice, for the storage and loss modulus, respectively, and at various frequencies: 600, 1000, 1500, 2000 Hz.

3. Results

Uniform and homogeneous phantoms of 5% w/v and 15% w/v crosslinked gelatin were tested separately through MRE experiments to identify the viscoelastic properties of the single constituents of the composite. Figure 9 shows the average values of the real and imaginary parts of the shear modulus for the constituents. In the considered frequency range both gelatins exhibited increasing moduli with increasing frequency. The error bars define values within a standard deviation from the average and they do not overlap between the 5% and 15% curves at each frequency. The shear storage and loss moduli in Figure 9 were used as input data for the homogenization process of the composite phantom.

Figure 9.

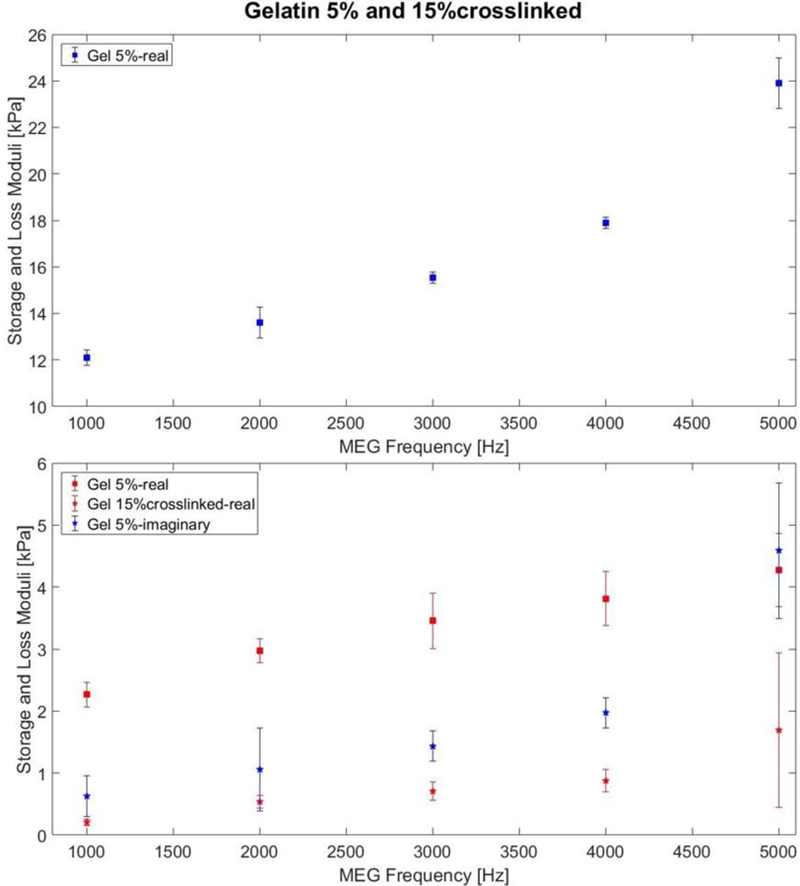
Shear storage modulus and loss modulus of the 5% w/v gelatin and 15% w/v crosslinked gelatin at different frequencies.

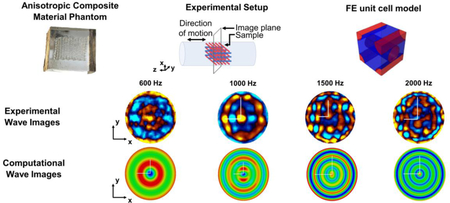
Among the 16 slices captured with the MRI from the 3D printed phantom, shown in Figure 10, the highlighted slice is the one chosen for the MRE experiment. By inspection of the highlighted image, the fibers were found to be aligned along the vertical direction, with respect to the image orientation on this page. Figure 11 shows snapshots of the MRE wave images at 600, 1000, 1500 and 2000 Hz. These images represent the experimental axial displacement maps in the xy plane, where the red and blue colors indicate the positive (out-of-plane) and negative displacements (into-plane), respectively. They refer to the slice selected in red in Figure 10.

Figure 10.

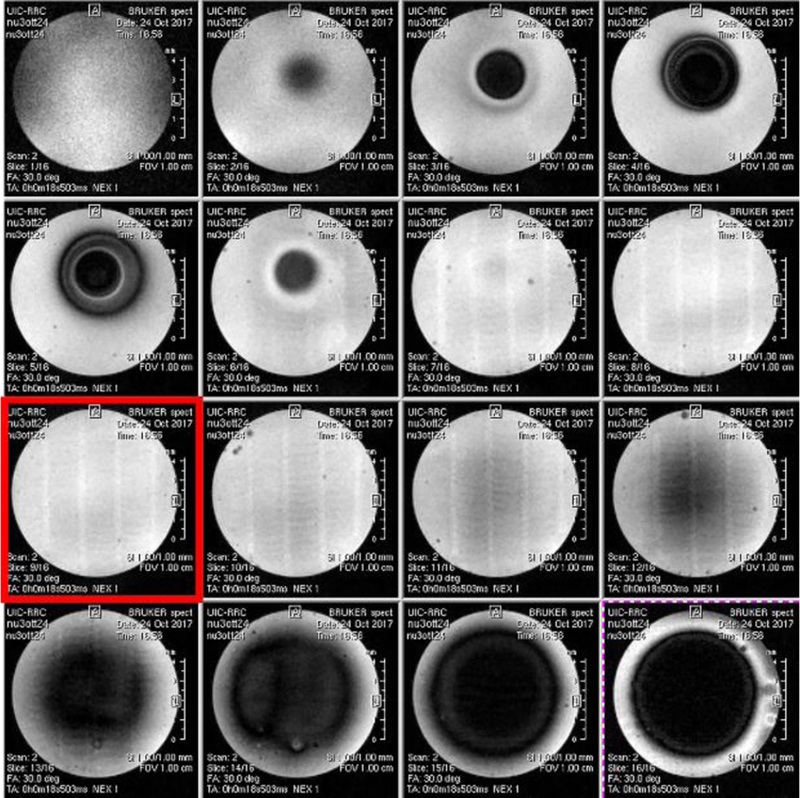
MRI images of the 3D printed phantom.

Figure 11.

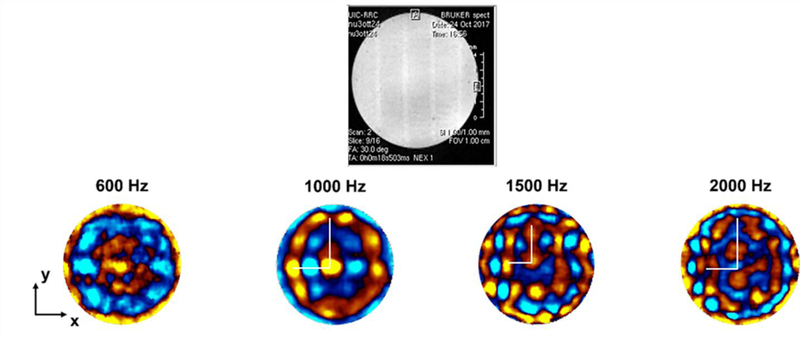
Top panel shows an MR magnitude image of the selected slice for the MRE experiment. In the second row, starting from the left, axial displacement maps as encoded by the MR phase are reported at 600, 1000, 1500, and 2000 Hz of mechanical excitation (red indicating positive displacement out of plane and blue indicating negative displacement into plane). The white lines correspond to the two semi-axes of the elliptical wavefront (long semi-axis in the vertical direction, short semi-axis in the horizontal direction).

For frequencies lower than 1000 Hz, only one wavelength is visible. The elastic anisotropy can be noticed at 1000 and 1500 Hz (Figure 11). To study the behavior of the anisotropy as a function of frequency, the length of the two semi-axes in the displacement maps were computed considering a FOV of 10 mm x 10 mm. Then, the anisotropic ratio was computed as the ratio between the long and the short semi-axes (see Table 1).

Table 1.

Lengths of the long and displacement maps at 1000, 1500, 2000 semi-axis/short semi-axis). short semi-axes of the elliptic wavefront in the Hz. Last column shows the anisotropic ratio (long

	Long semi-axis	Short semi-axis	Anisotropic ratio
1000 Hz	3.53mm	2.76mm	1.28
1500 Hz	2.64mm	1.75mm	1.5
2000 Hz	3.56mm	2.25mm	1.58

The homogenization process provided the elastic moduli of the composite phantoms. From the elastic (storage and loss) tensors, the shear moduli can be calculated. The results indicate that the plane containing the two families of fibers (yz plane) exhibit a lower shear modulus (µ_yz=µ_tt) with respect to that on the perpendicular planes (xz and xy planes, shear modulus µ_at). The values of the complex shear moduli in kPa are reported in Table 2.

Table 2.

Mechanical parameters resulting from homogenization used as input material properties for finite element simulations at 600, 1000, 1500 and 2000 Hz. Values are reported in kPa, with the real and imaginary parts referring to the storage and loss moduli, respectively.

	600 Hz	1000 Hz	1500 Hz	2000 Hz
µtt	2.47+i*0.262	2.77+i*0.196	3.16+i*0.427	3.56+i*0.592
µat	2.52+i*0.26	2.82+i*0.2	3.21+i*0.43	3.62+i*0.59
Ex=Ez=Et	8.58+i*0.82	9.48+i*0.68	10.65+i*1.32	11.89+i*1.78
Ey=Ea	8.07+i*0.8	8.98 +i*0.63	10.15+i*1.29	11.37+i*1.77

The axial displacements found through the finite element model, using material parameters in Table 2, are shown in Figure 12.

Figure 12.

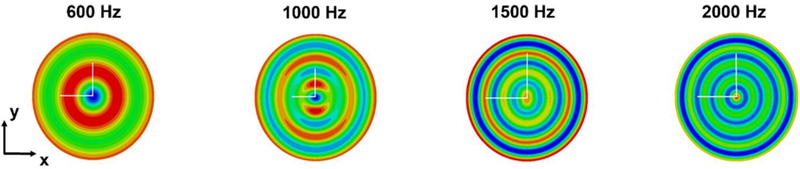
Displacement maps obtained simulating MRE experiments at 600, 1000, 1500 and 2000 Hz of mechanical excitation (red indicating positive displacement out of plane and blue indicating negative displacement into plane). Simulations are performed on a homogenized model of the composite structure phantom made of gelatin. In the slice model used to obtain these results the fibers are in the y and z direction. The white lines correspond to the two semi-axes of the elliptical wave front (long semi-axis in the vertical direction, short semi-axis in the horizontal direction).

The anisotropic ratios at different frequencies are reported in Table 3 as computed for the experimental case.

Table 3.

Lengths of the long and short semi-axes of the elliptic wavefront in the displacement maps at 1000, 1500, 2000 Hz. Last column shows the anisotropic ratio (long semi-axis/short semi-axis).

	Long semi-axis	Short semi-axis	Anisotropic ratio
1000 Hz	1.67mm	1.52mm	1.09
1500 Hz	2.64mm	1.61mm	1.63
2000 Hz	2.53mm	1.5mm	1.68

4. Discussion and Conclusions

The aim of muscle MRE is to identify alterations in mechanical properties of muscle tissue induced by diseases. There are still no commonly accepted standards to directly quantify the intrinsic stiffness of individual muscles, especially if anisotropic properties are also analyzed. This is a major obstacle to identifying, treating, and monitoring stiffness-related contributions to muscle impairments. The long-term goal of this project is to improve treatments for musculoskeletal disorders associated with changes to the intrinsic properties of muscle by providing a better means of assessing and monitoring intrinsic anisotropic properties noninvasively. Objective measures of muscle stiffness may clarify the role of muscle in stiffness-related impairments, and lead to personalized treatments.

In this study composite phantoms were designed for MRE; they exhibited anisotropic heterogeneous viscoelastic properties. This is a key feature for phantoms which have to mimic muscles and other biological tissues. This was accomplished using a novel 3D bioprinting process to fabricate samples with controlled geometry and mechanical properties using a fiber-based support structure embedded in gelatin, analogous to fibrous tissue structure.

MRE experimental tests as well as numerical simulations were performed with the aim to characterize anisotropic and viscoelastic mechanical properties of the phantom. The experimental displacement maps (Figure 11) obtained from the designed 3D printed grid structure show elliptical wavefronts elongated in the vertical direction, which were formed during the propagation of the mechanical wave from the walls towards the center of the test tube. This elongation means that the wavelengths are shorter in the vertical direction since the shear modulus is lower in the yz plane than in the xz one. This result is confirmed by previous computational findings from Clayton et al., 2013. Considering the analyzed frequencies, the acceptable lower limit of excitation frequency is above 600 Hz, while the highest one is below 2000 Hz for the size of the cylindrical container used here. Below 1000 Hz, less than one entire wavelength occurs and the wavelength of the propagating wave is higher than the spacing between fibers and the wave is not able to catch all the details of the lattice structure, while above 1500 Hz the phase-to-noise ratio of the experimental image becomes too low in places. The anisotropic ratios as found from the experimental displacement maps (Table 1) show that the anisotropic nature of the phantom is better caught at a higher frequency (1.58 at 2000Hz versus 1.28 at 1000 Hz). This indicates that the optimal selection of the frequency for the mechanical characterization of anisotropic fiber-reinforced material is a trade-off between the wave length interacting with the material characteristic size (fiber separation) and the phase to noise ratio which is decreasing for increasing frequency of excitation.

With regard to the computational study, the anisotropic mechanical properties used as input for the FE model come from a homogenization process performed on a RVE of the fiber reinforced structure characterizing the phantom. The homogenization approach, chosen to identify composite mechanical parameters, is more efficient as compared to the time required to perform simulations when fibers are explicitly defined; thus, it enables faster and cheaper exploration of the whole range of frequencies used in the MRE experiments. On the other hand, the homogenization procedure leads to losing some features: the influence of heterogeneities, such as fiber intersection knots, the effect of fiber diameters with respect to the wavelength and the scattering phenomena.

The displacement maps resulting from the simulations on the homogenized phantom (Figure 12) show similar patterns to those obtained from the experiment except for the scattering patterns (Figure 11). The result given by the FE model of the 3D printed phantom exhibits a degree of anisotropy comparable to the experimental results, with increasing values with increasing frequency. The anisotropic ratios for the experimental phantom are about 1.28 at 1000 Hz, 1.5 at 1500 Hz and 1.58 at 2000 Hz, while for the computational phantom are about 1.09 at 1000 Hz, 1.63 at 1500 Hz and 1.68 at 2000 Hz. These values are consistent with previous findings on skeletal muscle anisotropy from Qin et al., 2013. Thus, FE simulations of MRE experiments on these phantoms can be used to extract mechanical parameters of the individual constituents of anisotropic tissue by developing an optimization procedure that compares experimental and computational displacement profiles to extract shear modulus maps or elastograms.

The mismatch between experimental and computational displacement maps can be noticed at 2000 Hz where eventually the wavelength becomes too short and is comparable to the dimensions of the inhomogeneities of the sample. Thus, the homogenization technique is applicable only if the distance between the fibers and the diameter of the fibers is significantly smaller than the wavelength. Another requirement to be met is that the wavelength should be short enough with respect to the radius of the cylindrical sample. This prerequisite is essential if the goal is to be able to visualize elliptical shaped wavefronts: indeed, an anisotropic material would produce elliptical shaped waves in an infinite space but, in presence of circular boundary (test tube walls), the waves will adapt to the circular geometry. Moreover, the radius cannot be too large due to the damping effect of the material that, at higher frequencies, would cause the vibration to be too attenuated and thus no longer visible towards the center of the test tube despite the compensation provided by the geometric focusing effect. These limitations impose a trade-off in regards to the choice of the range of frequencies and the geometrical parameters. Furthermore, another possible reason for the differences between the experimental and computational results can be the scattering effect due to the inhomogeneities of the structure. This aspect is not considered in the computational simulations on the homogenized material where, differently from the experimental model, the fibers are not physically present; thus, they are not a source of scattering during the simulated wave propagation.

For future developments of the experimental phantom, new design strategies can be carried out. The ideal mechanical phantom to mimic skeletal muscle structure should be a transversely isotropic model. The approach followed in this study was to build viscoelastic and fibrous phantom structures resembling muscular tissue with 3D printing. The obtained structure is a gelatin grid formed by fibers oriented in perpendicular directions from one layer to the next one. Then this structure is embedded in a softer gelatin matrix. This strategy has been adopted with the purpose to provide suitable mechanical support to the embedded fibers, although the final phantom exhibits orthotropic properties, which may not be fully suitable to simulate transverse isotropy found in muscle. An improvement for a closer approximation of skeletal muscle would be having smaller fibers with lower spacing between them and enhanced transversely isotropic properties. 3D printing of such refined structures remains challenging and time consuming. Improvements in 3D printing capability may also solve the problem of mismatch between the resolution of the grid structure of the phantom and that of the muscle. A scaling down in the fiber diameter of the 3D printed fibers may be desirable so to be more consistent with physiological size of muscle fibers which are about 50 µm in diameter. Reaching these dimensions is challenging because of the current technical constraints like the nozzle diameter (200 μm) or fiber interspacing.

Despite the limitations hereby discussed, the results herein reported support the initial hypothesis that the experimental and numerical analysis of anisotropic viscoelastic materials are a prerequisite for identification of frequency dependent material parameters and, in perspective, to detect alterations in mechanical properties of muscle induced by diseases.

Highlights.

• In this study composite phantoms were designed for MRE; they exhibited anisotropic heterogeneous viscoelastic properties.

• The degree of anisotropy obtained from the MRE experiments and the FE simulations is comparable with values for muscle found in the literature, exhibiting increasing shear and storage moduli with increasing frequency.

• Experimental and numerical analyses of anisotropic viscoelastic materials provide insight into and may lead to improvements in the experimental identification of disease-correlated changes in anisotropic materials, such as muscle.