Tuning the Photoreactivity of Z-Hexatriene Photoswitches by Substituents - A Non-Adiabatic Molecular Dynamics Study

Abstract

To understand how substituents can be used to increase the quantum yield of photochemical electrocyclic ring-closing of the Z-hexa-1,3,5-triene (HT) photoswitch forming cyclohexadiene (CHD), we investigate the S₁ photo dynamics of HT and its derivatives 2,5-dimethyl-HT (DMHT), 2-isopropyl-5-methyl-HT (2,5-IMHT), 1-isopropyl-4-methyl-HT (1,4-IMHT), and 2,5-diisopropyl-HT (DIHT) using time-dependent density functional theory surface hopping dynamics. We report detailed photoproduct distributions, formation mechanisms, branching ratios, and wavelength-dependent product quantum yields. Most products have been confirmed experimentally and include alltrans HT derivatives, cyclopropanes, cyclobutenes, cyclopentene, cyclohexadienes, and bicyclic compounds. Regarding CHD formation, we find that for the 2,5-substituted derivatives DMHT, 2,5-IMHT, and DIHT, the branching ratios increase with increasing size of the substituents. In contrast the branching ratios of the E/Z-isomerization decrease with increasing size of the substituents. Due to steric interactions, increasing the size of the substituents increases the amount of gZg rotamers in the ground state, which are prone to CHD formation and have lower E/Z-isomerization probability. Furthermore, we find [1,4], [1,5], and [1,6]-sigmatropic hydrogen shift reactions occurring at large percentages (5% to 15%); for sterical reasons these reactions stem from tZg conformers. DIHT shows the lowest percentage of side product formation among the 2,5-substituted molecules and highest CHD branching ratio; its CHD quantum yield can be increased up to more than 64%, by excitation of DIHT on the red tail of its absorption spectrum, whereas the Z/E-isomerization is reduced below 5% and side reactions practically vanish. This makes DIHT the best candidate for applications in molecular switches.

Introduction

Photochemical switches are a key component in numerous applications on the molecular level, such as molecular machines, photoinduced drug delivery systems, and data storage.^1,2 One of the commonly used photochemical reactions in molecular switches is the reversible reaction of the Z-hexa-1,3,5-triene (HT) photoactive unit to cyclohexadiene (CHD). This reaction is common in diarylethenes, furylfulgides, and spiropyrans;^2–6 besides, it also plays a key role in vitamin D photochemistry.⁷ The ideal candidate for a photochemical switch maximizes the quantum yield of the desired product, exhibits controllable absorption properties, and stays stable over a large number of switching cycles. A large number of experimental studies focus on how structural modifications can be used to tune specific switching properties.^8,9 Most theoretical studies on that subject^10–16 are based on static geometries and minimum energy pathways;¹⁷ fewer studies^5,18,19 take into account the dynamic nature of the photo switching process, which can be expected to be highly dependent on vibrational excess energy due to photorelaxation and thermal energy in general. This has motivated us to investigate the influence of substituents on the hexatriene backbone on the excited state dynamics. In particular, we want to investigate how substituents can be used to alter the quantum yield of a specific product, such as CHD or the all-trans HT isomer that results from Z/E-isomerization. By calculating the wavelength-dependent product quantum yields (PQYs)²⁰ we want to assess how the quantum yield can further be increased by the selection of a specific switching wavelength.

Experimentally, these questions have been investigated in the 1970s by Havinga and coworkers²¹ in the context of vitamin D photochemistry, as well for the purpose of using photochemical reactions in organic synthesis to achieve a particular stereochemistry. These studies have contributed to understanding of the Non-Equilibrium of Excited State Rotamers (NEER)^22,23 principle, that states that the excited state life time is too short to allow for the conformational distribution too adapt to the different potential energy surface in the excited state, leading to a distinct photochemistry and photophysics for each rotamer.^24,25

To obtain mechanistic information beyond of what can be deducted from experiments, and to develop a methodology that allows to make theoretical predictions for the development of photochemical switches, we study the photochemical reactivity of several HT derivatives in the photochemically active first excited singlet state (S₁) by non-adiabatic molecular dynamics.

The molecules we studied are 1,3,5-Z-hexatriene (HT), 2,5-dimethyl-HT (DMHT), 2-isopropyl-5-methyl-HT (2,5-IMHT), 1-isopropyl-4-methyl-HT (1,4-IMHT)¹, and 2,5-diisopropyl-HT (DIHT), as shown in Fig. 1. All molecules share the photoactive HT unit but carry different substituents either in the 1,4-position or in the 2,5-position of the HT unit (Fig. 2). 2,5-IMHT and 1,4-IMHT are the open-ring isomers of natural compounds α-terpinene and α-phellandrene, respectively, which are relevant in atmospheric chemistry as secondary organic pollutants.^26,27 Common to all derivatives are the two major rotational degrees of freedom defined by the dihedral angles C1-C2-C3-C4 (∅₁) and C3-C4-C5-C6 (∅₃), allowing for four conformers (Fig. 2): gauche-Z-gauche (gZg), gauche-Z-trans (gZt), trans-Z-gauche (tZg), and trans-Z-trans (tZt). Here gauche/trans refers to the rotation around the single bonds and Z refers to the rotation around the central double bond. The gauche conformation describes a dihedral angle |∅| < 90°, and the trans conformation refers to |∅| > 90°. The definitions of the exact angles used to define the rotamers are given in caption of Fig. 2.

Figure 1:

Z-hexatriene derivatives studied here.

Figure 2:

Rotational isomers of the hexatriene derivatives, defined by the dihedral angles C1-C2-C3-C4 (∅₁) and C3-C4-C5-C6 (∅₃). The substituents that define the molecules are HT: R₁=R₂=R₃=R₄=H, DMHT: R₁=R₃=H R₂=R₄=CH₃, 2,5-IMHT: R₁=R₃=H R₂=CH₃ R₄=isopropyl, 1,4-IMHT: R₂=R₄=H R₁=CH₃ R₃=isopropyl, and DIHT: R₁=R₃=H R₂=R₄=isopropyl. gZg: −90° < ∅₁ < 90° and −90° < ∅₃ < 90°; gZt: −90° < ∅₁ < 90° and either ∅₃ > 90° or ∅₃ < −90°; tZg: ∅₁ > 90° or ∅₁ < −90° and −90° < ∅₃ < 90°; and tZt: ∅₁ > 90° or ∅₁ < −90° and either ∅₃ > 90° or ∅₃ < −90°.

Computational Details

We used ab-initio molecular dynamics (AIMD) to generate a Boltzmann ensemble of the molecules in the ground state at room temperature. Snapshot structures of the ensemble are used as starting structures for the simulation of the excited state reactions non-adiabatic molecular dynamics and they are used to compute average absorption spectra. We analyzed the trajectories with respect to their product formation and the absorption properties of their initial structure.

All calculations were performed with the density functional theory (DFT),²⁸ time-dependent density functional theory (TDDFT),²⁹ and algebraic diagrammatic construction through second order (ADC(2))³⁰ modules as implemented in the TURBOMOLE quantum chemistry program.³¹

Ground State Molecular Dynamics

The ground state Boltzmann ensemble of rotamers of the HT derivatives at 300K was sampled with ab initio Replica exchange molecular dynamics (REMD)³² based on the formulation of Sugita et al.³³ and Born-Oppenheimer molecular dynamics.³⁴ All REMD simulations were performed with the PBE functional³⁵ and accelerated using the resolution of identity approximation;³⁶ calculations employed the def-SVP³⁷ basis set. Simulations were performed at four temperatures (300 K, 600 K, 900 K, and 1200 K) and switches between the trajectories at different temperatures were evaluated every 200 molecular dynamics steps. The temperature was controlled by a Nosé-Hoover thermostat.^38,39 A time step of 50au (≈ 1fs) was used to propagate the nuclear degrees of freedom. Each REMD simulation was propagated for a total time of at least 100ps. More details about the REMD implementation can be found elsewhere.³²

Absorption Spectra

Electronic absorption spectra of the Boltzmann ensembles of the molecules were obtained by averaging the calculated spectra of more than one thousand individual structures (HT: 3241, DMHT: 1512, 2,5-IMHT : 1722, 1,4-IMHT: 2761, DIHT: 2214) from REMD trajectories taken every 80 time steps (96.8 fs). For the calculation of the product quantum yields (PQYs), spectra were calculated for smaller subsets of structures (Table 1, column 3). The ten lowest singlet excitation energies and oscillator strengths were calculated for each individual structure using linear response TDDFT²⁹ employing the hybrid PBE0 approximation to the exchange-correlation functional⁴⁰ and using ADC(2)³⁰ within the resolution of identity method.^41,42 TDDFT calculations employed the def2-SVP basis set, whereas ADC(2) calculations employed the def2-TZVP basis set.³⁷ In both cases, oscillator strengths were converted into molar decadic extinction coefficients and individual spectra were broadened with a Gaussian line shape with a full-width half-maximum of 0.15 eV and averaged to obtain the macroscopic absorption spectrum.^43–45 In ADC(2) calculations, we applied the conductor-like screening model (COSMO)⁴⁶ to include the presence of the solvent implicitly. To model n-pentane at 20°C, a dielectricity constant of 1.844 and a refractive index of 1.3575 was used.⁴⁷

Table 1:

Total number of trajectories started (column 2), number of trajectories used in analysis (column 3), number of trajectories that exhibit negative excitation energies at the transition from the excited state to the ground state (column 4), and number of trajectories failed due to numerical instabilities (column 5).

	Number of trajectories
	total	used in analysis	with negative excitation energies	failed
HT	897	870	57	27
DMHT	1012	991	106	21
2,5-IMHT	1389	1386	104	3
1,4-IMHT	1323	1322	39	1
DIHT	1213	1204	41	9

Non-adiabatic Molecular Dynamics

Non-adiabatic molecular dynamics was carried out with the TDDFT Surface Hopping method (TDDFT-SH)⁴⁸ as implemented in TURBOMOLE.^7,49 The hybrid PBE0 approximation to the exchange-correlation functional was used,⁴⁰ and calculations employed the def-SVP³⁷ basis set. From the ground-state Boltzmann ensemble generated by REMD, we sequentially choose between 800–1400 snapshot structures (Table 1, column 2) and their instantaneous velocities every 80 time steps (96.7fs) as starting geometry for an excited state dynamics simulation. The total simulation time of TDDFT-SH simulation was 900fs, which was sufficient to describe the full excited-state decay and eventual hot ground-state reactions. The Tamm-Dancoff approximation (TDA)⁵⁰ to TDDFT was used, since it shows less instabilities at conical intersections.^51,52 Within the TDA, singlet instabilities are characterized by negative excitation energies. In the case a trajectory exhibited a negative excitation energy (Table 1, column 4), a transition to the ground state was enforced. In some trajectories, however, it was not possible to converge either ground or excited state energies, or discontinuities in the PESs⁵³ did not allow to properly integrate Newton’s equations of motion. These trajectories terminated abnormally and were excluded from the analysis (Table 1, column 5). TDDFT-SH simulations were carried out in the gas phase in the NVE ensemble.

Calculation of Product Quantum Yields

Following our recently published method,²⁰ the product quantum yield (PQY) was calculated as the ratio of the average absorption spectrum of initial structures of the product-forming trajectories σ_P(λ) and the average absorption spectrum of all initial structures σ_tot(λ):

$$\mathrm{\Phi }(\lambda )=\frac{\frac{1}{N_{\text{traj}}^{\text{P}}}{\sum }_i^{N_{\text{traj}}^{\text{P}}}{\sigma }_i(\lambda )}{\frac{1}{N_{\text{traj}}^{\mathrm{tot}}}{\sum }_i^{N_{\mathrm{traj}}^{\mathrm{tot}}}{\sigma }_i(\lambda )}=\frac{{\sigma }_P(\lambda )}{{\sigma }_{tot}(\lambda )}.$$ (1)

To this end, successful TDDFT-SH trajectories (Table 1, column 3) were grouped according to the photoproduct P formed. In particular, we were interested in the CHD derivatives, the all-trans derivatives, and the quantum yield of the different products resulting from hydrogen transfer reaction. For each of the 3 groups, the absorption spectrum σ_P(λ) was computed by averaging the individual spectra of the initial structures of each subset of trajectories. The total absorption spectrum σ_tot(λ) is computed as average of the initial structures of all trajectories. Spectra of initial structures were obtained following the procedure described above.

Results and Discussion

Ground State Distribution

Analyzing the structures of the ground state Boltzmann ensemble obtained from REMD at 300 K, we find varying dihedral angle distributions for the different molecules (Fig. 3). Using the specifications for the rotamers defined in Fig. 2, we assigned each structure of the simulations to one of the rotamers gZg, gZt, tZg, or tZt and evaluated their relative populations (Table 2).

Figure 3:

Dihedral angle (∅₁/∅₃) distribution in the ground state obtained from REMD at 300 K. The color code indicates the percentage of structures in an area of 5°×5°. A: HT, B: DMHT, C: 2,5-IMHT, D: 1,4-IMHT, E: DIHT.

Table 2:

Number of structures of ground state rotamers gZg, gZt, tZg, and tZt, obtained by REMD simulations. Rotamers are defined in Fig. 2. Percentages are given in parenthesis.

	gZg	gZt	tZg	tZt	Total
HT	5763 (2.2%)	57525 (22.2%)	40906 (15.8%)	154682 (59.8%)	258876 (100%)
DMHT	17872 (14.8%)	40663 (33.7%)	41564 (34.4%)	20608 (17.1%)	120707 (100%)
2,5-IMHT	50525 (36.7%)	19616 (14.3%)	59009 (42.9%)	8319 (6.1%)	137469 (100%)
1,4-IMHT	2852 (1.30%)	48367 (22.5%)	40986 (19.1%)	122440 (57.1%)	214645 (100%)
DIHT	98297 (55.6%)	31040 (17.6%)	40747 (23.0%)	3503 (3.8%)	77005 (100%)

HT and 1,4-IMHT both exhibit a high number of structures in the tZt conformation (59.8% and 57.1%, respectively), which is reflected by the high density of structures in the corners of Fig. 3, A and D. DMHT, 2,5-IMHT, and DIHT, in contrast, have significantly less tZt structures (17.1%, 6.10%, and 3.80%, respectively). For the gZg configuration (central region in Fig. 3), we note the opposite trend: there is a high amount of structures for DMHT (14.8%), 2,5-IMHT (36.7%), and DIHT (55.6%), but there is a considerably smaller population in HT (2.20%) and 1,4-IMHT (1.30%).

Regarding gZt and tZg conformations, the differences between the molecules are less drastic than for gZg and tZt conformers. Total percentages range from 38 % (HT) to 68 % (DMHT). For the symmetrically substituted derivatives HT, DMHT, and DIHT, we expect gZt and tZg populations to be equal. However, the obtained percentages (Table 2) are slightly different due to imperfect sampling. For the asymmetrically substituted 2,5-IMHT we note the largest discrepancy between gZt and tZg populations.

Previous studies confirm our distributions; the ∅₁/∅₃-map of HT (Fig. 2) is similar to the map reported by Henseler et al.⁵⁴ and the dihedral angle conformations of some minimum energy structures of 2,5-IMHT previously determined by DFT²⁵ are consistent with the high-density regions in Fig. 3 C.

In summary, the HT and 1,4-IMHT share a similar rotamer distribution, whereas the 2,5-substituted molecules DMHT, 2,5-IMHT, and DIHT show a similar distribution. We note that for the 2,5-substituted molecules, the amount of gZg structures increases with increasing size of the substituents, whereas the tZt populations show the opposite trend.

Absorption Spectra

For a large number of structures of the ground-state ensemble we calculated electronic excitation energies and oscillator strengths (Fig. 4, columns 1 and 2, respectively) and converted them to absorption spectra (Fig. 4, column 3). The average S₁ excitation energy for HT calculated by ADC(2)/COSMO (4.86 eV, Table 3) is in good agreement with the experimentally found values of 4.88 eV in solution²¹ and 4.92 eV in the gas phase⁵⁵ and theoretical calculations.^56,57 Considering the molecules HT, DMHT, and 2,5-IMHT, where experimental absorption spectra have been published, ADC(2)/COSMO predicts the peak positions of the maxima (λ_max) more accurately than TDDFT. For the following computation of PQYs, we therefore rely on the spectra computed by ADC(2)/COSMO. From Fig. 4, column 3, we note the much stronger absorption band in the spectra of HT and 1,4-IMHT, compared to the other molecules. Looking at the dependency between dihedral angle conformation and oscillator strength (column 2 Fig. 4) we see that, both, TDDFT (Fig. S2, column 2) and ADC(2)/COSMO (Fig. 4, column 2), predict tZt structures to exhibit larger oscillator strengths than gZg and most of the other rotamers. Thus, HT and 1,4-IMHT having more structures in the tZt configurations, gives rise to the strong absorption band. In addition we note that throughout the series of molecules, tZt conformers possess on average higher excitation energies than gZt, tZg, and gZg conformers (Table 3). In contrast, for all molecules gZg rotamer have on average the lowest excitation energies and oscillator strengths.

Figure 4:

ADC(2)/COSMO S₁ ← S₀ excitation energies in eV (left column), oscillator strengths (length gauge) in atomic units (middle column) as a function of dihedral angles ∅₁ and ∅₃. Right column: absorption spectra of the HT derivatives and their conformers.22 Molecules are listed by rows. A: HT, B: DMHT, C: 2,5-IMHT, D: 1,4-IMHT, E: DIHT.

Table 3:

Average first excitation energies (ω₁) for the different rotamers in eV and average oscillator strengths (f) in atomic units (length representation).

		gZg	gZt	tZg	tZt	Total	λmax	λmax (Exp.)
HT	TDPBE0	4.56	4.62	4.62	4.71	4.67	4.68	4.88 a
		(0.21)	(0.42)	(0.42)	(0.75)	(0.61)		4.92 b
	ADC(2)	4.89	4.87	4.87	4.90	4.89	4.86
		(0.30)	(0.62)	(0.62)	(1.08)	(0.89)
DMHT	TDPBE0	4.76	4.77	4.78	4.88	4.79	4.68	5.28 a,c
		(0.13)	(0.28)	(0.28)	(0.30)	(0.26)
	ADC(2)	5.17	5.10	5.10	5.21	5.13	5.32
		(0.23)	(0.55)	(0.56)	(0.76)	(0.54)
2,5-IMHT	TDPBE0	4.61	4.78	4.74	4.98	4.71	4.68	5.06 a
		(0.14)	(0.21)	(0.29)	(0.19)	(0.22)
	ADC(2)	4.96	5.15	5.07	5.38	5.06	5.32
		(0.22)	(0.43)	(0.54)	(0.63)	(0.41)
1,4-IMHT	TDPBE0	4.30	4.39	4.42	4.41	4.40	4.40
		(0.23)	(0.46)	(0.44)	(0.80)	(0.65)
	ADC(2)	4.67	4.65	4.72	4.62	4.64	4.59
		(0.32)	(0.63)	(0.67)	(1.08)	(0.89)
DIHT	TDPBE0	4.59	4.74	4.73	4.92	4.66	4.64
		(0.14)	(0.22)	(0.23)	(0.22)	(0.18)
	ADC(2)	4.95	5.09	5.08	5.29	5.02	5.10
		(0.22)	(0.42)	(0.43)	(0.60)	(0.31)

^aRef.²¹ (solvent unknown)

^bRef.⁵⁵ (gas phase)

^cRef.⁶¹ (solvent: n-pentane)

Excited-State Dynamics

Z-Hexatriene

Analysis of the TDDFT-SH trajectories of HT reveals six distinct photo products (Fig. 5) and a non-reactive relaxation channel. About half of the trajectories decay unreactively (Table 4). The second most common relaxation pathway (20.1 %) occurs through Z/E-isomerization of the central double bond (Fig. 6). Furthermore, we observe [1,5]-hydrogen shift reactions forming allene 2 (13.8 %) (Fig. 7) and only 5.4 % of the trajectories lead to cyclohexadiene (CHD) through electrocyclic ring-closing. Besides, we find small amounts (< 1 %) of the trajectories forming cyclobutene derivative 3, and bicyclic compounds 4 and 5. All these products have been previously found in experimental studies,^58–60 although there was some uncertainty about the experimental characterization of 5.

Figure 5:

Excited state reaction pathways and products of HT, obtained from TDDFT-SH. Reactions are depicted for the conformer in which they occur most likely.

Table 4:

Branching ratios of the major products/reaction channels for each molecule, obtained from TDDFT-SH simulations.

	Non-reactive	CHD formation	cis/trans isomerization	H-transfer	other reactions
HT	57.1 %	5.29 %	22.2 %	14.3 %	1.15 %
DMHT	53.9 %	9.78 %	17.0 %	15.8 %	3.56 %
2,5-IMHT	53.1 %	18.8 %	11.7 %	13.0 %	3.38 %
1,4-IMHT	84.2 %	1.06 %	6.58 %	7.41 %	0.76 %
DIHT	55.5 %	24.2 %	9.57 %	7.84 %	2.89 %

Figure 6:

Upper panel: Potential energy surfaces and snapshot structures of an example trajectory that forms all-trans hexatriene 6 via Z/E-isomerization in HT. Total simulation times of the snapshot structures are 0fs (A), 186fs (B), 263fs (C), and 429fs (D). Lower panel: Dihedral angle of the central double bond (∅₂) as a function of time.

Figure 7:

Upper panel: Potential energy surfaces and snapshot structures of an example trajectory that forms allene 2 via [1,5]-sigmatropic hydrogen shift in HT. Lower panel: Time evolution of the distance between carbon C2 and hydrogen (blue) and carbon C6 and hydrogen (red).

We notice a strong dependence between the product of a particular trajectory and the ∅₁/∅₃-conformation and its initial structure (Fig. 8, A). While non-reactive decay occurs in all regions of the ∅₁/∅₃-space, the main products are almost exclusively found in specific regions only. Electrocyclic CHD formation is almost exclusively found to originate from gZg rotamers in the central region of Fig. 8, A. Z/E-isomerization is typical for tZt rotamers, but a spurious amount of Z/E-isomerizations also originates from other regions. [1,5]-hydrogen shift reactions are only found to occur in gZt conformers. Minor products 3 and 5 originate from gZt and tZt rotamers, respectively.

Figure 8:

Correlation between product/reaction pathway of HT derivatives (A: HT, B: DMHT, C: 2,5-IMHT, D: 1,4-IMHT, E: DIHT) and the dihedral angles ∅₁ and ∅₃ of the initial structures of TDDFT-SH. Gray dots: non-reactive, blue circles: ring-closure, green triangles: Z/E-isomerization, red diamonds: hydrogen transfer, pink squares: four-ring formation, yellow stars: five-ring formation, teal triangles: double-triangle formation.

DMHT

Reaction pathways for the symmetrically substituted DMHT are summarized in Fig. 9. Similar to HT, about half of the trajectories decay unreactively and the second most common decay channel is Z/E-isomerization, forming all-trans compound 14 (17 %). To a similar amount, we observe [1,6]-hydrogen transfer (Fig. 9, channel B), which occurs during the S₁-S₀ transition, forming an intermediate (structure C, Fig. 10). The intermediate further stabilizes by hot ground state reactions, forming mainly product 8 (10.8 %) (structure D in Fig. 10), and small amounts products 9 and 10 (both ≈ 3 %). Compared to HT, we find an increased amount of trajectories (9.78 %) forming the CHD derivative 7 and the cyclobutene derivative 11 (1.92%, Fig. 11). The major reaction products with branching ratios larger than 9%, 7, 8, and 14, as well as minor product 11 have all been confirmed experimentally.⁶¹

Figure 9:

Excited state reaction pathways and products of DMHT, obtained from TDDFT-SH. Reactions are depicted for the conformer in which they occur most likely.

Figure 10:

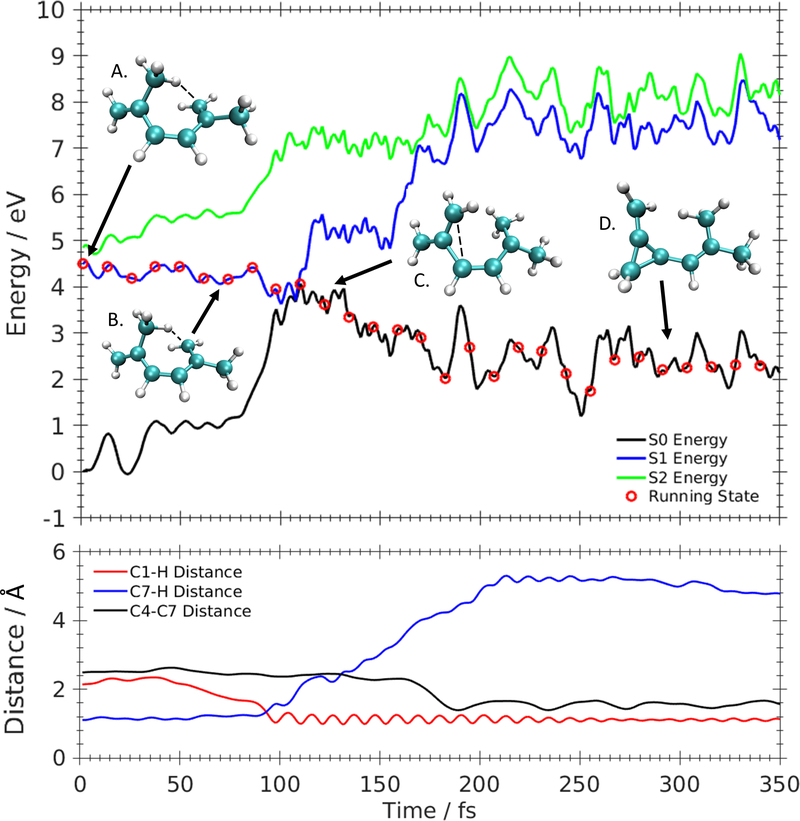
Upper panel: Potential energy surfaces and snapshot structures of an example trajectory that forms cyclopropane 8 from DMHT via [1,6]-sigmatropic hydrogen shift. Total simulation times of the snapshot structures are0fs (A), 70fs (B), 120fs (C), and 287fs (D). Lower panel: Time evolution of the distance between C1 and hydrogen, C7 and hydrogen, and C7 and C4.

Figure 11:

Upper panel: Potential energy surfaces and snapshot structures of an example trajectory that forms cyclobutene derivative 11 from DMHT. Total simulation times of the snapshot structures are 0fs (A), 72fs (B), 99fs (C), and 248fs (D). Lower panel: Time evolution of the distance between C1 and C4.

Also in DMHT, we find a correlation between the reaction product and the initial dihedral angle conformation (Fig. 8, B). Again, unreactive decay is found for all regions in the ∅₁/∅₃-space, and CHD formation is found almost exclusively in the gZg region. The larger amount of CHD formation compared to HT correlates with the higher density in the gZg region (Fig. 3, B), but we also find a larger amount of Z/E-isomerization in the gZg region.

2,5-IMHT

In 2,5-IMHT, we find the analogs of all reactions found in DMHT, plus a second family of products arising from the introduced isopropyl group (channel C in Fig. 12). Again, about half of the trajectories decay unreactively, but the amount of trajectories leading to the CHD derivative (19.8 %) is doubled compared to DMHT (Table 4). In contrast, the amount of Z/E-isomerization has decreased to 11 %. Minor products 16, 19, 20, 22, 26, 27 have been confirmed experimentally.²⁴ The larger amount of CHD formation compared to DMHT can again be explained by the increased density in the gZg region due the replacement of one methyl group by an isopropyl group when going from DMHT to 2,5-IMHT. Similarly, the lower amount of the all-trans product compared to DMHT can be explained by the fewer tZt structures.

Figure 12:

Excited state reaction pathways and products of 2,5-IMHT, obtained from TDDFT-SH. Reactions are depicted for the conformer in which they occur most likely.

1,4-IMHT

1,4-IMHT shows a much higher portion (84 %) of unreactive trajectories than the other molecules (51–54 %) (Table 4) and has the smallest amount of trajectories forming the CHD derivative (1.13 %). In general, similar products as in HT are observed (Fig. 13), but due to its asymmetric substitution two different allene compounds (32 and 35) and two different bicyclic [1.1.0] compounds (33 and 37) are found. Also regarding Z/E-isomerization and [1,5]-hydrogen shift reactions, 1,4-IMHT has the smallest branching ratios among the molecules studied (Table 4).

Figure 13:

Excited state reaction pathways and products of 1,4-IMHT, obtained from TDDFT-SH. Reactions are depicted for the conformer in which they occur most likely.

DIHT

Comparing DIHT to the other molecules, we find the highest amount of CHD formation (25 %) (Fig. 14) and the second lowest amount of Z/E-isomerization (9.57 %), after 1,4-IMHT. The high CHD formation correlates well with DIHT having the highest amount of gZg structures, and the low Z/E-isomerization probability correlates with the lower amount of tZt structures. Furthermore, we note a small amount of side reactions that are initiated by hydrogen transfer reactions, which is accompanied by a small amount of gZt structures in the ground state ensemble. Qualitatively, the product distribution of the symmetrically substituted DIHT is very similar to the one of DMHT, but a larger variety of products arise from the hot ground state reactions following [1,6]-hydrogen transfer (channel B in Fig. 15). The total amount of products caused by the hydrogen transfer (7.75 %), however, is halved compared to DMHT (15.8 %). Apart from the rather unreactive 1,4-IMHT, DIHT has the lowest amount of products other than CHD (Table 4).

Figure 14:

Upper panel: Potential energy surfaces and snapshot structures of an example trajectory that forms cyclohexadiene derivative 39 from DIHT. Total simulation times of the snapshot structures are 0fs (A), 60fs (B), 83fs (C), and 177fs (D). Lower panel: C1-C6 distance as a function of time. Atom numbers are defined in Fig. 2.

Figure 15:

Excited state reaction pathways and products of DIHT, obtained from TDDFT-SH. Reactions are depicted for the conformer in which they occur most likely.

Comparison of the Molecules

Comparing the product distributions of the excited state simulations of the different molecules, we note that there is a strong correlation between their ground state distribution of rotamers and the type and amount of products formed (Fig. 8). In particular, there is a positive correlation between the amount of gZg rotamers and the amount of trajectories that formed the CHD derivative (Fig. 16). At the same time, the number of trajectories that decayed through Z/E-isomerization correlates negatively with the amount of gZg rotamers (Fig. 16). With the exception of 1,4-IMHT, the two correlations are almost linear (Fig. 16). The higher probability of gZg rotamers forming CHD can be rationalized by the closer distance between the two carbon atoms C1 and C6 that are involved in the ring-closing reaction (Fig. 14). Increasing the amount of gZg structures by increasing the size of the side groups consequently leads to enhanced CHD formation. Regarding Z/E-isomerization, we see a high probability of tZt structures to decay through this channel in HT and 1,4-IMHT; in the other molecules, we observe this reaction also in tZg rotamers and spuriously in gZg rotamers. Hence, the decrease in E/Z-isomerization with increasing size of the substituents seems to be mainly a consequence of the increasing amount of gZg structures, which have low Z/E-isomerization probability. Furthermore, when we compare the three substituted molecules DMHT, 2,5-IMHT and DIHT, we find that increasing the size of the side groups leads to a decrease of the total tZg and gZt population (Table 2). Havinga and coworkers²¹ proposed that tZg and gZt rotamers are prone to decay through hydrogen transfer reactions because their conformation exhibits a close distance between the critical hydrogen and carbon atoms that are involved in the hydrogen shift reaction. Our simulations confirm this (Fig. 7 and 10). Consequently, a decrease in tZg and gZt rotamers reduces the amount of trajectories that exhibit a hydrogen transfer.

Figure 16:

Amount of six-ring formation (o) and Z/E-isomerization (X) as a function of the amount of gZg rotamers in the ground state.

In summary, within the series of 2,5-substituted HT derivatives increasing the size of the side groups has 3 distinct effects that lead to more desirable properties for a photoswitch that is based on the HT → CHD conversion: more CHD formation, less Z/E-isomerization, and less hydrogen transfer reactions.

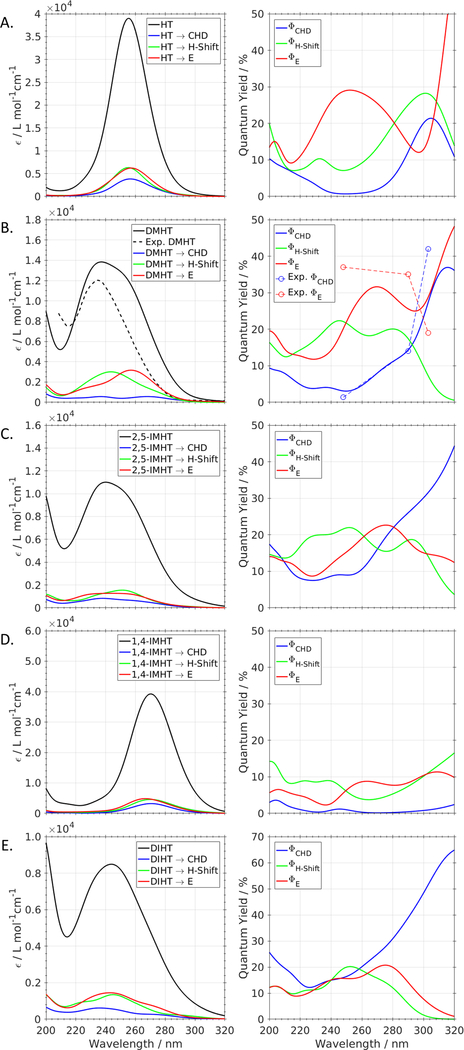
To further explore possibilities to manipulate product quantum yield (PQYs), we computed the wavelength-dependent PQYs for CHD formation, E/Z-isomerization and hydrogen transfer (Fig. 17). As previously shown for DMHT and previtamin D,²⁰ computed PQYs agree qualitatively and partially quantitatively within a few percent with experimentally measured wavelength-dependent PQYs. Turning to the results of our five molecules (Fig. 17), we note that the 2,5-substituted molecules DMHT, 2,5-IMHT, and DIHT exhibit a strong increase in CHD formation on the red side of the spectrum, leading to PQYs up to 37, 44, and 60% at 320nm, respectively. At the same time, the all-trans PQYs decrease with increasing wavelength. DMHT, however, exhibits a relatively large Z/E-isomerization probability at ≈ 320nm; this is a sampling problem due to the small number of trajectories with initial structures that can be excited by wavelengths larger than 290nm.²⁰

Figure 17:

Left: ADC(2)/COSMO absorption spectra of all TDDFT-SH initial structures (black), and initial structures of product-forming trajectories (CHD, H-Transfer, and all-trans product (E)). Right: Wavelength-dependent product quantum yields for CHD (blue), all-trans HT derivatives (red), and hydrogen-transfer products (green). A: HT, B: DMHT,35 C: 2,5-IMHT, D: 1,4-IMHT, E: DIHT.

The observed increase of the CHD PQY at long wavelengths is due to the fact that gZg rotamers have on average lower excitation energies (Fig. 4). Thus, excitation on the red side of the spectrum favors excitation of the gZg rotamers, which are prone to form CHD.

Regarding the lifetimes of the S₁ state, obtained from a monoexponential fit of the TDDFT-SH popuations (Table 5, Fig. S2), we note that HT and the 2,5-substituted derivatives exhibit similar decay times between 115fs to 157fs, whereas the decay time of 1,4-IMHT is longer (257fs). Thus, the size of the substituents has little effect on the excited state lifetimes.

Table 5:

Comparison of excited state lifetimes (fs) of the major products for each molecule. Lifetimes were obtained from a monoexponential fit of the TDDFT-SH S₁ populations Fig. S2.

	Total	Non-Reactive	Ring-Closure	Cis-Trans	H-Transfer
HT	115	114	80.3	118	102
DMHT	157	158	156	167	113
2,5-IMHT	142	142	141	189	117
1,4-IMHT	256	257	123	214	159
DIHT	147	147	149	184	103

Conclusion

We simulated the excited state photoreactions of five different HT derivatives and reported detailed product distributions. For the molecules where experimental products have been characterized (HT, DMHT, IMHT), the found photoproducts are largely consistent with the products characterized in experimental studies. Despite the many short-comings of the single-reference method TDDFT^51,62 and the approximations to the exchange-correlation functional used,^63,64 the good agreement between predicted and experimental product distributions illustrates the predictive power of the surface hopping method using TDDFT potential energy surfaces. While it would be desireable to use more accurate electronic structure methods to simulate the excited state dynamics,^65–68 presently only TDDFT, due to its computational efficiency, allows to carry out the extensive calculations necessary to obtain sufficient amount of sampling to give accurate statistics.

Our calculations show that substituents can be used to manipulate product distributions of photoreactions, mainly by modifying the ground state equilibrium of rotational isomers, consistent with NEER principle.^22,23 For the particular goal of increasing the CHD yield while minimizing side reactions, we find that DIHT best fulfills this requirement. The large isopropyl groups in positions 2 and 5 force the majority of the molecules into the gZg conformation, supressing most side reactions other than CHD formation. Nevertheless, besides CHD there are still other photoproducts formed and also the large amount of unreactive trajectories leaves room for improvements through structural modifications in order to approach a more complete HT → CHD conversion. In particular, we find hydrogen transfer reactions as common side reactions; this has been widely neglected in the study of photochemical switches and warrants to be focus of future studies. Regarding the unsuccessful trajectories, a previous study⁶⁹ showed that the nuclear momenta at the time of the transition to the ground state determine whether a product is formed or not. It is not obvious how the momenta at the time of the transition can be directly influenced by a change of substituent groups. More sophisticated methods that take into account the shape of the excitation pulse^70,71 might have the potential to answer how the number of reactive trajectories could be increased.

The computed wavelength dependent PQYs show that the HT → CHD conversion can further be enhanced by selective excitation of DIHT on the red side of the spectrum; this also suppresses effectively the formation of side products. However, there is still a large number of unreactive molecules. In the context of photochemical switches for molecular applications it will be the challenge to optimize a compound in such way that high conversion is achieved and no side reactions occur.

An important aspect, neglected in this study is the role of the solvent. At first, the ground state ensemble of rotamers might be affected by the presence of a solvent. A different ensemble of rotamers could lead to different absorption spectra, and also spectra themselves are in general solvent dependent. Furthemore, excited state reactions are potentially influenced by a solvent; this could for instance occur due to viscosity or caging effects. In future studies, the solvent could be included by a hybrid molecular mechanics/quantum mechanics approach,^66,72 or even on a full quantum level.⁷³ To further improve the quality of absorption spectra, it is also possible to refine the method by including the quantum nature of the nuclear vibrations.^44,74

Despite the approximations used, at the present level of theory, the presented methodology is able to give insights on the mechanisms of how substituents can be used to tune the excited state reactivity of photochemical switches. It constitutes a valuable tool that can be used to assist the design and optimization of more effective photoswitches. The method goes beyond static calculations, by intrinsically including dynamical effects during excited state dynamics and by considering the conformational equilibrium of structures in the ground state.