Normative human brain volume growth

Abstract

OBJECTIVE

While there is a long history of interest in measuring brain growth, as of yet there is no definitive model for normative human brain volume growth. The goal of this study was to analyze a variety of candidate models for such growth and select the model that provides the most statistically applicable fit. The authors sought to optimize clinically applicable growth charts that would facilitate improved treatment and predictive management for conditions such as hydrocephalus.

METHODS

The Weibull, two-term power law, West ontogenic, and Gompertz models were chosen as potential models. Normative brain volume data were compiled from the NIH MRI repository, and the data were fit using a nonlinear least squares regression algorithm. Appropriate statistical measures were analyzed for each model, and the best model was characterized with prediction bound curves to provide percentile estimates for clinical use.

RESULTS

Each model curve fit and the corresponding statistics were presented and analyzed. The Weibull fit had the best statistical results for both males and females, while the two-term power law generated the worst scores. The statistical measures and goodness of fit parameters for each model were provided to assure reproducibility.

CONCLUSIONS

The authors identified the Weibull model as the most effective growth curve fit for both males and females. Clinically usable growth charts were developed and provided to facilitate further clinical study of brain volume growth in conditions such as hydrocephalus. The authors note that the homogenous population from which the normative MRI data were compiled limits the study. Gaining a better understanding of the dynamics that underlie childhood brain growth would yield more predictive growth curves and improved neurosurgical management of hydrocephalus.

IN the neurosurgical treatment of childhood hydrocephalus, diversion or drainage of cerebrospinal fluid is performed. Although the focus is on fluid accumulation, it is brain growth that has been shown to importantly correlate with neurocognitive development in the treatment of infants with myelomeningocele.¹⁹ A randomized clinical trial contrasting surgical treatments of postinfectious hydrocephalus is currently underway (ClinicalTrials.gov registration number NCT01936272), wherein brain volumes are being followed as secondary outcome measures and correlated with neurocognitive development.¹⁷ Although such efforts point to the potential value of tracking brain volume in the management of childhood hydrocephalus, as of yet there are no existing clinical brain growth charts suitable for the management of such cases. In this study, we seek to create such growth curves. Since this is an area of active research, we propose to create such charts at this stage to facilitate clinical research trials. Our expectation is that if brain volumes are validated as useful in managing hydrocephalus in clinical trials, brain growth charts could constitute a useful tool for routine clinical use.

The most commonly used growth metric for children with hydrocephalus is the head circumference chart. These standard charts were generated using smoothed growth curves that had been fit to a family of mathematical functions using a nonlinear iterative method.²⁴ While this technique resulted in extremely smooth curves that represent the input data respectfully, it bears little biological relevance. Our conjecture is that normative brain growth provides a predictive target for managing conditions such as hydrocephalus, and as such, it serves as a model of age-dependent brain growth much as a map serves navigation targets. If so, then such a model can be incorporated into the sophisticated machinery of model-based control in engineering.²⁶ Although empirical models can be very effective in such strategies, it is best to seek fundamental models that reflect the underlying biology as they may be the most predictive for new out-of-training-sample data and offer a route to improve understanding of the pathophysiology.

In previous work, we characterized normative versus hydrocephalic brain volume growth curves in mice.²¹ In that work, normative brain volume growth data from healthy mice were fit with a natural log least squares curve over time. This curve could then be compared with mice with induced hydrocephalus, and different growth patterns were identified.²¹

We subsequently compiled normative brain volume growth data for humans using the NIH repository of normal pediatric brain MRI.² The resulting data were fit with a one-term power law based on the common use of the power law in the literature on biological allometric growth. The normative volumes were validated using historical imaging and postmortem data, and the power law goodness of fit was quantified using a coefficient of determination.²⁰ Furthermore, the shapes of the curves were contrasted to those of smoothed growth curves for human head circumference.²⁴

Seeking a more fundamental basis for creating brain growth curves, we chose to study a variety of methods that have shown connection to biological growth, as well as several empirical methods that have been used in biological growth studies. Our goal was to select clinically usable brain growth curves with confidence limits similar to those of the existing clinically applied head circumference curves. We found that at least one of the prominent biologically based growth models (West model) may not be as good as an older growth model (Weibull) for accounting for early childhood brain growth. Our aim is to prepare charts for employing such curves in clinical trials, such as in predictive management of patients with hydrocephalus.

Methods

Compilation of Normative Data

With oversight from the Penn State institutional review board (under exemption 27423EM, required by the NIH repository image guidelines), normative brain volume data were determined using MRI scans from the NIH Pediatric MRI Data Repository assembled by the Montreal Neurological Institute (https://pediatricmri.nih.gov/nihpd/info/index.html). This database consists of MRI studies of subjects representative of the US population with respect to sex, socioeconomic status, and race/ethnicity. Extensive screening and exclusion criteria were present to exclude intrauterine risk factors, abnormal neurological examinations, family history, behavioral or cognitive abnormalities, and other physical abnormalities.⁸ Mandell et al. calculated 64 brain volumes from this database by employing a particle filter–based image segmentation algorithm.²⁰

Candidate Models Fit to the Normative Data

To determine the best curves for representing normative brain growth, we focused on models that have been previously successfully applied to biological growth data, comparing a two-term power law, a Gompertz model, a Weibull model, and the West ontogenic model as shown in Table 1.^3,18,31

TABLE 1.

Candidate normative brain growth models

Model	Equation	Variables
Two-term power law	V = atb + c	V = volume t = time a, b, c = best-fit parameters
Gompertz	$\mathit{V}=\mathit{a}{\mathit{e}}^{-{\mathit{e}}^{\left(\mathit{b}\mathit{c}/\mathit{a}\right)\left(\mathit{d}-\mathit{t}\right)\mathbf{+}\mathbf{1}}}$	V = volume t = time a, b, c, d = best-fit parameters
Weibull	$\mathit{V}={\mathit{V}}_{\mathit{m}}-\mathit{a}{\mathit{e}}^{-\mathit{b}{\mathit{t}}^{\mathit{c}}}$	V = volume t = time a, b, c = best-fit parameters Vm = maximum volume
West ontogenic	${\left(\frac{\mathit{V}}{{\mathit{V}}_{\mathit{m}}}\right)}^{1/4}=1-\left(1-{\left[\frac{{\mathit{V}}_t}{{\mathit{V}}_{\mathit{m}}}\right]}^{\frac{\mathbf{1}}{\mathbf{4}}}\right){\mathit{e}}^{-\mathit{a}\mathit{t}/\mathbf{4}{\mathit{V}}_{\mathbf{m}}{\mathbf{1}\mathbf{/}}^{\mathbf{4}}}$	V = volume t = time a = best-fit parameter Vm = maximum volume Vi = initial volume

Each of the 4 models explored in this study, the two-term power law and the Gompertz, Weibull, and West ontogenic models, are described in this table. Their respective equations and corresponding parameters and variables are shown. In this paper all volumes, V, are calculated in cm³.

Power Law

A power law is one where two quantities change in proportional amounts, regardless of their initial values, but with one of the quantities raised to an exponential power. Growth power laws have a long precedence in allometric growth modeling,¹⁴ yet in this present instance a one-term power law was not deemed applicable. At the initiation of the growth curves, the one-term power law implied that the brain volume would be zero, which is not true at birth because of brain growth during gestation.¹⁰ Therefore, a two-term power law fit must be the minimum required for normative brain growth after delivery, accounting for brain volume at birth. In addition, volumetric brain size peaks during the 2nd decade, which is not reflected in the endlessly growing power law.²⁰ Therefore, other options had to be explored.

Gompertz

The Gompertz distribution was originally described to fit survivals and was instrumental in the early development of the insurance industry.³ Its cumulative distribution can be parameterized to have an S-shaped curve and fit animal growth. Such parameters have been used to compare growth rates between species such as the Tyrannosaurus rex, Diomedia exulans (albatross), and Loxodonta africana (African elephant).²³ The Gompertz distribution can also model the slowing of tumor growth with necrosis such as in gliomas.²⁷ It has also been successfully used to track the growth of myelinated white matter in the brain of young children.²⁵

Weibull

The Weibull function’s cumulative distribution can also be parameterized to produce an S-shaped curve. Weibull³⁰ initially designed this function to model chain failure, which occurs when any member of the chain links fail. It is thus used in hazard and survival analysis, but it can also model growth since an ensemble grows when any member grows or divides. Weibull also recognized that his function could be fit to the height distribution of boys.³⁰

West

The West et al. model of ontogenic growth³¹ was introduced as a fundamental model of organism (and organ) growth based upon cell division and the energy requirements for cellular maintenance and division. It has been shown to fit the growth of a wide variety of animal species. Nevertheless, we note that the postnatal human brain does not grow as a simple function of neuronal division, since most neurons are present at birth. Furthermore, we note that West et al. projected that it is the imbalance of supply (capillaries) and demand (number of cells) within an organ or organism that fundamentally limits growth, and that growth over time for an organism bears a consistent exponential relationship to final size. We therefore anticipate that the human brain might be exceptional in this regard vis-à-vis other organ systems due to its exceptional metabolic demand per unit mass.

Curve-Fitting Procedures

Once appropriate models had been established as potential fits for the normative data, it was possible to fit the models to the data using a curve-fitting algorithm (cftool, Matlab, The MathWorks). We applied nonlinear least squares regression and a trust-region algorithm critical to evaluating the curve-fitting fidelity.

Statistical Measurements Used for Analysis

To establish quantitative measures for ranking the models, statistical calculations were performed as described in detail in Table 2. All of the statistical measures provided insight into the applicability of each model. Note that the Akaike information criterion goes further than simply evaluating how well a model accounted for the data by penalizing the fit by the complexity (number of variables) in the model.¹

TABLE 2.

Statistical measures for model evaluation

Statistical Measure	Equation	Variables
Sum of squared errors (SSE)	$\mathit{SSE}={\displaystyle \sum {\left({\mathit{y}}_{\mathit{i}}-{\widehat{y}}_{\mathit{i}}\right)}^{\mathbf{2}}}$	yi = sample value ŷi = predicted sample value
Akaike information criterion (AIC)	$\mathit{AIC}=\mathbf{2}\mathit{S}+\mathit{N}\left[\mathit{l}\mathit{n}\left(\frac{\mathit{SSE}}{\mathit{N}}\right)\right]$	S = parameter number N = sample number
Total sum of squares (SST)	$\mathit{SST}={{\displaystyle \sum \left({\mathit{y}}_{\mathit{i}}-{\overline{y}}_{\mathit{i}}\right)}}^{\mathbf{2}}$	yi = sample value $\overline{y}$ = sample mean
Coefficient of determination (R2)	R2 = 1 – SSE/SST
Adjusted coefficient of determination (R2adj)	${\mathit{R}}_{\mathit{adj}}^{\mathbf{2}}=\mathbf{1}-\left[\frac{\mathit{N}-\mathbf{1}}{\mathit{N}-\mathit{p}}\right]\left(\frac{\mathit{SSE}}{\mathit{SST}}\right)$	p = total number of explanatory variables N = sample number
Root mean square error (RMSE)	$\mathit{RMSE}=\sqrt{{\displaystyle \sum {\left({\mathit{y}}_{\mathit{i}}-{\widehat{y}}_{\mathit{i}}\right)}^{\mathbf{2}}/\mathit{N}}}$	yi = sample value ŷi = predicted sample value N = sample number

Each statistical measure used is described, as well as the corresponding variables and parameters.

Defining Prediction Bounds and Percentiles

Upon analyzing the statistical measures calculated in this study, we sought the optimal curve that best represented the data. To provide clinical applicability, the male and female growth models were characterized with percentiles. To develop these percentiles, we defined prediction bounds dependent upon confidence limits. We employed the confidence bound statistical algorithms in the curve fitting routines from Matlab. In particular, the confidence limits were determined by applying the formula

$$C=b\pm t\sqrt{S},$$

where b represents the initial goodness of fit coefficient, C is the new confidence level coefficient, S is the vector of diagonal components from estimated covariance matrix of the coefficient estimates (X^T X)⁻¹z², where T represents transpose, z represents the mean squared error, and X is the Jacobian matrix of the fitted values with respect to the coefficients b. The variable t is reliant on the confidence level and is found using the inverse of the cumulative Student t-distribution function. The prediction bound curves are then developed by applying

$$y\pm t\sqrt{mS{m}^T},$$

where y is the model fit and m is a row vector of the Jacobian determined at a specific predictor value, and the percentiles are established by setting the initial model fit as the mean of the standard deviation curve.^4,6

Results

Curve Fit Models

The various models were fit to the brain growth data from birth to the age of 18 years for both males and females. These global fits resulted in the plots for the Weibull models, West ontogenic models, Gompertz models, and two-term power law models shown in Fig. 1. The insets in these plots are the residual errors that describe the difference between the model and the data at each point. For both sexes, all of the models show rapid growth within the first 2 years, and then the growth rate rapidly decreases. For the West ontogenic, Weibull, and Gompertz models, a stationary asymptote is reached. It is only the two-term power law that continues to show slow yet consistent growth up until and beyond age 18 years.

FIG. 1.

Normative model curve fits. The open circles represent different brain volumes at different ages. The curves fit to these data represent the models described above each plot. A–D represent female models, while E–H represent male models. The insets in each plot are the residual errors describing the difference between the model and the data at each point.

Statistical Analysis

Statistical measures were calculated for each model as shown in Table 3. The Weibull model gives the best statistical fits for the male and female data. The two-term power law gives the worst fits. Since human brain volume reaches a peak in the 2nd decade of life, a power law fit may have limited applicability beyond the early childhood period of rapid brain development.²⁰

TABLE 3.

Statistical measures for model fits

Growth Functions	RMSE	R2	R2adj	SSE	AIC
F Weibull	80	0.90	0.90	1.8e+05	275
F West ontogenic	91	0.87	0.87	2.5e+05	281
F Gompertz	112	0.82	0.80	3.4e+05	296
F Two-term power law	118	0.81	0.80	4.2e+05	301
M Weibull	87	0.91	0.90	2.3e+05	298
M West ontogenic	90	0.89	0.89	2.6e+05	298
M Gompertz	92	0.90	0.89	2.5e+05	303
M Two-term power law	140	0.79	0.78	6.2e+05	330

AIC = Akaike information criterion; RMSE = root mean squared error; R² = coefficient of determination; R²_adj = coefficient of determination adjusted for the number of terms; SSE = sum of the squared errors.

The growth functions preceded by an F represent the female models, while the functions preceded by an M represent the male models. The statistical measurements for each global fit are shown. There were 31 female and 33 male scans in the data set.

Weibull Clinical Curves

To achieve the objectives of this paper, the Weibull fits were plotted as clinically usable female and male growth charts displaying the Weibull model with percentiles in Fig. 2. The supplementary material for this report (available online) contains high-resolution images of the plots in Fig. 2 for printing, as well as a MATLAB algorithm that permits the user to change the percentiles or axis limits as desired to customize these growth charts for clinical study use.

FIG. 2.

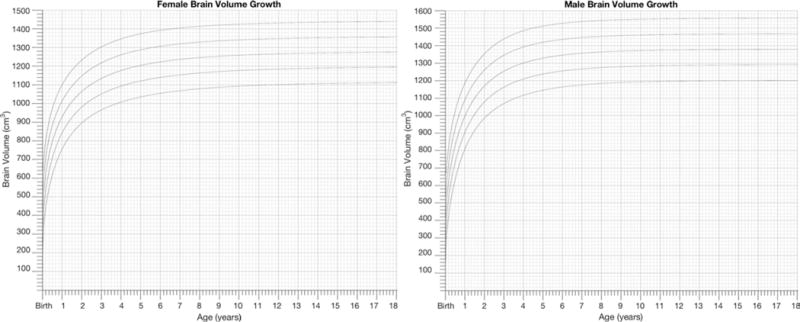
Weibull growth charts. The Weibull curve fits for the NIH female and male normative data are shown in this figure as growth charts. High-resolution versions are available in the supplementary material, along with a modifiable software code.

Model Parameters

For reproducibility purposes, the best-fit model parameters are presented in Table 4.

TABLE 4.

Best-fit parameters

Model Parameters	a	b	c	d
Gompertz female	1300	11.4	0.342	−305
Gompertz male	1300	13.3	0.338	−305
Two-term power law female		126	0.224	450
Two-term power law male		165	0.209	440
Weibull female		917	0.029	0.595
Weibull male		975	0.014	0.711
West ontogenic female		0.058
West ontogenic male		0.066

The parameters a, b, c, and d are shown, representing the optimally fit coefficients determined for each model fitting the brain volume as in Table 1.

Discussion

Brain growth has often been studied in relation to whole body growth, and there is a long history of comparative but static measurements of brain size.¹² In 1897, Eugène Dubois discussed the use of a power law relationship between the weight of the mammalian brain and the weight of the body.⁹ In his classic 1917 work On Growth and Form, D’Arcy Wentworth Thompson observed: “The changing ratio with increased magnitude is especially marked in the case of the brain, which constitutes an eighth of the body-weight at birth, and but one fiftieth at twenty-five.”²⁸ Julian Huxley and Georges Teissier used the term allometry in 1936 to define the relative changes in body part dimensions corresponding to the overall growth of the body.¹⁵

Despite this long history of interest, there is still no definitive method for describing normative brain volume growth. Moreover, the volumetric growth of the brain over time has not received as much attention as has relative growth. And with respect to neurosurgery, the dynamics of brain growth have not been a metric that has been used to guide surgical management.

Mechanistic Versus Empirical Models

Empirical models, such as the human head circumference curves, have proven to be invaluable in characterizing growth and for their clinical utility.

While “All models are wrong,”¹ it is important to acknowledge the value of a fundamental mechanistic model.²⁶ Although all of the models explored within this study are mechanistic in principle, only the West ontogenic model³¹ has a strong biological basis.

Asymptotic Versus Continuous Growth

It is clear from Fig. 1 that the two-term power law represents a different growth pattern from the other models. While the West ontogenic, Weibull, and Gompertz functions all show the brain volume growth reaching a maximum value, the two-term power law shows continuous growth throughout the entire age range. There are some animals, such as the Nile crocodile, that continue to grow throughout life, and in those animals such a simple power law is a superb fit to long-term brain growth.²² For the human brain, however, our statistical metrics reveal the worst applicability for the two-term power law, while the best overall statistical fit belonged to the Weibull model.

The Weibull Model

Although Huxley’s power law is prominent in the literature as a model for biological allometric growth, the Weibull model appears to be a better model for normative human brain volume growth. Weibull introduced his model in 1951 as a general statistical distribution that represents phenomena such as failure of “weakest links in the chain.”³⁰ This chain link failure principle has found much utility in survival analysis, because the probability of not dying requires that one not have died of any one of many different causes (e.g., tyrannosaur ageing²³). Viewed from the reverse standpoint, an ensemble of elements grows when any of its elements grow. The distribution follows an S-shaped sigmoidal curve, and most growth in plants or animals follows such a qualitative sigmoid curve with an inflection point.¹⁸ Weibull himself applied this distribution to a distribution of growth as measured in heights of boys,³⁰ and the Weibull growth function has found much success in modeling growth from certain species (e.g., fast-growing mule ducks²⁹) but less so for others (e.g., slow-growing California turkeys⁷).

We were surprised that the West ontogenic model did not fit brain growth as well as the Weibull distribution.³¹ The West model was designed as a biologically based growth curve and has shown great universality for body mass growth dynamics across a wide range of the animal kingdom.³² One of the key elements in the West formulation is that the mass of the body is a direct function of cell replication and the number of cells. However, neuronal replication is largely completed by the time of birth, and postnatal brain growth results more from synaptogenesis, axonal and dendritic sprouting, and myelination than from cellular proliferation.⁵ In addition, a key element of the West formulation for the brain is that the relative relationship between capillary supply and cellular demand ultimately limits growth in mammals. We speculate that the unique relationship between brain metabolic demand and supply might further push the mammalian brain away from the basic assumptions of the West model.

Study Limitations

The limitations of this study include a relatively small sample number and the fact that the sample population consisted of a representative group of children from North America. Our brain volumetrics were semiautomated, but we curated the results by hand to ensure that each image was accurately segmented.²⁰ Our findings should be followed up with research on larger data sets as more automated approaches to brain volume determination render such larger-scale studies increasingly feasible.

It would be useful to consider an alternative set of curves for brain volumes of individuals who have been born prematurely,¹³ but to our knowledge there is no existing imaging database of growth of such individuals. In addition, the normal growth curves of prematurely born infants would need to be developed from uncomplicated clinical courses, without for instance hemorrhagic stroke or ischemic damage to the brain. This would be an increasingly difficult task in terms of the most premature infants for whom such curves would be most needed.

Another difficult task is how to best handle the congenital malformations associated with hydrocephalus, such as spina bifida with myelomeningocele, frequently associated with polymicrogyria, or aqueductal stenosis complicated by neuronal migration anomalies.¹⁶ Similarly, one might ask whether the ventriculomegaly associated with skeletal dysplasia, such as achondroplasia,¹¹ might be better managed by the effect on normative growth if normal growth could be defined for such syndromes. Our conjecture is that studying the range of growth of such conditions in relationship to normal growth may be a way forward to better define clinical management goals. Correlating such growth with neurocognitive outcome¹⁷ might be a way to define optimal brain growth in the management of such children. It is also of interest to consider whether geographical region-specific brain growth curves would be advantageous to develop for applications to different regions of the world.^12,19

Conclusions

Since the Weibull model provided the best fit for male and female normative human brain volume growth, we developed curves for clinical and research use (available at high-resolution for printing, along with source code for further customizing the curves, in the supplemental material). These curves provide a new tool for clinicians and researchers to measure brain growth in clinical studies, and monitor growth along with treatment for conditions such as hydrocephalus. We anticipate that further work will refine these model fits, and their percentiles, and may lead to a standard tool for clinical rather than research use when consensus curves are established.