Use of the NESMA filter to improve myelin water fraction mapping with brain MRI

Abstract

Background and Purpose:

Myelin water fraction (MWF) mapping permits direct visualization of myelination patterns in the developing brain and in disease. MWF is conventionally measured through multiexponential T₂ analysis which is very sensitive to noise, leading to inaccuracies in derived MWF estimates. While noise reduction filters may be applied during post-processing, conventional filtering can introduce bias and obscure small structures and edges. Advanced non-blurring filters, while effective, exhibit a high level of complexity and the requirement for supervised implementation for optimal performance. The purpose of this paper is to demonstrate the ability of the recently introduced nonlocal estimation of multispectral magnitudes (NESMA) filter to greatly improve determination of MWF parameter estimates from gradient and spin echo (GRASE) imaging data.

Methods:

We evaluated the performance of the NESMA filter for MWF mapping from clinical GRASE imaging data of human brain, and compared the results to those calculated from unfiltered images. Numerical and in vivo analyses of the brains of three subjects, representing different ages, were conducted.

Results:

Our results demonstrate the potential of the NESMA filter to permit high quality in vivo MWF mapping. Indeed, NESMA permits substantial reduction of random variation in derived MWF estimates while preserving detail.

Conclusions:

In vivo estimation of MWF in the human brain from GRASE imaging data was markedly improved through use of the NESMA filter. The use of NESMA may contribute to the goal of high quality MWF mapping in clinically feasible imaging times.

INTRODUCTION

Myelin is an electrical insulator essential for action potential conduction and for transporting trophic support to the neuronal axons of the central nervous system (CNS).¹ Patterns of myelination represent an important biomarker for CNS diseases and neurodevelopment.^2,3 In 1994, Mackay and colleagues demonstrated the possibility of in vivo mapping of the myelin water fraction (MWF), a surrogate for myelin content, in human brain using magnetic resonance imaging (MRI).⁴ Since then, several methods have been introduced to either accelerate image acquisition or to improve data analysis.^2,5–7 Among them, multi-spin-echo (MSE)-based MRI sequences, namely the Carr-Purcell-Meiboom-Gill sequence (CPMG) or its accelerated version, the gradient and spin echo (GRASE) sequence,^8,9 remain the reference methods.^2,5 This is likely due to the availability of these imaging sequences on most pre-clinical and clinical MRI systems, the simplicity of the signal model, and the extensive histological validation conducted over the last two decades.^2,10,11

MWF can be measured from MSE imaging data through multicomponent T₂ analysis using the nonnegative least-squares algorithm (NNLS)^4,9,12,13 which does not require any a priori assumptions about the number of distinct underlying relaxation components. However, a well-known difficulty in MWF estimation is the sensitivity and instability of multiexponential decay analysis to noise,¹⁴ whether using NNLS or other analytic methods, leading to inaccuracies in derived MWF estimates.^5,15,16 Increased accuracy may be achieved though application of noise reduction filters during post-processing.^16–19 However, conventional linear filtering can introduce bias, leading to inaccurate parameter estimation, and can obscure small-scale structures by partial volume effect.²⁰ While attempts have been made to improve MWF mapping using more advanced filtering methods,^{15–18,21–24} performance was limited, especially at moderate signal-to-noise ratio (SNR); in addition, these applications required several user-defined parameters, adding substantially to difficulty in implementation.

In previous work, we introduced a new denoising image filter that is nonlocal (NL), that is, incorporates information from non-adjacent voxels, and multispectral (MS), that is, incorporates image intensities from different acquisition modalities or experimental parameter values, based on maximum likelihood (ML) estimation of voxel intensities using the intensities of M selected similar voxels. In the case of multiecho data sets, the selected voxels are defined as those that exhibit signal intensities over the full range of echo times (TEs) that are similar to the signal intensities of the index voxel, according to a specified metric.²⁰ In our most recent implementation, we replaced the maximum likelihood estimation (MLE) by the simple average of the amplitudes of these similar voxels. This markedly decreases both computational time and implementation complexity while maintaining nearly equivalent filtering performance. This filter outperforms currently available advanced filters, including nonlocal and multispectral filters, in term of noise reduction and detail preservation^20,25 and has been denoted nonlocal estimation of multi-spectral magnitudes (NESMA).²⁵ In addition to its improved performance as compared to other state-of-the-art filters, NESMA i) is straightforward to implement, ii) is very fast, rendering it suitable for routine use and analysis of large datasets, and iii) requires minimal user-defined parameters.^20,25

The main purpose of this study is to evaluate the performance of the NESMA filter for clinical MWF determination from in vivo human brain GRASE imaging data, and to compare the results to those calculated from unfiltered images. In vivo studies and numerical simulations were conducted to evaluate the performance of the filter in the clinical setting.

MATERIALS & METHODS

The NESMA filter

We consider perfectly registered multispectral images defined on a discrete grid I, which describes the bounded 3D spatial domain spanned by the image, given by S = {S(i) | i ∈ I, S(i) ∈ R^K}, where K is the total number of frames of the multispectral dataset. In this work, we define a frame k as an image within the multispectral dataset obtained with a particular value of TE. The underlying idea of quantitative filters is to reduce noise by replacing the noisy intensity of a given voxel by an unbiased estimation of its underlying amplitude. This requires selection of voxels that are likely to come from similar tissue. The NESMA filter restores the amplitude, A, of an index voxel, i, based on M preselected voxels with similar multispectral signal patterns through:

$${\widehat{\text{A}}}_{\text{k}}(\text{i})=\frac{1}{\text{M}}{\displaystyle \sum _j^{\text{M}}{\text{S}}_{\text{k}}}(\text{j}).$$ [1]

The number M of similar voxels is conventionally held constant in the construction of nonlocal MLE filters, including in our previous implementations.^20,26 However, the optimal value may in fact vary among different image regions. We therefore implemented a spatially adaptive selection of M using the relative Manhattan distance (RMD), defined as²⁵

$$\text{RMD}(\text{i},\text{j})=100\times \frac{{\displaystyle {\sum }_{\text{k=1}}^{\text{K}}\left|{\text{S}}_{\text{k}}{\text{(i)-S}}_{\text{k}}\text{(j)}\right|}}{{\displaystyle {\sum }_{\text{k=1}}^{\text{K}}{\text{S}}_{\text{k}}\text{(i)}}}.$$ [2]

In this work, the RMD was calculated between the index voxel and all voxels belonging to a relatively large search window of size R, centered around the index voxel i, in which emission and reception B₁ fields and noise standard deviation (SD) were assumed to be approximately constant.^13,27,28 The size of the search window, R, was fixed to to 21 mm x 21 mm x 21 mm, corresponding, in this work, to 21 voxels x 21 voxels x 7 voxels. Voxels with RMD < 5% were considered similar to the index voxel. Preliminary comparisons of NESMA with advanced filters in terms of noise reduction, small structure preservation, speed, and simplicity in implementation have been presented elsewhere.^20,25 All analyses were performed with MATLAB (MathWorks, Natick, MA, USA) using a 2.4 GHz computer.

MWF mapping

In each voxel, MWF was calculated via the inverse Laplace transform (ILT) using a regularized NNLS algorithm.^4,5,12 The regularization factor, λ, was defined based on the discrepancy principle such that 1.02${\text{χ}}_{mim}^2\le {\text{χ}}_{\text{reg}}^2\le 1.025\cdot {\text{χ}}_{\text{min}}^2$, where χ²_min and χ²_reg are the calculated misfit between the data and the model obtained from the nonregularized and regularized solution, respectively.^4,12,27 The input kernel matrix was created using 60 possible T₂ values, logarithmically spaced from 8 to 2000 ms, and 32 TE values corresponding to the experimental values indicated below. For each T₂ and TE combination, we used the extended phase graph (EPG) algorithm to correct for stimulated echoes.^13,27 The input normalized B₁ value was first obtained by fitting the experimental signal to a single component decay using the EPG; this allows fast and accurate determination of B_1.²⁹ Finally, the MWF was calculated as the integral of the T₂ distribution between 8 and 40 ms, normalized by the total area under the distribution.^4,9,12,27,30

In vivo analysis

3D GRASE images were acquired from the brains of three healthy subjects (males, ages 24 and 85, and female, age 43). For each participant, 32 echoes were acquired with TE_n = n * ΔTE, where ΔTE = 11.3 ms, TR = 1000 ms, EPI factor = 3, field-of-view = 278 mm x 200 mm x 30 mm, acquisition matrix size = 185 × 133 × 10, acquisition voxel size = 1.5 mm x 1.5 mm x 3 mm, reconstructed to 1 mm x 1 mm x 3 mm using zero-filling in k-space. The total acquisition time was ~10 min. All experiments were performed on a 3T whole body Philips MRI system (Achieva, Best, The Netherlands) using the internal quadrature body coil for transmission and an eight-channel phased-array head coil for reception. The approximate SNRs, defined as the mean signal at the first TE divided by the signal SD at the last TE calculated over large white matter regions, were ∼190, ~180, and ~165, for the 24, 43, and 85 year old participants, respectively. The nature of the experimental procedures was fully explained to the subjects, from whom written informed consent was obtained prior to participation. All examinations were performed in compliance with the standards established by our local Institutional Review Board.

The first analysis consisted of illustrating the sensitivity of NNLS to noise, and the spatial variation of the regularization factor, λ, before and after NESMA-filtering. The optimal value of λ, as determined by the χ² criterion described above, is itself highly nosie-dependent. Thus, for each participant, we compared signal decay curves and corresponding T₂-distributions from four different voxels before and after image NESMA-filtering. In addition, we constructed maps of λ for corresponding unfiltered and filtered images for a representative slice. This provides a quantitative visual representation of the values of λ required for regularization as defined above; in general, larger values of λ, with potential masking of fine structure in the T₂ histogram, are required for worse SNR.

The second analysis consisted of comparing MWF maps derived from unfiltered and NESMA-filtered datasets obtained from the brains of the three participants. For each participant, results were displayed for three representative slices. Moreover, the mean and SD of MWF values were calculated in five different regions-of-interest (ROI). The first ROI lay within the centrum semiovale (CS), the second within the genu of the corpus callosum (GCC), the third within splenium of the corpus callosum (SCC), the fourth within the limbs of the internal capsule (LIC), and the last region encompasses all previous regions. Results for this last ROI are presented as smoothed Gaussian histograms using the MATLAB command histfit.

Numerical analysis

Numerical simulations were conducted to further assess the performance of NESMA for MWF determination from GRASE imaging data. Noise-free 3D GRASE brain images were generated at 32 TEs, linearly spaced between 11 ms and 352 ms, assuming a biexponential signal model that incorporates myelin and intra/extra cellular water peaks. MWF maps and relaxation times derived from NESMA-filtered images of the brain of the 43-year-old participant were used as input parameters since that participant showed the greatest range of MWF values. Input relaxation time maps were calculated by defining the T₂ of myelin as the short component peak ranging from 8 ms to 40 ms, while the T₂ of the intra/extra cellular water as the component peak ranging from 40.1 ms to 200 ms. For each voxel, these MWF and relaxation time values were used to generate a distribution of relaxation times rather than two distinct components, following the method described by Dula et al.³¹ Gaussian noise was then added to produce images with SNR of 200, corresponding to in vivo values.^27,29 MWF images were derived as outlined above from unfiltered or NESMA-filtered images. For each slice, mean and SD MWF values were calculated in a large white matter region defined by manual segmentation. In addition to visual inspection, MWF absolute error (AE) maps were calculated as a quantitative measure of filtering performance, with maps derived from infinite SNR taken as the reference. In each voxel, AE was defined as the absolute difference between the estimated and reference MWF values. These MWF and AE maps were displayed for three different slices. AE histograms and the mean and SD of AE values were calculated from white matter voxels over the entire imaged volume.

RESULTS

Figure 1 shows an illustration of the sensitivity of the NNLS algorithm to noise and and the spatial variation of the regularization factor, λ, required in the NNLS algorithm before and after NESMA-filtering. Signal decay curves from four different voxels (left panel) as a function of TE from unfiltered and NESMA-filtered images and corresponding T₂-distributions obtained using NNLS (middle panel) are displayed for each participant. There is clearly a large variation in the morphology of the derived T₂-distributions from the unfiltered voxels, with much less variation seen after filtering. Two distinct peaks, corresponding to MWF and intra/extra cellular water, are clearly visible in the T₂-distribution obtained from the filtered signal. This analysis illustrates the high degree of sensitivity of the NNLS analysis of transverse relaxation to noise, and the substantial improvement obtained through NESMA filtering. This is further illustrated by λ-maps calculated from unfiltered and filtered images (right panel). The substantial decrease in the required degree of regularization after filtering is evident. Indeed, the values of λ were approximately a factor of 2 to 4 lower in parenchymal regions after filtering. Finally, the λ-maps derived from unfiltered images showed a much greater degree of random variation than the NESMA-filtered images.

Figure 1.

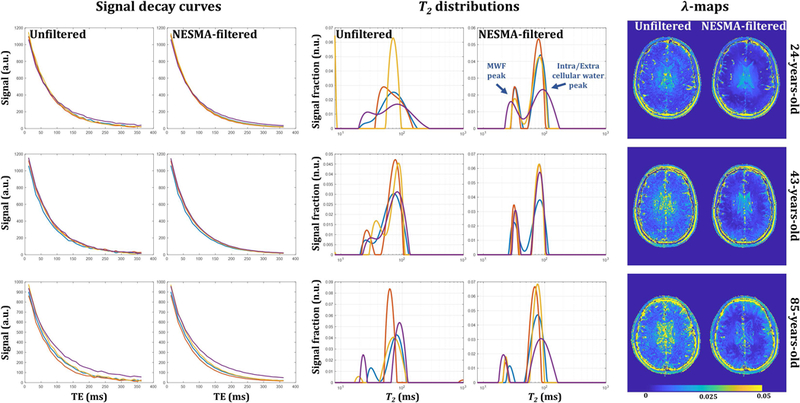
Illustration of the sensitivity of nonnegative least squares (NNLS) to noise and the spatial variation of the regularization factor, λ, required in the NNLS algorithm before and after NESMA-filtering. Left panel: representative signal decay as a function of TE from four different voxels before and after filtering. Middle panel: corresponding T₂-distributions obtained using NNLS. Each voxel is described by a T₂ distribution with two dominant components corresponding to myelin or intra/extra cellular water. There is clearly a large variation in the morphology of the T₂-distributions derived from the unfiltered voxels; in fact, the two underlying signal components are not resolved in several voxels, especially those with large values of λ. This result was found to be typical for white-matter voxels. In contrast, markedly decreased variation is seen in the T₂ distributions obtained after filtering. This illustrates the sensitivity of the NNLS analysis to noise, and the significant improvement obtained through NESMA filtering. Right panel: maps of the λ values used for regularization, calculated by the optimization procedure described in the text, for unfiltered and filtered myelin water fraction (MWF) maps derived from GRASE imaging data. The random variation evident in the λ-maps derived from unfiltered images is virtually absent in the λ-maps derived from NESMA-filtered images. Furthermore, the values of λ are substantially reduced after NESMA filtering, especially in parenchymal regions, indicating greatly improved data quality and reduced distortion of the T₂ histogram derived from the NNLS analysis.

Figure 2 shows a comparison of derived MWF maps from the brains of three subjects of different ages. Maps calculated from unfiltered and NESMA-filtered images are displayed for three different slices. As is readily seen, there is substantial random variation in MWF maps derived from unfiltered images, as well as “voids”,¹⁶ that is, voxels with very low MWF values, as indicated by the white arrows. However, MWF maps calculated from NESMA-filtered images exhibited preservation of edges and small structures, as well as greatly reduced random variation and nearly complete absence of voids as compared to unfiltered images. Further, the mean MWF values obtained from the unfiltered images were, overall, lower than those obtained from the filtered images (Fig. 3). We attribute this to underestimation of MWF due to the presence of artefactual voids as defined above. In addition, the SD of MWF values derived from unfiltered images was substantially larger than the SD derived from filtered images. This is likely due to the presence of voids as well as the direct effect of noise. The computation times required to filter the entire dataset using NESMA was ∼130 s.

Figure 2.

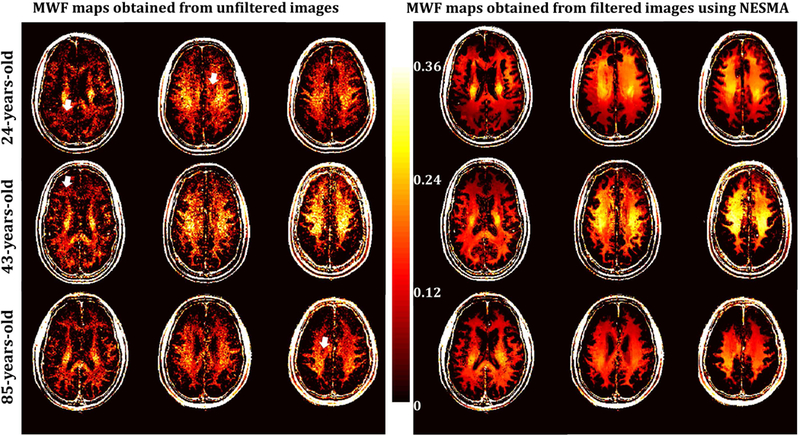
Myelin water fraction (MWF) maps derived using GRASE acquisition with non-negative least squares analysis from unfiltered or NESMA-filtered images. Results are shown for three different slices obtained from the brains of three subjects of different ages. As is readily seen, MWF maps derived from NESMA-filtered images exhibited more consistency and less variation than those derived from unfiltered images. Moreover, maps derived from unfiltered images shows substantial voids, that is, voxels with very low MWF values, as indicated by the white arrows. Further, the brain of the middle-aged subject exhibits greater MWF values than seen in the younger or the older subjects in several regions; this is in good agreement with the results of Arshad et al.⁶⁷.

Figure 3.

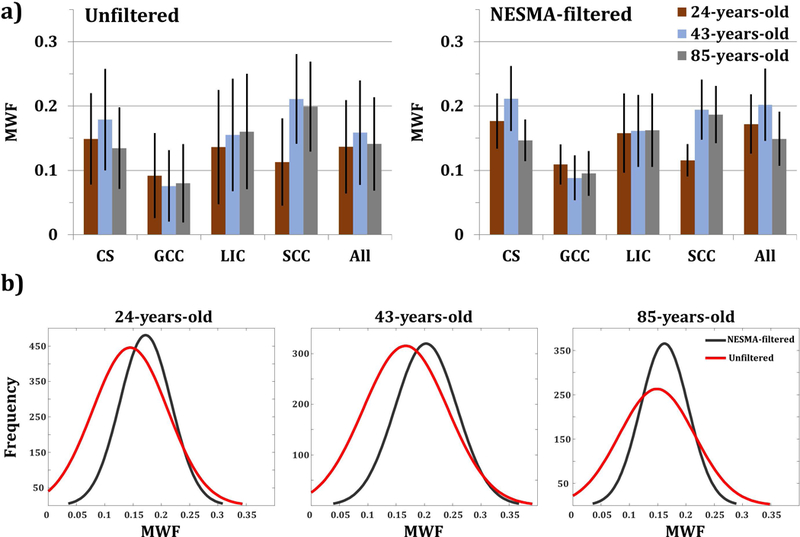
a) Mean and standard deviation myelin water fraction (MWF) values calculated in five different regions-of-interest (ROI). The first ROI lay within the centrum semiovale (CS), the second within the genu of the corpus callosum (GCC), the third within splenium of the corpus callosum (SCC), the fourth within the limbs of the internal capsule (LIC), and the last encompasses all previous regions. b) Smoothed Gaussian histograms showing the distribution of MWF within the composite ROI, using unfiltered and filtered images for each participant.

Figure 4 shows examples of MWF maps, AE maps, and AE histograms derived from simulated GRASE images obtained from three slices of the brain of the 43-year old participant. Results are shown from NNLS analysis of unfiltered and NESMA-filtered images. As is readily seen, MWF maps derived from the NESMA-filtered images exhibited preservation of edges and small structures, as well as greatly reduced random variation as compared to those derived from unfiltered images. Furthermore, the mean and SD of MWF values derived from NESMA-filtered images were very close to reference values derived from infinite SNR data. In contrast, mean MWF values derived from unfiltered images exhibited systematic underestimates, as well as larger SD. These results are in good agreement with our in vivo results (Figs. 2–3). Moreover, quantitative analysis of the filtered images showed negligible AE in the brain parenchyma, in contrast to the significant AE obtained from unfiltered images.

Figure 4.

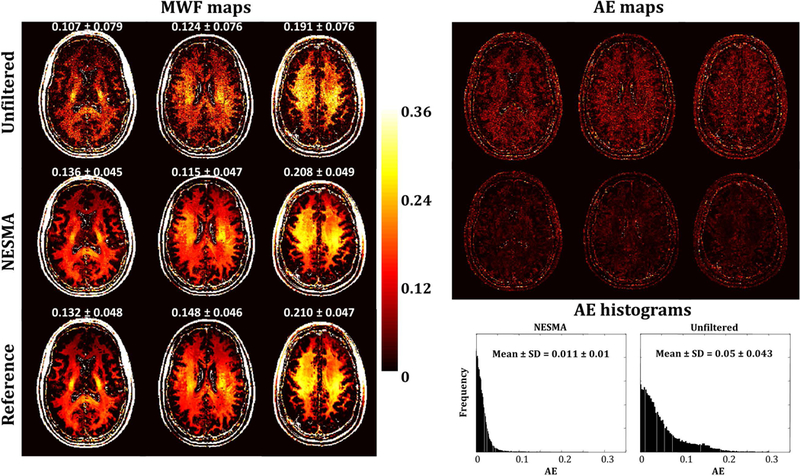
Myelin water fraction (MWF) maps, absolute error (AE) maps, and AE histograms derived from unfiltered and NESMA-filtered simulated GRASE images. Mean and standard deviation (SD) MWF values were calculated over a large region laying within white matter and are reported above each slice. AE histograms and mean and SD AE values were obtained from large white matter regions over the entire imaged volume. As is readily seen, derived MWF maps from NESMA-filtered images exhibited more consistency and less variation with lower AE than those derived from unfiltered images. Further, mean and SD MWF values derived from NESMA-filtered images were very close to the reference values derived from noiseless images. In contrast, mean MWF values derived from unfiltered images were systematically underestimated and exhibited larger SD. These results are in good agreement with the in vivo results (Figs. 1, 2 and 4). Finally, as expected, AE histograms indicate that MWF estimates from unfiltered images exhibit larger dispersion than those derived from NESMA-filtered images.

DISCUSSION

Regional alterations in myelin content have been found to be associated with a number of CNS diseases, including multiple sclerosis,^{2,10,30,32–39} neuromyelitis optica,⁴⁰ epilepsy,⁴¹ Parkinson’s disease,⁴² mild cognitive impairment,⁴³ Alzheimer’s disease,^44–46 phenylketonuria,⁴⁷ stroke,⁴⁸ schizophrenia,⁴⁹ and autism.⁵⁰ However, high-quality, high-resolution MR imaging of MWF is challenging, especially in the clinical setting,^{15,24,29,51–58} in which scan times are necessarily limited. In the present work, we investigated the ability of our recently introduced NESMA filter^20,25 to enhance the quality of derived MWF maps from clinical GRASE imaging data. Our in vivo analysis showed that estimation of MWF was markedly improved through use of the NESMA filter (Figs. 1–4). Indeed, our results indicate that NESMA filtering results in MWF maps with increased anatomic detail and delineation of local myelin patterns as compared to results obtained from unfiltered images. Further, our numerical analysis showed markedly reduced AE in MWF maps calculated from NESMA-filtered as compared to unfiltered images (Fig. 4).

It is well-known that the ILT is an ill-posed problem;^59–61 this renders the result of the ILT highly sensitive to noise and of potentially limited accuracy. While regularization may reduce these limitations,⁶² derived MWF values are highly sensitive to the degree of regularization, λ,⁶³ especially at clinical SNR. Our results showed that as expected, larger values of λ were required to regularize the signal decays from the unfiltered images. The histogram blurring resulting from this greater degree of regularization led to the inability to resolve underlying signal components of the T₂-distribution in a substantial number of voxels in these images (Fig. 1).^{9,12,13,16,27} In contrast, the dominant components of the T₂-distributions were well-resolved in all voxels in the filtered images, demonstrating the ability of NESMA to reduce the impact of regularization on MWF determination. We note that several slices showed myelin content extending to the brain periphery, especially in the brains of relatively young participants (Fig. 2). This is in accorda with previous data.^27,64 In addition, we note that this pattern is visible in MWF maps derived both with and without filtering (Fig. 2), and so is not attributable to a filtering artifact. Similarly, it is seen independently of the use of, or degree of, regularization (data not shown).

Most of the post-processing approaches for improved determination of MWF^15,21–24 require ad hoc adjustment of tuning parameters, adding further complexicity to their implementation. While a detailed comparison of these methods is beyond the scope of the present description of the effect of the NESMA filter on MWF measurement accuracy using GRASE, Fig. 5 shows a simulation-based comparision of MWF determination from unfiltered images and from images filtered using the NESMA and the multispectral nonlocal means (MS-NLM) filters.²¹ At high SNR, both filters performed well. However, it is readly seen that at low-to-moderate SNR, the NESMA filter exhibits greater preservation of detail than the MS-NLM filter. MS-NLM is based on a weighted mean of signal intensities calculated between the voxel being filtered and each of the other voxels in a large search window. In the case of low contrast between tissues or low SNR, these calculated weights are likely to be inaccurate.²⁰ This translates directly into inappropriate weighting of voxels in the calculation of the estimated intensity of the index voxel, leading to, in effect, partial volume effects. In contrast, NESMA uses only similar voxels to restore the amplitude of the index voxel.^20,25 Detailed comparison analysis can be found in our previous studies.^20,25

Figure 5.

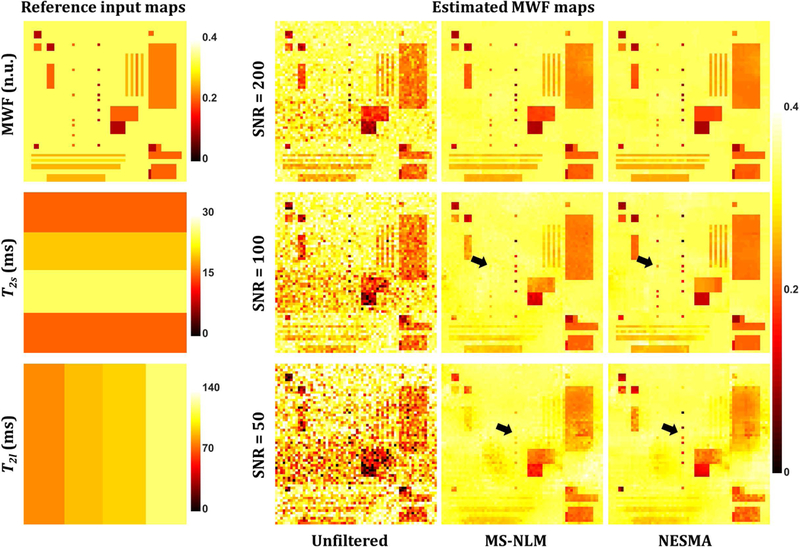
Left-hand panel: myelin water fraction (MWF), T_2s, and T_2l reference images used as inputs to evaluate filter performance. These reference images were derived from a simulated sequence of noise-free 3D T₂-weighted images generated at 32 TEs, linearly spaced between 10 ms and 320 ms, assuming a biexponential signal model that incorporates myelin and intra/extra-cellular water peaks. Gaussian noise was added to produce images with signal-to-noise ratio (SNR) of 200, corresponding to an in vivo value,^27,29 as well as 100 and 50, as may result from implementation of high-resolution fast imaging. Right-hand panel: Estimated MWF maps derived from unfiltered images or from images filtered using multi-spectral nonlocal means (MS-NLM) and NESMA, obtained as described in the text. Black arrows indicate example of regions where NESMA shows higher performance than MS-NLM.

An additional advantage to the high-resolution methodology we have introduced is the reduction of the partial volume effects that can lead to substantial errors in quantitative brain mapping. A related effect is the potential heterogeneity of tissue microstructure within an ROI selected for analysis; this has been recently addressed in the related context of myelin fiber mapping,⁶⁵ including in the investigation of dementia.⁶⁶ In fact, this approach to tract-specific structural measures represents an advance over what is currently possible with MWF mapping. On the other hand, MWF mapping has the potential to reflect underlying myelin content in a quantitative manner, while diffusivity, magnetization transfer, and relaxation times are less readily interpretable as quantitative measures of myelination.

Our results are consistent with recent studies indicating larger MWF values in the brain of middle aged subjects as compared to younger or old subjects.^45,67 This may be attributed to the process of myelination in the young-middle age, followed by demyelination in later years.^45,67 Further, our calculated MWF mean values were overall in good agreement with those previously reported using other techniques.^45,67. In contrast, both numerical and in vivo analyses revealed a systematic underestimation of mean MWF values and a larger SD of MWF values derived from unfiltered images. We believe that the presence of MWF voids,¹⁶ representing voxels in which the MWF is not resolvable from the larger non-bound water pool, is the major contributor to these effects, with additional variation deriving from the highly noise-sensitive determination of MWF from the unfiltered images, characteristic of ill-posed problems (Figs. 2–4). However, an important limitation of our study is the limited sample size in this initial study, so that no statistical conclusions can be drawn regarding disease status. However, our goal here was to establish the applicability of NESMA to improve MWF determination. and to indicate the potential of this approach for investigations of age and disease status.

In the present study, we showed that the NESMA filter permits substantial improvement in the quality of MWF maps derived from GRASE imaging datasets. However, NESMA is readily applicable to other multispectral imaging modalities to improve the quality of parameter estimates. This includes MWF mapping from multi-gradient echo imaging datasets,^68–71 relaxation time mapping,^72–74 diffusion imaging,^75–77 diffusion tensor imaging,^78–81 quantitative magnetization transfer,^82,83 quantitative susceptibility mapping,^84,85 perfusion mapping,^86,87 dynamic contrast enhanced measurements,⁸⁸ and other quantitative modalities in which successive images are obtained leading to multispectral characterization of individual voxels.^81,89 Moreover, the increase in SNR without loss of resolution in the filtered images may lead to enhanced clinical applicability of advanced signal models known to exhibit high sensitivity to noise.^90–92

Advantages of NESMA filtering include speed, with denoising of a whole brain volume requiring only few minutes, ease of implementation, quality of denoising while preserving resolution, and reliance on only a single user-defined parameter, the similarity threshold, RMD.²⁵ In fact, RMD must be carefully selected. Large values of RMD degrade the quality of noise reduction by including voxels that are progressively less similar to the index voxel. This translates directly into incorporation of inappropriate voxels into the calculation of the estimated intensity of the index voxel, leading to, in effect, inaccuracy in estimated signal intensity. To avoid this, we suggest the use of a small value of RMD, as it is the case in the present work. While this may penalize homogenous regions where large values of RMD would provide further increase in SNR, our analysis showed that use of small values still leads to excellent filtering performance, while preserving small structures and edges (Figs. 1, 2, 4). We note that an optimal value of RMD can also be estimated using numerical simulations with representative conditions, although this additional complexity may not lead to substantive improvements in filtering quality. Further, we have recently introduced a method for automatically selecting RMD²⁵ that permits variation of this parameter across the image, as appropriate for each index voxel. This requires a priori knowledge of the noise SD, which, while available in many cases, may be difficult to estimate in multichannel acquisitions due to potential correlation between coils and SENSE reconstruction.^93,94

In this work, we defined the MWF as the integrated area of the T₂ distribution over the range of 8 to 40 ms, divided by the total area of the distribution. While this corresponds to the conventional definition adopted in several studies,^{9,10,12,13,27,47,95} several other studies used 50 ms as an upper integration limit.^16,30,33,96 Levesque and colleagues have shown substantially different derived MWF values from the two ranges in several brain structures;⁹⁷ this is in accordance with our own observations (data not shown). We found that implementing their proposed method for adaptive selection of the T₂-range of MWF led to results similar to the ones we have presented. Indeed, in our NESMA-filtered images, ~40 ms appears to be an optimal upper limit; one example is seen in Fig. 1. However, using the same algorithm, derived MWF from unfiltered images showed substantial random variation; this is in agreement with Levesque’s et al. results.⁹⁷ Other factors may affect MWF estimation from MSE-based sequences such as CPMG and GRASE; this represents limitations of the present work as well as literature results. Indeed, the MSE signal model analyzed by ourselves and others neglects several factors including, i) exchange between water pools,^98–100 ii) magnetization transfer between free water protons and macromolecules, iii) T₁ effects resulting from the short TRs usually used, iv) off-resonance effects,^101–103 iv) J-coupling,^98,104 v) spin locking,^105,106 and vi) internal gradients.¹⁰⁷ Finally, as with any MRI sequence, the spatial gradients modulate the degree of signal attenuation due to water diffusion in underlying compartments, which is not modeled in the MSE formalism.

We note that the details of the T₂-distribution may be variable, with two or three relatively prominent histogram components. Because of this variation, assessment of MWF relies upon measurement of the total amplitude within a certain T₂ range, as described above, without direct consideration of the details of the underlying distribution.^{5,10,11,30,67,97} The precise interpretation of these components is a topic of current interest, but beyond the scope of the present manuscript, which centers on the improvement in MWF determination through use of the NESMA filter. In general, in all voxels examined, there were two dominant histogram components, attributable to relatively unbound water and to myelin water.

In conclusion, in vivo estimation of MWF in the human brain from GRASE imaging data was markedly improved through use of the NESMA filter. The use of NESMA may contribute significantly to the goal of high quality MWF mapping in clinically feasible imaging times, and is readily extendable to other quantitative modalities that use multispectral imaging datasets.