A fully automatic method yielding initial models from high-resolution electron cryo-microscopy maps

Abstract

A fully automated procedure for optimization and interpretation of reconstructions from cryo-EM is developed and applied to 476 datasets with resolution of 4.5 Å or better, including reconstructions of 47 ribosomes and 32 other protein-RNA complexes. The median fraction of residues in the deposited structures reproduced automatically was 71% for reconstructions determined at resolutions of 3 Å or better and 47% for those at lower resolution.

Improvements in electron cryo-microscopy (cryo-EM) data collection and image reconstruction methods have made it possible to obtain 3D images of macromolecules at resolutions where structural details such as locations of side chains can be readily visualized^1,2. A key limiting factor in structure determination by cryo-EM is now the effort required for interpretation of these reconstructed images in terms of an atomic model. Algorithms for de novo model-building using cryo-EM maps have been reported recently^3–8 and are capable of building very complete models in some cases. We have developed an integrated procedure that carries out map interpretation without user intervention and requires as inputs only a cryo-EM map, the nominal resolution of the reconstruction, the sequences of the molecules present, and any symmetry used in the reconstruction. Map interpretation begins with automatic image sharpening using an algorithm that maximizes connectivity and detail in the map⁹. The unique parts of the structure in the sharpened map are then identified with a segmentation algorithm that extends previous methods¹⁰ by taking into account reconstruction symmetry and choosing a contour level based on the expected contents of the structure (see Online Methods for details and Supplementary Fig. 1 and Ref. 11 for examples). For each part of the structure and for each type of macromolecule present, atomic models are generated using several independent methods, followed by extensive real-space refinement¹² using restraints based on automatically-identified secondary structure elements. Finally, our automated procedure carries out assembly and refinement of the entire structure including any symmetry that is present.

The steps in map interpretation are illustrated in Fig. 1. Part of a deposited cryo-EM reconstruction for lactate dehydrogenase (EMDB¹³ entry 8191¹⁴) obtained at a resolution of 2.8 Å is illustrated in Fig. 1A along with an atomic model (PDB¹⁵ entry 5k0z¹⁴) representing the authors’ interpretation of the reconstructed map. Our procedure optimizes map sharpening and yields an atomic model as an interpretation of that map (Fig. 1B). In the sharpened map in Fig. 1B, features such as side-chains can be clearly visualized without the need for a researcher to manually adjust the sharpening of the map. In this case (Fig. 1B) our automated interpretation does not determine the identity of the side-chains in this region of the map, but in other cases such as the reconstruction of β-galactosidase¹⁶ at a resolution of 2.2 Å (Fig. 1C) side chains are identified automatically for most of the structure.

Fig. 1.

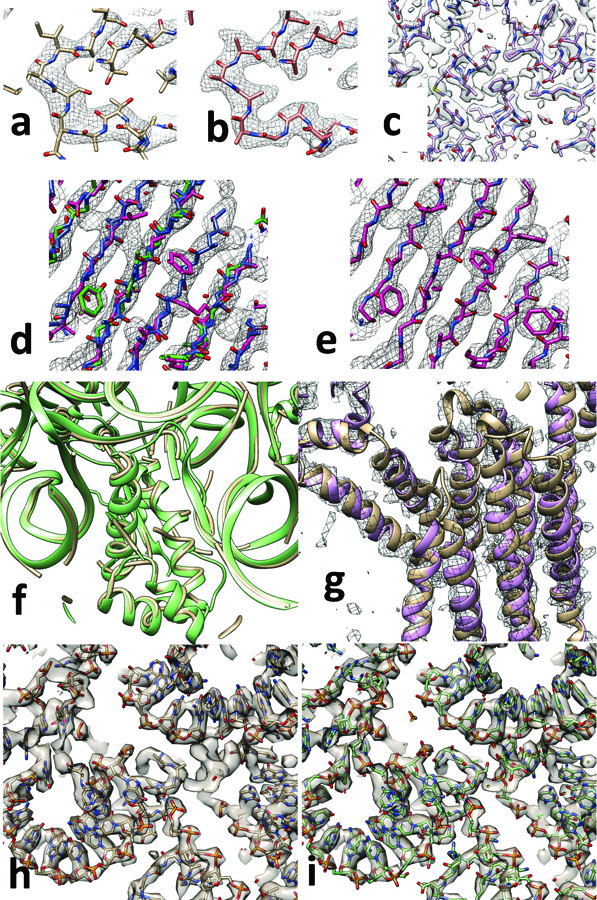
Automated interpretation of cryo-EM maps. A. Section through deposited cryo-EM reconstruction and deposited interpretation for lactate dehydrogenase¹⁴ (EMDB entry 8191). B. Automatically sharpened version of map in A with automatically generated model (PDB entry 5k0z). C. Automatic interpretation of β-galactosidase¹⁶ at a resolution of 2.2 Å. D. Automatically sharpened version of map for EMDB entry 6630 (glutamate dehydrogenase¹⁷) with three independent automatically-generated interpretations (using chain-tracing, green model, feature-based helix and strand identification, blue model, and pattern-based secondary structure identification with fragment-based extension, magenta model). E. Composite model derived from the three models in D. F. Automatically interpreted reconstruction of the Mycobacterium smegmatis ribosome (yellow tubes) compared with deposited model (green ribbons). G. Automatically generated model of the ERAD channel Hrd1 (purple ribbons) compared with deposited model (brown ribbons). H. detail of automatically-built Mycobacterium smegmatis ribosome, and I, corresponding portion of deposited model. See text for details. Graphics created with Chimera²².

Fig. 1D illustrates the procedure in more detail for the deposited cryo-EM reconstruction of glutamate dehydrogenase (EMDB¹³ entry 6630¹⁷) obtained at a resolution of 3.3 Å. Using the automatically sharpened map, three models were created, each using a different algorithm so as to minimize correlated errors. For each model-building algorithm, the main chain is built first, then the sequence is assigned and side chains are added based on the fit to density¹⁸. These three models are superimposed on the map in Fig. 1D (after applying reconstruction symmetry). The best-fitting parts of each model were combined and extended to fill gaps and the resulting composite model was refined to yield an interpretation of the reconstruction (Fig. 1E). For this glutamate dehydrogenase structure, 66% of the residues in the deposited model were reproduced by the automatically-generated model (C_α atoms in the deposited model matched within 3 Å), with a root-mean-square (rms) coordinate difference of 0.8 Å for matching C_α atoms.

We used a similar procedure to automatically generate interpretations of cryo-EM reconstructions containing complexes of RNA and protein. In addition to generating multiple models interpreting each part of a map as protein, further models were generated interpreting them as RNA, and the best-fitting parts of each model were combined to represent the protein-RNA complex. Fig. 1F shows such an automatically interpreted reconstruction of the Mycobacterium smegmatis ribosome¹⁹ (EMDB entry 6789) analyzed at a resolution of 3.1 Å and compared with the deposited model. Figs 1H and 1I compare a portion of automatically generated and deposited models in detail. The automatically generated model represents 60% of the RNA and 48% of the protein in the deposited model (PDB entry 5xym).

At lower resolution, a smaller fraction of the structures is typically reproduced by our methods, but secondary structural elements such as protein or RNA helices are often identifiable. Fig. 1G illustrates the automatically sharpened map and compares the automatic interpretation for the protein-conducting ERAD channel Hrd1²⁰ (EMDB entry 8637) with the deposited model. This reconstruction at a resolution of 4.1 Å was previously interpreted using a combination of fitting helices into density, manual model-building and Rosetta²⁰ modeling with distance restraints from evolutionary analysis (PDB entry 5v6p).

We evaluated the overall effectiveness of our procedure by applying it to all 476 high-resolution cryo-EM reconstructions in the EMDB database that we could extract with simple tools and match to an entry in the PDB. For chains in maps reconstructed at resolutions of 3 Å or better, the median fraction of protein and RNA residues in the deposited models reproduced by our approach was 71% and 45%, respectively (Fig. 2A). At lower resolutions, 47% of protein residues and 34% of RNA residues were reproduced. The median rms coordinate differences for matching C_α atoms in protein chains and for matching P atoms in RNA chains were each about 1/3 the resolution of the reconstructions (Fig. 2B). The median fraction of the sequence of the deposited structure that could be reproduced (Fig. 2C) was 28% for protein chains at higher resolution and 9% at lower resolutions (where random is about 6%). For RNA chains the sequence match was 49% at higher resolution and 42% at lower resolutions (random is about 25%). An analysis of the geometries of the models is presented in Supplementary Figs. 2 and 3. Substantial structural information can be obtained even at resolutions lower than the resolution of 4.5 Å for which the procedure was designed. Fig 2D and 2E show a comparison of our automatic analysis of horse spleen apoferritin at a resolution of 4.7 Å with the deposited model.

Fig. 2.

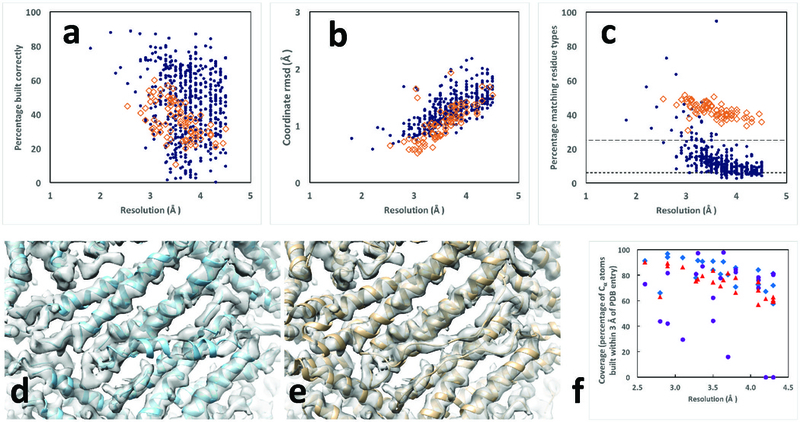
Residues in deposited models reproduced by automated analysis of cryo-EM reconstructions. Protein chains are indicated by blue dots and RNA chains are indicated by open brown diamonds. Residues are considered matched if C_α atom or P atom coordinates match within 3 Å (see Methods). Rms coordinate differences are assessed for all matched residues. A. Fraction of residues in deposited structure reproduced by automated analysis. Blue dots are protein chains and orange squares are RNA chains in panels A-C. B. Rms coordinate differences between matched residues in deposited structure and automated analysis. C. Fraction of residues in automated analysis matching a residue in the deposited model that also share the residue type of the matching residue in the deposited structure. The expected fraction matching based on random sequence assignment is roughly 6% for protein with 20 amino acids with frequencies in eukaryotes and roughly 25% for RNA with 4 bases and similar frequencies, illustrated by the horizontal lines in Fig. 2C. D and E, automatically generated and deposited models of horse spleen apoferritin (EMDB entry 2788 and PDB entry 4v1w). F. Comparison of fraction of deposited models reproduced by MAINMAST (blue diamonds), de novo Rosetta modeling (purple circles), and using the automated procedure described here (red triangles), all based on maps cut out from deposited maps based on a single chain of the deposited model as described⁸. Graphics created with Chimera²².

We carried out a comparison of our automatic model-building approach with two other recently-developed methods, MAINMAST⁸ and de novo Rosetta²¹ model-building. We applied our automated approach to 22 unique maps in the EMDB with a matching entry in the PDB, segmented to show a single chain as described⁸ and compared the models (Fig 2F and Supplementary Table I) with those obtained previously⁸. Our method (red triangles) yields an average coverage higher than Rosetta (purple circles) and lower than MAINMAST (blue diamonds). The models built by our automated procedure had the same or better accuracy (rms difference from deposited models of matching C_α atoms of 1.31 Å) as the MAINMAST models (rmsd of 1.51 Å) and the Rosetta models (rmsd of 1.33 Å).

With our automated procedure, essentially any high-resolution reconstruction with suitable meta-data describing the reconstruction, its resolution and reconstruction symmetry can be interpreted and a first atomic model generated without any manual intervention. The models produced are not complete at this stage. We anticipate that combining the integration available in our approach with others’ algorithms^3–8 may lead to both a high degree of automation and high model completeness.

One of the strengths of our automated model-building procedure is that a novice user will generally obtain the same result as an expert. Although most automatic tools have many parameters that the user can adjust to improve results in difficult cases, our approach, generally speaking, does not. Each time we can identify a parameter that needs to be adjusted depending on the situation, that parameter is automatically varied and optimized in our procedure. For example, the sharpening of a map is a highly important adjustable parameter, set by the user in most approaches. We developed a metric that we could use to evaluate map sharpening and use it to automatically optimize the sharpening of the map during the analysis. The result of this strategy is that our procedure has just one overall parameter (quick or not quick) that a user might normally adjust in order to ask the procedure to try harder for a difficult case. Another strength of automated procedures such as this is that they make analyses that would be challenging to carry out with tools that require manual input. With automated interpretation of a map, for example, error estimates can be obtained by repeating the interpretation using different algorithms or different random seeds in appropriate stages of analysis (see Supplementary Results).

Online Methods

Map optimization

Maps are automatically sharpened (or blurred) with phenix.auto_sharpen⁹, which maximizes the level of detail in the map and the connectivity of the map by optimizing an overall sharpening factor²³ B_sharpen applied to Fourier coefficients representing the map up to the effective resolution of the map. Beyond this resolution a blurring exponential factor B_blur with a value of 200 Ų is applied. This blurring procedure provides a way to dampen high-resolution information without requiring a precise knowledge of the optimal resolution cutoff.

Map segmentation is carried out by identifying all regions of density above an automatically-determined threshold, choosing a unique set of density regions that maximizes connectivity and compactness, taking into account the symmetry that is present.

Contiguous regions above a threshold in a map are identified using a region-finding algorithm. This algorithm chooses all the grid points in a map that are above a given threshold. Then it groups these grid points into regions in which every point in a region is above the threshold and is connected to every other point in that region through adjacent grid points that are also above the threshold.

The choice of threshold for defining regions of density is a critical parameter in segmentation¹⁰. We set this value automatically by finding the threshold that optimizes a target function that is based on three factors. One factor targets a specific volume of the map above the threshold. A second factor targets the expectation that if n-fold symmetry is present, then groups of n regions should have approximately equal volumes. A third factor is targets regions of density of a specific size. The desired volume above the threshold is chosen based on the molecular volumes of the molecules expected to be present in the structure and the assumption that a fraction f, (typically 0.2) of the volume inside a molecule will have high density (the parts very near atoms) and that only these high-density locations should be above the threshold. The desired size of individual regions of density is set to be about the size occupied by 50 residues of the macromolecule, chosen because this is a suitable size for model-building of one or a few segments of a macromolecule. The exact size of regions is not crucial.

The details of setting this threshold depend on n, the number of symmetry copies in the reconstruction, n_res the total number of residues in the reconstruction, the total volume of the reconstruction v_total, the volume occupied by the macromolecule, v_protein, a target fraction f of grid points inside the macromolecular regions desired to be above the threshold, and a target number of residues in each region of r. Prior to segmentation, the map is normalized, taking into account the fraction v_protein /v_total of volume of the map that contains macromolecule. The map is first transformed by subtraction of its mean followed by division by its variance to yield a map with a mean value of zero and variance of unity. Then a multiplicative scale factor of

$$s={\left(v_{protein}/v_{total}\right)}^{1/2}$$ (1)

is applied. This transformation has the property that if the density for the molecule has uniform variance everywhere inside the molecule, removing part of the molecule from the map would lead to a transformed map that is unchanged for the remainder of the molecule.

The desired total volume v_target corresponding to high density within the macromolecule is given by the product of the total volume within the macromolecule, v_total, and the desired fraction of grid points within the macromolecule that are to be above the threshold, f,

$$v_{target}=f{v}_{total}$$ (2)

The number of desired regions m_target is given by the number of residues in the macromolecule, divided by the desired residues in each region,

$$m_{target}=n_{nres}/r$$ (3)

The desired volume per region v_{region_target} is the ratio of the total target volume to the total number of regions,

$$v_{region\_target}=v_{target}/m_{target}$$ (4)

The desired volume ratio of the n’th region, v_n, to that of the first, v₁, is unity, and the value of this ratio is,

$$v_{ratio}=v_n/v_1$$ (5)

For a specific threshold, the volumes of regions above the threshold and the median volume v_median of the first m_target of these regions, after sorting from largest to smallest, are noted.

The desired median volume v_median is v_{region_target}. We use the target function,

$$\begin{gathered} v_{ratio\_median}=a\{v_{median}/v_{region\_target,}if<1, \\ {v}_{region\_target}/v_{median},otherwise\} \end{gathered}$$ (6)

to express this, so that a high value of v_{ratio_median} is always preferred. If all regions are about equal in size then this volume ratio v_{ratio_median} is not informative. The weight on the volume ratio is therefore scaled, increasing with variation in the size of regions, using the formula,

$$a=v_{target}/v_{median,}$$ (7)

where a is expected to increase from a value of 1 if all regions are the same size, to larger values if regions are of different sizes, as the largest regions will have more than median volumes.

The desired volume of the largest region, v₁, is also v_{region_target}. The target function,

$$\begin{gathered} v_{ratio\_1}=\{v_1/v_{region\_target,}if<1, \\ {v}_{{}_{region\_target}}/v_{1,}otherwise\} \end{gathered}$$ (7)

expresses this.

Finally, empirically we find that a threshold t on the order of unity is typically optimal (after scaling of the map as described above). We express this with a final ratio,

$$\begin{gathered} v_{ratio\_threshold}=\{t,if<1, \\ 1/t,otherwise\} \end{gathered}$$ (8)

where larger is again desired.

The total score Q for a threshold t is given by,

$$Q=A{v}_{ratio}+B*(v_{ratio\_median}+v_{ratio\_1})**2+C*v_{ratio\_threshold}$$ (9)

where A, B and C have default values we set by limited experimentation using a few test cases. Values of the threshold t are automatically tested and the value that maximizes the total score is used.

Once a threshold is chosen and the resulting set of regions of connected density above that threshold are found, these regions are assembled into groups with members related by symmetry (if any is present).

A unique set of density regions is chosen by picking one region from each symmetry-related group. The choice of regions is optimized to yield a compact structure and high connectivity. The compactness of the structure is represented by the radius of gyration of randomly-sampled points from all chosen regions. The connectivity of a set of regions is calculated based on finding the rms of the maximum gaps that would have to be spanned to connect each region to one central region, going through any number of regions in between. For any pair of regions, the gap is defined as the smallest distance between randomly-sampled points in the two regions. For a set of regions, the overall gap is the largest of the individual gaps that would have to be crossed to go from one region to another, going through any other regions in the process. The overall connectivity score is the rms of these gaps for connections between each region and one central region.

The central region and all the other regions are chosen to minimize both the connectivity score and the radius of gyration. The relative weighting of the two scores is determined by a user-definable parameter with a default value of weight on the radius of gyration of weight_rad_gyr=0.1. The weight on the radius of gyration is then normalized to the size of the molecule by multiplying this parameter by the largest cell dimension divided by 300 Å. (This dimension is arbitrary; the key relationship is that the radius of gyration scales with the size of the molecule).

The goal of the segmentation procedure described so far is to yield density corresponding to a single molecular unit. If the segmentation procedure yields only density corresponding to parts of several molecular units then complete chain tracing would not be possible. To increase the proportion of complete chains, regions neighboring the initial regions that would lead to an increase in the overall radius of gyration of 1 Å or less are added to the segmented region.

Chain types to be examined

The chain types (protein, RNA, DNA) to be tested in model-building were automatically deduced from the contents of the sequence file using the Phenix method guess_chain_types_from_sequences.

Protein model-building

In our new core method for protein model-building, the Phenix trace_chain algorithm²⁴ is used to build a polypeptide backbone through a map following high contour levels. These preliminary models are then improved by automatic iterative identification of secondary structure and refinement of the models including hydrogen-bond restraints representing this secondary structure with the phenix.real_space_refine approach¹². As the connectivity in a map can sometimes be more evident at lower resolution, a series of maps blurred with different values of a blurring exponential factor B_blur ranging from 0 to 105 Ų (8 choices in increments of 15 Ų) are created and each one is used in chain tracing.

Automatic identification of secondary structure is carried out by a feature-based method that is relatively insensitive to large errors. Helices are identified from a helical geometry of C_α positions. Segments with 6 or more residues in length are considered, and ${\text{C}}_{\text{α,i}}->{\text{C}}_{\text{α,i+3}}$ and ${\text{C}}_{\text{α,i}}->{\text{C}}_{\text{α,i+4}}$ vectors are calculated. The helical rise from a C_α atom is taken to be the mean value of the length of the corresponding $C_{\alpha ,i}->C_{\alpha ,i+3}$ and $C_{\alpha ,i}->C_{\alpha ,i+4}$ vectors, divided by the mean number of intervening residues (3.5). The overall helical rise is taken to be the average rise over all suitable C_α atoms and the segment is rejected if the helical rise is not within 0.5 Å of the target of 1.54 Å. Then the mean of all $C_{\alpha ,i}->C_{\alpha ,i+3}$ vectors is computed and the segment is considered helical if the mean dot product of individual vectors with the overall mean vector is at least 0.9 and no individual dot product is less than 0.3 (throughout this work, parameters are user-adjustable but values specified are used for all the work described here).

β-sheets are found by identification of parallel or antiparallel extended structure with at least 4 residues in each segment. For suitable C_α atoms within a single segment, $C_{\alpha ,i}->C_{\alpha ,i+3}$ vectors are calculated. If the mean length of these vectors is within 1.5 Å of the target of 10 Å, the mean dot product of individual vectors with the overall average is at least 0.75 and no individual dot product is less than 0.5, the segment is considered as a possible strand. Two strands are considered part of the same sheet if the C_α in the strands can be paired 1:1 with rms side-to-side $C_{\alpha ,i}->C_{\alpha ,i},$ distances of 6 Å or less. As above, all parameters are user-adjustable but default values were used throughout this work.

Once helices, parallel or antiparallel strands are identified, the corresponding hydrogen-bonding pattern is used to generate restraints that are used in real-space refinement.

A second method for model-building of proteins, previously used for crystallographic model-building, is based on examination of a map, typically at lower resolution, to identify features diagnostic of specific types of secondary structure²⁵.

A third method used to build protein models into segmented regions was the RESOLVE model-building algorithm²⁶ as implemented in phenix.resolve. This model-building method uses template matching to identify secondary structure elements (which can be protein helices or strands). Once secondary structure elements are identified, they are extended with tripeptide (or trinucleotide) fragments to create a full model.

Sequence assignment (matching of the sequence to residues in the model) for protein model-building is carried out using the tool phenix.assign_sequence which has been described recently²⁷.

Nucleic acid model-building

We have developed two approaches for nucleic acid model-building. The first is related to the template-matching methods for protein model-building described above²⁶. Regular A-form RNA helices (or B-form DNA helices) are identified with a convolution-based 6-dimensional search of a density map using regular base-paired templates 4 bases in length. Longer single-strands from base-paired templates of up to 19 bases are then superimposed on the templates that have been identified and portions that best match the density map are kept. These helical fragments are extended using libraries of trinucleotides based on 749 nucleotides in 6 RNA structures determined at resolutions of 2.5 Å or better (PDB entries 1gid, 1hr2, 3d2g, 4p95, 4pqv and 4y1j, using only one chain in each case) and filtered to retain only nucleotides where with the average B-value (atomic displacement parameter) was 50 Ų or lower. Extension in the 5’ direction using trinucleotides was done by superimposing the C4', C3', and C2' atoms of the 3’ nucleotide base of the trinucleotide to be tested on the corresponding atoms of the 5’ nucleotide in a placed segment, examining the map-model correlation for each trinucleotide, and choosing the one that best matches the map. A corresponding procedure was used for extension in the 3’ direction. The matching of nucleic acid sequence to nucleotides in the model was carried with an algorithm similar to the one used in the tool phenix.resolve for protein sequence assignment¹⁸. Four to six conformations of each the bases were identified from the six RNA structures described above. For each conformation of each base, average density calculated at a resolution of 3 Å from the examples in these structures (after superimposing nucleotides using the C4', C3', and C2' atoms) was used as a density template for that base conformation. Then after a nucleotide chain was built with our algorithm, the map correlation between each of these templates and each position along the nucleotide chain is calculated and used to estimate the probability of each base at each position¹⁸. All possible alignments of the supplied sequence and each nucleotide chain built are considered and the best matches with a confidence of 95% or greater are considered matched. For these matched nucleotides the corresponding conformation of the matched base is then placed in the model. For residues where no match is found, the best-fitting nucleotide is used. For base-paired nucleotides, the same procedure is carried out, except that pairs of base-paired nucleotides are considered together, essentially doubling the amount of density information available for sequence identification.

A second for nucleic acid model-building used here is to build duplex RNA helices directly into the density map with the tool phenix.build_rna_helices. The motivation for this algorithm was that the nucleic-acid model-building approach described above, which builds the two chains of duplexes separately, frequently resulted in poorly base-paired strands. To build RNA helices directly, very similar overall strategies were used, except that the templates were all base-paired and base-paired nucleotides were always considered as a single unit. This automatically led to the same favorable base-pairing found in the structures used to derive the templates. The atoms used to superimpose chains and bases were the O4’ and C3’ atoms of one nucleotide and the C1’ atom of the base-paired nucleotide. As in the previous method for sequence assignment, both bases in each base-paired set were considered together, leading again to a substantial increase in map-based information about the identities of bases in the model. Supplementary Fig. 4 illustrates the models obtained with the two methods for a small region of RNA density from the Leishmania ribosome²⁸ at a resolution of 2.5 Å (EMDB entry 7025).

Combining model information from different sources and removal of overlapping fragments

Model-building into local regions of density and into the entire asymmetric unit of the map normally yielded a set of partially overlapping segments. These segments were refined based on the sharpened map with the Phenix tool phenix.real_space_refine¹². The refined segments were scored based on map-model correlation multiplied by the square root of the number of atoms in the segment (related to fragment scoring in RESOLVE model-building except that density at the coordinates of atoms was used instead of map-model correlation in that work²⁶). Then a composite model was created from these fragments, starting from the highest-scoring one and working down, and including only non-overlapping parts of each new fragment considered, as implemented in the Phenix tool phenix.combine_models. When symmetry was used in reconstruction, all the symmetry-related copies of each fragment were considered in evaluating whether a particular part of a new fragment would overlap with the existing composite model.

Construction and refinement of full model including reconstruction symmetry

In cases where symmetry had been used during the reconstruction process, we assumed that this symmetry was nearly perfect and applied this symmetry to the model that we generated. We began with our model that represented the asymmetric unit of the reconstruction. Then reconstruction symmetry was applied to this model and the model was refined against the sharpened map with the Phenix tool phenix.real_space_refine. Finally one asymmetric unit of this final model was extracted to represent the unique part of the molecule and both the entire molecule with symmetry and the unique part are written out.

Evaluation of model similarity to deposited structures

We developed the Phenix tool phenix.chain_comparison as a way of comparing the overall backbone (C_α or P atoms only) similarity of two models. The unique feature of this tool is that it considers each segment of each model separately so that it does not matter whether the chain is complete or broken into segments. Additionally the tool can separately identify segments that have matching C_α or P atoms that proceed in the same direction and those that are reversed as well as those that have insertions and deletions, as is common in low-resolution model-building. The phenix.chain_comparison tool also identifies whether the sequences of the two models match by counting the number of matching C_α or P atoms that are associated with matching residue names. These analyses are carried out with a default criteria that C_α or P atoms that are within 3 Å are matching and those further apart are not. This distance is arbitrary but was chosen to allow atoms to match in chains that superimpose secondary structure elements such as helices even if the register of the secondary structure elements do not superimpose exactly.

When comparing models corresponding to a reconstruction that has internal symmetry, the appropriate pairs of matching atoms may require application of that symmetry. The phenix.chain_comparison tool allows the inclusion of symmetry in the analysis.

Datasets used

We selected reconstructions to analyze based on:

• (1)availability of a reconstruction in the EMDB as of Nov, 2017
• (2)resolution of the reconstruction 4.5 Å or better
• (3)presence of a unique deposited model in the PDB matching the reconstruction
• (4)consistent resolution in the PDB and EMDB
• (5)ability to use Phenix tools to automatically extract model and map from PDB and EMDB, apply symmetry if present in the metadata, and write the model

This resulted in 502 map-model pairs extracted from a total of 882 single-particle and helical reconstructions in the EMDB in this resolution range. (Note that only 660 of the 882 have one or more associated PDB entries).

After our initial analysis we further excluded reconstructions that had the following characteristics:

• (1)map-model correlation for the deposited map and deposited model of less than 0.3 after extraction of map and model and analysis with phenix.map_model_cc (18 reconstructions)
• (2)deposited model in the PDB represents less than half of the structure (9 reconstructions)

This yielded the 476 map-model pairs that are described in this work. We downloaded the maps from the EMDB¹³ and used them directly in phenix.map_to_model, with the exception of one map (EMDB entry 6351). For EMDB entry 6351, a pseudo-helical reconstruction²⁹, we could only deduce reconstruction symmetry for the part of the map corresponding to deposited model (PDB entry 3jar), so we used the phenix.map_box tool to cut out a box of density around the region defined by the deposited model, analyzed this map, and at the conclusion of the process translated the automatically-generated models to match the deposited map.

Parameters used when running phenix.map_to_model

All of the reconstructions selected were analyzed with official version 1.13–3015 of Phenix, with all default values of parameters except those specifying file names for the reconstructed map, sequence file, and symmetry information, the resolution of the reconstruction, and any control parameters specific to the computing system and processing approach (e.g., the number of processors to use, queue commands, parameters specifying what parts of the calculation to carry out or what parts to combine in a particular job, and level of verbosity in output).

The phenix.map_to_model tool allows an analysis to be broken up into smaller tasks, followed by combining all the results to produce essentially the same result as would be obtained by running the entire procedure in one step. We used this approach for two purposes in this work. First, some of the datasets we analyzed required a very large amount of computer memory in certain stages of the analysis, and in particular in the map segmentation and final model construction steps. For other datasets such as ribosomes, the analysis could be substantially sped up by running smaller tasks on many processors.

Computation

We carried out most of the analyses in this work on the grizzly high performance computing cluster at Los Alamos National Laboratory, typically with one task per node. Some of the analyses were carried out using a dedicated computing cluster at Lawrence Berkeley National Laboratory and some large analyses in particular were carried out on a machine with 1 TB of memory.

We monitored the CPU use for 175 of our analyses (generally smaller structures) that were each carried out in a single step on a single machine using a single processor. These analyses took from 15 minutes to 12 hours to complete on the grizzly cluster. For example, the analysis of EMDB entry 6630 in Fig. 2C required 3 CPU hours. We also monitored the CPU use for one of the largest structures (EMDB entry 9565), which required 129 CPU hours to complete.