Statistical Binning for Barcoded Reads Improves Downstream Analyses

SUMMARY

Sequencing technologies are capturing longer-range genomic information at lower error rates, enabling alignment to genomic regions that are inaccessible with short reads. However, many methods are unable to align reads to much of the genome, recognized as important in disease, and thus report erroneous results in downstream analyses. We introduce EMA, a novel two-tiered statistical binning model for bar-coded read alignment, that first probabilistically maps reads to potentially multiple “read clouds” and then within clouds by newly exploiting the nonuniform read densities characteristic of barcoded read sequencing. EMA substantially improves downstream accuracy over existing methods, including phasing and genotyping on 10x data, with fewer false variant calls in nearly half the time. EMA effectively resolves particularly challenging alignments in genomic regions that contain nearby homologous elements, uncovering variants in the pharmacogenomically important CYP2D region, and clinically important genes C4 (schizophrenia) and AMY1A (obesity), which go undetected by existing methods. Our work provides a framework for future generation sequencing.

In Brief

Researchers are applying barcoded read sequencing to capture longer-range information in the genome at low error rates. We introduce a two-tiered statistical binning model, named EMA, which probabilistically assigns reads to “clouds” and then optimizes read assignments within clouds based on read densities. Unlike previous approaches, our efficient method enables alignment to highly homologous regions of the genome important in disease and substantially improves downstream genotyping and haplotyping. Our method also uncovers rare variants in clinically important genes.

INTRODUCTION

Sequencing is the most fundamental operation in genomics, transcriptomics, and metagenomics. As sequencing technologies continue to advance beyond the initial introduction of next-generation sequencing (NGS), we have begun to see the emergence of the so-called “third-generation” sequencing platforms, which seek to improve on the standard short-read sequencing that has thus far been at the heart of most NGS (Mardis, 2017). Several organizations are at the center of this new sequencing revolution, including Pacific Biosciences (Eid et al., 2009), Oxford Nanopore (Wang et al., 2014), and 10x Genomics (Zheng et al., 2016). While the former two have developed sequencing technologies that produce much longer physical reads (e.g., 10–200 kb) at typically higher error rates, the latter is an example of a barcoded sequencing technology, which typically produces short reads (up to 300 bp) with low error rates (Goodwin et al., 2016).

At a high level, barcoded sequencing is any sequencing method where long DNA fragments are sheared and the sheared pieces have some identifier (“barcode”) relating them back to the source fragment. These barcodes can be explicit (a physical barcode is ligated to each sheared piece, e.g., as in 10x sequencing) or implicit (the fragments are distributed to identifiable wells, e.g., as in Illumina’s TruSeq Synthetic Long-Read sequencing, henceforth referred to as TruSeq SLR). These sheared pieces are then sequenced using standard short-read sequencing, thereby producing barcoded short reads (Figure 1A). Other barcoded sequencing technologies include Illumina’s Continuity Preserving Transposition technology (CPT-seq), Complete Genomics’ Long Fragment Read technology, Drop-seq, and CEL-Seq2 (Zheng et al., 2016; McCoy et al., 2014; Macosko et al., 2015; Hashimshony et al., 2016; 10x Genomics, 2018). Because they help identify the original source fragment, these barcodes implicitly carry long-range information, which can have a significant impact on alignment and many downstream analyses such as structural variation detection and phasing.

Figure 1. Overview of EMA Pipeline.

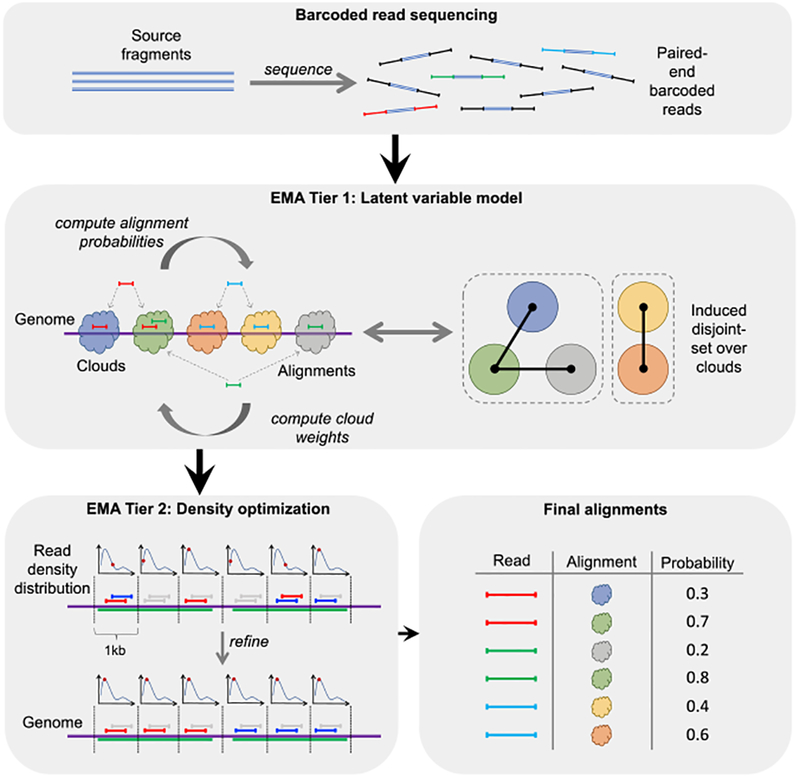
(A) An idealized model of barcoded read sequencing, wherein some number of unknown source fragments in a single droplet or well are sheared, barcoded, and sequenced to produce barcoded reads.

(B) EMA’s “read clouds” are constructed by grouping nearby-mapping reads sharing the same barcode; these clouds represent possible source fragments. EMA then partitions the clouds into a disjoint-set induced by the alignments, where two clouds are connected if there is a read aligning to both; connected components in this disjoint-set (enclosed by dashed boxes) correspond to alternate possibilities for the same unknown source fragment. EMA’s latent variable model optimization is subsequently applied to each of these connected components individually to deduce each of the potentially many fragments sharing this barcode.

(C) EMA applies a novel read density optimization algorithm to clouds containing multiple alignments of the same read to pick out the most likely alignment, by optimizing a combination of alignment edit distances and read densities within the cloud. The green regions of the genome are homologous, thereby resulting in multi-mappings within a single cloud.

(D) While the read density optimization operates within a single cloud, EMA’s latent variable model optimization determines the best alignment of a given read between different clouds and produces not only the final alignment for each read but also interpretable alignment probabilities (see Figure S1).

Barcoded reads have several advantages over physically long reads. First, and perhaps most important, barcoded read sequencing is substantially cheaper than long-read sequencing; whereas PacBio’s and Oxford Nanopore’s sequencing platforms currently cost anywhere from $750 to $1,000 per GB of data, barcoded sequencing is a comparatively cheap add-on to standard short-read sequencing and therefore bears the same cost (e.g., 10x sequencing costs $30 per GB plus a $500 overhead per sample) (Goodwin et al., 2016). Second, the error profile of barcoded reads is very similar to that of standard short reads (roughly 0.1% substitution errors), which enables us to augment the tools and algorithms that have been developed for regular short reads to handle their barcoded counterparts. By contrast, long-read sequencing typically produces high rates of erroneous indels (ranging from 12%–13%), which presents a challenge when trying to use preexisting algorithms. Beyond these advantages, barcoded reads are compatible with doing hybrid capture exome sequencing, and not sequencing introns (which is not possible with long-read sequencing technologies, as a contiguous long-read cannot only sequence the exons in a gene). This is a very substantial additional cost-advantage for barcoded reads (exome sequencing can mean a 10- to 20-fold reduction in sequencing cost over whole genome sequencing) (Schwarze et al., 2018). These and other benefits have led to the recent proliferation of barcoded sequencing technologies for various use cases; for example, 10x and TruSeq SLR sequencing for whole genome sequencing, as well as Drop-seq and CEL-Seq2 for single-cell RNA sequencing (RNA-seq), 10x for single-cell VDJ sequencing and so on (Zheng et al., 2016; McCoy et al., 2014; Macosko et al., 2015; Hashimshony et al., 2016; 10x Genomics, 2018). A comprehensive review of many of these methods is available (Ziegenhain et al., 2017). Furthermore, barcoded sequencing is also playing a greater role in downstream applications such as the generation of transcriptomic profiles (Cleary et al., 2017).

As with virtually all sequencing data, the first step in the analysis pipeline for barcoded reads is typically alignment. While barcoded reads can, in theory, be aligned by a standard short-read aligner (e.g., CORA [Yorukoglu et al., 2016] (COmpressive Read-mapping Accelerator), BWA (Burrows-Wheeler Aligner) [Li and Durbin, 2009], Bowtie2 [Langmead and Salzberg, 2012]), this would fail to take advantage of the information provided by the barcodes. An alternative approach (McCoy et al., 2014) is to assemble the reads for each particular barcode and to treat the result as a single “synthetic long read.” While this strategy works well for technologies such as TruSeq SLR, in which source fragments are generally sequenced with high coverage, it is not practical when fragments are shallowly sequenced as with 10x, which achieves high coverage not by having high per-barcode coverage but rather by having many barcodes. Also worth noting is the fact that TruSeq SLR’s sequencing fragments at high coverage inflate their sequencing costs to be on par with PacBio’s and Oxford Nanopore’s, whereas 10x circumvents this high cost via shallow fragment sequencing (Goodwin et al., 2016).

Currently, the state-of-the-art in terms of barcoded read alignment employs “read clouds”—groups of reads that share the same barcode and map to the same genomic region—to choose the most likely alignment from a set of candidate alignments for each read. Intuitively, read clouds represent the possible source fragments from which the barcoded reads are derived. The read cloud approach to alignment effectively begins with a standard all-mapping to a reference genome to identify these clouds, followed by an iterative update of the reads’ assignments to one of their possible alignments, guided by a Markov random field that is used to evaluate the probability of a given read-to-cloud configuration (taking into account the alignment scores, clouds, etc.). This method was first implemented for Moleculo data as Random Field Aligner (RFA) and was subsequently the foundation for the 10x aligner Lariat, which we compare to extensively in this work (Bishara et al., 2015). Notably, in this framework, clouds are inherently fixed entities to which some number of reads are assigned at any given point, which does not take into account the fact that reads can have suitable alignments in several different clouds. Since this information can be valuable in downstream analyses such as genotyping, phasing, and structural variation detection, we wish to account for it.

Confounding barcoded read alignment is the fact that multiple fragments can share the same barcode; it is in general not possible to infer the source fragment of a read (and thus its correct alignment within a reference genome) merely by looking at its barcode. In order to deduce the correct placement of a read, and thus its unknown source fragment, all possible alignments of that read need to be examined. Even then, it can be difficult to determine the correct alignment, particularly in homologous regions of the genome that result in multi-mappings within a single cloud.

Here, we propose a general paradigm for barcoded read alignment that newly employs a probabilistic interpretation of clouds: EMerAld, or EMA for short (Figure 1). Our two-tiered statistical binning approach enables the more accurate placement of reads in and within read clouds, which is the critical step in barcoded read alignment. The two tiers consist of (1) a novel latent variable model to probabilistically assign reads to clouds, which introduces the notion of clouds as distributions over generated reads rather than simply fixed groups of reads; and (2) newly exploiting expected read coverage (read density) to resolve the difficult case of multiple alignments of reads within clouds. The idea and subsequent observation of the fixed read density distribution within source fragments are novel to EMA and can be utilized by many barcoded read analysis tools: for example, an assembler might use our idea to model the distance between reads within the same source fragment and thus break ties, if any. Note that these ambiguous alignments account for a large fraction of the rare variants that currently cannot be resolved and are of great interest to biologists (Ingelman-Sundberg, 2004; Sekar et al., 2016; Falchi et al., 2014).

By thinking of clouds not as arbitrary clusters of reads but rather as distributions, EMA’s latent variable model (tier I) is able to generate more accurate alignments and to newly assign interpretable probabilities to its alignments, which greatly improves downstream analyses. Genotyping improvements and, more generally, the resolution of distant homologs (e.g., longer than fragment length or interchromosomol) stem from our probabilistic interpretation. We demonstrate EMA’s performance by evaluating downstream genotyping and phasing accuracy first using real 10x data. We discovered that roughly 20% of all reads in our datasets had multiple suitable alignments and were therefore able to be targeted by EMA’s optimization algorithm. We also found that genotypes called from EMA’s alignments contained over 30% fewer false positives than those called from 10x’s Lariat aligner—and at the same time contained fewer false negatives—on independent 10x datasets of NA12878, NA24149, NA24143, and NA24385. The National Institute of Science and Technology’s “Genome in a Bottle” high-confidence variant calls were used as a gold standard. EMA also improved phasing performance by reducing switch errors and producing larger phased blocks.

Focusing on uncovering novel biology, we additionally demonstrate that—through its read density optimization (tier II)—EMA improves alignments in several clinically important and highly homologous genes: CYP2D6/CYP2D7 (of great pharmacogenomic importance [Ingelman-Sundberg, 2004]), C4 (linked to schizophrenia [Sekar et al., 2016]), and AMY1A (conjectured association with obesity [Falchi et al., 2014]). We discovered using EMA and validated through published studies (Jain et al., 2017; Mostovoy et al., 2016; Pendleton et al., 2015) several variants in these regions that go undetected by Lariat and BWA. Moreover, we sought to demonstrate that our approach generalizes to other barcoded sequencing technologies by applying it to TruSeq SLR data as well as CPT-seq data, where we observe similar results. Intuitively, EMA’s ability to handle shorter homologies (i.e., those within a cloud) leads to these novel findings.

In addition to achieving superior accuracy, providing interpretable probabilities, and uncovering novel biology, the EMA pipeline is up to 2× faster than Lariat—which translates into days faster for typical 10x datasets—and does not add any memory overhead to the alignment process. Thus, we expect the algorithms introduced here to be a fundamental component of barcoded read methods in the future.

RESULTS

Experimental Setting

We first compared the performance of EMA against Lariat (10x Genomics, 2017) (10x’s own aligner and a component of the Long Ranger software suite) and BWA-MEM (“Maximal Exact Matches”) (Li and Durbin, 2009) (which does not take advantage of barcoded data and was therefore used as a baseline for what can be achieved with standard short reads). In order to benchmark the quality of the aligners, we examined downstream genotyping accuracy, alignments in highly homologous regions, and downstream phasing accuracy.

We ran each tool on four 10x Homo sapiens datasets for NA12878, NA24149, NA24143, and NA24385 and used the corresponding latest NIST GIAB (Zook et al., 2014, 2016) high-confidence variant calls as a gold standard for each. For both EMA and BWA, we performed duplicate marking after alignment using Picard’s MarkDuplicates tool (URL: https://broadinstitute.github.io/picard/), with barcode-aware mode enabled in the case of EMA; Long Ranger performs duplicate marking automatically. Genotypes were called by HaplotypeCaller from the Genome Analysis Toolkit (GATK) (McKenna et al., 2010; DePristo et al., 2011) with default settings, while phasing was done by HapCUT2 (Edge et al., 2016) in barcode-aware mode. Genotyping accuracies were computed using RTG (“Real Time Genomics”) Tools (Cleary et al., 2014). We also ran EMA and Lariat on a much higher coverage NA12878 dataset (“NA12878 v2”) to test genotyping accuracy at high coverage as well as scalability.

To test EMA’s improvements on other barcoded read sequencing technologies, we ran EMA and BWA on an NA12878 TruSeq SLR dataset (Bishara et al., 2015) as well as an NA12878 CPT-seq dataset (Amini et al., 2014). All analyses in this paper were performed with respect to the GRCh37 human reference genome.

EMA Improves Downstream Genotyping Accuracy

EMA’s genotyping accuracy surpasses that of other aligners (Figure 2). We found that for each of the four 10x H. sapiens datasets, EMA produced 30% fewer false positive variant calls compared to Lariat and produced fewer false negative calls as well. Interestingly, BWA-MEM (which does not take barcodes into account) performed marginally better than Lariat here. Nevertheless, EMA also outperforms BWA-MEM, attaining the fewest false positive and false negative variant calls between the three aligners on each dataset. To verify that EMA’s superior accuracy scales to higher coverage datasets, we tested it on a high-coverage NA12878 dataset (Supplementary Figure S3). EMA attains an even more substantial improvement on the high-coverage dataset, eliminating nearly 37% of Lariat’s false positives and 6% of its false negatives.

Figure 2. Genotyping and Phasing Results for Each Aligner.

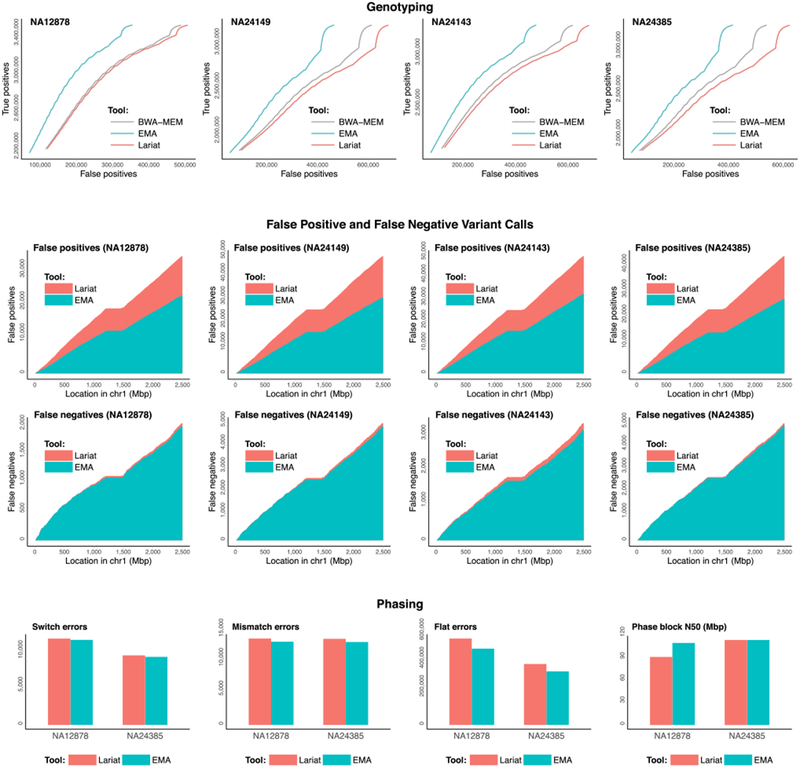
The top row shows true positive variant calls as a function of false positives for alignments produced by EMA (turquoise), Lariat (orange), and BWA-MEM (gray) on the well-studied samples NA12878, NA24149, NA24143, and NA24385. Genotype confidences are determined by the genotype quality (GQ) annotations generated by GATK’s HaplotypeCaller. The middle two rows contain cumulative histograms of false positives (top) and false negatives (bottom) throughout chromosome 1 for each dataset, for both EMA (turquoise) and Lariat (orange). EMA achieves more than a 30% average improvement over the other methods in terms of eliminating erroneous variant calls. The bottom row shows EMA and Lariat’s phasing results for several metrics: switch errors, mismatch errors, flat errors (Edge et al., 2016), and phase block N50 (lower is better for the first three, while higher is better for the last). EMA outperforms Lariat in phasing on every metric.

When run on TruSeq SLR and CPT-seq data, we did not observe any significant differences in genotyping accuracy between EMA and BWA. This finding is likely due to the fact that these platforms divide the source fragments into just 384 and 9,128 wells (“barcodes”), respectively, limiting the utility of the barcodes in unambiguous regions of the genome, which is primarily what our NIST GIAB gold standard consists of. However, for both technologies, we did observe improvements in resolving ambiguous regions of the genome, which we detail below.

Overall, we found that typically ~20% of all reads in our various datasets had multiple suitable alignments and were therefore able to be targeted by EMA’s two-tiered statistical binning optimization algorithm. These are precisely those reads that are most challenging to align and can occur in clinically important regions of the genome, as we next demonstrate.

EMA Improves Alignments and Analysis of Highly Homologous Regions

Among the principal promises of barcoded read sequencing is better structural variation detection, which invariably requires resolving alignments in homologous regions. One such important region is the CYP2D region in chromosome 22, which hosts CYP2D6—a gene of great pharmacogenomic importance (Ingelman-Sundberg, 2004)—and the two related and highly homologous regions CYP2D7 and CYP2D8. The high homology between CYP2D6 and CYP2D7 makes copy number estimation and variant calling in this region particularly challenging. Indeed, the majority of aligners misalign reads in this region. The difficulty is especially evident in NA12878, which, in addition to the two copies of both CYP2D6 and CYP2D7, contains an additional copy that is a fusion between these two genes (Twist et al., 2016), as well as CYP2D7 mutations that introduce even higher homology with the corresponding CYP2D6 region. Especially problematic is exon/intron 8 of CYP2D6, where many reads originating from CYP2D7 end up mapping erroneously (see Figure 3 for a visualization). Even the naive use of barcoded reads is not sufficient: both homologous regions in CYP2D are typically covered by a single cloud. For example, Lariat performs no better than BWA in this region (Figure 3). For these reasons, we chose to evaluate EMA in CYP2D to benchmark its accuracy in such highly homologous regions.

Figure 3. Positive Effect of EMA’s Statistical Binning in the Clinically Important Genes CYP2D6, CYP2D7, C4, and AMY1A.

The green inset shows the read coverage for the region around exon/intron 8 of CYP2D6 (top row) and CYP2D7 (bottom row). Spurious coverage peaks (i.e., increases in observed coverage likely to be false) in CYP2D6 are shaded black. EMA is clearly able to remove the problematic peaks and correctly assign them to CYP2D7. The insets below show the newly assigned mappings to CYP2D7: EMA’s alignments agree with the assembly consensus sequence (observe the insertion and two neighboring SNPs detected by EMA). By contrast, both Lariat and BWA-MEM aligned virtually no reads to this region and were thus unable to call these mutations. Analogous images are shown for C4 and AMY1A, as well as for TruSeq SLR and CPT-seq data.

As can be seen in Figure 3, EMA’s statistical binning strategy significantly smooths out the two problematic peaks in CYP2D6 and CYP2D7. This technique enabled us to detect three novel mutations in CYP2D7 (Figure 3), which exhibit high homology with the corresponding region in CYP2D6. Thus, all reads originating from these loci get misaligned to CYP2D6, especially if one only considers edit distance during the alignment (as Lariat and BWA do). Such misalignments are evident in the “peaks” and “holes” shown in Figure 3. We additionally cross-validated this region with the consensus sequence obtained from available NA12878 assemblies (Jain et al., 2017; Mostovoy et al., 2016; Pendleton et al., 2015) and confirmed the presence of novel mutations. Notably, we found similar enhancements in other clinically important and highly homologous genes: C4 and AMY1A, as depicted in the same figure.

In addition, the copy number derived from EMA’s alignments in this problematic region (spanning from exon 7 up to exon 9 in CYP2D6 and CYP2D7) was closer to the “expected” copy number by 20% compared to the copy number derived from Lariat’s alignments (we used Aldy [Numanagić et al., 2018] to obtain this data). We further ran Aldy on our high-coverage NA12878 v2 dataset, where it correctly detected the *3/*68+*4 allelic combination on both EMA’s and Lariat’s alignments, and EMA’s overall copy number error over the whole region was around 4% better than Lariat’s. Finally, statistical binning did not adversely impact phasing performance in this region as we were able to correctly phase CYP2D6*4A alleles in our NA12878 sample from EMA’s alignments.

To demonstrate the generalizability of our paradigm to other similar barcoded sequencing technologies, we tested it on TruSeq SLR (BioProject: PRJNA287848) and CPT-seq (BioProject: PRJNA241346) data, where the bin distributions follow a similar pattern as 10x’s. We alone were able to detect the same novel CYP2D7, C4, and AMY1A variants in an NA12878 TruSeq SLR dataset (even with shallow coverage) and to detect the CYP2D7 variants in an NA12878 CPT-seq dataset, as shown in the right-hand side of Figure 3.

EMA Improves Downstream Phasing

We applied the state-of-the-art phasing algorithm HapCUT2 (Edge et al., 2016), which supports 10x barcoded reads, to phase (i.e., link variants into haplotypes) the variants called by GATK for both EMA’s and Lariat’s alignments. We evaluated our results with the phasing metrics defined in the HapCUT2 manuscript. As shown in Figure 2, EMA provides more accurate phasing with respect to every metric in comparison to Lariat.

EMA Is Computationally More Efficient

Runtimes and memory usage for each aligner are provided in Table 1 for our small and large NA12878 datasets. These times include alignment, duplicate marking, and any other data post processing (e.g., BAM sorting and merging). The reported memory usages are per each instance of the given mapper. We found that EMA scales better than Lariat: specifically, we observe a 1.5x speedup on our smaller dataset and a nearly 2x speedup on our larger one, over Lariat’s runtimes. We ran EMA on a total of four high-coverage datasets and have observed that EMA scales linearly in the size of the dataset.

Table 1.

Runtime and Memory Usages on Two NA12878 Datasets

	NA12878		NA12878 v2
Tool	Time (hh:mm)	Mem./core (GB)	Time (hh:mm)	Mem./core (GB)
EMA	14:58 (10:40)	5.4	28:30 (17:45)	8.7
Lariat	21:49 (12:45)	7.0	54:53 (26:01)	8.2
BWA-MEM	14:49 (9:52)	5.5

“NA12878”—used also in Figure 2—is about 287 GB of raw data; “NA12878 v2” is about 823 GB. Numbers in parenthesis indicate the performance of the aligner alone (i.e., without sorting, merging, or duplicate marking). For the small dataset, each mapper was allocated 40 Intel Xeon E5–2650 CPUs @2.30GHz. For the large dataset, each was allocated 48 Intel Xeon E5–2695 CPUs @ 2.40GHz. Memory measurements include only the actual aligner’s memory usage and do not include the memory requirements of pre- and post-processing steps, as they are virtually the same for all methods. BWA-MEM was used only as a baseline on the smaller dataset.

Runtime and memory usages on two NA12878 datasets (“NA12878”—used also in Figure 2—is about 287 GB of raw data; “NA12878 v2” is about 823 GB). Numbers in parentheses indicate the performance of the aligner alone (i.e., without sorting, merging, or duplicate marking). For the small dataset, each mapper was allocated 40 Intel Xeon E5–2650 CPUs @ 2.30 GHz. For the large dataset, each was allocated 48 Intel Xeon E5–2695 CPUs @ 2.40 GHz. Memory measurements include only the actual aligner’s memory usage and do not include the memory requirements of pre- and post-processing steps as they are virtually the same for all methods. BWAMEM was used only as a baseline on the smaller dataset.

DISCUSSION

EMA’s unique ability to assign interpretable probabilities to alignments has several benefits, the most immediate of which is that it enables us to set a meaningful confidence threshold on alignments. Additionally, these alignment probabilities can be incorporated into downstream applications such as genotyping, phasing, and structural variation detection. We demonstrate this feature here by computing mapping qualities based on these probabilities, which consequently enhance genotyping and phasing. Nevertheless, specialized algorithms centered around these probabilities are also conceivable.

Moreover, EMA is able to effectively discern between multiple alignments of a read in a single cloud through its read density optimization algorithm. This capability addresses one of the weaknesses of barcoded read sequencing as compared to long-read sequencing; namely, that only a relatively small subset of the original source fragment is observed—and, more specifically, that the order of reads within the fragment is not known—making it difficult to produce accurate alignments if the fragment spans homologous elements. By exploiting the insight that read densities within a fragment follow a particular distribution, EMA more effectively aligns the reads produced by such fragments, which can overlap regions of phenotypic or pharmacogenomic importance, such as CYP2D, C4, or AMY1, as we demonstrated. In summary, EMA’s first tier (latent variable model) helps resolve the case of distant homologs, and its second tier, the case of proximal homologs.

As we usher in the next wave of the NGS technologies, barcoded read sequencing will undoubtedly play a central role, and fast and accurate methods for aligning barcoded reads, such as EMA, will ultimately prove invaluable in downstream analyses.

STAR*METHODS

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
NA12878 WGS (10x)	10x Genomics	https://support.10xgenomics.com/genome-exome/datasets/2.1.0/NA12878_WGS_210
NA12878 WGS v2 (10x)	10x Genomics	https://support.10xgenomics.com/genome-exome/datasets/2.2.1/NA12878_WGS_v2
NA12878 WGS (Illumina TruSeq Synthetic Long-Read)	Bishara et al. (2015)	BioProject: PRJNA287848
NA12878 WGS (CPT-seq)	Amini et al. (2014)	BioProject: PRJNA241346
Software and Algorithms
Long Ranger	10x Genomics	https://support.10xgenomics.com/genome-exome/software/downloads/latest
BWA	Li and Durbin (2009)	https://github.com/lh3/bwa
GATK	Broad Institute	https://software.broadinstitute.org/gatk/
HapCUT2	Edge etal. (2016)	https://github.com/vibansal/HapCUT2
Picard	Broad Institute	https://broadinstitute.github.io/picard/
Samtools	Li et al. (2009)	https://github.com/samtools/samtools
RTG Tools	Cleary et al. (2014)	https://github.com/RealTimeGenomics/rtg-tools
EMA	This paper	https://github.com/arshajii/ema
Other
NISTGIAB	Zook etal. (2016)	http://jimb.stanford.edu/giab/
NA24149, NA24143 and NA24385 WGS (10x)	Broad Institute	http://ema.csail.mit.edu

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Bonnie Berger (bab@mit.edu).

METHOD DETAILS

General barcoded read sequencing begins with splitting the source DNA into long fragments (10–200kb) where each such fragment is assigned some barcode (e.g. a short 16bp DNA sequence in 10x sequencing). These fragments are sheared and each sheared piece has the assigned barcode ligated to it (or, alternatively, resides in an identifiable well), whereupon standard short-read sequencing is applied to the sheared pieces. As a result, barcoded reads have the same low error rates as typical Illumina whole-genome sequencing reads. An idealization of this process is illustrated in Figure 1A.

Standard Data Preprocessing

The first stage in the alignment process is to preprocess the data and to identify the barcodes. Currently, EMA uses an in-house 10x barcode preprocessor, which extracts and corrects the barcodes from the raw data. Data from many other barcoded read technologies (e.g. TruSeq SLR) can be preprocessed in a more straightforward manner, as the barcodes are given as well identifiers for each read, meaning the preprocessing stage consists of a simple demultiplexing step.

For 10x data preprocessing we largely follow the same practices used by 10x Genomics’ WGS software suite, Long Ranger. The purpose of this preprocessing is to:

• extract the barcode from the read sequence,

• error-correct the barcode based on quality scores and a list of known barcode sequences,

• and group reads by barcode into “barcode buckets” to enable parallelism during alignment.

In summary, in the barcode extraction stage, we remove the 16bp barcode from the first mate of each read pair, and trim an additional 7bp to account for potential ligation artifacts resulting from the barcode ligation process during sequencing (the second mate shares the same barcode as the first mate). Subsequently, we compare each barcode to a list B of known barcodes to produce a count for each barcode in B, and compute a prior probability for each based on these counts (specifically, this prior is proportional to the fraction of times we see the given barcode in our data). Note that this list is provided by 10x Genomics, and is designed so that no two barcodes are Hamming-neighbors of one another. Now for each barcode b not appearing in B, we examine each of its Hamming-1 neighbors b′ and, if b′ appears in B, compute the probability that b′ was the true barcode based on its prior and the quality score of the changed base. Similarly, for each b appearing in B, we consider each Hamming-2 neighbor b′ and compute the probability that b′ was the true barcode in an analogous way. The reason we examine the Hamming-2 neighbors of barcodes that are already in our whitelist is because it is possible, albeit unlikely, that two sequencing errors in the barcode changed it from a barcode on the list to another also on the list (in practice we found this Hamming-2 correction step to be largely unnecessary as described below, but it is performed in Lariat’s data preprocessing nonetheless). Lastly, we employ a probability cutoff on the barcodes, and thereby omit the barcodes of reads that do not meet this cutoff. Any read not carrying a barcode after this stage is aligned with a standard WGS mapper such as CORA or BWA.

While in standard read alignment parallelism can be achieved at the read-level, for barcoded read alignment we can only achieve parallelism at the barcode-level. Therefore, the last preprocessing step is to group reads by barcode into some number of buckets. Each such bucket contains some range of barcodes from B, which are all grouped together within the bucket. This enables us to align the reads from each bucket in parallel, and to merge the outputs in a post-processing step.

We note that the Hamming-2 search takes a substantial fraction of the total time, but is often unnecessary: on a large 980GB 10x dataset, only 276 out of almost 1.5 billion reads are affected by the Hamming-2 correction (amounting to <0:0001% overall effect). Thus, it is safe to skip the Hamming-2 correction step. Nevertheless, we applied Hamming-2 correction on all our datasets for the sake of consistency with Lariat. Finally, EMA offers a parallelized barcode correction implementation, which significantly speeds up the overall pipeline.

Latent Variable Model for Aligning Barcoded Reads to Clouds

Here we employ a latent variable model for determining the optimal assignment of reads to their possible clouds. A “cloud” is defined to be a group of nearby alignments of reads with a common barcode, thereby representing a possible source fragment (Bishara et al., 2015). We consider all the reads for an individual barcode simultaneously, all-mapping and grouping them to produce a set of clouds for that barcode (Figure 1B). The clouds are deduced from the all-mappings by grouping any two alignments that are on the same chromosome and within 50kb of one another into the same cloud, which is the same approach employed by Lariat (for TruSeq SLR or CPT-seq data, we use 15kb as a cutoff; this is a tuneable parameter that can be adjusted depending on the underlying technology). While this heuristic works well in the majority of cases, it can evidently run into issues if, for example, a single read aligns multiple times to the same cloud. We address such cases below, but assume in the subsequent analysis that clouds consist of at most one alignment of a given read.

As notation, we will denote by c the set of alignments contained in a given cloud. We restrict our analysis to a single set of clouds $\mathcal{C}=\left\{c_1,c_2,\dots ,c_n\right\}$ that corresponds to a connected component in the disjoint-set over clouds induced by alignments, as shown in Figure 1B (i.e. two clouds c_i and c_j will be connected if there is a read that has an alignment to both c_i and c_j). Conceptually, the clouds in $\mathcal{C}$ can be thought of as alternate possibilities for the same latent source fragment. By definition, for any given read aligning to some cloud in $\mathcal{C}$, we will have to consider only the clouds in $\mathcal{C}$ when determining the best alignment for that read, so we focus on each such set of clouds separately. Note that we make the same implicit assumption made by Lariat: namely that distinct fragments sharing a common barcode (i.e. fragments in the same droplet/well) do not overlap on the genome. In reality, there is nothing preventing this from happening, but we can see that it occurs rarely since fragments are effectively sampled uniformly from the entire genome. If we partition the 3Gb genome into 100kb bins (as a reasonable upper bound on mean fragment length) and assume a droplet/well contains about 10 fragments (also a reasonable bound), we can observe that only about $1-{\displaystyle \prod }_{i=1}^{10}\left(1-\left(i-1/3\text{Gb}/100\text{kb}\right)\right)\approx 0.15\%$ will contain overlapping fragments, where (as an approximation) we assume fragments overlap Q if they are contained in the same bin. By comparison, about 5%–6% of all 10x reads are usually left without a barcode after standard barcode correction, so the additional 0.15% is rather marginal. A second possible undesirable scenario would be if two fragments with the same barcode originated from distinct but homologous regions. In this case, we would find two connected clouds in the disjoint-set that we would wrongly consider to be alternate possibilities of a single fragment. Nevertheless, we expect our optimization algorithm to handle this situation gracefully, assigning some probability to each read of mapping to either homolog (arguably, this is more of a problem with the previously employed read cloud methods wherein reads are only ever assigned to a single cloud).

For $\mathcal{C}=\left\{c_1,\dots ,c_n\right\},$ let C_i denote the event that cloud c_i represents the true source fragment. Since the clouds c₁,…,c_n are different possibilities for the same source fragment, we have Pr(C_i ∩ C_j) = 0 (i ≠ j) and ${\displaystyle \sum }_{i=1}^{n}1\left(C_i\right)=1$ (where 1(·) ∈ {0, 1} is an indicator for the specified event). We assume uniform priors on the clouds so that Pr (C_i) = (1/n) (while it is possible to devise a prior that takes into account features such as cloud length, we observed a large variance between clouds in our datasets that renders this unhelpful). Now, a cloud c_i can be conceptualized as an entity that generates some number of reads K_i, parameterized by some weight ${\theta }_{c_i},$ so that we can say $K_i~\text{Cloud}\left({\theta }_{c_i}\right)$ for some unknown “cloud” distribution over generated reads. We make the key assumption that, in expectation, $\mathrm{Pr}\left(C_i|{\theta }_{c_i}\right)\propto K_i\propto {\theta }_{c_i}$ for all $c_i\in \mathcal{C}.$ In other words, if a cloud is expected to have generated a large number of reads, then the probability that the cloud represents a true source fragment is high. Let $\theta =\left({\theta }_{c_1},\dots ,{\theta }_{c_n}\right)$ be the vector of cloud weights. We assume the cloud weights are normalized so that $\mathrm{Pr}\left(C_i/{\theta }_{c_i}\right)={\theta }_{c_i},$ and that they are drawn from a uniform Dirichlet distribution so that θ ~ Dir(1). Consider now the probability ${\gamma }_{r,c_i}$ that a read r truly originates from cloud c_i (denoted as an event by ${\Gamma }_{r,c_i}$) given the cloud parameters θ (i.e. ${\Gamma }_{r,c_i}/\theta ~\text{Ber}\left({\gamma }_{r,c_i}\right),$ where Ber(p) is the Bernoulli distribution with parameter p). By Bayes’ rule, we can say:

$${\gamma }_{r,c_i}=\mathrm{Pr}\left({\Gamma }_{r,c_i}/\theta \right)=\frac{1}{Z_{\mathcal{C}}}\mathrm{Pr}\left(\theta /{\Gamma }_{r,c_i}\right)\mathrm{Pr}\left({\Gamma }_{r,c_i}\right),$$

where $Z_{\mathcal{C}}\text{s}$ (and variants thereof) are normalization constants that are the same for each $c\in \mathcal{C}.$ Since ${\Gamma }_{r,c_i}$ occurs if and only if C_i occurs, we have

$${\gamma }_{r,c_i}=\frac{1}{Z_{\mathcal{C}}}\mathrm{Pr}\left(\theta /C_i\right)\mathrm{Pr}\left({\Gamma }_{r,c_i}\right).$$

Applying Bayes’ rule again to Pr(θ/C_i) and using the fact that both Pr(θ) and Pr(C_i) are uniform, we obtain

$${\gamma }_{r,c_i}=\frac{1}{Z_{\mathcal{C}}}\frac{\mathrm{Pr}\left(\theta \right)\mathrm{Pr}\left(C_i/\theta \right)}{\mathrm{Pr}\left(C_i\right)}\mathrm{Pr}\left({\Gamma }_{r,c_i}\right)=\frac{1}{{Z^{\prime }}_{\mathcal{C}}}\mathrm{Pr}\left(C_i/\theta \right)\mathrm{Pr}\left({\Gamma }_{r,c_i}\right)=\frac{{\theta }_{c_i}}{{Z^{\prime }}_{\mathcal{C}}}\mathrm{Pr}\left({\Gamma }_{r,c_i}\right),$$

where ${Z^{\prime }}_{\mathcal{C}}=\left[\mathrm{Pr}\left(C_i\right)/\mathrm{Pr}\left(\text{θ}\right)\right]Z_{\mathcal{C}}.$ Note that $\mathrm{Pr}\left({\Gamma }_{r,c_i}\right)$ is a prior on the probability that r truly originates from c_i, which is not dependent on the barcode but rather only on edit distance, mate alignment, and mapping quality as in standard short-read alignment. Henceforth, we refer to $\mathrm{Pr}\left({\Gamma }_{r,c_i}\right)$ as ${\gamma }_{r,c_i}^{\left(0\right)},$ so that ${\Gamma }_{r,c_i}~\text{Ber}\left({\gamma }_{r,c_i}^{\left(0\right)}\right).$

Now we can form a prior ${\theta }^{\left(0\right)}=\left({\theta }_{c_1}^{\left(0\right)},\dots ,{\theta }_{c_n}^{\left(0\right)}\right),$ which is intuitively the initial vector of cloud weights. If we are given a set of alignment probabilities and a “current” θ estimate ${\theta }^{\left(t\right)}=\left({\theta }_{c_1}^{\left(t\right)},\dots ,{\theta }_{c_n}^{\left(t\right)}\right)$ (initially t = 0), we can iteratively compute a better estimate θ^{(t + 1)} using the fact that ${\theta }_{c_i}\propto K_i$ in expectation:

$$\begin{gathered} {\theta }_{C_i}^{\left(t+1\right)}=\frac{1}{\left|\mathcal{R}\right|}\mathbb{E}\left(K_i\right)=\frac{1}{\left|\mathcal{R}\right|}\mathbb{E}\left({\displaystyle \sum }_{r\in \mathcal{R}}1\left({\Gamma }_{r,c_i}\right)/{\theta }^{\left(t\right)}\right) \\ =\frac{1}{\left|\mathcal{R}\right|}{\displaystyle \sum }_{r\in \mathcal{R}}\mathrm{Pr}\left({\Gamma }_{r,c_i}|{\theta }^{\left(t\right)}\right) \\ =\frac{1}{\left|\mathcal{R}\right|}{\displaystyle \sum }_{r\in \mathcal{R}}{\gamma }_{r,c_i}^{\left(t\right)}, \end{gathered}$$

where $\mathcal{R}$ is the set of reads mapping to any cloud in $\mathcal{C},$ and the $1/\left|\mathcal{R}\right|$ factor ensures that $\sum _{c\in \mathcal{C}}{\theta }_c=1$ This latent variable model formulation naturally to an expectation-maximization algorithm—one of the widely used ways of maximizing likelihood in such models—for determining the cloud weights and, thereby, the final alignment probabilities ${\gamma }_{r,c_i}^{★}.$ An implementation of this algorithm is given in Algorithm 1 (in practice we use T = 5 EM iterations).

Algorithm 1

Barcoded read alignment via expectation – maximization

Require:$\mathcal{R}$, $\mathcal{C}$

Ensure : ${\gamma }_{r,c}^{★}$ for each $r\in \mathcal{R},$ $c\in \mathcal{C}$

${\gamma }_{r,c}^{\left(0\right)}\leftarrow \mathrm{Pr}\left(r\in c\right),\forall r\in \mathcal{R},c\in \mathcal{C}$

${\theta }_c^{\left(0\right)}\leftarrow \frac{1}{\left(\mathcal{C}\right)},\forall c\in \mathcal{C}$

for t ∈ {0, 1, …, T − 1} do

E step: ${\gamma }_{r,c}^{\left(t+1\right)}\leftarrow \mathrm{Pr}\left(r\in c_i|{\theta }_c^{\left(t\right)}\right)\forall r\in \mathcal{R},c\in \mathcal{C}$

M step : ${\theta }_c^{\left(t+1\right)}\leftarrow \frac{1}{\left|\mathcal{R}\right|}{\displaystyle \sum }_{r\in \mathcal{R}}{\gamma }_{r,c}^{\left(t\right)}\forall r\in \mathcal{R}$

end for

${\gamma }_{r,c}^{★}\leftarrow {\gamma }_{r,c}^{\left(T\right)}\forall r\in \text{R},c\in \text{C}$

Each of the described variables and their interactions with one another is summarized in Supplementary Figure S1. Once we determine the final alignment probabilities through this method (as in Figure 1D), we use them to compute mapping qualities (“MAPQs”), which are a standard per-alignment metric reported by all aligners and are frequently used by downstream analysis pipelines. Specifically, we take the MAPQ to be the minimum of the alignment probability, the barcode-oblivious alignment score and the MAPQ reported by BWA-MEM’s API (which is used in EMA’s current implementation to find candidate alignments). Importantly, we also report the actual alignment probabilities determined by EMA via a special standard-compliant SAM tag, so that they are available to downstream applications.

Read Density Optimization to Handle Multi-Mappings in a Single Cloud

While the 50kb-heuristic described above is typically effective at determining the clouds, it does not take into account the fact that a single read may align multiple times to the same cloud (which can occur if a cloud spans two or more homologous regions). In such cases, rather than simply picking the alignment with lowest edit distance within the cloud, as is the current practice, we propose a novel alternative approach that takes into account not only edit distance but also read density. We take advantage of the insight that there is typically only a single read pair per 1kb bin in each cloud; the exact distribution of read counts per 1kb bin is shown in Supplementary Figure S2. Now consider the case where one of our source fragments spans two highly similar (homologous) regions, and thereby produces a cloud with multi-mappings, as depicted in Figure 1C. If we pick alignments solely by edit distance, we may observe an improbable increase in read density (as shown in the figure). Consequently, we select alignments for the reads so as to minimize a combination of edit distance and abnormal density deviations.

Specifically, consider any cloud with multi-mappings consisting of a set of reads R ={r₁,…,r_n}, and denote by A_r the set of alignments for read r ∈R in the cloud. Additionally, let a_r∈A_r denote the currently “selected”falignment for r. We will initially partition the cloud, spanning the region from its leftmost to its rightmost alignment, into the set of bins B ={b₁,…, b_n} of equal width w, where each bin b_i covers the alignments whose starting positions are located in the interval $\left[i\cdot w,\left(i+1\right)\cdot w\right),$ as shown in Figure 1C. In practice, we set w to 1kb. Denote by C_bi the random variable representing the number of reads in bin b_i, where C_bi is drawn from the bin density distribution CloudBin(i). Lastly, let ${\gamma }_{a_r}$ denote the prior probability that alignment a_r is the true alignment of read r based on edit distance and mate alignments alone. Our goal is to maximize the objective:

$$\left[{\displaystyle \prod }_{r\in R}{\gamma }_{a_r}\right]\cdot \left[{\displaystyle \prod }_{b_i\in B}\mathrm{Pr}{\left(C_{b_i}={\displaystyle \sum }_{r\in R}1\left(a_r\in b_i\right)\right)}^{\alpha }\right],$$

where α is a parameter that dictates the relative importance of the density probabilities compared to the alignment probabilities (we use a = 0:05 in practice). We determine the distribution CloudBin(i) of each C_bi beforehand by examining uniquely-mapping clouds that we are confident represent the true source fragment. Taking the logarithm, this objective becomes:

$$J\left(a_{r_1},\dots ,a_{r_n}\right)={\displaystyle \sum }_{r\in R}\log {\gamma }_{a_r}+\alpha {\displaystyle \sum }_{b_i\in B}\log \mathrm{Pr}\left(C_{b_i}={\displaystyle \sum }_{r\in R}1\left(a_r\in b_i\right)\right).$$

We optimize J through simulated annealing by repeatedly proposing random changes to a_r and accepting them probabilistically based on the change in our objective (the corresponding algorithm is described in Algorithm 2, in which K is the number of simulated annealing iterations, and τ(⋅) defines the annealing schedule, which can be taken to be an exponentially decreasing function).

Algorithm 2

Read density optimization via simulated annealing

Require : $\begin{array}{ll}R;A_r\hfill & \forall r\in R\hfill \end{array}$

Ensure : $\begin{array}{ll}{a}_r^{★}\hfill & \forall r\in R\hfill \end{array}$

a_r ← random(A_r) ∀r ∈ R

$z\leftarrow J\left(a_{r_1},\dots ,a_{r_n}\right)$

for k ∈ {1,…,K} do

r′ ← random({r ∈ R : |A_r|>1})

${a^{\prime }}_r\leftarrow \text{random}\left(A_r\backslash \left\{a_r\right\}\right)$

$z^{\prime }\leftarrow J\left(a_{r_1},\dots ,a_{r^{\prime }},\dots ,a_{r_n}\right)$

if z′>z or $\exp \left(-\frac{z-z^{\prime }}{\tau \left(k\right)}\right)>\text{random}\left(\left[0,1\right)\right)$ then

a_r ← a′_r

z ← z′

end if end for

$\begin{array}{ll}{a}_r^{★}\leftarrow a_r\hfill & \forall r\in \text{R}\hfill \end{array}$

We apply the preceding latent variable optimization algorithm to deduce optimal alignments between clouds and, if necessary, use this statistical binning algorithm to find the best alignments within a given cloud.

DATA AND SOFTWARE AVAILABILITY

EMA’s full source, links to all datasets used and detailed guidelines for reproducing our results are available online at http://ema.csail.mit.edu and https://github.com/arshajii/ema.

Highlights.

• We devise a two-tiered statistical binning model to align barcoded reads to the genome

• We can map highly homologous regions to uncover rare variants important in disease

• Our method greatly improves downstream genotyping and haplotyping accuracy

• We determine not only alignments but also interpretable alignment probabilities