Abstract
Parkinson's Disease (PD) is associated with decreased ability to perform habitual tasks, relying instead on goal-directed behaviour subserved by different cortical/subcortical circuits, including parts of the putamen. We explored the functional subunits in the putamen in PD using novel dynamic connectivity features derived from resting state fMRI recorded from thirty PD subjects and twenty-eight age-matched healthy controls (HC). Dynamic functional segmentation of the putamina was obtained by determining the correlation between each voxel in each putamen along a moving window and applying a joint temporal clustering algorithm to establish cluster membership of each voxel at each window. Contiguous voxels that had consistent cluster membership across all windows were then considered to be part of a homogeneous functional subunit. As PD subjects robustly had two homogenous clusters in the putamina, we also segmented the putamina in HC into two dynamic clusters for a fair comparison. We then estimated the dynamic connectivity using sliding windowed correlation between the mean signal from the identified homogenous subunits and 56 other predefined cortical and subcortical ROIs. Specifically, the mean dynamic connectivity strength and connectivity deviation were then compared to evaluate subregional differences.
HC subjects had significant differences in mean dynamic connectivity and connectivity deviation between the two putaminal subunits. The posterior subunit connected strongly to sensorimotor areas, the cerebellum, as well as the middle frontal gyrus. The anterior subunit had strong mean dynamic connectivity to the nucleus accumbens, hippocampus, amygdala, caudate and cingulate. In contrast, PD subjects had fewer differences in mean dynamic connectivity between subunits, indicating a degradation of subregional specificity. Overall UPDRS III and MoCA scores could be predicted using mean dynamic connectivity strength and connectivity deviation. Side of onset of the disease was also jointly related with functional connectivity features.
Our results suggest a robust loss of specificity of mean dynamic connectivity and connectivity deviation in putaminal subunits in PD that is sensitive to disease severity. In addition, altered mean dynamic connectivity and connectivity deviation features in PD suggest that looking at connectivity dynamics offers an additional dimension for assessment of neurodegenerative disorders.
Keywords: fMRI, Dynamic parcellation, Dynamic connectivity, Temporal homogeneous subunits, Parkinson's Disease, Putamen
Highlights
-
•
Dynamic connectivity features are utilized for functional subunits parcellation by a joint temporal clustering method.
-
•
Temporal homogenous subregions in the putamen and their connectivity patterns are investigated in the HC and PD groups.
-
•
The decreased subregional specificity in the putamen is found in the PD group.
-
•
The subregional connectivity features predict the disease severity in PD.
1. Introduction
Corticostriatal connections are important for the cognitive and motivational aspects of goal directed motor behaviours. Traditionally, the ventral striatum, which includes the nucleus accumbens, medial and ventral aspects of the caudate and putamen, part of the olfactory tubercle, and anterior perforated substance, has been associated with reward processing. The dorsal striatum consists of the majority of the caudate and the putamen, and has been implicated in cognitive function (particularly working memory (Provost et al., 2010)), and sensorimotor processing (Haber, 2016) respectively. However, it is becoming increasingly clear that such delineations of reward, cognitive and motor processing being directly attributed to the ventral striatum, caudate and putamen respectively is an oversimplification, as there is considerable overlap in function between these basal ganglia structures (Cardinal et al., 2002; Haber, 2016; Postuma and Dagher, 2006; Robbins, 2007).
Motor-related striatal areas such as the putamen subserve different motor functions with dorsomedial regions important for goal-directed control, and more laterally located sensorimotor regions important for habitual movements (Gruber and McDonald, 2012; Redgrave et al., 2010). Goal-directed learning is usually slow, continuous and learning on purpose. In contrast, in habitual learning, motor behavior is based on the default stimulus-response, and is fast, unconditioned and spontaneous (Dolan and Dayan, 2013). When a new motor task is repeatedly performed, it becomes more habitual and requires less goal-directed effort. The ventrolateral substantia nigra projecting to the caudolateral sensorimotor putamen may be particularly susceptible to degeneration early on in PD (Pavese and Brooks, 2009) affecting habitual motor control.
Elucidating the role of cortical striatal communications in PD is facilitated by non-invasive brain imaging methods such as functional MRI (fMRI). In addition to the local activity changes seen in fMRI, prior studies have demonstrated altered motor-related fMRI connectivity patterns in PD. A reduced overall connectivity of the left putamen during resting state is seen in drug-naive PD subjects, which is relatively restored with L-dopa medication (Wu et al., 2009). By contrasting early-stage PD subjects with healthy controls, (Luo et al., 2014) demonstrated decreased putaminal connectivity with mesolimbic regions, and especially reduced connectivity between the posterior putamen and sensorimotor cortex. Other studies have found remapping of striatal connectivity in PD at rest, with reduced spatial segregation between different cortico-striatal loops (Hacker et al., 2012; Helmich et al., 2010), and even accurately predicting whether PD subjects would develop dyskinesia (Herz et al., 2016). Task-based alterations in striatal connectivity in PD have also been investigated (Palmer et al., 2009; Wu et al., 2011a, Wu et al., 2011b). For instance, during a self-initiated right hand tapping task, connectivity between the putamen and M1, PMC, SMA and cerebellum were found to be decreased in PD patients (Wu et al., 2011a, Wu et al., 2011b). Therefore, striatal connectivity profiles associated with PD are important in understanding the pathophysiology of disease and may potentially provide an additional biomarker for PD.
Connectivity studies are often performed at the ROI (Region-of-Interest) level, as opposed to the individual voxel level as this is computational efficient, robust against noise, and eases neurological interpretation. However, parcellation of brain regions into biologically-meaningful ROIs is challenging. Conventionally, ROIs have been defined using atlases based on cytoarchitecture or anatomical structure (Tzourio-Mazoyer et al., 2002; Zilles and Amunts, 2009), although this requires the fairly strong assumption that functional activity closely follows anatomical divisions across all individuals. However, a single anatomical ROI, such as the putamen or amygdala, may in fact encompass distinct functional subdivisions (Mishra et al., 2014; Zhang et al., 2016), leading to inaccurate connectivity estimation. Thus a compromise between voxel-level connectivity and ROI-level connectivity studies is to parcellate an anatomically-derived given ROI into functionally homogeneous subregions. This may have particular clinical applications with respect to e.g., deep brain stimulation electrode placement.
A number of data-driven approaches have thus been proposed to parcellate brain regions based on functional connectivity. In clustering methods, features derived from the connectivity patterns between voxels are computed, then different clustering approaches can be used, including K-means clustering (Jung et al., 2014), hierarchical clustering (Blumensath et al., 2013), self-organized mapping (Mishra et al., 2014), spectral clustering (Shen et al., 2013) and region growing techniques (Lu et al., 2003). Another category of methods for connectivity based parcellation is based on modularity detection, where the voxels are considered as the nodes in a graph and it separates the graph into distinct modules (Barnes et al., 2010).
However, most methods for functional parcellation have not considered connectivity dynamics, neglecting the possibility that spatial patterns of functional homogeneous coactivations may change over time. Estimating dynamic changes provides another dimension in which to investigate brain alterations (Calhoun et al., 2014; Hutchison et al., 2013; Liu et al., 2016). Rajtmajer et al. proposed to define the temporal consensus of brain subdivisions by first estimating the parcellation using modularity at different time points and then aggregating the parcellations based on label propagation (Rajtmajer et al., 2015). To account for temporal dynamics, Instantaneous Correlation Parcellation (ICP) can be used to transform the original fMRI signals into an instantaneous correlation map, and selected features across sliding windows can be used to create a detailed parcellation of the thalamus (Ji et al., 2016; van Oort et al., 2018).
A number of studies have proposed to investigate the subdivisions in the striatum and its subregions based on their connectivity patterns in both health and disease (Bohanna et al., 2011; Choi et al., 2012; Cohen et al., 2009; de Wit et al., 2012; Helmich et al., 2010; Horga et al., 2015; Janssen et al., 2015; Jung et al., 2014). The putamina and caudate have been segmented into seven subregions according to their white matter connections to cortical areas in Huntington's disease (Bohanna et al., 2011). Using functional connectivity features, the striatum has been divided into functional subregions and coupled to cortical association networks by assigning each voxel in the striatum to its most strongly correlated cortical network (Choi et al., 2012). In (Jung et al., 2014), the authors parcellated the human striatum based on resting state connectivity using K-means clustering and reported multiple parallel corticostriatal loops with distinct connectivity maps. A reinforcement learning study suggested that the functional connections between the sensorimotor cortex and the posterior putamina strengthened progressively during learning (Horga et al., 2015). However, those studies did not consider the dynamic connectivity features, nor focused on the functional subdivisions associated with habitual learning, as would be relevant for PD.
Here we aim to estimate the functionally homogenous subunits in the putamina to reveal the altered functional connectivity in PD. We take account the voxel-wise connectivity dynamics into the functional region definition and study their subregional mean dynamic connectivity and connectivity deviation patterns.
2. Materials and methods
2.1. Subjects
Thirty PD subjects (11 females; age: 57.77 ± 9.85; UPDRS III: 32.53 ± 15.93; Hoehn and Yahr scale: 1.95 ± 0.62) and twenty-eight age-matched healthy controls (HC, 14 females; age: 58.39 ± 7.64) participated in this study. The demographical data is summarized in Table 1. All participants were recruited from the Movement Disorders Clinic of Xuanwu Hospital of Capital Medical University, and provided written, informed consent prior to participation. All studies were approved by the Institutional Review Board of Xuanwu Hospital of Capital Medical University, Beijing, China.
Table 1.
Demographical data.
| Variables | PD (n = 30) | NC (n = 28) | P-values |
|---|---|---|---|
| Gender (female/male) | 11/19 | 14/14 | 0.305 |
| Age (years) | 57.77 ± 9.85 | 58.39 ± 7.64 | 0.787 |
| Disease duration (years) | 5.07 ± 3.19 (1−13) | – | – |
| Onset side (B/R/L) | 3/17/10 | – | – |
| H-Y stage | 1.95 ± 0.62 (1–3) | – | – |
| MDS-UPDRS III (off) | 32.53 ± 15.93 (13–73) | – | – |
| LEDD (mg/d) | 395.75 ± 285.29 | – | – |
| MMSE | 27.93 ± 1.68 | 28.46 ± 1.45 | 0.202 |
| MoCA | 25.20 ± 3.55 | 26.00 ± 3.60 | 0.3980 |
2.2. fMRI data
Resting state imaging data were collected on a SIEMENS Trio 3 T scanner equipped with a head-coil. During scanning, all the participants were instructed to lie awake with eyes closed. Earplugs were used to minimize machine noise. PD subjects were scanned in the off-medication state (after a 12-h period of medication withdrawal).
High-resolution T1 weighted anatomical images were acquired using a sagittal, magnetization prepared rapid gradient echo three-dimensional T1-weighted sequence with a repetition time of 1970 ms, echo time of 3.9 ms, inversion time of 1100 ms and flip angle of 15°. A radiologist assessed the images of all participants to exclude those with space-occupying lesions and extensive cerebrovascular disease. Blood oxygenation level-dependent (BOLD) contrast echo-planar (EPI) T2*-weighted images were acquired with the following specifications: repetition time of 2000 ms, echo time of 30 ms, flip angle of 90°, field of view of 256 mm × 256 mm, matrix size of 64 × 64, voxel size of 3.0 mm × 3.0 mm × 4.0 mm, axial slices of 33 layers and the scanning time of 8 mins.
2.3. Imaging Preprocessing
A custom designed pipeline based on AFNI (http://afni.nimh.nih.gov/afni), FreeSurfer (https://surfer.nmr.mgh.harvard.edu/) and FSL (http://www.fmrib.ox.ac.uk/fsl) was utilized to preprocess imaging data in subject's native space. Despiking was first performed on the voxel-wise basis to remove the potential artefacts. The remaining images were then corrected for slice timing in order to eliminate the slice intensity differences due to interleaved acquisition, and further resliced to 3 mm isotropic voxels. Motion correction for any major head movements during the scan was performed using rigid body alignment. Standard brain parcellation was done on T1-weighted images in FreeSurfer. Functional data and parcellated structural images were co-registered with the functions from FSL as FSL performs well without too much computational demand. Since we were interested in the putamina in elderly population, who might be sensitive to misregistration, all analysis was done in the individual subject's native space, as opposed to spatially registering to a common template.
Sources of spurious variance, along with their temporal derivatives, were voxel-wise regressed from processed data including six parameters obtained by motion correction for rigid body head motion, the white-matter signal and the CSF signal. In the next step, fMRI signals were detrended by removing any linear or quadratic trends. The fMRI data were then spatially smoothed by a 6 × 6 × 6 FWHM (Full Width at Half Maximum) Gaussian kernel to further improve its SNR (Signal to noise ratio) in the subsequent analysis. The temporal bandpass filter was finally applied at 0.01 Hz to 0.08 Hz as suggested in previous studies.
2.4. Joint temporal parcellation
To incorporate the connectivity properties into the voxel selection, the Normalized Cut (NC), a graph-based spectral clustering algorithm, was used (Shi and Malik, 2000). Suppose the number of voxels in a target brain region is N, we construct a graph G = {V, E}, where the vertex set V represents all N voxels, and E is the edge set. Let W denotes the weight matrix between vertices, and W(i, j) is defined as a function of correlation between nodes i and j. To divide the graph into two disjoint sets A and B, we try to minimize the connections between two sets while maximizing the connections within each set, and the objective function of NC is defined as,
where is the sum of weighted connections between sets A and B, and is the total weights of connections from nodes in A to all other nodes in the graph.
The NC algorithm can be further extended to a K-way partition (Yu and Shi, 2003). Let D be an N ∗ N diagonal matrix with , and indicator matrix Y ∈ {0, 1}N∗K represents the partition of graph G. Then if node i belongs to partition set j, Y(i, j) = 1, otherwise, Y(i, j) = 0. This optimization problem can be efficiently solved as a generalized eigenvalue problem,
where Z′Z = IK and IK is the identity vector with length K. The solution of Z is the matrix with the k eigenvectors associated with the first K eigenvalues of matrix . Z can be considered as the new set of coordinates for the graph and we further apply the K-means to obtain the cluster indicator matrix Y.
Here, we extend the NC approach into a time varying setting. Under the assumption that brain activity recorded by fMRI changes relatively slowly over time, a sliding window framework is utilized. Assume that the window length is L and t ∈ {1, 2, …, T} is the index of time windows. We could construct the graph Gt = (Vt, Et) at each time window respectively. For convenience, we use the subscript t to represent the time index.
Suppose Zt ∈ RN∗K is the new set of coordinates obtained at each time point by solving the optimization problem , Yt is the cluster indicator matrix at time window t, and Ycom is the common cluster indicator matrix for the samples at all the time epochs. Similar to the multiple graph clustering formulation (Shen et al., 2013), the cost function of this joint temporal clustering problem could be formulated as,
where Rt′Rt = IK is the generalized rotation matrix of Zt. It tries to rotate individual coordinates to create a joint parcellation Ycom as well as obtaining the time dependent parcellation Yt by the rounding procedure of ZtRt. This optimization estimates the clustering membership jointly for all time windows by iteratively updating Rt and Ycom until they converge. We thus finally obtain the joint time dependent ROI parcellation. The performance of multiple graph clustering approach has been sufficiently validated in a group parcellation scenario (Shen et al., 2013).
2.5. Homogeneous subunits parcellation of the putamen
To apply the joint temporal parcellation approach, we first constructed the dynamic connectivity networks within the right and left putamina across time using a sliding window framework. The window length was chosen to be 60 s (= 30 samples) as suggested in previous studies, which is long enough to overcome the random fluctuations while still capable of detecting the underlying dynamics in the connectivity (Zalesky and Breakspear, 2015). The window moved 2 time points (4 s) forward at each Pearson's pairwise correlation, which resulted in 101 windowed connectivity matrices of regional networks involving the bilateral putamina. Because the significance of negative correlations is still unclear, and we were interested in spatially confluent parcellations, correlations between spatially discontinuous voxels or negative correlations were removed from the network, resulting in the symmetric, positive and spatially continuous time-dependent similarity matrices.
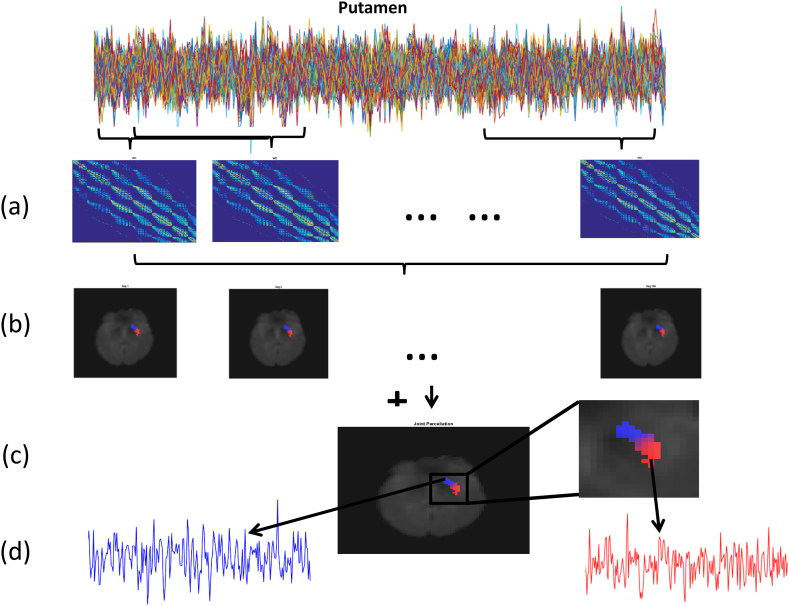
The joint temporal parcellation approach would simultaneously segment the target ROI at each time point into functional subunits. Voxels that were consistently assigned to the same cluster over time, i.e. the homogeneous subunits, were further investigated. We found that dividing each putamen into three or more subunits in the PD group resulted in some subjects having clusters that did not have any voxels with consistent cluster membership over time. We therefore restricted ourselves to parcellating the putamina into two clusters. For a fair comparison, we also parcelleated the putamina in the HC group using two clusters. The overview of the framework is demonstrated in Fig. 1.
Fig. 1.
Framework for studying the homogeneous subregions in the putamen. (a). Estimate the connectivity network at each time point for the target region. (b). Apply joint temporal clustering model to simultaneously segment the target region over time. (c). Based on the temporal clustering results, define the dynamic homogeneous subregions. (d). Extract the average time courses of homogenous subunits for subsequent dynamic connectivity analysis.
2.6. Functional connectivity maps of the subunits
Once the parcellation had been computed, the average signal of the voxels within each consistent cluster was used in subsequent dynamic connectivity analysis with other ROIs by windowed Pearson's pairwise correlation. The window length was 60 s and moved forward 4 s each window. In addition to the bilateral putamina, 56 ROIs were selected as shown in Table 2. These included representative ROIs from visual, motor, sensory, attentional, cerebellar and basal ganglia regions. The homogeneous subunits' connectivity to ROIs were then compared between HC and PD groups. Specifically, the mean and standard deviation of the dynamic connectivity strength between each putaminal homogenous subunits and all other ROIs were computed.
Table 2.
58 ROIs (including Left and Right Putamen) used in the dynamic connectivity analysis.
| Index | Name | Index | Name |
|---|---|---|---|
| 1 | L-Putamen | 30 | R-Putamen |
| 2 | L-Cerebellum-Ctx | 31 | R-Cerebellum-Ctx |
| 3 | L-Thalamus | 32 | R-Thalamus |
| 4 | L-Caudate | 33 | R-Caudate |
| 5 | L-Pallidum | 34 | R-Pallidum |
| 6 | L-Hippocampus | 35 | R-Hippocampus |
| 7 | L-Amygdala | 36 | R-Amygdala |
| 8 | L-Accumbens-area | 37 | R-Accumbens-area |
| 9 | L-Caudal-Anterior-Cingulate-Ctx | 38 | R-Caudal-Anterior-Cingulate-Ctx |
| 10 | L-Caudal-Middle-Frontal-Ctx | 39 | R-Caudal-Middle-Frontal-Ctx |
| 11 | L-Cuneus | 40 | R-Cuneus |
| 12 | L-Entorhinal | 41 | R-Entorhinal |
| 13 | L-Inferior-Parietal-Ctx | 42 | R-Inferior-Parietal-Ctx |
| 14 | L-Inferior-Temporal-Ctx | 43 | R-Inferior-Temporal-Ctx |
| 15 | L-Lateral-Orbitofrontal-Ctx | 44 | R-Lateral-Orbitofrontal-Ctx |
| 16 | L-Medial-Orbitofrontal-Ctx | 45 | R-Medial-Orbitofrontal-Ctx |
| 17 | L-Middle-Temporal-Ctx | 46 | R-Middle-Temporal-Ctx |
| 18 | L-Parahippocampal–Ctx | 47 | R-Parahippocampal-Ctx |
| 19 | L-Paracentral-Ctx | 48 | R-Paracentral-Ctx |
| 20 | L-Postcentral-Ctx | 49 | R-Postcentral-Ctx |
| 21 | L-Posterior-Cingulate-Ctx | 50 | R-Posterior-Cingulate-Ctx |
| 22 | L-Precentral-Ctx | 51 | R-Precentral-Ctx |
| 23 | L-Precuneus | 52 | R-Precuneus |
| 24 | L-Rostral-Anterior-Cingulate-Ctx | 53 | R-Rostral-Anterior-Cingulate-Ctx |
| 25 | L-Rostral-Middle-Frontal-Ctx | 54 | R-Rostral-Middle-Frontal-Ctx |
| 26 | L-Superior-Frontal-Ctx | 55 | R-Superior-Frontal-Ctx |
| 27 | L-Superior-Parietal-Ctx | 56 | R-Superior-Parietal-Ctx |
| 28 | L-Superior-Temporal-Ctx | 57 | R-Superior-Temporal-Ctx |
| 29 | L-insula | 58 | R-Insula |
L and R represent left and right hemisphere respectively, and Ctx represents the cortex.
2.7. Disease severity prediction using functional connectivity features
We examined the relationship between the derived connectivity features and the Unified Parkinson's Disease Rating Scale III (UPDRS III) by correlation analysis. A False Discovery Rate (FDR) multiple comparison correction was performed and the significance level was set to be 0.05. In addition, we further examined the capability of connectivity features for disease severity prediction and identified potential biomarkers for PD. Prior to analysis, we excluded the effects of age, disease duration and LEDD by first standardising these variables and then regressing them from the UPDRS III scores. Considering that the number of connectivity features with the bilateral putaminal subunits was large (e.g., 228 pairs of connections), we first applied a LASSO (Least absolute shrinkage and selection operator) regression model to choose the most related features in order to narrow down the features pool (Tibshirani, 1996). Suppose we have N subjects, leaving one subject out in each run, we chose a sparse set of features using LASSO with N − 1 subjects. The LASSO model was applied (with 5-fold cross validation to avoid overfitting), and the optimal tuning parameter was determined based on the minimal mean square error in each run. As a result, we obtained the frequency of the selected features over all runs. According to the frequency of selected features, we chose the subset of features that produced the highest prediction accuracy using a leave one subject out regression model. More specifically, we gradually increased the number of features according to their frequency. With fixed number of features, the leave one subject out simple regression was applied where N − 1 subjects were used as the training set and one subject was used for prediction. We reported the set of features obtaining the highest prediction accuracy. The prediction accuracy was estimated by the correlation of the predicted UPDRS III against the measured true UPDRS III.
2.8. Associating the cognitive profiles with functional connectivity features
To assess the multivariate association between cognitive profiles and functional connectivity features, we estimated the maximized correlations between MoCA (Montreal Cognitive Assessment) subscores and subregional connectivity features using Canonical Correlation Analysis (CCA) (Chen et al., 2016; Chen et al., 2018; Hardoon et al., 2004). The effects of age, disease duration and LEDD were first excluded by first standardising these variables and then regressing them out from the MoCA subscores. Let X ∈ RS∗N and Y ∈ RS∗M represent normalized connectivity features and cognitive profiles, respectively. CCA aims to estimate the projections of X and Y which achieve the maximum correlation between the projected variables. It can be formulated as,
where w and v are the weight vectors, and Xw and Yv are the projected canonical variables. CCA sequentially seeks each pair of canonical variables with maximized correlation between them, and each pair is uncorrelated with the other pairs of canonical variables. Due to the possible collinearity of cognitive scores and connectivity features, instead of using projection weights, the loadings were utilized to infer the contribution of each feature to the canonical variables. The loading is defined as the correlation between each measurement with the estimated canonical variable. A permutation test was then used to estimate the significance of canonical correlation coefficients. Briefly, the samples were randomized, and canonical correlation coefficients were estimated with the permuted signals. Suppose this procedure is repeated K times, and L is the number of permuted results that are greater than the estimated coefficients without permutation, then significance level of the coefficients could be estimated by Pval = L/K. Here we set K = 500. To robustly assess the loadings for each measurement, a leave-one-subject-out procedure was utilized in our analysis and the significance of the loadings was then evaluated by the one sample t-test. Prior to analysis, to avoid the collinearity, we first applied Principal Component Analysis (PCA) to reduce the dimensionality of the connectivity features before applying CCA, retaining enough components to capture >90% of the variance (in this case, 21 components).
Finally, we also examined the capability of connectivity features for MoCA total score prediction in PD. The same procedure was performed as described for UPDRS III prediction, the LASSO model was used for evaluating the importance of features and then leave one subject out simple regression was utilized for prediction. The set of features obtaining the highest prediction accuracy was reported.
3. Results
3.1. Homogeneous subunits identification in putamen
In this study, we applied a joint temporal parcellation model to simultaneously parcellate the bilateral putamina into two functional subclusters at each time epoch. Two homogeneous subunits of the bilateral putamina were thus obtained by taking into account the regional variations.
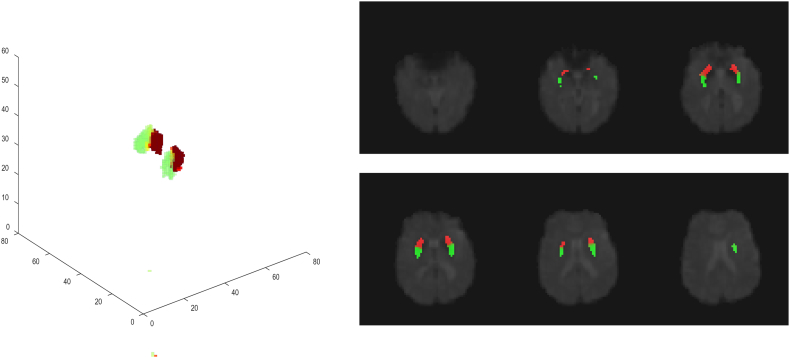
One typical example of the parcellation on left and right putamina in a HC subject is demonstrated in Fig. 2. With the proposed approach, parcellations appeared to create a predominantly anterior/posterior division. The ratio of the voxels with changing cluster memberships to the total number of voxels in the left putamen was 0.17 ± 0.083 (mean ± std) in the HC group and 0.206 ± 0.124 in the PD group. In the right putamen, it was 0.176 ± 0.079 and 0.167 ± 0.088 in the HC and PD groups respectively, which was not significantly different.
Fig. 2.
Example of the parcellation results on bilateral putamen of one HC subject. Green color represents the posterior subunit and the red color represents the anterior subunit.
We further examined the posterior and anterior homogenous subregional volumes in both HC and PD groups. In the right putamen, the sizes (defined as the number of voxels) of posterior and anterior subregions were 78.71 ± 18.78 and 68.04 ± 18.09 respectively in the HC group, and 77.5 ± 21.18 and 67.76 ± 13.26 in the PD group. Both groups had significant differences in the sizes of the two subregions (Student's t-test, p < .05). In the left putamen, the size of posterior subregion (75.68 ± 17.80) was significantly larger than that of anterior subregion (66.03 ± 16.26) in the HC group (p < .05). No significant difference in subregional sizes was found in the PD group in the left putamen.
3.2. Functional connectivity maps with homogeneous subunits in each putamen
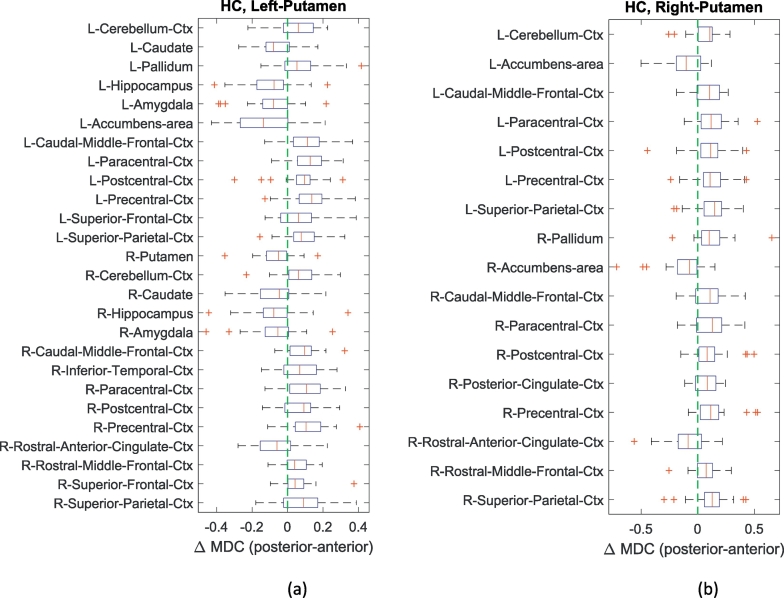
In the functional connectivity analysis, we investigated the dynamic connectivity between homogeneous putaminal subunits and all other ROIs using sliding windowed correlation. The differences of mean dynamic connectivity strength between the two homogenous clusters in the left and right putamen were compared in HC group in Fig. 3. Only the significant different mean dynamic connectivity between the two subclusters with other ROIs were reported (FDR corrected p value <.05). Cluster 1, located in the posterior putamen, demonstrated stronger mean dynamic connections with cortical areas and the cerebellar cortex, while cluster 2, which was located more anteriorly, connected strongly with the hippocampus, amygdala and other subcortical areas such as the caudate and the nucleus accumbens. Differences in the subregional mean dynamic connectivity between the clusters were more obvious in the left putamen in HC.
Fig. 3.
The comparisons of mean dynamic connectivity (MDC) of homogeneous subclusters in HC group. (a). The significant differences in MDC between homogenous left posterior and anterior putamen. (b). The significant differences in MDC between homogenous right posterior and anterior putamen. The significance level is 0.05 (FDR corrected). For ROI names, L and R represent left hemisphere and right hemisphere respectively. Ctx represents cortex.
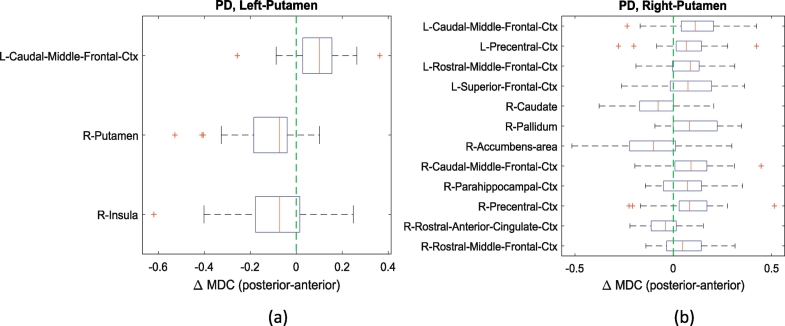
In the PD group, the posterior subunit in the left putamen exhibited stronger mean dynamic connections with the left caudal middle frontal cortex as the mean dynamic connectivity difference between two homogenous clusters was positive, while the anterior subunit in the left putamen showed stronger mean dynamic connections with the right putamen and insula (Fig. 4a). The mean dynamic connectivity between clusters in the right putamen and other regions is shown in Fig. 4b. Similar to the observations in the HC group, the posterior subunit in the right putamen had stronger mean dynamic connections with cortical areas, whilst the anterior subunit showed stronger mean dynamic connectivity to the right caudate, accumbens area and anterior cingulate cortex. Note that the subregional specificity is decreased in the PD group.
Fig. 4.
The comparisons of mean dynamic connectivity (MDC) of homogenous subclusters in PD group. (a). The significant differences in MDC between homogenous left posterior and anterior putamen. (b). The significant differences in MDC between homogenous right posterior and anterior putamen. The significance level is 0.05 (FDR corrected). For ROI names, L and R represent left hemisphere and right hemisphere respectively. Ctx represents cortex.
The standard deviation of the dynamic connectivity between the two homogenous subunits and other ROIs was also investigated (Supplementary Figs. S1 and S2). In both PD and HC groups, the posterior subunit demonstrated lower connectivity variability with cortical areas, while the anterior subunit demonstrated lower variations with subcortical areas (and the hippocampus in PD). However, compared to HC, the reduced difference between the two subunits in PD was also observed in the connectivity variations.
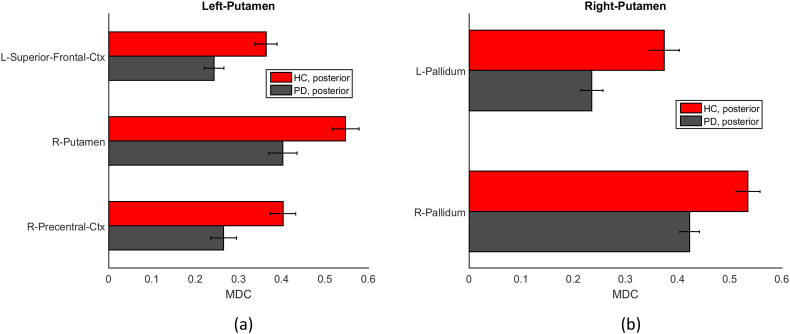
We compared the subregional connections of the two putaminal subunits between HC and PD groups. Only the mean dynamic connections associated with the posterior subunit was found to be significantly different between groups (<0.05, FDR corrected) (Fig. 5). We found that the mean dynamic connections between the posterior subunit in the left putamen and the following ROIs were decreased in PD: the left superior frontal gyrus, right putamen and the right precentral gyrus (Fig. 5(a)). With the right homogenous posterior putamen, the left and right pallidum showed decreased mean dynamic connectivity strength in PD (Fig. 5(b)).
Fig. 5.
The group comparison of mean dynamic connectivity (MDC) of (a). homogenous left posterior putamen and (b). homogenous right posterior putamen. The significance level is 0.05 (FDR corrected). Red color represents HC group, and gray color represents PD group. For ROI names, L and R represent left hemisphere and right hemisphere respectively. Ctx represents cortex.
3.3. Linking the connectivity features with disease severity
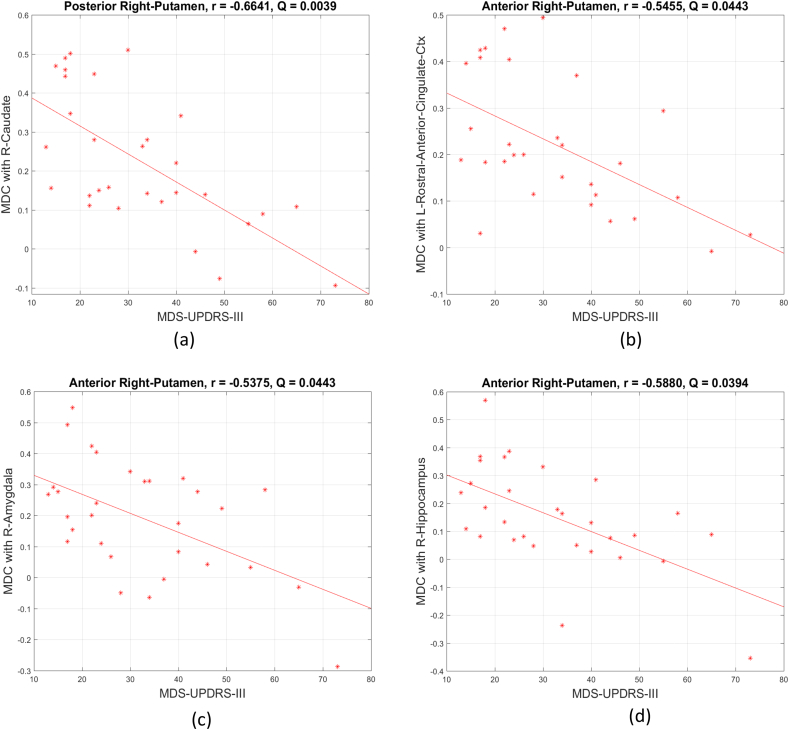
Further analysis was performed to determine the relation of the subregional connectivity features and each subject's UPDRS III score. Significant linear associations were found between mean dynamic connectivity of the right posterior putamen and the right caudate and UPDRS III (correlation coefficient = −0.6641, FDR corrected q value = 0.0039), mean dynamic connectivity between the right anterior putamen and the left rostral anterior cingulate cortex and UPDRS III (correlation coefficient = −0.5455, q = 0.0443), mean dynamic connectivity of right anterior putamen and right amygdala and UPDRS III (correlation coefficient = −0.5375, q = 0.0443), mean dynamic connectivity of right anterior putamen and right hippocampus and UPDRS III (correlation coefficient = −0.588, q = 0.0394) as shown in Fig. 6. Significant anti-correlations were also found between age and right putaminal subregional dynamic connectivity with the left caudal middle frontal cortex, the left rostral middle frontal gyrus, and the right paracentral gyrus (Supplementary Fig. S3). No significant correlations were found between the putaminal homogeneous subregional mean dynamic connectivity/connectivity deviation and other demographical features.
Fig. 6.
The significant negative correlations between homogenous subcluster mean dynamic connectivity (MDC) and UPDRS III. Those dynamic connections include (a) right caudate and homogenous right posterior putamen, (b) left anterior cingulate cortex and homogenous right anterior putamen, (c) right amygdala and homogenous right anterior putamen, and (d) right hippocampus and homogenous right anterior putamen. The significance level is 0.05 (FDR corrected). For ROI names, L and R represent left hemisphere and right hemisphere respectively. Ctx represents cortex.
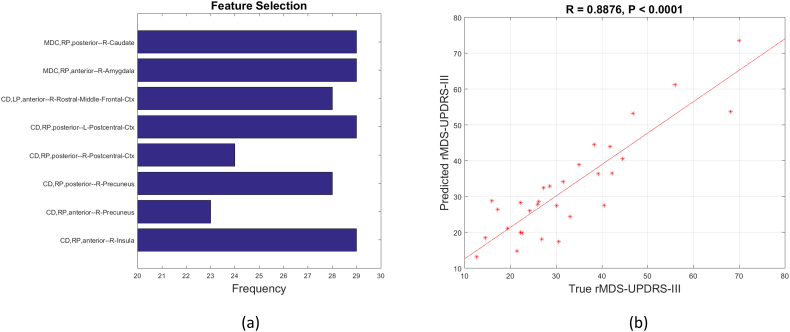
With a sparse set of connectivity features selected by LASSO, we accurately predicted UPDRS III scores. Two mean dynamic connectivity features and six connectivity deviation features jointly demonstrated the best ability to predict disease severity (R = 0.8876). As demonstrated in Fig. 7, mean dynamic connectivity features included: the right posterior putamen and right caudate, and the right anterior putamen and right amygdala. Six connectivity deviation features included the following pairs: left anterior putamen and right rostral middle frontal cortex, right posterior putamen and left postcentral gyrus, right posterior putamen and right postcentral gyrus, right posterior putamen and right precuneus, right anterior putamen and right precuneus, and right anterior putamen and right insula.
Fig. 7.
Prediction of UPDRS III using selected mean dynamic connectivity (MDC) and connectivity deviation (CD) as features. (a). The frequency of selected features using leave one subject out LASSO. (b). The prediction of UPDRS III with two mean dynamic connectivity features and six dynamic deviation features using leave one subject out simple regression. LP and RP represent the left putamen and right putamen respectively. For ROI names, L and R represent left hemisphere and right hemisphere respectively. Ctx represents cortex. rMDS-UPDRS-III means the effects of age, disease duration and LEDD have been regressed out from UPDRS III score.
3.4. Associating the cognitive functions with connectivity features
We also evaluated the associations between a set of cognitive profiles (MoCA subscores) and a set of connectivity features using CCA analysis.
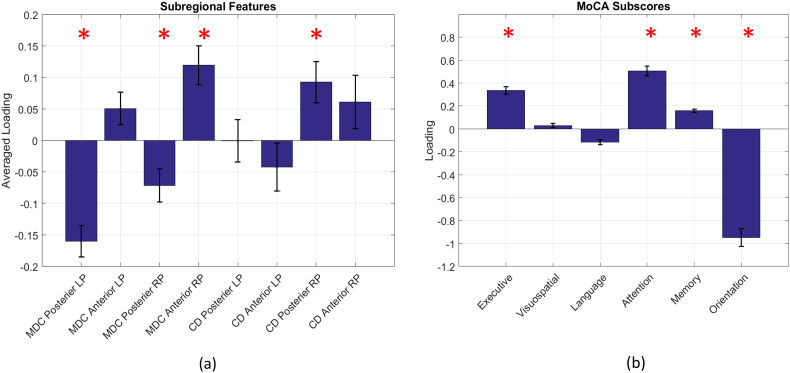
One CCA component was identified to be significant (R = 0.746, P < .05). Four MoCA subscores, Executive, Attention, Memory and Orientation were identified significantly correlated with the connectivity features as shown in Fig. 8(b). For all 228 connectivity features, we noticed that the signs of the significant loadings were relatively consistent within each subregion for each type of feature. Therefore, we used averaged loadings for significant mean dynamic connectivity and connectivity deviation features of each subregion to evaluate the overall subregional associations between connectivity profiles and cognitive performances as demonstrated in Fig. 8(a). Overall mean dynamic connectivity of bilateral posterior putamen was positively correlated with the orientation MoCA subscore. Overall mean dynamic connectivity of anterior right putamen and connectivity deviation of right posterior putamen were positively correlated with Executive, Attention and Memory MoCA subscores.
Fig. 8.
The significantly correlated cognitive profiles with overall subregional connectivity features estimated by CCA (R = 0.746, P < .05). (a). Loadings of overall subregional connectivity features. (b). Loadings of MoCA subscores. MDC and CD denote mean dynamic connectivity and connectivity deviation respectively. LP and RP represent left putamen and right putamen respectively. * indicates the significance level (p value) smaller than 0.05.
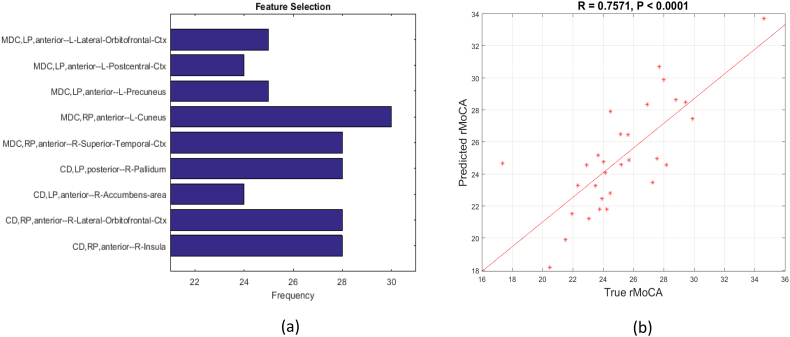
We further explored the relation between connectivity features and MoCA total score. With the LASSO model and leave-one-subject-out simple regression, a sparse set of features including five mean dynamic connectivity features and four connectivity deviation features were chosen with prediction accuracy at 0.7571. As demonstrated in Fig. 9, the mean dynamic connectivity features included the left anterior putamen and left lateral orbitofrontal cortex, left anterior putamen and left postcentral gyrus, left anterior putamen and left precuneus, right anterior putamen and left cuneus, and right anterior putamen and right superior temporal cortex. The four connectivity deviation features selected included: the left posterior putamen and right pallidum, left anterior putamen and right accumbens area, right anterior putamen and right lateral orbitofrontal cortex, and right anterior putamen and right insula. Note that majority of selected features involved the anterior putamen.
Fig. 9.
Prediction of total MoCA score using selected mean dynamic connectivity (MDC) and connectivity deviation (CD) as features. (a). The frequency of selected features using leave one subject out LASSO. (b). The prediction of total MoCA score with five mean dynamic connectivity features and four dynamic deviation features using leave one subject out simple regression. LP and RP represent the left putamen and right putamen respectively. For ROI names, L and R represent left hemisphere and right hemisphere respectively. Ctx represents cortex. rMoCA means the effects of age, disease duration and LEDD have been regressed out from total MoCA score.
Finally, we examined the side of onset of the disease with dynamic connectivity features. The mean dynamic connectivity features from left posterior putamen–right putamen, right posterior putamen–right caudal anterior cingulate, and right anterior putamen–right superior temporal were able to identify onset of disease with joint p value as 0.0384 using Hotelling t2 test. With connectivity deviation features, left posterior putamen connectivity–right medial orbitofrontal, left posterior putamen–right posterior cingulate, left anterior putamen–left thalamus, left anterior putamen–left amygdala, left anterior putamen-right putamen and right anterior putamen–right superior temporal were jointly related with side of onset (p = .0012).
4. Discussion
In this paper, we were able to parcellate the putamina into finer functionally-homogeneous spatial subunits based on regional dynamics of fMRI connectivity. Overall, the posterior putaminal subunit demonstrated stronger mean dynamic connectivity and lower connectivity variations to cortical areas. This subunit connected mostly to sensorimotor (including cerebellar) regions and fronto-parietal regions. The other subunit mainly occupied the very anterior part of putamen and showed stronger mean dynamic connectivity and lower connectivity variations to the anterior cingulate cortex and mostly subcortical regions, including the amygdala, nucleus accumbens, and caudate.
Our results are partly consistent with what has been previously described, albeit using static connectivity features in individuals with and without PD. In healthy individuals, a limbic-related subdivision localized to the ventral striatum, an associative-related subdivision localized to the anterior caudate and putamen, and a motor-related subdivision localized to the posterior putamen (Choi et al., 2012). K-means clustering has also been applied to putaminal parcellation in healthy adults, and two, three and six clusters were examined (Jung et al., 2014). Subsequent connectivity analysis demonstrated that the anterior putamen clusters were positively connected to affective and cognitive control areas, whereas the posterior putamen clusters were positively connected to the motor control areas, similar to what has been described here. Changes in connectivity in the posterior putamen have also been described in healthy individuals during reinforcement learning (Horga et al., 2015). Similar to what we found, PD subjects have shown decreased static coupling between the posterior putamen and the inferior parietal cortex (Helmich et al., 2010). Dynamic coupling in PD is starting to be explored both from the theoretical perspective in response to DBS (Saenger et al., 2017) and with respect to PD subjects with Mild Cognitive Impairment (MCI), although at the network level as opposed to the subROI level (Díez-Cirarda et al., 2018).
We found that the distinct connectivity patterns of homogenous subunits were clearly different between PD and HC. The connectivity differences between the two subunits, quite prominent in HC, became less apparent in PD. The exception was the caudal middle frontal gyrus (MFG) (Fig. 3, Fig. 4), which plays a particular role in working memory (Boisgueheneuc et al., 2006) and orienting attention between exogenous and endogenous stimuli (Japee et al., 2015). This region consistently demonstrated significant regional mean dynamic connectivity differences in both HC and PD, implying that these putaminal connections were relatively intact in our non-demented cohort of PD subjects.
We found relative differences in connectivity between the right insula and the left anterior/posterior putamen in PD that was not seen in controls (Fig. 4). Normally, the ventral striatopallidum receives specific afferents from the insular cortices (Reynolds and Zahm, 2005). In PD, the insula has decreased connectivity with the pre-SMA (Wu et al., 2011a, Wu et al., 2011b) and directional influence from the substantia nigra (Wu et al., 2012). Our results further refine these prior results by suggesting that the posterior putaminal subunit selectively loses mean dynamic insular connectivity in PD.
We tested the ability of subregional connectivity features to distinguish PD and HC (Fig. 5). As expected, given the early degeneration of the caudolateral sensorimotor putamen, mean dynamic connectivity strengths of the posterior putaminal subunit was significantly different between the two groups. A number of mean dynamic connectivity strengths were negatively correlated with the UPDRS III score (Fig. 6). It may seem paradoxical that the anterior putaminal subunit connectivity was more closely related with disease severity than the more severely affected posterior subunit. Our interpretation is that the posterior subunit must already have sufficiently reduced connectivity for the disease to become apparent; worsening disease may then result in connectivity changes spreading to the anterior subunit. The connectivity features that collectively predicted UPDRS III included the precuneus (Fig. 7), a prominent part of the default mode network (DFM). Dynamics in the default mode network are being increasingly recognized as being important for task performance (Lin et al., 2017) which is also affected early on in cognitive impairment (Lee et al., 2016).
Relating subregional functional connectivity in the putamen to the cognitive performance measured with MoCA in a multivariate fashion, two patterns were discovered (Fig. 8). First, higher mean dynamic connectivity strength in bilateral posterior putaminal connectivity was associated with higher scores of orientation test, suggesting that stronger mean dynamic connectivity strength in the posterior putamen was associated with better ability of orienting themselves in terms of time and location. The significance of the association between altered connectivity in the posterior putamen and orientation in the MoCA is unclear, as the posterior putamen is affected early, and normally related to motor dysfunctions. A recent study found that higher education in PD is associated with significantly higher cognitive scores, but also lower DAT binding to the posterior putamen than lower education PD subjects with similar disease duration (Sunwoo et al., 2016). This may suggest a blurring between traditionally considered “cognitive” and “motor” putaminal subdivisions in PD.
In addition, the other CCA pattern demonstrated that 1) mean connectivity strength in the right anterior putamen and 2) connectivity variation of the right posterior putamen were associated with better performance in executive, attention, and memory domains. This is partly consistent with prior studies: a decrease in [11C] raclopride binding in the right anterior putamen is seen during a screen for executive function, namely the Montreal Card Sorting Task (Monchi et al., 2006). The ‘cognitive’ corticostriatal loop involves the prefrontal cortex that projects to the anterior putamen (Alexander et al., 1986). Dopamine transporter (DAT) availability in the anterior putamen is directly associated with attention/working memory, frontal/executive, and visuospatial functions in de novo Parkinson's' disease (Chung et al., 2018). The connectivity-behaviour relation that we observed was that better cognitive function was not only related to stronger connectivity strength but also connectivity variation (i.e. how different the connections are across time). Executive functioning has been shown to require dynamic functional connectivity (Mattar et al., 2015; Nomi et al., 2017) and modulate performance of memory retrieval in elderly subjects (Angel et al., 2016), which partially explained the associations between connectivity deviation and executive/memory performance in our results. Moreover, decreased functional connectivity in subcortical regions, including the putamen, has been observed in children with attention deficits (Cao et al., 2009), implying that attention may require putaminal functional connectivity. Taken together, our results demonstrated that connectivity variation and mean dynamic connectivity strength in the right putamen were associated with better cognitive performance.
Finally, we also demonstrated that these connectivity features were able to predict overall MoCA score (Fig. 9). Interestingly, the connectivity deviation of short-range connections (including subcortico-subcortical) and the mean dynamic connectivity strength of cortico-subcortical connections were required to predict MoCA scores. The results implied that dynamic connectivity in short-range connections is a key factor to support overall cognition; while in cortico-subcortical connections, connectivity strength might be more important. To conclude, our findings of connectivity-behaviour associations illustrates that different aspects of resting-state functional connectivity were all required for overall cognitive functioning but served different effects in specific cognitive domains.
Our results are also partly consistent with previous studies. Recently, Hanakawa et al. performed a task-based fMRI and diffusion tractography study to explore the relationship of the identified basal ganglia-thalamo-cortical circuit dysfunctions with the motor and cognitive slowing in PD patients (Hanakawa et al., 2017). They demonstrated that motor slowing in PD patients is associated with the impaired motor basal ganglia-thalamo-cortical circuits, while the cognitive slowing is ascribed to the dysfunctions of the premotor and language basal ganglia-thalamo-cortical circuits. Consistent with their findings, we also found that the connectivity of posterior putamen, which is part of the motor basal ganglia-thalamo-cortical circuits, is correlated with UPDRS III scores; and connectivity of the anterior putamen, which is part of the language basal ganglia-thalamo-cortical circuits, is correlated with MoCA scores.
There are several limitations. In this study, we only identified two temporal homogenous subunits in the putamina, inspired by the conceptualization of two different motor control circuits and study their connectivity with other brain areas. Dividing putamen into two subunits by simple anatomical criteria, such as using the anterior commissure, has been previously reported in a number of studies in PD (Hacker et al., 2012; Helmich et al., 2010; Luo et al., 2014). However, an anatomical separation doesn't take into account the functionality of voxels and neglects inter-subject variability. Based on static connectivity features, the putamen has been segmented into finer structures with variable number of subregions. However, more subunits may represent finer subsets of the main two subregions described here (Jung et al., 2014). While we did not allow overlap between our subunits, other studies have relaxed this criterion (Marquand et al., 2017). When we attempted to divide each putamen into three or more subunits, this resulted in some subjects having clusters that did not have any voxels with consistent cluster membership over time. Collectively, we thus restricted ourselves to parcellate the putamina into two clusters. To achieve a finer parcellation using the temporal dynamics, fMRI with higher spatial resolution using multi-band techniques would allow for connectivity dynamics at a finer scale and therefore overcome the limitation of nonstable/noncontiguous regional dynamics. Instead of assigning the voxels with stable cluster memberships as homogenous subunits, a statistical probability model where the weighted signals represent the subunits in a fuzzy clustering framework could be explored in future work.
In addition, we note that we performed all analysis in the subjects' native space to prevent errors of misregistration, but with increasing number of clusters, the correspondence of a large number of clusters between differently-shaped putamina from different subjects may prove difficult. It was also hard to quantitatively describe the spatial locations of the subclusters as there was no common space. A more sophisticated group model would be potential in our future work.
We have utilized the sliding windowed correlation to examine the subregional dynamics in the putamen in this study. With the increased complexity of estimated time varying connectivity networks, a set of connectivity features such as mean, variance and state properties of functional connectivity have been generally adopted to study the temporal dynamics (Allen et al., 2014; Chiang et al., 2018; Hutchison et al., 2013; Liu et al., 2016; Liu et al., 2017). For instance, the dynamic connectivity mean strength, the stability and variability have been used to quantitatively describe the temporal variations of functional connectivity for characterizing an individual “fingerprint” of brain (Liu et al., 2017). Mean connectivity strength has been used in our previous study to reveal the regional dynamic differences between PD and HC groups (Liu et al., 2016), and more recently the mean and variance of dynamic functional connectivity have been used to discriminate between people with temporal lobe epilepsy and normal controls (Chiang et al., 2018). However, the interpretation of temporal variations in dynamic connectivity is still challenging. The mean dynamic connectivity strength may be closely related to the static functional connectivity, and the connectivity deviation represents the second order statistics of temporal variations. These two measures are limited in capturing the comprehensive information contained in dynamic connectivity patterns. Other connectivity measures such as spectral properties and range of the connectivity strength may also provide the meaningful characterizations. For example, we found that the correlation range of the right accumbens area and left posterior putamen was significantly correlated with disease severity in our cohort (Fig. Error! Reference source not found.). Finally examining concomitant behavioural data from task-based paradigms instead of utilizing resting state fMRI may guide which dynamic features may be post important.
5. Conclusion
In this paper, we employed a data-driven joint temporal parcellation method to identify spatially contiguous subunits in the putamina. In HC, there were distinct differences in the connectivity between the subunits, that was largely lost in PD. PD subjects had overall decreased connectivity in the posterior subunit, distinguishing them from controls. Interestingly, changes in the anterior subunit's mean dynamic connectivity were associated with overall disease severity, presumably as the disease progress to involve more anterior structures. Overall UPDRS III, MoCA scores could be predicted with putaminal connectivity features suggesting a role for static and dynamic putaminal connectivity as part of an imaging biomarker for PD.
Acknowledgement
This work was partly supported by the National Natural Science Foundation of China (61701158), Anhui Provincial Natural Science Foundation (1808085QF184) and UBC/PPRI Chair in Parkinson's Research.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.nicl.2018.10.022.
Contributor Information
Aiping Liu, Email: aipingl@ece.ubc.ca.
Xun Chen, Email: xunchen@ustc.edu.cn.
Appendix A. Supplementary data
Supplementary figures
References
- Alexander G.E., Delong M.R., Strick P.L. Parallel organization of functionally segregated circuits linking basal ganglia and cortex. Annu. Rev. Neurosci. 1986;9(1):357–381. doi: 10.1146/annurev.ne.09.030186.002041. [DOI] [PubMed] [Google Scholar]
- Allen E.A., Damaraju E., Plis S.M., Erhardt E.B., Eichele T., Calhoun V.D. Tracking Whole-Brain Connectivity Dynamics in the Resting State. Cerebral Cortex (New York, NY) 2014;24(3):663–676. doi: 10.1093/cercor/bhs352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angel L., Bastin C., Genon S., Salmon E., Fay S., Balteau E., Collette F. Neural correlates of successful memory retrieval in aging: do executive functioning and task difficulty matter? Brain Res. 2016;1631:53–71. doi: 10.1016/j.brainres.2015.10.009. [DOI] [PubMed] [Google Scholar]
- Barnes K.A., Cohen A.L., Power J.D., Nelson S.M., Dosenbach Y.B.L., Miezin F.M., Schlaggar B.L. Identifying Basal Ganglia Divisions in individuals using Resting-State Functional Connectivity MRI. Front. Syst. Neurosci. 2010;4 doi: 10.3389/fnsys.2010.00018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blumensath T., Jbabdi S., Glasser M.F., Van Essen D.C., Ugurbil K., Behrens T.E., Smith S.M. Spatially constrained hierarchical parcellation of the brain with resting-state fMRI. NeuroImage. 2013;76:313–324. doi: 10.1016/j.neuroimage.2013.03.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bohanna I., Georgiou-Karistianis N., Egan G.F. Connectivity-based segmentation of the striatum in Huntington's disease: vulnerability of motor pathways. Neurobiol. Dis. 2011;42(3):475–481. doi: 10.1016/j.nbd.2011.02.010. [DOI] [PubMed] [Google Scholar]
- Boisgueheneuc F.d., Levy R., Volle E., Seassau M., Duffau H., Kinkingnehun S., Dubois B. Functions of the left superior frontal gyrus in humans: a lesion study. Brain. 2006;129(12):3315–3328. doi: 10.1093/brain/awl244. [DOI] [PubMed] [Google Scholar]
- Calhoun V.D., Miller R., Pearlson G., Adali T. The chronnectome: time-varying connectivity networks as the next frontier in fMRI data discovery. Neuron. 2014;84(2):262–274. doi: 10.1016/j.neuron.2014.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao X., Cao Q., Long X., Sun L., Sui M., Zhu C., Wang Y. Abnormal resting-state functional connectivity patterns of the putamen in medication-naive children with attention deficit hyperactivity disorder. Brain Res. 2009;1303:195–206. doi: 10.1016/j.brainres.2009.08.029. [DOI] [PubMed] [Google Scholar]
- Cardinal R.N., Parkinson J.A., Hall J., Everitt B.J. Emotion and motivation: the role of the amygdala, ventral striatum, and prefrontal cortex. Neurosci. Biobehav. Rev. 2002;26(3):321–352. doi: 10.1016/s0149-7634(02)00007-6. [DOI] [PubMed] [Google Scholar]
- Chen X., Wang Z.J., McKeown M. Joint blind source separation for neurophysiological data analysis: Multiset and multimodal methods. IEEE Signal Process. Mag. 2016;33(3):86–107. [Google Scholar]
- Chen X., Xu X., Liu A., McKeown M.J., Wang Z.J. The use of multivariate EMD and CCA for denoising muscle artifacts from few-channel EEG recordings. IEEE Trans. Instrum. Meas. 2018;67(2):359–370. [Google Scholar]
- Chiang S., Vankov E.R., Yeh H.J., Guindani M., Vannucci M., Haneef Z., Stern J.M. Temporal and spectral characteristics of dynamic functional connectivity between resting-state networks reveal information beyond static connectivity. PLoS One. 2018;13(1) doi: 10.1371/journal.pone.0190220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi E.Y., Yeo B.T., Buckner R.L. The organization of the human striatum estimated by intrinsic functional connectivity. J. Neurophysiol. 2012;108(8):2242–2263. doi: 10.1152/jn.00270.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung S.J., Yoo H.S., Oh J.S., Kim J.S., Ye B.S., Sohn Y.H., Lee P.H. Effect of striatal dopamine depletion on cognition in de novo Parkinson's disease. Parkinsonism Relat. Disord. 2018;51:43–48. doi: 10.1016/j.parkreldis.2018.02.048. [DOI] [PubMed] [Google Scholar]
- Cohen M.X., Schoene-Bake J.C., Elger C.E., Weber B. Connectivity-based segregation of the human striatum predicts personality characteristics. Nat. Neurosci. 2009;12(1):32–34. doi: 10.1038/nn.2228. [DOI] [PubMed] [Google Scholar]
- de Wit S., Watson P., Harsay H.A., Cohen M.X., van de Vijver I., Ridderinkhof K.R. Corticostriatal connectivity underlies individual differences in the balance between habitual and goal-directed action control. J. Neurosci. 2012;32(35):12066–12075. doi: 10.1523/JNEUROSCI.1088-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Díez-Cirarda M., Strafella A.P., Kim J., Peña J., Ojeda N., Cabrera-Zubizarreta A., Ibarretxe-Bilbao N. Dynamic functional connectivity in Parkinson's disease patients with mild cognitive impairment and normal cognition. NeuroImage: Clinical. 2018;17:847–855. doi: 10.1016/j.nicl.2017.12.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dolan Ray J., Dayan P. Goals and Habits in the Brain. Neuron. 2013;80(2):312–325. doi: 10.1016/j.neuron.2013.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gruber A.J., McDonald R.J. Context, emotion, and the strategic pursuit of goals: interactions among multiple brain systems controlling motivated behavior. Front. Behav. Neurosci. 2012;6 doi: 10.3389/fnbeh.2012.00050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haber S.N. Corticostriatal circuitry. Neuroscience in the 21st Century. 2016:1–21. doi: 10.31887/DCNS.2016.18.1/shaber. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hacker C.D., Perlmutter J.S., Criswell S.R., Ances B.M., Snyder A.Z. Resting state functional connectivity of the striatum in Parkinson's disease. Brain. 2012;135(12):3699–3711. doi: 10.1093/brain/aws281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanakawa, T., Goldfine, A. M., & Hallett, M. (2017). A Common Function of Basal Ganglia-Cortical Circuits Subserving Speed in both Motor and Cognitive Domains. eneuro, ENEURO. 0200–0217.2017. [DOI] [PMC free article] [PubMed]
- Hardoon D.R., Szedmak S., Shawe-Taylor J. Canonical correlation analysis: an overview with application to learning methods. Neural Comput. 2004;16(12):2639–2664. doi: 10.1162/0899766042321814. [DOI] [PubMed] [Google Scholar]
- Helmich R.C., Derikx L.C., Bakker M., Scheeringa R., Bloem B.R., Toni I. Spatial Remapping of Cortico-striatal Connectivity in Parkinson's Disease. Cereb. Cortex. 2010;20(5):1175–1186. doi: 10.1093/cercor/bhp178. [DOI] [PubMed] [Google Scholar]
- Herz D.M., Haagensen B.N., Nielsen S.H., Madsen K.H., Løkkegaard A., Siebner H.R. Resting-state connectivity predicts levodopa-induced dyskinesias in Parkinson's disease. Mov. Disord. 2016;31(4):521–529. doi: 10.1002/mds.26540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horga G., Maia T.V., Marsh R., Hao X., Xu D., Duan Y., Peterson B.S. Changes in corticostriatal connectivity during reinforcement learning in humans. Hum. Brain Mapp. 2015;36(2):793–803. doi: 10.1002/hbm.22665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison R.M., Womelsdorf T., Allen E.A., Bandettini P.A., Calhoun V.D., Corbetta M., Chang C. Dynamic functional connectivity: promise, issues, and interpretations. NeuroImage. 2013;80:360–378. doi: 10.1016/j.neuroimage.2013.05.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janssen R.J., Jylänki P., Kessels R.P.C., van Gerven M.A.J. Probabilistic model-based functional parcellation reveals a robust, fine-grained subdivision of the striatum. NeuroImage. 2015;119:398–405. doi: 10.1016/j.neuroimage.2015.06.084. [DOI] [PubMed] [Google Scholar]
- Japee S., Holiday K., Satyshur M.D., Mukai I., Ungerleider L.G. A role of right middle frontal gyrus in reorienting of attention: a case study. Front. Syst. Neurosci. 2015;9:23. doi: 10.3389/fnsys.2015.00023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji B., Li Z., Li K., Li L., Langley J., Shen H., Hu X. Dynamic thalamus parcellation from resting-state fMRI data. Hum. Brain Mapp. 2016;37(3):954–967. doi: 10.1002/hbm.23079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung W.H., Jang J.H., Park J.W., Kim E., Goo E.-H., Im O.-S., Kwon J.S. Unravelling the Intrinsic Functional Organization of the Human Striatum: a Parcellation and Connectivity Study based on Resting-State fMRI. PLoS One. 2014;9(9) doi: 10.1371/journal.pone.0106768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee E.-S., Yoo K., Lee Y.-B., Chung J., Lim J.-E., Yoon B., Jeong Y. Default Mode Network Functional Connectivity in early and late Mild Cognitive Impairment. Alzheimer Dis. Assoc. Disord. 2016;30(4):289–296. doi: 10.1097/WAD.0000000000000143. [DOI] [PubMed] [Google Scholar]
- Lin P., Yang Y., Gao J., De Pisapia N., Ge S., Wang X., Niu C. Dynamic default mode network across different brain states. Sci. Rep. 2017;7 doi: 10.1038/srep46088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu A., Chen X., Dan X., McKeown M.J., Wang Z.J. A combined Static and Dynamic Model for Resting-State Brain Connectivity Networks. IEEE Journal of Selected Topics in Signal Processing. 2016;10(7):1172–1181. [Google Scholar]
- Liu J., Liao X., Xia M., He Y. Chronnectome fingerprinting: Identifying individuals and predicting higher cognitive functions using dynamic brain connectivity patterns. Hum. Brain Mapp. 2017;39(2):902–915. doi: 10.1002/hbm.23890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu Y., Jiang T., Zang Y. Region growing method for the analysis of functional MRI data. NeuroImage. 2003;20(1):455–465. doi: 10.1016/s1053-8119(03)00352-5. [DOI] [PubMed] [Google Scholar]
- Luo C., Song W., Chen Q., Zheng Z., Chen K., Cao B., Shang H.-F. Reduced functional connectivity in early-stage drug-naive Parkinson's disease: a resting-state fMRI study. Neurobiol. Aging. 2014;35(2):431–441. doi: 10.1016/j.neurobiolaging.2013.08.018. [DOI] [PubMed] [Google Scholar]
- Marquand A.F., Haak K.V., Beckmann C.F. Functional corticostriatal connection topographies predict goal-directed behaviour in humans. Nat. Hum. Behav. 2017;1(8):0146. doi: 10.1038/s41562-017-0146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattar M.G., Cole M.W., Thompson-Schill S.L., Bassett D.S. A functional cartography of cognitive systems. PLoS Comput. Biol. 2015;11(12) doi: 10.1371/journal.pcbi.1004533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mishra A., Rogers B.P., Chen L.M., Gore J.C. Functional connectivity-based parcellation of amygdala using self-organized mapping: a data driven approach. Hum. Brain Mapp. 2014;35(4):1247–1260. doi: 10.1002/hbm.22249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monchi O., Ko J.H., Strafella A.P. Striatal dopamine release during performance of executive functions: A [11C] raclopride PET study. NeuroImage. 2006;33(3):907–912. doi: 10.1016/j.neuroimage.2006.06.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nomi J.S., Vij S.G., Dajani D.R., Steimke R., Damaraju E., Rachakonda S., Uddin L.Q. Chronnectomic patterns and neural flexibility underlie executive function. NeuroImage. 2017;147:861–871. doi: 10.1016/j.neuroimage.2016.10.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer S.J., Eigenraam L., Hoque T., McCaig R.G., Troiano A., McKeown M.J. Levodopa-sensitive, dynamic changes in effective connectivity during simultaneous movements in Parkinson's disease. Neuroscience. 2009;158(2):693–704. doi: 10.1016/j.neuroscience.2008.06.053. [DOI] [PubMed] [Google Scholar]
- Pavese N., Brooks D.J. Imaging neurodegeneration in Parkinson's disease. Biochimica et Biophysica Acta (BBA)-Molecular Basis of Disease. 2009;1792(7):722–729. doi: 10.1016/j.bbadis.2008.10.003. [DOI] [PubMed] [Google Scholar]
- Postuma R.B., Dagher A. Basal ganglia functional connectivity based on a meta-analysis of 126 positron emission tomography and functional magnetic resonance imaging publications. Cereb. Cortex. 2006;16(10):1508–1521. doi: 10.1093/cercor/bhj088. [DOI] [PubMed] [Google Scholar]
- Provost J.S., Petrides M., Monchi O. Dissociating the role of the caudate nucleus and dorsolateral prefrontal cortex in the monitoring of events within human working memory. Eur. J. Neurosci. 2010;32(5):873–880. doi: 10.1111/j.1460-9568.2010.07333.x. [DOI] [PubMed] [Google Scholar]
- Rajtmajer S., Roy A., Albert R., Molenaar P., Hillary F. A voxelwise approach to determine consensus regions-of-interest for the study of brain network plasticity. Front. Neuroanat. 2015;(97):9. doi: 10.3389/fnana.2015.00097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Redgrave P., Rodriguez M., Smith Y., Rodriguez-Oroz M.C., Lehericy S., Bergman H., Obeso J.A. Goal-directed and habitual control in the basal ganglia: implications for Parkinson's disease. Nat. Rev. Neurosci. 2010;11(11):760–772. doi: 10.1038/nrn2915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reynolds S.M., Zahm D.S. Specificity in the projections of prefrontal and insular cortex to ventral striatopallidum and the extended amygdala. J. Neurosci. 2005;25(50):11757–11767. doi: 10.1523/JNEUROSCI.3432-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robbins T.W. Shifting and stopping: fronto-striatal substrates, neurochemical modulation and clinical implications. Philosophical Transactions of the Royal Society of London B: Biological Sciences. 2007;362(1481):917–932. doi: 10.1098/rstb.2007.2097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saenger V.M., Kahan J., Foltynie T., Friston K., Aziz T.Z., Green A.L., Deco G. Uncovering the underlying mechanisms and whole-brain dynamics of deep brain stimulation for Parkinson's disease. Sci. Rep. 2017;7(1):9882. doi: 10.1038/s41598-017-10003-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen X., Tokoglu F., Papademetris X., Constable R.T. Groupwise whole-brain parcellation from resting-state fMRI data for network node identification. NeuroImage. 2013;82:403–415. doi: 10.1016/j.neuroimage.2013.05.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi J., Malik J. Normalized Cuts and image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2000;22(8):888–905. [Google Scholar]
- Sunwoo M.K., Hong J.Y., Lee J.J., Lee P.H., Sohn Y.H. Does education modify motor compensation in Parkinson's disease? J. Neurol. Sci. 2016;362:118–120. doi: 10.1016/j.jns.2016.01.030. [DOI] [PubMed] [Google Scholar]
- Tibshirani R. Regression Shrinkage and selection via the Lasso. J. R. Stat. Soc. Ser. B Methodol. 1996;58(1):267–288. [Google Scholar]
- Tzourio-Mazoyer N., Landeau B., Papathanassiou D., Crivello F., Etard O., Delcroix N., Joliot M. Automated Anatomical labeling of Activations in SPM using a Macroscopic Anatomical Parcellation of the MNI MRI Single-Subject Brain. NeuroImage. 2002;15(1):273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
- van Oort E.S.B., Mennes M., Schröder T.N., Kumar V.J., Zaragoza Jimenez N.I., Grodd W., Doeller C.F., Beckmann C.F. Functional parcellation using time courses of instantaneous connectivity. NeuroImage. 2018;170:31–40. doi: 10.1016/j.neuroimage.2017.07.027. ISSN 1053-8119. [DOI] [PubMed] [Google Scholar]
- Wu T., Wang L., Chen Y., Zhao C., Li K., Chan P. Changes of functional connectivity of the motor network in the resting state in Parkinson's disease. Neurosci. Lett. 2009;460(1):6–10. doi: 10.1016/j.neulet.2009.05.046. [DOI] [PubMed] [Google Scholar]
- Wu T., Long X., Wang L., Hallett M., Zang Y., Li K., Chan P. Functional connectivity of cortical motor areas in the resting state in Parkinson's disease. Hum. Brain Mapp. 2011;32(9):1443–1457. doi: 10.1002/hbm.21118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu T., Wang L., Hallett M., Chen Y., Li K., Chan P. Effective connectivity of brain networks during self-initiated movement in Parkinson's disease. NeuroImage. 2011;55(1):204–215. doi: 10.1016/j.neuroimage.2010.11.074. [DOI] [PubMed] [Google Scholar]
- Wu T., Wang J., Wang C., Hallett M., Zang Y., Wu X., Chan P. Basal ganglia circuits changes in Parkinson's disease patients. Neurosci. Lett. 2012;524(1):55–59. doi: 10.1016/j.neulet.2012.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu S.X., Shi J. 2003. Multiclass spectral clustering. Paper presented at the Proceedings Ninth IEEE International Conference on Computer Vision. 13-16 Oct. 2003. [Google Scholar]
- Zalesky A., Breakspear M. Towards a statistical test for functional connectivity dynamics. NeuroImage. 2015;114:466–470. doi: 10.1016/j.neuroimage.2015.03.047. [DOI] [PubMed] [Google Scholar]
- Zhang Y., Liu A., Tan S.N., McKeown M.J., Wang Z.J. Connectivity-based parcellation of functional SubROIs in putamen using a sparse spatially regularized regression model. Biomedical Signal Processing and Control. 2016;27:174–183. [Google Scholar]
- Zilles K., Amunts K. Receptor mapping: architecture of the human cerebral cortex. Curr. Opin. Neurol. 2009;22(4):331–339. doi: 10.1097/WCO.0b013e32832d95db. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary figures