Abstract
We propose and numerically demonstrate two novel terahertz absorbers made up of periodic single- and double-layer decussate graphene ribbon arrays. The simulated results show that the proposed absorbers have narrowband near-unity terahertz absorption with ultra-wide frequency reconfiguration and angular stability. By tuning the Fermi level of graphene ribbons, the over 90% absorbance peak frequency of the absorber with single-layer graphene structure can be flexibly adjusted from 6.85 to 9.85 THz for both the transverse magnetic (TM) and transverse electric (TE) polarizations. This absorber with single-layer graphene demonstrates excellent angular stability with the absorbance peaks of the reconfigurable absorption bands remaining over 99.8% in a wide angle of incidence ranging from 0 to 70°. The tuning frequency can be significantly enhanced by using the absorber with double-layer graphene structure from 5.50 to 11.28 THz and 5.62 to 10.65 THz, approaching two octaves under TM and TE polarizations, respectively. The absorbance peaks of the reconfigurable absorption band of this absorber for both polarizations maintain over 70%, even at a large angle of incidence up to 70°. Furthermore, an analytical fitting model is also proposed to accurately predict the absorbance peak frequencies for this variety of absorbers. Benefitting from these attractive properties, the proposed absorber may have great potential applications in tunable terahertz trapping, detecting, sensing, and various terahertz optoelectronic devices.
Keywords: terahertz, graphene, frequency reconfigurable absorber, surface plasmons
1. Introduction
Terahertz waves generally refer to electromagnetic waves with a frequency of 0.1–10 THz. Terahertz technology has broad applications in terahertz communication, spectroscopy, detecting, sensing, and imaging [1,2,3,4]. THz metamaterial absorbers (MAs) have aroused increasing attention since Landy et al. proposed a perfect MA in 2008 [5]. For many applications, frequency-tunable narrowband MAs would be preferred over typical broadband MAs, owing to their ability to absorb given frequency resonance without influencing neighboring spectrums. For conventional MAs, the absorption characteristics can only be manipulated by changing the resonator geometry or the surrounding medium [6]. Recently, by integrating varactors [7], semiconductors [8], microelectromechanical systems (MEMS) [9], diodes [10], and liquid crystals [11], various tunable MAs with frequency, bandwidth, and strength adjustability have been achieved. However, such tunable absorbers usually have very limited frequency tuning range and also require large external controls and complicated manufacturing techniques.
Graphene is a monatomic carbon layer two-dimensional material that has attracted a great deal of attention in the past decade because of its unique electrical performance, low intrinsic loss, and photonic properties [12]. Since graphene possesses the ability to support long propagation and strongly localized surface plasmon polaritons (LSPPs) in the terahertz and infrared regions, it has become an excellent electromagnetic film material widely used in various terahertz components and devices [13,14,15]. To date, many graphene-based MAs have been proposed and investigated in a wide frequency spectrum ranging from microwave to ultraviolet light [16,17,18,19,20]. Via the chemical or electrostatic doping of graphene, both strong absorption and flexible tunability can be easily achieved. Especially, as a new type of MAs with broad potential applications in electromagnetic wave sensing, modulation, detection, and stealth, graphene-based frequency reconfigurable absorbers have recently attracted increasing attention. For example, Ning et al. proposed a tunable mid-infrared absorber made up of a graphene–metal nanostructure with angular-insensitive absorption within −12° to 12° [21]. Meanwhile, by tuning the graphene Fermi level from 0.2 to 0.8 eV, the absorbance peak wavelength (frequency) shifts from 9969 nm (30.1 THz) to 9318 nm (32.2 THz), corresponding to the relative frequency tuning range (RFTR) of 7%, where the RFTR is defined as the absolute absorbance peak frequency tuning range over the lowest absorbance peak frequency, (fH − fL)/fL × 100%. Li et al. demonstrated a tunable mid-infrared narrowband absorber using parallel double-layer graphene ribbons with an RFTR of 18.7% from 22.73 to 27 THz and a wide angular stability of 60° [22]. Wu investigated a tunable absorber using a dielectric grating-graphene-Bragg grating structure with an RFTR of 1.1% from 8.92 to 9.02 THz [23]. He et al. presented an active graphene-based terahertz MA with an RFTR of 20.6% from 1.31 to 1.58 THz [24]. Zhang et al. proposed a graphene-based tunable MA with an RFTR of 14.9% from 0.94 to 1.08 THz [25]. An enhanced angular stability up to 70° (50°) was achieved in that absorber for transverse magnetic (TM) (transverse electric, TE) polarized terahertz waves at 0.94 THz, but the insensitive angle of incidence was drastically decreased to 25° as the absorption band shifted to the higher-frequency end at 1.08 THz. In addition, dual-band tunable terahertz and mid-infrared MAs with RFTRs of 31.4% and 19.5% were also achieved [26,27]. Despite the recent progress in tunable MAs, most of these graphene-based absorbers still suffer from the disadvantages of small angular stability and very limited RFTR range, usually less than 35%. How to achieve tunable graphene-based absorbers with larger RFTR and wider angular stability remains a challenge.
To address this issue, we propose a new variety of frequency-reconfigurable narrowband near-unity terahertz absorbers with significantly enhanced RFTR and angular stability using single/double-layer decussate graphene ribbon arrays (S/DLDGRAs). To demonstrate the properties and mechanisms of the absorbers, we present the geometric configurations and study their performance, including terahertz absorbance spectra, effective impedance characteristics, field distributions, frequency reconfiguration, and angular stability of the proposed absorbers. It was found that by tuning graphene Fermi level, the RFTR for the over 90% absorbance peak frequency of the proposed absorber with SLDGRA reached 43.8%, ranging from 6.85 to 9.85 THz for both TM and TE polarizations under normal incidence. The RFRT for the over 90% absorbance peak frequency of the absorber with DLDGRA could be further extended to 105.1% (89.5%), ranging from 5.50 (5.62) to 11.28 (10.65) THz, approaching two octaves for the TM (TE) polarization under normal incidence. The absorbance peaks of the different absorption bands for both absorbers maintained over 70% in a wide range of angle of incidence from 0° to 70°. Furthermore, we propose a simple analytical fitting model to accurately predict the reconfigurable absorbance frequencies of the absorbers. Finally, we systematically draw the conclusion of the whole work.
2. Geometric Configurations of the Absorbers
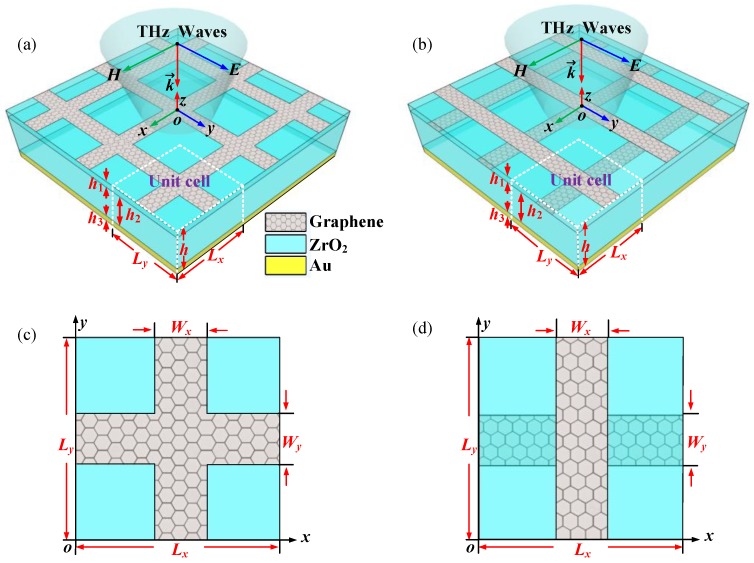
The schematic of the proposed frequency-reconfigurable wide-angle terahertz absorbers with S/DLDGRAs is illustrated in Figure 1. The absorber with a SLDGRA is made up of a periodic graphene ribbon array, a ZrO2 dielectric layer, and a gold (Au) reflection layer from the top to the bottom. The absorber with DLDGRAs can be interpreted as the transformation of the absorber with a SLDGRA by separating two graphene ribbon arrays into different layers with a distance of h1 while keeping the identical thickness of the dielectric layer. Here, we display the top views of the unit cells of the proposed absorbers with S/DLGRAs in Figure 1c,d, respectively. In the terahertz region, the surface conductivity of the graphene is calculated by the Kubo formula as σg = σintra + σinter (Unit: S) [28,29], where the intraband contribution σintra and interband contribution σinter are given by:
| (1) |
| (2) |
where is the Fermi–Dirac distribution, ω is the radian frequency, μc is the chemical potential or Fermi level, T0 is the temperature, Γ is the phenomenological scattering rate, Γ = 2τ−1, τ is the relaxation time, e is the charge of an electron, ξ is energy, ћ is the reduced Plank’s constant, and kB is Boltzmann’s constant. The relative dielectric constant of ZrO2 was set as εr = 4.41 [30,31] and the relative dielectric constant of Au was obtained by the Drude Model [32]. In the absorber designs, Lx and Ly are the periods of the unit cell, and Wx and Wy are the widths of the graphene ribbons in x and y directions, respectively. The thickness of the upper and lower ZrO2 spacers, the Au reflecting layer, and the total thickness of the absorbers were set as h1, h2, h3, and h = h1 + h2 + h3, respectively. In this study, we assumed the parameters as Lx = Ly = 4 µm, Wx = Wy = 0.9 μm, h1 = 1 μm, h2 = 4 μm, h3 = 1 μm, T0 = 300 K, τ = 0.6 ps [33], respectively. In the numerical simulations, graphene ribbons were modeled as equivalent two-dimensional surface impedance layers with Zg = 1/σg without thickness [34,35] and the finite element method-based frequency domain solver of the commercial software CST Studio was used to study the properties of the absorbers. The absorbance of the absorbers is defined as A = 1−T–R, where reflectance R = |S11|2, transmission T = |S21|2, and S denotes the scattering parameter, respectively [20]. In addition, the theoretical and experimental available Fermi level μc of graphene can be easily tuned from 0 to 1.0 eV via chemical or electrostatic doping [29,36,37], making it possible to achieve flexible control of the absorbance properties of the absorbers.
Figure 1.
Schematic illustrations of the proposed frequency-reconfigurable wide-angle terahertz absorbers. (a) The absorber with a single-layer decussate graphene ribbon array (SLDGRA); (b) The absorber with double-layer decussate graphene ribbon arrays (DLDGRAs); (c) top view of the unit cell of the proposed absorber with SLDGRA; (d) top view of the unit cell of the proposed absorber with DLDGRA. The geometric parameters of the absorbers were set as Lx = Ly = 4 µm, Wx = Wy = 0.9 μm, h1 = 1 μm, h2 = 4 μm, h3 = 1 μm.
3. Results and Discussion
In this section, we first study terahertz absorbance spectra, frequency reconfiguration and angular stability of the proposed absorbers with SLDGRA. Then, to demonstrate a wider frequency reconfiguration, we present and investigate the properties of the absorbers with DLDGRA. Furthermore, we also proposed a simple analytical fitting model to accurately predict the reconfigurable absorbance peak frequencies of this variety of absorbers.
3.1. The Terahertz Absorption Performance of the Absorber with a SLDGRA
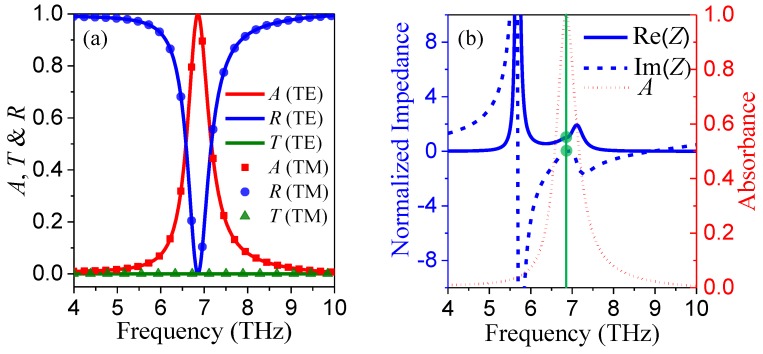
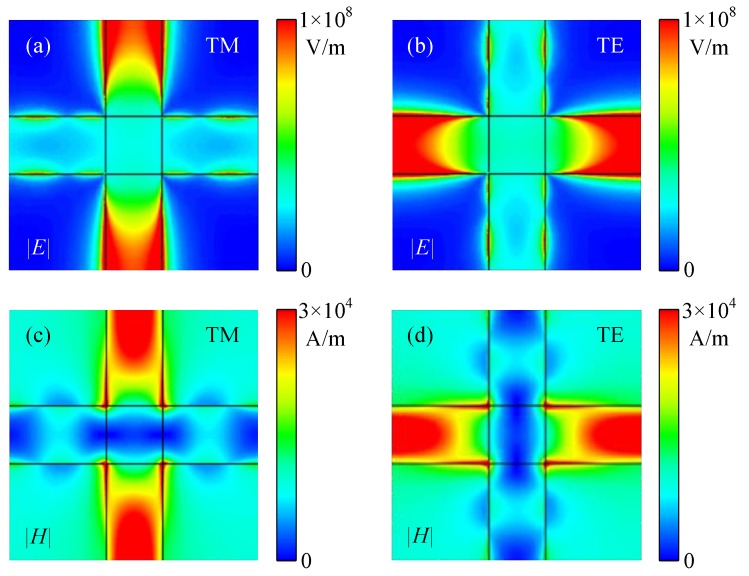
First, we investigated the terahertz absorption performance of the proposed absorber with a SLDGRA under normal incidence. The identical geometric parameters are shown in Figure 1a. This structure can be regarded as an asymmetric Fabry–Perot-like resonant cavity. Figure 2a shows the simulated absorbance A, transmission T, and reflectance R for both TE and TM polarizations with μc = 0.3 eV under normal terahertz incidence (θ = 0°). It is clear that excellent narrow-band terahertz absorption was achieved with the absorbance peak approaching 100% at 6.85 THz. Because of the axisymmetric unit cell, as shown in Figure 1c, this absorber demonstrated polarization independence for the TE- and TM-polarized incident terahertz waves under normal incidence. The underlying absorption mechanism can be interpreted by the effective medium theory [38], where the normalized effective impedance is given by . As shown in Figure 2b, the blue solid and dashed curves denote the real and imaginary parts of Z, respectively. We observed that for upper green point, Re(Z) = 1.0004, and for the lower green point, Im(Z) = −0.00114, at the absorbance peak frequency of 6.85 THz, implying the impedance of the absorber matched the free space well. Therefore, since the extremely low reflectance resulting from smooth impedance matching together with zero transmission enabled by the thick gold layer, the near-unity absorbance of the absorber was achieved. Figure 3a–d display the electric field distributions, |E|, and magnetic field distributions, |H|, for the TM and TE polarizations along the cut-plane on the top graphene layer at 6.85 THz. The localized surface plasmon polaritons (LSPPs) were excited and strongly confined on the graphene ribbons, leading to ultra-high terahertz absorption. As expected from the symmetric configuration and polarization-independent property, the |E| and |H| for TM polarization were exactly 90° shifted from that of the TE polarization. Therefore, this absorber with a SLDGRA showed a clear independence of polarization, which has a significant advantage over the polarization-sensitive absorber with single graphene ribbon array.
Figure 2.
(a) Simulated absorbance (A), transmission (T), and reflectance (R) of the proposed absorbers with SLDGRAs for both transverse magnetic (TM) and transverse electric (TE) polarizations at μc = 0.3 eV under normal terahertz incidence; (b) The real and imaginary parts of the retrieved effective impedance (Z) of the absorber for both TM and TE polarization, where the black and red curves indicate the Re(Z) and Im(Z), respectively, and the vertical green solid cut-line denotes the frequency of absorbance peak at 6.85 THz.
Figure 3.
(a–d) are the electric field distributions, |E|, and magnetic field distributions, |H|, for TM and TE polarizations of the absorbers with SLDGRAs along the cut-plane on the top graphene layer at 6.85 THz with μc = 0.3 eV under normal terahertz incidence, respectively.
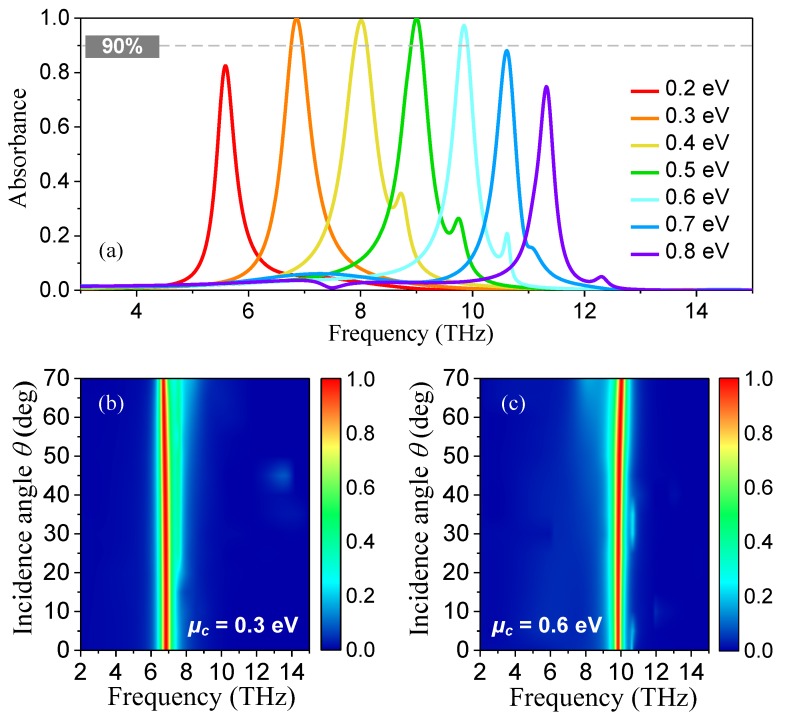
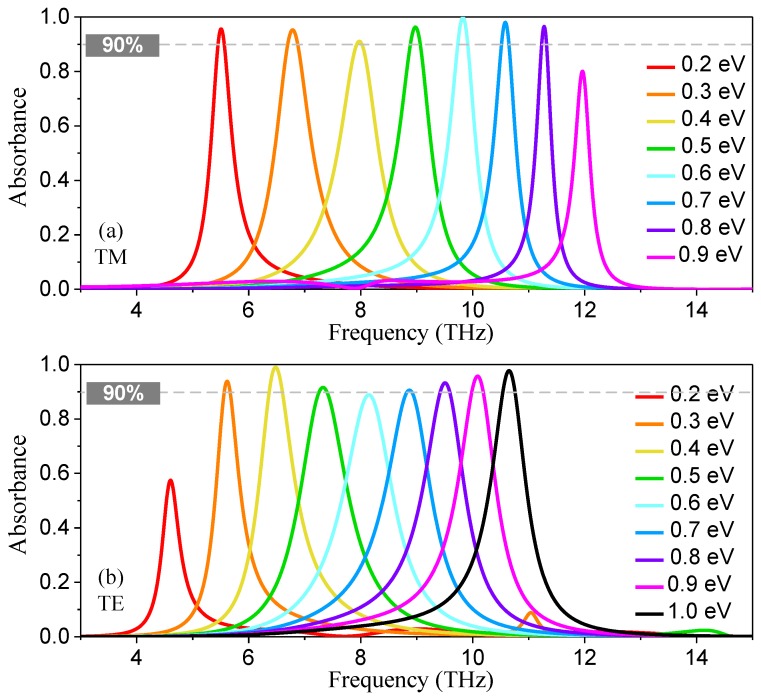
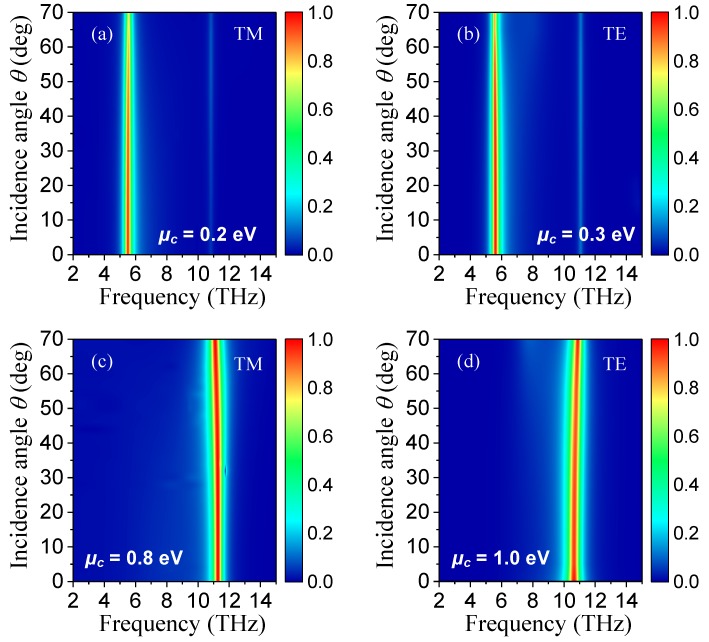
To demonstrate the properties of wide frequency reconfiguration and angular stability, we studied the dependence of Fermi level μc and angle of incidence θ on the absorbance spectra. Figure 4a depicts the absorbance spectra for both TM and TE polarizations under normal incidence with various μc. It was found that changing the μc of the graphene ribbon had a significant influence on the absorption frequency band. As μc increased from 0.2 to 0.8 eV, the absorbance peak frequency band red-shifted accordingly from 5.58 to 11.32 THz. Especially, good frequency reconfiguration characteristics were clearly observed. As μc increased from 0.3 to 0.6 eV, the over 90% absorbance peak frequency varied from 6.85 to 9.85 THz, demonstrating a wide absolute frequency tuning range of 3 THz with the RFTR of 43.8%, which was larger than the recently reported works [21,22,23,24,25,26,27]. Figure 4b,c display the simulated absorbance spectra as a function of incidence angle and operating frequency with μc of 0.3 and 0.6 eV, for the first and the last absorption bands with over 90% peak absorbance, respectively. The results showed that the absorber also possessed an excellent angular stability for narrowband terahertz absorption characteristics. Owing to the wide-angle localized resonance of SPPs in the SLDGRA structure, the peak absorbance remained over 99.8%, even at a large oblique incidence angle of 70° for both cases. This absorber with wide frequency reconfiguration, absolute polarization independence, and excellent angular stability may have significant potential applications in the terahertz regime.
Figure 4.
(a) Simulated absorption spectra for both TM and TE polarizations under normal incidence with μc ranging from 0.2 to 0.8 eV; (b,c) are the absorbance spectra as a function of incidence angle and operating frequency with μc fixed as 0.3 and 0.6 eV, respectively.
3.2. Terahertz Absorption Performance of the Absorber with DLDGRAs
To further enhance the absorbance peak frequency tuning range, we propose the absorber with DLDGRAs, as shown in Figure 1b,d. The ZrO2 separation (h1) of the double-layer decussate graphene ribbon arrays was set as 1 µm while the rest of the geometric parameters of this absorber were fixed to be the same as the absorber with a SLDGRA. The simulated absorbance spectra for TM and TE polarizations with different μc at normal terahertz incidence are displayed in Figure 5a,b, respectively. Clearly, ultra-wide frequency tuning of the narrowband terahertz absorption was obtained by varying μc. For TM polarizations, the reconfigurable over 90% absorbance peak frequency significantly switched from 5.50 to 11.28 THz, corresponding an enhanced RFTR of 105.1%, as the μc increased from 0.2 to 0.8 eV. For TE polarization, the reconfigurable over 90% absorbance peak frequency switched from 5.62 to 10.65 THz, corresponding to a RFTR of 89.5%, as the μc varied from 0.3 to 1.0 eV. Compared with the RFTR of the absorber with a SLDGRA, ultra-wide frequency reconfiguration with 2× more RFTR was achieved in the absorber with DLDGRAs.
Figure 5.
Simulated absorbance spectra of the proposed absorber with DLDGRAs with different μc under normal terahertz incidence. (a) Absorbance spectra for TM polarization with μc ranging from 0.2 to 0.9 eV; (b) absorbance spectra for TE polarization with μc ranging from 0.2 to 1.0 eV.
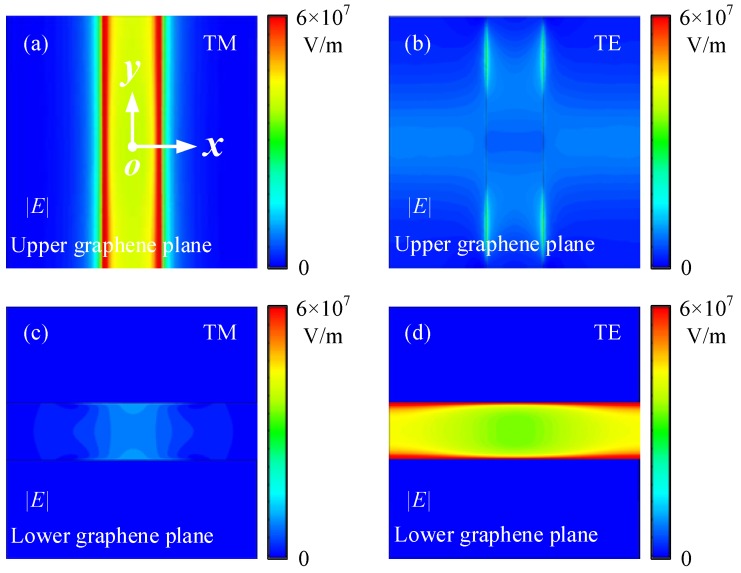
Next, it is remarkable that this absorber was no longer polarization-independent because of the non-axisymmetric DLDGRA structure. To better understand this characteristic, we depict the simulated electric field distributions for TM and TE polarizations along the cut-planes on upper and lower graphene layers with μc = 0.3 eV under normal incidence. For TM polarization, |E| distributions of the LSPPs at the absorbance peak frequency of 6.81 THz along upper and lower graphene plane are shown in Figure 6a,c, respectively. It was clearly observed that |E| were mainly confined around upper-layer graphene ribbon edges. Therefore, the terahertz absorption for the TM polarization was mainly caused by LSPPs located at the upper-layer graphene ribbons. Similarly, the electric distributions for the TE polarization at the absorbance peak frequency of 5.62 THz along upper and lower graphene plane are shown in Figure 6b,d. The LSPPs were strongly excited and concentrated around the lower graphene ribbons, leading to strong terahertz absorption. Clearly, the absorption is largely dependent on the localized resonance of SPPs in the individual layer of graphene ribbons rather than the interplay of SPPs between upper- and lower-layer graphene ribbons. The different field distributions of LSPPs determine the different terahertz absorbance spectra of the proposed absorber with DLDGRAs under TM and TE polarizations.
Figure 6.
Electric field distributions of the absorber with DLDGRAs at μc = 0.3 eV under normal incidence, where (a,c) are respectively the |E| for the TM polarization along the upper and lower graphene planes at the absorbance peak frequency of 6.81 THz; (b,d) are the |E| for the TE polarization along the upper and lower graphene planes at the absorbance peak frequency of 5.62 THz, respectively.
Furthermore, we also investigated the angular stability of the proposed absorber with DLDGRAs. Here, for example, we present the simulated absorbance spectra as a function of incidence angle θ and operating frequency with μc of 0.2 and 0.8 eV for TM polarization in Figure 7a,c, and with μc of 0.3 and 1.0 eV for TE polarization in Figure 7b,d, respectively. These results show that the absorbance could still maintain above 71.7%, 82.7%, 88.9%, and 96.9% for Figure 7a–d over a wide angle of incidence ranging from 0° to 70°, respectively. Therefore, the proposed absorber with DLDGRAs demonstrated ultra-wide angular stability, which can be mainly attributed to the wide-angle property of localized resonance of SPPs in individual graphene ribbons.
Figure 7.
Simulated absorption spectra of the proposed absorber with different incident angles θ under the (a) TM polarization with μc = 0.2 eV and (b) TE polarization with μc = 0.3 eV. (c) TM polarization with μc = 0.8 eV and (d) TE polarization with μc = 1.0 eV.
3.3. Analytical Prediction of the Reconfigurable Absorbance Peak Frequencies
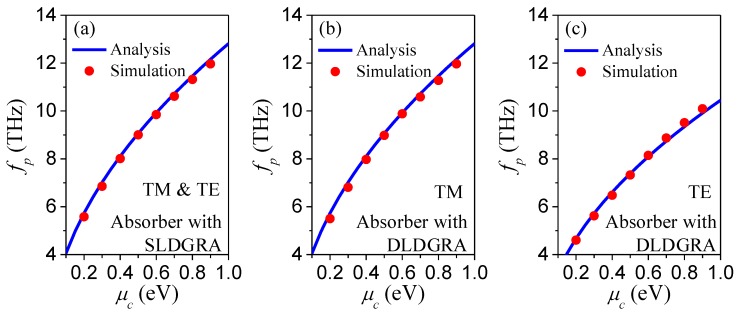
To predict the reconfigurable frequencies of the proposed absorbers, we further studied the relationship between the absorbance peak frequency fp and μc. According to the quasi-static analysis in References [39,40], a fitting mode for fp and μc is given by , where k = 0.1 denotes a dimensionless fitting constant, W is the width of graphene ribbon, εe is the effective permittivity of the background materials surrounding the graphene ribbon array, and εo is the permittivity of vacuum, respectively. Here, we first compared the fp of the absorber with a SLDGRA obtained from this analytical fitting mode and the simulated results, as shown in Figure 8a. In this case, the εe was expressed as εe = (εZro2 + 1)/2. It was found that with μc varying from 0.2 to 0.9 eV, fp increased from 5.58 to 11.97 THz. The analytical fitting results matched well with the simulation results. Then, we verified this analytical fitting mode for the absorber with the DLDGRA case. Because it is polarization-dependent, we compared the fitting and simulation results separately for TM and TE polarizations, as shown in Figure 8b,c. For TM polarization, the terahertz LSPPs predominated on the upper-layer graphene ribbon, as shown in Figure 6a. Therefore, εe was also approximately expressed as εe = (εZro2 + 1)/2. With the same values of εe for the absorber with DLDGRAs under TM polarization and the absorber with SLDGRA, the same analytical predictions of fp are shown in both Figure 8a,b. On contrary, the LSPPs mainly concentrated on the lower-layer graphene ribbon for the TE polarization, and εe should be calculated by εe = εZro2 instead. Both analytical prediction and the simulation results clearly showed that fp increased from 5.50 (4.60) to 11.97 (10.09) THz for TM (TE) polarization with μc varying from 0.2 to 0.9 eV with good agreement. Therefore, this analytical fitting mode can be used for the efficient prediction of the reconfigurable absorbance peak frequencies of this variety of absorbers.
Figure 8.
The variation of analytical and simulation absorbance peak frequency with different μc (a) for the absorber with a SLDGRA under both TM and TE polarizations; (b) for the absorber with DLDGRAs under TM polarization, and (c) for the absorber with DLDGRAs under TE polarization.
4. Conclusions
We systematically demonstrated a new variety of frequency-reconfigurable absorbers using S/DLDGRAs. The absorbers had excellent properties of narrowband near-unity terahertz absorbance, ultra-wide frequency reconfiguration, and angular stability. For the absorber with a SLDGRA, the over 90% absorbance peak frequency could be flexibly adjusted from 6.85 to 9.85 THz for both polarizations under normal incidence by tuning μc from 0.3 to 0.6 eV. For the absorber with DLDGRAs, the absorbance peak frequencies of each reconfigurable bands could be significantly extended from 5.50 to 11.31 THz and 5.60 to 10.61 THz under TM and TE polarizations, respectively, approaching two octaves. Good angular stability of these absorbers was achieved, with the absorbance peaks of the reconfigurable absorbance bands maintained over 70% in a wide angle of incidence ranging from 0° to 70° for both polarizations. We proposed an analytical fitting model to predict the absorbers’ reconfigurable absorbance peak frequencies. Our results demonstrated that the proposed frequency-reconfigurable absorbers offer significant potential to realize novel reconfigurable optoelectronic devices, which may have great applications in the emerging terahertz regime.
Author Contributions
L.Y. and F.Z. conceived the research, undertook the simulations and analysis, and wrote the manuscript. Y.Z., X.X., X.Y. and Q.H.L. contributed to the analysis and the manuscript review.
Funding
This research was funded by the National Natural Science Foundation of China (61601393 and 61601472); the Shenzhen Science and Technology Innovation Committee (Project No. 201887656); the Natural Science Foundation of Fujian Province of China (2016J01321).
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Tonouchi M. Cutting-edge THz technology. Nat. Photonics. 2007;1:97–105. doi: 10.1038/nphoton.2007.3. [DOI] [Google Scholar]
- 2.Ye L., Xu R., Wang Z., Lin W. A novel broadband coaxial probe to parallel plate dielectric waveguide transition at THz frequency. Opt. Express. 2010;18:21725–21731. doi: 10.1364/OE.18.021725. [DOI] [PubMed] [Google Scholar]
- 3.Vicarelli L., Vitiello M.S., Coquillat D., Lombardo A., Ferrari A.C., Knap W., Polini M., Pellegrini V., Tredicucci A. Graphene field-effect transistors as room-temperature terahertz detectors. Nat. Mater. 2012;11:865–871. doi: 10.1038/nmat3417. [DOI] [PubMed] [Google Scholar]
- 4.Liu L., Rahman S.M., Jiang Z., Li W., Fay P. Advanced Terahertz Sensing and Imaging Systems Based on Integrated III-V Interband Tunneling Devices. Proc. IEEE. 2017;105:1020–1034. doi: 10.1109/JPROC.2016.2636245. [DOI] [Google Scholar]
- 5.Landy N.I., Sajuyigbe S., Mock J.J., Smith D.R., Padilla W.J. A perfect metamaterial absorber. Phys. Rev. Lett. 2008;100:207402. doi: 10.1103/PhysRevLett.100.207402. [DOI] [PubMed] [Google Scholar]
- 6.Chen H.T., O’Hara J.F., Azad A.K., Taylor A.J., Averitt R.D., Shrekenhamer D.B., Padilla W.J. Experimental demonstration of frequency-agile terahertz metamaterials. Nat. Photonics. 2008;2:295–298. doi: 10.1038/nphoton.2008.52. [DOI] [Google Scholar]
- 7.Zhao J., Cheng Q., Chen J., Qi M., Jiang W., Cui T. A tunable metamaterial absorber using varactor diodes. New J. Phys. 2013;15:043049. doi: 10.1088/1367-2630/15/4/043049. [DOI] [Google Scholar]
- 8.Zhao X., Zhang J., Fan K., Duan G., Metcalfe G.D., Wraback M., Zhang X., Averitt R.D. Nonlinear terahertz metamaterial perfect absorbers using GaAs. Photonics Res. 2016;4:A16–A21. doi: 10.1364/PRJ.4.000A16. [DOI] [Google Scholar]
- 9.Liu M.K., Susli M., Silva D., Putrino G., Kala H., Fan S.T., Faraone L., Wallace V.P., Padilla W.J., Powell D.A., et al. Ultrathin tunable terahertz absorber based on MEMS-driven metamaterial. Microsyst. Nanoeng. 2017;3:17033–17045. doi: 10.1038/micronano.2017.33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zhu B., Feng Y., Zhao J., Huang C., Wang Z., Jiang T. Polarization modulation by tunable electromagnetic metamaterial reflector/absorber. Opt. Express. 2010;18:23196–23203. doi: 10.1364/OE.18.023196. [DOI] [PubMed] [Google Scholar]
- 11.Wang L., Ge S., Hu W., Nakajima M., Lu Y. Graphene-assisted high-efficiency liquid crystal tunable terahertz metamaterial absorber. Opt. Express. 2017;25:23873–23879. doi: 10.1364/OE.25.023873. [DOI] [PubMed] [Google Scholar]
- 12.Novoselov K.S., Fal’ko V.I., Colombo L., Gellert P.R., Schwab M.G., Kim K. A roadmap for graphene. Nature. 2012;490:192–200. doi: 10.1038/nature11458. [DOI] [PubMed] [Google Scholar]
- 13.Grigorenko A.N., Polini M., Novoselov K.S. Graphene plasmonics. Nat. Photonics. 2012;6:749–758. doi: 10.1038/nphoton.2012.262. [DOI] [Google Scholar]
- 14.Koppens F.H., Chang D.E., García de Abajo F.J. Graphene plasmonics: A platform for strong light-matter interactions. Nano Lett. 2011;11:3370–3377. doi: 10.1021/nl201771h. [DOI] [PubMed] [Google Scholar]
- 15.Low T., Avouris P. Graphene plasmonics for terahertz to mid-infrared applications. ACS Nano. 2014;8:1086–1101. doi: 10.1021/nn406627u. [DOI] [PubMed] [Google Scholar]
- 16.Meng F., Wang H., Huang F., Guo Y., Wang Z., Hui D., Zhou Z. Graphene-based microwave absorbing composites: A review and prospective. Compos. Part B. 2018;137:260–277. doi: 10.1016/j.compositesb.2017.11.023. [DOI] [Google Scholar]
- 17.Ye L., Chen Y., Cai G., Liu N., Zhu J., Song Z., Liu Q.H. Broadband absorber with periodically sinusoidally-patterned graphene layer in terahertz range. Opt. Express. 2017;25:11223–11232. doi: 10.1364/OE.25.011223. [DOI] [PubMed] [Google Scholar]
- 18.Thongrattanasiri S., Koppens F.H., Garcia F.J. Complete optical absorption in periodically patterned graphene. Phys. Rev. Lett. 2012;108:047401. doi: 10.1103/PhysRevLett.108.047401. [DOI] [PubMed] [Google Scholar]
- 19.Ye L., Chen X., Cai G., Zhu J., Liu N., Liu Q.H. Electrically Tunable Broadband Terahertz Absorption with Hybrid-Patterned Graphene Metasurfaces. Nanomaterials. 2018;8:562. doi: 10.3390/nano8080562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhu J., Yan S., Feng N., Ye L., Ou J.Y., Liu Q.H. Near unity ultraviolet absorption in graphene without patterning. Appl. Phys. Lett. 2018;112:153106. doi: 10.1063/1.5022768. [DOI] [Google Scholar]
- 21.Ning Y., Dong Z., Si J., Deng X. Tunable polarization-independent coherent perfect absorber based on a metal-graphene nanostructure. Opt. Express. 2017;25:32467–32474. doi: 10.1364/OE.25.032467. [DOI] [Google Scholar]
- 22.Li H., Wang L., Zhai X. Tunable graphene-based mid-infrared plasmonic wide-angle narrowband perfect absorber. Sci. Rep. 2016;6:36651. doi: 10.1038/srep36651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wu J. Tunable ultranarrow spectrum selective absorption in a graphene monolayer at terahertz frequency. J. Phys. D. Appl. Phys. 2016;49:215108. doi: 10.1088/0022-3727/49/21/215108. [DOI] [Google Scholar]
- 24.He X., Yao Y., Zhu Z., Chen M., Zhu L., Yang W., Yang Y., Wu F., Jiang J. Active graphene metamaterial absorber for terahertz absorption bandwidth, intensity and frequency control. Opt. Mater. Express. 2018;8:1031–1042. doi: 10.1364/OME.8.001031. [DOI] [Google Scholar]
- 25.Zhang Y., Feng Y., Zhu B., Zhao J., Jiang T. Graphene based tunable metamaterial absorber and polarization modulation in terahertz frequency. Opt. Express. 2014;22:22743–22752. doi: 10.1364/OE.22.022743. [DOI] [PubMed] [Google Scholar]
- 26.Yao G., Ling F., Yue J., Luo C., Ji J., Yao J. Dual-band tunable perfect metamaterial absorber in the THz range. Opt. Express. 2016;24:1518–1527. doi: 10.1364/OE.24.001518. [DOI] [PubMed] [Google Scholar]
- 27.Vasic B., Gajic R. Graphene induced spectral tuning of metamaterial absorbers at mid-infrared frequencies. Appl. Phys. Lett. 2013;103:207403. doi: 10.1063/1.4858459. [DOI] [Google Scholar]
- 28.Hanson G.W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene. J. Appl. Phys. 2008;103:064302. doi: 10.1063/1.2891452. [DOI] [Google Scholar]
- 29.Hanson G.W. Dyadic Green’s functions for an anisotropic, non-local model of biased graphene. IEEE Trans. Antennas Propag. 2008;56:747–757. doi: 10.1109/TAP.2008.917005. [DOI] [Google Scholar]
- 30.Du D., Liu J., Zhang X., Cui X., Lin Y. One-step electrochemical deposition of a graphene-ZrO2 nanocomposite: Preparation, characterization and application for detection of organophosphorus agents. J. Mater. Chem. 2011;21:8032–8037. doi: 10.1039/c1jm10696a. [DOI] [Google Scholar]
- 31.Cho B.H., Ko W.B. Preparation of graphene-ZrO2 nanocomposites by heat treatment and photocatalytic degradation of organic dyes. J. Mater. Chem. 2013;13:7625–7630. doi: 10.1166/jnn.2013.7819. [DOI] [PubMed] [Google Scholar]
- 32.Ordal M.A., Long L.L., Bell R.J., Bell S.E., Bell R.R., Alexander R.W., Jr., Ward C.A. Optical properties of the metals Al, Co, Cu, Au, Fe, Pb, Ni, Pd, Pt, Ag, Ti, and W in the infrared and far infrared. Appl. Opt. 1983;22:1099. doi: 10.1364/AO.22.001099. [DOI] [PubMed] [Google Scholar]
- 33.Guo J., Jiang L., Dai Y., Xiang Y., Fan D. Low threshold optical bistability in one-dimensional gratings based on graphene plasmonics. Opt. Express. 2017;25:5972–5981. doi: 10.1364/OE.25.005972. [DOI] [PubMed] [Google Scholar]
- 34.Gómez-Díaz J.S., Esquius-Morote M., Perruisseau-Carrier J. Plane wave excitation-detection of nonresonant plasmons along finite-width graphene strips. Opt. Express. 2013;21:24856–24872. doi: 10.1364/OE.21.024856. [DOI] [PubMed] [Google Scholar]
- 35.Ye L., Sui K., Liu Y., Zhang M., Liu Q.H. Graphene-based hybrid plasmonic waveguide for highly efficient broadband mid-infrared propagation and modulation. Opt. Express. 2018;26:15935–15947. doi: 10.1364/OE.26.015935. [DOI] [PubMed] [Google Scholar]
- 36.Bokdam M., Khomyakov P.A., Brocks G., Zhong Z., Kelly P.J. Electrostatic doping of graphene through ultrathin hexagonal boron nitride films. Nano Lett. 2011;11:4631. doi: 10.1021/nl202131q. [DOI] [PubMed] [Google Scholar]
- 37.Balci S., Balci O., Kakenov N., Atar F.B., Kocabas C. Dynamic tuning of plasmon resonance in the visible using graphene. Opt. Lett. 2016;41:1241. doi: 10.1364/OL.41.001241. [DOI] [PubMed] [Google Scholar]
- 38.Smith D.R., Vier D.C., Koschny T., Soukoulis C.M. Electromagnetic parameter retrieval from inhomogeneous metamaterials. Phys. Rev. E. 2005;71:036617. doi: 10.1103/PhysRevE.71.036617. [DOI] [PubMed] [Google Scholar]
- 39.Ju L., Geng B., Horng J., Girit C., Martin M., Hao Z., Bechtel H.A., Liang X., Zettl A., Shen Y.R., et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotechnol. 2011;6:630. doi: 10.1038/nnano.2011.146. [DOI] [PubMed] [Google Scholar]
- 40.Nikitin A.Y., Guinea F., Garca-Vidal F.J., Martin Moreno L. Surface plasmon enhanced absorption and suppressed transmission in periodic arrays of graphene ribbons. Phys. Rev. B. 2012;85:081405. doi: 10.1103/PhysRevB.85.081405. [DOI] [Google Scholar]